1
The Erlang Multirate Loss Model
We start with random arriving calls of fixed bandwidth requirements and fixed bandwidth allocation during service.
Before the study of multirate teletraffic loss models where multiple service‐classes of different bandwidth per call requirements are accommodated in a service system, let us begin with the simpler case where all calls belong to just one service‐class, and afterwards consider the multi‐service system.
1.1 The Erlang Loss Model
1.1.1 The Service System
Consider that a single service‐class (e.g., telephone service) is accommodated to a loss system, say a transmission link, of capacity ![]() b.u. Each call arrives in the system according to a Poisson process with mean value
b.u. Each call arrives in the system according to a Poisson process with mean value ![]() and requires 1 b.u. to be serviced. If this bandwidth is available, then a call is accepted in the system and remains under service for an exponentially distributed service time, with mean value
and requires 1 b.u. to be serviced. If this bandwidth is available, then a call is accepted in the system and remains under service for an exponentially distributed service time, with mean value ![]() . Otherwise, when all b.u. are occupied, a call is blocked and lost without further affecting the system (e.g., a blocked call is not allowed to retry).
. Otherwise, when all b.u. are occupied, a call is blocked and lost without further affecting the system (e.g., a blocked call is not allowed to retry).
Now, let ![]() be the number of in‐service calls at the time instant
be the number of in‐service calls at the time instant ![]() . Since each call occupies 1 b.u. then
. Since each call occupies 1 b.u. then ![]() also expresses the number of occupied b.u. at the time instant
also expresses the number of occupied b.u. at the time instant ![]() , i.e.,
, i.e., ![]() . Assume that at time instant
. Assume that at time instant ![]() , (
, (![]() ), the number of in‐service calls is
), the number of in‐service calls is ![]() , that is,
, that is, ![]() ; in the teletraffic jargon, we say that the system is in state
; in the teletraffic jargon, we say that the system is in state ![]() . Let
. Let ![]() denote the probability of being in state
denote the probability of being in state ![]() . Since calls arrive at random, based on (I.10) the system's state becomes
. Since calls arrive at random, based on (I.10) the system's state becomes ![]() at
at ![]() , if one of the following events takes place:
, if one of the following events takes place:
- (a)
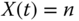 and (no arrival or departure occurs in
and (no arrival or departure occurs in  ).
). - (b)
 and (one new call arrives in
and (one new call arrives in  ).
). - (c)
 and (one in‐service call departs from the system in
and (one in‐service call departs from the system in  ).
).
The probability of the first event equals ![]() . Note that the probability for a specific call to depart within
. Note that the probability for a specific call to depart within ![]() is
is ![]() ; given that there are
; given that there are ![]() in‐service calls, one departure is possible due to the first or the second or the
in‐service calls, one departure is possible due to the first or the second or the ![]() th call, and therefore the probability of one departure becomes the sum of
th call, and therefore the probability of one departure becomes the sum of ![]() probabilities:
probabilities: ![]() .
.
The probability of the second event equals ![]() , while the probability of the last event equals
, while the probability of the last event equals ![]() (because of the
(because of the ![]() in‐service calls).
in‐service calls).
Therefore, because the above events are exclusive, we take:

or

In (1.2), when ![]() , the limit of the LHS defines the derivative of
, the limit of the LHS defines the derivative of ![]() :
:

According to the notion of derivative, (1.3) shows the rate of changes of the instantaneous value of ![]() , which is of little interest. Instead, of great interest is to find the state probability in the steady state, that is, when the system operates normally for a long time period. Service systems normally have a steady state; this means that as
, which is of little interest. Instead, of great interest is to find the state probability in the steady state, that is, when the system operates normally for a long time period. Service systems normally have a steady state; this means that as ![]() . Then, the probability
. Then, the probability ![]() approaches a limiting value
approaches a limiting value ![]() , which is constant over time and is determined through ( 1.3) when the LHS is zero:
, which is constant over time and is determined through ( 1.3) when the LHS is zero:
where ![]() and
and ![]() .
.
Since (1.4) holds for all ![]() , we say that the system is in statistical equilibrium. To find the limiting probabilities
, we say that the system is in statistical equilibrium. To find the limiting probabilities ![]() , also called steady state probabilities, we solve ( 1.4) by applying the so‐called ladder method:
, also called steady state probabilities, we solve ( 1.4) by applying the so‐called ladder method:

By adding these equations side by side, we obtain the following recurrent formula:
where ![]() is the offered traffic‐load in erl.
is the offered traffic‐load in erl.
From (1.5), by successive substitutions, we relate ![]() to the probability that the system is empty,
to the probability that the system is empty, ![]() :
:
One more equation is needed between ![]() and
and ![]() to formulate a system of two equations with two unknowns. Since the system will always be in one of the states
to formulate a system of two equations with two unknowns. Since the system will always be in one of the states ![]() , we have:
, we have:

that is,

By substituting (1.8) to (1.6), we determine ![]() :
:

which is the well‐known Erlang distribution.1
1.1.2 Global and Local Balance
It is important at this point to interpret ( 1.4) and ( 1.5). Let us rewrite them as follows, while multiplying them by ![]() :
:
The LHS of (1.10a) shows the probability sum of two events while the system is in state ![]() : a call arrival (
: a call arrival (![]() ) and a call departure (
) and a call departure (![]() ), which transfer the system out of state
), which transfer the system out of state ![]() , obviously to the adjacent state
, obviously to the adjacent state ![]() or
or ![]() , respectively. Likewise, the RHS of (1.10a) shows the probability of moving to state
, respectively. Likewise, the RHS of (1.10a) shows the probability of moving to state ![]() from the adjacent states
from the adjacent states ![]() and
and ![]() , due to a call arrival and a call departure, respectively. Let us remove
, due to a call arrival and a call departure, respectively. Let us remove ![]() from this equation. Then, (1.10a) denotes the fact that rate‐out = rate‐in and is named the global balance (GB) equation of state
from this equation. Then, (1.10a) denotes the fact that rate‐out = rate‐in and is named the global balance (GB) equation of state ![]() .
.
Even more interesting is the interpretation of (1.10b), where the RHS shows the probability of moving up, from state ![]() to state
to state ![]() , due to a call arrival, while the LHS shows the probability of moving down, from state
, due to a call arrival, while the LHS shows the probability of moving down, from state ![]() to state
to state ![]() , due to a call departure. When removing
, due to a call departure. When removing ![]() , this equation denotes the fact that rate‐down = rate‐up and is named the local balance (LB) equation between the adjacent states
, this equation denotes the fact that rate‐down = rate‐up and is named the local balance (LB) equation between the adjacent states ![]() and
and ![]() .
.
Having removed ![]() from (1.10a), its graphical representation is shown in Figure 1.1 by the state transition diagram of the system. Two LB equations are presented (the first one between states
from (1.10a), its graphical representation is shown in Figure 1.1 by the state transition diagram of the system. Two LB equations are presented (the first one between states ![]() and
and ![]() and the second one between states
and the second one between states ![]() and
and ![]() ). Note at this point that the existence of GB between adjacent states does not guarantee the existence of LB. The opposite holds.
). Note at this point that the existence of GB between adjacent states does not guarantee the existence of LB. The opposite holds.
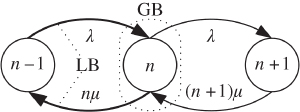
Figure 1.1 State transition diagram for the Erlang loss model ( /
/ /
/ /0).
/0).
Equations (1.10) introduce the following methodology, called classical methodology, in analyzing a service system in equilibrium, i.e., in determining its steady state probabilities:
- (i) Start with the state transition diagram of the system.
- (ii) Write the GB equations.
- (iii) Apply the ladder method to the GB equations in order to obtain simpler equations, usually the LB equations.
- (iv) If steps (ii) and (iii) are too complicated, assume that LB equations hold and go on, but check for atopy.
- (v) Consider the normalization condition.2
- (vi) Solve the resultant linear system of equations of the steady state probabilities.
Example 1.2
Consider the queuing system of Figure 1.2, as an ![]() /
/![]() /
/![]() /
/![]() FIFO system. Determine:
FIFO system. Determine:
- (a) the probability of having
 calls in the system (both in the queue and in the service mechanism) in steady state
calls in the system (both in the queue and in the service mechanism) in steady state - (b) the probability that a call delays (i.e., enters the queue)
- (c) the mean queue length

- (d) the mean call waiting time

- (a) To determine the steady state probabilities

- (i)
Starting with the state transition diagram of this system, we have to consider two cases: (a) when
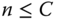 and (b) when
and (b) when  . This is due to the fact that in the latter case the rate whereby calls depart from the system remains constant and equals
. This is due to the fact that in the latter case the rate whereby calls depart from the system remains constant and equals  , while in case (a) this rate depends on the number of in‐service calls and equals
, while in case (a) this rate depends on the number of in‐service calls and equals  . The state transition diagram of Figure 1.1 stands for case (a). Case (b) is shown in Figure 1.2.
. The state transition diagram of Figure 1.1 stands for case (a). Case (b) is shown in Figure 1.2. - (ii)
According to the two state transition diagrams, the GB equations are:
(1.11)

- (iii)
The applicability of the ladder method on (1.11) for
 results in ( 1.5) and finally in ( 1.6). Let us rewrite ( 1.6) (remembering that
results in ( 1.5) and finally in ( 1.6). Let us rewrite ( 1.6) (remembering that  ):
(1.12)
):
(1.12)
- (iv) To speed up the procedure for
 , let us consider that the LB equation between states
, let us consider that the LB equation between states  and
and  holds:
(1.13)
holds:
(1.13)
From (1.13), by successive substitutions and based on (1.12), we obtain:

Or, since
 ,(1.14)
,(1.14)
- (v) The normalization condition is:
 (1.15)
(1.15)
Let us emphasize that the summation in (1.15) converges if and only if
 . Only under this condition can we determine
. Only under this condition can we determine  and, consequently,
and, consequently, 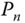 . To summarize:(1.16)
. To summarize:(1.16)
where
 is given by ( 1.15).
is given by ( 1.15). - (i)
Starting with the state transition diagram of this system, we have to consider two cases: (a) when
- (b) The probability that a call delays,
 : This equals the probability that the system is in state
: This equals the probability that the system is in state  , where
, where  :
(1.17)
:
(1.17)
Again, only when
 , can
, can  be determined via (1.17), which is the well‐known Erlang‐C formula.3 It is worth mentioning the following recursive form of the Erlang‐C formula (
be determined via (1.17), which is the well‐known Erlang‐C formula.3 It is worth mentioning the following recursive form of the Erlang‐C formula ( ), which is based on the Erlang‐B recursion (I.8):(1.18)
), which is based on the Erlang‐B recursion (I.8):(1.18)
- (c) To determine the mean queue length,
 : We apply the definition of the expected value of the number of calls waiting in the queue, as follows:
(1.19)
: We apply the definition of the expected value of the number of calls waiting in the queue, as follows:
(1.19)
since
 . From ( 1.17),
. From ( 1.17),  , then (1.19) can be written as:(1.20)
, then (1.19) can be written as:(1.20)
- (d) To determine the mean call waiting time
 (mean delay in the queue): We apply Little's law (I.32):
(1.21)where
(mean delay in the queue): We apply Little's law (I.32):
(1.21)where
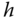 is the mean call holding time (in the service mechanism).
is the mean call holding time (in the service mechanism).

Figure 1.2  /
/ /
/ /
/ FIFO – state transition diagram for
FIFO – state transition diagram for  (Example 1.2).
(Example 1.2).
1.1.3 Call Blocking Probability
The most3 important question in a loss system is “What is the CBP?” or, equivalently, “What is the GoS?”. Call blocking occurs when the system is fully occupied, that is, CBP equals ![]() , the probability that the system is in state
, the probability that the system is in state ![]() . From ( 1.9) we have
. From ( 1.9) we have

Equation (1.22) is the famous Erlang‐B formula also met in (I.5). As we discussed there (Example I.5), the closed form of the Erlang‐B formula is not appealing for large values of ![]() and
and ![]() , instead its recurrent form (I.8) is not only preferred but necessary.
, instead its recurrent form (I.8) is not only preferred but necessary.
It is worth mentioning at this point that, as has been investigated (e.g., [1–3]), ( 1.9) and consequently ( 1.22) are insensitive to the distribution of service time, and depend only on the mean holding time, ![]() , which is inherently included in the traffic‐load (
, which is inherently included in the traffic‐load (![]() ). Besides, ( 1.22) refers to the proportion of time that all
). Besides, ( 1.22) refers to the proportion of time that all ![]() b.u. are occupied (i.e., the system is congested). This probability is named time congestion (TC) probability and can be measured by an outside observer. Due to the PASTA property, an inside observer sees the same probability, therefore ( 1.22) is also called call congestion (CC) probability or CBP.
b.u. are occupied (i.e., the system is congested). This probability is named time congestion (TC) probability and can be measured by an outside observer. Due to the PASTA property, an inside observer sees the same probability, therefore ( 1.22) is also called call congestion (CC) probability or CBP.
Example 1.3
Consider an Erlang loss system of capacity ![]() b.u. and let
b.u. and let ![]() be the probability that there exist
be the probability that there exist ![]() users in the system occupying
users in the system occupying ![]() b.u. at a chosen time, randomly selected.
b.u. at a chosen time, randomly selected.
- (a)Assuming a long time interval
 , determine the portion of time that the system accommodates
, determine the portion of time that the system accommodates  users.
users. - (b)Assume that users arrive in the system according to a Poisson process with rate
 . Show that the probability
. Show that the probability  seen by an arriving user, that
seen by an arriving user, that  users exist in the system just prior to its arrival, equals
users exist in the system just prior to its arrival, equals  .
.
- (a)The portion of time that the system accommodates
 users is
users is  .
. - (b)Based on the Bayes' and the total probability theorems, we have:
(1.23)where

 , according to (I.10).
, according to (I.10).
Having found a relationship between ![]() ,
, ![]() and GoS, i.e.,
and GoS, i.e., ![]() , let us now provide graphs of them (Figure 1.3) in order to compare them with the qualitative graphs of Figure I.2. The first graph of Figure 1.3 presents the required system capacity
, let us now provide graphs of them (Figure 1.3) in order to compare them with the qualitative graphs of Figure I.2. The first graph of Figure 1.3 presents the required system capacity ![]() versus the offered traffic‐load
versus the offered traffic‐load ![]() (for two certain values of GoS: 1% and 3%) and corresponds to the LHS graph of Figure I.2. However, the anticipated curve of Figure I.2 is hardly followed in Figure 1.3; the function
(for two certain values of GoS: 1% and 3%) and corresponds to the LHS graph of Figure I.2. However, the anticipated curve of Figure I.2 is hardly followed in Figure 1.3; the function ![]() is rather a straight line in a wide range of the presented values of traffic‐load. The second graph of Figure 1.3 presents CBP versus
is rather a straight line in a wide range of the presented values of traffic‐load. The second graph of Figure 1.3 presents CBP versus ![]() , for
, for ![]() erl and
erl and ![]() erl, and corresponds to the middle graph of Figure I.2. Due to the reverse meaning of CBP,4 the convex curvature of the middle graph in Figure I.2 appears in the middle graph of Figure 1.3, as a concave (reverse) curvature. The third graph of Figure 1.3 presents CBP versus traffic‐load
erl, and corresponds to the middle graph of Figure I.2. Due to the reverse meaning of CBP,4 the convex curvature of the middle graph in Figure I.2 appears in the middle graph of Figure 1.3, as a concave (reverse) curvature. The third graph of Figure 1.3 presents CBP versus traffic‐load ![]() for two values of
for two values of ![]() : 5 and 6 b.u. Herein, the corresponding qualitative graph of Figure I.2 (RHS) is followed pretty well.
: 5 and 6 b.u. Herein, the corresponding qualitative graph of Figure I.2 (RHS) is followed pretty well.

Figure 1.3 Quantitative relationships between traffic‐load, system capacity, and CBP.
Example 1.4
The terms GoS and CBP are not always interchangeable, although they both express blocking probability in loss systems. The different use of these terms arises when integer values of the system capacity ![]() are considered. For instance, we say: Determine
are considered. For instance, we say: Determine ![]() when
when ![]() erl, for GoS
erl, for GoS ![]() ; we cannot say for CBP
; we cannot say for CBP ![]() , because it is extremely seldom that it completely satisfies this CBP equality. By using the term GoS, we actually mean that the resultant CBP must not exceed
, because it is extremely seldom that it completely satisfies this CBP equality. By using the term GoS, we actually mean that the resultant CBP must not exceed ![]() . Indeed,
. Indeed, ![]() (Figure 1.3, first) and
(Figure 1.3, first) and ![]() (Figure 1.3, middle).
(Figure 1.3, middle).
1.1.4 Other Performance Metrics
- Utilization: The utilization,
 , is expressed by the average number of occupied b.u.:
(1.24)
, is expressed by the average number of occupied b.u.:
(1.24)
Equation (1.24) verifies (I.34). Because of property (4) of traffic‐load,
 .
. - Trunk efficiency: According to (I.35), the trunk efficiency
 is:
(1.25)
is:
(1.25)
Since
 expresses traffic‐load per trunk,
expresses traffic‐load per trunk,  (property (3) of traffic‐load). Thus, again,
(property (3) of traffic‐load). Thus, again,  . As Figure 1.4 shows, the trunk efficiency increases as the system capacity increases, for a certain GoS. This is called the large‐scale effect and leads to the conclusion that loss systems must be designed with the greatest possible capacity in order for trunks to be used efficiently. The latter happens because the larger the system capacity, the greater the carried traffic conveyed under a certain GoS.
. As Figure 1.4 shows, the trunk efficiency increases as the system capacity increases, for a certain GoS. This is called the large‐scale effect and leads to the conclusion that loss systems must be designed with the greatest possible capacity in order for trunks to be used efficiently. The latter happens because the larger the system capacity, the greater the carried traffic conveyed under a certain GoS.

Figure 1.4 Trunk efficiency for various values of GoS and  .
.
Example 1.5
- (a)
A transmission link is designed for GoS
 % to convey an offered traffic‐load of 2.5 erl in one traffic‐flow direction. For the reverse traffic‐flow direction, another transmission link with the same characteristics is used. What is the trunk efficiency in these two links?
% to convey an offered traffic‐load of 2.5 erl in one traffic‐flow direction. For the reverse traffic‐flow direction, another transmission link with the same characteristics is used. What is the trunk efficiency in these two links? - (b) The two links are replaced by one bi‐directional link, which is designed to convey the sum of the traffic‐loads with the same GoS. What is the trunk efficiency of the bi‐directional link?
- (a)
Using uni‐directional links: In each transmission link for each traffic‐flow direction, the capacity is determined as
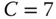 b.u., so that GoS
b.u., so that GoS  % is guaranteed. Indeed,
% is guaranteed. Indeed,  . By applying (1.25), we have
. By applying (1.25), we have  .
. - (b) Using bi‐directional links: The bi‐directional link will have a greater capacity than the uni‐directional link in order to accommodate the same total offered traffic‐load with the same GoS, thus the large‐scale effect takes place and a better
 is anticipated for the bi‐directional link. The total offered traffic‐load is 5.0 erl and the capacity is determined as
is anticipated for the bi‐directional link. The total offered traffic‐load is 5.0 erl and the capacity is determined as 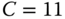 b.u. for GoS
b.u. for GoS  %. Note that
%. Note that  , while
, while  . Precisely,
. Precisely,  . By applying ( 1.25), we have
. By applying ( 1.25), we have  ; indeed, clearly better than 35%.
; indeed, clearly better than 35%.
On the other hand, this example reveals the importance of the large‐scale effect through the savings in system capacity, when a system of a larger capacity replaces smaller systems. The bi‐directional transmission link requires a capacity of 11 b.u., which is less than the total capacity of 14 b.u. required by the two uni‐directional transmission systems.
- A low bound of
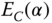 : Since
: Since  always, we have:
(1.26)
always, we have:
(1.26)
Equation (1.26) can be used for a fast evaluation of CBP measurements or CBP calculations, given that the offered traffic‐load
 estimation is correct. For instance, according to ( 1.26), if
estimation is correct. For instance, according to ( 1.26), if  b.u. and
b.u. and  erl, the anticipated CBP
erl, the anticipated CBP  % at least. Note that the actual CBP value is
% at least. Note that the actual CBP value is  . The interested reader may resort to [4] and the references therein for an in‐depth analysis of the lower and upper bounds on the Erlang‐B and Erlang‐C formulas.
. The interested reader may resort to [4] and the references therein for an in‐depth analysis of the lower and upper bounds on the Erlang‐B and Erlang‐C formulas.
1.2 The Erlang Multirate Loss Model
1.2.1 The Service System
Let us now consider the multi‐service system or, as we call it, the Erlang multirate loss model (EMLM). A single link of capacity ![]() b.u. accommodates calls of
b.u. accommodates calls of ![]() different service‐classes under the CS policy. Each call of service‐class
different service‐classes under the CS policy. Each call of service‐class ![]() arrives in the system following a Poisson process with mean rate
arrives in the system following a Poisson process with mean rate ![]() and requires
and requires ![]() b.u. to be serviced. If the requested bandwidth is available, then a call is accepted in the system and remains under service for an exponentially distributed service time, with mean
b.u. to be serviced. If the requested bandwidth is available, then a call is accepted in the system and remains under service for an exponentially distributed service time, with mean ![]() . Otherwise, the call is blocked and lost, without further affecting the system. After service completion, the
. Otherwise, the call is blocked and lost, without further affecting the system. After service completion, the ![]() b.u. are released and become available to new arriving calls.
b.u. are released and become available to new arriving calls.
Let ![]() denote the number of in‐service calls of service‐class
denote the number of in‐service calls of service‐class ![]() in the steady state,
in the steady state, ![]() ) the corresponding vector of all in‐service calls of all service‐classes, and
) the corresponding vector of all in‐service calls of all service‐classes, and ![]() ) the corresponding vector of the required bandwidth per call of all service‐classes in the system. Because of the CS policy, the set
) the corresponding vector of the required bandwidth per call of all service‐classes in the system. Because of the CS policy, the set ![]() of the system (state space) is given by (I.36). The product
of the system (state space) is given by (I.36). The product ![]() expresses the occupied link bandwidth in system state
expresses the occupied link bandwidth in system state ![]() and plays a decisive role in CAC:
and plays a decisive role in CAC:
In terms of ![]() , the CAC is expressed as follows. A new call of service‐class
, the CAC is expressed as follows. A new call of service‐class ![]() that finds the system in state
that finds the system in state ![]() is accepted in the system if
is accepted in the system if ![]() , where
, where ![]() .
.
Example 1.6
Consider a single link with ![]() b.u. The link accommodates
b.u. The link accommodates ![]() service‐classes with
service‐classes with ![]() b.u. and
b.u. and ![]() b.u. Figure 1.5 illustrates this service system under the CS policy.
b.u. Figure 1.5 illustrates this service system under the CS policy.
- (a)Draw the complete state transition diagram of the system.
- (b)Is there an indication that the system has a PFS?

Figure 1.5 A service system of  b.u. and two service‐classes under the CS policy (Example 1.6).
b.u. and two service‐classes under the CS policy (Example 1.6).
- (a) State transition diagram: According to the CS policy,
 , each state
, each state  should satisfy the inequality
should satisfy the inequality  . Figure 1.6 shows the state space
. Figure 1.6 shows the state space  (12 states), together with the complete state transition diagram of the system.
(12 states), together with the complete state transition diagram of the system. - (b) Indication of the PFS: As we discussed in Section I.12, the state space of this example satisfies the coordinate convexity conditions and the steady state probability
 can be expressed by the PFS (I.40). Based on Figure 1.6, we can intuitively understand the existence of a PFS. If only one service‐class exists in the system, say service‐class 1, then the steady state probability
can be expressed by the PFS (I.40). Based on Figure 1.6, we can intuitively understand the existence of a PFS. If only one service‐class exists in the system, say service‐class 1, then the steady state probability  will be given by the Erlang distribution ( 1.9). Likewise, if this system accommodates only service‐class 2, its steady state probability
will be given by the Erlang distribution ( 1.9). Likewise, if this system accommodates only service‐class 2, its steady state probability  will be given again by the Erlang distribution, under the assumption that each call of service‐class 2 requests 1 b.u. (instead of two), while the system capacity is half (suppose that
will be given again by the Erlang distribution, under the assumption that each call of service‐class 2 requests 1 b.u. (instead of two), while the system capacity is half (suppose that  is integer). That is:
(1.28)
is integer). That is:
(1.28)
where
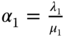 and
and  .
.The steady state probability
 is the joint probability that
is the joint probability that  calls of service‐class 1 coexist in the system with
calls of service‐class 1 coexist in the system with  calls of service‐class 2, by sharing the bandwidth
calls of service‐class 2, by sharing the bandwidth  under the CS policy. Thanks to the CS policy, the two service‐classes do not further influence each other; in this sense, the events
under the CS policy. Thanks to the CS policy, the two service‐classes do not further influence each other; in this sense, the events  and
and  can be considered independent. Therefore, their joint probability is expressed by the product of marginal (individual) probabilities. This consideration would be absolutely correct if
can be considered independent. Therefore, their joint probability is expressed by the product of marginal (individual) probabilities. This consideration would be absolutely correct if  . Now, because of the restricted
. Now, because of the restricted  , the presence of calls of one service‐class does influence the number of calls of the other service‐class at the borders of the system (only). For this reason, we can accept the principle of independency (i.e., multiplication of probabilities), but we have to reconsider the normalization condition, so that the state probabilities of all possible states sum up to 1. Thus, we multiply not the marginal probabilities but a proper function of them:(1.29)where
, the presence of calls of one service‐class does influence the number of calls of the other service‐class at the borders of the system (only). For this reason, we can accept the principle of independency (i.e., multiplication of probabilities), but we have to reconsider the normalization condition, so that the state probabilities of all possible states sum up to 1. Thus, we multiply not the marginal probabilities but a proper function of them:(1.29)where
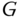 is a normalization constant (to be determined).
is a normalization constant (to be determined).

Figure 1.6 The state space  (CS policy) and the state transition diagram (Example 1.6).
(CS policy) and the state transition diagram (Example 1.6).
In any case, the best way to prove that a system has a PFS,5 is to find it!
1.2.2 The Analytical Model
1.2.2.1 Steady State Probabilities
In analyzing a service system, the first target is to determine the steady state probability ![]() . For the EMLM, it can be determined, obviously, by extending the PFS (1.29) of Example 1.6 to
. For the EMLM, it can be determined, obviously, by extending the PFS (1.29) of Example 1.6 to ![]() service‐classes, as follows:
service‐classes, as follows:

where ![]() the normalization constant, which is determined through
the normalization constant, which is determined through ![]() :
:

Of course, the PFS (1.30) must satisfy the set of GB and LB equations of the system. To verify it, follow the aforementioned classical methodology:
- (i)
Draw the state transition diagram and write the GB equations. Figure 1.7 shows the one‐dimensional state transition diagram of the EMLM when a general state
 is considered. Normally, the state transition diagram has as many dimensions (axes) as the number of service‐classes
is considered. Normally, the state transition diagram has as many dimensions (axes) as the number of service‐classes  ; see the LHS of Figure 1.8. To be converted to a one‐dimensional diagram, we define the equivalent diagram at the RHS of Figure 1.8. This consideration is justified because both diagrams lead to the same GB equation (see 1.32). Thus, the GB equation (rate in = rate out) for state
; see the LHS of Figure 1.8. To be converted to a one‐dimensional diagram, we define the equivalent diagram at the RHS of Figure 1.8. This consideration is justified because both diagrams lead to the same GB equation (see 1.32). Thus, the GB equation (rate in = rate out) for state  is given by:
(1.32)where
is given by:
(1.32)where
 are the probability distributions of the corresponding states
are the probability distributions of the corresponding states  ; parameters
; parameters  validate a state transition through the following expressions:
(1.33)
validate a state transition through the following expressions:
(1.33)

Figure 1.7 State transition diagram of the EMLM.

Figure 1.8 GB in the system of Example 1.6 (Example 1.7).
Example 1.7
Explanation of ( 1.32) and the usage of parameters ![]() .
.
Figure 1.8 illustrates the GB equation ( 1.32) of Example 1.6. As far as the use of parameters ![]() is concerned, if state
is concerned, if state ![]() (Figure 1.8) stands for
(Figure 1.8) stands for ![]() (Figure 1.6), then both
(Figure 1.6), then both ![]() and
and ![]() equal 1 because all transfers to all adjacent states are permitted from
equal 1 because all transfers to all adjacent states are permitted from ![]() . However, if
. However, if ![]() stands for any other state, not all transfers are possible, and therefore parameters
stands for any other state, not all transfers are possible, and therefore parameters ![]() should properly be used (0 or 1). For instance, if
should properly be used (0 or 1). For instance, if ![]() , then according to ( 1.32), we have:
, then according to ( 1.32), we have:

On the other hand, the use of parameter ![]() in each arrow of Figure 1.8 denotes that only one term at a time occurs, e.g., the pair of
in each arrow of Figure 1.8 denotes that only one term at a time occurs, e.g., the pair of ![]() can be
can be ![]() or
or ![]() .
.
- (ii) Assume that LB exists and check for atopy.
Assuming the existence of LB between any adjacent states (
 and
and  , or
, or  and
and  , for
, for  ), then the following LB equations (rate up = rate down) are extracted from the state transition diagram (Figure 1.8, LHS) (correspondingly):(1.34a)
), then the following LB equations (rate up = rate down) are extracted from the state transition diagram (Figure 1.8, LHS) (correspondingly):(1.34a) (1.34b)
(1.34b)
- (iii) Solve the resultant linear system of equations of the equilibrium probabilities, while considering the normalization condition. Check for atopy, again.
It can be verified that the probability distribution
 has a PFS by substituting ( 1.30) into (1.34a) or (1.34b).
has a PFS by substituting ( 1.30) into (1.34a) or (1.34b).
Example 1.8
Let us verify that the PFS ( 1.30) stands for the state probability ![]() of Example 1.6. For simplicity reasons, let
of Example 1.6. For simplicity reasons, let ![]() .
.
The steady state probabilities ( 1.29) result from ( 1.30) when ![]() , while
, while ![]() is given by (1.31). From Figure 1.6, the state space
is given by (1.31). From Figure 1.6, the state space ![]() is:
is:
![]() .
.
Thus, we have to verify that:

satisfies the LB equations obtained via (1.34), when considering any pair of states and any service‐class.
For instance, for the pair ![]() (Figure 1.6), the LB equation is:
(Figure 1.6), the LB equation is:
Since ![]() , the denominator of (1.35) becomes:
, the denominator of (1.35) becomes:

Then:

For the pair ![]() (Figure 1.6), the LB equation is:
(Figure 1.6), the LB equation is:
Indeed:

Having calculated the steady state probability ![]() , we proceed to determine the CBP. To this end, we denote by
, we proceed to determine the CBP. To this end, we denote by ![]() the admissible state space of service‐class
the admissible state space of service‐class ![]() :
: ![]() . A new service‐class
. A new service‐class ![]() call is accepted in the system, if, at the time point of its arrival, the system is in a state
call is accepted in the system, if, at the time point of its arrival, the system is in a state ![]() . Hence, the CBP of service‐class
. Hence, the CBP of service‐class ![]() is determined by the state space
is determined by the state space ![]() , as follows:
, as follows:

Example 1.9
In Example 1.6 (![]() ), assume that
), assume that ![]() . Find both the admissible and blocking states of each service‐class and, based on (1.36), determine the CBP.
. Find both the admissible and blocking states of each service‐class and, based on (1.36), determine the CBP.
As shown in Figure 1.6:
![]()
![]()
According to ( 1.36), the CBP are determined as the summation of the probabilities of (blocking) states:
![]() and
and ![]()
![]() . Hence,
. Hence,
![]() .
.
![]() .
.
Equation ( 1.35) provides the CBP of the EMLM based on a PFS. A recurrent form for the CBP calculation can be obtained by expressing ( 1.36), as follows:

where ![]() ; the values of
; the values of ![]() can be determined recursively via:
can be determined recursively via:

For large values of ![]() the computational complexity of (1.38) is
the computational complexity of (1.38) is ![]() 6. A simpler formula follows with a computational complexity
6. A simpler formula follows with a computational complexity ![]() ,7 for the determination of the state probabilities of the system, when the system state is represented not by the number of in‐service calls of each service‐class, but by the total occupied b.u.
,7 for the determination of the state probabilities of the system, when the system state is represented not by the number of in‐service calls of each service‐class, but by the total occupied b.u. ![]() in the link, where
in the link, where ![]() . This state representation is more effective when aimed at calculating the key performance metrics of the system, like CBP and link utilization. The unnormalized values
. This state representation is more effective when aimed at calculating the key performance metrics of the system, like CBP and link utilization. The unnormalized values ![]() of the link occupancy distribution, i.e., the probability that
of the link occupancy distribution, i.e., the probability that ![]() out of
out of ![]() b.u. are occupied, are given by:
b.u. are occupied, are given by:

Equation (1.39), known in the literature as the Kaufman–Roberts8 recursion, is accurate and computationally efficient with an easy computer implementation. Because of this, it is the springboard to derive other more complex but efficient teletraffic models. In order for the ![]() values of ( 1.39) to become probabilities, they must be normalized through division by the sum of them,
values of ( 1.39) to become probabilities, they must be normalized through division by the sum of them, ![]() :
:

Note that ![]() denotes either a normalized or unnormalized value of the link occupancy distribution, but, in any case, it will be explicitly mentioned (unless it is clear), while
denotes either a normalized or unnormalized value of the link occupancy distribution, but, in any case, it will be explicitly mentioned (unless it is clear), while ![]() denotes a normalized value of the link occupancy distribution.
denotes a normalized value of the link occupancy distribution.
Proof of ( 1.39): According to [5], let us consider the occupied link bandwidth ![]()
![]() , as a system state. Thus, the system can be seen either via state
, as a system state. Thus, the system can be seen either via state ![]() (multi‐dimensional system) or via the new (aggregate) state
(multi‐dimensional system) or via the new (aggregate) state ![]() (one‐dimensional system). The link occupancy distribution
(one‐dimensional system). The link occupancy distribution ![]() is defined as:
is defined as:

where ![]() is the set of states in which exactly
is the set of states in which exactly ![]() b.u. are occupied by all in‐service calls:
b.u. are occupied by all in‐service calls: ![]() (Figure 1.9).
(Figure 1.9).

Figure 1.9 Sets 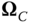 and
and  for the EMLM of two service‐classes, under the CS policy.
for the EMLM of two service‐classes, under the CS policy.
The key point for the recursive calculation of ![]() is to associate the values of
is to associate the values of ![]() values with the “previous” values of
values with the “previous” values of ![]() . In other words, we have to relate the values of
. In other words, we have to relate the values of ![]() with the (“previous”) values of
with the (“previous”) values of ![]() , since in state
, since in state ![]() there are
there are ![]() in‐service calls of service‐class
in‐service calls of service‐class ![]() , while in state
, while in state ![]() there are
there are ![]() in‐service calls (assuming that
in‐service calls (assuming that ![]() ). This relation will be achieved by the use of the LB equation (1.34a), as we will shortly show.
). This relation will be achieved by the use of the LB equation (1.34a), as we will shortly show.
Since ![]() , we can write (1.41) as follows:
, we can write (1.41) as follows:
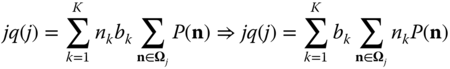
From the LB equation (1.34a), the product ![]() is determined by:
is determined by:

where the parameter ![]() is replaced by
is replaced by ![]() (another binary parameter) to denote that:
(another binary parameter) to denote that:

We take sums of both sides of (1.43) over ![]() to have:
to have:

Equation ( 1.43) has no meaning when ![]() ; since the RHS of (1.45) refers to state
; since the RHS of (1.45) refers to state ![]() , the previous state
, the previous state ![]() (in which the LHS of ( 1.45) refers to) belongs to
(in which the LHS of ( 1.45) refers to) belongs to ![]() given that
given that ![]() . This is expressed through the parameters
. This is expressed through the parameters ![]() . More formally, when
. More formally, when ![]() , the LHS of ( 1.45) is written as:
, the LHS of ( 1.45) is written as:

and the set ![]() defines the state space
defines the state space ![]() . To individuate the case where
. To individuate the case where ![]() , we introduce the following variable:
, we introduce the following variable:

By using (1.47), and because of the definition ( 1.41), we can write (1.46) as follows:

From ( 1.45), ( 1.46), and (1.48), we obtain:

Based on (1.49), (1.42) is written as:

which is the Kaufman–Roberts recursion ( 1.39). For an alternative proof see Example 1.12.
Q.E.D.
According to [ 5], ( 1.39) can be used for arbitrary distributed service times. An interesting interpretation of ( 1.39) is that it stands for an LB equation of a birth–death process, in which ![]() is the birth rate of service‐class
is the birth rate of service‐class ![]() calls,
calls, ![]() is the corresponding death rate, and
is the corresponding death rate, and ![]() is the mean number of service‐class
is the mean number of service‐class ![]() calls in state
calls in state ![]() (Figure 1.10):
(Figure 1.10):
Indeed, (1.51) is derived from ( 1.49) because the RHS of ( 1.49) is written as follows:
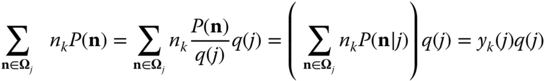
Note that ( 1.39) can be derived from ( 1.51) by multiplying both sides of ( 1.51) by ![]() and summing over
and summing over ![]() .
.

Figure 1.10 The Kaufman–Roberts recursion as a birth–death process.
1.2.2.2 CBP, Utilization, and Mean Number of In‐service Calls
The following performance measures are determined based on ( 1.39):
- CBP: The determination of CBP of service‐class
 , is given by:
(1.53)
, is given by:
(1.53)
where
 is given by (1.40).
is given by (1.40).Figure 1.11 depicts a helpful visualization regarding (1.53).

Figure 1.11 Visualization of CBP calculation.
Note that ( 1.53) refers to the TC probabilities of service‐class
 calls. These probabilities coincide with the CBP due to the PASTA property.
calls. These probabilities coincide with the CBP due to the PASTA property.Needless to say that in the case of one service‐class in the system, the CBP obtained by ( 1.53) coincides with the results of the Erlang‐B formula; hence, we name this model the Erlang multirate loss model.
- Utilization: The link utilization,
 , is calculated by:
(1.54)
, is calculated by:
(1.54)
- Mean number of in‐service calls in state
 : The mean number of in‐service calls of service‐class
: The mean number of in‐service calls of service‐class  in state
in state  is given (because of ( 1.51)) by:
(1.55)
is given (because of ( 1.51)) by:
(1.55)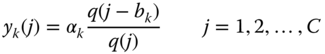
Note that
 , if
, if  .
. - Mean number of in‐service calls in the system: The mean number of in‐service calls for service‐class
 in the system,
in the system,  , is given by:
(1.56)
, is given by:
(1.56)
Example 1.10
In the system of Example 1.6 (![]() ):
):
- (a)Calculate the state probabilities
 , by applying the Kaufman–Roberts recursion.
, by applying the Kaufman–Roberts recursion. - (b)Verify the probability
 (that 5 b.u. are occupied) through the state probabilities
(that 5 b.u. are occupied) through the state probabilities  obtained from Example 1.9.
obtained from Example 1.9. - (c)Calculate the CBP of the two service‐classes through ( 1.53).
- (d)Calculate the link utilization.
- (e)Calculate the trunk efficiency.
- (f)Calculate the mean number of in‐service calls of the two service‐classes when the system is full.
- (g)Calculate the mean number of in‐service calls of the two service‐classes in the system.
- (h)Apply the classical methodology of solving the system of GB equations to check the accuracy of the state probabilities calculated by the Kaufman–Roberts recursion.
- (a) State probabilities through the Kaufman–Roberts recursion: For
 ,
,  ,
,  ,
, 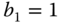 , and
, and 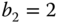 , the Kaufman–Roberts recursion is written as:
, the Kaufman–Roberts recursion is written as:

Starting with
 , we recursively calculate the
, we recursively calculate the  values for
values for  :
:
The normalization constant is
 .
.The state probabilities (link occupancy distribution) are:
 ,
, ,
, ,
, ,
, ,
, .
. - (b)Comparison–verification between the state probabilities
 and
and  : From Figure 1.6, we have that
: From Figure 1.6, we have that  . In Example 1.9, we have calculated that
. In Example 1.9, we have calculated that  , which coincides with
, which coincides with  calculated in (a) in this example.
calculated in (a) in this example. - (c)CBP calculation: According to ( 1.53), the CBP of each service‐class is:

- (d)Utilization: According to (1.54), the link utilization is:

- (e) Trunk efficiency: On average, 2.3562 b.u. (out of 5 b.u.) are occupied, that is, a percentage of
 , which is the trunk efficiency.
, which is the trunk efficiency.
In case of two service‐classes, an alternative estimation of the trunk efficiency is achieved by considering an equivalent single service‐class in the link, with the following offered traffic‐load and CBP:
 erl and
erl and 
Then,
 .
. - (f) Mean number of calls, when the system is full: The system is full in state
 (
( ). Then, according to (1.55), we have:
). Then, according to (1.55), we have:

Indeed,
 .
. - (g)Mean number of calls in the system: Based on (1.56), the mean numbers of calls of the first and second service‐classes are
 and
and  , respectively.
, respectively. - (h) Accuracy of the Kaufman–Roberts recursion, examined by classical methodology: According to classical methodology, we have to formulate a linear system of equations obtained from the GB equations of the system, together with the normalization condition that all state probabilities
 sum up to 1. Therefore, for each of the 12 states of Figure 1.6, we write the corresponding GB equation (rate in = rate out):
sum up to 1. Therefore, for each of the 12 states of Figure 1.6, we write the corresponding GB equation (rate in = rate out): 







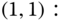















To finalize the formation of the system of equations, let us now replace the longest, the GB equation of (1,1), with the normalization condition:

































and  .
.Although the above linear system can be solved on paper by the simple method of successive substitutions, the procedure is tedious and therefore a computer program is used to obtain the results:



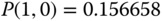








These results verify the results of the Kaufman–Roberts recursion in (a), since:












Example 1.11
Based on Example 1.6 (![]() ), show that:
), show that:
- (a)The Kaufman–Roberts recursion holds for any initial value of
 (not only for
(not only for  ).
). - (b)Find a way to reduce the value of
 so that register overflow is avoided in the computer implementation of the Kaufman–Roberts recursion.
so that register overflow is avoided in the computer implementation of the Kaufman–Roberts recursion.
- (a) Initial value of
 for the Kaufman–Roberts recursion: Let
for the Kaufman–Roberts recursion: Let  and apply the Kaufman–Roberts recursion ( 1.39), or (1.50), for
and apply the Kaufman–Roberts recursion ( 1.39), or (1.50), for  :
: 


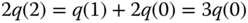














The normalization constant becomes
 .
.By dividing the
 values by
values by  , we have exactly the same results as if
, we have exactly the same results as if  .
. - (b)Method of reducing the value of
 : Since
: Since  is a product of
is a product of  , by choosing a small value for
, by choosing a small value for  , for instance
, for instance  ,
,  is reduced. Furthermore, thanks to the recurrent calculations, it is possible to check the value of
is reduced. Furthermore, thanks to the recurrent calculations, it is possible to check the value of  in each iteration, and if
in each iteration, and if  exceeds a threshold, then (at that iteration) all the already determined values (including
exceeds a threshold, then (at that iteration) all the already determined values (including  ) can be divided by a large number to obtain smaller values (without affecting the final probabilities). For instance, starting with
) can be divided by a large number to obtain smaller values (without affecting the final probabilities). For instance, starting with  and setting the threshold value of
and setting the threshold value of  at 4, we find that
at 4, we find that  just after the iteration for
just after the iteration for  . Before continuing, we can divide by 10 in order to take smaller values:
. Before continuing, we can divide by 10 in order to take smaller values:  ,
,  ,
,  and
and  . When continuing, we have
. When continuing, we have  and
and  , resulting in
, resulting in  . This technique is useful for systems with a large capacity
. This technique is useful for systems with a large capacity  and many service‐classes.
and many service‐classes.
Example 1.12
Prove ( 1.39), based on the CBP definition (I.2b) and property (4) of the traffic‐load.
Proof: An alternative proof of the Kaufman–Roberts recursion ( 1.39) (and consequently of ( 1.53)) is given in [6]. Since call blocking of service‐class ![]() occurs when the total occupied link bandwidth
occurs when the total occupied link bandwidth ![]() , the CBP of service‐class
, the CBP of service‐class ![]() becomes:
becomes:

From the definition ((I.2b)), ![]() , and property (4) of traffic‐load, i.e., the mean number of service‐class
, and property (4) of traffic‐load, i.e., the mean number of service‐class ![]() calls under service,
calls under service, ![]() , equals the carried traffic
, equals the carried traffic ![]() of service‐class
of service‐class ![]() , so we have:
, so we have:
From (1.58), we have the mean number of occupied b.u. in the link, ![]() :
:

which is also written as (according to the probabilistic notion of mean value):

Because of (1.57), ( 1.58) can be rewritten as (see also ( 1.36)):

where ![]() is the set of all admissible states of service‐class
is the set of all admissible states of service‐class ![]() (e.g.,
(e.g., ![]() for service‐class 1, in Figure 1.6).
for service‐class 1, in Figure 1.6).
By multiplying the LHS and RHS of (1.61) by ![]() and summing up to
and summing up to ![]() , we have:
, we have:

Combining (1.60) with (1.62), we have:

From the LHS and RHS of (1.63), we have ( 1.39).
Q.E.D.
Although this proof is more tractable, the proof given by Kaufman in [ 5] provides interesting insights of the EMLM, like the interpretation of a multi‐dimensional system by an one‐dimensional Markov chain through the parameters ![]() and ( 1.49).
and ( 1.49).
Example 1.13
Consider again Example 1.6 (![]() ) and let
) and let ![]() . Herein, we determine the CBP of both service‐classes by using an alternative approach, called convolution algorithm [7]. The same CBP results as in Example 1.10 are provided.
. Herein, we determine the CBP of both service‐classes by using an alternative approach, called convolution algorithm [7]. The same CBP results as in Example 1.10 are provided.
The convolution algorithm for ![]() service‐classes is as follows.
service‐classes is as follows.
- (a)
For each service‐class
 calculate the link occupancy distribution
calculate the link occupancy distribution  , assuming that only one (the
, assuming that only one (the  th) service‐class is accommodated in the link,
th) service‐class is accommodated in the link,  for
for 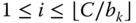 and
and  , while
, while  (
( ).
).
- First service‐class (
 erl,
erl,  b.u.). For
b.u.). For  , we have:
, we have: 

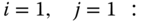







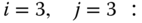

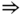







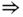

Therefore:
 , and the normalized values of
, and the normalized values of  are:
are:





- Second service‐class (
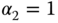 erl,
erl,  b.u.). For
b.u.). For 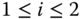 , we have:
, we have: 









Therefore
 , and the normalized values of
, and the normalized values of  are:
are:


- First service‐class (
- (b) By applying successive convolutions we calculate the link occupancy distribution
 for all states
for all states  . Letting the symbol
. Letting the symbol  denote the convolution operator, we have the following formula for the calculation of
denote the convolution operator, we have the following formula for the calculation of  for both service‐classes:
for both service‐classes:  . Thus:
. Thus: 




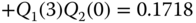




Thus,
 . The CBP are exactly the same as in Example 1.10(c):
. The CBP are exactly the same as in Example 1.10(c):  .
.
In general, convolution algorithms can be applied only in PFS models. If a PFS does not hold, there are other methods that are computationally more effective. As an example, consider the application of the BR policy in the EMLM. As we will see in Section 1.3.2, this policy destroys the PFS of the steady state probabilities, but the CBP calculation can be easily determined through recursive formulas. However, the CBP calculation based on convolution algorithms is much more complex, as [8] and [9] reveal.
Example 1.14
Consider a single link of capacity ![]() b.u. that accommodates calls of
b.u. that accommodates calls of ![]() service‐classes with the following traffic characteristics: first service‐class
service‐classes with the following traffic characteristics: first service‐class ![]() erl,
erl, ![]() b.u., second service‐class
b.u., second service‐class ![]() erl,
erl, ![]() b.u. Calculate the CBP
b.u. Calculate the CBP ![]() ,
, ![]() of the two service‐classes, when
of the two service‐classes, when ![]() increases in steps of 1 erl (up to 40 erl), while
increases in steps of 1 erl (up to 40 erl), while ![]() remains constant. Observe how each CBP varies versus the offered traffic‐load. In particular, the graph of
remains constant. Observe how each CBP varies versus the offered traffic‐load. In particular, the graph of ![]() differs a lot from the corresponding graph of Figure 1.3 (last) because of the observed oscillations. Such oscillations are a characteristic of the CS policy, especially when
differs a lot from the corresponding graph of Figure 1.3 (last) because of the observed oscillations. Such oscillations are a characteristic of the CS policy, especially when ![]() and the bandwidth per call requirements between the service‐classes highly differ.
and the bandwidth per call requirements between the service‐classes highly differ.
We present the exact CBP ![]() and
and ![]() in Figure 1.12. The oscillations that occur in the CBP of the first service‐class can be intuitively explained. The fact that
in Figure 1.12. The oscillations that occur in the CBP of the first service‐class can be intuitively explained. The fact that ![]() does not increase (actually decreases) when, for instance,
does not increase (actually decreases) when, for instance, ![]() increases from 4 to 7 erl can be justified by the great number
increases from 4 to 7 erl can be justified by the great number ![]() of b.u. which become available to the first service‐class calls at the time points that the second service‐class calls suffer from blocking. An in‐depth analysis of this phenomenon is found in [10].
of b.u. which become available to the first service‐class calls at the time points that the second service‐class calls suffer from blocking. An in‐depth analysis of this phenomenon is found in [10].

Figure 1.12 CBP oscillations in the EMLM (CS policy) (Example 1.14).
1.3 The Erlang Multirate Loss Model under the BR policy
1.3.1 The Service System
We consider again the multi‐service system of the EMLM, but with the following CAC. A new service‐class ![]() call is accepted in the link if, after its acceptance, the link has at least
call is accepted in the link if, after its acceptance, the link has at least ![]() b.u. available to serve calls of other service‐classes. This service system is called EMLM under the BR policy (EMLM/BR). By properly selecting the BR parameters
b.u. available to serve calls of other service‐classes. This service system is called EMLM under the BR policy (EMLM/BR). By properly selecting the BR parameters ![]() , we can achieve CBP equalization among service‐classes; this is the main target of the BR policy. Assuming that
, we can achieve CBP equalization among service‐classes; this is the main target of the BR policy. Assuming that ![]() , then for CBP equalization the parameters
, then for CBP equalization the parameters ![]() are chosen so that
are chosen so that ![]() , that is,
, that is, ![]() , since it is reasonable not to reserve bandwidth against the service‐class which requires the maximum bandwidth per call. Obviously, due to CBP equalization, we avoid the CBP oscillations observed in the EMLM under the CS policy.
, since it is reasonable not to reserve bandwidth against the service‐class which requires the maximum bandwidth per call. Obviously, due to CBP equalization, we avoid the CBP oscillations observed in the EMLM under the CS policy.
Figure 1.13 illustrates the case of a single link with ![]() that accommodates calls of two service‐classes with
that accommodates calls of two service‐classes with ![]() and
and ![]() b.u. To achieve CBP equalization we reserve
b.u. To achieve CBP equalization we reserve ![]() b.u. in favor of calls of the second service‐class.
b.u. in favor of calls of the second service‐class.

Figure 1.13 An example of the EMLM under the BR policy.
1.3.2 The Analytical Model
The basic characteristic of the BR policy is that the steady state probabilities cannot be calculated via a PFS. This is because LB between some adjacent states is destroyed (see the following example).
Example 1.15
Consider a single link of capacity ![]() b.u. which accommodates calls of two service‐classes, under the BR policy, with
b.u. which accommodates calls of two service‐classes, under the BR policy, with ![]() b.u. and
b.u. and ![]() b.u. The BR parameters are
b.u. The BR parameters are ![]() and
and ![]() . Let
. Let ![]() , and
, and ![]() be the corresponding traffic parameters of each service‐class; for simplicity suppose that
be the corresponding traffic parameters of each service‐class; for simplicity suppose that ![]() . Present graphically the state space
. Present graphically the state space ![]() of this system and show the states in which the LB does not exist.
of this system and show the states in which the LB does not exist.
The state space ![]() of this system consists of 11 states and is presented in Figure 1.14. Each state
of this system consists of 11 states and is presented in Figure 1.14. Each state ![]() satisfies the inequality
satisfies the inequality ![]() .
.

Figure 1.14 The state space  of the EMLM under the BR policy (Example 1.15).
of the EMLM under the BR policy (Example 1.15).
LB is destroyed between the adjacent states: (a) (0,2) and (1,2) and (b) (2,1) and (3,1). For instance, consider that the system is in state ![]() when a call of the first service‐class arrives; due to the BR policy, the call is blocked and lost. On the other hand, let the system state be
when a call of the first service‐class arrives; due to the BR policy, the call is blocked and lost. On the other hand, let the system state be ![]() . In that case, the first service‐class call may complete its service and leave the system. Then, the system state becomes
. In that case, the first service‐class call may complete its service and leave the system. Then, the system state becomes ![]() .
.
1.3.2.1 Accurate CBP Calculation
The absence of a PFS in the EMLM/BR leads to approximate solutions as far as the recursive calculation of the state probabilities (and consequently the CBP) is concerned. An accurate CBP calculation is achieved only by solving the linear system of GB equations; however, this is applicable only to small systems with a few service‐classes. Otherwise, the computational requirements become quite excessive.
Example 1.16
Consider Example 1.15 (![]() ) and determine the CBP of both service‐classes based on the GB equations.
) and determine the CBP of both service‐classes based on the GB equations.
For each of the 11 states of Figure 1.14, we write the corresponding GB equation (rate in = rate out):
By setting the numerical values, the linear system of equations becomes:
To finalise the formation of the linear system of equations, we have to replace one of the above equations with the normalization condition ![]() . The solution of the system of the 11 equations with the 11 variables (state probabilities) is:
. The solution of the system of the 11 equations with the 11 variables (state probabilities) is:
The CBP are determined based on the state probabilities. New calls of the first service‐class are blocked whenever the occupied link bandwidth is ![]() . Hence:
. Hence:
Similarly, new calls of the second service‐class are blocked if less than 2 b.u. are available in the link, hence:
As anticipated, ![]() , since
, since ![]() .
.
1.3.2.2 Approximate CBP Calculation based on the Roberts Method
In the EMLM/BR, the link occupancy distribution, q(j), is given in an approximate way by the following recursive formula [11]:

where:

This formula has a form similar to the Kaufman–Roberts recursion ( 1.39), and its existence is based on the assumption that, for a service‐class ![]() with
with ![]() , the mean number of service‐class
, the mean number of service‐class ![]() calls in state
calls in state ![]() ,
, ![]() , is zero in all states
, is zero in all states ![]() which belong to the prohibitive space of this service‐class:
which belong to the prohibitive space of this service‐class: ![]() . Thanks to this assumption, which is reflected in the variable
. Thanks to this assumption, which is reflected in the variable ![]() , the one‐dimensional Markov chain of the system is transformed to an approximate reversible Markov chain,9 which leads to the recurrent formula (1.64). Markov chain reversibility is a strong indication of the existence of a PFS.
, the one‐dimensional Markov chain of the system is transformed to an approximate reversible Markov chain,9 which leads to the recurrent formula (1.64). Markov chain reversibility is a strong indication of the existence of a PFS.
Example 1.17
In Example 1.15 (![]() ), find in which (macro‐) states
), find in which (macro‐) states ![]() the population of calls is negligible (
the population of calls is negligible (![]() ), for each service‐class, according to the Roberts' assumption.
), for each service‐class, according to the Roberts' assumption.
According to the Roberts' assumption, the population of calls of the first service‐class is negligible in states ![]() , that is, in state
, that is, in state ![]() we have
we have ![]() . However, state
. However, state ![]() corresponds to the detailed states
corresponds to the detailed states ![]() and
and ![]() , which both belong to the state space of the system (Figure 1.14). In both states, the value of
, which both belong to the state space of the system (Figure 1.14). In both states, the value of ![]() ; this shows why Roberts' formula provides an approximate way for the calculation of
; this shows why Roberts' formula provides an approximate way for the calculation of ![]() . For the second service‐class, the assumption does not hold, since
. For the second service‐class, the assumption does not hold, since ![]() .
.
The CBP of service‐class ![]() ,
, ![]() , is given by:
, is given by:

where ![]() is the normalization constant, given by ( 1.40).
is the normalization constant, given by ( 1.40).
The link utilization, ![]() , is given by ( 1.54).
, is given by ( 1.54).
The mean number of service‐class ![]() calls, in state
calls, in state ![]() , is determined by:
, is determined by:

The mean number of service‐class ![]() calls in the system,
calls in the system, ![]() , is given by ( 1.56).
, is given by ( 1.56).
Example 1.18
For the system of Example 1.15 (![]() ), draw the state transition diagram (one‐dimensional Markov chain) for all states
), draw the state transition diagram (one‐dimensional Markov chain) for all states ![]() and calculate the CBP of the service‐classes by using the Roberts' method.
and calculate the CBP of the service‐classes by using the Roberts' method.
The state transition diagram of this example is depicted in Figure 1.15. In state ![]() , due to the BR parameters, there is no rate in of the first service‐class from state
, due to the BR parameters, there is no rate in of the first service‐class from state ![]() . Also, in state
. Also, in state ![]() , there is no rate out of the first service‐class (backward to state
, there is no rate out of the first service‐class (backward to state ![]() ) because of the Roberts' assumption that y1(5) = 0. To calculate CBP, from ( 1.64) and (1.65), we obtain that:
) because of the Roberts' assumption that y1(5) = 0. To calculate CBP, from ( 1.64) and (1.65), we obtain that:

Thus, starting with ![]() , we recursively calculate the
, we recursively calculate the ![]() values for
values for ![]() :
:
The normalization constant is
 . . |
Then, from (1.66) we have:
 and and 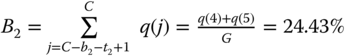 |
which are close to the accurate values of ![]() (calculated in Example 1.16).
(calculated in Example 1.16).

Figure 1.15 The one‐dimensional Markov chain of the EMLM/BR (Roberts' assumption, Example 1.18) .
1.3.2.3 CBP Calculation Recursively based on the Stasiak–Glabowski Method
When aiming at QoS equalization among service‐classes, the recursive CBP calculation of the EMLM/BR according to the Roberts method can be improved by the following method proposed by Stasiak and Glabowski10 [12]. The average number of service‐class ![]() calls,
calls, ![]() , in state
, in state ![]() is not zero but positive, and can be determined approximately in a recurrent way by:
is not zero but positive, and can be determined approximately in a recurrent way by:

where for the calculation of ![]() the corresponding EMLM system under the CS policy is assumed (i.e., the Kaufman–Roberts recursion ( 1.39)), while
the corresponding EMLM system under the CS policy is assumed (i.e., the Kaufman–Roberts recursion ( 1.39)), while ![]() is a weight given by:
is a weight given by:

The weight ![]() determines the proportion of
determines the proportion of ![]() that is transferred in state
that is transferred in state ![]() by a call of service‐class
by a call of service‐class ![]() (other than
(other than ![]() ), assuming that
), assuming that ![]() . Although the system cannot be in state
. Although the system cannot be in state ![]() due to an arriving call of service‐class
due to an arriving call of service‐class ![]() (because of the BR policy), the system can be in state
(because of the BR policy), the system can be in state ![]() due to arriving calls of other service‐classes (calls of other service‐classes may coexist in previous states together with service‐class
due to arriving calls of other service‐classes (calls of other service‐classes may coexist in previous states together with service‐class ![]() calls). Thus, when the system is transferred to state
calls). Thus, when the system is transferred to state ![]() by a service‐class
by a service‐class ![]() call, this call also transfers to state
call, this call also transfers to state ![]() the population of service‐class
the population of service‐class ![]() . Therefore, the assumption that the average number of calls is positive even in a prohibitive state of a service‐class is more realistic compared to the Roberts assumption. Figure 1.16 illustrates the fact that calls from different service‐classes may contribute in transferring the population of service‐class
. Therefore, the assumption that the average number of calls is positive even in a prohibitive state of a service‐class is more realistic compared to the Roberts assumption. Figure 1.16 illustrates the fact that calls from different service‐classes may contribute in transferring the population of service‐class ![]() to a prohibitive state
to a prohibitive state ![]() . Consequently, given that in state
. Consequently, given that in state ![]() the population of service‐class
the population of service‐class ![]() does exist, a backward transition to state
does exist, a backward transition to state ![]() is true.
is true.

Figure 1.16 Calls of service‐classes  contribute in
contribute in  by transferring the population of service‐class
by transferring the population of service‐class  to state
to state  .
.
Having determined the average number of calls in each state ![]() via (1.68), then the Roberts method is followed by replacing
via (1.68), then the Roberts method is followed by replacing ![]() in the RHS of
in the RHS of ![]() in ( 1.64) by
in ( 1.64) by ![]() , in order for the average number of calls of each service‐class in state
, in order for the average number of calls of each service‐class in state ![]() to be determined:
to be determined:

The philosophy behind this method is that the approximated reversible Markov chain of the Roberts method is kept, but each state ![]() of the prohibited state space is now substituted by state
of the prohibited state space is now substituted by state ![]() . The Stasiak–Glabowski method is summarized in the following procedure:
. The Stasiak–Glabowski method is summarized in the following procedure:
- Step 1:
Assuming that the system is under the CS policy (instead of the BR policy), calculate
 via ( 1.39).
via ( 1.39). - Step 2:
Calculate the average number of service‐class
 calls in state
calls in state  ,
,  , according to ( 1.68) and (1.69).
, according to ( 1.68) and (1.69). - Step 3: Determine
 for the EMLM/BR, as follows:
(1.71)
for the EMLM/BR, as follows:
(1.71)
- Step 4: Determine the CBP of each service‐class according to ( 1.66).
Example 1.19
For the system of Example 1.15 (![]() ), explain the Stasiak–Glabowski assumption by properly modifying the one‐dimensional Markov chain of Figure 1.15, and calculate the CBP of both service‐classes by using the Stasiak–Glabowski method.
), explain the Stasiak–Glabowski assumption by properly modifying the one‐dimensional Markov chain of Figure 1.15, and calculate the CBP of both service‐classes by using the Stasiak–Glabowski method.
Let the system be in state ![]() , in which there are in‐service calls of the first service‐class. Assume now that a new call of the second service‐class arrives in the system and requires
, in which there are in‐service calls of the first service‐class. Assume now that a new call of the second service‐class arrives in the system and requires ![]() b.u. After the acceptance of this call in the system, the population not only of the second service‐class but also of the first service‐class is transferred in the new state
b.u. After the acceptance of this call in the system, the population not only of the second service‐class but also of the first service‐class is transferred in the new state ![]() . Thus, since it is realistic to assume that the average population of first service‐class calls in state
. Thus, since it is realistic to assume that the average population of first service‐class calls in state ![]() is positive, we also assume the backward transition to state
is positive, we also assume the backward transition to state ![]() , due to a first service‐class call departure. This transition is shown in Figure 1.17 as a modification of Figure 1.15. To calculate the CBP according to the Stasiak–Glabowski method, we proceed as follows:
, due to a first service‐class call departure. This transition is shown in Figure 1.17 as a modification of Figure 1.15. To calculate the CBP according to the Stasiak–Glabowski method, we proceed as follows:
- Step 1: Assuming that the system is under the CS policy, we calculate
 via ( 1.39). These results have been obtained in Example 1.10:
via ( 1.39). These results have been obtained in Example 1.10: 





with normalization constant:
 .
. - Step 2: The average number of service‐class
 calls in state
calls in state  ,
, 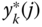 , according to ( 1.68) and ( 1.69), is:
, according to ( 1.68) and ( 1.69), is: 









The value of
 (in bold) is positive, while it is zero according to the Roberts method. All other values are exactly the same in both methods.
(in bold) is positive, while it is zero according to the Roberts method. All other values are exactly the same in both methods. - Step 3: We determine
 for the EMLM/BR via (1.71):
for the EMLM/BR via (1.71): 





















The normalization constant is
 .
. - Step 4: The CBP of each service‐class is calculated according to ( 1.66):
 and
and 
which are closer to the accurate values of
 (calculated in Example 1.16) than the results of the Roberts method (
(calculated in Example 1.16) than the results of the Roberts method ( , calculated in Example 1.18).
, calculated in Example 1.18).

Figure 1.17 The one‐dimensional Markov chain of the EMLM/BR under the Stasiak–Glabowski assumption (Example 1.19).
Example 1.20
A single link of capacity ![]() b.u. accommodates three service‐classes under the BR policy, with
b.u. accommodates three service‐classes under the BR policy, with ![]() b.u. and offered traffic‐load of
b.u. and offered traffic‐load of ![]() erl (so that
erl (so that ![]() ). Determine the CBP of each service‐class, according to the Roberts method and the Stasiak–Glabowski method, for the following three sets of the BR parameters
). Determine the CBP of each service‐class, according to the Roberts method and the Stasiak–Glabowski method, for the following three sets of the BR parameters ![]() : (A)
: (A) ![]() , (B)
, (B) ![]() , and (C)
, and (C) ![]() (obtained from [ 12]). Compare the CBP results with the corresponding CBP results when the CS policy is applied in the link.
(obtained from [ 12]). Compare the CBP results with the corresponding CBP results when the CS policy is applied in the link.
Observe that only the last set of BR parameters leads to CBP equalization among these three service‐classes, while both sets (A) and (B) lead to CBP equalization between the first and second service‐classes only (since ![]() b.u. and
b.u. and ![]() b.u.). In respect of CBP, the last set of BR parameters benefits the third service‐class most, while the least benefit for the third service‐class is anticipated by set (A). Notice that by set (A), less b.u. (than set (B) or (C)) are reserved to benefit the third service‐class.
b.u.). In respect of CBP, the last set of BR parameters benefits the third service‐class most, while the least benefit for the third service‐class is anticipated by set (A). Notice that by set (A), less b.u. (than set (B) or (C)) are reserved to benefit the third service‐class.
The following table contains the CBP results under the CS policy and the BR policy for each set of BR parameters:
| CS policy | 0.82 | 1.90 | 29.18 |
| Set (A) Roberts | 10.74 | 10.74 | 25.22 |
| Set (A) Stasiak–Glabowski | 10.79 | 10.79 | 25.27 |
| Set (A) Simulation | 9.91 |
9.90 |
28.27 |
| Set (B) Roberts | 14.32 | 14.32 | 23.32 |
| Set (B) Stasiak–Glabowski | 14.42 | 14.42 | 23.40 |
| Set (B) Simulation | 14.38 |
14.36 |
27.86 |
| Set (C) Roberts | 19.70 | 19.70 | 19.70 |
| Set (C) Stasiak–Glabowski | 20.44 | 20.44 | 20.44 |
| Set (C) Simulation | 24.28 |
24.29 |
24.30 |
The rows referring to “ Simulation” provide CBP results from simulation as mean values of 12 runs with a confidence interval of 95%. These values are considered reference values in order to check the accuracy of the other CBP results. Thus, based on simulation, we found that, indeed, the Stasiak–Glabowski method provides better results than the Roberts method for CBP equalization (set (C)), but not for set (A). For set (B) the CBP results of the two methods are pretty close to each other.
Comparing the CBP results under the CS and BR policies (set (C)), it is worth noticing that the BR policy achieves CBP equalization at the expense of high traffic losses of low‐speed calls (while the traffic savings of the high‐speed calls are relatively low).
1.4 The Erlang Multirate Loss Model under the Threshold Policy
1.4.1 The Service System
We consider again the multi‐service system of the EMLM and adopt a TH‐type CAC, as follows: A new call of service‐class k is accepted in the system, of C b.u., if:
- (i) its bandwidth requirement, bk b.u., is less or equal to the available link bandwidth
- (ii) the number nk of in‐service calls of service‐class k does not exceed a predefined threshold parameter, after its acceptance. Otherwise, the call is blocked and lost without affecting the system.
By definition a policy is called a TH policy if there exists a set of positive integers ![]() such that a service‐class
such that a service‐class ![]() call is accepted in the system when in state
call is accepted in the system when in state ![]() , if and only if the new system state fulfils the relations
, if and only if the new system state fulfils the relations ![]() and
and ![]() [13].
[13].
Example 1.21
A single link of ![]() b.u. accommodates calls of two service‐classes with
b.u. accommodates calls of two service‐classes with ![]() and
and ![]() b.u., respectively. The TH policy is applied only to calls of service‐class 1, by assuming that in‐service calls of that service‐class can be at most three, i.e.,
b.u., respectively. The TH policy is applied only to calls of service‐class 1, by assuming that in‐service calls of that service‐class can be at most three, i.e., ![]() . For example, because of this threshold, a new service‐class 1 call will be blocked even if there are two available b.u. in the link, upon the call's arrival. Describe this TH policy according to (I.38).
. For example, because of this threshold, a new service‐class 1 call will be blocked even if there are two available b.u. in the link, upon the call's arrival. Describe this TH policy according to (I.38).
For ![]() , we have
, we have ![]()
Example 1.22
The following example shows an interesting application of the TH policy in the case of tree networks. Consider calls of ![]() service‐classes accommodated in a tree network. The network consists of
service‐classes accommodated in a tree network. The network consists of ![]() access links of capacity
access links of capacity ![]() b.u. and a common link of capacity
b.u. and a common link of capacity ![]() b.u. Calls of service class
b.u. Calls of service class ![]() follow a Poisson process with mean arrival rate
follow a Poisson process with mean arrival rate ![]() and have an exponentially distributed service time with mean
and have an exponentially distributed service time with mean ![]() . The offered traffic‐load of service‐class
. The offered traffic‐load of service‐class ![]() is
is ![]() (in erl). Calls of service class
(in erl). Calls of service class ![]() request
request ![]() b.u. simultaneously on the
b.u. simultaneously on the ![]() th access link and the common link (Figure 1.18). Without loss of generality, we assume that
th access link and the common link (Figure 1.18). Without loss of generality, we assume that ![]() is a multiple integer of
is a multiple integer of ![]() for all
for all ![]() . If these
. If these ![]() b.u. are available, then the call is accepted in the system, otherwise the call is blocked and lost. Show how the tree network of Figure 1.18 can be described by the EMLM/TH.
b.u. are available, then the call is accepted in the system, otherwise the call is blocked and lost. Show how the tree network of Figure 1.18 can be described by the EMLM/TH.

Figure 1.18 A multirate access tree network that accommodates  service‐classes of Poisson input (Example 1.22).
service‐classes of Poisson input (Example 1.22).
If ![]() denotes the vector of all in‐service calls, then the state space
denotes the vector of all in‐service calls, then the state space ![]() of the tree network is written as
of the tree network is written as ![]() , with
, with ![]() and
and ![]() .
.
Now, let ![]() be the maximum number of service‐class
be the maximum number of service‐class ![]() calls serviced by the tree network. Then, we rewrite the state space as
calls serviced by the tree network. Then, we rewrite the state space as ![]() . This form of
. This form of ![]() represents a link of capacity
represents a link of capacity ![]() b.u. that accommodates calls of
b.u. that accommodates calls of ![]() service‐classes, which compete for the available bandwidth under the EMLM/TH.
service‐classes, which compete for the available bandwidth under the EMLM/TH.
According to the aforementioned definition of the TH policy, the topology of Figure 1.18 can be replaced by the single link of Figure 1.19, and the analytical formulas obtained for the first topology can be used in the second one and vice versa. For simplicity, we adopt the topology of Figure 1.19, which corresponds to the EMLM/TH.

Figure 1.19 A single link that accommodates  service‐classes of Poisson input described by the EMLM/TH (Example 1.22).
service‐classes of Poisson input described by the EMLM/TH (Example 1.22).
1.4.2 The Analytical Model
1.4.2.1 Steady State Probabilities
Due to the fact that the TH policy is a coordinate convex policy (as the CS policy is) the steady state probabilities in the EMLM/TH have a PFS whose form is the same as that of the EMLM (only the definition of ![]() differs):
differs):

where ![]() and
and ![]()
Example 1.23
Consider again Example 1.6 (![]() ) and assume that the TH policy is applied to calls of service‐class 1, with
) and assume that the TH policy is applied to calls of service‐class 1, with ![]() . By assuming that
. By assuming that ![]() :
:
- (a)Present graphically the state space
 and calculate the state probabilities
and calculate the state probabilities  and, based on them, the corresponding values of
and, based on them, the corresponding values of  .
. - (b)Verify that the PFS of (1.72) results in the same values of
 as those obtained in (a).
as those obtained in (a). - (c)Calculate the CBP of both service‐classes.
- (d)Assume an increase in
 from 0.1 to 1.0 erl in steps of 0.1 erl. Present graphically the CBP of each service‐class obtained by the EMLM, the EMLM/BR (let
from 0.1 to 1.0 erl in steps of 0.1 erl. Present graphically the CBP of each service‐class obtained by the EMLM, the EMLM/BR (let  and
and  , for CBP equalization), and the EMLM/TH when
, for CBP equalization), and the EMLM/TH when  . Comment on the results.
. Comment on the results.
- (a) The state space
 of this system consists of 10 states and is presented in Figure 1.20. This state space is actually a subset of the EMLM presented in Example 1.6. Each state
of this system consists of 10 states and is presented in Figure 1.20. This state space is actually a subset of the EMLM presented in Example 1.6. Each state  satisfies the inequalities
satisfies the inequalities 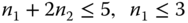 . To determine the state probabilities, we write the GB equations for the 10 states
. To determine the state probabilities, we write the GB equations for the 10 states 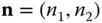 of Figure 1.20:
of Figure 1.20: 










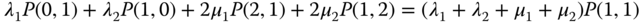













By replacing a GB equation (e.g., of (1,1)) with the normalization condition
 , we have the solution of this linear system of 10 equations:
, we have the solution of this linear system of 10 equations:









Based on the values of
 we have:
we have:





- (b)It is easy to verify that the PFS of
 , where
, where  gives exactly the same results as those obtained in (a).
gives exactly the same results as those obtained in (a). - (c) The CBP of service‐class 1 is given by the formula:

where the second summation refers to the TH policy.
The CBP of service‐class 2 is given by the formula:

Note that exactly the same CBP are obtained when considering two concatenated links with
 and
and  b.u. (substituting the single link of
b.u. (substituting the single link of  b.u.), and calls of the first service‐class traverse both links, while calls of the second service‐class utilize only the second link of
b.u.), and calls of the first service‐class traverse both links, while calls of the second service‐class utilize only the second link of  b.u. (see Section 1.5 and Example 1.25 where the similar case of
b.u. (see Section 1.5 and Example 1.25 where the similar case of  and
and  b.u. is examined).
b.u. is examined). - (d)
Figure 1.21 presents
 and
and  , in the LHS and the RHS, respectively, for the EMLM, the EMLM/BR, and the EMLM/TH. Based on Figure 1.21, we see that:
, in the LHS and the RHS, respectively, for the EMLM, the EMLM/BR, and the EMLM/TH. Based on Figure 1.21, we see that:
- increasing the value of
 decreases the CBP of service‐class 1 and increases the CBP of service‐class 2
decreases the CBP of service‐class 1 and increases the CBP of service‐class 2 - the EMLM and the EMLM/BR cannot capture the behavior of the EMLM/TH. Especially for the case of
 one would expect that the CBP of service‐class 1 for the EMLM/BR and the EMLM/TH would be quite close due to the selection of the BR parameter
one would expect that the CBP of service‐class 1 for the EMLM/BR and the EMLM/TH would be quite close due to the selection of the BR parameter  , which prevents
, which prevents  becoming 5. However, this is not the case since
becoming 5. However, this is not the case since 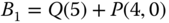 for the EMLM/TH, while
for the EMLM/TH, while  for the EMLM/BR.
for the EMLM/BR.
- increasing the value of

Figure 1.20 The state space  of system under the TH policy (Example 1.23).
of system under the TH policy (Example 1.23).

Figure 1.21 Comparison of the EMLM, the EMLM/BR, and the EMLM/TH (Example 1.23) .
For the determination of the unnormalized values of q(j), the following accurate and recursive formula can be used [14]:

where ![]() is the probability that
is the probability that ![]() b.u. are occupied, while the number of service‐class
b.u. are occupied, while the number of service‐class ![]() calls is
calls is ![]() or:
or:
In (1.73) the fact that ![]() implies that:
implies that:
- (i)
 and therefore
and therefore  for
for  and
and - (ii)
 is a blocking probability factor for service‐class
is a blocking probability factor for service‐class  calls.
calls.
The proof of ( 1.73) is similar to the proof of the Kaufman–Roberts formula (see e.g., [ 14]). The only difference is that ( 1.48) now takes the form:

due to the existence of the TH policy.
Intuitively, the form of (1.75) is expected, since the term ![]() is a factor that blocks a new service‐class
is a factor that blocks a new service‐class ![]() call from being accepted in the system and therefore blocks the transition from state
call from being accepted in the system and therefore blocks the transition from state ![]() to state
to state ![]() .
.
1.4.2.2 CBP, Utilization and Mean Number of In‐service Calls
The following performance measures can be determined:
- To determine the CBP of service‐class
 ,
,  , we consider two groups of macro‐states:
, we consider two groups of macro‐states:
- (i)
those where there is no available bandwidth to accept a new service‐class
 call; this happens when
call; this happens when 
- (ii)
those where available bandwidth exists, i.e.,
 but
but  ; the latter implies that
; the latter implies that  .
.
The values of
 are given by:(1.76)
are given by:(1.76)
where
 is the normalization constant.
is the normalization constant. - (i)
those where there is no available bandwidth to accept a new service‐class
- The link utilization is given by ( 1.54).
- The mean number
 of service‐class
of service‐class  calls, in state
calls, in state  , is given by:
(1.77)
, is given by:
(1.77)
- The mean number of service‐class
 calls in the system is given by ( 1.56).
calls in the system is given by ( 1.56).
Equations (1.76) and (1.77) require knowledge of ![]() . The latter takes positive values when
. The latter takes positive values when ![]() . Thus, we consider a subsystem of capacity
. Thus, we consider a subsystem of capacity ![]() that accommodates all service‐classes but service‐class
that accommodates all service‐classes but service‐class ![]() . For this subsystem, we define
. For this subsystem, we define ![]() , which is analogous to
, which is analogous to ![]() of ( 1.73):
of ( 1.73):

We can now compute ![]() for
for ![]() , as follows:
, as follows:

In (1.79), the term ![]() is expected, since for states
is expected, since for states ![]() , the number of in‐service calls of service‐class
, the number of in‐service calls of service‐class ![]() is always
is always ![]() .
.
The computational complexity of the EMLM/TH is in the order of ![]() , where
, where ![]() ; for more details, see [ 14].
; for more details, see [ 14].
Note: In (1.78), each time that the calculation of ![]() requires knowledge of
requires knowledge of ![]() (this happens when
(this happens when ![]() , for
, for ![]() , an extra subsystem is needed for the calculation of
, an extra subsystem is needed for the calculation of ![]() and
and ![]() via ( 1.78) and ( 1.79) (see also Section IV, pp. 12–69 in [ 14]). Instead of using subsystems, we may calculate
via ( 1.78) and ( 1.79) (see also Section IV, pp. 12–69 in [ 14]). Instead of using subsystems, we may calculate ![]() for those values of
for those values of ![]() that result in
that result in ![]() (in ( 1.78)), while for the rest values of
(in ( 1.78)), while for the rest values of ![]() we can use the following formula (which is based on the fact that the EMLM/TH has a PFS):
we can use the following formula (which is based on the fact that the EMLM/TH has a PFS):

for ![]() and
and ![]() .
.
This method can be useful especially for systems with small to moderate state spaces (see Example 3.10). This topic remains open to investigation.
1.5 The Erlang Multirate Loss Model in a Fixed Routing Network
1.5.1 The Service System
According to ITU‐T, a fixed routing network is a network in which a route11 providing a connection between an originating node and a destination node is fixed for every service‐class (or for every traffic flow of the same service‐class). Let us consider that a fixed routing network consists of ![]() links. Each link
links. Each link ![]() has a fixed capacity of
has a fixed capacity of ![]() b.u. The network accommodates calls of
b.u. The network accommodates calls of ![]() service‐classes under the CS policy. Calls of service‐class
service‐classes under the CS policy. Calls of service‐class ![]() follow a Poisson process with rate
follow a Poisson process with rate ![]() , require
, require ![]() b.u. and have a generally distributed service time with mean
b.u. and have a generally distributed service time with mean ![]() . Let
. Let ![]() be the fixed route of service‐class
be the fixed route of service‐class ![]() calls in the network, where
calls in the network, where ![]() . A call of service‐class
. A call of service‐class ![]() is accepted in the network if its
is accepted in the network if its ![]() b.u. are available in every link
b.u. are available in every link ![]() , otherwise the call is blocked and lost.
, otherwise the call is blocked and lost.
1.5.2 The Analytical Model
Let ![]() be the number of in‐service calls of service‐class
be the number of in‐service calls of service‐class ![]() in the steady state of the system and
in the steady state of the system and ![]() be the corresponding steady state vector of all service‐classes in the fixed routing network. If
be the corresponding steady state vector of all service‐classes in the fixed routing network. If ![]() is the set of service‐classes whose calls are accommodated in link
is the set of service‐classes whose calls are accommodated in link ![]() , i.e.,
, i.e., ![]() , then the state space
, then the state space ![]() of the system is given by:
of the system is given by:

Example 1.24
Consider two service‐classes whose calls require ![]() and
and ![]() b.u., respectively. All calls are accommodated to a network of three sequential links of capacity
b.u., respectively. All calls are accommodated to a network of three sequential links of capacity ![]() and
and ![]() b.u., respectively. Draw the bounds of the state space
b.u., respectively. Draw the bounds of the state space ![]() of this system.
of this system.
The bounds of the state space ![]() consist of three linear constraints; they are drawn in Figure 1.22, where
consist of three linear constraints; they are drawn in Figure 1.22, where ![]() and
and ![]() are the numbers of calls of the two service‐ classes, respectively,
are the numbers of calls of the two service‐ classes, respectively, ![]() is the largest integer not exceeding
is the largest integer not exceeding ![]() , and
, and  .
.

Figure 1.22 The state space  of the three link network (Example 1.24) .
of the three link network (Example 1.24) .
1.5.2.1 Steady State Probabilities
The steady state probabilities ![]() have a PFS whose form is the following [ 13,15]:
have a PFS whose form is the following [ 13,15]:
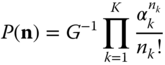
where  is the normalization constant, and
is the normalization constant, and ![]() is the offered traffic‐load of service‐class
is the offered traffic‐load of service‐class ![]() calls.
calls.
If we denote by ![]() the occupied b.u. of link
the occupied b.u. of link ![]() , where
, where ![]() , and
, and ![]() is the corresponding vector of the entire fixed routing network, then the unnormalized values of the occupancy distribution
is the corresponding vector of the entire fixed routing network, then the unnormalized values of the occupancy distribution ![]() in the fixed routing network are given by the following L‐dimensional accurate recursive formula [ 15]:
in the fixed routing network are given by the following L‐dimensional accurate recursive formula [ 15]:

where 
![]() is the
is the ![]() th row of a (
th row of a (![]() ) matrix (routing table), and shows the route (sequence of links) for the
) matrix (routing table), and shows the route (sequence of links) for the ![]() th service‐ class.
th service‐ class.
Note: In the case of a single link, (1.83) becomes the Kaufman–Roberts recursion ( 1.39).
1.5.2.2 CBP, Utilization, and Mean Number of In‐service Calls in the System
Having determined the values of ![]() , the following performance measures can be determined:
, the following performance measures can be determined:
- We calculate the CBP of service‐class
 , as follows:
(1.84)where
, as follows:
(1.84)where
 .
. - The utilization of link
 , is given by the following formula:
(1.85)where
, is given by the following formula:
(1.85)where
 .
. - The mean number of service‐class k calls in state
 ,
,  , is determined by the formula:
(1.86)
, is determined by the formula:
(1.86)
- The mean number of service‐class k calls in the system,
 , is given by:
(1.87)
, is given by:
(1.87)
Example 1.25
Consider the fixed routing network of Figure 1.23. The first link has a capacity of ![]() b.u. while the second one has a capacity of
b.u. while the second one has a capacity of ![]() b.u. This system accommodates calls of
b.u. This system accommodates calls of ![]() service‐classes, with
service‐classes, with ![]() and
and ![]() b.u., respectively. Calls of service‐class 1 traverse both links, while calls of service‐class 2 traverse only the second link.
b.u., respectively. Calls of service‐class 1 traverse both links, while calls of service‐class 2 traverse only the second link.
- (a)Calculate the CBP of both service‐classes via ( 1.83) and (1.84), when
 erl.
erl. - (b)Calculate the utilization of each link.
- (a) Since calls of service‐class 1 traverse both links, while calls of service‐class 2 traverse the second link, the (2
 2) matrix of this example is
2) matrix of this example is  =
=  . According to ( 1.83), we have
. According to ( 1.83), we have  , with
, with  and
and  .
.
Starting with
 and considering the second link only (i.e.,
and considering the second link only (i.e.,  in ( 1.83), we recursively calculate
in ( 1.83), we recursively calculate  for
for  :
:


= 0.0 




= 2.0 




= 0.0 




= 2.0 




= 0.0 

Indeed, given that
 b.u., when the second link is occupied by calls of the second service‐class only, we cannot have an odd number of occupied b.u., hence
b.u., when the second link is occupied by calls of the second service‐class only, we cannot have an odd number of occupied b.u., hence  . Likewise, since calls of the first service‐class occupy b.u. in both links, we have
. Likewise, since calls of the first service‐class occupy b.u. in both links, we have  .
.We now consider the first link (i.e.,
 in ( 1.83)), and we recursively calculate
in ( 1.83)), and we recursively calculate  (for
(for  and
and  ) as follows:
) as follows:  Since
Since 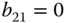 , the term
, the term  is not included in the rest of the calculations:
is not included in the rest of the calculations:
= 
= 0.0 

= 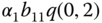
= 1.0 
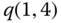
= 
= 0.0 

= 
= 0.5 

= 
= 0.0 

= 
= 1.0 

= 
= 0.0 

= 
= 1.0 

= 
= 0.0 
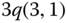
= 
= 0.0 

= 
= 0.0 

= 
= 0.5 

= 
= 0.0 

= 
= 0.5 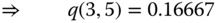

= 
= 0.0 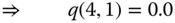

= 
= 0.0 

= 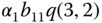
= 0.0 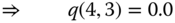

= 
= 0.16667 

= 
= 0.0 
The normalization constant is
 . Thus:
. Thus:
It is worth mentioning that exactly the same
 and
and  are obtained by the EMLM/TH when assuming a single link of capacity
are obtained by the EMLM/TH when assuming a single link of capacity  b.u. and
b.u. and  .
. - (b)
 where:
where: 

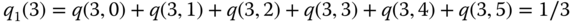
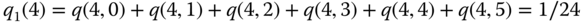
Similarly,
 where:
where:

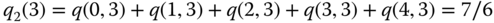

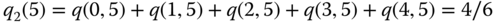

Figure 1.23 Two service‐classes accommodated in a fixed routing network of two links (Example 1.25).
Although ( 1.83) determines CBP in an accurate way, it has a high computational complexity of the order ![]() [16]. The latter shows the necessity for approximate methods that can be used instead of ( 1.83), especially in the case of large networks. The most popular method is the reduced load approximation (RLA) (see e.g., [ 13, 15,17], and [18]) and is the subject of the next subsection.
[16]. The latter shows the necessity for approximate methods that can be used instead of ( 1.83), especially in the case of large networks. The most popular method is the reduced load approximation (RLA) (see e.g., [ 13, 15,17], and [18]) and is the subject of the next subsection.
1.5.3 CBP Calculation by the RLA Method
1.5.3.1 A Fixed Routing Network Supporting a Single Service‐class
We assume that a fixed routing network supports K different traffic flows of a single service‐class requiring 1 b.u. per traffic flow, that is, ![]() . Traffic flows are distinguished by the different sequence of links traversing the various end‐to‐end connections in a fixed routing network. Let
. Traffic flows are distinguished by the different sequence of links traversing the various end‐to‐end connections in a fixed routing network. Let ![]() be the total offered traffic‐load to a link
be the total offered traffic‐load to a link ![]() , where
, where ![]() :
:

where ![]() is the set of traffic flows utilizing link
is the set of traffic flows utilizing link ![]() .
.
The CBP of traffic‐flow ![]() , can be upper bounded by the following product (based on the Erlang‐B formula) [19]:
, can be upper bounded by the following product (based on the Erlang‐B formula) [19]:

This product‐bound provides a good CBP approximation only if the number of links used by traffic flows in the network is small. If not, this bound is unreliable, for example consider only one traffic flow traversing ![]() links of the same capacity
links of the same capacity ![]() . Then, from (1.89), we have [ 13]:
. Then, from (1.89), we have [ 13]:
where ![]() for every link
for every link ![]() .
.
The bound of (1.90) approaches unity when ![]() increases, although
increases, although ![]() for every link and, consequently, for the entire fixed routing network.
for every link and, consequently, for the entire fixed routing network.
A better CBP approximation is achieved by reducing the offered traffic‐load ![]() so that blocking in the other links (excluding
so that blocking in the other links (excluding ![]() ) is taken into account. Specifically, this is done by substituting in (1.88) the term
) is taken into account. Specifically, this is done by substituting in (1.88) the term ![]() with
with ![]() , where the reduced factor
, where the reduced factor ![]() is the probability that there is at least 1 b.u. available in every link of the route
is the probability that there is at least 1 b.u. available in every link of the route ![]() . Denoting the approximate CBP in link
. Denoting the approximate CBP in link ![]() by
by ![]() , we obtain:
, we obtain:

Assuming that blocking is independent from link to link (an assumption that is incorrect), we have [ 13]:

The combination of (1.91) and (1.92) gives the following fixed‐point equation12 for the approximate CBP determination in link l:

Assuming again that blocking is independent from link to link, we approximate the CBP of traffic flow k, ![]() , as follows [ 13]:
, as follows [ 13]:

The combination of (1.93) and (1.94) constitutes the RLA method (or the so‐called Erlang fixed point equation, see e.g., [20]) for fixed routing networks that support traffic flows of a single service‐class.
Note that the fixed point equation has a unique solution (see e.g., Theorem 5.9 in [ 13]) which satisfies the bound:

This solution can be obtained via a simple method that relies on repeated substitutions, as the following example shows.
Example 1.26
Consider the telephone network of Figure 1.24 that accommodates ![]() telephone traffic flows of equal offered traffic‐load:
telephone traffic flows of equal offered traffic‐load: ![]() erl. Estimate the CBP for each traffic flow (
erl. Estimate the CBP for each traffic flow (![]() b.u.), as well as each link.
b.u.), as well as each link.
According to ( 1.91) and ( 1.92), for ![]() , we have:
, we have:
Thus, we can proceed according to ( 1.93) and ( 1.94):
To solve the above system of equations, we initially set ![]() and calculate the new values of
and calculate the new values of ![]() and the corresponding values of
and the corresponding values of ![]() . We repeat the calculations by considering the new values as initial values and so on. We terminate this iterative process when the new values differ from the previous values by less than a predefined value, say 0.00001; in this example, we need eight repetitions. The results are:
. We repeat the calculations by considering the new values as initial values and so on. We terminate this iterative process when the new values differ from the previous values by less than a predefined value, say 0.00001; in this example, we need eight repetitions. The results are:
| Repetition | ||||||
| 1 | 0.000000 | 0.000000 | 0.000157 | 1.000000 | 0.000157 | 0.000157 |
| 2 | 0.000157 | 0.036466 | 0.180316 | 0.036618 | 0.210207 | 0.180316 |
| 3 | 0.000013 | 0.010778 | 0.168421 | 0.010791 | 0.177384 | 0.168421 |
| 4 | 0.000020 | 0.019001 | 0.176808 | 0.019021 | 0.192450 | 0.176808 |
| 5 | 0.000018 | 0.011104 | 0.176442 | 0.011122 | 0.185557 | 0.176442 |
| 6 | 0.000018 | 0.011138 | 0.176701 | 0.011156 | 0.185871 | 0.176701 |
| 7 | 0.000018 | 0.011114 | 0.176690 | 0.011133 | 0.185841 | 0.176690 |

Figure 1.24 Application of the RLA method in a telephone network of three links (Example 1.26).
1.5.3.2 A Fixed Routing Network Supporting Multiple Service‐classes
Consider now that ![]() service‐classes are accommodated in a fixed routing network of
service‐classes are accommodated in a fixed routing network of ![]() links, according to the service system described in Section 1.5.1. Suppose that a service‐class
links, according to the service system described in Section 1.5.1. Suppose that a service‐class ![]() traverses a link
traverses a link ![]() of capacity
of capacity ![]() b.u. and experiences there CBP,
b.u. and experiences there CBP, ![]() .
. ![]() can be determined approximately by:
can be determined approximately by:

where it is assumed that the offered traffic‐load ![]() of service‐class
of service‐class ![]() to the whole fixed routing network is the same as the offered traffic‐load of service‐class
to the whole fixed routing network is the same as the offered traffic‐load of service‐class ![]() in link
in link ![]() ;
; ![]() is the unnormalized probability of having
is the unnormalized probability of having ![]() occupied b.u. in this link (calculated by the Kaufman–Roberts recursion, ( 1.39), over all
occupied b.u. in this link (calculated by the Kaufman–Roberts recursion, ( 1.39), over all ![]() ) and
) and ![]() is the corresponding normalization constant.
is the corresponding normalization constant.
The CBP expression (1.96) can be improved by considering that the offered traffic‐load of a service‐class to a link is actually reduced when traversing through a sequence of links. Let us denote by ![]() the improved CBP of service‐class
the improved CBP of service‐class ![]() in link
in link ![]() . Based on ( 1.92), the offered traffic‐load
. Based on ( 1.92), the offered traffic‐load ![]() is reduced to
is reduced to ![]() . Then,
. Then, ![]() is given by [ 13]:
is given by [ 13]:

Based on (1.97), the approximate CBP calculation of service‐ class ![]() , in the entire route
, in the entire route ![]() , is given by:
, is given by:

The combination of ( 1.97) and (1.98) constitutes the RLA method for fixed routing networks that support calls of different service‐class. The values of ![]() can be obtained via repeated substitutions as Example 1.27 shows.
can be obtained via repeated substitutions as Example 1.27 shows.
The extension of the RLA method to include different service‐ classes appears in the literature as the knapsack approximation [21]. This term is justified by the fact that the EMLM resembles the stochastic knapsack/problem in combinatorial optimization [22]. The knapsack approximation does not always lead to a unique solution (for an analytical example see [ 13]), however in most cases it approximates CBP quite satisfactorily.
Example 1.27
Consider again Example 1.25 (Figure 1.23, ![]() ) and calculate the CBP of both service‐classes by applying the RLA method.
) and calculate the CBP of both service‐classes by applying the RLA method.
Let ![]() and
and ![]() be the CBP of service‐ class 1 in the first and second links, respectively, and
be the CBP of service‐ class 1 in the first and second links, respectively, and ![]() the CBP of service‐class 2 in the second link. Then, according to ( 1.96), we have:
the CBP of service‐class 2 in the second link. Then, according to ( 1.96), we have:



where the values of ![]() are determined by the Kaufman–Roberts recursion ( 1.39).
are determined by the Kaufman–Roberts recursion ( 1.39).
Based on ( 1.92), we determine the reduced offered traffic‐load of service‐class 1 to the first and second links by (1.100a) and (1.100b), respectively, and the reduced offered traffic‐ load of service‐class 2 to the second link by (1.100c):



Then, according to ( 1.97), the improved CBP of service‐class 1 in the first and second links, ![]() and
and ![]() , respectively, and the improved CBP of service‐class 2 in the second link,
, respectively, and the improved CBP of service‐class 2 in the second link, ![]() , are:
, are:
In the following, we calculate ![]() and
and ![]() by repeated substitutions, starting with
by repeated substitutions, starting with ![]() :
:
| Repetition 1 |
 |
| Repetition 2 |
 |
 |
 |
| Repetition 3 |
| Repetition 6 |
We stop at Repetition 6 since the values of ![]() and
and ![]() are pretty close to those obtained in the previous step.
are pretty close to those obtained in the previous step.
Then, we calculate the CBP according to ( 1.98):
which are quite close to the accurate values of Example 1.25:
Example 1.28
Consider the ring network of Figure 1.25 that accommodates ![]() service‐classes with the following traffic characteristics:
service‐classes with the following traffic characteristics: ![]() , and
, and ![]() , respectively. Calls of service‐class 1 follow the routes AB and EA, calls of service‐class 2 follow the routes ABC, BCD, CD, DE, and DEA, calls of service‐class 3 follow the routes AB, ABC, BCD, DE, DEA, and EA, while calls of service‐class 4 follow the route CD. Calculate the CBP of all service‐classes in their routes, assuming the existence of the BR policy with BR parameters
, respectively. Calls of service‐class 1 follow the routes AB and EA, calls of service‐class 2 follow the routes ABC, BCD, CD, DE, and DEA, calls of service‐class 3 follow the routes AB, ABC, BCD, DE, DEA, and EA, while calls of service‐class 4 follow the route CD. Calculate the CBP of all service‐classes in their routes, assuming the existence of the BR policy with BR parameters ![]() , and
, and ![]() , and compare the analytical with simulation results.
, and compare the analytical with simulation results.

Figure 1.25 A ring network supporting service‐classes under the BR policy (Example 1.28).
For the analytical calculation of ![]() , we apply the Roberts method (see recursive formula ( 1.64)). Equations ( 1.97) and ( 1.98) remain unchanged, while ( 1.96) becomes:
, we apply the Roberts method (see recursive formula ( 1.64)). Equations ( 1.97) and ( 1.98) remain unchanged, while ( 1.96) becomes:

in order to take into account the BR parameters ![]() . Observe that
. Observe that ![]() , and therefore the CBP among the service‐classes are equalized.
, and therefore the CBP among the service‐classes are equalized.
In Table 1.1 we present the equalized CBP of all service‐classes for all routes. The differences between the analytical CBP results (obtained by the RLA method) and the simulation results (mean values of 12 runs with 95% confidence interval), are within an acceptable range for the call‐level network performance. The simulation language used is SIMSCRIPT III [23].
Table 1.1 Equalized CBP under the BR policy in the network of Figure 1.25.
| Route | Offered | RLA method | Simulation | Route | Offered | RLA method | Simulation |
| traffic (erl) | CBP (%) | CBP (%) | traffic (erl) | CBP (%) | CBP (%) | ||
| AB | 60.0 | 20.48 | 22.03 |
AB | 2.0 | 20.48 | 22.11 |
| ABC | 30.0 | 34.02 | 33.41 |
ABC | 2.0 | 34.02 | 33.04 |
| BCD | 30.0 | 36.68 | 36.89 |
BCD | 2.0 | 36.68 | 36.74 |
| CD | 30.0 | 23.69 | 26.92 |
CD | 1.0 | 23.69 | 27.12 |
| DE | 30.0 | 22.24 | 24.10 |
DE | 2.0 | 22.24 | 24.00 |
| DEA | 30.0 | 37.29 | 37.60 |
DEA | 2.0 | 37.29 | 38.14 |
| EA | 60.0 | 19.36 | 20.11 |
EA | 2.0 | 19.36 | 20.35 |
1.6 Applications
1.6.1 The Erlang‐B Formula
Although the Erlang loss model is now obsolete, since it is applicable to single service‐class systems only, it is still useful when a network operator wants to guarantee a specific QoS for a service (of streaming traffic) and, to achieve it, reserves a certain amount of bandwidth, ![]() b.u. for this service (not recommended, because of no statistical multiplexing gain [24]). For the applicability of the Erlang‐B formula ( 1.22) when a call requires a service rate
b.u. for this service (not recommended, because of no statistical multiplexing gain [24]). For the applicability of the Erlang‐B formula ( 1.22) when a call requires a service rate ![]() b.u., we have to consider a system capacity of
b.u., we have to consider a system capacity of ![]() and traffic‐load
and traffic‐load ![]() :
: ![]() . Thus, we transform the system as if it were
. Thus, we transform the system as if it were ![]() . When the system capacity is a real number,
. When the system capacity is a real number, ![]() is determined through the gamma function
is determined through the gamma function ![]() [25]:
[25]:

1.6.2 The Erlang‐C Formula
For the Internet, more interesting is the case of the Erlang‐C formula (1.18). As has been investigated (e.g., [26], [27]), the Erlang‐C formula can provide an upper bound of the congestion probability in a lightly loaded link of the Internet with ![]() b.u., when a max–min fairness policy is applied among traffic flows sharing the link (see [28] and [29]). Assume that we can distinguish
b.u., when a max–min fairness policy is applied among traffic flows sharing the link (see [28] and [29]). Assume that we can distinguish ![]() different peak rates
different peak rates ![]() (in increasing order) among the flows traversing the link. Let
(in increasing order) among the flows traversing the link. Let ![]() be the offered traffic‐load of flows which corresponds to peak rate
be the offered traffic‐load of flows which corresponds to peak rate ![]() ; then, the overall traffic‐load is
; then, the overall traffic‐load is ![]() (for a steady state).13 If
(for a steady state).13 If ![]() is the number of active flows (calls) with peak rate
is the number of active flows (calls) with peak rate ![]() , then congestion occurs when
, then congestion occurs when ![]() . In this case, when a fair rate
. In this case, when a fair rate ![]() is determined based on the max–min fairness policy, flows of higher rates (say, all flows with peak rates from
is determined based on the max–min fairness policy, flows of higher rates (say, all flows with peak rates from ![]() to
to ![]() ,
, ![]() ) must reduce their bandwidth to the fair rate
) must reduce their bandwidth to the fair rate ![]() (so that
(so that ![]() ) in order for the total rate to satisfy the link bandwidth capacity
) in order for the total rate to satisfy the link bandwidth capacity ![]() . The proportion of time where any active flow of rate
. The proportion of time where any active flow of rate ![]() would suffer loss or has to reduce its bandwidth should be less than a targeted value (i.e., the GoS); this proportion of time is defined as the rate‐
would suffer loss or has to reduce its bandwidth should be less than a targeted value (i.e., the GoS); this proportion of time is defined as the rate‐![]() congestion probability14 [ 26]:
congestion probability14 [ 26]:

Equivalently, the rate‐![]() congestion probability is the probability that the max–min fair rate
congestion probability is the probability that the max–min fair rate ![]() is less than
is less than ![]() (because
(because ![]() is determined so that the system capacity
is determined so that the system capacity ![]() is not violated). This probability increases when all higher peak rates are reduced to
is not violated). This probability increases when all higher peak rates are reduced to ![]() (or all lower peak rates increase to
(or all lower peak rates increase to ![]() ), while keeping constant the overall traffic‐load
), while keeping constant the overall traffic‐load ![]() . When the peak rates of higher peak rates are reduced to
. When the peak rates of higher peak rates are reduced to ![]() , the number
, the number ![]() of flows increases to
of flows increases to ![]() (suppose for all
(suppose for all ![]() ), so that the overall traffic‐load remains constant. Thus, the corresponding probability of rate‐
), so that the overall traffic‐load remains constant. Thus, the corresponding probability of rate‐![]() congestion also increases:
congestion also increases:

Intuitively, the max–min fair rate of the original system cannot be less than that of the new system (since ![]() and higher peak rates have been reduced in the new system).
and higher peak rates have been reduced in the new system).
The worst case of the distribution of the peak rates in the link for the rate‐![]() congestion probability under the max–min fair policy is the case where all flows have an equal peak rate
congestion probability under the max–min fair policy is the case where all flows have an equal peak rate ![]() . In that case, the rate‐
. In that case, the rate‐![]() congestion probability cannot be increased since the max‐min fair rate cannot be reduced, and therefore it becomes an upper bound of the congestion probability. The total number of flows
congestion probability cannot be increased since the max‐min fair rate cannot be reduced, and therefore it becomes an upper bound of the congestion probability. The total number of flows ![]() (each flow with the same peak rate
(each flow with the same peak rate ![]() bps) offering a total traffic‐load
bps) offering a total traffic‐load ![]() in the link of capacity
in the link of capacity ![]() (bps) resembles a FIFO queuing system with no loss (if it is lightly loaded), and thus can be modeled as
(bps) resembles a FIFO queuing system with no loss (if it is lightly loaded), and thus can be modeled as ![]() . Specifically, if
. Specifically, if ![]() is an integer and
is an integer and ![]() , then the probability of congestion (i.e., the proportion of time where
, then the probability of congestion (i.e., the proportion of time where ![]() ) is given by the Erlang‐C formula ( 1.18) when the system capacity is
) is given by the Erlang‐C formula ( 1.18) when the system capacity is ![]() and the offered traffic‐load is
and the offered traffic‐load is ![]() . Thus, we have:
. Thus, we have:

The applicability of the Erlang‐C formula in the Internet fits well to the IntServ resource (bandwidth) allocation strategy, but not to the DiffServ strategy (see Section I.14). Max–min fairness can be implemented through TCP congestion control.
1.6.3 The Kaufman–Roberts Recursion
Applications of the EMLM (Kaufman–Roberts recursive formula ( 1.39)) in contemporary communications networks are numerous. Its applicability to integrated services digital networks (ISDN) or global system for mobile (GSM) communications networks is straightforward and there is no need for additional explanation.
In optical networks of wavelength division multiplexing (WDM) technology, each fiber supports multiple communication channels, each one operating at a different wavelength. In view of the fact that only a small number of network users necessitate the entire bandwidth of the channel (e.g., up to ![]() bps data rate), the network mostly supports traffic demands with data rates significantly lower than the full wavelength capacity. Therefore, the channel bandwidth is divided into lower sub‐rate units (called traffic grooming), while traffic streams use one or multiple of these units, i.e., b.u. Considering a single link and a certain capacity (in b.u.) in each wavelength of the link supporting several service‐classes, the application of ( 1.39) for the calculation of the occupancy distribution of each separate wavelength is also straightforward under the Poisson traffic assumption [30].
bps data rate), the network mostly supports traffic demands with data rates significantly lower than the full wavelength capacity. Therefore, the channel bandwidth is divided into lower sub‐rate units (called traffic grooming), while traffic streams use one or multiple of these units, i.e., b.u. Considering a single link and a certain capacity (in b.u.) in each wavelength of the link supporting several service‐classes, the application of ( 1.39) for the calculation of the occupancy distribution of each separate wavelength is also straightforward under the Poisson traffic assumption [30].
Let us concentrate now on wideband code division multiple access (WCDMA) wireless networks like the Universal Mobile Telecommunication System (UMTS) in Europe [31]. In a WCDMA cell, all users transmit in the same frequency band by using (pseudo) orthogonal codes to have their signals separated. The basic idea is that a user considers interference (noise) all other signals of all other users. The interference increases as the number of users increases, whereas the cell capacity of the uplink decreases; thus, the applicability of the EMLM is not straightforward but possible. We need to interpret the several sources of noise in terms of the EMLM (see also Section 2.11). The maximum cell load (![]() ) can be seen as the system capacity
) can be seen as the system capacity ![]() , while the required bandwidth per call
, while the required bandwidth per call ![]() corresponds to the occupied cell's resources per call/user (load factor,
corresponds to the occupied cell's resources per call/user (load factor, ![]() ). The latter is determined by the bit‐error‐rate (BER) parameter,
). The latter is determined by the bit‐error‐rate (BER) parameter, ![]() 15 and the transmission bit rate
15 and the transmission bit rate ![]() of the corresponding mobile station
of the corresponding mobile station ![]() [32], [33]:
[32], [33]:

where ![]() is the chip rate of the WCDMA carrier.16
is the chip rate of the WCDMA carrier.16
Since discretization is necessary to apply ( 1.39), this is achieved through the introduction of a cell load unit ![]() :
: ![]() ,
, ![]() . The
. The ![]() controls the granularity of the state space of the system, which increases as
controls the granularity of the state space of the system, which increases as ![]() decreases. On the other hand, the smaller the
decreases. On the other hand, the smaller the ![]() , the better the analytical results (CBP on the uplink) we obtain. For a thorough study, several other parameters (such as local blocking (expressing the fact that a call may be blocked due to noise even if the cell accommodates a very few number of users), user activity, interference from other cells) must be incorporated in the EMLM for WCDMA networks [ 32]. Having understood the applicability of the EMLM to WCDMA systems, then it can readily be applied to more complex systems like the one presented in [34].
, the better the analytical results (CBP on the uplink) we obtain. For a thorough study, several other parameters (such as local blocking (expressing the fact that a call may be blocked due to noise even if the cell accommodates a very few number of users), user activity, interference from other cells) must be incorporated in the EMLM for WCDMA networks [ 32]. Having understood the applicability of the EMLM to WCDMA systems, then it can readily be applied to more complex systems like the one presented in [34].
We concentrate now on the downlink of an orthogonal frequency division multiplexing (OFDM)‐based cell that services calls from different service‐classes with different traffic description parameters and consequently different QoS requirements. The cell has ![]() subcarriers and let
subcarriers and let ![]() and
and ![]() be the average data rate per subcarrier, the available power in the cell and the system's bandwidth, respectively. Let the entire range of channel gains or signal‐to‐noise ratios per unit power be partitioned into
be the average data rate per subcarrier, the available power in the cell and the system's bandwidth, respectively. Let the entire range of channel gains or signal‐to‐noise ratios per unit power be partitioned into ![]() consecutive (but non‐overlapping) intervals and denoted as
consecutive (but non‐overlapping) intervals and denoted as ![]() the average channel gain of the
the average channel gain of the ![]() interval. Considering
interval. Considering ![]() subcarrier requirements and
subcarrier requirements and ![]() average channel gains, there are
average channel gains, there are ![]() service‐classes. A newly arriving service‐class
service‐classes. A newly arriving service‐class ![]() call
call ![]() requires
requires ![]() subcarriers in order to be accepted in the cell (i.e., the call has a data rate requirement
subcarriers in order to be accepted in the cell (i.e., the call has a data rate requirement ![]() ) and has an average channel gain
) and has an average channel gain ![]() . If these subcarriers are not available, the call is blocked and lost. Otherwise, the call remains in the cell for a generally distributed service time with mean
. If these subcarriers are not available, the call is blocked and lost. Otherwise, the call remains in the cell for a generally distributed service time with mean ![]() . To calculate the power
. To calculate the power ![]() required to achieve the data rate
required to achieve the data rate ![]() of a subcarrier assigned to a call whose average channel gain is
of a subcarrier assigned to a call whose average channel gain is ![]() , we use the Hartley–Shannon theorem:
, we use the Hartley–Shannon theorem: ![]() . Assuming that calls follow a Poisson process with rate
. Assuming that calls follow a Poisson process with rate ![]() and that
and that ![]() is the number of in‐service calls of service‐class
is the number of in‐service calls of service‐class ![]() , then the system can be described as a multirate loss model with a PFS for the steady state probabilities
, then the system can be described as a multirate loss model with a PFS for the steady state probabilities ![]() [35]:
[35]:

where ![]() ,
, ![]() is the state space of the system,
is the state space of the system, ![]() is the normalization constant, and
is the normalization constant, and ![]() is the offered traffic‐load (in erl) of service‐class
is the offered traffic‐load (in erl) of service‐class ![]() calls.
calls.
Note that the derivation of (1.108) requires that ![]() and
and ![]() are integers (which is generally not true). In order to have an equivalent representation of the constraint
are integers (which is generally not true). In order to have an equivalent representation of the constraint ![]() , we multiply both sides of this expression by a constant to get
, we multiply both sides of this expression by a constant to get ![]() , where
, where ![]() and
and ![]() are integers [ 35]. Thus, without loss of generality, we assume that
are integers [ 35]. Thus, without loss of generality, we assume that ![]() and
and ![]() are integers. Now, let
are integers. Now, let ![]() (i.e.,
(i.e., ![]() ) be the occupied subcarriers and
) be the occupied subcarriers and ![]() (i.e.,
(i.e., ![]() ) the occupied power in the cell. Then, it is proved in [36] that there exists a recursive formula, which resembles the Kaufman–Roberts recursion, for the determination of
) the occupied power in the cell. Then, it is proved in [36] that there exists a recursive formula, which resembles the Kaufman–Roberts recursion, for the determination of ![]() and consequently all performance measures.
and consequently all performance measures.
Finally, it is worth mentioning a remarkable application of the EMLM on smart grid, which is an example showing the wide applicability range of the model. To control energy consumption, all appliances are connected to a central controller. Each appliance has a power demand (in power units), while the appliances are distinguished into different types according to the demand. For a specific type of appliance, the power demand arrival processes (to the controller) can be assumed Poisson. The controller activates each power demand request upon arrival, if it is possible, given that the total amount of power (capacity in total power units) that can be distributed to the appliances is limited. Each appliance operates for an operating time (depending on its type), which is generally distributed. Assuming that the amounts of power can be discretized, the analogy between a communication link and the smart grid case becomes obvious: the total amount of power corresponds to the link bandwidth capacity, the various types of appliances to service‐ classes, the power demand of a specific appliance to the required bandwidth per service‐class call, the arrival process for power request to the call arrival process, and the operating time of appliances to the service time of calls. In this way, the probability distribution of the total power units devoted to the appliances can be determined through the EMLM. Alternatively, the EMLM can be used as a tool to calculate the total amount of power needed for guaranteeing power demands under a specific GoS per type of appliances [37].
1.7 Further Reading
There is a vast number of papers related to extensions and applications of the models presented in this chapter. In this section we present only an indicative list of papers for further reading in various directions.
Although we would like to focus on works beyond the Erlang‐B formula, it would be an omission if we did not mention several extensions of the Erlang‐B formula in wireless ([38], [39]), optical ([40], [41]), and satellite networks [42] that have emerged in recent years. In [ 38], a multi‐cell mobility model for cellular networks is considered and a two‐dimensional Erlang loss model is proposed for the determination of loss probabilities. In [ 39], the Erlang‐B formula has been adopted in order to provide approximate CBP in a two WiFi access link system in which the two links share their bandwidth. In [ 40], an analytical model is proposed for the determination of burst blocking probabilities in optical burst switching (OBS) networks. The model extends the Erlang‐B formula by considering multiple priority classes and the notion of preemption. In [ 41], an analytical model, based on the Erlang fixed point approximation, is proposed for the approximate network‐wide blocking probability determination in any cast routing and wavelength assignment optical WDM networks. In [ 42], a fixed point approximation method is proposed for the CBP calculation in a low earth orbit (LEO) satellite network. The CBP calculation uses the Erlang‐B formula, but the offered traffic‐load is modified in order to take into account the time and location in which the calls are made.
Many remarkable extensions of the EMLM in wired ([43–57]), wireless ([58–66]), optical ([67–69]), and satellite networks ([70–72]) have been published. In [ 43], a recursive formula is proposed for the determination of the link occupancy distribution in a link that accommodates Bernoulli–Poisson–Pascal (BPP) traffic. In [44] and [45], and [46] and [47], the EMLM is extended to handle unicast/multicast connections in a single link and a network, respectively. In [48–51] and [52], CBP derivatives with respect to offered traffic‐load, arrival rate or service rate are studied in the EMLM and in the EMLM/BR, respectively. CBP derivatives are significant in multirate loss systems since they enable the study of the interaction between different service‐classes that share the same link. In [53–56], the EMLM is extended to handle overflow traffic, i.e., traffic that is lost in a primary link and is routed to a secondary link. In [ 57], a recent review on loss networks is presented. In [ 58], the EMLM/BR is extended to include a reservation policy in which the reserved b.u. can have a real (not integer) value. In [59], an EMLM‐ based model is proposed for the CBP determination in the X2 interface that interconnects neighboring eNBs in a LTE network. In [60] and [61], the EMLM is applied to the CBP calculation in the downlink of orthogonal frequency division multiple access cellular networks. In [62], an EMLM‐based model is proposed for the CBP calculation in a multicast 3G network. The authors of [63] investigated strategies for active sharing of radio access among multiple operators, assuming the existence of Cloud‐RAN. For their analysis a BPP multirate loss model is considered. In [64], the EMLM is used in the call‐ level analysis of the access part of a 3G mobile network that incorporates priorities between calls of different service‐classes. In [65], a probabilistic threshold policy is proposed that extends the EMLM/TH. In [ 66], the two WiFi access link system of [ 39] (which accommodates a single service‐class) has been extended to include the case of multiple service‐classes. In [ 67], EMLM‐based models are proposed for calculating connection failure probabilities (due to unavailability of a wavelength) and CBP (due to the restricted bandwidth capacity of a wavelength) in hybrid TDM‐WDM passive optical networks with dynamic wavelength allocation (DWA). In [68], an analytical methodology for computing approximate blocking probabilities in multirate optical WDM networks is proposed which is based on the EMLM and the RLA. In [ 69], the EMLM is applied in elastic optical networks. Based on the EMLM, an analytical framework is proposed for evaluating the performance of the CS and the fixed channel reservation policies [ 70] as well as the complete partitioning and the threshold call admission policies [71] that are applied in LEO mobile satellite systems. An extension of [ 70] and [ 71] that includes efficient formulas for various performance measures (including CBP and handover failure probabilities) has been proposed in [ 72].
References
- 1 B. Sevastyanov, An ergodic theorem for Markov processes and its application to telephone systems with refusals. Theory of Probability & Its Applications, 2(1): 104–112, 1957.
- 2 L. Takacs, On Erlang's Formula. The Annals of Mathematical Statistics, 40(1): 71–78, 1969.
- 3 P. Taylor, Insensitivity in Stochastic Models, Chapter 3 in Queueing Networks: A Fundamental Approach, N. van Dijk and R. J. Boucherie (eds.), Springer‐Verlag, pp. 121–140, 2011.
- 4 A. Harel, Sharp and simple bounds for the Erlang delay and loss formulae. Queueing Systems, 64(2):119–143, February 2010.
- 5 J. Kaufman, Blocking in a shared resource environment. IEEE Transactions on Communications, 29(10): 1474–1481, October 1981.
- 6 M. Schwartz and B. Kraimeche, An analytic control codel for an integrated node. Proceedings of the IEEE Infocom, pp. 540–545, 1983.
- 7 V. Iversen, The exact evaluation of multi‐service loss system with access control. Teleteknik [English edn], 31(2): 56–61, 1987.
- 8 M. Glabowski, A. Kaliszan and M. Stasiak, Asymmetric convolution algorithm for blocking probability calculation in full‐availability group with bandwidth reservation. IET Circuits Devices & Systems, 2(1): 87–94, February 2008.
- 9 Q. Huang, K. Ko and V. Iversen, A new convolution algorithm for loss probability analysis in multiservice networks. Performance Evaluation, 68(1):76–87, January 2011.
- 10 S. Johnson, A performance analysis of integrated communications systems. British Telecom Technology Journal, 3(4): 36–45, 1985.
- 11 J. Roberts, Teletraffic models for the Telecom 1 Integrated Services Network. Proceedings of ITC‐10, Montreal, Canada, 1983.
- 12 M. Stasiak and M. Glabowski, A simple approximation of the link model with reservation by a one‐dimensional Markov chain. Performance Evaluation, 41(2–3):195–208, July 2000.
- 13 K. Ross, Multiservice Loss Models for Broadband Telecommunication Networks, Springer, Berlin, 1995.
- 14 D. Tsang and K. Ross, Algorithms to determine exact blocking probabilities for multirate tree networks. IEEE Transactions on Communications, 38(8):1266–1271, August 1990.
- 15 Z. Dziong and J. Roberts, Congestion probabilities in a circuit switched integrated services network. Performance Evaluation, 7(4):267–284, November 1987.
- 16 G. Awater and H. van de Vlag, Exact computation of time and call blocking probabilities in large, multi‐traffic, multi‐resource loss systems. Performance Evaluation, 25(1): 41–58, March 1996.
- 17 D. Bear, Principles of Telecommunication‐Traffic Engineering, Peter Peregrinus Ltd, 1976.
- 18 A. Girard, Routing and Dimensioning in Circuit Switched Networks, Addison Wesley, 1990.
- 19 W. Whitt, Blocking when service is required from several facilities simultaneously. AT&T Technical Journal, 64:1807–1856, 1985.
- 20 F. Kelly, Loss networks. Annals of Applied Probability, 1(3):319–378, August 1991.
- 21 S. Chung and K. Ross, Reduced load approximations for multirate loss networks. IEEE Transactions on Communications, 41(8):1222–1231, August 1993.
- 22 H. Wagner, Principles of Operations Research, Prentice‐Hall, 1969.
- 23 SIMSCRIPT III, http://www.simscript.com/.
- 24 H. Saito, Teletraffic Technologies in ATM Networks, Artech House, 1994.
- 25 H. Akimaru and K. Kawashima, Teletraffic – Theory and Applications, 2nd edn, Springer, Berlin, 1999.
- 26 T. Bonald and J. Roberts, Internet and the Erlang formula. ACM SIGCOMM Computer Communication Review, 42(1):23–30, January 2012.
- 27 V.B. Iversen, The Internet Erlang formula, in NEW2AN/ruSMART 2012, S. Andreev et al. (eds), LNCS 7469, pp. 328–337, Springer‐Verlag, Berlin, Heidelberg, 2012.
- 28 I. Moscholios and M. Logothetis, New algorithm for the generalized max–min fairness policy based on linear programming. IEICE Transactions on Communications, E88‐B(2):775–780, February 2005.
- 29 M. Logothetis, I. Moscholios and G. Kokkinakis, The generalized max–min fairness policy based on linear programming. Mediterranean Journal of Electronics and Communications, 2(1):1–10, 2006.
- 30 J.S. Vardakas, V.G. Vassilakis and M.D. Logothetis, Calculating blocking probabilities in single‐hop WDM traffic groomed optical networks. Proceedings of the International Conference on Transparent Optical Networks (ICTON 2007), Rome, 1–5 July, 2007.
- 31 H. Holma and A. Toskala (eds), WCDMA for UMTS, 5th edn, John Wiley & Sons Ltd, 2010.
- 32 D. Staehle and A. Mäder, An analytic approximation of the uplink capacity in a UMTS network with heterogeneous traffic. Proceedings of the 18th International Teletraffic Congress (ITC18), Berlin, September 2003.
- 33 M. Logothetis, V. Vassilakis and I. Moscholios, Call‐level performance modeling and QoS assessment of W‐CDMA networks, in Wireless Networks: Research, Technology and Applications, pp. 57–90, Nova Science Publishers, New York, 2009.
- 34 J.S. Vardakas, V.G. Vassilakis and M.D. Logothetis, Call‐level analysis of hybrid WDM‐OCDMA PONs. Proceedings of the International Conference on Transparent Optical Networks (ICTON 2008), Athens, Greece, June 22–26, 2008.
- 35 C. Paik and Y. Suh, Generalized queueing model for call blocking probability and resource utilization in OFDM wireless networks. IEEE Communication Letters, 15(7):767–769, July 2011.
- 36 I. Moscholios, V. Vassilakis, P. Panagoulias and M. Logothetis, On call blocking probabilities and resource utilization in OFDM wireless networks. Proceedings of the IEEE/IET CSNDSP, Budapest, Hungary, 18–20 July 2018.
- 37 J.S. Vardakas, N. Zorba and C.V. Verikoukis, Performance evaluation of power demand scheduling scenarios in a smart grid environment. Applied Energy, 142:164–178, March 2015.
- 38 K. Kim and H. Choi, A mobility model and performance analysis in wireless cellular network with general distribution and multi‐cell model. Wireless Personal Communications, 53(2):179–198, April 2010.
- 39 V. Burger, M. Seufert, T. Hossfeld and P. Tran‐Gia, Performance evaluation of backhaul bandwidth aggregation using a partial sharing scheme. Physical Communication, 19:135–144, June 2016.
- 40 G. Zeng, A review on a new conservation law in optical burst switching networks. Mathematical and Computer Modelling, 57(5–6):1504–1513, March 2013.
- 41 Y. Cui and V. Vokkarane, Analytical blocking model for anycast RWA in optical WDM networks. IEEE/OSA Journal of Optical Communications and Networking, 8(10):787–799, October 2016.
- 42 D. Yiltas and A. Zaim, Evaluation of call blocking probabilities in LEO satellite networks. International Journal of Satellite Communications and Networking, 27(2):103–115, March/April 2009.
- 43 L. Delbrouck, On the steady‐state distribution in a service facility carrying mixtures of traffic with different peakedness factors and capacity requirements. IEEE Transactions on Communications, 31(11):1209–1211, November 1983.
- 44 K. Boussetta and A. Beylot, Multirate resource sharing for unicast and multicast connections, in Broadband Communications – Convergence of Network Technologies, Volume 30 of the IFIP series, pp. 561–570, 2000.
- 45 I. Gudkova and O. Plaskina, Performance measures computation for a single link loss network with unicast and multicast traffics, in Lecture Notes in Computer Science, Volume 6294, Springer, Berlin, 2010.
- 46 K. Samouylov and N. Yarkina, Blocking probabilities in multiservice networks with unicast and multicast connections. Proceedings of the 8th International Conference on Telecommunications (ConTEL), Zagreb, Croatia, June 2005.
- 47 M. Glabowski, M. Stasiak and P. Zwierzykowski, Modeling of virtual‐circuit switching nodes with multicast connections. European Transactions on Communications, 20(2):123–137, March 2009.
- 48 J. Virtamo, Reciprocity of blocking probabilities in multiservice loss systems. IEEE Transactions on Communications, 36(10):1257–1260, October 1988.
- 49 S. Jordan and P. Varaiya, Throughput in multiple service multiple resource communications networks. IEEE Transactions on Communications, 39(8):1216–1222, August 1991.
- 50 C. Aswakul and J. Barria, Error analysis of multiservice single‐link system studies using linear approximation model. Proceedings of the IEEE ICC, Seoul, South Korea, May 2005.
- 51 V. Iversen and S. Stepanov,Derivatives of blocking probabilities for multi‐service loss systems and their applications, in Lecture Notes in Computer Science, Volume 4712, Springer, Berlin, 2007.
- 52 I. Moscholios, J. Vardakas, M. Logothetis and A. Boucouvalas, New algorithms for performance measures derivatives in the Erlang multirate loss model including the bandwidth reservation policy. Mediterranean Journal of Computers and Networks, 7(4):304–316, October 2011.
- 53 Q. Huang, K. Ko and V. Iversen, Approximation of loss calculation for hierarchical networks with multiservice overflows. IEEE Transactions on Communications, 56(3):466–473, March 2008.
- 54 M. Glabowski, K. Kubasik and M. Stasiak, Modeling of systems with overflow multi‐rate traffic. Telecommunication Systems, 37(1–3):85–96, March 2008.
- 55 M. Glabowski, S. Hanczewski, and M. Stasiak, Modelling of cellular networks with traffic overflow. Mathematical Problems in Engineering, article ID 286490, 15 pp, 2015, doi: 10.1155/2015/286490.
- 56 M. Glabowski, A. Kaliszan and M. Stasiak, Modelling overflow systems with distributed secondary resources. Computer Networks, 108:171–183, October 2016.
- 57 S. Zachary and I. Ziedins, Loss networks, in Queueing Networks: A fundamental approach, R. Boucherie and N. van Dijk (eds), pp. 701–728, Springer, Berlin, 2011.
- 58 F. Cruz‐Pérez, J. Vázquez‐Ávila and L. Ortigoza‐Guerrero, Recurrent formulas for the multiple fractional channel reservation strategy in multiservice mobile cellular networks. IEEE Communication Letters, 8(10): 629–631, October 2004.
- 59 I. Widjaja and H. La Roche, Sizing X2 bandwidth for inter‐connected eNBs. Proceedings of the IEEE Vehicle Technology Conference, Fall, Anchorage, USA, September, 2009.
- 60 B. Blaszczyszyn and M. Karray, Dimensioning of the downlink in OFDMA cellular networks via an Erlang's loss model. Proceedings of the European Wireless Conference, Aalborg, Denmark, May 2009.
- 61 M. Karray, Analytical evaluation of QoS in the downlink of OFDMA wireless cellular networks serving streaming and elastic traffic. IEEE Transactions on Wireless Communications, 9(5):1799–1807, May 2010.
- 62 D. Parniewicz, M. Stasiak and P. Zwierzykowski, Traffic engineering for multicast connections in multiservice cellular networks. IEEE Transactions on Industrial Informatics, 9(1):262–270, February 2013.
- 63 A. Avramova and V. Iversen, Radio access sharing strategies for multiple operators in cellular networks. IEEE ICC Workshop on 5G & Beyond,London, UK, June 2015.
- 64 S. Hanczewski, M. Stasiak and P. Zwierzykowski, Modelling of the access part of a multi‐service mobile network with service priorities. Eurasip Journal on Wireless Communications and Networking, 2015:194, December 2015, doi: 10.1186/s13638‐015‐0420‐4.
- 65 I. Moscholios, V. Vassilakis, M. Logothetis and A. Boucouvalas, A probabilistic threshold‐based bandwidth sharing policy for wireless multirate loss networks. IEEE Wireless Communication Letters, 5(3):304–307, June 2016.
- 66 S. Sagkriotis, S. Pantelis, I. Moscholios and V. Vassilakis, Call blocking probabilities in a two‐link multi rate loss system for Poisson traffic, IET Networks, 7(4):233–241, July 2018.
- 67 J. Vardakas, V. Vassilakis and M. Logothetis, Blocking analysis in hybrid TDM‐WDM passive optical networks. Proceedings of the 5th HET‐NETs, Karlskrona, Sweden, February 2008.
- 68 K. Kuppuswamy and D. Lee, An analytical approach to efficiently computing call blocking probabilities for multiclass WDM networks. IEEE/ACM Transactions on Networking, 17(2):658–670, April 2009.
- 69 H. Beyranvand, M. Maier and J. Salehi, An analytical framework for the performance evaluation of node‐and network‐wise operation scenarios in elastic optical networks. IEEE Transactions on Communications, 62(5):1621–1633, May 2014.
- 70 Z. Wang, P.T. Mathiopoulos and R. Schober, Performance analysis and improvement methods for channel resource management strategies of LEO‐MSS with multiparty traffic. IEEE Transactions on Vehicle Technology, 57(6):3832–3842, November 2008.
- 71 Z. Wang, P.T. Mathiopoulos and R. Schober, Channeling partitioning policies for multi‐class traffic in LEO‐MSS. IEEE Transactions on Aerospace and Electronic Systems, 45(4):1320–1334, October 2009.
- 72 I. Moscholios, V. Vassilakis, N. Sagias and M. Logothetis, On channel sharing policies in LEO mobile satellite systems. IEEE Transactions on Aerospace and Electronic Systems, 54(4):1628–1640, August 2018.
