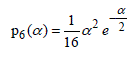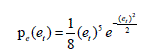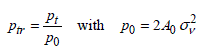Appendix 3

Total Field and Total Power Variables

This appendix includes the calculations of the probability density functions and the moments of the total field and power variables. By total variables, we mean the fields or the powers measured by probes or antennas, which simultaneously collects the three E_x, E_y, E_z complex field projections.

A3.1. Total field variables

The total field variable taking E_t as a notation is given by the square root of the sum of six terms made up of all the square complex components of each E_{x y z}projection i.e.:

[A3.1]

The normalized variable of the total field is designated for the occasion by the lower case e_t notation. This variable comes from the extension of the definition introduced in section 3.2.3:

[A3.2]

We find in this formula the standard deviation σ_ν, which is attached to the complex components of E_{x y z}.

A3.2. χ² variable attached to the total field

Knowing that the E_{x y z} variables all follow the normal probability distribution,the square amplitude of the normalized total e_t field will be the χ² variable with six degrees of freedom:

[A3.3]

We can thus add to this variable, the pdf of χ², which is expressed by the notation conventions of formulas[3.23] and [3.24].

Hence:

[A3.4]

After use of simplified notations and insertion of the numerical value of Γ(3),this equation takes the final form:

[A3.5]

A3.3. Total field probability density function

A3.3.1. The pdf related to the total “e_t” normalized field variable

The pdf brought back to the normalized variable of the total field e_t relates to the p_e(e_t) notation.

Under the previous notation, taking the derivate of p₆(α) and convert the resultdp in respect of the normalized field e_t variables, we obtain a new equation in order to determine p_e(e_t).

[A3.6]

After insertion of function [A3.5] then immediately gives access to p_e(e_t), i.e.:

[A3.7]

A3.3.2. The pdf related to the absolute amplitude of the total field “E_t”

Using the change of variable suggested in [A3.2] and after insertion into [A3.6],we reach the p_E(E_t) function giving the pdf of the total field where the absolute amplitude E_t of the total field projections appears.

[A3.8]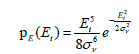

We will notice the use of simplified exponents notations in place of (E_t)⁵ and(E_t)².

A3.4. Calculation of the mean of the total field

A3.4.1. Mean of the normalized “e_t” amplitude

By using the suitable notation, the mean amplitude of the normalized total field variable will be determined by the calculation of the moment of e_t, i.e.:

[A3.9]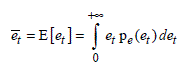

After insertion of function [A3.7] and solving the integral analytically, we reach the numerical value of . i.e.:

[A3.10]

A3.4.2. Mean of the absolute “E_t” amplitude

From the previous equation and from the change of variable [A3.2], we take :

[A3.11]

A3.5. The pdf of the total power

A3.5.1. Variables of total power “p_t” variable

The total power variable taking the symbol p_t is the extension of the definition of the power found in equation [3.33] where the term |E_x,y,z|² is replaced by (E_t)² with the E_t variable previously introduced, hence:

[A3.12]

We find in equation [A3.12] the coefficient of physical scale A₀.

A3.5.2. Computation of the pdf related to the total power

The pdf of the total power taking the notation p₆(p_t) comes from algebraic computations linking the variable α, which is defined in [A2.4], to the variable p_t:

[A3.13]

Using the derivate form of [A3.5], we reach the sought after relationships:

[A3.14]

After insertion of function [A3.5], we take the pdf of p_t:

[A3.15]

A3.5.3. The pdf of the normalized total power variable “p_tr”

The establishment of the previous equation suggests adopting as the definition of the total reduced power, the ratio of p_t with the p₀ parameter defined below:

[A3.16]

A3.5.4. Computation of the pdf of the total normalized power

The probability density function of the total normalized power using the notation p₆(p_tr), is easily deduced from equation [A3.15] after a few simple transformations:

[A3.17]

We establish the pdf of the total normalized power, i.e.:

[A3.18]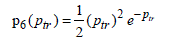

A3.6. Calculation of the mean total powers

A3.6.1. Mean of the total normalized power “p_tr”

The mean of the total normalized power, taking the symbol , comes from the calculation of the moment of p_tr as found below:

[A3.19]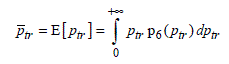

After solving the integral, we obtain:

[A3.20]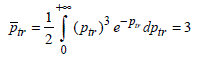

A3.6.2. Mean of the total power “p_t”

By using equation [A3.16], we easily find the mean of the total power:

[A3.21]

We will notice that the obtained numerical value is exactly similar to three times the p_mv mean power, which is determined on an electric field component. A comparison of this result to formulas [3.32] and [A3.11] shows that the ratio of the mean powers is indeed different from the ratio of the square roots of the mean fields:

[A3.22]

The result shows that the ratio of the moment of the total power p_t over the mean power of one field projection p_mv is not similar to the square of the ratio of the mean value of the absolute total field E_t over the moment of one E_x,y,z projection. Taking the square root of the previous [A3.22] equation then leads to:

[A3.23]