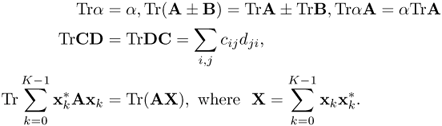Appendix A

Matrix Analysis

A.1 Vector Spaces and Hilbert Space

Finite-dimensional random vectors are the basic building blocks of many applications. Halmos (1958) [1472] is the standard reference. We just take the most elementary material from him.

These axioms are not claimed to be logically independent.

Example A.1

1. Let be the set of all complex numbers; If we regard x + y and αx as ordinary complex numerical addition and multiplication, becomes a complex vector space.

2. Let be the set of all n-tuples of complex numbers. If

are elements of we write, by definition,

is a vector space since all parts of our axioms are satisfied; it will be called n-dimensional complex coordinate space.

---

Definition A.2 (Linear dependence and linear independence

A finite set x_i of vectors is linear dependent if there exists a corresponding set α_i of scalars, not all zero, such that

If, on the other hand, implies that α_i for each i, the set x_i is linearly independent.

---

Recall that the basic building block in “Big Data” is a random vector which is defined in a finite-dimensional vector space. The dimension is high but still finite-dimensional. The high-dimensional data processing is critical to many modern applications.

Definition A.4 (Isomorphism)

Two vector spaces and (over the same field) are isomorphic, if there is a one-to-one correspondence between the vectors x of and the vectors y of , say y = T(x), such that

In other words, and are isomorphic if there is an isomorphism (such as T) between them, where an isomorphism is a one-to-one correspondence that preserves all linear relations.

---

Theorem A.4 (Isomorphic)

Every n-dimensional vector space Ω over a field is isomorphic to

---

If y₁ and y₂ are linear functions on Ω and α₁ and α₂ are scalars, let us define the function by

It is easy to check that y is also a linear functional; we denote it by α₁y₁ + α₂y₂. With these definitions of the linear concepts (zero, addition, scalar multiplication), the set Ω′ forms a vector space, the dual space of Ω.

A.2 Transformations

Linear transformations can be regarded as vectors.

Definition A.8 (Matrices)

Let Ω be an n-dimensional vector space, let be any basis of Ω, and let A be a linear transformation on Ω. Since every vector is a linear combination of the x_i, we have in particular

The set α_ij of n² scalars, indexed with the double subscript i, j, is the matrix of A in the coordinate system A matrix (α_ij) is usually written in the form of a square array:

the scalars (α_i1, ···, α_in) form a column; (α_1j, ···, α_nj) form a row, of A.

---

A.3 Trace

The trace function, TrA = ∑_ia_ii, satisfies the following properties [110] for matrices A, B, C, D, X and scalar α:

A.1

To prove the last property, note that since is a scalar, the left side of (A.1) is

A.4 Basics of C*-Algebra

C*-algebras (pronounced “C-star”) are an important area of research in functional analysis. The prototypical example of a C*-algebra is a complex algebra of linear operators on a complex Hilbert space with two additional properties:

1. is a topologically closed set in the norm topology of operators.

2. is closed under the operation of taking adjoints of operators.

C*-algebras [138, 1473] are now an important tool in the theory of unitary representations of locally compact groups, and are also used in algebraic formulations of quantum mechanics. Another active area of research is the program to obtain classification, or to determine the extent of which classification is possible. It is through the latter area that its connection with our interest in hypothesis detection is made.

A.5 Noncommunicative Matrix-Valued Random Variables

We mainly follow [11] this section, but with different notations that are convenient for our context. Random variables are functions defined on a measure space, and they are often identified by their distributions in probability theory [11]. In the simplest case when the random variables are real valued, the distribution is a probability measure on the real line. In this appendix probability distributions can be represented by means of linear Hilbert space operators, as well. (In this appendix an operator is an infinite-dimensional matrix.) This observation is as old as quantum mechanics; the standard probabilistic interpretation of the quantum mechanical formalism is related.

In an algebraic generalization, elements of a typically noncommutative algebra together with a linear functional on the algebra are regarded as noncommutative random variables. The linear functional evaluated on this element is the expectation value, its use to powers of this selected element leads to the moments of the noncommunicative random variables. One does not distinguish between two random variables, when they have the same moments. A very new feature of this theory occurs when these noncommunicative random variables are truly noncommuting with each other. Then, one cannot have a joint distribution in the sense of classical probability theory, but a functional of the algebra of polynomials of noncommuting indeterminates may work as an abstract concept of joint distribution [11]. Random matrices with respect to the expectation of their trace are natural “noncommuniting” noncommutative (matrix-valued) random variables.

Random variables over a probability space form an algebra. Indeed, they are measurable functions defined on a set Ω, and so are the product and sum of two of them, that is, A B and A + B. As mentioned before, the expectation value is a linear functional on this algebra. The algebraic approach to probability stresses this point. An algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it is an algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as an algebra, this multiplication must satisfy certain compatibility axioms with the given vector space structure, such as distributivity. In other words, an algebra over a field is a set together with operations of multiplication, addition, and scalar multiplication by elements of the field [1474].

If is a unital algebra (a vector space defined above) over the complex numbers and ϕ is a linear functional of such that

then will be called a noncommutative probability space and an element A of will be called a noncommunicative random variable. of course, a random matrix is such a noncommunitative random variable. The number ϕ(A^k) is called the n-th moment of a noncommutative random variable.

Example A.2 (Bounded operators [11])

Let denote the algebra of all bounded operators acting on a Hilbert space . If the linear functional is defined by means of a unit vector as

then any element of is a noncommunitative random variable.

---

If is, further, self-adjoint (or Hermitian for the finite-dimensional case), then a probability measure is associated to A and φ, as mentioned above. The algebra used in the definition of a noncommunitative random variable is often replaced with a *-algebra. In fact, is a *-algebra, if the operation A* stands for the adjoint of A. The most familiar example of a *-algebra is the field of complex numbers C where * is just complex conjugation. Another example is the matrix algebra of n × n matrices over C with * given by the conjugate transpose. Its generalization, the Hermitian adjoint of a linear operator on a Hilbert space is also a *-algebra (or star-algebra).

A *-algebra is a unital algebra over the complex numbers which is equipped with an involution*. The revolution recalls the adjoint operation of Hilbert space operators as follows:

1. is conjugate linear.

2. (AB)* = (BA)*,

3. A** = A.

When is a noncommunitative probability space over a *-algebra ϕ is always assumed to be a state on that is, a linear function such that

1. φ(1) = 1,

2. and φ(A*A) ≥ 0 for every

A matrix X whose entries are (classical) random variables on a (classical) probability space is called a random matrix, such as a sample covariance matrix XX^H. Here H stands for the conjugate and transpose (Hermitian) of a complex matrix.

Random matrices form a *-algebra. For example, consider X₁₁, X₁₂, X₂₁, X₂₂ to be four bounded (classical) scalar random variables on a probability space. Then

is a bounded 2 × 2 random matrix. The set X of all such matrices has a *-algebra structure when the unit matrix operations are considered, and is a noncommunitative probability space when, for example,

A C*-algebra is a *-algebra which is endowed with a norm such that

and furthermore, is a Banach space with respect to this norm.

Gelfand and Naimark give two important theorems concerning the representation of C*-algebras.

Combination of the above two theorems yields a form of the spectral theorem. For a linear functional φ of a C*-algebra,

is equivalent to

A noncommunitative probability space will be called a C*-probability space when is a C*-algebra and φ is a state on .

All real bounded classical scalar random variables may be considered as noncommunicative random variables.

A.6 Distances and Projections

For projections, we freely use [1475]. Let denote the algebra of linear operators acting on a finite-dimensional Hilbert space . The von Neumann entropy of a state ρ, i.e. that is, a positive operator of unit trace in , is given by S(ρ) = − Trρlogρ.

For , the absolute value |A| is defined as and it is a positive matrix. The trace norm of A − B is defined as

This trace norm||A − B||₁ is a nature distance between complex n × n matrices A and B, . Similarly,

is also a natural distance. We can define the p-norm as

It was Von Neumann who showed first that the Hoelder inequality remains true in the matrix setting

If A is a self-adjoint and written as

where the vector e_i form an orthonormal basis, then it is defined as

Then A = {A ≥ 0} + {A < 0} = A₊ + A₋ and |A| = {A ≥ 0} − {A < 0} = A₊ − A₋. The decomposition is called the Jordan decomposition of A. Corresponding definitions apply for the other spectral projections {A < 0}, {A > 0}, and {A ≤ 0}. For two operators, {A < B}, {A > B}, and {A ≤ B}.

For self-adjoint operators A, B and any positive operator 0 ≤ P ≤ I we have

Identical conditions hold for strict inequalities in the spectral projections {A < B} and {A > B}.

The trace distance between operators A and B is given by

The fidelity of states ρ and ρ′ is defined as

The trace distance between two states is related to the fidelity as follows:

For self-adjoint operators A, B and any positive operator 0 ≤ P ≤ I, the inequality

for any > 0, implies that

The “gentle measurement” lemma is given here: For a state ρ and any positive operator 0 ≤ P ≤ I, if Tr(ρP) ≥ 1 − δ, then

The same holds if ρ is only a subnormalized density operator, that is, Trρ ≤ 1.

If ρ is a state and P is a projection operator such that Tr(Pρ) > 1 − δ for a given δ > 0, then

where

and .

Consider a state ρ and a positive operator σ ∈ B^ε(ρ), for some > 0. If π_σ denote the projection onto the support of σ, then

Lemma A.1 (Hoffman-Wielandt)

[16, 34] Let A and B be N × N self-adjoint matrices, with eigenvalues and . Then,

---

The singular values of a matrix A ∈ M_n are the eigenvalues of its absolute value , we have fixed the notation s(A) = (s₁(A), …, s_n(A)) with s₁(A) ≥…≥ s_n(A). Singular values are closely related to the unitary invariant norm. Singular values inequalities are weaker than Löwner partial order inequalities and stronger than unitarily invariant norm inequalities in the following sense [133]:

for all unitarily invariant norms. The norm ||A||₁ = Tr|A| is unitarily invariant. Singular values are unitarily invariant: s(UAV) = s(A) for every A and all unitary U, V. A norm || · || is called unitarily invariant if

A.2

for all A ∈ M_n and all unitary U, V ∈ M_n. ||A|| ≤ ||B|| for all unitarily invariant norms if and only if that is,

A.3

The differences of two positive semidefinite matrices A, B ∈ M_n are often encountered. Denote the block diagonal matrix

by the notation A ⊕ B. Then [133]

1. s_i(A − B) ≤ s_i(A ⊕ B), i = 1, 2, …, n,

2. ||A − B|| ≤ ||A ⊕ B|| for all unitarily invariant norms,

3.

4. ||A − |z|B|| ≤ ||A + zB|| ≤ ||A + |z|B||, for any complex number z.

Note that the weak log majorization is stronger than the weak majorization .

A.6.1 Matrix Inequalities

Let be a linear mapping from finite-dimensional Hilbert spaces and . α is called positive if it sends positive (semidefinite) operators to positive (semidefinite) operators. Let be a positive, unital linear mapping and be a convex function. Then, it follow [34, p. 189] that

A.4

for every Here sa denotes the self-adjoint case.

Let A and B be positive operators, then for 0 ≤ s ≤ 1,

The triangle inequality for the matrix is [114, p. 237]

A.5

where A and B are any square complex matrices of the same size, and U and V are unitary matrices. Taking the trace of (A.5) leads to the following

A.6

Replacing B in (A.6) with B + C leads to

Similarly, we have

A.7

For positive operators A and B,

The n-tuples of the coefficients of real numbers may be regarded as diagonal matrices and the majorization can be extended to self-adjoint matrices. Suppose that A, B ∈ M_n are so. Then means that the n-tuple of eigenvalues of A is majorized by the n- tuple of eigenvalues of B; similarly for the weak majorization. Since the majorization depends only on the spectrums, holds if and only if for some unitaries U and V. It follows from Birkhoff's theorem [34] that implies that

for some p_i > 0 with ∑_ip_i = 1 and for some unitaries.

Theorem A.8

Let ρ₁ and ρ₂ be states. Then the following statements are equivalent.

1. .

2. ρ₁ is more mixed than ρ₂.

3. for some convex combination λ_i and for some unitaries U_i.

4. for any convex function .

---

A.6.2 Partial Ordering of Positive Semidefinite Matrices

Let A ≥ 0 and B ≥ 0 be of the same size. Then

1. A + B ≥ B,

2. ,

3. Tr(AB) ≤ Tr(A)Tr(B),

4. , when n > 1,

5. the eigenvalues of AB are all nonnegative, λ_i(AB) ≥ 0.

6. AB is positive semidefinite, AB ≥ 0, if and only if AB = BA. AB may not be even Hermitian.

If A ≥ B ≥ 0, then

Let A, B ∈ M_n be positive semidefinite. Then for any complex number and any unitarily invariant norm [133],

A.6.3 Partial Ordering of Hermitian Matrices

We follow [126, p. 273] for a short review. [115] has the most exhaustive collection. Positive definite and semi-definite matrices are important since covariance matrix and sample covariance matrix (used in practice) are semi-definite. A Hermitian matrix is called positive definite if

and positive semidefinite if the weaker condition x^HAx ≥ 0 holds. A Hermitian matrix is positive definite if and only if all of its eigenvalues are positive, and positive semidefinite if and only if all of its eigenvalues are nonnegative. For , we write A > B when A − B is positive definite, and A ≤ B if B − A is positive definite. This is a partial ordering of the set of n × n Hermitian matrices. It is partial because we may have and .

Let A ≥ 0 and B ≥ 0 be of the same size and C is nonsingular. We have

1. C^HAC > 0,

2. C^HBC > 0,

3. A⁻¹ > 0,

4. A + B ≥ B,

5. ,

6. Tr(AB) ≤ TrATrB,

7. A ≥ B ⇒ λ_i(A) ≥ λ_i(B), where λ_i are the eigenvalues (sorted in decreasing order),

8. det (A) ≥ det (B) and TrA ≥ TrB.

9. the eigenvalues of AB are all nonnegative. Furthermore, AB is positive semidefinite if and only if AB = BA.

The partitioned Hermitian matrix

with square blocks A and D, is positive definite if and only if A > 0 and its Schur complement D − B^HA⁻¹B > 0, or D > B^HA⁻¹B.

The Hadamard determinant inequality for a positive semidefinite is

The Minkowski determinant inequality for positive definite is

with equality if and only if B = cA for some constant c.

If f is convex then

and

A.8