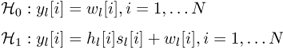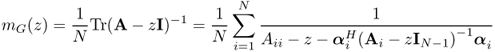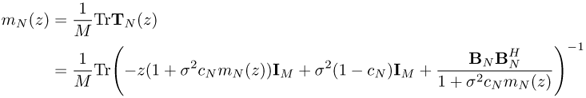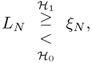Chapter 5

Large Random Matrices

5.1 Large Dimensional Random Matrices: Moment Approach, Stieltjes Transform and Free Probability

The necessity of studying the spectra of large dimensional random matrices, in particular, the Wigner matrices, arose in nuclear physics in the 1950s. In quantum mechanics, the energy levels of quantum are not directly observable (very similar to many problems in today's wireless communications and the Smart Grid), but can be characterized by the eigenvalues of a matrix of observations [10].

Let X_ij be i.i.d. standard normal variables of n × p matrix X

The sample covariance matrix is defined as

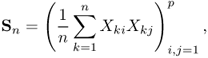
where n vector samples of a p-dimensional zero-mean random vector with population matrix I.

The classical limit theorem are no longer suitable for dealing with large dimensional data analysis. In the early 1980s, major contributions on the existence of the limiting spectral distribution (LSD) were made. In recent years, research on random matrix theory has turned toward second-order limiting theorems, such as the central limit theorem for linear spectral statistics, the limiting distributions of spectral spacings, and extreme eigenvalues.

Many applied problems require an estimate of a covariance matrix and/or of its inverse, where the matrix dimension is large compared to the sample size [20]. In such situations, the usual estimator, the sample covariance matrix, is known to perform poorly. When the matrix dimension p is larger than the number n of observations available, the sample covariance matrix is not even invertible. When the ratio p/n is less than one but not negligible, the sample covariance matrix is invertible but numerically ill-conditioned, which means that inverting it amplifies estimation error dramatically. For a large value of p, it is difficult to find enough observations to make p/n negligible, and therefore it is important to develop a well-conditioned estimator for large-dimensional covariance matrices such as in [20].

Suppose A_N is an N × N matrix with eigenvalues λ₁(A_N), …, λ_N(A_N). If all these eigenvalues are real (e.g., if A_N is Hermitian), we can define a one-dimensional distribution function. The empirical cumulative distribution of the eigenvalues, also called the empirical spectrum distribution (ESD), of an N × N Hermitian matrix A is denoted by

5.1

where 1{} is the indicator function.

Following [10], we divide available techniques into three categories: (1) Moment approach; (2) Stieltjes transform; (3) Free probability. Applications for these basic techniques will be covered.

The significance of ESD is due to the fact that many important statistics in multivariate analysis can be expressed as functionals of the ESD of some random matrices. For example, the determinant and the rank functions are the most common examples. The most significant theorem relevant to our applications is the convergence of the sample covariance matrix: the Marchenko-Pastur law.

 

 

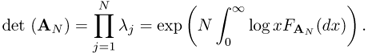
The ultimate goal of hypothesis testing is to search for some metrics that are “robust” for decision making by setting a threshold. For example, the trace functions are commonly used. To represent the trace functions, we suggest four methodologies: moment method, Stieltjes transform, orthogonal polynomial decomposition and free probability. We only give the basic definitions and their relevance to our problems of spectral sensing. We refer to [14] for details.

The goal of random matrix theory is to present several aspects of the asymptotics of random matrix “macroscopic” quantities [252] such as

where i_k ∈ {1, …, m}, 1 ≤ k ≤ p and are some n × n random matrices whose size n goes to infinity. are most often Wigner matrices, that is Hermitian matrices with independent entries, and Wishart matrices.

5.2 Spectrum Sensing Using Large Random Matrices

5.2.1 System Model

The most remarkable intuition of random matrices is that in many cases the eigenvalues of matrices with random entries turn out to converge to some fixed distribution, when both the dimensions of the signal matrix tend to infinity with the same order [253]. For Wishart matrices, the limiting joint distribution called Marchenko-Pastur Law has been known since 1967 [251]. Then, most recently, the marginal distribution of single ordered eigenvalues have been found. By exploiting these results, we are able to express the largest and the smallest eigenvalues of sample covariance matrices using their asymptotic values in closed form. The closed-form, exact expression for the standard condition number (defined as the ratio of the largest to the smallest eigenvalue) is available.

We often treat the asymptotic limiting results for large matrices to the finite-size matrices. The power of large random matrices is such that the approximate technique is often stunningly precise. If the matrices under consideration are larger than 8 × 8, the asymptotic results are accurate enough to approximate the simulated results.

The received signal contains L vectors y_l, l = 1, …, L

5.6

where h_l[i] is the channel gain (often having a Rayleigh fading distribution) for the i-th sample time of the l-th sensor. This is similar for signal vector s_l and noise vector w_l. Let y be a n × 1 vector modeled as

where H is an n × L matrix, s is an L × 1 “signal” vector and w is an n × 1 “noise” vector. This model appears frequently in many signal processing and communications applications. If s and w are modeled as independent Gaussian vectors with independent elements with zero mean and unit variance matrix (identity covariance matrix), then y is a multivariate Gaussian with zero mean and covariance matrix written as

5.7

In most practical applications, the true covariance matrix is unknown. Instead, it is estimated from N independent observations (“snapshots”) y₁, y₂, …, y_N as:

where Y_n = [y₁, y₂, …, y_N] is referred to as the “data matrix” and S_Y is the sample covariance matrix.

When n is fixed and N → ∞, it is well-known that the sample covariance matrix converges to the true covariance matrix. However, when both n, N → ∞ with

this is no longer true. Such a scenario is very relevant in practice where stationarity constraints limit the amount of data (N) that can be used to form the sample covariance matrix. Free probability is an invaluable tool in such situations when attempting to understand the structure of the resulting sample covariance matrices [254].

In matrix form, we have the following L × N matrix:

5.8

Similarly, we do this for H, S, W. (5.8) can be rewritten in matrix form as

5.9

where X = HS. Using (5.9), (5.6) becomes our standard form:

5.10

where we have made the assumption that

5.11

(5.11) can be justified rigorously using random matrix theory.

In general, knowing the eigenvalues of two matrices, say A, B, is not enough to find the eigenvalues of the sum or product of the two matrices, unless they commute. Free probability gives us a certain sufficient condition, called asymptotic freeness, under which the asymptotic spectrum of the sum A + B or product AB can be obtained from the individual asymptotic spectra, without involving the structure of the eigenvectors of the matrices [255]. [13, p. 9] [256]

The sample covariance matrix S_Y based on Y, which contains N samples and L column vectors, is

The sample covariance matrix S_Y is related to the true covariance matrix by the property of Wishart distribution (see Theorem 5.2)

5.12

where Z is a L × N i.i.d. Gaussian zero mean matrix. In fact,

5.13

is the Wishart matrix.

For a standard signal plus noise model, the true covariance matrix has the form

5.14

where and are, respectively, the true covariance matrix of the signal and the noise; also if the white noise is assumed.

Comparing the true covariance matrix (5.14) with its sample counterpart (5.11) reveals the fundamental role of a rigorous random matrix theory. We really cannot say much about the relation between the two versions of equations, generally for small sample size N. Luckily, when the sample size N is very large, the two versions can be proven equivalent (which will be justified later). This is the reason why random matrix theory is so relevant to wireless communications since a majority of wireless systems can be expressed in the form of (5.9). For example, CDMA, MIMO and OFDM systems can be expressed in such a form.

5.2.2 Marchenko-Pastur Law

The Marchenko Pastur law stated in Theorem 5.1 serves as a theoretical prediction under the assumption that the matrix is “all noise” [255]. Deviations from this theoretical limit in the eigenvalue distribution should indicate nonnoisy components, in other words, they should suggest information about the matrix.

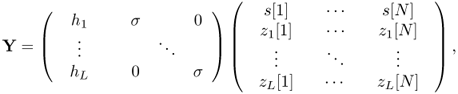
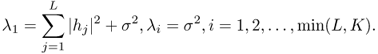
5.2.2.1 Noise Distribution Unknown, Variance Known

The criteria is

where a and b are defined in Theorem 5.1. The results are based on the asymptotic eigenvalue distribution.

5.2.2.2 Both Noise Distribution and Variance are Unknown

The ratio of the maximum and the minimum eigenvalues in the case does not depend on the variance of the noise. This allows us to circumvent the need for the knowledge of the noise:

The test provides a good estimator of the SNR γ. The ratio of the largest eigenvalue b₁ and the smallest a of is related solely to γ and α

For extremely low SNR such as γ = 0.01, that is, −20 dB, the above relation becomes

Typically, we have α = 1/2 and α = 1/10.

5.2.2.3 On the Empirical Distribution of Eigenvalues of Large Dimensional Information-Plus-Noise Type Matrices

Sample covariance matrices for systems with noise are the starting point in many problems, for example, spectrum sensing. Multiplicative free deconvolution has been shown in [262] to be a method. This method can assist in expressing limit eigenvalues distributions for sample covariance matrices, and to simplify estimators for eigenvalue distributions of covariance matrices.

We adopt a problem formulation from [263]. Let X_n be n × N containing i.i.d. complex entries and unit variance (sum of variances of real and imaginary parts equals 1), σ > 0 constant, and R_n an n × N random matrix independent of X_n. Assume, almost surely, as n → ∞, the empirical distribution function (e.d.f.) of the eigenvalues of converges in distribution to a nonrandom probability distribution function (p.d.f.), and the ratio tends to a positive number. Then it is shown that, almost surely, the e.d.f. of the eigenvalues of

5.18

converges in distribution. The limit is nonrandom and is characterized in terms of its Stieltjes transform, which satisfies a certain equation. n and N both converge to infinity but their ratio converges to a positive quantity c. The aim of [263] is to show that, almost surely, converges in distribution to a nonrandom p.d.f. F. (5.18) can be thought of as the sample covariance matrices of random vectors r_n + σx_n, where r_n can be a vector containing the system information and x_n is additive noise, with σ a measure of the strength of the noise.

The matrix C_N can be viewed as the sample correlation matrix of the columns of R_n + σX_n, which models situations where relevant information is contained in the R_.i′s and can be extracted from . Since R_.i is corrupted by X_.i, the creation of this matrix C_N is hindered. If the number of samples N is sufficiently large and if the noise is centered, then C_N would be a reasonable estimate of (I denoting the n × n identity matrix), which could also yield significant (if not all) information. Under the assumption

5.19

C_N models situations where, due to the size of n, the number of samples N needed to adequately approximate is unattainable, but is of the same order of magnitude as n. (5.19) is typical of many situations arising in signal processing where one can gather only a limited number of observations during which the characteristics of the signal do not change. This is the case for spectrum sensing when fading changes rapidly.

One application of the matrix C_N defined in (5.18) is the problem of spectrum sensing, for example, in Example 5.3. The beauty of the above model is that σ is arbitrary. Of course, this model applies to the low SNR detection problem for spectrum sensing.

Assume that N observations for n sensors. These sensors form a random vector r_n + σx_n, and the observed values form a realization of the sample covariance matrix C_n. Based on the fact that C_n is known, one is interested in inferring as much as possible about the random vector r_n, and hence on the system (5.18). Within this setting, one would like to connect the following quantities:

5.2.2.4 Statistical Eigen-Inference from Large Wishart Matrices

The measurements are of the form

where denotes a p-dimensional (real or complex) Gaussian noise vector with covariance matrix , denotes a k-dimensional zero-mean (real or complex) Gaussian signal vector with covariance matrix , and A is a p × k unknown nonrandom matrix.

5.3 Moment Approach

Most of the material in this section can be found in [10]. Throughout this section, only Hermitian matrices are considered. Real symmetric matrices are treated as special cases.

Let A be an n × n Hermitian matrix, and its eigenvalues be denoted by

Then, from the Definition 5.1, the k-th moment of F_A can be expressed as

5.20

(5.20) plays a fundamental role in random matrix theory. Most results in finding limiting spectral distribution were obtained by estimating the mean, variance or higher moments of .

To motivate our development, let us see an example first.

When sample covariance matrices S that are random matrices are used instead of Σ, the moments of S are scalar random variables. Girko studied the random determinants det S for decades [111]. Repeat (5.21) here for convenience:

5.21

5.3.1 Limiting Spectral Distribution

To show that F_A converges to a limit, say F, we often employ the Moment Convergence Theorem,

in some sense, for example, almost surely (a.s.) or in probability and the Carleman's condition

Thus the Moment Convergence Theorem can be used to show the existence of the limiting spectral distribution.

5.3.1.1 Wigner Matrix

The celebrated semicircle law (distribution) is related to a Wigner matrix. A Wigner matrix W of order n is defined as an n × n Hermitian matrix whose entries above the diagonal are i.i.d. complex random variables with variance σ², and whose diagonal elements are i.i.d. real random variables (without any moment requirement). We have the following theorem.

For each n, the entries above the diagonal of W are independent complex random variables with mean zero and variance σ², but they may not be identically distributed and depend on n. We have the following theorem.

In Girko's book (1990) [111], (5.23) is stated as a necessary and sufficient condition for the conclusion of Theorem 5.4.

5.3.1.2 Sample Covariance Matrix

Suppose that x_jn, j, n = 1, 2, … is a double array of i.i.d. complex random variables with mean zero and variance σ². Write

The sample covariance matrix is defined as

Marchenko and Pasture (1967) [251] had the first success in finding the limit spectral distribution of S. The work also provided the tool of Stieltjes transform. Afterwards, Bai and Yin (1988) [264], Grenander and Silverstein (1977) [265], Jonsson (1982) [266], Wachter (1978) [267] and Yin (1986) [268] did further research on the sample covariance matrix.

The limit distribution of Theorem 5.5 is called the Marchenko-Pastur law (distribution) with ratio index c and scale index σ². The existence of the second moment of the entries is necessary and sufficient for the Marchenko-Pastur law since the limit spectral distribution involves the parameter σ². The condition of zero mean can be relaxed to have a common mean.

Sometimes, in practice, the entries of X depend on N and for each N, they are independent but not identically distributed. We have the following theorem.

Now consider the case p → ∞, but . Almost all eigenvalues tend to 1 and thus the empirical spectrum distribution of S tend to a degenerate one. For convenience, we consider instead the matrix

When X is real, under the existence of the fourth moment, Bai and Yin (1988) [264] showed that its empirical spectrum distribution tends to the semicircle law almost surely as p → ∞. Bai (1988) [10] gives a generalization of this result.

Conditions (5.25) and (5.26) hold if the entries of X have bounded fourth moments.

 

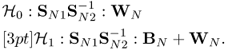
5.3.1.3 Product of Two Random Matrices

The motivation of studying products of two random matrices arises from the fact that the true covariance matrix is not a multiple of an identity matrix I, and that of multivariate F = S₁S₂⁻¹. When S₁ and S₂ are independent Wishart, the limit spectral distribution of F follows from Wachter (1980) [267].

5.3.2 Limits of Extreme Eigenvalues

5.3.2.1 Limits of Extreme Eigenvalues of the Wigner Matrix

The real case of the following theorem is obtained in [269] and the complex case is in [10].

For the Wigner matrix, symmetry between the largest and smallest eigenvalues exists. Thus, Theorem 5.10 actually proves the following: the necessary and sufficient conditions (for both the largest and the smallest eigenvalues) to have finite limits almost surely are (1) the diagonal entries have finite second moments; (2) the off-diagonal entries have zero mean and finite fourth moments.

5.3.2.2 Limits of Extreme Eigenvalues of Sample Covariance Matrix

Geman (1980) [270] proved that, as , the largest eigenvalue of a sample covariance matrix tends to b(c) almost surely, assuming a certain growth condition on the moments of the underlying distribution, where defined in Theorem 5.5. The real case of the following theorem is in [271], and their result is extended to the complex case in [10].

If we define the smallest eigenvalue as the (p − N + 1)-st smallest eigenvalue of S when p > N, then from Theorem 5.11, we immediately reach the following conclusion:

The first work to exploit Theorem 5.12 for spectrum sensing is [258] with their conference version published in 2007. Denote the eigenvalues of S_N by λ₁ ≤ λ₂ ≤ ··· ≤ λ_N. Write λ_max = λ_N and

Using the convention above, Theorem 5.12 is true [14] for all c ∈ (0, ∞).

5.3.2.3 Limiting Behavior of Eigenvectors

Relatively less work has been done on the limiting behavior of eigenvectors than eigenvalues. See [272] for the latest additions to the literature.

There is a good deal of evidence that the behavior of large random matrices is asymptotically distribution-free. In other words, it is asymptotically equivalent to the case where the basic entries are i.i.d. mean 0 normal, provided that some moment requirements are met.

5.3.2.4 Miscellanea

The norm (N^−1/2X)^k is sometimes important.

The following theorem is proven independently by [273] and [269].

5.3.2.5 Circular Law–Non-Hermitian Matrices

We consider the non-Hermitian matrix. Let

be an N × N complex matrix with i.i.d. entries x_jn of mean zero and variance 1. The eigenvalues of Q are complex and thus the empirical spectral distribution of Q, denoted by F_N(x, y), is defined in the complex plane. Since the 1950s, it has been conjectured that F_N(x, y) tends to the uniform distribution over the unit disc in the complex plane, called the circular law. The problem was open until Bai (1997) [274].

5.3.3 Convergence Rates of Spectral Distributions

5.3.3.1 Wigner Matrix

Consider the model of Theorem 5.4, and assume that the entries of W above or on the diagonal are independent and satisfy

5.27

 

5.3.3.2 Sample Covariance Matrix

Assume the following conditions are true.

5.28

 

 

Consider , where X_N = (x_ij) is a p × p matrix consisting of independent complex entries with mean zero and variance one, T_N is a p × p nonrandom positive definite Hermitian matrix with spectral norm uniformly bounded in p. If

and c_N = p/N < 1 uniformly as N → ∞, we obtain [277] that the rate of the expected empirical spectral distribution of S_N converging to its limit spectral distribution is . Under the same assumption, it can be proved that for any η > 0, the rates of the convergence of the empirical spectral distribution of S_N in probability and the almost sure convergence are and .

5.3.4 Standard Vector-In, Vector-Out Model

Random vectors are our basic building blocks in our signal processing. We define the standard vector-in, vector-out model (VIVO)¹ as

where y_n is an M × 1 complex vector of observations collected from M sensors, x_n is K × 1 complex vector of transmitted waveform, H is an M × K matrix, and w_n is an M × 1 complex vector of additive Gaussian noise with mean zero and variance .

Defining

we have

The sample covariance matrix is defined as

For the noise-free case, that is, , we have

We can formulate the problem as a hypothesis testing problem

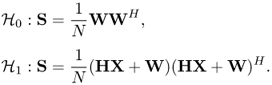
5.3.5 Generalized Densities

In the generalized densities, the moments of the matrix play a critical role. Assume that the matrix A has a density

The joint density function of its eigenvalues is of the form

For example for a real Gaussian matrix, β = 1 and h_n = 1, for a complex Gaussian matrix, β = 2 and h_n = 1, for a quaternion Gaussian matrix, β = 4 and h_n = 1, and for a real Wishart matrix with n ≥ p, β = 1 and h_n = x^n−p. The following examples illustrate this.

For generalized densities, we have

The book of [14] mainly concentrates on results without assuming density conditions.

5.4 Stieltjes Transform

We follow [10] closely for the definition of the Stieltjes transform. Let G be a function of bounded variation defined on the real line. Then, its Stieltjes transform is defined by

5.29

where z = u + iv with v > 0. The integrand in (5.29) is bounded by 1/v, the integral always exists, and

This is the convolution of G with a Cauchy density with a scale parameter v. If G is a distribution function, then its Stieltjes transform always has a positive imaginary part. Thus, we can easily verify that, for any continuity points x₁ < x₂ of G,

5.30

(5.30) provides a continuity theorem between the family of distribution functions and the family of their Stietjes transforms.

Also, if Im(m(z)) is continuous at x₀ + i0, then G(x) is differentiable at x = x₀ and its derivative equals . (5.30) gives an easy way to find the density of a distribution if its Stieltjes transform is known.

Let G be the empirical spectral distribution of a Hermitian matrix A_N of N × N. It is seen that

5.31

where is the i-th column vector of A with the i-th entry removed and A_i is the matrix obtained from A with the i-th row and column deleted. (5.31) is a powerful tool in analyzing the spectrum of large random matrix. As mentioned above, the mapping from distribution functions to their Stieltjes transforms is continuous.

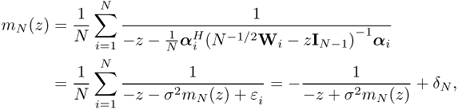
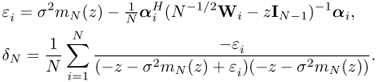
Let A_N be an N × N Hermitian matrix and be its empirical spectral distribution. If the measure μ admits a density f(x) with support Ω:

Then, the Stieltjest transform of is given for complex arguments by

5.34

where M_k = ∫_Ωx^kf(x) dx is the k-th moment of F. This provides a link between the Stieltjes transform and the moments of A_N. The moments of random Hermitian matrices become practical if direct use of the Stieltjes transform is too difficult.

Let , such that AB is Hermitian. Then, for , we have [12, p. 37]

In particular, we can apply AB = XX^H.

Let be Hermitian and a be a nonzero real. Then, for

There are only a few kinds of random matrices for which the corresponding asymptotic eigenvalue distributions are known explicitly [278]. For a wider class of random matrices, however, explicit calculation of the moments turns out to be unfeasible. The task of finding an unknown probability distribution given its moments is known as the problem of moments. It was addressed by Stieltjes in 1894 using the integral transform defined in (5.34). A simple Taylor series expansion of the kernel of the Stieltjes transform

shows how the moments can be found given the Stieltjes transform, without the need for integration. The probability density function can be obtained from the Stieltjes transform, simply taking the limit

which is called the Stieltjes inverse formula [11].

We follow [279] for the following properties:

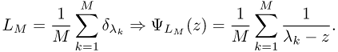
Gaussian tools [280] are useful. Let the s be independent complex Gaussian random variables denoted by z = (Z₁, ···, Z_n).

5.4.1 Basic Theorems

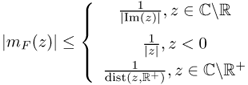
Our version of the above theorem is close to [12] with slightly different notation.

Let t > 0 and m_F(z) be the Stieltjes transform of a distribution function F. Then, for we have [12]

Let and be Hermitian, nonnegative definite. Then, for we have [12]

The fundamental result in the following theorem [282] states the equivalence between pointwise convergence of Stieltjes transform and weak onvergence of probability measures.

Let the random matrix W be square N × N with i.i.d. entries with zero mean and variance . Let Ω be the set containing eigenvalues of W. The empirical distribution of the eigenvalues

converges a nonrandom distribution functions as N → ∞. Table 5.2 lists commonly used random marices and their density functions.

Table 5.1 compiles some moments for commonly encountered matrices from [278]. Calculating eigenvalues λ_k of a matrix X is not a linear operation. Calculation of the moments of the eigenvalue distribution is, however, conveniently done using a normalized trace since

Thus, in the large matrix limit, we define tr(X) as

Table 5.1 Common random matrices and their moments (The entries of W are i.i.d. with zero mean and variance ; W is square N × N, unless otherwise specified. )

Convergence Laws	Definitions	Moments
Full-Circle Law	W square N × N
Semicircle Law
Quarter Circle Law
	Q2
Deformed Quarter Circle Law
	R2
Haar Distribution
Inverse Semicircle Law	Y = T + TH

Table 5.2 is made self-contained and only some remarks are made here. For Haar distribution, all eigenvalues lie on the complex unit circle since the matrix T is unitary. The essential nature is that the eigenvalues are uniformly distributed. Haar distribution demands for Gaussian distributed entries in the random matrix W. This condition does not seem to be necessary, but allowing for any complex distribution with zero mean and finite variance is not sufficient.

Table 5.2 Definition of commonly encountered random matrices for convergence laws (the entries of W are i.i.d. with zero mean and variance ; W is square N × N, unless otherwise specified)

Convergence Laws	Definitions	Density Functions
Full-Circle Law	W square N × N
Semicircle Law
Quarter Circle Law
	Q2
Deformed Quarter Circle Law
	R2
Haar Distribution
Inverse Semicircle Law	Y = T + TH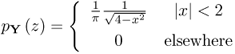

Table 5.3² lists some transforms (Stieltjes, R-, S- transforms) and their properties. The Stieltjes transform is more fundamental since both R-transform and S-transform can be expressed in terms of the Stieltjes transform.

Table 5.3 Table of Stieltjes, R- and S-transforms

Stieltjes Transform	R-Transform	S-Transform
,
		,
GK(z) =
		SY(z) = undefined
		SAB(z) = SA(z)SB(z)
,

5.4.1.1 Products of Random Matrices

Almost surely, the eigenvalue distribution of the matrix product

converges in distribution, as K, N → ∞ but β = K/N.

5.4.1.2 Sums of Random Matrices

Consider the limiting distribution of random Hermitian matrices of the form [251, 283]

where W(N × K), D(K × K), A(N × N) are independent, with W containing i.i.d. entries having second moments, D is diagonal with real entries, and A is Hermitian. The asymptotic regime is

The behavior is expressed using the limiting distribution function . The remarkable result is that the convergence of

to a nonrandom F.

 

 

 

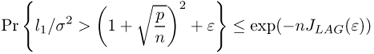
Consider the standard model for signals with p sensors. Let denote p-dimensional i.i.d. observations of the form

5.36

sampled at n distinct times t_i, where A = [a₁, …, a_K]^T is the p × K matrix of K linearly independent p-dimensional vectors. The K × 1 vector s(t) = [s₁(t), …, s_K(t)]^T represents the random signals, assumed zero-mean and stationary with full rank covariance matrix. σ is the unknown noise level, and bfn(t) is a p × 1 additive Gaussian noise vector, distributed and independent of s(t).

 

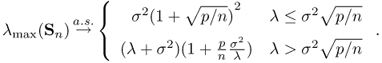
Theorem 5.29 says, assuming sufficiently fast decay of the residual eigenvalues, samples ensure that the top l eigenvalues are captured with relative precision.

5.4.2 Large Random Hankel, Markov and Toepltiz Matrices

Two most significant matrices, whose limiting spectral distributions have been extensively studied, are the Wigner and the sample covariance matrices. Here, we study other structured matrices. The important papers include Bryc, Dembo, and Jiang [287], Bose et al. [288–294], and Miller et al. [295, 296]. We mainly follow Bryc, Dembo, and Jiang (2006) [287] for this development. For a symmetric n × n matrix A, let λ_j(A), 1 ≤ j ≤ n, denote the eigenvalues of the matrix A, written in a nonincreasing order. The spectral measure of A, denoted , is the empirical spectral distribution (ESD) of its eigenvalues, namely

where δ_x is the Dirac delta measure at x. So when A is a random matrix, is a random measure on .

The ensembles of random matrices are studied here. Let X_k:k = 0, 1, 2, … be a sequence of i.i.d. real-valued random variables. We can visualize the Wigner matrix as

It is well known that almost surely, the limiting spectral distribution of n^−1/2(W_p) is the semicircle law.

The sample covariance matrix S is defined as

where W_p = ((X_ij))_{1≤i≤p, 1≤j≤n}.

In view of the above discussion, it is thus natural to study the limiting spectral distribution of matrices of the form where X_p is a p × n suitably patterned (asymmetric) random matrix. Asymmetry is used very loosely. It just means that X_n is not necessarily symmetric. One may ask the following questions [290]:

For , define a random n × n Hankel matrix H_n = [X_i+j−1]_{1≤i, j≤n},

and a random n × n Toeplitz matrix T_n = [X_|i−j|]_{1≤i, j≤n},

 

A symmetric distribution ν is said to be unimodal, if the function is convex for x < 0.

To state the theorem on the Markov matrices, define the free convolution of two probability measures μ and ν as the probability measure whose nth cumulant is the sum of the nth cumulants of μ and ν.

Let us define the Markov matrices M_n. Let X_ij:j ≥ i ≥ 1 be an infinite upper triangular array of i.i.d. random variables and define X_ij = X_jiforj ≥ i ≥ 1. Let M_n be a random n × n symmetric matrix given by

where X_n = [X_ij]_{1≤i, j≤n} and 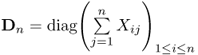is a diagonal matrix, so each of the rows of M_n has a zero sum. The values of X_ij are irrelevant for M_n.

Wigner's classical result says that converges weakly as n → ∞ to the (standard) semicircle law with the density on (− 2, 2). For normal X_n and normal i.i.d. diagonal independent of X_n, the weak limit of is the free convolution of the semicircle and standard normal measures; see [297] and the references therein. The predicted result holds for the Markov matrix M_n, but the problem is nontrivial since D_n strongly depends on X_n.

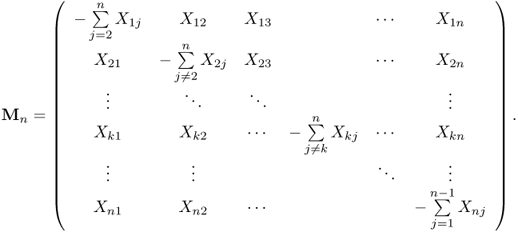
5.4.3 Information Plus Noise Model of Random Matrices

We follow [282] for this subsection. We consider such that N = M(N), M < N and c_N = M/N → c ∈ (0, 1) as N → ∞. A Gaussian information plus noise model matrix is a M × N random matrix defined by

5.37

where matrix B_N is deterministic such that

and the entries W_{i, j, N} of W_N are i.i.d. and satisfy

Most results can be also extended to the non-Gaussian case.

The convergence of the empirical spectral measure of defined by

with δ_x is the Dirac measure at point x.

We define the resolvent of matrix by

. Its normalized trace can be written as the Stieltjes transform of defined as

The weak convergence of can be studied by characterizing the convergence of as N → ∞, with the aid of (5.4.3). The main result is summarized in this theorem.

This result was first proven by Girko [298] and later Dozier-Silverstein [263]. This result is also valid for the non-Gaussian case.

If the spectral distribution

of matrix converges to the distribution F(x) as N → ∞, then

with μ probability measure, whose Stieltjes transform

satisfies

The convergence of can be guaranteed by the following theorem.

According to Theorem 5.33, is a good approximation of . The following theorem shows that the entries of Q_N(z) also approximate the entries of T_N(z).

Theorem 5.35 is valid for the non-Gaussian case that is proven in [299].

 

The support of μ_N is studied in [300]. Under further assumption such as Assumption 5.1, this is studied in [299]. Assumption 5.2 is stronger than Assumption 5.1. Assumption 5.2 says the rank of B_NB_N^H is independent of N.

Under the spiked model assumption, measure μ_N is intuitively expected to be very close to the Marchenko-Pastur distribution μ, and particularly Ω_N should be close to

Theorem 5.36 shows that the first cluster is very close to the support of the Marchenko-Pastur distribution; we have the presence of additional clusters, if the eigenvalues of B_NB_N^H are large enough. Indeed, if K_s eigenvalues of B_NB_N^H converge to different limits, above the threshold , then there will be K_s additional clusters in the support of Ω_N for all large N.

Theorem 5.36 also states that the smallest M − K_s eigenvalues of B_NB_N^H are associated with the first cluster, or equivalently that

and that

The conditions for the support Ω_N to split into several clusters depend in a nontrivial way on σ, the eigenvalues of B_NB_N^H, the distance between them. However, under stronger Assumption 5.2 (K independent of N and convergence of the eigenvalues to different limits), explicit conditions for the separation of the eigenvalues are obtained: an eigenvalue of B_NB_N^H is separated from the others if its limit is greater than . The nonseparated eigenvalues are those associated with . Therefore, in the spiked model case, the behaviors of the clusters of Ω_N are completely characterized.

The spectral decomposition of and are expressed as

with unitary matrices and , . The eigenvalues of and are decreasingly ordered such that 0 ≤ λ_{1, N} ≤…≤ λ_{M, N} and , respectively.

Let us consider the eigenvectors of and . Let us first start with a problem of DOA estimation, and then convert the problem into the standard information plus noise model defined in (5.37).

The observed M-dimensional time series y_n for the n-vector sample are expressed as

with

where s_n collects K < M nonobservable “source signals,” the matrix A of M × K is deterministic with an unknown rank K < M, and is additive white Gaussian noise such that . Here denotes the set of all integers.

In matrix form, we have Y_N = (y₁, …, y_N), observation matrix of M × N. Similarly, we do this for S_N and V_N. Then,

Using the normalized matrices

we obtain the standard model

5.39

which is identical to (5.37). Recall that

• B_N is a rank K deterministic matrix;
• W_N is a complex Gaussian matrix with i.i.d. entries having zero mean and variance σ²/N.

The “noise subspace” is defined as

that is, the eigenstate associated with 0 of , and the “signal space” the orthogonal complement, that is, the eigenspace associated with the non-null eigenvalues of . The goal of subspace estimation is to find the projection matrix onto the noise subspace, that is,

The subspace estimation problem we consider here is to find a consistent estimation of

where (d_N) is a sequence of deterministic vectors such that .

Traditionally, η_N is estimated by

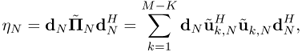
in other words, by replacing the eigenvectors of true signal covariance (information only) with those of their empirical estimates (information plus noise). This estimator only makes sense in the regime where M does not depend on N (thus c_N → 0), because from the classical law of large numbers, we have

whose convergence is not true in general, if c_N → c > 0. It can be shown that does not converge to zero.

Fortunately, we can derive a consistent estimate of η_N by using the results concerning the convergence of bilinear forms of the resolvent of .

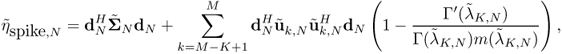
where , and m(x) is the Stieltjes transform of the Marchenko-Pastur law, expressed as

and

Then, under Assumption 5.2, if

it holds that

This theorem is derived using a different method [301].

5.4.4 Generalized Likelihood Ratio Test Using Large Random Matrices

The material in this subsection can be found in [302]. Denote by N the number of observed samples

where

• (w[n]), n = 0, …, N − 1 represents an indepdent and identically distributed (i.i.d.) process of K × 1 vectors with circular complex Gaussian entries with mean zero and covariance matrix σ²I_K;
• vector 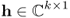is deterministic, signal s[n], n = 0, …, N − 1 denotes a scalar i.i.d. circular complex Gaussian process with zero mean and unit variance;
• (w[n]), n = 0, …, N − 1 and s[n], n = 0, …, N − 1 are assumed to be independent processes.

We stack the observed data into a K × N matrix

Denote by the sample covariance matrix defined as

5.40

We denote by p₀(Y;σ²) and p₁(Y;σ²) the likelihood functions of the observation matrix Y indexed by the unknown parameters h and σ² under hypotheses and .

As Y is a K × N matrix whose columns are i.i.d Gaussian vectors with covariance matrix

When parameters h and σ² are known, the Neyman-Pearson procedure gives a uniformly most power test, defined by the likelihood function

In practice, this is not the case: parameters h and σ² are not known. We will deal with this case in the following. No simple procedure guarantees a uniformly most powerful test, and a classical approach called GLRT considers

The GLRT rejects hypothesis when L_N is above some threshold ξ_N

5.41

where ξ_N is selected in order that the probability of false alarm does not exceed a given level α.

With the aid of [303, 304], the closed form expression of the GLRT L_N is derived in [302]. Denote by

the ordered eigenvalues of (all distinct with probability one).

Since T_N ∈ (1, K) and ϕ(·) is an increasing function in this interval, (5.43) is equivalent to

5.44

Using (5.44), (5.41) is rewritten as

5.45

with

The GLRT (5.45) requires setting the threshold γ_N which is a function of N. Let p_N(t) be the complementary c.d.f. of the statistics T_N under the null hypothesis

The threshold γ_N is thus defined as

which guarantees that the probability of false alarm is kept under a desired level α ∈ (0, 1).

Since p_N(t) is continuous and decreasing from 1 to 0 in the interval t ∈ [0, ∞), the threshold is well defined. It is more convenient to rewrite the GLRT (5.45) as the final form

5.46

The exact expression required in (5.46) has been derived in [302]. The fundamental point is that T_N is only a function of the eigenvalues of λ₁, …, λ_K of the sample covariance matrix defined in (5.40). The adopted approach is to study the asymptotic behavior of the complex c.d.f. p_N as the number of observations N goes to infinity. The asymptotic regime is defined as the joint limit where both the number K of sensors and the number N of snapshots go to infinity at the same speed

5.47

This asymptotic regime (5.47) is relevant in cases where the sensing system must be able to perform source detection in a moderate amount of time, that is, both the number K of sensors and the number N of snapshots are of the same order. Very often, the number of sensors is lower than the number of snapshots; hence, the ratio c is lower than 1.

(5.47) is particularly the case for “cognitive radio network as sensors” presented in Chapter 12. The basic idea behind this concept is that spectrum sensing is required in the cognitive radio systems. The availability of so much information that is used for spectrum sensing can also be exploited for sensing the radio environment (as “sensors”); in this manner, a cognitive radio network is used as sensors. Note that the cognitive radio network has much more information at its disposal than the traditional sensors such as ZigBee and Wi-Fi. The programmability of software defined radios must be exploited. Waveforms are programmable in these systems. Waveform diversity for remote sensing is thus enabled.

Under hypothesis , . Sample covariance matrix is a complex Wishart matrix. Its mathematical properties are well studied.

Under hypothesis , . Sample covariance matrix follows a single spiked model, in which all the population eigenvalues are one except for a few fixed eigenvalues [26].

The sample covariance matrix is not only central to the GLRT, but also to multivariate statistics. In many examples, indeed, a few eigenvalues of the sample covariance matrix are separated from the rest of the eigenvalues. Many practical examples show that the samples have non-null covariance. It is natural to ask whether it is possible to determine which non-null population model can possibly lead to the few sample eigenvalues separated from the Marchenko-Pastur density.

The simplest non-null case would be when the population covariance is finite rank perturbation of a multiple of the identity matrix. In other words, all but finitely many eigenvalues of the population covariance matrix are the same, say equal to 1. Such a population model has been called “spiked population model”: a null or purely noise model “spiked” with a few significant eigenvalues. The spiked population model was first proposed by [22]. The question is how the eigenvalues of the sample covariance matrix would depend on the nonunit population eigenvalues as N, K → ∞, as for example, a few large population eigenvalues would possibly pull up a few sample eigenvalues.

Since the behavior of T_N is not affected if the entries of Y are multiplied by a given constant, we find it convenient to consider the model

Define the signal-to-noise ratio (SNR) as

The matrix

where U is a unitary matrix and

The limiting behavior of the largest eigenvalue λ₁ can change, if the signal-to-noise ratio ρ_K is large enough, above a threshold.

The support of the Marchenko-Pastur distribution is defined as [λ⁻, λ⁺], with λ⁻ the left edge and λ⁺ the right edge, where

5.48

A further result due to Johnstone [22] and Nadler [305] gives its speed of convergence . Let Λ₁ be defined as

5.49

then Λ₁ converges in distribution toward a standard Tracy-Widom random variable with c.d.f. F_TW defined in (5.50). The Tracy-Widom distribution was first introduced in [24, 25], as the asymptotic distribution of the centered and rescaled large eigenvalue of a matrix from the Gaussian Unitary Ensemble.

Tables of the Tracy-Widom law are available, for example, in [306], and a practical algorithm [307] is used to efficiently evaluate (5.50). Refer to [19] for an excellent survey.

We call ρ the limiting SNR. We also define

Under hypothesis , the largest eigenvalue has the following asymptotic behavior [26] as N, K → ∞

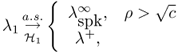
where is strictly larger than the right edge λ⁺. In other words, if the perturbation is large enough, the largest eigenvalue converges outside the support of Marchenko-Pastur distribution [λ⁻, λ⁺]. The condition for the detectability of the rank one perturbation is

5.51

In Theorem 5.39, we take advantage of the fundamental fact: the largest eigenvalues of the sample covariance matrix , defined in (5.40), converge in the asymptotic regime, defined in (5.47). The threshold and the p-value of interest can be expressed in terms of Tracy-Widom quantiles. Related work includes [24, 25, 308–311], Johnstone [9, 19, 22, 312–318], and Nadler [305].

 

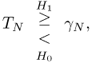
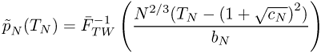
A related test [257] uses the ratio of the maximum to the minimum of the eigenvalues of the sample covariance matrix. As for T_N, χ_N is independent of the unknown noise power σ². This test χ_N is based on an observation based on (5.48).

Under hypothesis , the spectral measure of weakly converges to the Marchenko-Pastur distribution with support (λ⁻, λ⁺) with λ⁻ and λ⁺ defined in (5.48). The largest eigenvalue of , λ₁, converges toward λ⁺ under , and under .

The lowest eigenvalue of , λ_K, converges to [26, 271, 320]

under both and . Therefore, the statistic χ_N admits the following limit

The test is based on the observation that the limit of χ_N under the alternative is strictly larger than the ratio , at least when the SNR ρ is large enough.

The threshold must be determined before using the condition number test. It is proven in [302] that T_N outperforms χ_N. Λ₁ is defined in (5.49) (repeated below) and Λ_K is defined as

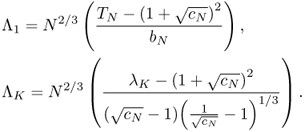
Then, both Λ₁ and Λ_K converge toward Tracy-Widom random variables

where X and Y are independent random variables, both distributed according to F_TW(x). A direct use of the Delta method [321, Chapter 3] gives the following convergence in distribution

where

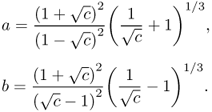
The optimal threshold is found to be

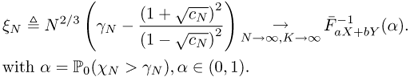
In particular, ξ_N is bounded as N, K → ∞.

5.4.5 Detection of High-Dimensional Signals in White Noise

We mainly follow [322] for this development. We observe M samples (“snapshots”) of possibly signal bearing N-dimensional snapshot vectors x₁, …, x_M. For each i,

where x_i are mutually independent. The snapshot vectors are modelled as

where

• , denotes an N-dimensional (real or circularly symmetric complex) Gaussian noise vector whose σ² is assumed to be unknown;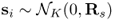
• denotes a K-dimensional (real or circularly symmetric complex) Gaussian signal vector with R_s;
• and H is a N × K unknown nonrandom matrix.
• H encodes the parameter vector associated with the j-th signal whose magnitude is described by the j-th element of s_i.

Since the signal and noise vectors are independent of each other, the covariance matrix of x_i can be decomposed as

where

The sample covariance matrix is defined as

where

is the matrix of observations (samples).

It is assumed that the rank of is K. Equivalently, the N − K smallest eigenvalues of are equal to zero. Denote the eigenvalues of R by

then the smallest N − K eigenvalues of R are all equal to σ² so that

In practice, we have to estimate the value of K, so called rank estimation.

We assume M > N and . Similarly to the case of the true covariance matrix, the eigenvalues of are ordered

Our estimator developed here is robust to high-dimensionality and sample size constraints.

A central object in the study of large random matrices is the empirical distribution function (e.d.f.) of the eigenvalues. Under , the e.d.f. of converges to the Marchenko-Pastur density F_W(x). The almost sure convergence of the e.d.f. of the signal-free sample covariance matrix (SCM) implies that the moments of the eigenvalues converge almost surely, so that

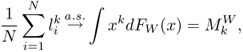
where [266]

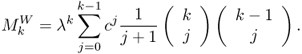
For finite N and M, the sample moments, that is, , will fluctuate about these limiting values.

 

The two Propositions 5.3 and 5.4 deal with . Now we introduce the two propositions in the signal-bearing case . In the signal-bearing case, a so-called phase transition phenomenon is observed, in that the largest eigenvalue will converge to a limit different from that in the signal-free case only if the “signal” eigenvalues are above a certain threshold.

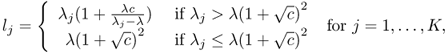
where convergence is almost certain.

This result appears in [26] for a very general setting. A matrix theoretic proof for the real-valued SCM case may be found in [27] while a determinental proof for the complex case may be found in [259]. A heuristic derivation appears in [323].

The “signal” eigenvalues strictly below the threshold described in Proposition 5.5 exhibit, on rescaling, fluctuations described by the Tracy-Widom distribution [24, 25]. An excellent survey is given in [19].

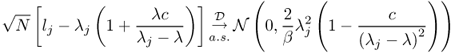
A matrix theoretic proof for the real-valued SCM case may be found in [27] while a determinental proof for the complex case may be found in [259]. The result has been strengthened for non-Gaussian situations by Baik and Silverstein for general c ∈ (0, ∞).

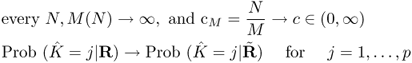
By Proposition 5.3, we heuristically define the effective number of (identifiable) signals as

Consider an example of

which has the N − 2 smallest eigenvalues λ₃ = ··· = λ_N = σ² and the two largest eigenvalues

respectively. Applying the result in Proposition 5.3, we can express the effective number of signals as

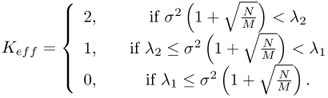
In the special situation when

we can (in an asymptotic sense) reliably detect the presence of both signals from the sample eigenvalues alone, whenever we have the following condition

We define as

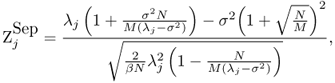
which measures the (theoretical) separation of the j-th “signal” eigenvalue from the largest “noise” eigenvalue in standard deviations of the j-th signal eigenvalue's fluctuations. Simulations suggest that reliable detection (with the empirical probability greater than 90%) of the effective number of signals is possible if lies between 5 and 15.

5.4.6 Eigenvalues of (A + B)⁻¹B and Applications

Roy's largest root test [324] is relevant under this context. We follow [325] for this development. Let X be an m × p normal data matrix: each row is an independent observation from . A p × p matrix A = X^HX is then said to have a Wishart distribution

Let

Assume that m ≥ p; then A⁻¹ exists and the nonzero eigenvalues of A⁻¹B generalize the univariate F ratio. The scale matrix has no effect on the distribution of these eigenvalues; without loss of generality we assume that . We follow the definition of [110, p. 84] for the greatest root statistic.

Since A is positive definite, 0 < λ_i < 1, for the i-th eigenvalue. Equivalently, λ₁(p, m, n) is the largest root of the determinantal equation

The parameter p stands for dimension, m the “error” degrees of freedom and n the “hypothesis” degrees of freedom. Thus m + n represents the “total” degrees of freedom.

The greatest root distribution has the property

5.53

useful in the case when n < p. [110, p. 84]

Assume p is even and that p, m = m(p), n = n(p) all go to infinity together such that

5.54

Define the logit transform W_p as

Johnstone (2008) [325] shows W_p, is, with appropriate centering and scaling, approximately Tracy-Widom distributed:

The distribution function was found by Tracy and Widom to be the limiting law of the largest eigenvalue of a p × p Gaussian symmetric matrix [25].

The centering and scaling parameters are

5.55

where the angle parameters γ, φ are defined by

5.56

Data matrices X based on complex-valued data rises frequently in signal processing and communications. If the rows of X are drawn independently from a complex normal distribution , then we say

In parallel with the real case definition, if

are independent, then the joint density of the eigenvalues

of (A + B)⁻¹B, or equivalently

is given by [326]

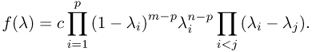
The largest eigenvalue λ^C(p, m, n) of (A + B)⁻¹B is called the greatest root statistic, with distribution λ^C(p, m, n). The property (5.53) carries over to the complex case.

Again, we define

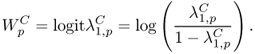
The centering and scaling are given in [325]. Software implementation is also available. See [325] for details.

We are now in a position to consider several settings in multivariate statistics using double Wishart models.

5.4.7 Canonical Correlation Analysis

Suppose that there are N observations on each of L + M variables. For definiteness, assume that L ≤ M. The first L variables are grouped into an N × L data matrix

and the last M into N × L data matrix

Write

for cross-product matrices. Canonical correlation analysis (CCA), or more precisely, the zero-mean version of CCA, seeks the linear combinations a^Tx and b^Ty that are most highly correlated, that is, to maximize

5.57

This leads to a maximal correlation ρ₁ and associated canonical vectors a₁ and b₁, usually each taken to have unit length. The procedure may be iterated. We restrict the search to vectors that are orthogonal to those already found:

The successive canonical correlations ρ₁ ≥ ρ₂ ≥ ··· ≥ ρ_L ≥ 0 may be found as the roots of the determinantal equation

5.58

See, for example, [110, p. 284]. A typical question in applications is how many of the ρ_k are significantly different from zero.

After some manipulations, (5.58) becomes

5.59

Now assume that Z = [XY] is an N × (L + M) Gaussian data matrix with mean zero. The covariance matrix is partitioned into

Under these Gaussian assumptions, X and Y variable sets will be independent if and only if

This is equivalent to asserting that

The canonical correlations (ρ₁, …, ρ_L) are invariant under block diagonal transformations

of the data (for B and C nonsingular L × L and M × M matrices, respectively). It follows that under hypothesis

the distribution of the canonical correlations can be found (without loss of generality) by assuming that

In this case, the matrices A and B of (5.59) are

From the definition, the largest squared canonical correlation has the Λ(L, N − M, M) distribution under the null hypothesis .

In practice, it is more common to allow each variable to have a separate, unknown mean. One can correct the mean using the approach, for example, in [325].

5.4.8 Angles and Distances between Subspaces

The cosine of the angle between two vectors is given by

(5.57) becomes

5.4.9 Multivariate Linear Model

In the multivariate model,

where

The model matrix H remains the same for each response; however, there are separate vectors of unknown coefficients and errors for each response; these are organized into X of regression coefficients and N × M matrix E of errors [327]. Assuming for now that the model matrix H has full rank, the least squares estimator is

Consider the linear hypothesis

where C₁ is a r × K matrix of rank r. For more details about C₁, we refer to [327].

The hypothesis sums and errors sums of squares and product matrices become

It follows [327] that

and under hypothesis ,

in addition, D and E are independent. Generalization of the -test is obtained from the eigenvalues of the matrix E⁻¹D, or equivalently, the eigenvalues of (D + E)⁻¹D.

Thus, under the null hypothesis C₁X = 0, Roy's maximum root statistic λ₁ has null distribution

5.4.10 Equality of Covariance Matrices

Suppose that independent samples from two normal distributions and lead to covariance estimates S₁ and S₂ which are independent and Wishart distributed on N₁ and N₂ degrees of freedom:

Then the largest root test of the null hypothesis

is based on the largest eigenvalue λ of (A₁ + A₂)⁻¹A₂, which under has the Λ(M, N₁, N₂) distribution [328].

5.4.11 Multiple Discriminant Analysis

Suppose that there are K populations, the i-th population being assumed to follow an M-variate normal distribution , with the covariance matrix assumed to be unknown, but common to all populations. A sample of size N_i (vector) observations is available from the i-th population, leading to a total of N = ∑N_i observations. Multiple discriminant analysis uses the “within groups” and “between groups” sums of squares and products matrices W and B to construct linear discriminant functions based on eigenvectors of W⁻¹B. A test of the null hypothesis that discrimination is not worthwhile

can be based, for example, on the largest root of W⁻¹B, which leads to use of the Λ(M, N − K, K − 1) distribution [110, pages 318 and 138].