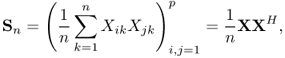Chapter 1
Introduction
1.1 Vision: “Big Data”
“Big Data” [1] refers to datasets whose size is beyond the ability of typical database software tools to capture, store, manage, and analyze.
There is a convergence of communications, sensing and computing towards the objective of achieving some control. In particular, cloud computing is promising. Sensors become cheaper. A network becomes bigger. In particular, powered by Internet protocols, the Smart Grid—a huge network, much bigger than the traditional networks—becomes an “energy Internet.”
Communications are becoming more and more like “backbones” for a number of applications. Sensing is a seamless ingredient in the future Internet of Things. In particular, it is the data acquisition mechanism to support the vision of “Big Data.” Computing will become a commodity that is affordable by the common needs of everyday applications.
The economy is becoming a “digital economy,” meaning that the jobs are more and more related to “soft power.” This does not necessarily imply software programming. Rather, it implies that more and more job functions will be finished by a smart system which is driven by sophisticated mathematics. While job functions become more and more “soft,” the needs for analytical analysis become more demanding. As a result, analytical skills, which are avoided by most of us at first sight, will be most useful in the lifelong education of a typical graduate student. Most often, our students know how to do their programing if they know the right mathematics. This is the central problem or dilemma. Analytical machinery is like our games of sports. Unless we practice with dedication, we will not become good players.
The book aims to focus on fundamentals, in particular, mathematical machinery. We primarily cover topics that are critical to cognitive radio network but hard to master without big efforts.
1.2 Cognitive Radio: System Concepts
Radio spectrum is one of the most scarce and valuable resources, like real estate, in modern society. Competition for these scare resources is the basic drive for the telecommunication industry.
In the most general sense, cognitive radio takes advantage of Moore's law to capitalize on the computational power of the semiconductor industry [2]. When information is accessible in the digital domain, the force behind this novel radio is computationally intelligent algorithms. Machine learning and artificial intelligence have become the new frontier toward this vision—the analogy of robotics. Converting information from the analog domain to the digital domain plays a central role in this vision: revolutionary compressed sensing is, therefore, critical to expanding the territory of this new system paradigm. The agile, software defined radios that can perform according to algorithms are basic building blocks. When each node is computationally intelligent, wireless networking faces a novel revolution. At the system level, functions such as cognitive radio, cognitive radar and anti-jamming (even electronic warfare) have no fundamental difference and are unified into a single framework that requires interdisciplinary knowledge. Radar and communications should be unified since both require dynamic spectrum access (DSA)—the bottleneck. Spectrum agile/cognitive radio is a new paradigm in wireless communications—a special application of the above general radio.
Cognitive radio [3] takes advantage of the waveform programmable hardware platform, that is, so-called software-defined radio. Signal processing and machine learning are the core of the whole radio, called cognitive core (engine). In its fundamental nature, cognitive radio is a “mathematically-intensive” radio. It is policy based. The policy can be reasoned through the cognitive engine. In some sense, the whole book is focused on the fundamentals that are responsible for the cognitive engine. Here, our radio stands for a generalized sense. The radios can be used for communication networks, or sensor networks. So-called cognitive radar [4] is even included in this sense [2]. Our whole book can be viewed as a detailed spelling-out of Haykin's vision [3, 4]. Similar to Haykin, our style is mathematical in its nature. At the time of writing, the IEEE 802.22 standard on cognitive radio [5] was just released in July 2011. This book can be viewed as the mathematical justification for some critical system concepts, such as spectrum sensing (random matrices being the unifying theme), radio resource allocation (enabled by the convex optimization engine), and game theory (understanding the competition and collaboration of radio nodes in networking).
1.3 Spectrum Sensing Interface and Data Structures
Dynamic spectrum sharing in time and space is a fundamental system building block. An intelligent wireless communication system will estimate or predict spectrum availability and channel capacity, and adaptively reconfigure itself to maximum resource utilization while addressing interference mitigation [6]. Cognitive radio [3] is an attempt in this direction. It takes advantage of the waveform programmable hardware platform, that is, so-called software-defined radio.
The interface and data structures are significant in the context of system concepts. For example, we adopt the view of IEEE 1900.6 [6], as shown in Figure 1.1. Let us define some basic terms:
Figure 1.1 Sample topology of an IEEE 1900.6 distributed RF sensing system [6].

Spectrum sensing is fundamental to a cognitive radio. In some sense, a cognitive radio includes two parts: (1) spectrum sensing; (2) the radio resources are “cognitively” allocated using the available sensed spectrum information. In future evolved schemes, every “object” connected to the Internet could provide sensing features. This approach is oriented toward both the Internet of Things (IoT) and green radio communication paradigms [6]. The approach is also to create dynamic wide-area maps of spectrum usage that are being rapidly updated to optimize the overall electromagnetic emission and global interference. In this context, the jointly merging the notion of the cognitive radio network and the Smart Grid is relevant. The latter is a huge network of power grids (many sensors, mobile or fixed). The size of the network is many times bigger than the usual wireless communications network. The idea of this merging was explored (for the first time in the proposal of R. Qiu to the office of naval research (ONR)) [7].
Sensing related information basically consists of four categories:
1.4 Mathematical Machinery
1.4.1 Convex Optimization
Optimization stems from human instinct. We always want to do things in the best way. Relying on mathematics, this human instinct can be written down in terms of mathematical optimization. Practical problems can be formulated as optimization problems with objective functions, constraint functions, and optimization variables. Mathematical optimization attempts to minimize or maximize the objective function by systematically selecting the values of optimization variables from a specific set defined by the constraint functions.
Convex optimization is a subfield of mathematical optimization, which investigates the problem of minimizing convex objective function based on a compact convex set. The strength of convex optimization is if a local minimum exists, then it is a global minimum. Hence, if a practical problem can be formulated as a convex optimization problem, then global optimum can be obtained. That is one reason why convex optimization has recently become popular.
The other reason for the popularity of convex optimization is that convex optimization can be solved by the cutting plane method, ellipsoid method, subgradient method, or interior point method. Thus the interior point method, which was originally developed to solve linear programming problems, can also be used to solve convex optimization problems [8]. By taking advantage of the interior point method, convex optimization problems can be solved efficiently [8].
Convex optimization includes the well-known linear programming, second order cone programming (SOCP), semidefinite programming (SDP), geometric programming, and so on. Convex optimization is a powerful signal processing tool which can be exploited anywhere, for example, system control, machine learning, operation research, logistics, finance, management, telecommunication, and so on, due to the prevalence of convex optimization problems in practice [8].
Besides convex optimization, mathematical optimization also includes integer programming, combinatorial programming, nonlinear programming, fractional programming, stochastic programming, robust programming, multi-objective optimization, and so on.
Unfortunately, there are still a large amount of nonconvex optimization problems in the real-world. Relaxation is the common way to address the nonconvex optimization issues. The nonconvex optimization problem is relaxed to the convex optimization problem. Based on the global optimum to the convex optimization problem, we can find the sub-optimal solution to the original nonconvex optimization problem. The second strategy to deal with the nonconvex optimization problems makes use of stochastic methods. Stochastic methods exploit random variables to get the solution to the optimization problem. Stochastic methods do not need to explore the structures of objective functions and constraints. Stochastic methods include simulated annealing, stochastic hill climbing, genetic algorithm, ant colony optimization, particle swarm optimization, and so on.
When we enjoy the beauty and benefit of mathematical optimization, we cannot forget the contributors and the important researchers in mathematical optimization. Joseph Louis Lagrange found a way to identify optima. Carl Friedrich Gauss and Isaac Newton gave iterative methods to search for an optimum. In 1939, Leonid Kantorovich published an article “Mathematical Methods of Organizing and Planning Production,” introducing the concept and theory of linear programming. Then George Bernard Dantzig developed simplex method for linear programming in 1947 and John von Neumann invented Duality Theorem for linear programming in the same year. Von Neumann's algorithm can be considered as the first interior-point method of linear programming. In 1984, a new polynomial-time interior-point method for linear programming was introduced by Narendra Karmarkar. Yurii Nesterov and Arkadi Nemirovski published a book Interior-Point Polynomial Algorithms in Convex Programming in 1994. Generally, the interior-point method is faster than the simplex method for the large-scale optimization problem. Besides, David Luenberger, Stephen P. Boyd, Yinyu Ye, Lieven Vandenberghe, Dimitri P. Bertsekas, and so on also made obvious contributions to mathematical optimization.
Mathematical optimization, especially convex optimization, has already greatly improved the performance of the current telecommunication system. For the next generation wireless communication system, that is, cognitive radio network, mathematical optimization will play a critical role. Cognitive radio network opens another stage for the show of mathematical optimization. Optimization will be the core of the cognitive engine. We can see the beauties of mathematical optimization in spectrum sensing, spectrum sharing, coding and decoding, waveform diversity, beamforming, radio resource management, cross-layer design, and security for cognitive radio network.
1.4.2 Game Theory
Game theory is an important analysis tool in cognitive radio. Essentially, a game involves multiple players, each of which makes individual decision and maximizes its own reward. Since the reward of each players is dependent on the actions of other players, the player must take the possible response of other players into account. All players will be satisfied at the equilibrium point, at which any individual deviation from the strategy only incurs reward loss. A natural question may arise, that is, why game theory is needed in cognitive radio?
The essential reason for the necessity of game theory is the existence of conflict or collaboration in cognitive radio. Some examples are given below:
- PUE attack: Primary user emulation (PUE) attack is a serious threat to the cognitive radio network, in which the attacker pretends to be a primary user and sends interference signals to scare secondary users away. Then, the secondary users need to evade the PUE attack. If there are multiple channels to choose, the secondary users need to make decisions on the channel use while the attacker needs to decide which channel to jam (if it is unable to jam all channels), thus forming a game.
- Channel synchronization: The control channel is of key importance in cognitive radio. Two secondary users need to convey control messages through the control channel. If the control channel is also in the unlicensed band, it is subject to the interruption of primary users. Hence, two secondary users need to collaborate to find a new control channel if the current one is no longer available. Such a collaboration is also a game.
- Suspicious collaborator: Collaborative spectrum sensing can improve the performance of spectrum sensing. However, the reports from a collaborator could be false if the collaborator is actually a malicious one. Hence, the honest secondary user needs to make a decision on whether trust the collaborator or not. Meanwhile, the attacker also needs to decide what type of report to share with the honest secondary user such that it can simultaneously spoof the honest user and disguise its goal.
The above examples concern zero-sum games, general sum games, Bayesian games and stochastic games. In this book, we will explain how to analyze a game, particularly the computation of Nash equilibrium, and apply the game theory to the above examples.
1.4.3 “Big Data” Modeled as Large Random Matrices
It turns out that random matrices are the unifying theme since “big data” can be modeled as large random matrices. With data acquisition and storage now easy, today's statisticians often encounter datasets for which the sample size, n, and the number of variables, p, are both large [9]: in the hundreds, thousands, millions and even billions in situations such as web search problems. This phenomenon is so-called “big data.” The analysis of these datasets using classical methods of multivariate statistical analysis requires some care. In the context of wireless communications, networks become more and more dense. Spectrum sensing in cognitive radio collects much bigger datasets than the traditional multiple input multiple output (MIMO)-orthogonal frequency-division multiplexing (OFDM), and code division multiple access (CDMA) systems. For example, for a duration of 4.85 milliseconds, a data record (digital TV) consisting of more than 105 sample points is available for data processing. We can divide this long data record into vectors consisting of only p sample points. A number of sensors n can cooperate for spectrum sensing. The analogy of sensors and particles is shown in Table 1.1. Alternatively, we can view n · p = 105 as using only one sensor to record a long data record. Thus we have p = 100 and n = 1, 000 for the current example. In this example, both n and p are large and in the same order of magnitude.
Table 1.1 Analogy of sensors and particles
| Particles | Sensors | Random Matrices |
| Total energy | Information | Degrees of freedom |
| Energy levels | Eigenvalues |
Let Xij be i.i.d. standard normal variables of p × n matrix X
The sample covariance matrix is defined as
where n vector samples of a p-dimensional zero-mean random vector with the population (or true covariance) matrix I and H stands for conjugate transpose (Hermitian) of a matrix.
The classical limit theorem is no longer suitable for dealing with large dimensional data analysis. The classical methods make an implicit assumption that p is fixed and n is growing infinitely large,
This asymptotic assumption (1.3) was consistent with the practice of statistics when these ideas were developed, since investigation of datasets with a large number of variables was very difficult. A better theoretical framework—that is, large p—for modern datasets, however, is the assumption of the so-called “large n, large p” asymptotics
where c is a positive constant.
There is a large body of work concerned with the limiting behavior of the eigenvalues of a sample covariance matrix Sn when p and n both go to ∞ (1.4). A fundamental result is the Marchenko-Pastur equation, which relates the asymptotic behavior of the eigenvalues of the sample covariance matrix to that of the population covariance in the “large n, large p” asymptotic setting. We must change points of view: from vectors to measures.
One of the first problems to tackle is to find a mathematically efficient way to express the limit of a vector whose size grows to ∞. (Recall that there are p eigenvalues to estimate in our problem and p goes to ∞.) A fairly natural way to do so is to associate to any vector a probability measure. More explicitly, suppose we have a vector (y1, …, yp) in ![]() . We can associate to it the following measure:
. We can associate to it the following measure:
![]()
where δx is the Dirac delta function at x. Gp is thus a measure with p point masses of equal weight, one at each of the coordinates of the vector. The change of focus from vector to measure implies a change of focus in the notion of convergence—weak convergence of probability measure.
Following [10], we divide available techniques into three categories: (1) Moment approach; (2) Stieltjes transform; (3) Free probability. Applications for these basic techniques will be covered.
The Stieltjes transform is a convenient and very powerful tool in the study of the convergence of spectral distribution of matrices (or operators), just as the characteristic function of a probability distribution is a powerful tool for central limit theorems. More important, there is a simple connection between the Stieltjes transform of the spectral distribution of a matrix and its eigenvalues. By definition, the Stieltjes transform of a measure G on ![]() is defined as
is defined as
![]()
where ![]() is the set of complex numbers with strictly positive imaginary part. The Stieltjes transform is sometimes referred to as Cauchy or Abel-Stieltjes transform. Good references on Stieltjes transforms include [11] and [12].
is the set of complex numbers with strictly positive imaginary part. The Stieltjes transform is sometimes referred to as Cauchy or Abel-Stieltjes transform. Good references on Stieltjes transforms include [11] and [12].
The remarkable phenomenon is that the spectral distribution of the sample covariance matrix is asymptotically nonrandom. Furthermore, it is fully characterized by the true population spectral distribution, through the Marchenko-Pastur equation. The knowledge of the limiting distribution of the eigenvalues in the population, ![]() , fully characterizes the limiting behavior of the eigenvalues of the sample covariance matrix, S.
, fully characterizes the limiting behavior of the eigenvalues of the sample covariance matrix, S.
In the market for wireless communications, an excellent book by Couillet and Debbah (2011) [12] has just appeared, in addition to Tulino and Verdu (2004) [13]. Our aim in this book is to introduce the relevance of random matrix theory in the context of cognitive radio, in particular spectrum sensing. Our treatment is more practical than in those two books. Although some theorems are also compiled in our book, no proofs are given. We emphasize how to apply the theory through a large number of examples. It is our belief that future engineers must be familiar with random matrix methods since “big data” is the dominant theme across layers of the wireless network.
“One of the useful features, especially of the large dimensional random matrix theory approach, is its ability to predict the behavior of the empirical eigenvalue distribution of products and sums of matrices. The results are striking in terms of accuracy compared to simulations with reasonable matrix sizes.” [12]
“Indeed, engineering education programs of the twentieth century were mostly focused on the Fourier transform theory due to the omnipresence of frequency spectrum. The twenty-first century engineers know by now that space is the next frontier due to the omnipresence of spatial modes, which refocuses the program towards a Stietjes transform theory.” [12]
In the eyes of engineers, Bai and Silverstein (2010) [14], Hiai and Petz (2000) [11] and Forrester (2010) [15] are most readable among the mathematical literature. Anderson (2010) is also accessible [16] and Girko (1998) is comprehensive [17]. One excellent survey [10] is a good starting point for the massive literature. It is still the best survey. Two surveys [18] and [19] are very readable.
In the early 1980s, major contributions on the existence of the limiting spectral distribution (LSD) were made. In recent years, research on random matrix theory has turned toward second-order limiting theorems, such as the central limit theorem for linear spectral statistics, the limiting distributions of spectral spacings, and extreme eigenvalues.
Many applied problems require an estimate of a covariance matrix and/or of its inverse, where the matrix dimension is large compared to the sample size [20]. In such situations, the usual estimator, the sample covariance matrix, is known to perform poorly. When the matrix dimension p is larger than the number of observations available, the sample covariance matrix is not even invertible. When the ratio p/n is less than one but not negligible, the sample covariance matrix is invertible but numerically ill-conditioned, which means that inverting it amplifies estimation error dramatically. For large p, it is difficult to find enough observations to make p/n negligible, and therefore it is important to develop a well-conditioned estimator for large-dimensional covariance matrices such as in [20].
1.4.3.1 Why is Random Matrix Theory So Successful?
Random matrix theory is very successful in nuclear physics [21]. Here are several reasons:
1.5 Sample Covariance Matrix
The study of sample covariance matrix is fundamental in multivariate analysis. With contemporary data, the matrix is often large, with number of variables comparable to sample size (so-called “big data”) [22]. In this setting, relatively little is known about the distribution of the largest eigenvalue, or principal component variance. A surprise of the random matrix theory, the domain of mathematical physics and probability, is that the results seem to give useful information about principal components for quite small values of n and p.
Let X, defined in (1.1), be an p × n data matrix. Typically, one thinks of n observations or cases xi of a p-dimensional column vector which has covariance matrix ![]() . For definiteness, assume that rows xi are independent Gaussian
. For definiteness, assume that rows xi are independent Gaussian ![]() . In particular, the mean has been subtracted out. If we also do not worry about dividing by n, we can call XXH a sample covariance matrix defined in (1.2). Under Gaussian assumption, XXH is said to have a Wishart distribution
. In particular, the mean has been subtracted out. If we also do not worry about dividing by n, we can call XXH a sample covariance matrix defined in (1.2). Under Gaussian assumption, XXH is said to have a Wishart distribution ![]() . If
. If ![]() , the “null” case, we call it a white Wishart, in analogy with time series setting where a white spectrum is one with the same variance at all frequencies.
, the “null” case, we call it a white Wishart, in analogy with time series setting where a white spectrum is one with the same variance at all frequencies.
Large sample work in multivariate analysis has traditionally assumed that n/p, the number of observations per variable, is large. Today, it is common for p to be large or even huge, and so n/p may be moderate to small and in extreme cases less than one.
The eigenvalue and eigenvector decomposition of the sample covariance matrix
![]()
with eigenvalues in the diagonal matrix L and orthogonal eigenvectors collected as columns of U. There is a corresponding population (or true) covariance matrix
![]()
with eigenvalues λi and orthogonal eigenvectors collected as columns of ![]() .
.
A basic phenomenon is that the same eigenvalues li are more spread out than the population λi. This effect is strongest in the null case when all population eigenvalues are the same.
Data matrices with complex Gaussian entries are of interest in statistics, signal processing and wireless communications. Suppose that X = (Xij)p×n with
![]()
all independently of one another. The matrix S = XXH has the complex Wishart distribution, and its (real) eigenvalues are ordered l1 > ··· > lp.
Define μnp and σnp as

Assume that n = n(p) increases with p so that both μnp and σnp are increasing in p.
![]()
The center and scale are essentially the same as the real case, but the limit distribution is
![]()
where q is still the Painleve II function defined as
![]()
and Ai(x) denotes the Airy function. This distribution was found by Tracy and Widom [24, 25] as the limiting law of the largest eigenvalue of an p by n Gaussian symmetric matrix (Wigner matrix).
Simulations show the approximation to be informative for n and p as small as 5.
1.6 Large Sample Covariance Matrices of Spiked Population Models
A spiked population model, in which all the population eigenvalues are one except for a few fixed eigenvalues, has been extensively studied [26, 27]. In many examples, a few eigenvalues of the sample covariance matrix are separated from the rest of the eigenvalues, the latter being packed together as in the support of the Marchenko-Pastur density. Examples are so common in speech recognition, mathematical finance, wireless communications, physics of mixture, and data analysis and statistical learning.
The simplest non-null case would be the population covariance ![]() is a finite rank perturbation of a multiple of the identity matrix I. In other words, we say
is a finite rank perturbation of a multiple of the identity matrix I. In other words, we say
![]()
As mentioned in the above, Johnstone (2001) [22] derived the asymptotic distribution for the largest sample eigenvalue under the setting of an identity matrix I under Gaussianity. Soshnikov (2002) proved the distributional limits under weaker assumptions, in addition to deriving distributional limits of the k-th largest eigenvalue, for fixed but arbitrary k [28].
A few of the sample eigenvalues under ![]() have limiting behavior that is different from
have limiting behavior that is different from ![]() when the covariance is identity matrix I.
when the covariance is identity matrix I.
A crucial aspect is the discovery of a phase transition phenomenon. Simply put, if the non-unit eigenvalues are close to one, then their sample versions will behave in roughly the same way as if the true covariance were the identity. However, when the true eigenvalues are larger than ![]() , the sample eigenvalues have a different asymptotic property. The eigenvectors also undergo a phase transition. By performing a natural decomposition of the sample eigenvectors into “signal” and “noise” parts, it is shown that when
, the sample eigenvalues have a different asymptotic property. The eigenvectors also undergo a phase transition. By performing a natural decomposition of the sample eigenvectors into “signal” and “noise” parts, it is shown that when ![]() , the “signal” part of the eigenvectors is asymptotically normal [27].
, the “signal” part of the eigenvectors is asymptotically normal [27].
1.7 Random Matrices and Noncommutative Random Variables
Random matrices are noncommutative random variables [11], with respect to the expectation

for an N × N random matrix H, where ![]() represents the expectation of a classical random variable. It is a form of the Wigner theorem that
represents the expectation of a classical random variable. It is a form of the Wigner theorem that
![]()
if the N × N real symmetric random matrix H(N) has independent identical Gaussian entries ![]() so that
so that
![]()
The semicircle law is the limiting eigenvalue distribution density of H(N). It is also the limiting law of the free central limit. The reason why this is so was made clear by Voiculescu. Let
![]()
be independent random matrices with the same distribution as X(N). It follows from the properties of Gaussians that the distribution of the random matrix
![]()
is the same as X(N). The convergence in moments to the semicircle law is understood in the sense that
![]()
are in free relation. The conditions for the free relation include
![]()
which is equivalently expressed as
![]()
Independent symmetric Gaussian matrices and independent Haar distributed unitary matrices are asymptotically free. The notion of asymptotic freeness may serve as a bridge connecting random matrix theory with free probability theory.
1.8 Principal Component Analysis
Every 20–30 years, principal component analysis (PCA) is reinvented with slight revision. It has many different names. We model the communication signal or noise as random field. The Karhunen-Loeve decomposition (KLD) is also known as PCA, the Proper Orthogonal Decomposition (POD), and Empirical Orthogonal Function (EOF). Its kernel version, that is, Kernel PCA, is very popular. We apply PCA to spectrum sensing.
PCA is a standard tool for dimensionality reduction. PCA finds orthogonal directions with maximal variance of the data and allows its low-dimensional representation by linear projections onto these directions. This dimensionality reduction is a typical preprocessing setup. A spiked covariance model [29–32] implies that the underlying data is low-dimensional but each sample is corrupted by additive Gaussian noise.
1.9 Generalized Likelihood Ratio Test (GLRT)
The GLRT is the culmination of the theoretical development for spectrum sensing. Its kernel version, Kernel GLRT, performs well, in contrast to Kernel PCA.
Both GLRT and PCA (its kernel version Kernel PCA) use sample covariance matrices as their starting points. As a result, large-dimensional random matrices are natural objects of mathematics to study.
1.10 Bregman Divergence for Matrix Nearness
When dealing with random matrices, we still need some measure of distance between them. Matrix nearness problems ask for the distance from a given matrix to the nearest matrix with a certain property. The use of a Bregman divergence in place of a matrix norm is, for example, proposed by Dhillon and Tropp (2007) [33]. Bregman divergence is equivalent to quantum information [34, p. 203]. Let ![]() is a convex set in a Banach space. For a smooth functional
is a convex set in a Banach space. For a smooth functional ![]()
![]()
is called the Bregman divergence of ![]() Now let
Now let ![]() be the set of density matrices and let
be the set of density matrices and let
![]()
A density matrix is a positive definite matrix whose trace equals one. It can be shown that the Bregman divergence is the quantum relative entropy which is the basis for measuring quantum information. Problems of Bregman divergence can be formulated in terms of convex optimization. The semicircle law, free (matrix-valued) random variables, and quantum entropy are related [11], when we deal with “big data.”
Functions of matrices are often needed in studying many problems in this book, for example, in spectrum sensing. The Matrix Function Toolbox contains MATLAB implementations to calculate functions of matrices [35]. It is available from http://www.maths.manchester.ac.uk/~higham/mftoolbox/