Chapter 4
Hypothesis Detection of Noncommutative Random Matrices
4.1 Why Noncommutative Random Matrices?
The most basic building block for quantum information is the covariance matrix. We are dealing with the matrix space whose elements are covariance matrices. The sufficient and necessary conditions for a matrix to be a covariance matrix are semidefinite positive. As a result, the basic elements for us to manipulate are the SDP matrices. Naturally, convex optimization (SDP matrices are of course convex) is the new calculus under this context.
For any two elements (matrices) A and B, we need to define the basic metric to order them. If they are random matrices, we call this order the stochastic order, for example,
![]()
if B is stochastically greater than A.
More generally, A and B are two matrix-valued random variables, in contrast with the scalar random variables. Recall that every entry of A and B is a scalar random variable. The focus of the current engineering curriculum is on the scalar random variable. When we deal with “Big Data” [1] in a high-dimensional vector space, the most natural objects of mathematical operations are such (SDP) matrix-valued random variables.
The matrix operation is fundamentally different from its scalar counterpart in that the matrix multiplication is not communicative. The quantum mechanics is built upon this mathematical fact.
When we process the data, we argue in this chapter that the so-called quantum information [127] must be preserved and extracted. Data mining is about quantum information processing [128, 129]. For more details, we refer to the standard text [128].
Now, random matrices are our new objects of interest. We will dedicate an entire chapter to study this connection. The fundamental reason for us to study random matrices is that a sample covariance matrix (in practice, we do not know the exact covariance matrix) is a large-dimensional random matrix. Random matrices are a special case of noncommunicative (matrix-valued1) random variables.
See Appendix A.5 for details on noncommunicative matrix-valued random variables: random matrices are their special cases.
4.2 Partial Orders of Covariance Matrices: A < B
![]()
![]()
For a general 2 × 2 matrix, it is easy to check the positivity:
![]()
since
![]()
If the entries are n × n matrices, then the condition for positivity is similar but it is more complicated. Matrices with matrix entries are called block-matrices.
![]()
![]()
![]()
The matrix C of the previous theorem is called the Hadamard (or Schur) product of the matrices A and B. In notation, C = A°B.
Let A and B be self-adjoint operators. A ≤ B if B − A is positive. The inequality A ≤ B implies XAX* ≤ XBX* for every operator X. The partial order between A and B can be defined. It is called Loewner's order [109, 114, 130–133]. Generally, stochastic order [132] can be defined for two random operators A and B.
4.1 ![]()
![]()
The hypothesis testing problem, see Example 4.2 for an illustraion, can be viewed as a problem of partial ordering of two covariance matrices ![]() and
and ![]() for two hypotheses. Matrix inequalities are the basis of the proposed formalism. Often, Hermitian matrices (or finite-dimensional self-adjoint operators) are objects of study. The positivity of these matrices is required for many recent results developed in quantum information theory. The fundamental role of positivity of covariance matrices is emphasized here.
for two hypotheses. Matrix inequalities are the basis of the proposed formalism. Often, Hermitian matrices (or finite-dimensional self-adjoint operators) are objects of study. The positivity of these matrices is required for many recent results developed in quantum information theory. The fundamental role of positivity of covariance matrices is emphasized here.
For positive operators A and B,
Let A and B be positive operators, then for 0 ≤ s ≤ 1,
4.4 ![]()
or
4.5 ![]()
If f is convex then
![]()
and
4.6 ![]()
In particular, for f(t) = tlogt, the relative entropy of two states is positive:
4.7 ![]()
This is the original Klein inequality. A stronger estimate is obtained [34, p. 174]:
From (4.3) to (4.8), the only requirement is that A and B are positive operators (matrices). Of course, they are valid for A < B.
Let A, B ∈ Mn be positive semidefinite. Then for any complex number z, and any unitarily invariant norm [133],
![]()
4.3 Partial Ordering of Completely Positive Mappings: Φ(A) < Φ(B)
It has long been realized that trace-preserving, completely positive maps seem to be the appropriate mathematical structure needed to model noise in quantum communication channels and quantum computers [134].
We define a quantum operation Φ as a map from the set of density operators of the input space Q1 to the set of density operators for the output space Q2, with the following three axiomatic properties [128]:
- A1: First, Tr[Φ(ρ)] is the probability that the transformation ρ → Φρ takes place;
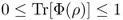 for any state ρ.
for any state ρ. - A2: Second, Φ is a convex-linear map on the set of density operators, that is, for probabilities {pi} of states ρi,
4.9 
- A3: Third, Φ is a completely positive map. That is, if Φ maps density operators of system Q1 to density operators of system Q2, then Φ(A) must be positive for any positive operator A. Furthermore, if we introduce an extra system R of arbitrary dimensionality, it must be true that
 is positive for any positive operator A on the combined system RQ1, where
is positive for any positive operator A on the combined system RQ1, where  denotes the identity map on system R.
denotes the identity map on system R.
The following theorem is fundamental to the adopted formalism: The map Φ satisfies axioms A1, A2, A3 if and only if
for some set of operators ![]() which map the input Hilbert space to the output Hilbert space, and
which map the input Hilbert space to the output Hilbert space, and ![]() where
where ![]() is the identity operator and * denotes the conjugate and transpose. Φ is obviously linear. The map Φ sends a density matrix into another one, thus
is the identity operator and * denotes the conjugate and transpose. Φ is obviously linear. The map Φ sends a density matrix into another one, thus ![]() and
and ![]() are density matrices that satisfy the conditions for 3.22. The hypothesis test 3.22 is, thus, generalized by replacing the expectation with the map Φ:
are density matrices that satisfy the conditions for 3.22. The hypothesis test 3.22 is, thus, generalized by replacing the expectation with the map Φ:
The map Φ in (4.11) is very general. The whole body of knowledge of quantum information theory [127] can be borrowed. Two maps are of the most important significance: (1) positive linear maps; (2) completely positive maps. The mathematical foundation is treated in textbooks [109, 130]. A positive linear map (also unital) Φ may be thought as a noncommutative analogue of an expectation map.
Since positivity is a useful and interesting property, it is natural to ask what linear transformations preserve it [109, Chapter 2]. It is instructive to think of positive maps as noncommutative (matrix) averaging operations [109, 115, 130, 133].
In this section we use the symbol Φ for a linear map from ![]() to
to ![]() . When k = 1, such a map is called a linear functional, and we use the lower-case symbol φ for it. A linear map Φ:
. When k = 1, such a map is called a linear functional, and we use the lower-case symbol φ for it. A linear map Φ: ![]() is called positive if
is called positive if ![]() where
where ![]() and
and ![]() is the space of n × n matrices. It is said to be unital if
is the space of n × n matrices. It is said to be unital if ![]() . We say Φ is strictly positive if
. We say Φ is strictly positive if ![]() where
where ![]() . It is easy to see that a positive linear map is strictly positive if and only if
. It is easy to see that a positive linear map is strictly positive if and only if ![]() .
.
Any positive linear combination of positive maps is positive. Any convex combination of positive, unital maps is positive and unital. There are ten basic examples in [109, Chapter 2]. The combination of these basic maps allows us to form many combined maps that are suitable for specific needs across the layers of the cognitive radio network. This subtask needs further investigation.
From (4.11), it is required that: (1) the map Φ is positive: positive matrices are mapped to positive matrices, that is, ![]() for any
for any ![]() ; (2) the map is trace-preserving, that is,
; (2) the map is trace-preserving, that is, ![]() . This special class of positive maps, called completely positive, trace-preserving (CPTP) linear maps [109, Chapter 3], is central to the proposed research. The map in (4.10) is such a map. A CPTP linear operation takes statistical operators to statistical operators. Such maps in (4.10) are also called quantum channels in quantum information theory.
. This special class of positive maps, called completely positive, trace-preserving (CPTP) linear maps [109, Chapter 3], is central to the proposed research. The map in (4.10) is such a map. A CPTP linear operation takes statistical operators to statistical operators. Such maps in (4.10) are also called quantum channels in quantum information theory.
4.4 Partial Ordering of Matrices Using Majorization: 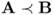
B > A is very strong condition at extremely low SNR such as − 20 dB. The weak majorization ![]() is equivalent to σk(A) ≤ σk(B) for all k. This is hardly satisfied at extremely low SNR, due to the presence of two random matrices, for example, X and Y in (4.2). The majorization
is equivalent to σk(A) ≤ σk(B) for all k. This is hardly satisfied at extremely low SNR, due to the presence of two random matrices, for example, X and Y in (4.2). The majorization ![]() holds if and only if
holds if and only if
4.12 ![]()
for some ![]() . By shifting a self-adjoint matrix, we can make it to be positive always. When discussing the properties of majorization, we can restrict ourselves to positive (definite) matrices.
. By shifting a self-adjoint matrix, we can make it to be positive always. When discussing the properties of majorization, we can restrict ourselves to positive (definite) matrices.
4.14 ![]()
4.15 ![]()
Here, ||| · ||| stands for the symmetric, unitarily invariant norm. Given two covariances ![]() and
and ![]() , these covariance matrices are affected by random signals experiencing fading and network control. It is difficult to guarantee that the covariance matrix of the noise or interference,
, these covariance matrices are affected by random signals experiencing fading and network control. It is difficult to guarantee that the covariance matrix of the noise or interference, ![]() = Rw, is known (due to noise power uncertainty). We can work on the “blind” version of the algorithms. The covariance matrices can be normalized by their traces. The impact of this normalization process is described by (4.13) in Wehrl's theorem.
= Rw, is known (due to noise power uncertainty). We can work on the “blind” version of the algorithms. The covariance matrices can be normalized by their traces. The impact of this normalization process is described by (4.13) in Wehrl's theorem.

Using the structure of 3.4 and considering the unit power of additive noise (without loss of generalization), ![]() , we have
, we have
4.16 ![]()
With the aid of (4.17) and Tr(A + B) = TrA + TrB, one detection algorithm using the preset threshold η0 can be stated as following:
The beauty of Algorithm 4.2 is that Tr(A) is independent of the measured signals. We can use the statistics of the additive noise (interference), TrA, a random variable, to set the threshold for the measured signals plus noise, TrB, also a random variable.
If we have the prior knowledge of Rs, we can consider
4.18 ![]()
where ![]() is used to match the signal covariance matrix Rs to get the absolute value |Rs|2. Recall that
is used to match the signal covariance matrix Rs to get the absolute value |Rs|2. Recall that ![]() .
.
Consider K independent copies Ak, k = 1, 2, …, K
Let Ck ≥ 0 and Dk ≥ 0 be of the same size. Then [114, p. 166]
For ![]() , with the aid of (4.20), both sides of these K inequalities in (4.19) are summed up to yield
, with the aid of (4.20), both sides of these K inequalities in (4.19) are summed up to yield
4.21 
4.22 ![]()
4.23 ![]()
Two covariances ![]() and
and ![]() are normalized first using (4.13) in Wehrl's theorem:
are normalized first using (4.13) in Wehrl's theorem:
4.24 ![]()
where X, Y and ![]() are self-adjoint random matrices with TrX = 0, TrY = 0 and
are self-adjoint random matrices with TrX = 0, TrY = 0 and ![]() , and N = TrI is the dimensionality of identity matrix I. X and Y are two independent, identical distributed copies whose rows are independent (see Section 3.4). It follows that
, and N = TrI is the dimensionality of identity matrix I. X and Y are two independent, identical distributed copies whose rows are independent (see Section 3.4). It follows that
Note that Tr(B − A) = 0 which implies that TrU*(B − A)U = 0, where U is an arbitrary unitary matrix. Consider
![]()
Using (A.6) [114, p. 239]: Tr|A + B| ≤ Tr|A| + Tr|B|, it follows that
4.26 ![]()
where ||X − Y||1 = Tr|Y − X| is the distance between two random matrices, also called trace norm. λi is the i − th eigenvalue. If ![]() and Tr|Y − X|, then Tr|B − A| = 0, which implies that A and B cannot be distinguished from each other.
and Tr|Y − X|, then Tr|B − A| = 0, which implies that A and B cannot be distinguished from each other.
In (4.25), generally we can not claim that B − A is positive, although B − A is still Hermitian. Let A and B be positive operators, then for 0 ≤ s ≤ 1,
In general, if A, B ≥ 0, we have
4.28 ![]()
However, the product of AB is not a Hermitian matrix. Note that although AB + BA is Hermitian, it is generally not positive semidefinite. In (4.27), we are interested in the absolute value of B − A only, in terms of ![]() This trace norm ||A − B||1 is a natural distance between complex n × n matrices A and B,
This trace norm ||A − B||1 is a natural distance between complex n × n matrices A and B, ![]() . Similarly,
. Similarly,

is also a natural distance. We can define the p − norm as
![]()
It was Von Neumann who showed first that the Hoelder inequality remains true in the matrix setting
![]()
For ![]() , the absolute value |A| is defined as
, the absolute value |A| is defined as ![]() and it is a positive matrix. If A is a self-adjoint and written as
and it is a positive matrix. If A is a self-adjoint and written as
![]()
where the vector ei forms an orthonormal basis, then it is defined as
![]()
Then A = {A ≥ 0} + {A < 0} = A+ + A− and |A| = {A ≥ 0} − {A < 0} = A+ − A−. The decomposition is called the Jordan decomposition of A.
4.5 Partial Ordering of Unitarily Invariant Norms: |||A||| < |||B|||
4.29 ![]()
4.30 ![]()
For the trace norm, Theorem 4.6 is a classical inequality. Recall that ||A||1 = ![]() , where σi is the singular value. Special cases: (1) f(t) = tm, m = 1, 2, …; (2)
, where σi is the singular value. Special cases: (1) f(t) = tm, m = 1, 2, …; (2) ![]()
4.6 Partial Ordering of Positive Definite Matrices of Many Copies: 
The function ![]() , defined by
, defined by ![]() satifies the inequality of (4.32). We interpret Theorem 4.7 as a norm-matrix generation of the scalar inequality f(a) + f(b) ≤ f(a + b), where a, b ≥ 0 and f:[0, ∞] → [0, ∞] is a convex function with f(0) = 0.
satifies the inequality of (4.32). We interpret Theorem 4.7 as a norm-matrix generation of the scalar inequality f(a) + f(b) ≤ f(a + b), where a, b ≥ 0 and f:[0, ∞] → [0, ∞] is a convex function with f(0) = 0.
4.7 Partial Ordering of Positive Operator Valued Random Variables: Prob(A ≤ X ≤ B)
Consider K matrix-valued observations:
where Xk, Yk, and Sk are of zero trace and denote the nondiagonal elements of the covariance matrices.
where the diagonal terms are associated with I with

Using the central limit theorem, the total trace (or total power) can be reduced to (scalar) Gaussian random variables.

Only diagonal elements are used in Algorithm 4.3; in (4.34), however, nondiagonal elements ![]() contain information of use to detection. The exponential of a matrix provides one tool. See Example 4.4. In particular, we have
contain information of use to detection. The exponential of a matrix provides one tool. See Example 4.4. In particular, we have
![]()
The following matrix inequality
![]()
is known to be false.
Let A and B be two Hermitian matrices of the same size. If A − B is positive semidefinite, we write [114]
4.35 ![]()
≥ is a partial ordering, referred to as Löwner partial ordering, on the set of Hermitian matrices, that is,
The statement A ≥ 0 ⇔ X*AX ≥ 0 is generalized as follows:
4.36 ![]()
for every complex matrix X.
A hypothesis detection problem can be viewed as a problem of partially ordering the measured matrices for individual hypotheses. If many (K) copies of the measured matrices Ak and Bk are at our disposal, it is nature to ask this fundamental question:
Is B1 + B2 + ··· + BK (statistically) larger than A1 + A2 + ··· + AK ?
To answer this question motivates this whole section. It turns out that a new theory is needed. We freely use [137] that contains a relatively complete appendix for this topic.
The theory of real random variables provides the framework of much of modern probability theory, such as laws of large numbers, limit theorems, and probability estimates for large deviations, when sums of independent random variables are involved. Researchers develop analogous theories for the case that the algebraic structure of the reals is substituted by more general structures such as groups, vector spaces, etc.
At the hands of our current problem of hypothesis detection, we focus on a structure that has vital interest in quantum probability theory and names the algebra of operators2 on a (complex) Hilbert space. In particular, the real vector space of self-adjoint operators (Hermitian matrices) can be regarded as a partially ordered generalization of the reals, as reals are embedded in the complex numbers.
A matrix-valued random variable ![]() , where
, where
4.37 ![]()
is the self-adjoint part of the C* − algebra ![]() [138], which is a real vector space. For more details, we refer to Appendix A.4. Let
[138], which is a real vector space. For more details, we refer to Appendix A.4. Let ![]() be the full operator algebra of the complex Hilbert space
be the full operator algebra of the complex Hilbert space ![]() . We denote
. We denote ![]() which is assumed to be finite. Here
which is assumed to be finite. Here ![]() means the dimensionality of the vector space. In the general case, d = TrI, and
means the dimensionality of the vector space. In the general case, d = TrI, and ![]() can be embedded into
can be embedded into ![]() as an algebra, preserving the trace.
as an algebra, preserving the trace.
The real cone
4.38 ![]()
induces a partial order ≤ in ![]() . We can introduce some convenient notation: for
. We can introduce some convenient notation: for ![]() the closed interval [A, B] is defined as
the closed interval [A, B] is defined as
4.39 ![]()
Similarly, open and half-open intervals (A, B), [A, B), etc.
For simplicity, the space Ω on which the random variable lives is discrete. Some remarks on the operator order is as follows.
4.40 ![]()
4.41 ![]()
Note that a rarely few of mappings (functions) are operator convex (concave) or operator monotone. Fortunately, we are interested in the trace functions that have much bigger sets. Take a look at (4.42) for example. In (4.33), since ![]() and
and ![]() (even stronger
(even stronger ![]() ), it follows from (4.42) that
), it follows from (4.42) that
The use of (4.42) allows us to separately study the diagonal part and the nondiagonal part of the covariance matrix of the noise, since all the diagonal elements are equal for a WSS random process (see 3.4). At low SNR, the goal is to find some ratio or threshold that is statistically stable over a large number of Monte Carlo trials.
![]()
![]()
![]()
![]()
![]()
![]()

4.43 ![]()
4.44 ![]()
4.45 ![]()
4.46 ![]()
Recall that
![]()
since ![]() is operator monotone.
is operator monotone.
If X, Y are independent, then Var(X + Y) = VarX + VarY. This is the same as in the classical case but one has to pay attention to the noncommunicativity that causes technical difficulty.
4.47 
4.48 ![]()
4.49 
Define the binary I-divergence as
4.50 ![]()
4.51 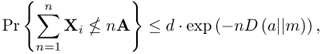
4.52 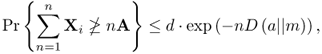
4.53 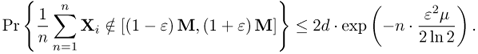
4.8 Partial Ordering Using Stochastic Order: A ≤ stB
If x ≤ sty, then ![]() .
.
Let x have a multivariate normal density with mean vector zero and variance matrix Σ1. Let y have a multivariate normal density with mean vector zero and variance matrix Σ1 + Σ2, where Σ2 is a nonnegative definite matrix. Then [132, p. 14]
4.54 ![]()
where || · || is the Euclidean norm defined as ![]() , for
, for ![]()
4.9 Quantum Hypothesis Detection
We consider the two hypotheses ![]() (null):ρ and
(null):ρ and ![]() (alternative):σ. We identify a state with a density operator, that is, a linear positive operator with trace one on finite-dimensional Hilbert space
(alternative):σ. We identify a state with a density operator, that is, a linear positive operator with trace one on finite-dimensional Hilbert space ![]() . Physically discriminating between the two hypotheses corresponds to performing a generalized (POVM) measurement on the quantum system. In analogy to the classical proceeding, one accepts
. Physically discriminating between the two hypotheses corresponds to performing a generalized (POVM) measurement on the quantum system. In analogy to the classical proceeding, one accepts ![]() or
or ![]() according to a decision rule based on the outcome of the measurement. There is no loss of generality assuming the POVM consists of only two elements, which denotes by {I − Π, Π}, where Π may be any linear operator on
according to a decision rule based on the outcome of the measurement. There is no loss of generality assuming the POVM consists of only two elements, which denotes by {I − Π, Π}, where Π may be any linear operator on ![]() with 0 ≤ Π ≤ I and I is identity operator. Neyman and Pearson introduces the idea of similarly making a distinction between type I and type II errors: (1) The type I error or false positive, denoted by α, is the error of accepting the alternative hypothesis when in reality the null hypothesis holds; (2) The type II error or false negative, denoted by β, is the error of accepting the null hypothesis when the alternative hypothesis is the true state of nature. The type-I and type-II error probabilities α and β are the probabilities of mistaking σ for ρ, and vice-versa, and are given by
with 0 ≤ Π ≤ I and I is identity operator. Neyman and Pearson introduces the idea of similarly making a distinction between type I and type II errors: (1) The type I error or false positive, denoted by α, is the error of accepting the alternative hypothesis when in reality the null hypothesis holds; (2) The type II error or false negative, denoted by β, is the error of accepting the null hypothesis when the alternative hypothesis is the true state of nature. The type-I and type-II error probabilities α and β are the probabilities of mistaking σ for ρ, and vice-versa, and are given by
![]()
The average error probability Pe is given by
The Bayesian distinguishably problem consists of finding the Π that minimizes Pe. A special case is the symmetric one where the prior probabilities π0 and π1 are equal.
Let us first introduce some basic notations. Abusing terminology, we will use the term ‘positive’ for ‘positive semidefinite’(denoted A ≥ 0). We use the positive semidefinite ordering on the linear operators on ![]() throughout, that is, A ≥ B if and only if A − B ≥ 0. For each linear operator
throughout, that is, A ≥ B if and only if A − B ≥ 0. For each linear operator ![]() the absolute value |A| is defined as
the absolute value |A| is defined as ![]() where A* is the transpose and conjugate (Hermitian) of A. The Jordan decomposition of a self-adjoint operator A is given by A = A+ − A−, where
where A* is the transpose and conjugate (Hermitian) of A. The Jordan decomposition of a self-adjoint operator A is given by A = A+ − A−, where
4.56 ![]()
are the positive part and negative part of A, respectively. Both parts are positive by definition, and A+A− = 0. There is a very useful variational characterization of the trace of the postitive part of a self-adjoint operator A:
In other words, the maximum is taken over all positive contractive operators. Since the extremal values of the set of positive contractive operators are exactly the orthogonal projector, we also have
The maximizer on the right-hand side is the orthogonal projector onto the range of A+.
4.59 ![]()
4.60 ![]()
![]()
The Lemmas say that the POVM {I − Π*, Π*} is the optimal one when the goal is to minimize the quantity α + cβ. In symmetric hypothesis testing the positive number c is taken to be the ratio π1/π0 of the prior probabilities. The goal of the Bayesian distinguishability problem is to minimize the average error probabilities Pe defined in (4.55) and can be rewritten as
![]()
By the Neyman-Pearson Lemma, the optimal test is given by the projector Π* onto the range of ![]() and the obtained minimal error probability is given by
and the obtained minimal error probability is given by
4.61 ![]()
where ||A||1 = Tr|A| is the trace norm. We call Π* the Holevo-Helstrom projector. Note Trρ = Trσ = 1 since ρ and σ are arbitrary density operators. Our goal in this task is to establish the connection of the heuristic hypothesis testing defined by 3.23 with quantum hypothesis testing. Consider a quantum system ![]() whose state is represented by the density matrix ρ and σ; more precisely,
whose state is represented by the density matrix ρ and σ; more precisely, ![]() and
and ![]() . This procedure may be expressed as a Hermitian matrix.
. This procedure may be expressed as a Hermitian matrix.
Let us define the projection {X ≥ 0} with respect to a Hermitian matrix X with a spectral decomposition X = ∑ixiEX, i:
![]()
When the state is ρ, the probability of the set {xi ≥ 0} is ![]() . This notation generalizes the concept of the subset to the noncommunicative case. It is known that two noncommunicative Hermitian matrices X and Y cannot be diagonalized simultaneously by a common orthonormal basis. This fact causes many technical difficulties.
. This notation generalizes the concept of the subset to the noncommunicative case. It is known that two noncommunicative Hermitian matrices X and Y cannot be diagonalized simultaneously by a common orthonormal basis. This fact causes many technical difficulties.
The two-valued POVM {T, I − T} for a Hermitian matrix T satisfying I ≥ T ≥ 0 allows us to perform the discrimination. Thus, T will be called a test. The following theorem [140, 141] holds for an arbitrary real number c > 0: The average probability of error is
4.62 ![]()
The minimum value is achieved when T = {ρ − σ ≥ 0}. In particular, if c = 13, it follows that
The optimal average probability of correct discrimination is
4.64 ![]()
Therefore, the trace norm gives a measure for the discrimination of two states. Here ![]() and the absolute value |A| is defined as
and the absolute value |A| is defined as ![]() . From (4.63), the necessary condition for quantum detection is: ||ρ − σ||1 = Tr|ρ − σ| > 0. Since only the absolute value is involved, the trace norm distance is symmetric. Without loss of generality, considering σ ≥ ρ ≥ 0 the necessary condition reduces to
. From (4.63), the necessary condition for quantum detection is: ||ρ − σ||1 = Tr|ρ − σ| > 0. Since only the absolute value is involved, the trace norm distance is symmetric. Without loss of generality, considering σ ≥ ρ ≥ 0 the necessary condition reduces to
if ![]() and
and ![]() . Condition (4.42) is exactly identical to 3.22 used in Algorithm 3.1. Therefore, it is shown that Algorithm 3.1 is equivalent to the Holevo-Helstrom tests [142, 143], which are noncommunicative generalizations of the classical LRT. The above “proof” paves the way for systematically exploiting the deep work done for quantum hypothesis testing [142, 144–217]. This subtask may lead to algorithms for spectrum sensing with unprecedented performance.
. Condition (4.42) is exactly identical to 3.22 used in Algorithm 3.1. Therefore, it is shown that Algorithm 3.1 is equivalent to the Holevo-Helstrom tests [142, 143], which are noncommunicative generalizations of the classical LRT. The above “proof” paves the way for systematically exploiting the deep work done for quantum hypothesis testing [142, 144–217]. This subtask may lead to algorithms for spectrum sensing with unprecedented performance.
4.10 Quantum Hypothesis Testing for Many Copies
A single copy of the quantum system is not enough for a good decision. One should make independent measurement on several identical copies, or joint measurements. The basic problem is to identify how the error probability Pe behaves in the asymptotic limit, that is, when one has to discriminate between the hypotheses ![]() and
and ![]() corresponding to either n copies of ρ or n copies of σ. To do so, we need to study the quantity
corresponding to either n copies of ρ or n copies of σ. To do so, we need to study the quantity
where ![]() is the nth-tensor powers of ρ. Such states can be regarded as the quantum version of independent, identical distributions (i.i.d). It turns out that
is the nth-tensor powers of ρ. Such states can be regarded as the quantum version of independent, identical distributions (i.i.d). It turns out that ![]() exponentially decreases in n:
exponentially decreases in n: ![]() This exponential decrease is very desirable for cooperative sensing of RF spectrum, where a large number n of copies are feasible.
This exponential decrease is very desirable for cooperative sensing of RF spectrum, where a large number n of copies are feasible.
Theorem [34, 142, 143]: For any two states ρ and σ on a finite-dimensional Hilbert space, occurring with prior probabilities π1 and π2, respectively, the rate limit of ![]() , as defined by (4.66), exists and is equal to the quantum Chernoff distance ξQCB
, as defined by (4.66), exists and is equal to the quantum Chernoff distance ξQCB
4.67 ![]()
This recent result provides a convenient tool for quantifying the asymptotic limit of the cooperative sensing of RF spectrum. For a general test with n different states ![]() and
and ![]() , the necessary condition for (4.66) to be valid takes a new look:
, the necessary condition for (4.66) to be valid takes a new look:
![]()
which, if σi > ρi, reduces to
![]()
This is equivalent to a special form of 3.23: by replacing the expectation with the average of n copies and letting f(x) = x in 3.23.
This subtask can borrow from the use of many copies for coding, basic to quantum information [34, 117, 127, 129, 140–143, 218–250].
1 After we get used to this notion, we can drop the words of “matrix-valued.”
2 The finite-dimensional operators and matrices are used interchangeably.
3 Two hypotheses have two equal prior probabilities in this Bayesian test.

