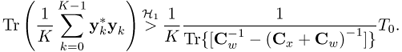Chapter 3

Classical Detection

3.1 Formalism of Quantum Information

Fundamental Fact: The noise lies in a high-dimensional space; the signal, by contrast, lies in a much lower-dimensional space.

If a random matrix A has i.i.d rows A_i, then A*A = ∑_iA_iA_i^T where A* is the adjoint matrix of A. We often study A through the n × n symmetric, positive semidefinite matrix, the matrix A*A. The eigenvalues of are therefore nonnegative real numbers.

An immediate application of random matrices is the fundamental problem of estimating covariance matrices of high-dimensional distributions [107]. The analysis of the row-independent models can be interpreted as a study of sample covariance matrices. For a general distribution in , its covariance can be estimated from a sample size of N = O(nlogn) drawn from the distribution. For sub-Gaussian distributions, we have an even better bound N = O(n). For low-dimensional distributions, much fewer samples are needed: if a distribution lies close to a subspace of dimension r in , then a sample of size N = O(rlogn) is sufficient for covariance estimation.

There are deep results in random matrix theory. The main motivation of this subsection is to exploit the existing results in this field to better guide the estimate of covariance matrices, using nonasymptotic results [107].

3.2 Hypothesis Detection for Collaborative Sensing

The density operator (matrix) ρ is the basic building block. An operator ρ satisfies: (1) (Trace condition) ρ has trace equal to one, that is, Trρ = 1; (2) (Positivity) ρ is a positive operator, that is, ρ ≥ 0. Abusing terminology, we will use the term “positive” for “positive semide finite (denoted A ≥ 0).” Covariance matrices satisfy the two necessary conditions. We say A > 0 when A is a positive definite matrix; B > A means that B − A is a positive definite matrix. Similarly, we say this for nonnegative definite matrix for B − A ≥ 0. The hypothesis test problems can be written as

3.1

where R_n is the covariance matrix of the noise and R_S that of the signal. The signal is assumed to be uncorrelated with the noise. From (3.1), it follows that R_S ≥ 0 and R_n > 0. In our applications, this noise is modeled as additive so that if x(n) is the “signal” and w(n) the “noise,” the recorded signal is

Often, this additive noise is assumed to have zero mean and to be uncorrelated with the signal. In this case, the covariance of the measured data, y(n), is the sum of the covariance of x(n) and w(n). Specifically, note that since

if x(n) and w(n) are uncorrelated, then

and it follows that

3.2

Discrete-time random processes are often represented in matrix form. If

is a vector of p + 1 values of a process x(n), then the outer product

is a (p + 1) × (p + 1) matrix. If x(n) is wide-sense stationary, taking the expected value and using the Hermitian symmetry of the covariance sequence, , leads to the (p + 1) × (p + 1) matrix of covariance values

3.3

referred to as the covariance matrix. The correlation matrix R_x has the following structure:

3.4

where I is identity matrix and TrA represents the trace of A. The covariance matrix has the following basic structures:

A complete list of properties is given in Table 3.1. When the mean values m_x and m_y are zero, the autocovariance and matrices are equal. We will always assume that all random processes have zero mean. Therefore, we use the two definitions interchangeably.

Table 3.1 Definition and properties for correlation and covariance matrices [108, p. 39]

Auto-correlation and covariance
Symmetry	Rx = Rx*	Cx = Cx*
Positive semidefinite	Rx ≥ 0	Cx ≥ 0
Interrelation	Rx = Cx + mxmx*
Cross-correlation and cross-covariance
Relation to Ryx and Cyx	Rxy = Ryx	Cxy = Cyx
Interrelation	Rxy = Cxy + mxmy*
Orthogonal and uncorrelated	x, y orthogonal: Rxy = 0	x, y uncorrelated: Cxy = 0
Sum of	Rx+y = Rx + Ry	Cx+y = Cx + Cy
x and y	if x, y orthogonal	if x, y uncorrelated

Let A be a Hermitian operator with qI ≤ A ≤ QI. The matrices QI − A and A − qI are positive and commute with each other [109, p. 95]. Since R_w is positive (of course, Hermitian), we have

The random matrix is Hermitian, but not necessarily positive. X is Hermitian, since its eigenvalues must be real. The Hoffman-Wielandt is relevant in this context.

(3.5) can be used to bound the difference of the eigenvalues between A and B.

3.3 Sample Covariance Matrix

In Section 3.2, the true covariance matrix is needed for hypothesis detection. In practice, we only have access to the sample covariance matrix which is a random matrix. We first present some basic definitions and properties related to a sample covariance matrix. The determinant of a random matrix S, det S, also called generalized variance, is of special interest. It is an important measure of spread in multidimensional statistical analysis.

3.3.1 The Data Matrix

The general (n × N) data matrix will be denoted X or X(n × N). The element in row i and column j is x_ij. We write the matrix X = (x_ij). The rows of X will be written as

Or

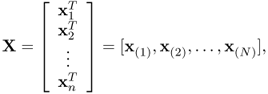
where

3.3.1.1 The Mean Vector and Covariance Matrix

The sample mean of the ith variable is

3.6

and the sample variance of the ith variable is

3.7

The sample covariance between the ith and jth variable is

3.8

The vector of means,

3.9

is called the sample mean vector, or simply the “mean vector.” The N × N matrix

is called the sample covariance matrix, or simply “covariance matrix.” It is more convenient to express the statistics in matrix notation. Corresponding to (3.6) and (3.9), we have

3.10

where 1 is a column vector of n ones. On the other hand,

so that

3.11

This may be expressed as

using (3.10). Writing

where H is called the centering matrix, we obtain the following standard form

3.12

which is a convenient matrix representation of the sample covariance matrix. We need a total of nN points of samples to estimate the sample covariance matrix S. Turning the table around, we can “summarize” information of nN points of samples into one single matrix S. In spectrum sensing, we are given a long record of data about some random variables, or a random vector of large data dimensionality.

Let us check the most important property of S: S is a positive semidefinite matrix. Since H is a symmetric idempotent matrix: H = H^T, H = H², for any N-vector a,

where y = HXa. Thus, the covariance matrix S is positive semidefinite, writing

For continuous data, we expect S is not only positive semidefinite, but positive definite, writing

if n ≥ N + 1.

It is often convenient to define the covariance matrix with a divisor of n − 1 instead of n. Set

If the data forms a random vector sample from a multivariate distribution, with finite second moments, then S_u is an unbiased estimate of the true covariance matrix. See Theorem 2.8.2 of [110, p. 50].

The sample correlation coefficient between the ith and the j variables is

Unlike s_ij, the correlation coefficient is invariant under both changes of scale and origin of the ith and the jth variables. This property is the foundation of detection of correlated structures among random vectors. Clearly,

where |a| is the absolute value of a. Define the sample correlation matrix as

with ρ_ii = 1. It follows that

If Σ = I, we say that the variables are uncorrelated. This is the case for white Gaussian noise. If D = diag(s_i), then

3.3.1.2 Measure of Multivariate Scatter

The matrix S is one possible multivariate generation of the univariate notion of variance, measuring scatter above the mean. Physically, the variance is equivalent to the power of the random vector. For example, for a white Gaussian random variable, the variance is its power.

Sometimes, for example, for hypothesis testing problems, we would rather have a single number to measure multivariate scatter. Of course, the matrix S contains many more structures (“information”) than this single real number. Two common such measures are

A motivation for these measures is in principle component analysis (PCA) that will be treated later. For both measures, large values indicate a high degree of scatter about the mean vector —physically larger power. Low values represent concentration about the mean vector . Two different measures reflect different aspects of the variability in the data. The generalized variance plays an important role in maximum likelihood (ML) estimation while the total variance is a useful concept in principal component analysis. In the context of low SNR detection, it seems that the total variance is a more sensitive measure to decide on two alternative hypotheses.

The necessity for studying the (empirical) sample covariance matrix in statistics arose during 1950s when practitioners were searching for a scalar measure of dispersion for the multivariate data [111, Chapter 2]. This scalar measure of dispersion is relevant under the context of hypothesis testing. We need a scalar measure to set the threshold for testing.

3.3.1.3 Linear Combinations

Linear transformations can simplify the structure of the covariance matrix, making interpretation of the data more straightforward. Consider a linear combination

where a₁, ···, a_N are given. From (3.10), the mean is

and the variance is

where (3.11) is used.

For a q-dimensional linear transformation, we have

which may be written as

where Y is a q × q matrix and b is a q-vector. Usually, q ≤ N.

The mean vector and covariance matrix of the new objects y_l are

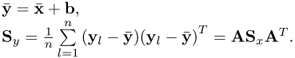
If A is nonsingular (so, in particular, q = N), then

Here we give three most important examples: (1) the scaling transform; (2) Mahalanobis transform; (3) principal component transformation (or analysis).

3.3.1.4 The Scaling Transform

The n vectors of dimension N are objects of interest. Define the scaling transform as

This transformation scales each variable to have unit variance and thus eliminates the arbitrariness in the choice of scale. For example, if x₍₁₎ measures lengths, then y₍₁₎ will be the same. We have

3.3.1.5 Mahalanobis Transformation

If S > 0, then S⁻¹ has a unique symmetric positive definite square root S^−1/2. See A.6.15 of [110]. We define the Mahalanobis transformation as

Then

so that this transformation eliminates the correlation between the variables and standardizes the variance of each variable.

3.3.1.6 Principle Component Analysis

In the era of high-dimensionality data processing, PCA is extremely important to reduce the dimension of the data. One is motivated to summarize the total variance using much fewer dimensions. The notion of rank of the data matrix occurs naturally in this context. For zero-mean random vector, it follows, from (3.12), that

This mathematical structure plays a critical role in its applications.

By spectrum decomposition theorem, the covariance matrix S may be written as

where U is an orthogonal matrix and Λ is a diagonal matrix of the eigenvalues of S,

The principal component transformation is defined by the unitary rotation

Since

the columns of W, called principal components, represent uncorrelated linear combinations of the variables. In practice, one hopes to summarize most of the variability in the data using only the principal components with the highest variances, thus reducing the dimensions. This approach is the standard benchmark for dimensionality reduction.

The principal components are uncorrelated with variances

It seems natural to define the “overall” spread of the data by some symmetric monotonically increasing function of λ₁, λ₂, ···, λ_n, such as the geometric mean and the arithmetic mean

Using the properties of linear algebra, we have

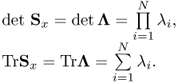
We have used the facts for a N × N matrix

where λ_i is the eigenvalues of the matrix A. See [110, A.6] or [112], since the geometric mean of the nonnegative sequence is always smaller than the arithmetic mean of the nonnegative sequence, or [113]

where a_i are nonnegative real numbers. Besides, the special structure of S ≥ 0, implies that all eigenvalues are nonnegative [114, p. 160]

The arithmetic mean-geometric mean inequality is thus valid for our case. Finally we obtain

3.13

The rotation to principal components provides a motivation for the measures of multivariate scatter. Let us consider one application in spectrum sensing. The key idea behind covariance-based primary user's signal detection that the primary user signal received at the CR user is usually correlated because of the dispersive channels, the utility of multiple receiver antennas, or even oversampling. Such correlation can be used by the CR user to differentiate the primary signal from white noise.

Since S_x is a random matrix, det S_x and are scalar random variables. Girko studied random determinants [111]. 5.14 relates the determinant to the trace of the random matrix S_x. In Chapter 4, the tracial functions of S_x are commonly encountered.

The max-min eigenvalue algorithm is simple and has a fairly good performance under the context of low SNR. At extremely low SNR, say − 25 dB, the calculated eigenvalues of the sample covariances matrix are random and look identical. This algorithm breaks down as a result of this phenomenon. Note that the eigenvalues are the variances of the principal components. The problem is that this algorithm depends on the variance of one dimension (associated with the minimum or the maximum eigenvalues).

The variances of different components are uncorrelated random variables. It is thus more natural to use the total variance or total variation.

3.4 Random Matrices with Independent Rows

We focus on a general model of random matrices, where we only assume independence of the rows rather than all entries. Such matrices are naturally generated by high-dimensional distributions. Indeed, given an arbitrary probability distribution in , one takes a sample of N independent points and arranges them as the rows of an N × n matrix A. Recall that n is the dimension of the probability space.

Let X be a random vector in . For simplicity we assume that X is centered, or . Here denotes the expectation of X. The covariance matrix of X is the n × n matrix . The simplest way to estimate is to take some N independent samples X_i from the distribution and form the sample covariance matrix . By the law of large numbers, almost surely as N → ∞. So, taking sufficiently many samples we are guaranteed to estimate the covariance matrix as well as we want. This, however, does not address the quantitative aspect: what is the minimal sample size N that guarantees approximation with a given accuracy?

The relation of this question to random matrix theory becomes clear when we arrange the samples X_i = :A_i as rows of the N × n random matrix A. Then, the sample covariance matrix is expressed as . Note that A is a matrix with independent rows but usually not independent entries. The reference of [107] has worked out the analysis of such matrices, separately for sub-Gaussian and general distributions.

We often encounter covariance estimation for sub-Gaussian distribution due to the presence of Gaussian noise. Consider a sub-Gaussian distribution in with covariance matrix , and let ∈ (0, 1), t ≥ 1. Then with probability at least 1 − 2exp(− t²n) one has

3.16

Here C depends only on the sub-Gaussian norm of a random vector taken from this distribution; the spectral norm of A is denoted as ||A||, which is equal to the maximum singular value of A, that is, s_max = ||A||.

Covariance estimation for arbitrary distribution is also encountered when a general noise interference model is used. Consider a sub-Gaussian distribution in with covariance matrix and supported in some centered Euclidean ball whose radius we denote . Let ∈ (0, 1) and t ≥ 1. Then, with probability at least , one has

3.17

Here C is an absolute constant and log denotes the natural logarithm. In (3.17), typically . The required sample size is N ≥ C(t/)²nlogn.

Low rank estimation is used, since the distribution of a signal in lies close to a low-dimensional subspace. In this case, a much smaller sample size suffices for covariance estimation. The intrinsic dimension of the distribution can be measured with the effective rank of the matrix , defined as

3.18

where denotes the trace of . One always has , and this bound is sharp. The effective rank always controls the typical norm of X, as . Most of the distribution is supported in a ball of radius where . The conclusion of (3.17) holds with sample size N ≥ C(t/)²rlogn.

Summarizing the above discussion, (3.16) shows that the sample size N = O(n) suffices to approximate the covariance matrix of a sub-Gaussian distribution in by the sample covariance matrix. While for arbitrary distribution, N = O(nlogn) is sufficient. For distributions that are approximately low-dimensional, such as that of a signal, a much smaller sample size is sufficient. Namely, if the effective rank of equals r, then a sufficient size is N = O(rlogn).

Each observation of the sample covariance matrix is a random matrix. We can study the expectation of the observed random matrix. Since the expectation of a random matrix can be viewed as a convex combination, and also the positive semidefinite cone is convex [115, p. 459], expectation preserves the semidefinite order [116]:

3.19

Noncommunicativity of two sample covariance matrices: If positive matrices X and Y commute, then the symmetrized product is: which is not true,¹ if we deal with two sample covariances. A simple MATLAB simulation using two random matrices can verify this observation. It turns out that this observation is of an elementary nature: Quantum information is built upon this noncommunicativity of operators (matrices). If the matrices A and B commute, the problem of (3.1) is equivalent to the classical likelihood ratio test [117]. A unifying framework including classical and quantum hypothesis testing (first suggested in [117]) is developed here.

When only N samples are available, the sample covariance matrices can be used to approximate the actual ones. A random vector is used to model the noise or interference. Similarly, a random vector models the signal. In other words, (3.1) becomes

3.20

where

For any A ≥ 0, all the eigenvalues of A are nonnegative. Since some eigenvalues of and are negative, they are indefinite matrices of small tracial values. Under extremely low signal-to-noise ratios, the positive term (signal) in (3.20) is extremely small, compared with the other three terms. All these matrices are random matrices with dimension n.

Our motivation is to use the fundamental relation of (3.19). Consider (sufficiently large) K i.i.d. observations of random matrices A and B:

3.21

The problem at hand is how the fusion center combines the information from these K observations. The justification for using the expectation is based on the basic observation of (3.20): expectation increases the effective signal-to-noise ratio. For the K observations, the signal term experiences coherent summation, while these other three random matrices go through incoherent summation.

Simulations: In (3.20), is no bigger than 0.5, so they do not have significant influence on the gap between and . Figure 3.1 shows that this gap is very stable. A narrowband signal is used. The covariance matrix is 4 × 4. About 25 observations are sufficient to recover this matrix with acceptable accuracy. Two independent experiments are performed to obtain and . In our algorithms, we need to set the threshold first for the hypothesis test of ; we rely on for . To obtain every point in the plot, N = 600 is used in (3.20).

Denote the set of positive-definite matrices by . The following theorem [115, p. 529] provides a framework: Let , assume that A and B are positive semidefinite, assume that A ≤ B, assume that f(0) = 0, f is continuous, and f is increasing. Then,

3.22

A trivial case is: f(x) = x. If A and B are random matrices, combining (3.22) with (3.19) leads to the final equation

3.23

Consider a general Gaussian detection problem: , where , , and s and w are independent. The Neyman-Pearson detector decides if . This LRT leads to a structure of a prewhitener followed by an EC [118, p. 167]. In our simulation, we assume that we know perfectly the signal and noise covariance matrices. This serves as the upper limit for the LRT detector. It is amazing to discover that Algorithm 3.1 outperforms the LRT by several dBs!

Related Work: Several sample covariance matrix based algorithms have been proposed in spectrum sensing. Maximum-minimum eigenvalue (MME)[119] and arithmetic-to-geometric mean (AGM) [120] uses the eigenvalues information, while feature template matching (FTM) [121] uses eigenvectors as prior knowledge. All these algorithms are based on covariance matrices. All the thresholds are determined by probability of false alarm.

Preliminary Results Using Algorithm 3.1: Sinusoidal signals and DTV signals captured in Washington D.C are used. For each simulation, zero-mean i.i.d. Gaussian noise is added according to different SNR. 2,000 simulations are performed on each SNR level. The threshold obtained by Monte Carlo simulations is in perfect agreement with that of the derived expression. The number of total samples contained in the segment is N_s = 100, 000 (corresponding to about 5 ms sampling time). The smoothing factor L is chosen to be 32. Probability of false alarm is fixed with P_fa = 10%. For simulated sinusoidal signal, the parameters are set the same.

Hypothesis detection using a function of matrix detection (FMD) is based on (3.23). For more details, we see [122]. It is compared with the benchmark EC, together with AGM, FTM, MME, as shown in Figure 3.2. FMD is 3 dB better than EC. While using simulated sinusoidal signal, the gain between FMD and EC is 5 dB. The longer the data, the bigger this gain.

3.5 The Multivariate Normal Distribution

The multivariate normal (MVN) distribution is the most important distribution in science and engineering [123, p. 55]. The reasons are manifold: Central limit theorems make it the limiting distributions for some sums of random variables, its marginal distributions are normal, linear transformations of multivariate normals are also multivariate normal, and so on. Let

denote an N × 1 random vector. The mean of X is

The covariance matrix of X is

The random vector X is called to be multivariate normal if its density function is

3.24

We assume that the nonnegetive definite matrix R is nonsingular. Since the integral of the density function is unit, this leads to

The quadratic form

is a weighted norm called Mahalanobis distance from x to m.

Characteristic Function

The characteristic function of X is the multidimensional Fourier transform of the density

By some manipulation [123], we have

3.25

The characteristic function itself is a multivariate normal function of the frequency variable .

Linear Transforms

Let Y be a linear transformation of a multivariate normal random variable:

The characteristic function of Y is

Thus, Y is also a multivariate normal random variable with a new mean vector and new variance matrix

if the matrix A^TRA is nonsingular.

Diagonalizing Transforms

The correlation matrix is symmetric and nonnegative definite. In other words, R ≥ 0. Therefore, there exists an orthogonal matrix U such that

The vector Y = U^TX is distributed as

The random variables Y₁, Y₂, …, Y_N are uncorrelated since

In fact, Y_n are independent normal random variables with mean U^Tm and variances :

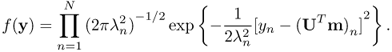
This transformation Y = U^TX is called a Karhunen-Loeve or Hotelling transform. It simply diagonalizes the covariance matrix

Such a transform can be implemented in MATLAB, using a function called eig or svd.

Quadratic Forms in MVN Random Variables

Linear functions of MVN random vectors remain MVN. In GLRT, quadratic forms of MVNs are involved. The natural question is what about quadratic forms of MVNs? In some important cases, the quadratic forms have a χ² distributions. Let X denote an random variable. The distribution

is distributed. The characteristic function of Q is

which is the characteristic function of a chi-squared distribution with N degrees of freedom, denoted . The density function for Q is the inverse Fourier transform

The mean and variance of Q are obtained from the characteristic function

Sometimes we encounter more general quadratic forms in the symmetric matrix P:

The mean and variance of Q are

The characteristic function of Q is

If PR is symmetric: PR = RP, the characteristic function is

where λ_n are eigenvalues of PR. This is the characteristic function of a random variable iff

If R = I, meaning X consists of indepedent components, then the quadratic form Q is iff P is idempotent:

Such a matrix is called a projection matrix. We have the following result: if X is and P is a rank r projection, the linear transformation Y = PX is , and the quadratic form Y^TY = X^TPX is . More generally, if X is , R = UΛ²U^T, and P is chosen to be with , then and the quadratic form Y^TY is .

Let Q = (X − m)^TR⁻¹(X − m) where X is . Equivalently,

is a quadratic form in the i.i.d. random variables X₁, X₂, ···, X_N. We have shown that Q is . Form the random variable

The new random variable V asymptotically has mean 0 and variance 1, that is, asymptotically .

The Matrix Normal Distribution

Let X(n × N) be a matrix whose rows , are independently distributed as . Then X has the matrix normal distribution and represents a random matrix observation from . Using (3.24), we find that the density function of X is [110]

where 1 is a column vector having the number 1 as its elements.

Transformation of Normal Data Matrices

We often encounter random vectors. Let

be a random sample from [110]. We call

a data matrix from or simply a “normal data matrix.” This matrix is a basic building block in spectrum sensing. We must understand it thoroughly. In practice, we deal with data with high dimensionality. We use this notion as our basic information elements in data processing.

Consider linear functions

where A(m × n) and B(p × q) are fixed matrices of real numbers. The most important linear function is the sample mean

where A = n⁻¹1^T and B = I_p.

 

 

Under the conditions of Theorem 3.3, is independent of HX, and thus is independent of S = n⁻¹X^THX.

The Wishart Distribution

We often encounter the form X^TCX where C is a symmetric matrix. This is a matrix-valued quadratic function. The most important special case is the sample covariance matrix obtained by putting C = n⁻¹H, where H is the centering matrix. These quadratic forms often lead to the Wishart distribution, which is a matrix generalization of the univariate chi-squared distribution, and has many similar properties.

If M(p × p) is

where X(m × p) is a data matrix from , then M is said to have a Wishart distribution with scale matrix and degrees of freedom parameter m. We write

When the distribution is said to be in standard form.

When p = 1, the W₁(σ², m) distribution is given by x^Tx, where the elements of x(m × 1) are i.i.d. variables; that is the W₁(σ², m) distribution is the same as the distribution.

The scale matrix plays the same role in the Wishart distribution as σ² does in the distribution. We shall usually assume

The diagonal submatrices of M themselves have a Wishart distribution. Also,

If M ~ W_p(I, m) and B(p × q) satisfies B^TB = I_q, then

Also, we have

 

 

The Hotelling T² Distribution

[110, p. 73] Let us study the functions such as d^TM⁻¹d, where d is normal, M is Wishart, and d and M are independent. For example, d may be the sample mean, and d proportional to the sample covariance matrix. Hotelling (1931) initiated the work to derive the general distribution of quadratic forms.

If α is used to represent md^TM⁻¹d where d and M are independently distributed as and W_p(I, m), respectively, then we say that α has the Hotelling T² distribution with parameters p and m. We write α ~ T²(p, m).

If and S are the mean vector and covariance matrix of a sample of size n from and S_u = (n/(n − 1))S, then

The T² statistic is invariant under any nonsingular linear transformation x → Ax + b. where B(·, ·) is a beta variable.

Wilks' Lambda Distribution

If and are independent and if m ≥ p, we say that

has a Wilks' lambda distribution with parameters p, m, n.

The Λ family of distributions occurs frequently in the context of likelihood ratio test. The parameter p is dimension. The parameter m represents the “error” degrees of freedom and n the “hypothesis” degrees of freedom. Thus m + n represents the “total” degrees of freedom. Like the T² statistic, Wilks' lambda distribution is invariant under changes of the scale parameters of A and B.

 

If is independent of where m ≥ p. Then, the largest eigenvalue θ of (A + B)⁻¹B is called the greatest root statistic and its distribution is denoted θ(p, m, n).

If λ is an eigenvalue of A⁻¹B, then is an eigenvalue of (A + B)⁻¹B. Since this is a monotone function of λ, θ is given by

where λ₁ is the largest eigenvalue of A⁻¹B. Since λ₁ > 0, we see that 0 ≤ θ ≤ 1.

For multisample hypotheses, we see [110, p. 138].

Geometric Ideas

The multivariate normal distribution in N dimensions has constant density on ellipses or ellipsoids of the form

3.26

where c is a constant. These ellipsoids are called the contour of the distribution or the ellipsoids of equal concentration. For , these contours are centered at x = 0, and when the contours are circles or in higher dimensions spheres or hyperspheres.

The principal component transformation facilitates interpretation of the ellipsoids of equal concentration. Using the spectral decomposition

where is the matrix of eigenvalues of , and is an orthogonal matrix whose columns are the corresponding eigenvectors. As in Section 3.3.1, define the principal component transform by

In terms of y, (3.26) becomes

so that the components of y represents axes of the ellipsoid.

In the GLRT, the following difference between two ellipsoids is encountered

3.27

where d is a constant. When the actual covariance matrices and are perfectly known, the problem is fine. Technical difficulty arises from the fact that sample covariance matrices and are used in replacement of and . The fundamental problem is to guarantee that (3.27) has a geometric meaning; in other words, this implies

3.28

As in Section A.3, the trace function, TrA = ∑_ia_ii, satisfies the following properties [110] for matrices A, B, C, D, X and scalar α:

3.29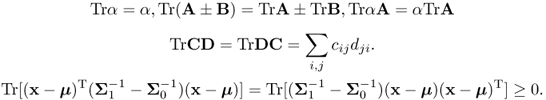

Using the fact that for A, B ≥ 0, we have

we have the necessary condition (for (3.28) to be valid)

3.30

since

3.31

The necessary condition (3.30) is easily satisfied when the actual covariance matrices and are known. When, in practice, the sample covariance matrices and

are known, instead, the problem arises

3.32

This leads to a natural problem of sample covariance matrix estimation and the related GLRT. The fundamental problem is that the GLRT requires the exact probability distribution functions for two alternative hypotheses. This condition is rarely met in practice. Another problem is intuition that the random vectors fit the exact probability distribution function. In fact, the empirical probability distribution function does not satisfy this condition. This problem is more obvious when we deal with high data dimensionality such as N = 10⁵, 10⁶ which are commonly feasible in real-world spectrum sensing problems. For example, N = 100, 000 corresponding to 4.65 milliseconds sampling time.

3.6 Sample Covariance Matrix Estimation and Matrix Compressed Sensing

Fundamental Fact: The noise lies in a high-dimensional space; the signal, on the contrast, lies in a much lower-dimensional space.

If a random matrix A has i.i.d column A_i, then

where A* is the adjoint matrix of A. We often study A through the n × n symmetric, positive semidefinite matrix, the matrix A*A; in other words

The absolute matrix is defined as

A matrix C is positive semidefinite,

if and only all its eigenvalues λ_i are nonnegative

The eigenvalues of |A| are therefore nonnegative real numbers or

An immediate application of random matrices is the fundamental problem of estimating covariance matrices of high-dimensional distributions [107]. The analysis of the row-independent models can be interpreted as a study of sample covariance matrices.

There are deep results in random matrix theory. The main motivation of this subsection is to exploit the existing results in this field to better guide the estimate of covariance matrices, using nonasymptotic results [107].

We focus on a general model of random matrices, where we only assume independence of the rows rather than all entries. Such matrices are naturally generated by high-dimensional distributions. Indeed, given an arbitrary probability distribution in , one takes a sample of N independent points and arranges them as the rows of an N × n matrix A. Recall that n is the dimension of the probability space.

Let X be a random vector in . For simplicity we assume that X is centered, or . Here denotes the expectation of X. The covariance matrix of X is the n × n matrix

The simplest way to estimate is to take some N independent samples X_i from the distribution and form the sample covariance matrix

By the law of large numbers,

almost surely as N → ∞. So, taking sufficiently many samples we are guaranteed to estimate the covariance matrix as well as we want. This, however, does not address the quantitative aspect: what is the minimal sample size N that guarantees approximation with a given accuracy?

The relation of this question to random matrix theory becomes clear when we arrange the samples

as rows of the N × n random matrix A. Then, the sample covariance matrix is expressed as

Note that A is a matrix with independent rows but usually not independent entries. The reference of [107] has worked out the analysis of such matrices, separately for sub-Gaussian and general distributions.

We often encounter covariance matrix estimation for sub-Gaussian distribution due to the presence of Gaussian noise. Consider a sub-Gaussian distribution in with covariance matrix , and let ∈ (0, 1), t ≥ 1. Then with probability of at least

one has

3.33

Here C depends only on the sub-Gaussian norm of a random vector taken from this distribution; the spectral norm of A is denoted as ||A||, which is equal to the maximum singular value of A, that is,

Covariance matrix estimation for arbitrary distribution is also encountered when a general noise interference model is used. Consider a sub-Gaussian distribution in with covariance matrix and supported in some centered Euclidean ball whose radius we denote . Let ∈ (0, 1) and t ≥ 1. Then, with probability at least , one has

3.34

Here C is an absolute constant and log denotes the natural logarithm. In (3.34), typically

Thus the required sample size is

Low rank estimation is often used, since the distribution of a signal in lies close to a low-dimensional subspace. In this case, a much smaller sample size suffices for covariance estimation. The intrinsic dimension of the distribution can be measured with the effective rank of the matrix , defined as

3.35

where denotes the trace of . One always has

and this bound is sharp. The effective rank

always controls the typical norm of X, as

Most of the distribution is supported in a ball of radius , where

The conclusion of (3.34) holds with sample size

Summarizing the above discussion, (3.34) shows that the sample size

suffices to approximate the covariance matrix of a sub-Gaussian distribution in by the sample covariance matrix. While for arbitrary distribution,

is sufficient. For distributions that are approximately low-dimensional, such as that of a signal, a much smaller sample size is sufficient. Namely, if the effective rank of equals r, then a sufficient size is

As in Section 3.3.1, our standard problem (3.15) is

where R_s and R_w are, respectively, covariance matrices of signal and noise. When the sample covariance matrices are used in replacement of actual covariance matrices, it follows that

3.36

We must exploit the fundamental fact that requires only O(rlogn) samples, while requires O(n). Here the effective rank r of R_s is small. For one real sinusoid signal, the rank is only two, that is, r = 2. We can sum up the K sample covariance matrices , for example, K = 200. Let us consider the three-step algorithm:

In Step 3, the signal part coherently adds up and the noise part randomly adds up. This step enhances SNR, which is especially relevant at low SNR signal detection. This basic idea will be behind the chapter on quantum detection.

Another underlying idea is to develop a nonasymptotic theory for signal detection. Given a finite number of (complex) data samples collected into a random vector , the vector length n is very large, but not infinity, in other words, n < ∞. We cannot simply resort to the central limit theorem to argue that the probability distribution function of this vector x is Gaussian since this theorem requires n → ∞.

The recent work on compressed sensing is highly relevant to this problem. Given n, we can develop a theory that is valid with an overwhelming probability. As a result, one cornerstone of our development here is compressed sensing to recover the “information” from n data points x. Another cornerstone is the concentration of measure to study sums of random matrices. For example what are the statistics of the resultant random matrix ?

This problem is closely related to classical multivariate analysis [110, p. 108]. Section 3.6.1 will show that the sum of the random matrices is the ML estimation of the actual covariance matrix.

3.6.1 The Maximum Likelihood Estimation

The problem of Section 3.6.1 is closely related to classical multivariate analysis [110, p. 108]. Given k independent data matrices

where the rows of X_i(n × p) are i.i.d.

what is the ML estimation of the sample covariance matrix?

In practice, the most common constraints are

or

If (b) holds, we can treat all the data matrices as constituting one matrix sample from a single population (distribution).

Suppose that x₁, …, x_n is a random vector sample from a population (distribution) with the pdf , where is a parameter vector. The likelihood function of the whole sample is

Given a matrix sample X, both and are considered as functions of the vector parameter .

Suppose x₁, …, x_n is a random sample from . We have

and

3.40

Let us simplify these equations. When the identity

is summed over the index i = 1, …, n, the final term on the right-hand side vanishes, giving

3.41

Since each term is a scalar, it equals the trace of itself. Thus using

we have

3.42

Summing (3.42) over index i and substituting in (3.41) gives

3.43

Writing

and using (3.40) in (3.43), we have

3.44

For the special case and then (3.44) becomes

3.45

To calculate the ML estimation if (a) holds, from (3.44), we have

3.46

where S_i is the covariance matrix of the i-th matrix sample, i = 1, .., k, and Since there is no restriction on the population means, the ML estimation of is . Setting

(3.46) becomes

3.47

Differentiating (3.47) with respect to and equating to zero yields

3.48

which is the ML estimation of under the conditions stated.

3.6.2 Likelihood Ratio Test (Wilks' Λ Test) for Multisample Hypotheses

Consider k independent normal matrix samples X₁, …, X_k, whose likelihood is considered in Section 3.6.1.

In Section 3.6.1, the ML estimation under is and S, since the observation can be viewed under as constituting a single random matrix sample. The ML estimation of under the alternative hypothesis is , the i-th sample mean, and the ML estimation of the common sample covariance matrix is n⁻¹W, where, following (3.47), we have

is the “within-groups” sum of squares and products (SSP) matrix and Using (3.46), the LRT is given by

3.49

Here

is the “total” SSP matrix, derived by regarding all the data matrices as if they constituted a single matrix sample. In contrast, the matrix W is the “within-group” SSP and

may be regarded as the “between-groups” SSP matrix. Thus, from (3.49), we have

The matrix W⁻¹B is an obvious generalization of the univariate variance ratio. It will tend to zero if is true.

If n ≥ p + k, under ,

3.50

where Wilks' Λ statistics is described in Section 3.5.

Let us derive the statistics of (3.50). Write the k matrix samples as a single data matrix

where X_i(n_i × p) is the i-th matrix sample, i = 1, …, k. Let 1_i be the n-vector with 1 in the places corresponding to the i-th sample and 0 elsewhere, and set I_i = diag(1_i). Then I = ∑I_i, and 1 = ∑1_i. Let

be the centering matrix for the i-th matrix sample. The sample covariance matrix can be expressed as

Set

We can easily verify that

Further, C₁ and C₂ are idempotent matrices of rank n − k and k − 1, respectively, and C₁C₂ = 0.

Under , H is data matrix from Thus by Theorem 3.7 and Theorem 3.8, we have

and, furthermore, W and B are independent. Therefore, (3.50) is derived.

3.7 Likelihood Ratio Test

3.7.1 General Gaussian Detection and Estimator-Correlator Structure

The most general signal assumption is to allow the signal to be composed of a deterministic component and a random component. The signal then can be modeled as a random process with the deterministic part corresponding to a nonzero mean and the random part corresponding to a zero mean random processes with a given signal covarance matrix. For generality the noise covariance matrix can be assumed to be arbitrary. These assumptions lead to the general Gaussian detection problem [118, 167], which mathematically is written as

Define the column vector

3.51

and similarly for x and w. In vector and matrix form

where , and , and x and w are independent. The LRT decides if

where

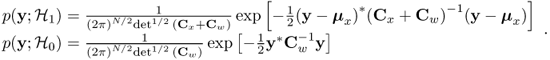
Taking the logarithm, retaining only the data-dependent terms, and scaling produces the test statistic

3.52

From the matrix inverse lemma [114, p. 43] [118, 167]

3.53

for , (3.52) is rewritten as

where

is the MMSE estimator of x. This is a prewhitener followed by an estimator-correlator.

Using the properties of the trace operation (see Section A.3)

3.54

where α is a constant, we have

3.55

where the matrix yy* is of size N × N and of rank one. We can easily choose T₀ > 0, since T(y) > 0 that will be obvious later. Therefore, (3.55) can be rewritten as

3.56

Let A ≥ 0 and B ≥ 0 be of the same size. Then [112, 329] (see Section A.6.2)

3.57

With the help of (3.57), on one hand, (3.56) becomes

Or,

3.58

if

3.59

Using (3.57), on the other hand, (3.55) becomes

3.60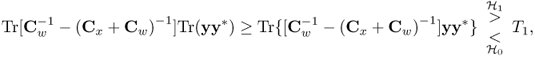

3.61

if

3.62

(which is identical to (3.59)) whose necessary condition to be valid is:

3.63

due to the following fact: If A ≤ B for A ≥ 0 and B ≥ 0, then (see Section A.6.2)

3.64

Note that A⁻¹ + B⁻¹ ≠ (B + A)⁻¹.

Starting from (3.53), we have

3.65

with

3.66

where (3.54) is used in the second step and, in the third step, we use the following [114, p. 43]

Let A > 0 and B > 0 be of the same size. Then [114, p. 181]

3.67

where λ_max(A) is the largest eigenvalue of A. Due to the facts A > 0 and B > 0 given in (3.66), with the help of (3.65) and (3.67), (3.61) becomes

3.68

Combining (3.65) and (3.67) yields

3.69

Using (3.69), (3.58) turns out to be

since

Here |a| is the absolutue value of a. The necessary condition of (3.63) is satisfied even if the covariance matrix of the signal C_x is extremely small, compared with that of the noise C_w. This is critical to the practical problem at hand: sensing of an extremely weak signal in the spectrum of interest. At first sight, the necessary condition of (3.63) seems be trivial to achieve; this intuition, however, is false. At extremely low SNR, this condition is too strong to be satisfied. The lack of sufficient samples to estimate the covariance matrices C_w and C_x is the root of the technical difficulty. Fortunately, the signal covariance matrix C_x lies in the space of lower rank than that of the noise covariance matrix C_w. This fundamental difference in their ranks is the departure point for most of developments in Chapter 4.

(3.68) is expressed in a form that is convenient in practice. Only the traces of these covariance matrices are needed! The traces are, of course, positive scalar real values, which, in general, are random variables. The necessary condition for (3.68) to be valid is (3.63) C_w < C_x + C_w.

3.7.1.1 Divergence

Let y:[0, C_y] denote an N × 1 normal random vector with mean zero and covariance matric C_y. The problem considered here is the test:

In particular, we have C₀ = C_w and C₁ = C_w + C_x. Divergence [123] is a coarse measure of how the log likelihood distinguishes between and :

where

The matrix Q can be rewritten as

The log likelihood ratio can be rewritten as

The transformed vector z is distributed as [0, C_z], with C_z = I for and C_z = S for . S is called the signal-to-noise-ratio matrix.

3.7.1.2 Orthogonal Decomposition

The matrix S has an orthogonal decomposition

where Λ is a diagonal matrix with diagonal elements λ_i and U satisfies U^TU = I. This implies that solves the generalized eigenvalue problem

With this representation for S, the log likelihood ratio may be expressed as

where the random vector y has covariance matrix under and I under :

3.7.1.3 Rank Reduction

A reduced-rank version of the log likelihood ratio is

where I_r and are reduced-rank versions of I and that retain r nonzero terms and N − r zero terms.

This rank reduction is fine, whenever the discarded eigenvalues λ_i are unity (noise components). The problem is that nonunity eigenvalues are sometimes discarded with much penalty. We introduce a new criterion, divergence, a coarse measure of how the log likelihood distinguishes between and

We emphasize that it is the sum of , not , that determines the contribution of an eigenvalue. It will lead to penalty when we discard the small eigenvalues. At extremely low SNR, the eigenvalues are almost uniformly distributed, it is difficult to do reduced-rank processing. The trace sum of S and S⁻¹ must be considered as a whole. Obviously, we require that

since

where A, B are Hermitian matrices. The matrix inequality condition implies

or,

The rank r divergence is identical to the full-rank divergence when N − r of the eigenvalues in the original diagonal matrix are unity. To illustrate, consider the case

The difference between C₁ and C₀ is

Assuming , then rank(R₁ − R₀) = rank(L) and a rank(L) detector has the same divergence as a full-rank detector.

 

3.7.2 Tests with Repeated Observations

Consider a binary hypothesis problem [124] with a sequence of independent distributed random vectors If

denotes the likelihood radio function of a single observation, an LRT for this problem takes the form

3.70

where τ(K) denotes a threshold that may depend on the number of observations, K. Taking the logarithms on both sides of (3.70), and denoting Z_k = ln(Λ(y_k)), we find that

When τ(K) tends to a constant as K → ∞,

Taking the logarithm, retaining only the data-dependent terms, and scaling produces the test statistic (setting μ_x for brevity)

3.71

Using the following fact

3.72

(3.71) becomes

3.73

If the following sufficient condition for the LRT for repeated observations is satisfied

3.74

implying (see Section A.6.2)

using (3.57), we have

3.75

Or,

3.76

The covariance matrix of y is defined as

The asymptotic case of K → ∞ is

3.77

since the sample covariance matrix converges to the true covariance matrix, that is

To guarantee (3.74), the following stronger condition is enough

3.78

due to (3.64).

3.7.2.1 Case 1. Diagonal Covariance Matrix on : Equal Variances

When x[n] is a complex Gaussian random process with zero mean and covariance matrix C_x and w[n] is complex white Gaussian noise (CWGN) with variance matrix . The probability distribution functions (PDFs) are given by

where I is the identity matrix of N × N, and TrI = N.

The log-likelihood ratio is

Consider the following special case:

and

The LRT of (3.79) becomes

3.79

Using the matrix inverse lemma

we have

3.80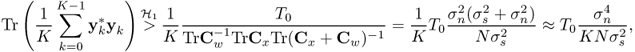

when the signal is very weak, or . TrC_y is the total power (variation) of the received signal plus noise. Note y_k are vectors of length N.

Consider the single observation case, K = 1, we have

which is the energy detector. Intuitively, if the signal is present, the energy of the received data increases. In fact, the equivalent test statistic can be regarded as an estimator of the variance. Comparing this to a threshold recognizes that the variance under is but under is

3.7.2.2 Case 2. Correlated Signal

Now assume N = 2 and

where ρ is the correlation coefficient between x[0] and x[1].

where

where

If A > 0, then

Obviously, C_w + C_x > 0. From (3.77), we have

3.81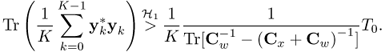

3.7.3 Detection Using Sample Covariance Matrices

If we know the covariance matrices perfectly, we have

In practice, estimated covariance matrices such as sample covariance matrices must be used:

where A₀ and A₁ are sample covariance matrices for the noise while B is the sample covariance matrix for the signal. The eigenvalues λ_i of

where A is positive semidefinite and B positive definite, satisfy

Let A be positive definite and B symmetric such that det (A + B) ≠ 0, then

The inequality, known as Olkin's inequality, is strict if and only if B is nonsingular.

Wilks' lambda test [110, p. 335]

where λ_j are the eigenvalues of A⁻¹B.

The equicorrelation matrix is [112, p. 241]

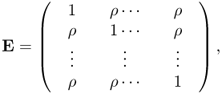
or,

where ρ is any real number and J is a unit matrix J_p = 11^T, 1 = (1, …, 1)^T. Then e_ii = 1, e_ij = ρ, for i ≠ j. For statistical purposes this matrix is most useful for − (p − 1)⁻¹ < ρ < 1. Direct verification shows that, if ρ ≠ 1, − (p − 1)⁻¹, then E⁻¹ exists and is given by

Its determinant is given by

Since J has rank 1 with eigenvalues p and corresponding eigenvector 1, we see that the equicorrelation matrix E = (1 − ρ)I + ρJ has eigenvalues:

and the same eigenvectors as J. logdet A is bounded:

where A and A + B are positive definite, with equality if and only if B = 0. If A ≥ 0 and B ≥ 0, then [112, 329]

3.7.4 GLRT for Multiple Random Vectors

The data is modeled as a complex Gaussian random vector with probability density function

mean , and covariance matrix R_xx. Consider M independent, identically distributed (i.i.d.) random vectors

drawn from this distribution. The joint probability density function of these vectors is written as

where S_xx is the sample covariance matrix

and m_x is the sample mean vector

Our task is to test whether R_xx has structure 0 or the alternative structure 1:

The GLRT statistic is

The actual covariance matrices are not known, they are replaced with their ML estimates computed using the M random vectors. If we denote by the ML estimate of R_xx under and by the ML estimate of R_xx under , we have

If we assume further that is the set of positive definite matrices (no special restrictions are imposed), then , and

The generalized likelihood ratio for testing whether R_xx has structure is

where a and g are the arithmetic and geometric means of the eigenvalues of :

Based on the desirable probability of false alarm or probability of detection, we can choose a threshold l₀. So if l > l₀, we accept hypothesis , and if l < l₀, we reject it. Consider a special case

where is the variance of each component of x. The ML estimate of R_xx under is , where the variance is estimated as . Therefore, the GLRT is

This test is invariant under scale and unitary transformation.

3.7.5 Linear Discrimination Functions

Two random vectors can be stochastically ordered by using their likelihood ratio. Here, we take our liberty in freely borrowing materials from [123]. Linear discrimination may be used to approximate a quadratic likelihood ratio when testing y:(0, C_i) under hypothesis _i. The Neyman-Pearson test of versus will have us compare the log likelihood ratio to a threshold:

We hope, on the average, L(y) will be larger than η under and smaller than η under . An incomplete measure of how the test of versus will perform is the difference in terms of L(y) under two hypotheses:

This function is the J-divergence between versus introduced previously in Section 3.7.1. It is related to information that a random sample can bring about the hypothesis _i. The J-divergence for the multivariate normal problem _i:y:N(0, C_i) is computed by carrying out the expectations:

This expression does not completely characterize the performance of a likelihood ratio statistic, but it does bring useful information about the “distance” between and .

3.7.5.1 Linear Discrimination

Assume that the data y is used to form the linear discriminant function (or statistic)

This statistic is distributed as under _i. If a log likelihood ratio is formed using the new variable z, then the divergence between versus is

Let us define the following ratio of quadratic forms

Then we may rewrite the divergence as

It is remarkable to note that the choice of the discriminant w that maximizes divergence is also the choice of w that maximizes a function of a quadratic form. The maximization of quadratic forms is formulated as a generalized eigenvalue problem [123, p. 163]. Let us rewrite divergence as

The function of J is convex in λ. It achieves its maximum either at λ_max or at λ_min, where λ_max and λ_min, respectively, are maximum and minimum values of

The divergence is maximized as follows:

The linear discriminant function is either the maximum eigenvector of or the minimum eigenvector of , depending on the nature of the maximum and minimum values. It is not always the maximum eigenvector. The choice of w = w_max or w = w_min is also called a principal component analysis (PCA). Without loss of generality, w may be normalized as w*w = 1. Then, if R₀ = I, the linear discriminant function is distributed as follows

3.7.6 Detection of Correlated Structure for Complex Random Vectors

For the assessment of multivariate association between two complex random vectors x and y, our treatment here draws materials from [125, 126]. Consider two real zero-mean vectors and with two correlation matrices

We assume both correlation matrices are invertible. The cross-correlation properties between x and y are described by the cross-correlation matrix

but this matrix is generally difficult to explain. In order to illuminate the underlying structure, many correlation analysis techniques transform x and y into p-dimensional internal representation

with p = min{m, n}. The full rank matrices A, B are chosen such that all partial sums over the absolute values of the correlations

are maximized

3.82

The solution to the maximization problem (3.82) leads to a diagonal cross-correlation matrix between and

3.83

with

In order to summarize the correlation between x and y, an overall correlation coefficient ρ is defined as a function of the diagonal correlations {k_i}. This correlation coefficient shares the invariance of the {k_i}. Because of the maximization (3.82), the assessment of correlation is allowed in a lower-dimensional subspace of rank

There is a variety of possible correlation coefficients that can be defined based on the first r canonical correlations for a given rank r.

For r = p, these coefficients can be expressed in terms of the original correlation matrices

where

These coefficients share the invariance of the canonical correlations, that is, they are invariant under a nonsingular linear transformation of x and y. For jointly Gaussian x and y, determines the mutual information between x and y

The complex version of correlation analysis is discussed in [125, 126].

 

 

¹ This is true, if we know the true covariance matrices, rather than the sample covariance matrices.