5.5 Case Studies and Applications
5.5.1 Fundamental Example of Using Large Random Matrix
We follow [279] for this development. Define an M × N complex matrix as

where (Xij)1≤i≤M, 1≤j≤N are (a number of MN) i.i.d. complex Gaussian variables ![]() . x1, x2, …, xN are columns of X. The covariance matrix R is
. x1, x2, …, xN are columns of X. The covariance matrix R is
![]()
The empirical covariance matrix is defined as

In practice, we are interested in the behavior of the empirical distribution of the eigenvalues of ![]() for large M and N. For example, how do the histograms of the eigenvalues (λi)i=1, …, M of
for large M and N. For example, how do the histograms of the eigenvalues (λi)i=1, …, M of ![]() behave when M and N increase? It is well known that when M is fixed, but N increases, that is,
behave when M and N increase? It is well known that when M is fixed, but N increases, that is, ![]() is small, the large law of large numbers requires
is small, the large law of large numbers requires

In other words, if N ![]() M, the eigenvalues of
M, the eigenvalues of ![]() are concentrated around σ2.
are concentrated around σ2.
On the other hand, let us consider the practical case when M and N are of the same order of magnitude. As
5.60 ![]()
it follows that
![]()
but
![]()
does not converge toward zero. Here || · || denotes the norm of a matrix. It is remarkable to find (by Marchenko and Pastur [251]) that the histograms of the eigenvalues of ![]() tend to concentrate around the probability density of the so-called Marchenko-Pastur distribution
tend to concentrate around the probability density of the so-called Marchenko-Pastur distribution
with
![]()
(5.61) is still true in the non Gaussian case. One application of (5.61) is to evaluate the asymptotic behavior of linear statistics
where f(x) is an arbitrary continuous function. The use of (5.61) allows many problems to be treated in closed forms. To illustrate, let us consider several examples:
![]()
![]()
![]()
The fluctuations of the linear statistics (5.62) can be cast into closed forms. The bias of the linear estimator is
![]()
The variance of the linear estimator is
![]()
where Δ2 is the variance and ![]() denotes the normal Gaussian distribution. In other words,
denotes the normal Gaussian distribution. In other words,
![]()
5.5.2 Stieltjes Transform
We here follow [329]. Let us consider
![]()
where ![]() is an N × K matrix with i.i.d. entries with zero mean and variance one, for
is an N × K matrix with i.i.d. entries with zero mean and variance one, for
![]()
Denote A = σ2I and D = IK, K. For this case, we have
![]()
Applying Theorem 5.25, it follows that
![]() is the Cauchy transform of the eigenvalue distribution of matrix σ2I. The solution of (5.64) gives
is the Cauchy transform of the eigenvalue distribution of matrix σ2I. The solution of (5.64) gives
![]()
The asymptotic eigenvalue distribution is given by

where δ(x) is a unit mass at 0 and [z]+ = max(0, z).
Another example is the standard vector-input, vector-output (VIVO) model3
where x and y are, respectively, input and output vectors, and H and n are channel transfer function and additive white Gaussian noise with zero mean and variance σ2. Here H is a random matrix. (5.65) covers a number of systems including CDMA, OFDM, MIMO, cooperative spectrum sensing and sensor network. The mutual information between the input vector x and the output vector y is a standard result in information theory

Differentiating C with respect to σ2 yields

It is interesting to note that we get the closed form in terms of the Stieltjes transform.
5.5.3 Free Deconvolution
We follow the definitions and notations of the example shown in Section 5.5.1. For more details, we see [12, 329, 330]. For a number of N vector observations of xi, i = 1, …, N, the sample covariance matrix is defined as
Here, W is an M × N matrix consisting of i.i.d. zero-mean, Gaussian vectors of variance 1/N. The main advantage of free deconvolution techniques is that asymptotic “kick-in” at a much earlier stage than other techniques available up to now [329]. Often, we know the values of R which are the theoretical values. We would like to find ![]() . If we know the behavior of the matrix WWH, with the aid of (5.66),
. If we know the behavior of the matrix WWH, with the aid of (5.66), ![]() can be obtained. Thus, our problem of finding
can be obtained. Thus, our problem of finding ![]() is reduced to understand WWH. Fortunately, the limiting distribution of the eigenvalues of WWH is well-known to be the Marchenko-Pastur law.
is reduced to understand WWH. Fortunately, the limiting distribution of the eigenvalues of WWH is well-known to be the Marchenko-Pastur law.
Due to our invariance assumption on one of the matrices (here WWH), the eigenvector structure does not matter. The result enables us to compute the eigenvalues of R, by knowing only the eigenvalues of ![]() . The invariance assumption “frees,” in some sense, one matrix from the other by “disconnecting” their eigenspaces.
. The invariance assumption “frees,” in some sense, one matrix from the other by “disconnecting” their eigenspaces.
5.5.4 Optimal Precoding of MIMO Systems
Given M receive antennas and N transmit antennas, the standard vector channel model is
5.67 ![]()
where the complex entries of H of M × N are the MIMO channel gains and H is a nonobservable Gaussian random matrix with known (or well estimated) second order statistics. Here, x is the transmitted signal vector and n is the additive Gaussian noise vector at the receiver with ![]() .
.
The optimum precoding problem is to find the covariance matrix Q of x in order to maximize some figure of merit of the system. For example, the optimization problem can be expressed as

A possible alternative is to maximize a large system approximation of I(Q). Closed-form expressions (5.63) can be used [331]. For more details, see [279].
5.5.5 Marchenko and Pastur's Probability Distribution
We follow [279] for this development. The Stieltjes transform is one of the numerous transforms associated with a measure. It is well suited to study large random matrices and was first introduced in this context by Marchenko and Pastur [251]. The Stieltjes transform is defined in (5.34).
Consider
where VN is a M × N matrix with i.i.d. complex Gaussian random variables ![]() . Our aim is the limiting spectral distribution of X = WNWNH. Consider the associated resolvent and its Stieltjes transform
. Our aim is the limiting spectral distribution of X = WNWNH. Consider the associated resolvent and its Stieltjes transform
The main assumption is: The ratio ![]() is bounded away from zero and upper bounded, as M, N → ∞.
is bounded away from zero and upper bounded, as M, N → ∞.
The approach is sketched here. First one derives the equation that is satisfied by the Stieltjes transform of the limiting spectral distribution ![]() defined in (5.69). Afterwards, one relies on the inverse formula (see (5.35)) of Stieltjes transform, to obtain the so-called Marchenko-Pastur distribution.
defined in (5.69). Afterwards, one relies on the inverse formula (see (5.35)) of Stieltjes transform, to obtain the so-called Marchenko-Pastur distribution.
There are three main steps:
The Stieltjes transform in this work of large random matrices plays a role analogous to the Fourier transform in a linear, time-invariant (LTI) system.
5.5.6 Convergence and Fluctuations Extreme Eigenvalues
We here follow [279] for presentation. Consider the WWH defined in (5.68). Denote by
![]()
the ordered eigenvalues of WWH. The support of Marchenko-Pastur distribution is
![]()
One theorem is: If cN → c*, we have

where “a.s.” denotes “almost surely.” The ratio of two limit expressions is used for spectrum sensing in Example 5.4.
A central limit theorem holds for the largest eigenvalue of matrix WWH, as M, N → ∞. The limiting distribution is known as Tracy-Widom Law's distribution (see (5.50)) for fluctuations of ![]() .
.
The function FTW2(s) stands for Tracy-Widom culmination distribution function. MATLAB codes are available to compute [332].
Let us cN → c*. When corrected centered and rescaled, ![]() converges to a Tracy-Widom distribution:
converges to a Tracy-Widom distribution:

5.5.7 Information plus Noise Model and Spiked Models
We refer to [263, 279, 299, 300, 302, 333–335] for more details. The observed M-dimensional time series yn for the n-vector sample are expressed as

with
![]()
where sn collects K < M nonobservable “source signals,” the matrix A is deterministic with an unknown rank K < M, and ![]() is additive white Gaussian noise such that
is additive white Gaussian noise such that ![]() . Here
. Here ![]() denotes the set of all integers.
denotes the set of all integers.
In matrix form, we have YN = (y1, …, yN)T, observation matrix of M × N. We do this for SN and VN. Then,
![]()
Using the normalized matrices
![]()
we obtain
Detection of the presence of signal(s) from matrix ![]() is to tell whether K = 1 versus K = 0 (noise only) to simplify. Since K does not scale with M, that is, K
is to tell whether K = 1 versus K = 0 (noise only) to simplify. Since K does not scale with M, that is, K ![]() M, a spiked model is reached.
M, a spiked model is reached.
We assume that the number of sources K is K ![]() N. (5.39) is a model of
N. (5.39) is a model of
![]()
The asymptotic regime is defined as
![]()
Let us further assume that SN is a random matrix with independent ![]() elements (Gaussian iid source signals), and AN is deterministic. It follows that
elements (Gaussian iid source signals), and AN is deterministic. It follows that
![]()
where BN is M × N with independent ![]() elements.
elements.
Consider a spectral factorization of ![]()
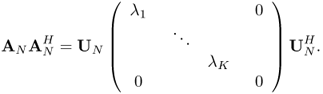
Let PN be the M × M matrix
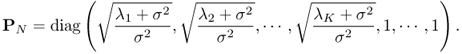
Then
![]()
where WN is M × N with independent ![]() elements and
elements and ![]() denotes weak convergence. Since PN is a fixed rank perturbation of identity, we reach the so-called multiplicative spike model
denotes weak convergence. Since PN is a fixed rank perturbation of identity, we reach the so-called multiplicative spike model
![]()
Similarly, we can define the additive spike model. Let us assume that SN is a deterministic matrix and
![]()
is such that
![]()
The additive spike model is defined as
![]()
A natural question arises: What is the impact of ![]() on the spectrum of
on the spectrum of ![]() in the asymptotic regime?
in the asymptotic regime?
Let ![]() and FN be the distribution functions of the spectral measures of
and FN be the distribution functions of the spectral measures of ![]() and
and ![]() , respectively. Then
, respectively. Then
![]()
Thus ![]() and
and ![]() have identical (Marchenko-Pastur) limit spectral measure, either for the multiplicative or the additive spike model.
have identical (Marchenko-Pastur) limit spectral measure, either for the multiplicative or the additive spike model.
We use our measured data to verify the Marchenko-Pastur law. There are five USRP platforms serving as sensor nodes. The data acquired from one USRP platform are segmented into twenty data blocks. All these data blocks are used to build large random matrices. In this way, we emulate the network with 100 sensor nodes. If there is no signal, the spectral distribution of noise sample covariance matrix is shown in Figure 5.1(a) which follows the Marchenko-Pastur law in (5.3). When signal exists, the spectral distribution of sample covariance matrix of signal plus noise is show in Figure 5.1(b). The experimental results well agree with the theory. The support of the eigenvalues is finite. The theoretical prediction offered by the Marchenko-Pastur law can be used to set the threshold for detection.
Figure 5.1 Spectral distribution. (a) Spectral distribution of noise sample covariance matrix; (b) Spectral distribution of sample covariance matrix of signal plus noise.

Main results on the eigenvalues can be summarized into the theorem [279].
![]()
![]()

5.5.8 Hypothesis Testing and Spectrum Sensing
This example is continued from the example shown in Section 5.5.7. For more details, we see [263, 279, 299, 300, 302, 333–335]. One motivation is to exploit the asymptotic limiting distribution for spectrum sensing.
The hypothesis test is formulated as
![]()
Assume further K = 1 source for convenience.
![]()
is a rank one matrix such that
![]()
The GLRT is
The natural question is: what is the asymptotic performance of TN under the assumption of large random matrices?
Under ![]() and
and ![]() , we have
, we have
![]()
As a consequence of Theorem 5.43, under ![]() , if
, if ![]() , then
, then
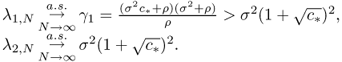
If ![]() , then
, then
![]()
Using the above result in (5.71), under ![]() , we have
, we have
![]()
Under ![]() , if
, if ![]() , we have
, we have
![]()
If ![]() , we have
, we have
![]()
Recall that
![]()
The limit of detectability by the GLRT is given by
![]()
Defining ![]() , we have
, we have
![]()
For extremely low SNR, it follows that c* must be very small, implying
![]()
With the help of the Tracy-Widom law, false alarm probability can be evaluated and linked with the decision threshold TN.
For finite, low rank perturbation of large random matrices, the eigenvalues and eigenvectors are studied in [335].

5.72 ![]()


5.5.9 Energy Estimation in a Wireless Network
Consider a wireless (primary) network [330] in which K entities are transmitted data simultaneously on the same frequency resource. Transmitter k ∈ (1, …, K) has transmitted power Pk and is equipped with nk antennas. We denote

the total number of transmit antennas of the primary network.
Consider a secondary network composed of a total of N, N ≥ n, sensing devices: they may be N single antennas devices or multiple devices embedded with multiple antennas whose sum is equal to N. The N sensors are collectively called the receiver. To ensure that every sensor in the second network roughly captures the same amount of energy from a given transmitter, it is assumed that the respective transmitter-sensor distances are alike. This is realistic assumption for anb in-house femtocell network.
Denote ![]() the multiple antenna channel matrix between transmitter k and the receiver. We assume that the entries of
the multiple antenna channel matrix between transmitter k and the receiver. We assume that the entries of ![]() are independent and identically distributed (i.i.d.), with zero mean, unit variance, and finite fourth-order moment.
are independent and identically distributed (i.i.d.), with zero mean, unit variance, and finite fourth-order moment.
At time instant m, transmitter k emits the multi-antenna signal vector ![]() , whose entries are assumed to be i.i.d., with zero mean, unit variance, and finite fourth-order moment.
, whose entries are assumed to be i.i.d., with zero mean, unit variance, and finite fourth-order moment.
Further, we assume that at time instant m, the received signal vector is impaired by an additive white Gaussian noise (AWGN) vector, denoted ![]() , whose entries are assumed to be i.i.d., with zero mean, variance σ2, and finite fourth-order moment on every sensor. The entries of
, whose entries are assumed to be i.i.d., with zero mean, variance σ2, and finite fourth-order moment on every sensor. The entries of ![]() have unit variance.
have unit variance.
At time m, the receiver senses the signal ![]() defined as
defined as

It is assumed that at least M consecutive sampling periods, the channel fading coefficients are constant. We concatenate M successive signal realizations into
![]()
we have
![]()
for every k. This can be further recast into the final form
where ![]() is diagonal with first n1 entries P1, subsequent n2 entries P2, …, last nK entries PK,
is diagonal with first n1 entries P1, subsequent n2 entries P2, …, last nK entries PK,
![]()
By convention, it is assumed that
![]() H, W and X have independent entries of finite fourth-order moment. The entries of X need not be identically distributed, but may originate from a maximum of K distinct distributions.
H, W and X have independent entries of finite fourth-order moment. The entries of X need not be identically distributed, but may originate from a maximum of K distinct distributions.
Our objective is to infer the values of P1, ···, PK from the realization of the random matrix Y. The problem at hand is to exploit the eigenvalue distribution of ![]() as N, n and M grow large at the same rate.
as N, n and M grow large at the same rate.
![]()
![]()
![]()
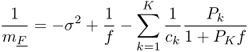
![]()
For Assumption 5.3 and Assumption 5.4—too long to be covered in this context—that are used in the following theorem, we refer to [330].
5.5.10 Multisource Power Inference
Let ![]() be defined as in Theorem 5.45, and
be defined as in Theorem 5.45, and
![]()
be the vector of the ordered eigenvalues of BN. Further assume that the limiting ratios c, c1, …, cK and P are such that Assumptions 5.3 and 5.4 are fulfilled for some ![]() . Then, as N, n, M grow large, we have
. Then, as N, n, M grow large, we have ![]() where the estimates
where the estimates ![]() is given by
is given by
- if M ≠ N,
![]()
- if M = N,

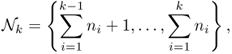
A blind multisource power estimation has been derived in [330]. Under the assumptions that the ratio between the number of sensors and the number of signals are not too small, and the source transmit powers are sufficiently distinct from one another, they derive a method to infer the individual source powers if the number of sources are known. This novel method outperforms the alternative estimation techniques in the medium to high SNR regime. This method is robust to small system dimensions. As such, it is particularly suited to the blind detection of primary mobile users in future cognitive radio networks.
5.5.11 Target Detection, Localization, and Reconstruction
We follow [336] for this development. A point reflector can model a small dielectric anomaly in electromagnetism; a small density anomaly in acoustics, or more generally, a local variation of the index of refraction in the scalar wave equation. The contrast of the anomaly can be of order one but its volume is small compared to the wavelength. In such a situation, it is possible to expand the solution of the wave equation around the background solution.
Consider the scalar wave equation in a d-dimensional homogeneous medium with the index of refraction n0. The reference speed of propagation is denoted by c. It is assumed that the target is a small reflector of inclusion D with the index of refraction nref ≠ n0. The support of the inclusion is of the form D = xref + B, where B is a domain with small volume. Thus the scalar wave equation with the source S(t, x) takes the form
![]()
where the index of refraction is given by
![]()
For any yn, zm far from xref the field Re[(yn, zm)e−jωt], observed at yn, when a point source emits a time-harmonic signal with frequency ω at zm, can be expanded as powers of the volume as
![]()
where k0 = n0ω/c is the homogeneous wavenumber, ρref is the scattering amplitude

and ![]() (y, z) is the Green's function or fundamental solution of the Helmhotz equation with a point source at z:
(y, z) is the Green's function or fundamental solution of the Helmhotz equation with a point source at z:
![]()
More explicitly, we have
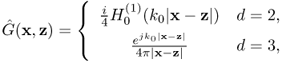
where ![]() is the Hankel function of the first kind of order zero.
is the Hankel function of the first kind of order zero.
When there are M sources (zm)m = 1, …, M and N receivers (yn)n = 1, …, N, the response matrix is the N × M matrix
![]()
defined by
![]()
This matrix has rank one:
![]()
The nonzero singular value is
The associated left and right singular vectors uref and vref are given by
![]()
where the normalized vectors of Green's functions are defined as

where * denotes the conjugation of the function.
The matrix H0 is the complete data set that can be collected. In practice, the measured matrix is corrupted by electronic or measurement noise that has the form of an additive noise. The standard acquisition gives
![]()
where the entries of W are independent complex Gaussian random variables with zero mean and variance ![]() . We assume that N ≥ M.
. We assume that N ≥ M.
The detection of a target can be formulated as a standard hypothesis testing problem
![]()
Without target ![]() , the behavior of W is has been extensively studied. With target
, the behavior of W is has been extensively studied. With target ![]() , the singular values of the perturbed random response matrix are of interest. This model is also called the information plus noise model or the spiked population model. The critical regime of practical interest is that the singular values of an unperturbed matrix are of the same order, as the singular values of the noise, that is, σref is of the same order of magnitude as σ. Related work is in [24, 25, 308–311], Johnstone [9, 19, 22, 312–318], and Nadler [305].
, the singular values of the perturbed random response matrix are of interest. This model is also called the information plus noise model or the spiked population model. The critical regime of practical interest is that the singular values of an unperturbed matrix are of the same order, as the singular values of the noise, that is, σref is of the same order of magnitude as σ. Related work is in [24, 25, 308–311], Johnstone [9, 19, 22, 312–318], and Nadler [305].

![]()
![]()

The type-3 Tracy-Widom distribution has the cdf ΦTW3(z) given by
![]()
The expectation of Z3 is ![]() and its variance is Var[Z3] = 1.22.
and its variance is Var[Z3] = 1.22.
The singular eigenvectors of the perturbed response matrix are described in the following proposition. Define the scalar product as
![]()


A standard imaging function for target localiztion is the MUSIC function defined by
![]()
where u(x) is the normalized vector of Green's function. It is a nonlinear function of a weighted subspace migration functional
![]()
The reconstruction can be formulated in this context. Using Proposition 5.7, we can see that the quantity
is an estimator of σref, provided that ![]() . From (5.74), we can estimate the scattering amplitude ρref of the inclusion by
. From (5.74), we can estimate the scattering amplitude ρref of the inclusion by
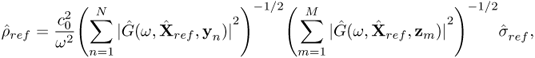
with ![]() the estimator of (5.75) of σref and
the estimator of (5.75) of σref and ![]() is an estimator of the position of the inclusion. This estimator is not biased asymptotically since it compensates for the level repulsion of the first singular value due to the noise.
is an estimator of the position of the inclusion. This estimator is not biased asymptotically since it compensates for the level repulsion of the first singular value due to the noise.
5.5.12 State Estimation and Malignant Attacker in the Smart Grid
A natural situation to use the large random matrices is in the Smart Grid where the big network is met. We use one example to illustrate this potential. We follow the model of [337] for our setting. State estimation and a malignant attack on it are considered in the context of large random matrices.
Power network state estimators are broadly used to obtain an optimal estimate from redundant noisy measurements, and to estimate the state of a network branch which, for economical or computational reasons, is not directly monitored.
The state of a power network at a certain instant of time is composed of the voltage angles and magnitudes at all the system buses. Explicitly, let ![]() and
and ![]() be, respectively, the state and measurements vector. Then, we have
be, respectively, the state and measurements vector. Then, we have
where h(x) is a nonlinear measurement function, and ![]() is a zero mean random vector satisfying
is a zero mean random vector satisfying
![]()
The network state could be obtained by measuring directly the voltage phasors by means of phasor measurement devices. We adopt the approximated estimation model that follows from the linearization around the origin of (5.76)
![]()
where
![]()
Because of the interconnection structure of the power network, the measurement matrix H is sparse.
We assume that zi is available from i = 1 to i = N. We denote by ZN the p × N observation matrix. (5.76) can be rewritten as
where
![]()
From this matrix ZN, we can define the sample covariance matrix of the observation as
![]()
while the empirical spatial correlation matrix associated with the noiseless observation will take the form
![]()
To simplify the notation in the future, we define the matrices
![]()
so that (5.77) can be equivalently formulated as
where ![]() is the (normalized) matrix of observations, BN is a deterministic matrix containing the signals contribution, and WN is a complex Gaussian white noise matrix with i.i.d. entries that have zero mean and variance σ2/N.
is the (normalized) matrix of observations, BN is a deterministic matrix containing the signals contribution, and WN is a complex Gaussian white noise matrix with i.i.d. entries that have zero mean and variance σ2/N.
If N → ∞ while M is fixed, the sample covariance matrix of the observations
![]()
of ZN converges toward the matrix
![]()
in the sense that
However, in the joint limits
![]()
which is the practical case, (5.79) is no longer true. The random matrix theory must be used to derive the consequences. (5.78) is a standard form in [282, 333, 338, 339].
Given the distributed nature of a power system and the increasing reliance on local area networks to transmit data to a control center, it is possible for an attacker to attack the network functionality by corrupting the measurements vector z. When a malignant agent corrupts some of the measurements, the new state to measurements relation becomes
where ![]() is chosen by the attacker, and thus, it is unknown and unmeasurable by any of the monitoring stations.
is chosen by the attacker, and thus, it is unknown and unmeasurable by any of the monitoring stations.
(5.80) is a standard hypothesis testing problem. The GLRT can thus be used, together with the random matrix theory. Following the same standard procedure as above, we have
![]()
where
![]()
By studying the sample covariance matrix
![]()
we are able to infer different behavior under hypothesis ![]() or
or ![]() . It seems that this result for this example is reported for the first time.
. It seems that this result for this example is reported for the first time.
5.5.13 Covariance Matrix Estimation
We see [340] for more details. Consider a discrete-time complex-valued K-user N-dimensional vector channel with M channel uses. We define ![]() and
and ![]() . We assume the system load β < 1(K < N); otherwise the signal subspace is simply the entire N-vector space. In the m-th channel use, the signal at the receiver can be represented by an N-vector defined by
. We assume the system load β < 1(K < N); otherwise the signal subspace is simply the entire N-vector space. In the m-th channel use, the signal at the receiver can be represented by an N-vector defined by
where hkm is the channel symbol of user k, having unit power, xk is the signature waveform of user k (note that sk is independent of the sample index m), and w(m) is additive noise. By defining
![]()
(5.81) is rewritten as
We do not assume specific distribution laws of the entries in H, x, w, thereby making the channel model more general [340]:
- The entries of X are mutually independent random variables, each having zero expectation and variance
 . Therefore,
. Therefore,  almost surely, as N → ∞.
almost surely, as N → ∞. - The entries of h(m) are mutually independent random variables. The random vectors
 are mutually independent for different values of m and satisfying
are mutually independent for different values of m and satisfying
![]()
- The entries of w(m) are mutually independent random variables. The random vectors w(m)m = 1, …, M are mutually independent for different values of m and satisfy
![]()
- X, h(m), w(m) are jointly independent.
Such a model is useful for CDMA and MIMO systems.
The covariance matrix of the received signal (5.81) is given by
5.83 ![]()
Based on (5.82) and
![]()
the unbiased sample covariance matrix estimate is defined as
5.84 
where
![]()
By applying the theory of noncrossing partitions, one can obtain explicit expressions for the asymptotic eigenvalue moments of the covariance matrix estimate [340]. Here we only give some key results.
5.5.13.1 Noise-Free Case
When ![]() , the sample covariance matrix is given by
, the sample covariance matrix is given by
![]()
The generic eigenvalue of ![]() is denoted by
is denoted by ![]() and one defines the eigenvalue moments as
and one defines the eigenvalue moments as
![]()
The explicit expressions are derived in [340].
The Stieltjes transform of ![]() is denoted by
is denoted by ![]() .
.
(5.85) can be used to derive the cumulation distribution function (CDF) and the probability distribution function (PDF) of ![]() , through the inverse formula for the Stieltjes transform.
, through the inverse formula for the Stieltjes transform.
![]()
![]()
The closed-form PDF of ![]() within its support has been derived in [340] and is too long to be included here.
within its support has been derived in [340] and is too long to be included here.
![]()
5.5.13.2 Noisy Case
We extend the anaysis to the general case of ![]() . When
. When ![]() , the exact covariance matrix is of full rank and there is a mass point at
, the exact covariance matrix is of full rank and there is a mass point at ![]() with probability 1 − β.
with probability 1 − β.
Similar to the noise-free case, the eigenvalue moments of ![]()
are derived in a closed form in [340]. Let us give the first four moments

The asymptotic eigenvalue moments of the estimated covariance matrix are larger than those of the exact covariance matrix (except for the expectation). This is true for both noisy and noise-free cases.
The Stieltjes transform of the eigenvalue ![]() , denoted by
, denoted by ![]() , is given by
, is given by

We define
![]()
Their counterparts for the exact covariance matrix, denoted by λmin, λmax, and ![]() , are given by
, are given by ![]() , and
, and ![]() , respectively.
, respectively.
The properties 3 and 4 in Theorem 5.47 are the same as in Theorem 5.49. Property 1 is completely different. The essential reason is the existence of a mass point at ![]() . When
. When ![]() , the mass point at 0 always exists with probability 1 − β and the support on positive eigenvalues is continuous. When
, the mass point at 0 always exists with probability 1 − β and the support on positive eigenvalues is continuous. When ![]() , and 1 < α < ∞, the estimated covariance matrix is of full rank and there is no mass point. When α → ∞, the support of positive eigenvalues has to be separated into at least two disjoint intervals such that the support around
, and 1 < α < ∞, the estimated covariance matrix is of full rank and there is no mass point. When α → ∞, the support of positive eigenvalues has to be separated into at least two disjoint intervals such that the support around ![]() shrinks to a point.
shrinks to a point.
5.5.14 Deterministic Equivalents
Deterministic equivalents for certain functions of large random matrices are of interest. The most important references are [281, 341–344]. Let us follow [281] for this presentation. Consider an N × n random matrix ![]() , where the entries are given by
, where the entries are given by
![]()
n. Here (σij(n), 1 ≤ i ≤ N, 1 ≤ j ≤ n) is a bounded sequence of real numbers called a variance profile; the ![]() are centered with unit variance, independent and identically distributed (i.i.d.) with finite 4 + ε moment. Consider now a deterministic N × n matrix An whose columns and rows are uniformly bounded in the Euclidean norm.
are centered with unit variance, independent and identically distributed (i.i.d.) with finite 4 + ε moment. Consider now a deterministic N × n matrix An whose columns and rows are uniformly bounded in the Euclidean norm.
Let
![]()
This model has two interesting features: the random variables are independent but not i.i.d. since the variance may vary and An, the centering perturbation of Yn, can have a very general form. The purpose of our problem is to study the behavior of
![]()
that is, the Stieltjes transform of the empirical eigenvalue distribution of ![]() when n → ∞, and N → ∞ in such a way that
when n → ∞, and N → ∞ in such a way that ![]() .
.
There exists a deterministic N × N matrix-valued function Tn(z) analytic in ![]() such that, almost surely,
such that, almost surely,
![]()
In other words, there exists a deterministic equivalent to the empirical Stieltjes transform of the distribution of the eigenvalues of ![]() . It is also proved that
. It is also proved that ![]() is the Stieltjes transform of a probability measure πn(dλ), and that for every bounded continuous function f, the following convergence holds almost surely
is the Stieltjes transform of a probability measure πn(dλ), and that for every bounded continuous function f, the following convergence holds almost surely
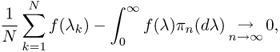
where the (λk)1≤k≤N are the eigenvalues of ![]() . The advantage of considering
. The advantage of considering ![]() as a deterministic approximation instead of
as a deterministic approximation instead of ![]() (which is deterministic as well) lies in the fact that Tn(z) is in general far easier to compute than
(which is deterministic as well) lies in the fact that Tn(z) is in general far easier to compute than ![]() whose computation relies on Monte Carlo simulations. These Monte Carlo simulations become increasingly heavy as the size of the matrix Σn increases.
whose computation relies on Monte Carlo simulations. These Monte Carlo simulations become increasingly heavy as the size of the matrix Σn increases.
This work is motivated by the MIMO wireless channels. The performance of these systems depends on the so-called channel matrix Hn whose entries ![]() represent the gains between transmit antenna j and receive antenna i. Matrix Hn is often modeled as a realization of a random matrix. In certain context, the Gram matrix
represent the gains between transmit antenna j and receive antenna i. Matrix Hn is often modeled as a realization of a random matrix. In certain context, the Gram matrix ![]() is unitarily equivalent to a matrix (Yn + An)(Yn + An)* where An is a possibly full rank deterministic matrix. As an application, we derive a deterministic equivalent to the mutual information:
is unitarily equivalent to a matrix (Yn + An)(Yn + An)* where An is a possibly full rank deterministic matrix. As an application, we derive a deterministic equivalent to the mutual information:

where σ2 is a known parameter.
Let us consider the extension of the above work. Consider
![]()
where (σij(n), 1 ≤ i ≤ N, 1 ≤ j ≤ n) is uniformly bounded sequence of real numbers, and the random variables ![]() are complex, centered, i.i.d. with unit variance and finite 8th moment.
are complex, centered, i.i.d. with unit variance and finite 8th moment.
We are interested in the fluctuations of the random variable
![]()
where Yn* is the Hermitian adjoint of Yn and ρ > 0 is an additional parameter. It is proved [342] that when centered and properly scaled, this random variable satisfies a Center Limit Theorem (CLT) and has a Gaussian limit whose parameters are identified. Understanding its fluctuations and in particular being able to approximate its standard deviation is of major interest for various applications such as for instance the computation of the so-called outage probability.
Consider the following linear statistics of the eigenvalues
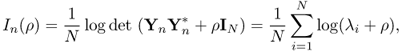
where λi is the eigenvalue of matrix ![]() . This functional is of course the mutual information for the MIMO channel. The purpose of [342] is to establish a CLT for In(ρ) whenever
. This functional is of course the mutual information for the MIMO channel. The purpose of [342] is to establish a CLT for In(ρ) whenever ![]() .
.
There exists a sequence of deterministic probability measure πn such that the mathematical expectation ![]() satisfies
satisfies
![]()
We study the fluctuations of
![]()
and prove that this quantity properly rescaled converges toward a Gaussian random variable. In order to prove the CLT, we study the quantity
![]()
from which the fluctuations arise and the quantity
![]()
which yields a bias.
The variance of Θ2 of ![]() takes a remarkably simple closed-form expression. In fact, there exists a n × n deterministic matrix An whose entries depend on the variance profile σij such that the variance takes the form:
takes a remarkably simple closed-form expression. In fact, there exists a n × n deterministic matrix An whose entries depend on the variance profile σij such that the variance takes the form:
![]()
where ![]() in the fourth cumulant of the complex variable X11 and the CLT is expressed as:
in the fourth cumulant of the complex variable X11 and the CLT is expressed as:
![]()
The bias can be also modeled. There exists a deterministic quantity Bn such that:
![]()
In [343], they study the fluctuations of the random variable:

where
![]()
as the dimensions of the matrices go to infinity at the same pace. Matrices Xn and An are respectively random and deterministic N × n matrices; matrices Dn and ![]() are deterministic and diagonal. Matrix Xn has centered, i.i.d., entries with unit variance, either real and complex. They study the fluctuations associated to noncentered large random matrices. Their contribution is to establish the CLT regardless of specific assumptions on the real or complex nature of the underlying random variables. It is in particular not assumed that the random variables are Gaussian, neither that whenever the random variables Xij are complex, their second moment
are deterministic and diagonal. Matrix Xn has centered, i.i.d., entries with unit variance, either real and complex. They study the fluctuations associated to noncentered large random matrices. Their contribution is to establish the CLT regardless of specific assumptions on the real or complex nature of the underlying random variables. It is in particular not assumed that the random variables are Gaussian, neither that whenever the random variables Xij are complex, their second moment ![]() is zero nor is it assumed that the random variables are circular.
is zero nor is it assumed that the random variables are circular.
The mutual information In has a strong relationship with the Stieltjes transform
![]()
of the spectral measure of ![]() :
:
![]()
Accordingly, the study of the fluctuations of In is also an important step toward the study of general linear statistics of the eigenvalues of ![]() which can be expressed via the Stieltjes transform:
which can be expressed via the Stieltjes transform:

5.5.15 Local Failure Detection and Diagnosis
The joint fluctuations of the extreme eigenvalues and eigenvectors are studied for a large dimensional sample covariance matrix [345], when the associated population covariance matrix is a finite-rank perturbation of the identity matrix, corresponding to the so-called spiked model in random matrix theory. The asymptotic fluctuations, as the matrix size grows large, are shown to be intimately linked with matrices from the Gaussian unitary ensemble (GUE). When the spiked population eigenvalues have unit multiplicity, the fluctuations follow a central limit theorem. This result is used to develop an original framework for the detection and diagnosis of local failure in large sensor networks, from known or unknown failure magnitude. This approach is relevant to the Cognitive Radio Network and the Smart Grid. This approach is to perform fast and computationally reasonable detection and localization of multiple failure in large sensor networks through this general hypothesis testing framework. Practical simulations suggest that the proposed algorithms allow for high failure detection and localization performance even for networks of small sizes, although for those much more observations than theoretically predicted are in general demanded.
5.6 Regularized Estimation of Large Covariance Matrices
Estimation of population covariance matrices from samples of multivariate data has always been important for a number of reasons [344, 346, 347]. Principals among these are:
(1) requires estimation of the eigenstructure of the covariance matrix while (2) and (3) require estimation of the inverse. In signal processing and wireless communication, the covariance matrix is always the starting point.
Exact expressions were cumbersome, and multivariate data were rarely Gaussian. The remedy was asymptotic theory for large sample and fixed relatively small dimensions. Recently, due to the rising vision of “big data” [1], datasets that do not fit into this framework have been very common—the data are very high-dimensional and sample sizes can be very small relative to dimension.
It is well known by now that the empirical covariance matrix for samples of size n from a p-variate Gaussian distribution, ![]() , is not a good estimator of the population covariance if p is large. Johnstone and his students [9, 19, 22, 312–318, 325, 327] are relevant here.
, is not a good estimator of the population covariance if p is large. Johnstone and his students [9, 19, 22, 312–318, 325, 327] are relevant here.
The empirical covariance matrix for samples of size n from a p-variate Gaussian distribution has unexpected features if both p and n are large. If p/n → c ∈ (0, 1), and the covariance matrix ![]() (the identity), then the empirical distribution of the eigenvalues of the sample covariance matrix
(the identity), then the empirical distribution of the eigenvalues of the sample covariance matrix ![]() follows the Marchenko-Pastur law [348], which is supported on
follows the Marchenko-Pastur law [348], which is supported on
![]()
Thus, the larger p/n (thus c), the more spread out the eigenvalues.
Two broad classes of covariance estimators [347] have emerged: (1) those that rely on a natural ordering among variables, and assume that variables far apart in the ordering are only weakly correlated, and (2) those invariant to variable permutations. However, there are many applications for which there is no notion of distance between variables at all.
Implicitly, some approaches, for example, [312], postulate different notions of sparsity. Thresholding of the sample covariance matrix has been proposed in [347] as a simple and permutation-invariant method of covariance regulation. A class of regularized estimators of (large) empirical covariance matrices corresponding to stationary (but not necessarily Gaussian) sequences is obtained by banding [344].
We follow [346] for notation, motivation, and background.
We observe X1, …, Xn, i.i.d. p-variate random variables with mean 0 and covariance matrix ![]() , and write
, and write
![]()
For now, we assume that Xi are multivariate normal. We want to study the behavior of estimates of ![]() as both p and n → ∞. It is well known that the ML estimation of
as both p and n → ∞. It is well known that the ML estimation of ![]() , the sample covariance matrix,
, the sample covariance matrix,
![]()
behaves optimally if p is fixed, converging to ![]() at rate n−1/2. If p → ∞,
at rate n−1/2. If p → ∞, ![]() can behave very badly, unless it is “regularized” in some fashion.
can behave very badly, unless it is “regularized” in some fashion.
5.6.1 Regularized Covariance Estimates
5.6.1.1 Banding the Sample Covariance Matrix
For any matrix A = [aij]p × p, and any 0 ≤ k ≤ p, define
![]()
and estimate the covariance ![]() . This kind of regularization is ideal in the situation where the indexes have been arranged in a such a way that in
. This kind of regularization is ideal in the situation where the indexes have been arranged in a such a way that in ![]() we have
we have
![]()
This assumption holds, for example, if ![]() is the covariance matrix of Y1, …, Yp, where Y1, …, Yp is a finite inhomogeneous moving average (MA) process,
is the covariance matrix of Y1, …, Yp, where Y1, …, Yp is a finite inhomogeneous moving average (MA) process,

and xj are i.i.d. mean 0. Banding an arbitrary covariance matrix does not guarantee positive definitiveness.
All our sets will be the subsets of the so-called well-conditioned covariance matrices, ![]() , such that, for all p,
, such that, for all p,
![]()
Here, ![]() and
and ![]() are the maximum and minimum eigenvalue of
are the maximum and minimum eigenvalue of ![]() , and
, and ![]() is independent of p.
is independent of p.
Examples of such matrices [349] include
![]()
where Xi is a stationary ergodic process, and Wi is a noise process independent of ![]() . This model also includes the “spiked model” of Paul [27], since a matrix of bounded rank is Hilbert-Schmidt. We discuss this model in detail elsewhere.
. This model also includes the “spiked model” of Paul [27], since a matrix of bounded rank is Hilbert-Schmidt. We discuss this model in detail elsewhere.
We define the first class of positive definite symmetric well conditioned matrices ![]()
as follows:
The class ![]() in (5.86) contains the Toeplitz class
in (5.86) contains the Toeplitz class ![]() defined by
defined by
![]()
where fΣ(m) denotes the mth derivative of f. By [350], ![]() is symmetric, Toeplitz,
is symmetric, Toeplitz, ![]() , with σ(− k) = σ(k), and
, with σ(− k) = σ(k), and ![]() has an absolutely continuous spectral distribution with Radon-Nikodym derivative fΣ(t), which is continuous on (− 1, 1), then
has an absolutely continuous spectral distribution with Radon-Nikodym derivative fΣ(t), which is continuous on (− 1, 1), then
![]()
A second uniformity class of nonstationary covariance matrices is defined by
![]()
The bound independent of dimension identifies any limit as being of “trace class” as operator for m > 1.
The main work is summarized in the following theorem.
5.87 ![]()
5.6.2 Banding the Inverse
Suppose we have
![]()
defined on a probability space, with probability measure ![]() , which is
, which is ![]() ,
, ![]() . Let
. Let
be the ![]() projection of
projection of ![]() on the linear span of X1, …Xj−1, with Zj = (X1, …, Xj−1)T the vector of coordinates up to j − 1, and aj = (aj1, …, aj, j−1)T the vector of coefficients. If j = 1, let
on the linear span of X1, …Xj−1, with Zj = (X1, …, Xj−1)T the vector of coordinates up to j − 1, and aj = (aj1, …, aj, j−1)T the vector of coefficients. If j = 1, let ![]() . Each vector aj can be computed as
. Each vector aj can be computed as
5.89 ![]()
Let the lower triangular matrix A with zeros on the diagonal contain the coefficients aj arranged in rows. Let ![]() ,
, ![]() and let
and let ![]() be a diagonal matrix. The geometry of
be a diagonal matrix. The geometry of ![]() or standard regression theory implies independence of the residuals. After applying the covariance operator to the identity
or standard regression theory implies independence of the residuals. After applying the covariance operator to the identity
![]()
we obtain the modified Cholesky decomposition of ![]() and
and ![]() :
:
Suppose now that k < p. It is natural to define an approximation to ![]() by restricting the variables in regression (5.88) to
by restricting the variables in regression (5.88) to
![]()
In other words, in (5.88), we regress each Xj on its closest k predecessors only. Let Ak be the k-banded lower triangular matrix containing the new vectors of coefficients ![]() , and let
, and let ![]() be the diagonal matrix containing the corresponding residual variance. Population k-banded approximations
be the diagonal matrix containing the corresponding residual variance. Population k-banded approximations ![]() and
and ![]() are obtained by plugging in Ak and Dk in (5.90) for A and D.
are obtained by plugging in Ak and Dk in (5.90) for A and D.
If
![]()
with ![]() lower triangular,
lower triangular, ![]() , let
, let
5.91 
5.92 ![]()
5.93 
5.6.3 Covariance Regularization by Thresholding
Bickel and Levina (2008) [347] considers regularizing a covariance matrix of p variables estimated from n (vector) observations, by hard thresholding. They show that the thresholded estimate is consistent in the operator norm as long as the true covariance matrix is sparse in a suitable sense, the variables are Gaussian or sub-Gaussian, and (logp)/n → 0, and obtain explicit rates.
The approach of thresholding of the sample covariance matrix is a simple and permutation-invariant method of covariance regularization. We define the thresholding operator by
![]()
which we refer to as A thresholded at s. Ts preserves symmetry and is invariant under permutations of variables labels, but does not necessarily preserve positive definiteness. However, if
![]()
then Ts(A) is necessarily positive definite, since for all vectors v with ||v||2 = 1, we have
![]()
Here, λmin(A) stands for the minimum eigenvalue of A.
![]() in (5.86) defines the uniformity class of “approximately bandable” covariance matrices. Here, we define the uniformity class of covariance matrices invariant under permutations by
in (5.86) defines the uniformity class of “approximately bandable” covariance matrices. Here, we define the uniformity class of covariance matrices invariant under permutations by

If q = 0, we have

is a class of sparse matrices. Naturally, there is a class of covariance matrices ![]() that satisfy both banding and thresholding conditions. Define a subset of
that satisfy both banding and thresholding conditions. Define a subset of ![]() by
by

for α > 0.
We consider n i.i.d. p-dimensional observations X1, …, Xn distributed according to a distribution ![]() , with
, with ![]() (without loss of generality), and
(without loss of generality), and ![]() . We define the empirical (sample) covariance matrix by
. We define the empirical (sample) covariance matrix by
![]()
where ![]() and write
and write ![]() .
.
![]()
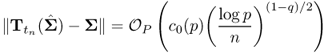

This theorem is in parallel with the banding result of Theorem 5.50.
5.6.4 Regularized Sample Covariance Matrices
Let us follow [344] to state a certain central limit theorem for regularized sample covariance matrices. We just treated how to band the covariance matrix ![]() ; here we consider how to band the sample covariance matrix
; here we consider how to band the sample covariance matrix ![]() . We consider regularization by banding, that is, by replacing those entries of XTX that are, at distance, exceeding b = b(p) away from the diagonal by 0. Let Y = Y(p) denote the thus regularized empirical matrix.
. We consider regularization by banding, that is, by replacing those entries of XTX that are, at distance, exceeding b = b(p) away from the diagonal by 0. Let Y = Y(p) denote the thus regularized empirical matrix.
Let X1, …, Xk be real random variables on a common probability space with moments of all orders, in which the characteristic function
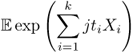
is an infinitely differentiable function of the real variables t1, …, tk. One defines the joint cumulant C(X1, …, Xk) by the formula
5.94 
(The middle expression is a convenient abbreviated notation.) The quantity C(X1, …, Xk) depends symmetrically and ![]() -multilinearly on X1, …, Xk. Moreover, dependence is continuous with respect to the
-multilinearly on X1, …, Xk. Moreover, dependence is continuous with respect to the ![]() -norm. One has in particular
-norm. One has in particular
![]()
Let
![]()
be a stationary sequence of real random variables, satisfying the following conditions:
Let us turn to random matrices. Let
![]()
be an i.i.d. family of copies of ![]() . Let X = X(p) be the n × p random matrices with entries
. Let X = X(p) be the n × p random matrices with entries
![]()
Let B = B(p) be the p × p deterministic matrix with entries
![]()
Let Y = Y(p) be the p × p random symmetric matrix with entries
and eigenvalues ![]() .
.
For integers j, let
![]()
For integers m > 0 and all integers i and j, we write
Here, the convolution ![]() is defined for any two summable functions
is defined for any two summable functions ![]() :
:
![]()
Now we are in a position to state a central limit theorem.
![]()
![]()
![]()
![]()
5.6.5 Optimal Rates of Convergence for Covariance Matrix Estimation
Despite recent progress on covariance matrix estimation, there has been remarkably little fundamental theoretical study on optimal estimation. Cai, Zhang and Zhou (2010) [351] establish the optimal rates for estimating the covariance matrix under both the operator norm and Frobenius norm. Optimal procedures under two norms are different, and consequently matrix estimation under the operator norm is fundamentally different from vector estimation. The minimax upper bound is reached by constructing a special class of tapering estimators and by studying their risk properties. The banding estimator treated previously in Section 5.6.1 is suboptimal and the performance can be significantly improved using the technique to be covered now.
We write an ≈ bn if there are positive constants c and C independent of n such that c ≤ an/bn ≤ C. For matrix A, its operator norm is defined as ![]() . We assume that p ≤ exp(γn) for some constant γ > 0.
. We assume that p ≤ exp(γn) for some constant γ > 0.
where ![]() is the maximum eigenvalue of the matrix
is the maximum eigenvalue of the matrix ![]() , and α > 0, M > 0 and M0 > 0.
, and α > 0, M > 0 and M0 > 0.
5.101 ![]()
The proposed procedure does not attempt each row/column optimally as a vector. This procedure does not optimally trade bias and variance for each row/column. This proposed estimator has good numerical performance; it nearly uniformly outperforms the banding estimator.
![]()
5.103 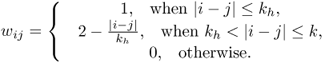
Assume that the distribution of the X1's are sub-Gaussian in the sense that there is ρ > 0 such that
Let ![]() denote the set of distributions of X1 that satisfy (5.100) and (5.105).
denote the set of distributions of X1 that satisfy (5.100) and (5.105).
From (5.106), it is clear that the optimal choice of k is of order n−2α/(2α+1). The upper bound given in (5.107) is thus rated optimal, among the class of the tapering estimators defined in (5.104). The minimax lower bound derived in Theorem 5.56 shows that the estimator ![]() with k = n−2α/(2α+1) is in fact rated optimal among all estimators.
with k = n−2α/(2α+1) is in fact rated optimal among all estimators.
![]()
Theorem 5.55 and Theorem 5.56 together show that the minimax risk for estimating the covariance matrices over the distribution space ![]() satisfies, for p > n1/(2α+1),
satisfies, for p > n1/(2α+1),
5.108 ![]()
The results also show that the tapering estimator ![]() with tapering parameter k = n1/(2α+1) attains the optimal rate of convergence
with tapering parameter k = n1/(2α+1) attains the optimal rate of convergence ![]() .
.
It is interesting to compare the tapering estimator with the banding estimator of [346]. A banding estimator with bandwidth ![]() was proposed and the rate of convergence of
was proposed and the rate of convergence of ![]() was proven.
was proven.
Both the tapering estimator and the banding estimator are not necessarily positive semidefinite. A practical proposal to avoid this would projecting the estimator ![]() to the space of positive semidefinite matrices under the operator norm. One may first diagonalize
to the space of positive semidefinite matrices under the operator norm. One may first diagonalize ![]() and then replace negative eigenvalues by zeros. The resulting estimator will be then positive semidefinite.
and then replace negative eigenvalues by zeros. The resulting estimator will be then positive semidefinite.
In addition to the operator norm, the Frobenius norm is another commonly used matrix norm. The Frobenius norm of a matrix A is defined as the l2 vector norm of all entries in the matrix

This is equivalent to treating the matrix A as a vector of length p2. It is easy to see that the operator norm is bounded by the Frobenius norm, that is, ||A|| ≤ ||A||F.
Consider estimating the covariance matrix ![]() from the sample
from the sample ![]() . We have considered the parameter space
. We have considered the parameter space ![]() defined in (5.100). Other similar parameter spaces can be also considered. For example, in time series analysis it is often assumed the covariance |σij| decays at the rate |i − j|−(α−1) for some α > 0. Consider the collection of positive-definite symmetric matrices satisfying the following conditions
defined in (5.100). Other similar parameter spaces can be also considered. For example, in time series analysis it is often assumed the covariance |σij| decays at the rate |i − j|−(α−1) for some α > 0. Consider the collection of positive-definite symmetric matrices satisfying the following conditions
where ![]() is the maximum eigenvalue of the matrix
is the maximum eigenvalue of the matrix ![]() .
. ![]() is a subset of
is a subset of ![]() as long as M1 ≤ αM.
as long as M1 ≤ αM.
Let ![]() denote the set of distribution of X1 that satisfies (5.105) and (5.109).
denote the set of distribution of X1 that satisfies (5.105) and (5.109).
5.110 ![]()
The inverse of the covariance matrix ![]() is of significant interest. For this purpose, we require the minimum eigenvalue of
is of significant interest. For this purpose, we require the minimum eigenvalue of ![]() to be bounded away from zero. For δ > 0, we define
to be bounded away from zero. For δ > 0, we define
Let ![]() denote the set of distributions of X1 that satisfy (5.100), (5.105), and (5.111), and similarly, distribution in
denote the set of distributions of X1 that satisfy (5.100), (5.105), and (5.111), and similarly, distribution in ![]() that satisfy (5.105), (5.109), and (5.111).
that satisfy (5.105), (5.109), and (5.111).
5.112 ![]()
5.6.6 Banding Sample Autocovariance Matrices of Stationary Processes
Nonstationary covariance estimators by banding a sample covariance matrix or its Cholesky factor were considered in [352] and [346] in the context of longitudinal and multivariate data. Estimation of covariance matrices of stationary processes was considered in [353]. Under a short-range dependent condition for a wide class of nonlinear processes, it is shown that the banded covariance matrix estimates converge, in operator norm, to the true covariance matrix with explicit rates of convergence. Their consistency was established under some regularity conditions when
![]()
where n and p are the number of subjects and variables, respectively. Many good references are included in [353].
Given a realization of X1, …, Xn of a mean-zero stationary process {Xt}, its autocovariance function σk = cov(X0, Xk) can be estimated by
5.113 
It is known that for fixed ![]() , under ergodicity condition,
, under ergodicity condition, ![]() in probability. Entry-wise convergence, however, does not automatically imply that
in probability. Entry-wise convergence, however, does not automatically imply that ![]() is a good estimator of
is a good estimator of ![]() . Indeed, although positive definite,
. Indeed, although positive definite, ![]() is not uniformly close to the population (true) covariance matrix
is not uniformly close to the population (true) covariance matrix ![]() , in the sense that the largest eigenvalue or the operator norm of
, in the sense that the largest eigenvalue or the operator norm of ![]() does not converge to zero. Such uniform convergence is important when studying the rate of convergence of the finite predictor coefficients and performance of various classification methods in time series.
does not converge to zero. Such uniform convergence is important when studying the rate of convergence of the finite predictor coefficients and performance of various classification methods in time series.
Not necessarily positive definite, the covariance matrix estimator is of the form
5.114 ![]()
where l ≥ 0 is an integer. It is a truncated version of ![]() preserving the diagonal and the 2l main subdiagonals; if l ≥ n − 1, then
preserving the diagonal and the 2l main subdiagonals; if l ≥ n − 1, then ![]() . By following [346],
. By following [346], ![]() is called the banded covariance matrix estimate and l its band parameter.
is called the banded covariance matrix estimate and l its band parameter.
Hannan and Deistler (1988) [354] have considered certain linear ARMA processes and obtained the uniform bound
![]()
Here, we consider the comparable results for nonlinear processes, mainly following the notation and results of [353].
Let ![]() , be independent and identically distributed (i.i.d.) random variables. Assume that
, be independent and identically distributed (i.i.d.) random variables. Assume that ![]() is a causal process of the form
is a causal process of the form
where g is a measurable function such that Xi is well-defined and ![]() . Many stationary processes fall within the framework of (5.115).
. Many stationary processes fall within the framework of (5.115).
To introduce the dependent structure, let ![]() be an independent copy of
be an independent copy of ![]() and ξi = (···, εi−1, ε i). Following [355], for i ≥ 0, let
and ξi = (···, εi−1, ε i). Following [355], for i ≥ 0, let
![]()
For α > 0, define the physical dependence of measure
5.116 ![]()
Here, for a random variable Z, we write ![]() , if
, if
![]()
and write || · || = || · ||2. Observe that ![]() is a coupled version of Xi = g(ξi) with ε 0 in the latter replaced by an i.i.d. copy
is a coupled version of Xi = g(ξi) with ε 0 in the latter replaced by an i.i.d. copy ![]() . The quantity δp(i) measures the dependence of Xi on ε 0. We say that
. The quantity δp(i) measures the dependence of Xi on ε 0. We say that ![]() is short-range dependent with moment α if
is short-range dependent with moment α if
That is, the cumulative impact of ε 0 on future values of the process or ![]() is finite, thus implying a short-range dependence.
is finite, thus implying a short-range dependence.

![]()
Let ρ2(A) is the largest eigenvalue of ATA. The n × n matrix A has the operator norm ρ(A).
We define the project operator ![]() as
as
![]()
![]()
5.118 
5.7 Free Probability
In quantum detection, tensor products are needed. For a large number of random matrices, tensor products are too computationally expensive for our problem at hand. Free probability is a highly noncommunicative probability theory with independence based on free products instead of tensor products [356]. Basic examples include the asymptotic behavior of large Gaussian random matrices. The freeness (its beauty and fruitfulness) is the central concept [357].
Independent symmetric Gaussian matrices which are random matrices (also noncommunitative matrix-valued random variables) are asymptotic free. See Appendix A.5 for details on noncommunicative matrix-valued random variables: random matrices are their special cases.
In this subsection, we take the liberty of drawing material from [12, 13]. Here we are motivated for spectrum sensing and (possible) other applications in cognitive radio network. Free probability is a mathematical theory that studies noncommunitative random variables. The “freeness” is the analogue of the classical notation of independence, and it is connected with free products. This theory was initiated by Dan Voiculescu around 1986, who made the statement [16]:
![]()
His first motivation was to study the von Neumann algebras of free groups. One of Voiculescu's central observations was that such groups can be equipped with tracial states (also called states), which resemble expectations in classical probability.
What is the spectrum of the sum A + B [358]? For deterministic matrices A and B one cannot in general determine the eigenvalues of A + B from those of A and B alone, as they depend on the eigenvectors of A and B as well. However, it turns out that for large random matrices A and B satisfying a property called freeness, the limiting spectrum of the sum A + B can indeed be determined from the individual spectra of A and B. This is a central result in free probability theory.
Define the functional φ as
![]()
ϕ stands for the normalized expected trace of a random matrix.
The matrices A1, …, Am are called free if
![]()
whenever
- p1, …, pk are polynomials in one variable;
- i1 ≠ i2 ≠ i3 ··· ≠ ik (only neighboring elements are required to be distinct);
 for all j = 1, …, k.
for all j = 1, …, k.
For independent random variables, the joint distribution can be specified completely by the marginal distributions [359]. For free random variables, the same result can be proven, directly from definition. In particular, if X and Y are free, then the moments φ[(X + Y)n] of X and Y can be completely specified by the moments of X and the moments of Y. The distribution is naturally called free convolution of the two marginal distributions. Classical convolution can be computed via transforms: the log moment generating function of the distribution of X + Y is the sum of the log moment generating function of the individual distributions of X and Y. In contrast, for free convolution, the appropriate transform is called the R-transform. This is defined via the Steltjes transform given by (5.34).
Asymptotic Freeness
To apply the theory of free probability to random matrix theory, we need to extend the definition of free to asymptotic freeness, by replacing the state functional φ by ϕ
![]()
The expected asymptotic pth moment is ϕ(Ap) and ϕ(I) = 1. The definition of asymptotic freeness is analogous to the concept of independent random variables. However, statistical independence does not imply asymptotic freeness.
The Hermitian random matrices A and B are asymptotic free if for all l and for all polynomials pi(·) and qi(·) with 1 ≤ i ≤ l such that
![]()
We state the following useful relationships for asymptotically free A and B
![]()
One approach to characterize the asymptotic spectrum of a random matrix is to obtain its moments of all orders. The moments of a noncommunicative polynomial p(A, B) of two asymptotically free random matrices can be computed from the individual moments of A and B. Thus, if p(A, B), A and B are Hermitian, the asymptotic spectrum of p(A, B) depends on only those of A and B, even if they do not have the same eigenvectors!

[13] compiles a list of some of the most useful instances of asympotic freeness that have been shown so far. Let us list some here:
Sum of Asymptotic Free Random Matrices
Free probability is useful mainly due to the following theorem.
![]()
In particular, the following translation property is valid
![]()
![]()

Let us revisit the problem of sum of K random matrices in Section 3.6. The K sample covariance matrices are asymptotic free.
![]()
![]()
![]()


Products of Asymptotic Free Random Matrices
The S-transform plays an analogous role to the R-transform for products (instead of sum) of asymptotically free matrices.
![]()
The S-transform is the free analog of the Mellin transform in classical probability theory, whereas the R-transform is the free analog of the log-moment generating function in classical probability theory.
There are useful theorems [11] to calculate ϕ[(A + B)n] and ϕ[(AB)n].
Moments of the Sums and Products

![]()
Finding an explicit formula for the coefficients ![]() is a nontrivial combinatorial problem that has been solved by Speicher [360]. From Theorem 5.64, ϕ(A1 ··· Al) is completely determined by the moments of the individual matrices.
is a nontrivial combinatorial problem that has been solved by Speicher [360]. From Theorem 5.64, ϕ(A1 ··· Al) is completely determined by the moments of the individual matrices.
![]()
Theorem 5.65 is based on the fact that, if A and B be nonnegative asymptotically free random matrices, the free cumulants of the sum satisfy
![]()
![]()
5.7.1 Large Random Matrices and Free Convolution
5.7.1.1 Random Matrices and Free Random Variables
In free probability, large random matrices is an example of “free” random variables. Let AN be an N × N symmetric (or Hermitian) random matrix with real eigenvalues. So the two-dimensional complex problem is converted into a one-dimensional real-value problem. The probability measure on the set of its eigenvalues
![]()
(counted with multiplicities) is given by

We are interested in the limiting spectral measure μA as N → ∞. This limiting spectral measure is uniquely characterized by its moments, when compactly supported. We refer to A as an element of the “algebra” with probability measure μA and moments above.
For two random matrices AN and BN with limiting probability distribution μA and μB, we would like to compute the limiting probability distribution for AN + BN and ANBN in terms of the moments of μA and μB. As treated above, the appropriate structure of “freeness,” analogous to independence for “classical” random variables, is what we need to impose on AN and BN, in order to compute these distributions. Since A and B do not commute we are dealing with noncommutative algebra. Since all possible products of A and B are allowed, we have the “free” products, that is, all words in A and B are allowed. We have already dealt with how to compute the moments of these products. The connection with random matrices comes in, because a pair of random matrices AN and BN are asymptotically free, that is, in the limit of N → ∞, so long as at least one of AN or BN has what amounts to eigenvectors that are uniformly distributed with Haar measure. This result is stated precisely in [356].
Table 5.3 lists definitions of R-transform and S-transform and their properties.
5.7.1.2 Free Additive Convolution
When AN and BN are asymptotically free, the (limiting) spectral measure μAB for random matrices of the form
![]()
is given by the free additive convolution of the probability measures μA and μB and written as [356]
5.120 ![]()
An algorithm in terms of the so-called R-transform exists for computing μA+B from μA and μB. See [356] for details and [361] for computational issues.
5.7.1.3 Free Multiplicative Convolution
When AN and BN are asymptotically free, the (limiting) spectral measure μAB for random matrices of the form
![]()
is given by the free multiplicative convolution of the probability measures μA and μB and written as [356]
5.121 ![]()
The algorithm for computing μAB is given in [254, 361–364].
The convolution operators on the noncommunicative algebra of large random matrices exist, and can be computed efficiently (e.g., in MATLAB codes). Symbolic computational tools are now available to perform these nontrial computations efficiently [361, 362]. These tools enable us to analyze the structure of sample covariance matrices and design algorithms that take advantage of this structure [254].
5.7.1.4 Applications to Rank Estimation and Spectrum Sensing
Since the Wishart matrix so formed in (5.13) has eigenvectors that are uniformly distributed with Haar measure, the matrices R and W(α) are asymptotically free! Thus the limiting probability measure ![]() can be obtained using free multiplication convolution as
can be obtained using free multiplication convolution as
where ![]() is the limiting probability measure on the true covariance matrix R and μW is the Marchenko-Pastur density [251], which is defined in (5.3). As given in (5.7), the limiting spectral measure of R is simply
is the limiting probability measure on the true covariance matrix R and μW is the Marchenko-Pastur density [251], which is defined in (5.3). As given in (5.7), the limiting spectral measure of R is simply
![]()
The free probability results are exact when N → ∞, but the predictions are very accurate for N ≈ 8, for rank estimation [254].


![]()
5.7.3 Vandermonde Matrices
For notation and some key theorems, we follow [365] closely. Vandermonde matrices have a central role in signal processing such as the fast Fourier transform or Hadamard transforms. A Vandermonde matrix with complex entries on the unit circle has the following form
where the factor ![]() and the assumption of
and the assumption of ![]() are included to ensure that the analysis will give limiting asymptotic behavior defined in the asymptotic regime of
are included to ensure that the analysis will give limiting asymptotic behavior defined in the asymptotic regime of
We are interested in the case where ω1, …, ωL are independent and identically distributed (i.i.d.), taking values in [0, 2π]. The ωi is called phase distributions. V will be only to denote Vandermonde matrices in this section with a given phase distribution, and the dimensions of the Vandermonde matrices will always be N × L.
[111] has some related results. The overwhelming majority of the known results are concerned about Gaussian matrices or matrices with independent entries. Very few results are available in the literature on matrices whose structure is strongly related to the Vandermonde case.
Often, we are interested in only the moments. It will be shown that asymptotically, the moments of the Vandermonde matrices V depend only on the ratio c and the phase distributions, and have explicit expressions. Moments are useful for performing deconvolution.
The normalized trace is defined as
![]()
The matrices Dr(N), 1 ≤ r ≤ n will denote nonrandom diagonal L × L matrices, where we implicitly assume that ![]() .
.
We say the ![]() have the joint limit distribution as N → ∞ if the limit
have the joint limit distribution as N → ∞ if the limit
![]()
exists for all choices of ![]() .
.
The concepts from partition theory are needed. We denote by ![]() the set of all partitions of
the set of all partitions of ![]() , and use ρ as notation for a partition in
, and use ρ as notation for a partition in ![]() . We write
. We write ![]() , where Wj will be used to denote the blocks of ρ. |ρ| = k denotes the number of blocks in ρ and |Wj| will represent the number of entries in a given block.
, where Wj will be used to denote the blocks of ρ. |ρ| = k denotes the number of blocks in ρ and |Wj| will represent the number of entries in a given block.
For ![]() , with
, with ![]() , we define
, we define
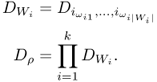
For ![]() , define
, define

where
are i.i.d. (indexed by the blocks of ρ), all with the same distribution as ω, and where b(k) is the block of ρ which contains k (notation is cyclic, that is, b(0) = b(n). If the limit
![]()
exists, then we call it a Vandermonde mixed moment expansion coefficient.
![]()
![]()
For the case of Vandermonde matrices with uniform phase distribution, the noncrossing partitions play a central role. Let u denote the uniform distribution on [0, 2π].


Let us consider generalized Vandermonde matrices defined as
where f is called the power distribution, and is a function from [0, 1] to [0, 1]. We also consider the more general case when f is replaced with a random variable λ,
with the λi i.i.d. and distributed as λ, defined and taking values in [0, 1], and also independent from the ωj.
For (5.128) and (5.129), define

where ![]() are defined as in (5.127). If the limits
are defined as in (5.127). If the limits

exist, then they are called Vandermonde mixed moment expansion coefficients.
![]()
![]()
![]()

![]()
In particular, when the phase distribution is uniform, the first three moments are given by
![]()
![]()
- yi is the N × 1 received vector,
- xi is the L × 1 transmit vector by the L users; we assume
 ,
, - wi is N × 1 additive, white, Gaussian noise of variance
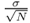 , and
, and - all components in xi and wi are assumed independent.

![]()
![]()
![]()
![]()

![]()


A generalized multipath model that has taken into account the per-path pulse distortion [367–373] is relevant to the context. The so-called scatter centers that are used for the radar community are mathematically modeled by the multiple maths that are used in wireless communications. As a result, this work bridges the gap between two communities. Deeper research can be pursued using this mathematical analogy between two different systems. Physically, the two systems are equivalent.
By sampling the continuous frequency signal at sampling rate ![]()
where B is the bandwidth (in Hertz), we have (for a given channel realization)
5.134 ![]()
where

We set here B = T = 1, which implies that the ωi of (5.125) are uniformly distributed over [0, 2π). When additive noise w is taken into account, our model again becomes that of (5.131): The only difference is that the phase distribution of the Vandermonde matrix now is uniform. L now is the number of paths, N the number of frequency samples, and P is the unknown L × L diagonal power matrix. Taking K observations, we reach the same form as in (5.133). We can do even better than Proposition 5.9. Our estimators for the moments are unbiased for any number of observations K and frequency samples N.
![]()


![]()
![]()

![]()
Consider a phase distribution ω which is uniform on [0, α], and 0 elsewhere. The density is thus ![]() on [0, α], and 0 elsewhere. In this case we have
on [0, α], and 0 elsewhere. In this case we have
![]()
The first of these equations, combined with (5.136), enable us to estimate α.
Certain matrices similar to Vandermonde matrices have analytical expressions for the moments. In [375], the matrices with entries of the form Ai, j = F(ωi, ωj) are considered. This is relevant to the Vandermonde matrices since
![]()
5.7.4 Convolution and Deconvolution with Vandermonde Matrices
In the large dimensional limit, certain random matrices a deterministic behavior of the eigenvalue distribution [377]. In particular, one can obtain the eigenvalue distribution of AB and A + B, based on only the individual eigenvalue distributions of A and B, when the matrices are independent and large. This operation is called convolution, and the inverse operation is called deconvolution.
Gaussian-like matrices fit into this setting, since the concept of freeness [11] can be used. [364] used large Wishart matrices. Random matrix theory was used in [9]; other deterministic equivalents [17, 281, 298, 378] are used; Although used successfully [366], all these techniques can only treat very simple models, that is, one of these considered matrices are unitarily invariant.
The method of moments, which is the focus in this section, is very appealing and powerful when freeness does not apply, for which we still do not have a general framework. It requires the combinatorial skills and can be used for a large class of random matrices. Compared with the Stieltjes transform, this approach has the main drawback that it rarely provides the exact eigenvalue distribution. In many applications, however, we only need a subset of the moments. We mainly follow Ryan and Debbah (2011) [377] for our development.
A N × N Vandermonde matrix V is defined in (5.125). We repeat it here for convenience:
5.137 
The ω1, …, ωL, also called phase distributions, will be assumed i.i.d., taking values in [0, 2π]. Similarly, we consider the asymptotic regime defined in (5.126): N and L go to infinity at the same rate, and write ![]() .
.
In Section 5.7.2, the limit eigenvalue distributions of combinations of VHV and diagonal matrices D(N) were shown to be dependent on the limit eigenvalue distributions of the two matrices.
Define
where V1, V2, … are assumed independent, with phase distributions ω1, …, ωL.
Consider the following four expressions:
5.140 
A special case of Theorem 5.72 is considered here. This theorem states in particular that
![]()
depends only on the moments. This expression characterizes the singular law of a sum of independent Vandermonde matrices. Also, expressions 1 and 3 are found to only rely on the spectra of the component matrices. For convolution expression 1, we have the following corollary.

For expression 3, we have the following corollary.

![]()
For expression 4, we have the following corollary.

The spectral separability seems to be a phenomenon for large N-limit. We are only aware of Gaussian and deterministic matrices where spectral separability occur in finite case [379]. The moments of Hankel, Markov, and Toeplitz matrices [287] are relevant to this context.
A practical example is studied in [377]:
The example only makes an estimate of the first moments of the component matrix D(N). These moments can give valuable information: in cases where it is known that there are few distinct eigenvalues, and the multiplicities are known, only some lower order moments are needed, in order to get an estimate of these eigenvalues.
5.7.5 Finite Dimensional Statistical Inference
We follow [379] for the development here, converting to our notation. Given X and Y are two N × N independent square Hermitian (or symmetric) random matrices:
The method of moments [380] and the Stieltjes transform method [381] can be used. The expression is simple, if some kind of asymptotic freeness [11] of the matrices is assumed. Freeness, however, is not valid for finite matrices. Remarkably, the method of moments can still be used for this purpose. The general finite-dimensional statistical inference framework was proposed [379], and the codes for MATLAB implementation are available [382]. The calculations are tedious. Only Gaussian matrices are addressed. But other matrices such as Vandermonde matrices can also be implemented in the same vein. The general case is more difficult.
Consider the doubly correlated Wishart matrix [383]. Let M, N be positive integers, W be M × N standard, complex, Gaussian, and D (deterministic) M × M and E N × N. Given any positive integer p,, the following moments

exist and can be calculated [379].
The framework of [379] enables us to compute the moments of many types of combinations of independent, Gaussian- and Wishart random matrices, without any assumptions on the matrix dimensions. Since the method of moments only encode information about the lower order moments, it lacks much information which is encoded naturally into the Stieltjes transform; spectrum estimation based on the Stieltjes transform is more accurate than the case when a few moments are used. One interesting question is to ask how many moments are typically required, in order to reach the performance close to that of the Stieltjes transform.
![]()


![]()
![]()

5.143 ![]()

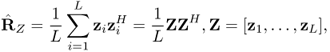
![]()
![]()
1 Multiple-input, multiple-output (MIMO) has a special meaning in wireless communications.
2 This table is primarily compiled from [278].
3 MIMO has a special meaning in the context of wireless communications. This informal name VIVO captures our perception of the problem. Vector nature is fundamental. Vector space is the fundamental mathematical space for us to optimize the system.


















