In the previous chapter, we gave a brief overview of various models for pricing options. In this chapter, we turn our attention to the key task of incorporating derivative securities into the portfolio risk model, which we developed in previous chapters. Just as the nonlinear payoff function was the key feature from the perspective of option pricing in the previous chapter, it is also driving the risk management discussion in this chapter. The nonlinear payoff creates asymmetry in the portfolio return distribution, even if the return on the underlying asset follows a symmetric distribution. Getting a handle on this asymmetry is a key theme of this chapter.

The chapter is structured as follows:

The delta of an option is defined as the partial derivative of the option price with respect to the underlying asset price, S_t. For puts and calls, we define

Notice that the deltas are not observed in the market, but instead are based on the assumed option pricing model.

Figure 11.1 illustrates the familiar tangent interpretation of a partial derivative. The option price for a generic underlying asset price, S, is approximated by

where S_t is the current price of the underlying asset. In Figure 11.1, S_t equals 100.

The delta of an option (in this case, a call option) can be viewed as providing a linear approximation (around the current asset price) to the nonlinear option price, where the approximation is reasonably good for asset prices close to the current price but gets gradually worse for prices that deviate significantly from the current price, as Figure 11.1 illustrates. To a risk manager, the poor approximation of delta to the true option price for large underlying price changes is clearly unsettling. Risk management is all about large price changes, and we will therefore consider more accurate approximations here.

Equipped with a formula for delta from our option pricing formula of choice, we are now ready to adapt our portfolio distribution model from earlier chapters to include portfolios of options.

Consider a portfolio consisting of just one (long) call option on a stock. The change in the dollar value (or the dollar return) of the option portfolio, is then just the change in the value of the option

Using the delta of the option, we have that for small changes in the underlying asset price

Defining geometric returns on the underlying stock as

and combining the previous three equations, we get the change in the option portfolio value to be

The upshot of this formula is that we can write the change in the dollar value of the option as a known value δ_t times the future return of the underlying asset, R_{t + 1}, if we rely on the delta approximation to the option pricing formula.

Notice that a portfolio consisting of an option on a stock corresponds to a stock portfolio with δ shares. Similarly, we can think of holdings in the underlying asset as having a delta of 1 per share of the underlying asset. Trivially, the derivative of a stock price with respect to the stock price is 1. Thus, holding one share corresponds to having δ = 1, and holding 100 shares corresponds to having δ = 100.

Similarly, a short position of 10 identical calls corresponds to setting , where δ^c is the delta of each call option. The delta of a short position in call options is negative, and the delta of a short position in put options is positive as the delta of a put option itself is negative.

The variance of the portfolio in the delta-based model is

where is the conditional variance of the return on the underlying stock.

Assuming conditional normality, the dollar Value-at-Risk (VaR) in this case is

where the absolute value, comes from having taken the square root of the portfolio change variance, Notice that since is measured in dollars, we are calculating dollar VaRs directly and not percentage VaRs as in previous chapters. The percentage VaR can be calculated immediately from the dollar VaR by dividing it by the current value of the portfolio.

In case we are holding a portfolio of several options on the same underlying asset, we can simply add up the deltas. The delta of a portfolio of options on the same underlying asset is just the weighted sum of the individual deltas as in

where the weight, m_j, equals the number of the particular option contract j. A short position in a particular type of options corresponds to a negative m_j.

In the general case where the portfolio consists of options on n underlying assets, we have

In this delta-based model, the variance of the dollar change in the portfolio value is again

Under conditional normality, the dollar VaR of the portfolio is again just

Thus, in this case, we can use the Gaussian risk management framework established in Chapter 4 and Chapter 7 without modification. The linearization of the option prices through the use of delta, together with the assumption of normality, makes the calculation of the VaR and other risk measures very easy.

Notice that if we allow for the standard deviations, to be time varying as in GARCH, then the option deltas should ideally be calculated from the GARCH model also. We recall that for horizons beyond one day, the GARCH returns are no longer normal, in which case the return distribution must be simulated. We will discuss simulation-based approaches to option risk management later. When volatility is assumed to be constant and returns are assumed to be normally distributed, we can calculate the dollar VaR at horizon K by

where σ_DV is the daily portfolio volatility and where K is the risk management horizon measured in trading days.

The linearization of the option price using the delta approach outlined here often does not offer a sufficiently accurate description of the risk from the option. When the underlying asset price makes a large upward move in a short time, the call option price will increase by more than the delta approximation would suggest. Figure 11.1 illustrates this point. If the underlying price today is $100 and it moves to $115, then the nonlinear option price increase is substantially larger than the linear increase in the delta approximation. Risk managers, of course, care deeply about large moves in asset prices and this shortcoming of the delta approximation is therefore a serious issue. A possible solution to this problem is to apply a quadratic rather than just a linear approximation to the option price. The quadratic approximation attempts to accommodate part of the error made by the linear delta approximation.

The Greek letter gamma, γ, is used to denote the rate of change of δ with respect to the price of the underlying asset, that is,

Figure 11.4 shows a call option price as a function of the underlying asset price.

The gamma approximation is shown along with the model option price. The model option price is approximated by the second-order Taylor expansion

For a European call or put on an underlying asset paying a cash flow at the rate q, and relying on the BSM model, the gamma can be derived as

and where ϕ (●) as before is the probability density function for a standard normal variable,

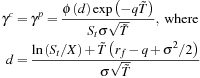
Figure 11.5 shows the gamma for an option using the BSM model with parameters as in Figure 11.2 where we plotted the deltas.

When the option is close to at-the-money, the gamma is relatively large and when the option is deep out-of-the-money or deep in-the-money the gamma is relatively small. This is because the nonlinearity of the option price is highest when the option is close to at-the-money. Deep in-the-money call option prices move virtually one-for-one with the price of the underlying asset because the options will almost surely be exercised. Deep out-of-the-money options will almost surely not be exercised, and they are therefore virtually worthless regardless of changes in the underlying asset price.

All this, in turn, implies that for European options, ignoring gamma is most crucial for at-the-money options. For these options, the linear delta-based model can be highly misleading.

Finally, we note that gamma can be computed using binomial trees as well. Table 11.2 shows the gamma for the American put option from Table 11.1.

The formula used for gamma in the tree is simply

and it is thus based on the change in the delta from point B to C in the tree divided by the average change in the stock price when going from points B and C.

In the previous delta-based model, when considering a portfolio consisting of options on one underlying asset, we have

where δ denotes the weighted sum of the deltas on all the individual options in the portfolio.

When incorporating the second derivative, gamma, we instead rely on the quadratic approximation

where the portfolio δ and γ are calculated as

where again m_j denotes the number of option contract j in the portfolio.

Linear and quadratic approximations to the nonlinearity arising from options can in some cases give a highly misleading picture of the risk from options. Particularly, if the portfolio contains options with different strike prices, then problems are likely to arise. We will give an explicit example of this type of problem.

In such complex portfolios, we may be forced to calculate the risk measure using what we will call full valuation. Full valuation consists of simulating future hypothetical underlying asset prices and using the option pricing model to calculate the corresponding future hypothetical option prices. For each hypothetical future asset price, every option written on that asset must be priced. While full valuation is precise, it is unfortunately also computationally intensive. Full valuation can, in principle, be done with any of the option pricing models discussed in Chapter 10.

To illustrate the three approaches to option risk management, consider the following example. On January 6, 2010, we want to compute the 10-day $VaR of a portfolio consisting of a short position in one S&P 500 call option. The option has 43 calendar days to maturity, and it has a strike price of . The price of the option is , and the underlying index is . The expected flow of dividends per day is , and the risk-free interest rate is per day. For simplicity, we assume a constant standard deviation of 1.5% per calendar day (for option pricing and delta calculation) or equivalently per trading day (for calculating VaR in trading days). We will use the BSM model for calculating as well as the full valuation option prices. We thus have

from which we can calculate the delta and gamma of the option as

for the portfolio, which is short one option; we thus have

where the −1 comes from the position being short.

In the delta-based model, the dollar VaR is

where we now use volatility in trading days.

Using the quadratic model and relying on the Cornish-Fisher approximation to the portfolio dollar return distribution, we calculate the first three moments for the K-day change in portfolio values, when the underlying return follows the 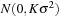distribution. Setting K = 10, we get

where we use volatility denoted in trading days since K is denoted in trading days. The dollar VaR is then

which is much higher than the VaR from the linear model. The negative skewness coming from the option γ and captured by increases the quadratic VaR in comparison with the linear VaR, which implicitly assumes a skewness of 0.

Using instead the simulated quadratic model, we generate 5000 10-trading day returns, with a standard deviation of . Using the δ and γ calculated earlier, we find

Notice again that due to the relatively high γ of this option, the quadratic VaR is more than 50% higher than the linear VaR.

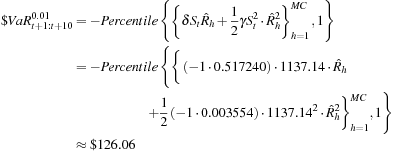
Finally, we can use the full valuation approach to find the most accurate VaR. Using the simulated asset returns to calculate hypothetical future stock prices, we calculate the simulated option portfolio value changes as

where 14 is the number of calendar days in the 10-trading-day risk horizon. We then calculate the full valuation VaR as

In this example, the full valuation VaR is slightly higher than the quadratic VaR. The quadratic VaR thus provides a pretty good approximation in this simple portfolio of one option.

To gain further insight into the difference among the three VaRs, we plot the entire distribution of the hypothetical future 10-day portfolio dollar returns under the three models. Figure 11.6 shows a normal distribution with mean zero and variance .

Figure 11.7 shows the histogram from the quadratic model using the 5000 simulated portfolio returns.

Finally, Figure 11.8 shows the histogram of the 5000 simulated full valuation dollar returns. Notice the stark differences between the delta-based method and the other two. The linear model assumes a normal distribution where there is no skewness. The quadratic model allows for skewness arising from the gamma of the option. The portfolio dollar return distribution has a negative skewness of around −1.29.

Finally, the full valuation distribution is slightly more skewed at −1.42. The difference in skewness arises from the asymmetry of the distribution now being simulated directly from the option returns rather than being approximated by the gamma of the option.

Further details on all the calculations in this section can be found on the web site.

While the previous example suggests that the quadratic approximation yields a good approximation to the true option portfolio distribution, we now show a different example, which illustrates that even the gamma approximation can sometimes be highly misleading.

To illustrate the potential problem with the approximations, consider an option portfolio that consists of three types of options all on the same asset, and that has a price of , all with 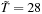calendar days to maturity. The risk-free rate is and the volatility is per calendar day. We take a short position in 1 put with a strike of 95, a short position in 1.5 calls with a strike of 95, and a long position in 2.5 calls with a strike of 105. Using the BSM model to calculate the delta and gamma of the individual options, we get

We are now interested in assessing the accuracy of the delta and gamma approximation for the portfolio over a five trading day or equivalently seven calendar day horizon. Rather than computing VaRs, we will take a closer look at the complete payoff profile of the portfolio for different future values of the underlying asset price, We refer to the value of the portfolio today as and to the hypothetical future value as .

We first calculate the value of the portfolio today as

The delta of the portfolio is similarly

Now, the delta approximation to the portfolio value in five trading days is easily calculated as

The gamma of the portfolio is

and the gamma approximation to the portfolio value in five trading days is

Finally, relying on full valuation, we must calculate the future hypothetical portfolio values as

where we subtract seven calendar days from the time to maturity corresponding to the risk management horizon of five trading days.

Letting the hypothetical future underlying stock price vary from 85 to 115, the three-option portfolio values are shown in Figure 11.9. Notice how the exact portfolio value is akin to a third-order polynomial. The nonlinearity is arising from the fact that we have two strike prices. Both approximations are fairly poor when the stock price makes a large move, and the gamma-based model is even worse than the delta-based approximation when the stock price drops. Further details on all the calculations in this section can be found on the web site.

The important lesson of this three-option example is as follows: The different strike prices and the different exposures to the underlying asset price around the different strikes create higher order nonlinearities, which are not well captured by the simple linear and quadratic approximations. In realistic option portfolios consisting of thousands of contracts, there may be no alternative to using the full valuation method.

This chapter has presented three methods for incorporating options into the risk management model.

First, the delta-based approach consists of a complete linearization of the nonlinearity in the options. This crude approximation essentially allows us to use the methods in the previous chapters without modification. We just have to use the option's delta when calculating the portfolio weight of the option.

Second, we considered the quadratic, gamma-based approach, which attempts to capture the nonlinearity of the option while still mapping the option returns into the underlying asset returns. In general, we have to rely on simulation to calculate the portfolio distribution using the gamma approach, but we only simulate the underlying returns and not the option prices.

The third approach is referred to as full valuation. It avoids approximating the option price, but it involves much more computational work. We simulate returns on the underlying asset and then use an option pricing model to value each option in the portfolio for each of the future hypothetical underlying asset prices.

In a simple example of a portfolio consisting of just one short call option, we showed how a relatively large gamma would cause the delta-based VaR to differ substantially from the gamma and full valuation VaRs.

In another example involving a portfolio of three options with different strike prices and with large variations in the delta across the strike prices, we saw how the gamma and delta approaches were both quite misleading with respect to the future payoff profile of the options portfolio.

The main lesson from the chapter is that for nontrivial options portfolios and for risk management horizons beyond just a few days, the full valuation approach may be the only reliable choice.

The delta, gamma, and other risk measures are introduced and discussed in detail in Hull (2011). Backus et al. (1997) give the formula for delta in the Gram-Charlier model. Duan (1995) provided the delta in the GARCH option pricing model. Garcia and Renault (1998) discussed further the calculation of delta in the GARCH option pricing model. Heston and Nandi (2000) provided the formula for delta in the closed-form GARCH option pricing model.

Risk measurement in options portfolios has also been studied in Alexander et al. (2006), Sorwar and Dowd (2010) and Simonato (2011).

The sample portfolio used to illustrate the pitfalls in the use of the delta and gamma approximations is taken from Britten-Jones and Schaefer (1999), which also contains the analytical VaR formulas for the gamma approach assuming normality.

The important issue of accuracy versus computation speed in the full valuation versus delta and gamma approaches is analyzed in Pritsker (1997).

In this and the previous chapter, we have focused attention on European options. American options and many types of exotic options can be priced using binomial trees as we discussed in the last chapter. Deltas and gammas can be calculated from the tree approach as well as we have seen in this chapter. Hull (2011) contains a thorough introduction to binomial trees as an approximation to the normal distribution with constant variance. Ritchken and Trevor (1999) price American options under GARCH using a time-varying trinomial tree. Duan and Simonato (2001) priced American options under GARCH using instead a Markov chain simulation approach. Longstaff and Schwartz (2001) established a convenient least squares Monte Carlo method for pricing American and certain exotic options. See also Stentoft (2008) and Weber and Prokopczuk (2011) for methods to value American options in a GARCH framework.

Derman (1999), Derman and Kani (1994) and Rubinstein (1994) suggested binomial trees, which allow for implied volatility smiles as in the IVF approach in the previous chapter.

Whether one relies on the delta, gamma, or full valuation approach, an option pricing model is needed to measure the risk of the option position. Because all models are inevitably approximations, they introduce an extra source of risk referred to as model risk. Analysis of the various aspects of model risk can be found in Gibson (2000).