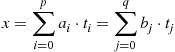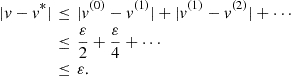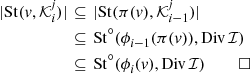Wait-Free Computability for General Tasks
Abstract
Although many tasks of interest are colorless, there are “inherently colored” tasks that cannot be defined without taking process names into account. Some have wait-free read-write protocols, and some do not. This chapter gives a characterization of wait-free read-write solvability for general tasks. We will see that general tasks are harder to analyze than colorless tasks. Allowing tasks to depend on process names seems like a minor change, but it will have sweeping consequences.
Keywords
Cauchy sequence; Lebesgue number; Chromatic subdivision; Deformation retraction; Hourglass task; Hyperplane; Link-connected; Mesh; Open cover; Safe agreement
Although many tasks of interest are colorless, there are “inherently colored” tasks that have no corresponding colorless task. Some are wait-free solvable, but not by any colorless protocol; others are not wait-free solvable. In this chapter we give a characterization of wait-free solvability of general tasks. We will see that general tasks are harder to analyze than colorless tasks. Allowing tasks to depend on process names seems like a minor change, but it will have sweeping consequences.
11.1 Inherently colored tasks: the hourglass task
Not all tasks can be expressed as colorless tasks. For example, the weak symmetry-breaking task discussed in Chapter 9 cannot be expressed as a colorless task, since one process cannot adopt the output value of another.
Theorem 4.3.1 states that a colorless task 
has an 
-process wait-free layered snapshot protocol if and only if there is a continuous map 
carried by 
. Can we generalize this theorem to colorless tasks? A simple example shows that a straightforward generalization will not work.
Consider the following Hourglass task, whose input and output complexes are shown in Figure 11.1. There are three processes: 
, and 
, denoted by black, white, and gray, respectively, and only one input simplex. The carrier map defining this task is shown in tabular form in Figure 11.2 and in schematic form in Figure 11.3. Informally, this task is constructed by taking the standard chromatic subdivision and “pinching” it at the waist to identify (that is, “glue together”) 
’s vertices on the edges representing its two-process executions.
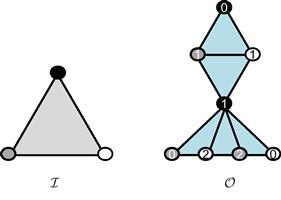
Figure 11.1 Input and output complexes for the Hourglass task. If a vertex 
is labeled with 
, then a process that chooses output vertex 
in the Hourglass task chooses 
’s input value for the 
-set agreement task. Note that each triangle is labeled with at most two process names.
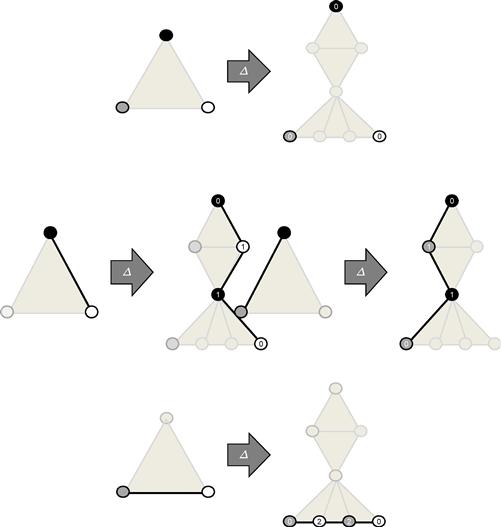
Figure 11.3 Carrier map for the Hourglass task. Single-process executions are at the top, executions for 
and 
on the middle left executions for 
and 
on the middle right, and executions for 
and 
on the bottom.
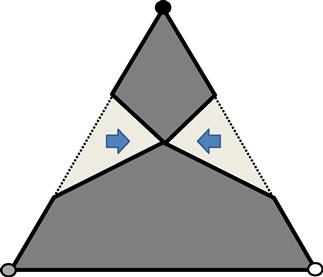
Note that the Hourglass task satisfies the conditions of Theorem 4.3.1: There is a continuous map 
carried by 
, shown schematically in Figure 11.4.1
Nevertheless, even though this task satisfies the conditions of Theorem 4.3.1, it does not have a wait-free layered immediate-snapshot protocol. Perhaps the simplest demonstration is merely to observe that we can solve 2-set agreement by composing a layered immediate snapshot protocol with a protocol for the Hourglass task. It follows that if we had a layered immediate snapshot hourglass protocol, then this composition would yield a layered immediate snapshot protocol for 2-set agreement, which we know to be impossible.
The composite protocol is shown in Figure 11.5. The processes share an array announce[], with one entry for each process, initially null. Process 
first writes its input value to announce[i]and then calls the layered snapshot Hourglass protocol. If that call returns 0, 
may be running by itself, so it decides its own input. Otherwise, the processes behave differently. If the Hourglass protocol returns 1 to 
, then 
is running concurrently with either 
or 
, or both, so it decides announce[1]if it is not null ; otherwise it decides announce[2]. If the Hourglass protocol returns 1 to 
or 
, it decides announce[0]. If the Hourglass protocol returns 2, the process decides its own input. Figure 11.6 labels each output vertex with its corresponding decision value. It is easy to check that in each execution, the processes decide at most two distinct values.
, and 
.
-set agreement values.Since there is no wait-free snapshot protocol for 
-set agreement, there cannot be a wait-free snapshot protocol for the Hourglass task. Why does Theorem 4.3.1 fail to hold for colored tasks? One direction still works: Given a protocol 
solving the task 
, it is easy to extend the proof of Theorem 4.3.1 to exploit the connectivity of the snapshot protocol complex to construct a continuous map 
. Composing this map with the decision map yields a continuous map 
carried by 
.
The other direction fails. Given a continuous map 
carried by 
, it is possible to construct a simplicial approximation 
carried by 
, but that simplicial approximation may not be color-preserving. In other words, one process may be assigned another’s output value. Such flexibility is not an issue with colorless tasks, where by definition a process’s inputs and outputs do not depend on its identity. By contrast, for tasks such as weak symmetry breaking or Hourglass, an output legal for one process may not be legal for another.
11.2 Solvability for colored tasks
Recall that a simplex 
is chromatic if each vertex is labeled with a distinct color, and a chromatic subdivision 
is a subdivision of 
where
(1) each simplex of the subdivision is chromatic,
(2) for each 
, each vertex in 
is labeled with a color from 
.
We are now ready to state our main theorem.
Theorem 11.2.1
A task 
has a wait-free layered immediate snapshot protocol if and only if 
has a chromatic subdivision 
and a color-preserving simplicial map
carried by 
.
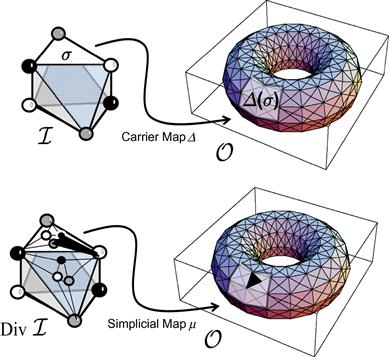
Theorem 11.2.1 is depicted schematically in Figure 11.7. The figure’s top half shows how a task is specified by a carrier map 
that takes each simplex 
of the input complex 
to a subcomplex 
of the output complex 
. The bottom half shows how the simplicial map 
maps each simplex of a chromatic subdivision 
to a simplex in the output complex such that every 
is carried to a simplex in 
.
It is impossible to build such a color-preserving simplicial map for the Hourglass task because the “pinch” in the middle makes it impossible for any simplicial map to be color-preserving.
In Chapter 10 we saw that the (colorless) consensus task has no wait-free layered immediate snapshot protocol. We can illustrate how Theorem 11.2.1 works by relaxing the consensus task’s requirements as follows:
Quasi-Consensus Each of 
and 
is given a binary input. If both have input 
, then both must decide 
. If they have mixed inputs, then either they agree or 
may decide 
and 
may decide 1 (but not vice versa).
Figure 11.8 shows the input and output complexes for the quasi-consensus task. Note that quasi-consensus is not a colorless task. Does it have a wait-free read-write protocol?
It is easy to see that there is no color-preserving simplicial map carried by 
from the input complex to the output complex. The vertices of input simplex 
map to 
and 
, but there is no single output simplex containing both vertices. Nevertheless, there is a map satisfying the conditions of the theorem from a subdivision 
of the input complex. If input simplex 
is subdivided as shown in Figure 11.9, then it can be “folded” around the output complex, allowing input vertices 
and 
to be mapped to their counterparts in the output complex.
Figure 11.10 shows a simple protocol for quasi-consensus. If 
has input 0 and 
has input 1, then this protocol admits three distinct executions: one in which both decide 
, one in which both decide 
, and one in which 
decides 0 and 
decides 1. These three executions correspond to the three simplices in the subdivision of 
, which are carried to the edges 
, and 
.
(left) and 
(right).11.3 Algorithm implies map
One direction of Theorem 11.2.1 is straightforward: If 
solves 
, then the protocol’s simplicial decision map
is color-preserving and carried by 
. On the other hand, any wait-free layered immediate snapshot protocol complex 
is a chromatic subdivision of the input complex 
.
11.4 Map implies algorithm
Assume we are given a task 
, a chromatic subdivision 
of the input complex, and a color-preserving simplicial map 
carried by 
. We will show that this task has a wait-free read-write protocol.
Our strategy is to show there exists a color-preserving simplicial map
for some 
such that for all 
. These maps compose as follows:
Here is how to turn these maps into a protocol. From an input simplex 
, each process performs the following three steps:
step 1. execute an 
-layer immediate snapshot protocol, halt on a vertex 
of the simplicial complex 
,
, yielding a vertex in 
,
, yielding an output vertex.It is easy to check that all processes halt on the vertices of a single simplex in 
. Moreover, because all maps are color-preserving, each process halts on an output vertex of matching color.
Because the identity map 
is continuous, it has a simplicial approximation 
carried by 
(Theorem 3.7.5). Unfortunately, there is no guarantee that this map is color-preserving. To provide such a guarantee, we will prove the following generalization of the Simplicial Approximation theorem:
Theorem 11.4.1
If 
is a chromatic complex, and 
is a chromatic subdivision of 
, then there exists a color-preserving simplicial map
such that for all 
, 
.
Both 
and 
are abstract complexes, defined in purely combinatorial terms. Nevertheless, we do not know how to prove the existence of this map in a combinatorial way. Instead, we will work with geometric complexes, embedded in high-dimensional Euclidean space, where we can exploit tools provided by point-set topology. Henceforth, all simplices and complexes will be geometric unless explicitly stated otherwise, so we will not always distinguish between a simplex or complex and its polyhedron. The exact meaning should be clear from context.
11.4.1 Basic concepts from point-set topology
Recall that geometric simplices “live” in a a Euclidean space of high but finite dimension. Any such space is a metric space, where the distance between points 
and 
is denoted 
. The open 
-ball 
around a point 
is the set of points 
such that 
for some 
. An 
-ball is an open set.
A Cauchy sequence is an infinite sequence of points 
with the property that the distance between successive points 
limits to zero.
Fact 11.4.2
In Euclidean space, every Cauchy sequence 
converges to a point 
, meaning that for any 
, there is an integer 
such that 
for all 
.
The set of points that can be expressed as affine combinations of points 
,
where 
, is called the hyperplane defined by those points. If a hyperplane is generated by 
affinely-independent points, then it has dimension 
. A set of points need not be affinely independent to define a hyperplane, so a hyperplane generated by 
arbitrary points has dimension at most 
.
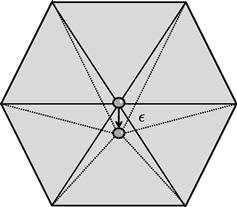
As long as a finite set of hyperplanes does not fill up the entire space, any point has arbitrarily small neighborhoods that include points not on any hyperplane.
Fact 11.4.3
If 
is a point and 
a finite set of hyperplanes, each of dimension less than 
, then there is an 
such that for every 
, 
contains a point not on any hyperplane in 
.
Moreover, any point not on any hyperplane has arbitrarily small neighborhoods that do not intersect the hyperplane.
Fact 11.4.4
If 
is a point and 
a finite set of hyperplanes, each of dimension less than 
, none of which contains 
, then there is an 
such that 
does not intersect any hyperplane in 
.
Definition 11.4.5
An open cover 
for a simplicial complex 
is a finite collection of open sets 
such that 
.
The following fact is the basis for the Simplicial Approximation theorem used in earlier chapters.
Fact 11.4.6
If 
an open cover for a finite simplicial complex 
, there exists a real number 
, called the Lebesgue number, such that any set of diameter less than 
lies in a single 
.
11.4.2 Geometric complexes
In Chapter 9, we defined the standard chromatic subdivision 
in a purely combinatorial way, as an abstract simplicial complex. Now we give an equivalent definition of 
as a geometric complex.
Definition 11.4.7
Recall that 
, as an abstract complex, is defined as follows. First, each vertex is a pair 
, where 
, and 
. Second, if 
and 
are vertices of 
, then 
or vice versa. Finally, if 
, then 
.
We need to assign a point within 
to each 
. Recall that 
is the barycenter of 
. Let 
be any real value such that 
. For each 
and simplex 
, define
See Figure 11.11.
.For any sufficiently small value of 
, it can be shown that this definition gives a geometric construction for the chromatic subdivision. We will use this construction for the remainder of this section. Since all simplices and complexes in this section are geometric, we will not distinguish between an abstract vertex 
and the point 
or an abstract simplex 
and its polyhedron 
.
Recall (Definition 3.6.7) that the mesh of a complex is the maximum diameter of any simplex.
Fact 11.4.8
For an 
-simplex 
, 
.
By taking sufficiently large 
can be made arbitrarily small.
11.4.3 Colors and covers
Fact 11.4.9
A set of vertices 
of a complex 
forms a simplex if and only if the intersection of their open stars is non-empty:
To construct a color-preserving simplicial map from 
to 
, we will need the vertex colors to “align” nicely. More specifically, the open stars of the vertices in a 
form an open cover for 
. This open-star cover has a natural coloring inherited from the coloring of 
. The open-star cover of 
is chromatic on 
if every simplex of 
is covered by open stars of vertices of a simplex in 
of matching color:
for some 
where 
.
We will show that without loss of generality, the geometric realization of 
can be chosen so that its open-star cover is chromatic on any iterated standard chromatic subdivision of 
.
Lemma 11.4.10
The geometric realization of 
can be chosen so that its open-star cover is chromatic on each of the subdivisions
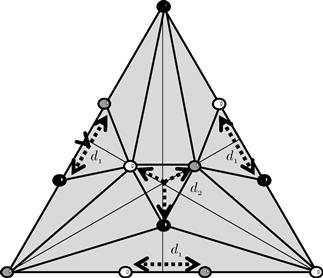
Figure 11.12 shows how an open-star covering can fail to be chromatic. Simplices of 
are shown with dotted lines and square vertices, whereas simplices of 
are shown with solid lines and round vertices. The gray vertex marked 
lies on the boundary between two gray open stars, so it is not covered by an open star of the same color.
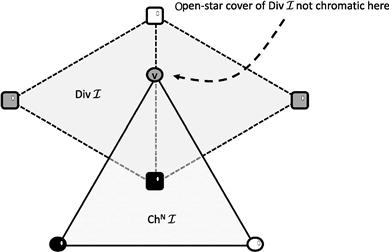
Figure 11.12 How an open-star covering can fail to be chromatic. Simplices of 
are shown with dotted lines and square vertices; simplices of 
are shown with solid lines and round vertices. The gray vertex marked 
lies on the boundary between two gray open stars, so this open-star covering fails to be chromatic.
Note, however, that if we perturb some of the square vertices by an arbitrarily small amount, then 
moves off the boundary and into the open star of a vertex of matching color. This observation suggests a strategy: We will pick an arbitrary geometric realization of 
, and if its open-star cover fails to be chromatic, then we will “perturb” vertex positions by very small amounts until the open-star cover becomes chromatic.
Readers willing to accept Lemma 11.4.10 can skip directly to Section 11.4.4.
We can recast some familiar concepts in terms of convex combinations. Every point 
in the polyhedron of a complex 
can be expressed uniquely as the convex combination of the vertices of a simplex 
of 
. The open star 
is just the set of points that can be expressed as the convex combination of the vertices of a simplex that includes 
.
In this definition and in the subsequent lemmas, 
and 
may be replaced by arbitrary chromatic subdivisions. Two simplices conflict if they share no colors.
Definition 11.4.11
A conflict point for 
and 
is a point that can be expressed as the convex combination of vertices of two conflicting simplices, 
and 
, were 
:
for 
and 
.
Lemma 11.4.12
The open-star cover of 
is chromatic for 
if and only if there are no conflict points.
Proof
As noted, every point 
in 
has a unique expression as the convex combination of the vertices of a 
, and similarly for a 
.
If 
is a conflict point, then it lies in the interior of 
but not in 
for any vertex 
where 
. The open stars of 
with colors from 
therefore fail to cover 
.
If the open-star cover is chromatic, then every 
lies in the open star of some vertex 
of 
and 
of 
such that 
, implying that 
is not a conflict point. 
Corollary 11.4.13 follows because the definition of conflict point is symmetric in terms of the two subdivisions.
Corollary 11.4.13
If the open-star cover of 
is chromatic on 
, then the open-star cover of 
is chromatic on 
.
We say that 
has an 
-perturbation at vertex 
for some 
if there is a point 
, such that replacing 
with 
in each simplex of 
yields a subdivision 
isomorphic to 
. (This isomorphism means that both complexes are geometric realizations of the same abstract complex.) See Figure 11.13. For brevity, we write such a perturbation as:
If 
is the result of applying 
-perturbations at multiple vertices, we write:
We will see that there is always an 
such that any vertex of a 
can be perturbed to any position within 
within its carrier.
Lemma 11.4.14
If 
is a vertex in 
whose carrier is an 
-simplex 
, then there is an 
-perturbation
for any 
.
Proof
We must check that any choice of 
yields a subdivision. We can pick 
small enough that 
lies in the open star of 
. We must check that 
can be made affinely independent of each simplex 
in 
. Each such 
defines a hyperplane 
of dimension 
. Because each 
is a simplex of 
, 
are affinely independent, and hence 
is not in any 
. By Fact 11.4.4, there is an 
so that for any 
, 
, and thus is affinely independent of the vertices of 
. 
Lemma 11.4.15
If 
is a vertex of 
whose carrier is an 
-simplex 
, then there is a perturbation 
such that 
contains no conflict points with 
.
Proof
Let 
be the set of hyperplanes defined by all pairs of conflicting simplices, one from 
and one from 
. By Fact 11.4.3, there is an 
so that some point 
within 
of 
does not intersect any of these hyperplanes. By Lemma 11.4.14, this choice of 
defines a perturbation 
.
We claim that 
and 
have no conflict points. Otherwise, if 
is a conflict point, then there are conflicting simplices 
in 
and 
in 
such that
where 
, and 
. And yet, this equation implies that 
lies on the hyperplane defined by the vertices of 
, which contradicts the choice of 
. 
Lemma 11.4.16
If 
is a vertex of 
whose carrier is an 
-simplex 
, then there is a perturbation 
such that 
has no conflict points with any of the subdivisions
Proof
By Lemma 11.4.14, there is a 
such that 
is a perturbation for any 
.
We inductively construct a sequence of subdivisions
such that 
has no conflict points with 
.
For the base case, the open-star cover of 
is already a chromatic cover for 
, so let 
and 
.
For the induction step, Lemma 11.4.15 states that there is a perturbation
such that 
has no conflict points with 
.
If we pick each
then 
is a Cauchy sequence that converges to 
, where
As a result, we have constructed a perturbation
where 
and 
have no conflict points for all 
. 
Lemma 11.4.17
Every chromatic subdivision 
has a perturbation
such that 
has no conflict points with any of the subdivisions
Proof
By induction on 
. In the base case, when 
, the claim is trivial because both complexes are discrete sets of vertices.
Inductively assume that the open-star cover of 
is chromatic for each of
For each vertex 
in 
whose carrier has dimension 
, Lemma 11.4.16 states that we can construct a perturbation that eliminates all conflict points from its open star. Successively applying this construction to each such vertex yields a perturbation
that has no conflict points with any iterated standard chromatic subdivision 
. 
-perturbation.Because 
and its perturbation 
are just different geometric realizations of the same abstract complex, we have completed the proof of Lemma 11.4.10.
11.4.4 Construction
We are now ready to prove Theorem 11.4.1, showing there exists a color-preserving simplicial map
such that for all 
, 
.
We will construct a sequence of chromatic subdivisions, 
, for 
, where 
, along with a sequence of simplicial maps
defined on 
, except for a subcomplex 
of dimension at most 
.
At the end of the sequence, 
is empty, so
is the desired map.
This sequence of subdivisions induces a parent map,
carrying each vertex of 
to the unique vertex of matching color in its carrier in 
. The ancestors of a vertex 
are the vertices 
.
Subdividing 
induces subdivisions on its subcomplexes. Given a subcomplex 
, define 
to be the maximal subcomplex of 
satisfying 
. Similarly, for 
, define 
to be the maximal subcomplex of 
satisfying 
.
Definition 11.4.18
The extended star 
of a simplex 
in a complex 
is the union of the stars of its vertices:
Like the star of a vertex, the extended star of a simplex is a subcomplex of 
, and its polyhedron is a closed set. Moreover,
For the base case of our construction, let 
, and 
is everywhere undefined.
For the inductive step, assume we are given 
and 
for all 
.
Lemma 11.4.10 states that we may assume, without loss of generality, that the open-star cover of 
is chromatic for 
, including 
, the subcomplex where 
is undefined. Let 
be the Lebesgue number of this cover of 
. Pick 
large enough that for every facet 
of 
,
(11.4.1)
We will use this inequality later.
We define 
as follows: Each vertex 
in 
not in 
“inherits” the map from its parent: 
. Otherwise, for each vertex in 
, if there exits a vertex 
such that
(11.4.2)
and 
, then 
.
The remaining vertices of 
define 
, the subcomplex of 
where 
is not defined. Note that this definition implies that for 
,
(11.4.3)
Lemma 11.4.19
Let 
be a vertex in 
, and 
its sequence of ancestors. Let 
be the least index (earliest ancestor) for which 
is defined. We claim that
Proof
We argue by induction on 
. For the base case, when 
, the claim follows because 
is defined for the first time by Equation 11.4.2.
Assume the result for 
. By the induction hypothesis,
where 
is the least index for which 
is defined for an ancestor of 
. Note that 
is a subdivision of 
, and 
is a vertex in the carrier of 
for this subdivision, so
Putting these containments together,
Lemma 11.4.20
Each 
is a color-preserving simplicial map.
Proof
The color-preserving property is immediate from Equation 11.4.2. To show that 
is simplicial, we argue by induction on 
. When 
, the claim holds vacuously. Let 
be a simplex of 
. We must show that 
is a simplex of 
.
By Lemma 11.4.19, for each 
, there is a 
such that for each vertex 
,
Assume without loss of generality that 
, so
In particular, 
is a vertex of them all.
for 
, so
It follows from Fact 11.4.9 that 
is a simplex of 
, completing the proof that 
is a simplicial map. 
Lemma 11.4.21
For 
.
Proof
Recall that the open-star cover of 
is chromatic on 
. Moreover, by Equation 11.4.1, the number 
is large enough to ensure that the diameter of the extended star of every facet 
of 
is less than the cover’s Lebesgue number:
for a vertex 
. Because the cover is chromatic, there is a vertex 
of matching color: 
. Because 
,
so by Equation 11.4.2, 
is defined, and 
is not a vertex of 
. In this way, 
is defined on at least one vertex of every facet of 
, so the dimension of 
drops by at least one. 
Lemma 11.4.20 states that the vertex map
is color-preserving and simplicial, whereas Lemma 11.4.21 states that 
is empty. Together these imply that
is a color-preserving simplicial map.
This completes the proof of the “map implies algorithm” direction of Theorem 11.2.1.
It is useful to observe that the “property implies protocol” part of the proof assumes only that the model of computation in which the protocol is constructed is strong enough to solve the immediate snapshot task.
Corollary 11.4.22
A task 
has a protocol in any model of computation that solves immediate snapshot if 
has a chromatic subdivision 
and a color-preserving simplicial map 
carried by 
.
Of course, the converse of this corollary does not hold in general.
11.5 A sufficient topological condition
We now give a simple topological condition that ensures that a colored task 
has a wait-free read-write protocol. We will use the following topological property.
Definition 11.5.1
A pure simplicial complex 
of dimension 
is called link-connected if for each simplex 
, 
is 
-connected.
The output complex for the Hourglass task shown in Figure 11.1 is not link-connected, since the vertex at the hourglass’s “waist” is disconnected, that is, not 0-connected.
Theorem 11.5.2
The colored task 
has a wait-free layered immediate snapshot protocol if for each 
, 
is 
-connected, and 
is link-connected.
This theorem establishes the existence of a protocol in terms of the topological properties of complexes and carrier maps.
By Theorem 11.2.1, it is enough to prove the following lemma.
Lemma 11.5.3
If for each 
, 
is 
-connected, and 
is link-connected, then there exists a chromatic subdivision 
and a color-preserving simplicial map
carried by 
.
We need the following lemma about link connectivity.
Lemma 11.5.4
If 
is a pure link-connected simplicial complex, then so is 
for any simplex 
.
Proof
Assume 
. Note that 
is a pure 
-complex, and for any 
in 
. We will show that for any 
in 
is 
-connected.
We claim that
If 
, then 
, and therefore 
, so
Moreover, if 
, then 
, and therefore 
, so
Because 
and 
are disjoint, 
. The complex 
is link-connected by hypothesis, so 
, and therefore 
, is 
-connected. 
We make use of the following fact, discussed in the chapter notes.
Fact 11.5.5
Let 
, and 
be complexes such that 
, and 
a continuous map such that the vertex map induced by 
restricted to 
is simplicial. There exists a subdivision 
of 
such that 
, and a simplicial map 
that agrees with 
on vertices of 
.
Lemma 11.5.6
Let 
and 
be 
-complexes such that there is a continuous map
such that the restriction of 
to 
is a rigid simplicial map. There exist a subdivision 
that 
and a rigid simplicial map 
that agrees with 
on vertices of 
.
Proof
We argue by induction on 
. For the base case, when 
is a graph, and 
is a set of discrete points. By way of contradiction, assume that every subdivision 
and every simplicial map
that agrees with 
on 
collapses an edge of 
.
Pick 
and 
to collapse a minimal number of edges. There is an edge 
in 
such that 
, where 
is a vertex in 
(see Figure 11.14). Because 
is link-connected, 
is non-empty and so contains a vertex 
. Define a new subdivision 
by taking the stellar subdivision of 
with center 
. Define 
to agree with 
except that 
. It is easy to check that 
agrees with 
on 
but collapses one fewer simplex than 
, contradicting our assumption that 
collapses a minimum number of simplices.
For the induction step, assume the claim for complexes of dimension less than 
. Let 
be an 
-complex, and 
a continuous map that is simplicial and rigid on 
. Fact 11.5.5 implies there exists a subdivision 
such that 
and a simplicial map 
that agrees with 
on 
.
Suppose, by way of contradiction, that for every such 
and 
, 
collapses a simplex of 
. Pick 
and 
to minimize the number of collapsed simplices. We will show how to adjust 
and 
to collapse one fewer simplex, a contradiction.
Pick 
in 
such that 
collapses 
to a single vertex 
but does not collapse any simplex strictly containing 
. Because 
does not collapse any simplices in 
, 
for some 
-simplex 
. Because 
is an 
-simplex, 
.
As before, pick a point 
in the interior of 
, and take the stellar subdivision 
with center 
. Because 
is a manifold, 
is an 
-sphere, and 
is an 
-disk with boundary 
.
The subcomplex 
is 
-connected by hypothesis and link-connected by Lemma 11.5.4. Because 
does not collapse any simplices strictly containing 
,
Because 
, we apply the induction hypothesis as follows: Because 
is connected and link-connected, there exists a subdivision 
and simplicial map
such that 
, 
agrees with 
on 
, and 
does not collapse any simplices of 
(see Figure 11.15).
Because 
does not subdivide any simplices of 
, it extends to a subdivision 
of all of 
. Define
Note that 
agrees with 
on every vertex not in 
and on every vertex of 
, so 
cannot collapse more of these simplices than 
. Moreover, 
cannot collapse any simplices of 
because it is rigid by the induction hypothesis. It follows that 
collapses one fewer simplex than 
, contradicting our assumption that 
collapses a minimum number of simplices. 
Lemma 11.5.7
Let 
be a chromatic 
-simplex, 
a chromatic subdivision, and 
is a rigid simplicial map. If 
is color-preserving on 
, then 
is color-preserving on 
.
Proof
is a manifold with boundary, so for any 
-simplex 
, there is a sequence of 
-simplices 
, where 
has an 
-face on the boundary, 
and 
share an 
-face, and 
.
We argue by induction on 
. When 
, the claim is trivial. Otherwise, assume that 
is color-preserving on 
. The map 
is color-preserving on the 
face shared by 
and 
. Because 
is rigid, it cannot send the remaining vertex of 
to any of the other 
colors in the shared face, so it must send it to a vertex of the same color. 
We are now ready to complete the proof of Lemma 11.5.3 (and hence Theorem 11.5.2). For 
, we inductively construct a sequence of chromatic subdivisions 
and a color-preserving simplicial map
carried by 
.
For the base case, let 
send any vertex 
of 
to any vertex of 
. This construction is well-defined because 
is 
-connected (non-empty) by hypothesis. This map is trivially color-preserving.
For the induction hypothesis, assume we have constructed a chromatic subdivision and color-preserving simplicial map
This simplicial map induces a continuous map that sends the boundary of each 
-simplex 
in 
to 
. By hypothesis, 
is 
-connected, so this map of the 
-sphere 
can be extended to a continuous map of the 
-disk 
:
These extensions agree on 
, so together they define a continuous map,
where for each 
, 
.
Note that the restriction of 
on the 
skeleton is just 
, a color-preserving simplicial map, so by Lemma 11.5.6, there is a subdivision 
of 
such that 
and a rigid simplicial map 
extending 
. By Lemma 11.5.7, 
is also color-preserving. These extensions agree on the 
-skeleton, so together they define a color-preserving simplicial map:
carried by 
.
When 
is a color-preserving simplicial map carried by 
, completing the proof.
By analogy with Corollary 11.4.22, the proof of Theorem 11.5.2 requires only that the protocol model support the immediate snapshot.
Corollary 11.5.8
Assume that for any input complex 
and any 
, there is a protocol that solves the chromatic agreement task 
. Then a task 
has a protocol if, for each 
, 
is 
-connected, and 
is link-connected.
One interesting and useful fact that emerges from this discussion is that if two different read-write models with different adversaries have the same minimal core size, then they solve the same set of colorless tasks. In this sense, an adversary’s minimum core size completely determines its computational power for colorless tasks.
11.6 Chapter notes
The results in this chapter originally appeared in Herlihy and Shavit [91].
Herlihy, Rajsbaum, and Raynal [87] present an implementation of the safe agreement task in a layered model. See Exercise 11.1.
Mostefaoui, Rajsbaum, and Raynal [122] and Mostefaoui, Rajsbaum, Raynal, and Travers [121] study “condition-based” variations of tasks such as consensus in which the input complexes are restricted to permit 
-resilient layered snapshot protocols. Such tasks provide simple, natural examples of colored tasks, where processes can adopt one another’s output values but not their input values.
Imbs, Rajsbaum, and Raynal [95] study generalized symmetry-breaking tasks (GSB) that include election, renaming, and other tasks that are not colorless. These are fixed-input in the sense that the only input to a process is its name.
Fact 11.5.5 is Theorem IV.2 of Glaser [72].
11.7 Exercises
Exercise 11.2
Consider the following fixed-input colored task: 
processes choose distinct values in the range 
. Prove that the output complex for this task is a manifold. (This task is a special case of the renaming task considered in the next chapter.)
Exercise 11.3
As a special case of Exercise 11.2, draw the output complex for the fixed-input colored task where three processes choose distinct values in the range 
. What is this surface called?
Exercise 11.4
be a continuous map and 
be the open-star cover of 
.
is an open cover of 
.
has Lebesgue number 
and every edge of 
has length 1. For what value of 
can we guarantee that for every vertex 
in 
, 
?
in 
, define 
, where 
is any vertex such that 
. Prove that 
is a simplicial approximation for 
.Exercise 11.5
For an 
-simplex 
, what is the Lebesgue number of the open-star cover of 
? Of 
?
Exercise 11.6
Prove Fact 11.4.3: If 
is a point in 
-dimensional Euclidean space, and 
is a finite set of hyperplanes, each of dimension less than 
, then there is an 
such that for every 
, 
contains a point not on any hyperplane in 
.
Exercise 11.7
Prove Fact 11.4.4: If 
is a point in 
-dimensional Euclidean space, and 
is a finite set of hyperplanes, each of dimension less than 
, none of which contains 
, then there is an 
such that 
does not intersect any hyperplane in 
.
Exercise 11.8
Prove Fact 11.4.9: A set of vertices 
of a complex 
forms a simplex if and only if the intersection of their open stars is non-empty.
Exercise 11.9
Let 
be a geometric complex. Define the distance between two simplices 
of 
to be 
. Show that the Lebesgue number of the open-star cover of 
is 
, taken over all pairs of simplices 
in 
such that 
.
1This map is a deformation retraction, a continuous deformation of the input complex’s polyhedron into the output complex’s polyhedron that leaves the output complex unchanged.