Solvability of Colorless Tasks in Different Models
Abstract
This chapter explores the circumstances under which colorless tasks can be solved in different communication models, satisfying different fault-tolerance requirements. We consider both shared memory and message-passing models, wait-free and ![]() -resilient protocols, and protocols that work against adversaries.
-resilient protocols, and protocols that work against adversaries.
Keywords
![]() -resilient; Adversaries; Layered snapshot protocols; Message-passing protocols; Wait-free
-resilient; Adversaries; Layered snapshot protocols; Message-passing protocols; Wait-free
In Chapter 4 we considered colorless layered immediate snapshot protocols and identified the colorless tasks that such protocols can solve while tolerating crash failures by any number of processes. This chapter explores the circumstances under which colorless tasks can be solved using other computational models.
We consider models with different communication mechanisms and different fault-tolerance requirements. We show that the ideas of the previous chapter can be extended to characterize the colorless tasks that can be solved when up to ![]() out of
out of ![]() processes may crash, when the processes communicate by shared objects that solve
processes may crash, when the processes communicate by shared objects that solve ![]() -set agreement, or when the processes communicate by message passing.
-set agreement, or when the processes communicate by message passing.
Once we have established necessary and sufficient conditions for a task to have a protocol in a particular model, it is natural to ask whether it is decidable whether a given task satisfies those conditions. We will see that the answer to that question depends on the model.
5.1 Overview of models
Recall from Chapter 4 that a colorless task is one where only the sets of input or output values matter, not which process has which. For such tasks, an initial configuration remains an initial configuration if one participating process exchanges its own input value for another’s, and the same holds true for final configurations. Consensus and ![]() -set agreement are examples of colorless tasks.
-set agreement are examples of colorless tasks.
In a model where the processes communicate by layered snapshots and any number of processes can fail by crashing, a protocol must be wait-free. A process cannot wait for another process to take a step, because it cannot tell whether that process has crashed or is merely slow. We have seen that a colorless task ![]() has a wait-free
has a wait-free ![]() -process layered immediate snapshot protocol if and only if there is a continuous map
-process layered immediate snapshot protocol if and only if there is a continuous map
![]() (5.1.1)
(5.1.1)
carried by ![]() (Theorem 4.3.1). Informally, this characterization says that wait-free layered snapshot protocols transform (sets of at most
(Theorem 4.3.1). Informally, this characterization says that wait-free layered snapshot protocols transform (sets of at most ![]() different) inputs to outputs in a continuous way.
different) inputs to outputs in a continuous way.
In this chapter we consider several other models for which the computational power can be measured by a parameter ![]() . The colorless tasks solvable in a model with parameter
. The colorless tasks solvable in a model with parameter ![]() are exactly those for which there is a continuous map
are exactly those for which there is a continuous map
![]()
carried by ![]() . Thus, the wait-free layered snapshot model is the weakest, having
. Thus, the wait-free layered snapshot model is the weakest, having ![]() , whereas a model with
, whereas a model with ![]() can solve any colorless task.
can solve any colorless task.
Sometimes the wait-free condition may be too demanding. Instead of tolerating failures by an arbitrary subset of processes, we may be willing to tolerate fewer failures. A protocol is ![]() -resilient if it tolerates halting failures by as many as
-resilient if it tolerates halting failures by as many as ![]() processes. (A wait-free protocol is
processes. (A wait-free protocol is ![]() -resilient.) We say that a colorless task has a t-resilient protocol in a model if, for all
-resilient.) We say that a colorless task has a t-resilient protocol in a model if, for all ![]() , there is a
, there is a ![]() -resilient
-resilient ![]() -process protocol for that task. In Section 5.2 we will see that a colorless task
-process protocol for that task. In Section 5.2 we will see that a colorless task ![]() has a
has a ![]() -resilient layered snapshot protocol if and only if there is a continuous map
-resilient layered snapshot protocol if and only if there is a continuous map
![]() (5.1.2)
(5.1.2)
carried by ![]() . Not surprisingly, the
. Not surprisingly, the ![]() -resilient Condition 5.1.2 is strictly weaker than its wait-free counterpart, Condition 5.1.1, since the map needs to be defined only over the
-resilient Condition 5.1.2 is strictly weaker than its wait-free counterpart, Condition 5.1.1, since the map needs to be defined only over the ![]() -skeleton of the input complex. The lower the dimension
-skeleton of the input complex. The lower the dimension ![]() , the easier it is to satisfy this condition and the more tasks that can be solved. In a sense, these two conditions capture the cost of fault tolerance. For colorless tasks, solvability is determined by the number of processes that can fail, whereas the total number of processes is irrelevant.
, the easier it is to satisfy this condition and the more tasks that can be solved. In a sense, these two conditions capture the cost of fault tolerance. For colorless tasks, solvability is determined by the number of processes that can fail, whereas the total number of processes is irrelevant.
We also show (Section 5.3) that if we augment layered snapshot protocols by also allowing processes to communicate through ![]() -set agreement objects, then a colorless task
-set agreement objects, then a colorless task ![]() has a wait-free layered protocol if and only if there is a continuous map
has a wait-free layered protocol if and only if there is a continuous map
![]()
carried by ![]() . Adding
. Adding ![]() -set agreement objects,
-set agreement objects, ![]() , increases the computational power of layered snapshot protocols by lowering the dimension of the skeleton on which a map must exist.
, increases the computational power of layered snapshot protocols by lowering the dimension of the skeleton on which a map must exist.
It follows that fault tolerance and communication power are, in a sense, interchangeable for colorless computability. A ![]() -resilient layered colorless protocol and a wait-free layered protocol augmented by
-resilient layered colorless protocol and a wait-free layered protocol augmented by ![]() -set agreement objects, are equivalent: They can solve the same colorless tasks. Notice that in the extreme case, where
-set agreement objects, are equivalent: They can solve the same colorless tasks. Notice that in the extreme case, where ![]() , any colorless task is solvable, either because there are no failures or because the processes can reach consensus (Exercise 5.2). More generally, let
, any colorless task is solvable, either because there are no failures or because the processes can reach consensus (Exercise 5.2). More generally, let ![]() be an integer,
be an integer, ![]() . Then, for any
. Then, for any ![]() such that
such that ![]() , there is a
, there is a ![]() -resilient
-resilient ![]() -set agreement layered snapshot protocol for a task
-set agreement layered snapshot protocol for a task ![]() if and only if there is a continuous map
if and only if there is a continuous map
![]()
carried by ![]() (see Exercise 5.4).
(see Exercise 5.4).
The previous chapter’s techniques extend even to the case where process failures are not independent. In Section 5.4, we show how to exploit knowledge of which potential failures are correlated and which are not. A parameter ![]() captures the power of such a model for solving colorless tasks. This parameter is the size of the smallest core in the system, a minimal set of processes that will not all fail in any execution. The result for
captures the power of such a model for solving colorless tasks. This parameter is the size of the smallest core in the system, a minimal set of processes that will not all fail in any execution. The result for ![]() -resilient solvability readily generalizes to dependent failures. A colorless task
-resilient solvability readily generalizes to dependent failures. A colorless task ![]() has a layered protocol with minimal core size
has a layered protocol with minimal core size ![]() if and only if there is a continuous map
if and only if there is a continuous map
![]()
carried by ![]() .
.
Next, in Section 5.5 we consider message-passing protocols. The layered snapshot model might appear to be stronger; once a process writes a value to shared memory, that value is there for all to see, whereas a value sent in a message is visible only to the process that received the message. Perhaps surprisingly, as long as a majority of processes is nonfaulty (that is, ![]() ), the two models are equivalent: Any task that has a
), the two models are equivalent: Any task that has a ![]() -resilient layered immediate snapshot protocol has a
-resilient layered immediate snapshot protocol has a ![]() -resilient message-passing protocol, and vice versa.
-resilient message-passing protocol, and vice versa.
Once we have established necessary and sufficient conditions for a task to have a protocol in a particular model, it is natural to ask whether it is decidable whether a given task satisfies those conditions. We will see in Section 5.6 that the answer depends on the model. Essentially, for any model in which solvable tasks are exactly those for which there is a continuous map
![]()
carried by ![]() , then solvability is decidable if and only if
, then solvability is decidable if and only if ![]() .
.
5.2 t-Resilient layered snapshot protocols
Recall that wait-free protocols tolerate crash failures by all processes but one (that is, ![]() out of
out of ![]() ). Sometimes this level of resilience is excessive, especially if there are many processes. Instead, it may be enough to tolerate only
). Sometimes this level of resilience is excessive, especially if there are many processes. Instead, it may be enough to tolerate only ![]() failures among
failures among ![]() processes, where
processes, where ![]() , a property called
, a property called ![]() -resilience.
-resilience.
A colorless ![]() -resilient layered immediate snapshot protocol (
-resilient layered immediate snapshot protocol (![]() -resilient layered protocol when clear from context) is structured as shown in Figure 5.1. As in the wait-free case, the processes share a two-dimensional memory array mem[
-resilient layered protocol when clear from context) is structured as shown in Figure 5.1. As in the wait-free case, the processes share a two-dimensional memory array mem[![]() ][i], where row
][i], where row ![]() is shared only by the processes participating in layer
is shared only by the processes participating in layer ![]() , and column
, and column ![]() is written only by
is written only by ![]() . During layer
. During layer ![]() writes its current view to mem[
writes its current view to mem[![]() ][i], waits for
][i], waits for ![]() views (including its own) to be written to that layer’s row, and then takes a snapshot of that row. The waiting step introduces no danger of deadlock because at least
views (including its own) to be written to that layer’s row, and then takes a snapshot of that row. The waiting step introduces no danger of deadlock because at least ![]() nonfaulty processes will eventually reach each level and write their views.
nonfaulty processes will eventually reach each level and write their views.
Notice that the wait-free layered snapshot protocol of Figure 4.1, where ![]() , is a degenerate form of the
, is a degenerate form of the ![]() -resilient protocol of Figure 5.1. In the wait-free protocol, once
-resilient protocol of Figure 5.1. In the wait-free protocol, once ![]() has written to mem[
has written to mem[![]() ][i], it can proceed immediately because
][i], it can proceed immediately because ![]() , and one view (its own) has already been written.
, and one view (its own) has already been written.
Right away we can see that even an ![]() -resilient protocol can solve colorless tasks that cannot be solved by a wait-free protocol (and in a single layer). The pseudo-code in Figure 5.2 solves
-resilient protocol can solve colorless tasks that cannot be solved by a wait-free protocol (and in a single layer). The pseudo-code in Figure 5.2 solves ![]() -set agreement if at most
-set agreement if at most ![]() processes may fail. In contrast, we know from Theorem 4.3.6 that there is no
processes may fail. In contrast, we know from Theorem 4.3.6 that there is no ![]() -set agreement protocol if
-set agreement protocol if ![]() processes can fail when
processes can fail when ![]() . More generally, this impossibility holds for any value of
. More generally, this impossibility holds for any value of ![]() (Theorem 5.2.9), so each additional level of resilience allows us to solve a harder instance of set agreement.
(Theorem 5.2.9), so each additional level of resilience allows us to solve a harder instance of set agreement.
In Exercise 5.22, we ask you to show that this protocol does not actually require immediate snapshots.
The following lemma will be useful for characterizing the colorless tasks that can be solved, tolerating ![]() failures, by a layered colorless protocol. It is similar to Theorem 4.2.8 for wait-free single-layer colorless immediate snapshot protocol complex, and indeed the proof is similar as well.
failures, by a layered colorless protocol. It is similar to Theorem 4.2.8 for wait-free single-layer colorless immediate snapshot protocol complex, and indeed the proof is similar as well.
By Definition 4.2.2 we can consider the triple ![]() for the protocol of Figure 5.1, where
for the protocol of Figure 5.1, where ![]() is the input complex of a task,
is the input complex of a task, ![]() is the protocol complex where each simplex is a colorless final configuration, and
is the protocol complex where each simplex is a colorless final configuration, and ![]() is the strict execution carrier map.
is the strict execution carrier map.
A simple induction, with Lemma 5.2.2 as the base, yields the following.
If a protocol solves a colorless task ![]() , then we are free to add a preprocessing step to the protocol, where first the processes agree on at most
, then we are free to add a preprocessing step to the protocol, where first the processes agree on at most ![]() of their inputs, where
of their inputs, where ![]() , using the protocol of Figure 5.2. The following lemma states this formally using the protocol composition Definition 4.2.5.
, using the protocol of Figure 5.2. The following lemma states this formally using the protocol composition Definition 4.2.5.
We may now combine the previous results to show that, for ![]() -resilient colorless task solvability, we may assume without loss of generality that a protocol complex is a barycentric subdivision of the
-resilient colorless task solvability, we may assume without loss of generality that a protocol complex is a barycentric subdivision of the ![]() -skeleton of the input complex.
-skeleton of the input complex.
Applying the Discrete Protocol Complex Lemma (4.2.7),
Without loss of generality, we can assume that any ![]() -resilient layered protocol consists of one
-resilient layered protocol consists of one ![]() -set agreement layer followed by any number of immediate snapshot layers. Moreover, only the first
-set agreement layer followed by any number of immediate snapshot layers. Moreover, only the first ![]() -set agreements layer requires waiting; the remaining layers can be wait-free.
-set agreements layer requires waiting; the remaining layers can be wait-free.
An important special case of the previous theorem occurs when ![]() , implying that consensus is not solvable by a layered protocol even if only a single process can fail.
, implying that consensus is not solvable by a layered protocol even if only a single process can fail.
5.3 Layered snapshots with k-set agreement
Practically all modern multiprocessor architectures provide synchronization primitives more powerful than simple read or write instructions. For example, the test-and-set instruction atomically swaps the value true for the contents of a memory location. If we augment layered snapshots with test-and-set, for example, it is possible to solve wait-free ![]() -set agreements for
-set agreements for ![]() (see Exercise 5.5). In this section, we consider protocols constructed by composing layered snapshot protocols with
(see Exercise 5.5). In this section, we consider protocols constructed by composing layered snapshot protocols with ![]() -set agreement protocols.
-set agreement protocols.
In more detail, we consider protocols in the form of Figure 5.3. The protocol is similar to the colorless wait-free snapshot protocol of Figure 4.1 except that in addition to sharing memory, the objects share an array of ![]() -set agreement objects (Line 3). In each layer
-set agreement objects (Line 3). In each layer ![]() , the processes first join in a
, the processes first join in a ![]() -set agreement protocol with the other processes in that layer (Line 8), and then they run an
-set agreement protocol with the other processes in that layer (Line 8), and then they run an ![]() -layer immediate snapshot protocol (Line 11) for some
-layer immediate snapshot protocol (Line 11) for some ![]() .
.
Recall that the ![]() -set agreement protocol with input complex
-set agreement protocol with input complex ![]() is
is ![]() , where the skeleton operator is considered as a strict carrier map (see Exercise 4.8).
, where the skeleton operator is considered as a strict carrier map (see Exercise 4.8).
Recall also that if ![]() and
and ![]() are protocols where the protocol complex for the first is contained in the input complex for the second, then their composition is the protocol
are protocols where the protocol complex for the first is contained in the input complex for the second, then their composition is the protocol ![]() , where
, where ![]() (Definition 4.2.3).
(Definition 4.2.3).
Applying the Discrete Protocol Complex Lemma (4.2.7):
The next corollary follows because Theorem 5.3.4 is independent of the order in which ![]() -set agreement layers are composed with immediate snapshot layers.
-set agreement layers are composed with immediate snapshot layers.
5.4 Adversaries
A ![]() -resilient protocol is designed under the assumption that failures are uniform: Any
-resilient protocol is designed under the assumption that failures are uniform: Any ![]() out of
out of ![]() processes can fail. Often, however, failures are correlated. In a distributed system, processes running on the same node, in the same network partition, or managed by the same provider may be more likely to fail together. In a multiprocessor, processes running on the same core, on the same processor, or on the same card may be likely to fail together. It is often possible to design more effective fault-tolerant algorithms if we can exploit knowledge of which potential failures are correlated and which are not.
processes can fail. Often, however, failures are correlated. In a distributed system, processes running on the same node, in the same network partition, or managed by the same provider may be more likely to fail together. In a multiprocessor, processes running on the same core, on the same processor, or on the same card may be likely to fail together. It is often possible to design more effective fault-tolerant algorithms if we can exploit knowledge of which potential failures are correlated and which are not.
One way to think about such failure models is to assume that failures are controlled by an adversary who can cause certain subsets of processes to fail, but not others. There are several ways to characterize adversaries. The most straightforward is to enumerate the faulty sets: all sets of processes that fail in some execution. We will assume that faulty sets are closed under inclusion; if ![]() is a maximal set of processes that fail in some execution, then for any
is a maximal set of processes that fail in some execution, then for any ![]() there is an execution in which
there is an execution in which ![]() is the actual set of processes that fail. There is a common-sense justification for this assumption: We want to respect the principle that fault-tolerant algorithms should continue to be correct if run in systems that display fewer failures than in the worst-case scenario. A model that permits algorithms that are correct only if certain failures occur is unlikely to be useful in practice.
is the actual set of processes that fail. There is a common-sense justification for this assumption: We want to respect the principle that fault-tolerant algorithms should continue to be correct if run in systems that display fewer failures than in the worst-case scenario. A model that permits algorithms that are correct only if certain failures occur is unlikely to be useful in practice.
Faulty sets can be described as a simplicial complex ![]() , called the faulty set complex, the vertices of which are process names and the simplices of which are sets of process names such that exactly those processes fail in some execution.
, called the faulty set complex, the vertices of which are process names and the simplices of which are sets of process names such that exactly those processes fail in some execution.
Faulty sets can be cumbersome, so we use a more succinct and flexible way to characterize adversaries. A core is a minimal set of processes that will not all fail in any execution. A core is a simplex that is not itself in the faulty set complex, but all of its proper faces are in ![]() . The following dual notion is also useful. A survivor set is a minimal set of processes that intersects every core (such a set is sometimes called a hitting set). In every execution, the set of nonfaulty processes includes a survivor set.
. The following dual notion is also useful. A survivor set is a minimal set of processes that intersects every core (such a set is sometimes called a hitting set). In every execution, the set of nonfaulty processes includes a survivor set.
Here are some examples of cores and survivor sets.
The Wait-Free Adversary. The entire set of processes is the only core, and the singleton sets are the survivor sets.
The ![]() -Faulty Adversary. The cores are the sets of cardinality
-Faulty Adversary. The cores are the sets of cardinality ![]() , and the survivor sets are the sets of cardinality
, and the survivor sets are the sets of cardinality ![]() .
.
An Irregular Adversary. Consider a system of four processes, ![]() ,
, ![]() , and
, and ![]() , where any individual process may fail, or
, where any individual process may fail, or ![]() and
and ![]() may both fail. Here
may both fail. Here ![]() is a core, since they cannot both fail, yet there is an execution in which each one fails. In all, there are five cores:
is a core, since they cannot both fail, yet there is an execution in which each one fails. In all, there are five cores:
![]()
and three survivor sets:
![]()
The set ![]() is a survivor set, since there is an execution where only these processes are nonfaulty. This adversary is illustrated in Figure 5.4.
is a survivor set, since there is an execution where only these processes are nonfaulty. This adversary is illustrated in Figure 5.4.
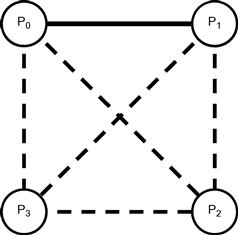
Figure 5.4 An irregular adversary: ![]() , and
, and ![]() can each fail individually, or
can each fail individually, or ![]() and
and ![]() may both fail. The faulty set complex consists of an edge linking
may both fail. The faulty set complex consists of an edge linking ![]() and
and ![]() , shown as a solid line, and two isolated vertices,
, shown as a solid line, and two isolated vertices, ![]() and
and ![]() . There are five cores, shown as dotted lines.
. There are five cores, shown as dotted lines.
Here is how to use cores and survivor sets in designing a protocol. Given a fixed core ![]() , it is safe for a process to wait until it hears from some member of
, it is safe for a process to wait until it hears from some member of ![]() , because they cannot all fail. It is also safe for a process to wait until it hears from all members of some survivor set, because the set of nonfaulty processes always contains a survivor set. See Exercise 5.14.
, because they cannot all fail. It is also safe for a process to wait until it hears from all members of some survivor set, because the set of nonfaulty processes always contains a survivor set. See Exercise 5.14.
Let ![]() be an adversary with minimum core size
be an adversary with minimum core size ![]() . We say that a protocol is
. We say that a protocol is ![]() -resilient if it tolerates any failure permitted by
-resilient if it tolerates any failure permitted by ![]() . As illustrated in Figure 5.5, an
. As illustrated in Figure 5.5, an ![]() -resilient layered snapshot protocol differs from a
-resilient layered snapshot protocol differs from a ![]() -resilient protocol as follows. At each layer, after writing its own value, each process waits until all the processes in a survivor set (possibly including itself) have written their views to that layer’s memory. As noted, there is no danger of deadlock waiting until a survivor set has written.
-resilient protocol as follows. At each layer, after writing its own value, each process waits until all the processes in a survivor set (possibly including itself) have written their views to that layer’s memory. As noted, there is no danger of deadlock waiting until a survivor set has written.
Notice that the ![]() -resilient layered snapshot protocol of Figure 5.1 is a degenerate form of the
-resilient layered snapshot protocol of Figure 5.1 is a degenerate form of the ![]() -resilient protocol of Figure 5.5 because, for the
-resilient protocol of Figure 5.5 because, for the ![]() -resilient protocol, any set of
-resilient protocol, any set of ![]() processes is a survivor set.
processes is a survivor set.
Applying the Discrete Protocol Complex Lemma (4.2.7):
5.5 Message-passing protocols
So far we have focused on models in which processes communicate through shared memory. We now turn our attention to another common model of distributed computing, where processes communicate by message passing.
There are ![]() asynchronous processes that communicate by sending and receiving messages via a communication network. The network is fully connected; any process can send a message to any other. Message delivery is reliable; every message sent is delivered exactly once to its target process after a finite but potentially unbounded delay. Message delivery is first-in, first-out (FIFO); messages are delivered in the order in which they were sent.
asynchronous processes that communicate by sending and receiving messages via a communication network. The network is fully connected; any process can send a message to any other. Message delivery is reliable; every message sent is delivered exactly once to its target process after a finite but potentially unbounded delay. Message delivery is first-in, first-out (FIFO); messages are delivered in the order in which they were sent.
The operational model is essentially unchanged from the layered snapshot model. The principal difference is that communication is now one-to-one rather than one-to-many. In Exercise 5.11, we ask you to show that barycentric agreement is impossible in a message-passing model if a majority of the process can fail. For this reason, we restrict our attention to ![]() -resilient protocols where
-resilient protocols where ![]() , the number of processes that can fail, is less than half:
, the number of processes that can fail, is less than half: ![]() .
.
We will see that as long as a majority of processes are nonfaulty, there is a ![]() -resilient message-passing protocol if and only if there is a
-resilient message-passing protocol if and only if there is a ![]() -resilient layered snapshot protocol. We will see, however, that message-passing protocols look quite different from their shared-memory counterparts.
-resilient layered snapshot protocol. We will see, however, that message-passing protocols look quite different from their shared-memory counterparts.
For shared-memory protocols, we focused on layered protocols because it is convenient to have a “clean” shared memory for each layer. For message-passing protocols, where there is no shared memory, we will not need to use layered protocols. Later, in Chapter 13, it will be convenient impose a layered structure on asynchronous message-passing executions.
In our examples we use the following notation. A process ![]() sends a message containing values
sends a message containing values ![]() to
to ![]() as follows:
as follows:
We say that a process broadcasts a message if it sends that message to all processes, including itself:
Here is how ![]() receives a message from
receives a message from ![]() :
:
Some message-passing protocols require that each time a process receives a message from another, the receiver forwards that message to all processes. Each process must continue to forward messages even after it has chosen its output value. Without such a guarantee, a nonfaulty process that chooses an output and falls silent is indistinguishable from a crashed process, implying that tasks requiring a majority of processes to be nonfaulty become impossible. We think of this continual forwarding as a kind of operating system service running in the background, interleaved with steps of the protocol itself. In our examples, such loops are marked with the background keyword:
We start with two useful protocols, one for ![]() -set agreement and one for barycentric agreement.
-set agreement and one for barycentric agreement.
5.5.1 Set agreement
As a first step, each process assembles values from as many other processes as possible. The getQuorum() method shown in Figure 5.7 collects values until it has received messages from all but ![]() processes. It is safe to wait for that many messages because there are at least
processes. It is safe to wait for that many messages because there are at least ![]() nonfaulty processes. It is not safe to wait for more, because the remaining
nonfaulty processes. It is not safe to wait for more, because the remaining ![]() processes may have crashed.
processes may have crashed.
Figure 5.8 shows a simple protocol for ![]() -set agreement. Each process broadcasts its input value, waits to receive values from a quorum of
-set agreement. Each process broadcasts its input value, waits to receive values from a quorum of ![]() messages, and chooses the least value among them. A proof of this protocol’s correctness is left as Exercise 5.9. Note that this protocol works for any value of
messages, and chooses the least value among them. A proof of this protocol’s correctness is left as Exercise 5.9. Note that this protocol works for any value of ![]() .
.
5.5.2 Barycentric agreement
Recall that in the barycentric agreement task, each process ![]() is assigned as input a vertex
is assigned as input a vertex ![]() of a simplex
of a simplex ![]() , and after exchanging messages with the others, chooses a face
, and after exchanging messages with the others, chooses a face ![]() containing
containing ![]() , such that for any two participating processes
, such that for any two participating processes ![]() and
and ![]() the faces they choose are ordered by inclusion:
the faces they choose are ordered by inclusion: ![]() , or vice versa. This task is essentially equivalent to an immediate snapshot, which it is convenient (but not necessary) to assume as a shared-memory primitive operation. In message-passing models, however, we assume send and receive as primitives, and we must build barycentric agreement from them.
, or vice versa. This task is essentially equivalent to an immediate snapshot, which it is convenient (but not necessary) to assume as a shared-memory primitive operation. In message-passing models, however, we assume send and receive as primitives, and we must build barycentric agreement from them.
Figure 5.9 shows a message-passing protocol for barycentric agreement. Each ![]() maintains a set
maintains a set ![]() of messages it has received, initially only
of messages it has received, initially only ![]() ’s input value (Line 2).
’s input value (Line 2). ![]() repeatedly broadcasts
repeatedly broadcasts ![]() , and waits to receive sets from other processes. If it receives
, and waits to receive sets from other processes. If it receives ![]() such that
such that ![]() (Line 7), then it increments its count of the number of times it has received
(Line 7), then it increments its count of the number of times it has received ![]() . If it receives
. If it receives ![]() such that
such that ![]() (Line 9). It sets
(Line 9). It sets ![]() to
to ![]() and starts over. When
and starts over. When ![]() has received
has received ![]() identical copies of
identical copies of ![]() from distinct processes, the protocol terminates, and
from distinct processes, the protocol terminates, and ![]() decides
decides ![]() . As usual, after the protocol terminates,
. As usual, after the protocol terminates, ![]() must continue to forward messages to the others (Lines 15–17).
must continue to forward messages to the others (Lines 15–17).
5.6 Decidability
This section uses more advanced mathematical techniques than the earlier sections.
Now that we have necessary and sufficient conditions for a task to have a protocol in various models, it is natural to ask whether we can automate the process of deciding whether a given task has a protocol in a particular model. Can we write a program (that is, a Turing machine) that takes a task description as input and returns a Boolean value indicating whether a protocol exists?
Not surprisingly, the answer depends on the model of computation. For wait-free layered snapshot protocols or wait-free ![]() -set layered snapshot protocols for
-set layered snapshot protocols for ![]() , the answer is no: There exists a family of tasks for which it is undecidable whether a protocol exists. We will construct one such family: the loop agreement tasks, discussed in Chapter 15. On the other hand, for wait-free
, the answer is no: There exists a family of tasks for which it is undecidable whether a protocol exists. We will construct one such family: the loop agreement tasks, discussed in Chapter 15. On the other hand, for wait-free ![]() -set layered snapshot protocols for
-set layered snapshot protocols for ![]() or 2, the answer is yes: For every task, it is decidable whether a protocol exists. For any model where the solvability question depends only on the 1-skeleton of the input complex, solvability is decidable (see Exercise 5.19).
or 2, the answer is yes: For every task, it is decidable whether a protocol exists. For any model where the solvability question depends only on the 1-skeleton of the input complex, solvability is decidable (see Exercise 5.19).
5.6.1 Paths and loops
Let ![]() be a finite 2-dimensional complex. Recall from Chapter 3 that an edge path between vertices
be a finite 2-dimensional complex. Recall from Chapter 3 that an edge path between vertices ![]() and
and ![]() in
in ![]() is a sequence of vertices
is a sequence of vertices ![]() such that each pair
such that each pair ![]() is an edge of
is an edge of ![]() for
for ![]() . A path is simple if the vertices are distinct.
. A path is simple if the vertices are distinct.
All edge loops considered here are assumed to be simple.
Informally, we would like to distinguish between edge loops that circumscribe “solid regions” and edge loops that circumscribe holes. To make this notion precise, we must introduce some continuous concepts.
All continuous loops considered here are assumed to be simple.
As illustrated in Figure 5.10, a continuous loop in ![]() is contractible if it can be continuously deformed to its base point in finite “time,” leaving the base point fixed. Formally, we capture this notion as follows.
is contractible if it can be continuously deformed to its base point in finite “time,” leaving the base point fixed. Formally, we capture this notion as follows.
A simple continuous loop ![]() is a representative of a simple edge loop
is a representative of a simple edge loop ![]() if their geometric images are the same:
if their geometric images are the same: ![]() .
.
Although any particular simple edge loop has an infinite number of representatives, it does not matter which one we pick.
In Exercise 5.18, we ask you to construct an explicit representative of an edge path.
Remarkably, the question remains undecidable even for complexes of dimension two (see Section 5.7, “Chapter notes”).
5.6.2 Loop agreement
Let ![]() denote the
denote the ![]() -simplex for which the vertices are labeled
-simplex for which the vertices are labeled ![]() , and
, and ![]() , and let
, and let ![]() denote an arbitrary
denote an arbitrary ![]() -dimensional complex. We are given three distinct vertices
-dimensional complex. We are given three distinct vertices ![]() , and
, and ![]() in
in ![]() , along with three edge paths
, along with three edge paths ![]() , and
, and ![]() , such that each path
, such that each path ![]() goes from
goes from ![]() to
to ![]() . We let
. We let ![]() denote the corresponding
denote the corresponding ![]() -dimensional simplicial subcomplex as well, in which case we let
-dimensional simplicial subcomplex as well, in which case we let ![]() . We assume that the paths are chosen to be nonself-intersecting and that they intersect each other only at corresponding end vertices.
. We assume that the paths are chosen to be nonself-intersecting and that they intersect each other only at corresponding end vertices.
In the loop agreement task, the processes start on vertices of ![]() and converge on a simplex in
and converge on a simplex in ![]() , subject to the following conditions. If all processes start on a single vertex
, subject to the following conditions. If all processes start on a single vertex ![]() , they converge on the corresponding vertex
, they converge on the corresponding vertex ![]() . If they start on two distinct input vertices,
. If they start on two distinct input vertices, ![]() and
and ![]() , they converge on some simplex (vertex or edge) along the path
, they converge on some simplex (vertex or edge) along the path ![]() linking
linking ![]() and
and ![]() . Finally, if the processes start on all three input vertices
. Finally, if the processes start on all three input vertices ![]() , they converge to some simplex (vertex, edge, or triangle) of
, they converge to some simplex (vertex, edge, or triangle) of ![]() . See Figure 5.11 for an illustration. More precisely:
. See Figure 5.11 for an illustration. More precisely:
5.6.3 Examples of loop agreement tasks
Here are some examples of interesting loop agreement tasks:
• A ![]() -set agreement task can be formulated as the loop agreement task
-set agreement task can be formulated as the loop agreement task ![]() , where
, where ![]() .
.
• Let ![]() be an arbitrary subdivision of
be an arbitrary subdivision of ![]() . In the
. In the ![]() -dimensional simplex agreement task, each process starts with a vertex in
-dimensional simplex agreement task, each process starts with a vertex in ![]() . If
. If ![]() is the face composed of the starting vertices, then the processes converge on a simplex in
is the face composed of the starting vertices, then the processes converge on a simplex in ![]() . This task is the loop agreement task
. This task is the loop agreement task ![]() , where
, where ![]() , with
, with ![]() denoting the unique simple edge path from
denoting the unique simple edge path from ![]() to
to ![]() in the subdivision of the edge
in the subdivision of the edge ![]() .
.
• The ![]() -dimensional
-dimensional ![]() -th barycentric simplex agreement task is simplex agreement for
-th barycentric simplex agreement task is simplex agreement for ![]() , the
, the ![]() -th iterated barycentric subdivision of
-th iterated barycentric subdivision of ![]() . Notice that
. Notice that ![]() -barycentric agreement is just the trivial loop agreement task
-barycentric agreement is just the trivial loop agreement task ![]() , where
, where ![]() , since a process with input
, since a process with input ![]() can directly decide
can directly decide ![]() .
.
• In the ![]() -dimensional
-dimensional ![]() -agreement task, input values are vertices of a face
-agreement task, input values are vertices of a face ![]() of
of ![]() , and output values are points of
, and output values are points of ![]() that lie within
that lie within ![]() of one another in the convex hull of the input values. This task can be solved by a protocol for
of one another in the convex hull of the input values. This task can be solved by a protocol for ![]() -barycentric simplex agreement for suitably large
-barycentric simplex agreement for suitably large ![]() .
.
• In the ![]() -dimensional approximate agreement task input values are taken from the set
-dimensional approximate agreement task input values are taken from the set ![]() , and output values are real numbers that lie within
, and output values are real numbers that lie within ![]() of one another in the convex hull of the input values. This task can be solved by a
of one another in the convex hull of the input values. This task can be solved by a ![]() -dimensional
-dimensional ![]() -agreement protocol.
-agreement protocol.
Of course, not all tasks can be cast as loop agreement tasks.
5.6.4 Decidability for layered snapshot protocols
We now show that a loop agreement task ![]() has layered snapshot protocol for
has layered snapshot protocol for ![]() if and only if the triangle loop
if and only if the triangle loop ![]() is contractible in
is contractible in ![]() . Loop contractibility, however, is undecidable, and therefore so is the question whether an arbitrary loop agreement task has a protocol in this model.
. Loop contractibility, however, is undecidable, and therefore so is the question whether an arbitrary loop agreement task has a protocol in this model.
5.6.5 Decidability with k-set agreement
Essentially the same argument shows that the existence of a wait-free loop agreement protocol is also undecidable for ![]() -set layered snapshot protocols for
-set layered snapshot protocols for ![]() .
.
It follows from Fact 5.6.6 that it is undecidable whether a loop agreement task has a protocol for three processes in this model.
The situation is different in models capable of solving 1-set or 2-set agreement, such as 1-resilient layered snapshot or message-passing protocols, or wait-free ![]() -set layered snapshot protocols for
-set layered snapshot protocols for ![]() or 2.
or 2.
5.7 Chapter notes
The layered approach used in this chapter was employed by Herlihy, Rajsbaum, and Tuttle [88,89] for message-passing systems. It was used to prove that connectivity is conserved across layers, something we will do later on. In this chapter we used the more direct approach of showing that subdivisions are created in each layer. Earlier work by Herlihy and Rajsbaum [79] and Herlihy and Shavit [91] was based on the “critical state” approach, a style of argument by contradiction pioneered by Fischer, Lynch, and Paterson [55]. This last paper proved that consensus is not solvable in a message-passing system, even if only one process may fail by crashing, a special case of Theorem 5.5.5. Our message-passing impossibility result is simplified by using layering.
In shared-memory systems the wait-free layered approach used in this chapter was introduced as an “iterated model” of computation by Borowsky and Gafni [26]; see the survey by Rajsbaum [128] for additional references. Algorithms in this model can be presented in a recursive form as described by Gafni and Rajsbaum [68] and in the tutorial by Herlihy, Rajsbaum, and Raynal [87]. Fault-tolerant versions of the model were studied by Rajsbaum, Raynal, and Travers [132]. In Chapter 14 we study the relationship of this model with a more standard model in which processes can write and read the same shared array any number of times.
The BG-simulation [27] provides a way to transform colorless tasks wait-free impossibilities bounds to ![]() -resilient impossibilities. As we shall see in Chapter 7, the
-resilient impossibilities. As we shall see in Chapter 7, the ![]() -resilient impossibility theorems proved directly in this chapter can be obtained by reduction to the wait-free case using this simulation. The BG simulation and layered models are discussed by Rajsbaum and Raynal [129]. Lubitch and Moran [111] provide a direct model-independent
-resilient impossibility theorems proved directly in this chapter can be obtained by reduction to the wait-free case using this simulation. The BG simulation and layered models are discussed by Rajsbaum and Raynal [129]. Lubitch and Moran [111] provide a direct model-independent ![]() -resilient impossibility proof of consensus.
-resilient impossibility proof of consensus.
Early applications of Sperner’s lemma to set agreement are due to Chaudhuri [38] and to Chaudhuri, Herlihy, Lynch, and Tuttle [40]. Herlihy and Rajsbaum [79] present critical state arguments to prove results about the solvability of set agreement using set agreement objects. We explore in Chapter 9 why renaming is weaker than ![]() -set agreement, as shown by Gafni, Rajsbaum, and Herlihy [69].
-set agreement, as shown by Gafni, Rajsbaum, and Herlihy [69].
Junqueira and Marzullo [99,98] introduced the core/survivor-set formalism for characterizing general adversaries used here, and they derived the first lower bounds for synchronous consensus against such an adversary. Delporte-Gallet et al. [46] investigate the computational power of more general adversaries in asynchronous shared memory using simulation. By contrast, the analogous impossibility results proved here use direct combinatorial arguments. The colorless task solvability characterization theorem for adversaries was proved by Herlihy and Rajsbaum [84] (and extended in [86], as discussed in Chapter 13).
Biran, Moran, and Zaks [19] showed that task solvability is decidable in a message-passing system where at most one process can fail by crashing, providing a characterization of solvable tasks in terms of graph connectivity, extending earlier work by Moran and Wolfstahl [118]. They further present a setting where the decision problem is NP-hard [20]. Gafni and Koutsoupias [63] were the first to note that three-process tasks are undecidable for wait-free layered snapshot protocols. This observation was generalized to other models by Herlihy and Rajsbaum [80].
The message-passing barycentric agreement protocol of Figure 5.9 is adapted from the stable vectors algorithm of Attiya et al. [9]. Attiya et al. [8] showed that it is possible to simulate shared memory using message-passing when a majority of processes are nonfaulty. One could use this simulation to show that our message-passing characterization follows from the shared-memory characterization.
The hierarchy of loop agreement tasks defined by Herlihy and Rajsbaum [83] will be presented in Chapter 15. Several variants and extensions have been studied. Degenerate loop agreement was defined in terms of two vertices of the output complex instead of three, by Liu, Pu, and Pan [108]. More general rendezvous task were studied by Liu, Xu, and Pan [109]. Similar techniques were used by Fraigniaud, Rajsbaum, and Travers [59] to derive hierarchies of tasks motivated by checkability issues.
Contractibility is undecidable because it reduces to the word problem for finitely presented groups: whether an expression reduces to the unit element. This problem was shown to be undecidable by S. P. Novikov [126] in 1955, and the isomorphism problem (whether two such groups are isomorphic) was shown to be undecidable by M. O. Rabin [127] in 1958. (For a more complete discussion of these problems, see Stillwell [142] or Sergeraert [140].)
Biran, Moran, and Zaks [21] study the round complexity of tasks in a message-passing system where at most one process can fail by crashing. Hoest and Shavit [94] consider nonuniform layered snapshot subdivisions to study the number of layers needed to solve a task in the wait-free case (see Exercise 5.21 about the complexity of solving colorless tasks).