Immediate Snapshot Subdivisions
Abstract
Throughout this book, we have relied on the fact that ![]() , the standard chromatic subdivision of the
, the standard chromatic subdivision of the ![]() -simplex
-simplex ![]() defined in Chapter 3, is indeed a subdivision of
defined in Chapter 3, is indeed a subdivision of ![]() . In this chapter, we give a rigorous proof of this claim.
. In this chapter, we give a rigorous proof of this claim.
Keywords
Schlegel diagram; Affinely independent; Cross-polytope; Polytope; Subdivision
Throughout this book, we have relied on the fact that ![]() , the standard chromatic subdivision of the
, the standard chromatic subdivision of the ![]() -simplex
-simplex ![]() defined in Chapter 3, is indeed a subdivision of
defined in Chapter 3, is indeed a subdivision of ![]() . In this chapter, we give a rigorous proof of this claim.
. In this chapter, we give a rigorous proof of this claim.
The complex ![]() captures all single-layer immediate snapshot executions for
captures all single-layer immediate snapshot executions for ![]() processes. Recall that a single-layer immediate snapshot execution is given by a schedule
processes. Recall that a single-layer immediate snapshot execution is given by a schedule ![]() , where each
, where each ![]() is the set of processes that participate in step
is the set of processes that participate in step ![]() , the
, the ![]() are disjoint, and the complete set of processes
are disjoint, and the complete set of processes ![]() is their union. We call
is their union. We call ![]() an ordered partition of
an ordered partition of ![]() .
.
16.1 A glimpse of discrete geometry
16.1.1 Polytopes
Recall from basic linear algebra that a hyperplane in ![]() is a solution of a single linear equation
is a solution of a single linear equation ![]() . Given such an equation, we also have two open half-spaces: the set of points for which
. Given such an equation, we also have two open half-spaces: the set of points for which ![]() and the set for which
and the set for which ![]() . It also defines two closed half-spaces: the unions of the hyperplane with the open half-spaces.
. It also defines two closed half-spaces: the unions of the hyperplane with the open half-spaces.
A ![]() -dimensional convex polytope1
-dimensional convex polytope1 ![]() is the convex hull of finitely many points in
is the convex hull of finitely many points in ![]() , where we assume that not all points lie on the same hyperplane. A face of a polytope
, where we assume that not all points lie on the same hyperplane. A face of a polytope ![]() is the intersection of
is the intersection of ![]() with a hyperplane that does not intersect the interior of
with a hyperplane that does not intersect the interior of ![]() . An
. An ![]() -dimensional polytope
-dimensional polytope ![]() is bounded by a number of
is bounded by a number of ![]() -dimensional faces, which are themselves polytopes. In fact,
-dimensional faces, which are themselves polytopes. In fact, ![]() is an intersection of the closed half-spaces associated to its
is an intersection of the closed half-spaces associated to its ![]() -faces.
-faces.
16.1.2 Schlegel diagrams
In general, it can be complicated to prove that one simplicial complex is a subdivision of another, even for a subdivision of a simplex. A straightforward argument would need to go into the technical details of topology of a geometric simplicial complex, possibly having to deal with explicit point descriptions as convex combinations of the vertices and so on.
Fortunately, in this case there is a short-cut: Schlegel diagrams. Informally, a Schlegel diagram is constructed by taking a “photograph” (perspective projection) of the polytope from a vantage point just outside of it, centered over a chosen ![]() -face
-face ![]() . Since the polytope is convex, it is possible to choose the vantage point so that all the faces project onto
. Since the polytope is convex, it is possible to choose the vantage point so that all the faces project onto ![]() and the projections of disjoint faces are themselves disjoint.
and the projections of disjoint faces are themselves disjoint.
Let us make this more specific. Pick a ![]() -dimensional face
-dimensional face ![]() of the polytope
of the polytope ![]() . As noted,
. As noted, ![]() itself is a
itself is a ![]() -dimensional polytope obtained as an intersection of
-dimensional polytope obtained as an intersection of ![]() with some hyperplane
with some hyperplane ![]() so that the rest of the polytope lies entirely on one side of this hyperplane. Let
so that the rest of the polytope lies entirely on one side of this hyperplane. Let ![]() denote the open half-space bordered by
denote the open half-space bordered by ![]() , which does not intersect the polytope
, which does not intersect the polytope ![]() . Choose a point
. Choose a point ![]() in
in ![]() very close to the barycenter of
very close to the barycenter of ![]() (in fact, any point in the interior of
(in fact, any point in the interior of ![]() will do). Now project the boundary of the polytope
will do). Now project the boundary of the polytope ![]() along the rays connecting it to
along the rays connecting it to ![]() into the hyperplane
into the hyperplane ![]() . If
. If ![]() is sufficiently close to the barycenter of
is sufficiently close to the barycenter of ![]() , the image of that projection will be contained in
, the image of that projection will be contained in ![]() . (In fact, topologically it will be precisely
. (In fact, topologically it will be precisely ![]() .) Furthermore, by linearity, the images of the faces on the boundary of
.) Furthermore, by linearity, the images of the faces on the boundary of ![]() , excluding
, excluding ![]() itself, will constitute a polyhedral subdivision of
itself, will constitute a polyhedral subdivision of ![]() , which we denote
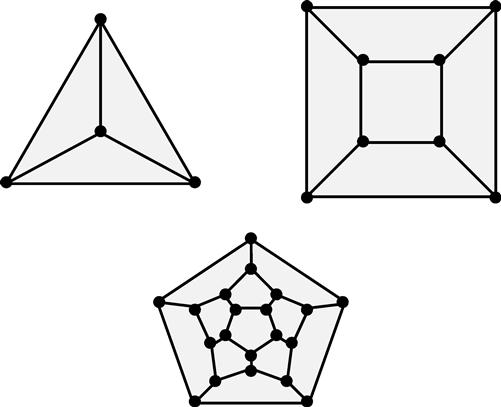
, which we denote ![]() . See Figure 16.1 for examples of Schlegel diagrams of a tetrahedron, cube, and dodecahedron.
. See Figure 16.1 for examples of Schlegel diagrams of a tetrahedron, cube, and dodecahedron.
16.1.3 Schlegel diagrams of cross-polytopes
A polytope whose ![]() -faces are simplices is said to be simplicial. If the polytope
-faces are simplices is said to be simplicial. If the polytope ![]() is simplicial, then the Schlegeldiagram is a simplicial subdivision of the
is simplicial, then the Schlegeldiagram is a simplicial subdivision of the ![]() -simplex
-simplex ![]() . We now consider a specific simplicial polytope in
. We now consider a specific simplicial polytope in ![]() . For
. For ![]() , let
, let ![]() denote the point whose
denote the point whose ![]() coordinate is
coordinate is ![]() , and all other coordinates are
, and all other coordinates are ![]() . Let
. Let ![]() be the convex hull of the point set
be the convex hull of the point set ![]() . It is easy to see that these
. It is easy to see that these ![]() points are in convex position and that the obtained polytope is simplicial. This is the so-called cross-polytope. Since for any pair of
points are in convex position and that the obtained polytope is simplicial. This is the so-called cross-polytope. Since for any pair of ![]() -faces of
-faces of ![]() there exists a symmetry of
there exists a symmetry of ![]() moving one of the faces to the other one, the Schlegel diagram will not depend on which face of
moving one of the faces to the other one, the Schlegel diagram will not depend on which face of ![]() we choose, so we just write
we choose, so we just write ![]() . Examples of Schlegel diagrams for crosspolytopes of dimensions 1 and 2 are shown in Figure 16.2. Note that the boundary complex of
. Examples of Schlegel diagrams for crosspolytopes of dimensions 1 and 2 are shown in Figure 16.2. Note that the boundary complex of ![]() is precisely the simplicial join of
is precisely the simplicial join of ![]() copies of the simplicial complex consisting of two points with no edge between them.
copies of the simplicial complex consisting of two points with no edge between them.
We shall need the following combinatorial description of the simplicial complex ![]() . The set of vertices is indexed by
. The set of vertices is indexed by ![]() , where for every
, where for every ![]() , the pair
, the pair ![]() denotes the inner point of
denotes the inner point of ![]() corresponding to the
corresponding to the ![]() axis, whereas the pair
axis, whereas the pair ![]() denotes the vertex of the
denotes the vertex of the ![]() -simplex used as the initial face for constructing the Schlegel diagram, corresponding to the
-simplex used as the initial face for constructing the Schlegel diagram, corresponding to the ![]() axis. The
axis. The ![]() -dimensional simplices of
-dimensional simplices of ![]() are all tuples
are all tuples ![]() such that
such that ![]() .
.
Clearly, the advantage of using Schlegel diagrams is that one gets the fact that the diagram is a subdivision of the face for free. Figure 16.2 shows that ![]() is isomorphic to
is isomorphic to ![]() , whereas
, whereas ![]() is different from
is different from ![]() . To get from
. To get from ![]() to
to ![]() one needs to further subdivide each of the edges of the triangle and extend these subdivisions to the subdivision of
one needs to further subdivide each of the edges of the triangle and extend these subdivisions to the subdivision of ![]() . For higher
. For higher ![]() , one needs to do this several times.
, one needs to do this several times.
16.1.4 Extending subdivisions of simplices
To generalize the construction to higher dimensions, we need the following standard fact about simplicial complexes. Let ![]() be an arbitrary simplicial complex, and let
be an arbitrary simplicial complex, and let ![]() be any simplex of
be any simplex of ![]() . Recall that the (closed) star of
. Recall that the (closed) star of ![]() is the union of all simplices that contain
is the union of all simplices that contain ![]() , denoted by
, denoted by ![]() . The complex
. The complex ![]() is the union of
is the union of ![]() and the deletion
and the deletion ![]() . The intersection of these two pieces is precisely the join of the link
. The intersection of these two pieces is precisely the join of the link ![]() with the boundary
with the boundary ![]() . The closed star itself is the simplicial join of
. The closed star itself is the simplicial join of ![]() with its link (see Section 3.3).
with its link (see Section 3.3).
Now assume that ![]() is a subdivision of
is a subdivision of ![]() that only subdivides the interior of
that only subdivides the interior of ![]() while leaving the boundary of
while leaving the boundary of ![]() unchanged. A Schlegel diagram is an example of such a subdivision. In this case, the join of
unchanged. A Schlegel diagram is an example of such a subdivision. In this case, the join of ![]() with
with ![]() is a subdivision of
is a subdivision of ![]() .
.
Back to our subdivision: We notice that since it does not change the link of ![]() , and it does not change the boundary
, and it does not change the boundary ![]() , it will also not change their join. Since this is precisely the space along which we attach
, it will also not change their join. Since this is precisely the space along which we attach ![]() , we can extend our local subdivision to a global subdivision of the entire
, we can extend our local subdivision to a global subdivision of the entire ![]() .
.
We now have all the tools at hand to describe how to obtain the chromatic subdivision ![]() . Start with
. Start with ![]() . Subdivide it as a Schlegel diagram of the cross-polytope. Proceed with the faces of
. Subdivide it as a Schlegel diagram of the cross-polytope. Proceed with the faces of ![]() of codimension
of codimension ![]() ; replace them with corresponding Schlegel diagrams and extend these subdivisions using the argument above to the global subdivision of the entire complex. After this, proceed to do the same for the faces of
; replace them with corresponding Schlegel diagrams and extend these subdivisions using the argument above to the global subdivision of the entire complex. After this, proceed to do the same for the faces of ![]() of codimension
of codimension ![]() and so on. We denote the simplicial complexes constructed in this way by
and so on. We denote the simplicial complexes constructed in this way by ![]() . In short: To go from
. In short: To go from ![]() to
to ![]() , we replace all boundary simplices of codimension
, we replace all boundary simplices of codimension ![]() of the original simplex
of the original simplex ![]() with Schlegel diagrams
with Schlegel diagrams ![]() and then extend this to the subdivision of the entire
and then extend this to the subdivision of the entire ![]() as described previously.
as described previously.
We are now ready to give a combinatorial description of the simplicial structure that we get at every step of the process.
16.2 Chapter notes
The material in this chapter is adapted from Kozlov [101].
More information on Schlegel diagrams can be found in Grunbaum [74] and more on cross-polytope in Coxeter [42].
1This is a special case of what is called polytope in some literature, which will be sufficient for our purposes.