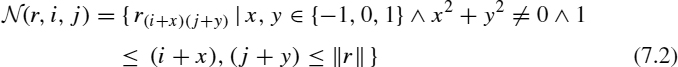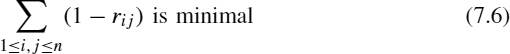CHAPTER 7

Solving Constrained Optimization Problems with Hybrid Evolutionary Algorithms

C. COTTA and A. J. FERNÁNDEZ

Universidad de Málaga, Spain

7.1 INTRODUCTION

The foundations for evolutionary algorithms (EAs) were established at the end of the 1960s [1,2] and strengthened at the beginning of the 1970s [3,4]. EAs appeared as an alternative to exact or approximate optimization methods whose performance in many real problems was not acceptable. When applied to real problems, EAs provide a valuable relation between the quality of the solution and the efficiency in obtaining it; for this reason these techniques attracted the immediate attention of many researchers and became what they now represent: a cutting-edge approach to real-world optimization. Certainly, this has also been the case for related techniques such as simulated annealing (SA) [5] and tabu search (TS) [6]. The term metaheuristics has been coined to denote them.

The term hybrid evolutionary algorithm (HEA) or hybrid metaheuristics refers to the combination of an evolutionary technique (i.e., metaheuristics) and another (perhaps exact or approximate) technique for optimization. The aim is to combine the best of both worlds, with the objective of producing better results than can be obtained by any component working alone. HEAs have proved to be very successful in the optimization of many practical problems [7,8], and as a consequence, there currently is increasing interest in the optimization community for this type of technique.

One crucial point in the development of HEAs (and hybrid metaheuristics in general) is the need to exploit problem knowledge, as was demonstrated clearly in the formulation of the no free lunch theorem (NFL) by Wolpert and Macready [9] (a search algorithm that performs in strict accordance with the amount and quality of the problem knowledge incorporated). Quite interestingly, this line of thinking had already been advocated by several researchers in the late 1980s and early 1990s (e.g., Hart and Belew [10], Davis [11], and Moscato [12]). This is precisely the foundation of one of the most known instances of HEAs, the memetic algorithms (MAs), a term used first in the work of Moscato [13,14,15]. Basically, an MA is a search strategy in which a population of optimizing agents synergistically cooperate and compete [12]. These agents are concerned explicitly with using knowledge from the problem being solved, as suggested in both theory and practice [16]. The success of MAs is evident, and one of the consequences is that currently the term memetic algorithm is used as synonym of for hybrid evolutionary algorithm, although in essence MAs are a particular case of HEAs.

As already mentioned, HEAs were born to tackle many problems that are very difficult to solve using evolutionary techniques or classical approaches working alone. This is precisely the case for constrained problems. Generally speaking, a constrained problem consists of a set of constraints involving a number of variables restricted to having values in a set of (possibly different) finite domains. Basically, a constraint is a relation maintained between the entities (e.g., objects or variables) of a problem, and constraints are used to model the behavior of systems in the real world by capturing an idealized view of the interaction between the variables involved. Solving a constrained problem consists of finding a possible assignment (of values in the computation domains) for the constrained variables that satisfies all the constraints. This type of problem can be solved using different techniques, ranging from traditional to modern. For example, some approaches to solving a problem are in the area of operational research (OR), genetic algorithms, artificial intelligence (AI) techniques, rule-based computations, conventional programs, and constraint-based approaches. Usually, solving is understood as the task of searching for a single solution to a problem, although sometimes it is necessary to find the set of all solutions. Also, in certain cases, because of the cost of finding all solutions, the aim is simply to find the best solution or an approximate solution within fixed resource bounds (e.g., in a reasonable time). Such types of constrained problems are called partially constrained problems (PCPs). An example of a PCP is a constrained combinatorial optimization problem (CCOP), which assigns a cost to each solution and tries to find an optimal solution within a given time frame [17]. In this chapter we focus on CCOPs.

Not surprisingly, HEAs have been used extensively to solve these types of problems. This chapter represents our particular share in this sense. In this work we analyze the deployment of HEAs on this domain. Initially, in Section 7.2 we provide a generic definition for these types of problems and an overview of general design guidelines to tackle CCOPs. In Section 7.3 we discuss a number of interesting and not well known (at least, in the EA community) CCOPs that the authors have recently attacked via HEAs. In particular, for each problem we provide a formal definition and discuss some interesting proposals that have tackled the problem. The chapter ends with a summary of lessons learned and some current and emerging research trends in HEAs for managing CCOPs.

7.2 STRATEGIES FOR SOLVING CCOPs WITH HEAs

In general terms, an unconstrained COP is often defined as a tuple , where is the search space, and is the objective function. Each D_i is a discrete set containing the values that a certain variable x_i can take. Therefore, any solution is a list , and we are interested in finding the solution minimizing (w log) the objective function f.

A constrained COP arises when we are just interested in optimizing the objective function within a subset S_val ⊂ S. This subset S_val represents valid or feasible solutions, and it may even be the case that f is a partial function defined only on these feasible solutions. The incidence vector of S_val on S defines a Boolean function [i.e., iff is a valid solution]. In practice, constrained COPs include a well-structured function such that it can be computed efficiently. Typically, this is achieved via the conjunction of several simpler Boolean functions [i.e., ]. Each of these functions is a constraint.

As an example, consider the vertex cover problem: Given a graph G(V, E), find a subset V′ ⊆ V of minimal size such that for any (u,υ) ∈ E, it holds that . In this case, S = {0, 1}^|V| the objective function (to be minimized) is , and there is a collection of binary constraints _uυ = min(1, x_u + x_υ), (u, υ) ∈ E.

The previous definition can easily be generalized to weighted CCOPs, where we do not simply have to know whether or not a solution satisfies a particular constraint, but we also have an indication how far that solution is from satisfying that constraint (in case it does not satisfy it at all). For this purpose, it is more convenient to denote each constraint as a function , where indicates fulfillment of the corresponding constraint, and any strictly positive value indicates an increasingly higher degree of violation of that constraint. Note that . The formulation above of weighted CCOPs allows a rather straightforward approach to tackling such a problem with HEAs: namely, incorporating the constraint functions within the objective function. This can be done in different ways [18], but the simplest method is aggregating all constraint functions within a penalty term that is added to the objective function: for example,

Different variants can be defined here, such as raising each δ_i term to a certain power (thus avoiding linear compensation among constraints and/or biasing the search toward low violation degrees) or adding an offset value in case of infeasibility to ensure that any feasible solution is preferable to any nonfeasible solution. This penalty approach can obviously be used only in those cases in which the objective function is defined on nonfeasible solutions. A typical example is the multidimensional 0–1 knapsack problem (MKP). This problem is defined via a row vector of profits , a column vector of capacity constraints , and a constraint matrix M. Solutions are binary column vectors , the objective function is , and the feasibility constraint is . Let . Then δ_i = − min(0, d_i).

This approach has the advantage of being very simple and allowing the use of rather standard EAs. Nevertheless, a HEA can provide a notably better solution if it is aware of these penalty terms and focuses on their optimization (see, e.g., the maximum density still life problem described in Section 7.3.2, or the social golfer problem described in Section 7.3.3). An alternative approach is trying to enforce the search being carried within the feasible region of the search space. This can be done in two ways:

1. By allowing the algorithm to traverse the infeasible region temporarily during the reproduction phase, but using a repairing procedure to turn nonfeasible solutions into feasible solutions before evaluation.
2. By restricting the search to the feasible region at all times. This can in turn be done in two ways:

   (a) By defining appropriate initialization, recombination, and mutation operators that take and produce feasible solutions.

   (b) By defining an unconstrained auxiliary search space S_aux and an adequate mapping dec: S_aux → S_val.

The repair approach is possibly the simplest option after the penalty approach, although it must be noted that a straightforward repair procedure is not always available. In any case it is interesting to note that in some sense (and depending on the particular procedure chosen for repairing), this stage can be regarded as a local search phase and some repair-based EAs can therefore qualify as memetic algorithms. An example of repairing can be found in the GA defined by Chu and Beasley for the MKP [19]. They define a heuristic order for traversing the variables and keep setting them to zero as long as the solution is nonfeasible (this procedure is complemented by a subsequent improvement phase in which variables are set to 1 in inverse order as long as the solution remains feasible). Another example of repairing can be found in the protein structure prediction problem [20], in which the search space is composed of all embeddings of a given string in a certain fixed lattice, and solutions are feasible only if they are self-avoiding. The repairing procedure is in this case more complex and requires the use of a backtracking algorithm to produce a feasible embedding. Nevertheless, even accounting for this additional cost, the HEA performs better than a simpler penalty-based approach.

Restricting the search to the feasible space via appropriate operators is in general much more complex, although it is the natural approach in certain problems, most notably in permutational problems. Feasible initialization and mutation are rather straightforward in this case, and there exists an extensive literature dealing with the definition of adequate operators for recombination, (see, e.g., ref. 21). Fixed-size subset problems are also dealt with easily using this method. As to the use of decoders, it is an arguably simpler and more popular approach. A common example, again on the MKP, is to define an auxiliary search space composed of all permutations of objects and to decode a particular permutation using a procedure that traverses the list of objects in the order indicated and includes objects in the solution if doing so does not result in a nonfeasible solution. Also for the MKP problem, a different approach was defined by Cotta and Troya [22] using lists of integers representing perturbations of the original instance data, and utilizing a greedy algorithm to obtain a solution from the instance modified. Note that contrary to some suggestions in the literature, it is not necessary (and often not even recommended) to have a decoder capable of producing any feasible solution or producing them with the same frequency: It is perfectly admissible to ignore suboptimal solutions and/or to bias the search to promising regions via overrepresentation of certain solutions (this is precisely the case with the previous example). Another example of a general approach can be found in a GRASP-like decoding procedure [23] in which solutions are encoded via a list of natural numbers that are used to control the level of greediness of a constructive heuristic. This approach has been used with success in the Golomb ruler problem (see Section 7.3.1).

A particular problem with this decoder approach is the fact that locality is easily lost; that is, a small change in the genotype can result in a large change in the phenotype [24,25]. This was observed, for example, in the indirect encoding of trees via Prüfer numbers [26].

7.3 STUDY CASES

In this section we review our recent work on solving CCOPs by applying hybrid collaborative techniques involving evolutionary techniques. In particular, we focus on four constrained problems that are not very well known in the evolutionary programming community and that we have tackled with a certain level of success in recent years.

7.3.1 Optimal Golomb Rulers

The concept of Golomb rulers was introduced by Babcock in 1953 [27], and described further by Bloom and Golomb [28]. Golomb rulers are a class of undirected graphs that, unlike most rulers, measure more discrete lengths than the number of marks they carry. The particularity of Golomb rulers is that on any given ruler, all differences between pairs of marks are unique, which makes them really interesting in many practical applications [29,30].

Traditionally, researchers are interested in discovering the optimal golomb ruler (OGR), that is, the shortest Golomb ruler for a number of marks. The task of finding optimal or nearly optimal Golomb rulers is computationally very difficult and results in an extremely challenging combinatorial problem. Proof of this is the fact that the search for an optimal 19-mark Golomb ruler took approximately 36,200 CPU hours on a Sun Sparc workstation using a very specialized algorithm [31]. Also, optimal solutions for 20 to 24 marks were obtained using massive parallelism projects, taking from several months up to four years (for the 24-mark instance) for each of those instances [30,32–34].

The OGR problem can be classified as a fixed-size subset selection problem, such as the p-median problem [35], although it exhibits some very distinctive features.

Formal Definition An n-mark Golomb ruler is an ordered set of n distinct nonnegative integers, called marks, a₁ < · · · < a_n, such that all the differences a_i − a_j (i > j) are distinct. We thus have a number of constraints of the form a_i − a_j ≠ a_k − a_m [i > j, k > m, (i, j) ≠ (k, m)]. Clearly, we may assume that a₁ = 0. By convention, a_n is the length of the Golomb ruler. A Golomb ruler with n marks is an optimal Golomb ruler if and only if:

• There exist no other n-mark Golomb rulers of shorter length.
• The ruler is canonically “smaller” with respect to equivalent rulers. This means that the first differing entry is less than the corresponding entry in the other ruler.

Figure 7.1 shows an OGR with four-marks. Observe that all distances between any two marks are different. Typically, Golomb rulers are represented by the values of the marks on the ruler [i.e., in a n-mark Golomb ruler, a_i = x (1 ≤ i ≤ n) means that x is the mark value in position i]. The sequence (0, 1, 4, 6) would then represent the ruler in Figure 7.1. However, this representation turns out to be inappropriate for EAs (e.g., it is problematic with respect to developing good crossover operators [36]). An alternative representation consists of representing the Golomb ruler via the lengths of its segments, where the length of a segment of a ruler is defined as the distance between two consecutive marks. Therefore, a Golomb ruler can be represented by n − 1 marks, specifying the lengths of the n − 1 segments that compose it. In the previous example, the sequence (1, 3, 2) would encode the ruler depicted in Figure 7.1.

Figure 7.1 Golomb ruler with four marks.

Solving OGRs In addition to related work discussed above, here we discuss a variety of techniques that have been used to find OGRs: for instance, systematic (exact) methods such as the method proposed by Shearer to compute OGRs up to 16 marks [37]. Basically, this method was based on the utilization of branch-and-bound algorithms combined with a depth-first search strategy (i.e., backtracking algorithms), making its use in experiments of upper bound sets equal to the length of the best known solution. Constraint programming (CP) techniques have also been used, although with limited success [38,39]. The main drawback of these complete methods is that they are costly computationally (i.e., time consuming). A very interesting hybridization of local search (LS) and CP to tackle the problem was presented by Prestwich [40]; up to size 13, the algorithm is run until the optimum is found, and for higher instances the quality of the solutions deteriorates.

Hybrid evolutionary algorithms were also applied to this problem. In this case two main approaches can be considered in tackling the OGR problem with EAs. The first is the direct approach, in which the EA conducts the search in the space _G of all possible Golomb rulers. The second is the indirect approach, in which an auxiliary _aux space is used by the EA. In the latter case, a decoder [41] must be utilized to perform the _aux → _G mapping. Examples of the former (direct) approach are the works of Soliday et al. [36] and Feeney [29]. As to the latter (indirect) approach, we cite work by Pereira et al. [42] (based on the notion of random keys [43]); also, Cotta and Fernández [23] used a problem-aware procedure (inspired in GRASP [44]) to perform genotype-to-phenotype mapping with the aim of ensuring the generation of feasible solutions; this method was shown to outperform other approaches.

A HEA incorporating a tabu search algorithm for mutation was proposed by Dotú and Van Hentenryck [45]. The basic idea was to optimize the length of the rulers indirectly by solving a sequence of feasibility problems (starting from an upper bound l and producing a sequence of rulers of length l₁ > l₂ > · · · > l_i > · · ·). This algorithm performed very efficiently and was able to find OGRs for up to 14 marks; in any case we note that this method requires an estimated initial upper bound, something that clearly favored its efficiency. At the same time, we conducted a theoretical analysis on the problem, trying to shed some light on the question of what makes a problem difficult for a certain search algorithm for the OGR problem. This study [46] consisted of an analysis of the fitness landscape of the problem. Our analysis indicated that the high irregularity of the neighborhood structure for the direct formulation introduces a drift force toward low-fitness regions of the search space. The indirect formulation that we considered earlier [23] does not have this drawback and hence would in principle be more amenable for conducting a local search. Then we presented an MA in which our indirect approach (i.e., a GRASP-based EA) was used in the phases of initialization and restarting of the population [47], whereas a direct approach in the form of a local improvement method based on the tabu search (TS) algorithm [45] was considered in the stages of recombination and local improvement. Experimental results showed that this algorithm could solve OGRs up to 15 marks and produced Golomb rulers for 16 marks that are very close to the optimal value (i.e., 1.1% distant), thus significantly improving the results reported in the EA literature.

Recently [48], we combined ideas from greedy randomized adaptive search procedures (GRASP) [49], scatter search (SS) [50,51], tabu search (TS) [52,53], clustering [54], and constraint programming (CP), and the resulting algorithm was able of solving the OGR problem for up to 16 marks, a notable improvement with regard to previous approaches reported in the literature in all the areas mentioned (i.e., EAs, LS, and CP). This algorithm yields a metaheuristic approach that is currently state of the art in relation to other metaheuristic approaches.

7.3.2 Maximum Density Still Life Problem

Conway's game of life [55] consists of an infinite checkerboard in which the only player places checkers on some of its squares. Each square has eight neighbors: the eight cells that share one or two corners with it. A cell is alive if there is a checker on it, and dead otherwise. The state of the board evolves iteratively according to three rules: (1) if a cell has exactly two living neighbors, its state remains the same in the next iteration; (2) if a cell has exactly three living neighbors, it is alive in the next iteration; and (3) if a cell has fewer than two or more than three living neighbors, it is dead in the next iteration.

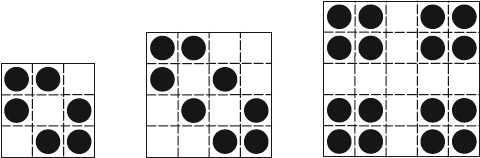
One challenging constrained optimization problem based on the game of life is the maximum density still life problem (MDSLP). To introduce this problem, let us define a stable pattern (also called a still life) as a board configuration that does not change through time, and let the density of a region be its percentage of living cells. The MDSLP in an n × n grid consists of finding a still life of maximum density. This problem is very difficult to solve, and although to the best of our knowledge, it has not been proved to be NP-hard, no polynomial-time algorithm for it is known. The problem has a number of interesting applications [56–58], and a dedicated web page (http://www.ai.sri.com/~nysmith/life) maintains up-to-date results. Figure 7.2 shows some maximum density still lives for small values of n.

Figure 7.2 Maximum density still lives for n ∈ {3, 4, 5}.

Formal Definition The constraints and objectives of the MDSLP are formalized in this section, in which we follow a notation similar to that used by Larrosa et al. [59,60]. To state the problem formally, let r be an n × n binary matrix, such that r_ij ∈ {0,1}, 1 ≤ i, j ≤ n [r_ij = 0 if cell (i, j) is dead, and 1 otherwise]. In addition, let (r, i, j) be the set comprising the neighborhood of cell r_ij:

where denotes the number of rows (or columns) of square matrix r, and let the number of living neighbors for cell r_ij be noted as η(r, i, j):

According to the rules of the game, let us also define the following predicate that checks whether cell r_ij is stable:

To check boundary conditions, we further denote by the (n + 2) × (n + 2) matrix obtained by embedding r in a frame of dead cells:

The maximum density still life problem for an n × n board, MDSLP(n), can now be stated as finding an n × n binary matrix r such that

subject to

Solving MDSLPs The MDSLP has been tackled using different approaches. Bosch and Trick [61] compared different formulations for the MDSLP using integer programming (IP) and constraint programming (CP). Their best results were obtained with a hybrid algorithm that mixed the two approaches. They were able to solve the cases for n = 14 and n = 15 in about 6 and 8 days of CPU time, respectively. Smith [62] used a pure constraint programming approach to attack the problem and proposed a formulation of the problem as a constraint satisfaction problem with 0–1 variables and nonbinary constraints; only instances up to n = 10 could be solved. The best results for this problem, reported by Larrosa et al. [59,60], showed the usefulness of an exact technique based on variable elimination and commonly used in solving constraint satisfaction problems: bucket elimination (BE) [63]. Their basic approach could solve the problem for n = 14 in about 10⁵ seconds. Further improvements pushed the solvability boundary forward to n = 20 in about twice as much time. Recently, Cheng and Yap [64,65] tackled the problem via the use of ad hoc global case constraints, but their results are far from those obtained previously by Larrosa et al.

Note that all the techniques discussed previously are exact approaches inherently limited for increasing problem sizes, whose capabilities as “anytime” algorithms are unclear. To avoid this limitation, we proposed the use of HEAs to tackle the problem. In particular, we considered an MA consisting of an EA endowed with tabu search, where BE is used as a mechanism for recombining solutions, providing the best possible child from the parental set [66]. Experimental tests indicated that the algorithm provided optimal or nearly optimal results at an acceptable computational cost. A subsequent paper [67] dealt with expanded multilevel models in which our previous exact/metaheuristic hybrid was further hybridized with a branch-and-bound derivative: beam search (BS). The experimental results show that our hybrid evolutionary proposals were a practical and efficient alternative to the exact techniques employed so far to obtain still life patterns.

We recently proposed [48] a new hybrid algorithm that uses the technique of minibuckets (MBs) [68] to further improve the lower bounds of the partial solutions that are considered in the BS part of the hybrid algorithm. This new algorithm is obtained from the hybridization, at different levels, of complete solving techniques (BE), incomplete deterministic methods (BS and MB), and stochastic algorithms (MAs). An experimental analysis showed that this new proposal consistently finds optimal solutions for MDSLP instances up to n = 20 in considerably less time than do all the previous approaches reported in the literature. Moreover, this HEA performed at the state-of-the-art level, providing solutions that are equal to or better than the best ones reported to date in the literature.

7.3.3 Social Golfer Problem

The social golfer problem (SGP), first posted at http://sci.op-research in May 1998, consists of scheduling n = g · s golfers into g groups of s players every week for w weeks so that no two golfers play in the same group more than once. The problem can be regarded as an optimization problem if for two given values of g and s, we ask for the maximum number of weeks w the golfers can play together. SGP is a combinatorial constrained problem that raises interesting issues in symmetry breaking (e.g., players can be permuted within groups, groups can be ordered arbitrarily within every week, and even the weeks themselves can be permuted). Note that symmetry is also present in both the OGR problem and the MDSLP. Notice, however, that problem symmetry is beyond the scope of this chapter and thus symmetry issues will not be discussed explicitly here.

Formal Definition As mentioned above, SGP consists of scheduling n = g · s golfers into g groups of s players every week for w weeks, so that no two golfers play in the same group more than once. An instance of the social golfer is thus specified by a triplet . A (potentially infeasible) solution for such an instance is given by a schedule , where , and |σ(i, j)| = s for all , , that is, a function that on input (i, j) returns the set of s players that constitute the ith group of the jth week. There are many possible ways of modeling for SGP, which is one of the reasons that it is so interesting. In a generalized way, this problem can be modeled as a constraint satisfaction problem (CSP) defined by the following constraints:

• A golfer plays exactly once a week:

  

  This constraint can be also formalized by claiming that no two groups in the same week intersect:

  

• No two golfers play together more than once:

  

  This constraint can also be formulated as a weighted constraint: Let #_σ(a, b) be the number of times that golfers a and b play together in schedule σ:

  

  where [·] is the Iverson bracket: namely, [true] = 1 and [false] = 0. Then we can define the degree of violation of a constraint a-and-b-play-together-at-most-once as max(0, #_σ(a, b) − 1).

As already noted, symmetries can appear in (and can be removed from) this problem in several forms; see refs. 69–71 for more details.

Solving the SGP The SGP was first attacked by CP techniques that addressed the SGP mainly by detecting and breaking symmetries (see, e.g., refs. 72–79). Due to the interesting properties of the problem, it also attracted attention in other optimization areas and has been tackled extensively using different techniques. Here we mention just some of the most recent advances in solving the SGP. For example, Harvey and Winterer [69] have proposed constructing solutions to the SGP by using sets of mutually orthogonal Latin squares. Also, Gent and Lynce [79] have introduced a satisfiability (SAT) encoding for the SGP. Barnier and Brisset [70] have presented a combination of techniques to find efficient solutions to a specific instance of SGP, Kirkman's schoolgirl problem. Global constraints for lexicographic ordering have been proposed by Frisch et al. [80], being used for breaking symmetries in the SGP. Also, a tabu-based local search algorithm for the SGP is described by Dotú and Van Hentenryck [81].

To the best of our knowledge, we presented the first attempt of tackling the SGP by evolutionary techniques [71]; it consisted of a memetic algorithm (MA) that is based on the hybridization of evolutionary programming and tabu search. The flexibility of MAs eased the handling of the problem symmetries. Our MA, based on selection, mutation, and local search, performed at a state-of-the-art level for this problem.

7.3.4 Consensus Tree Problem

The inference (or reconstruction) of phylogenetic trees is a problem from the bioinformatics domain that has direct implications in areas such as multiple sequence alignment [82], protein structure prediction [83], and molecular epidemiological studies of viruses [84], just to cite a few. This (optimization) problem seeks the best tree representing the evolutionary history of a collection of species, therefore providing a hierarchical representation of the degree of closeness among a set of organisms. This is typically done on the basis of molecular information (e.g., DNA sequences) from these species, and can be approached in a number of ways: maximum likelihood, parsimony, distance matrices, and so on [85]. A number of different high-quality trees (with quality measured in different ways) can then be found, each possibly telling something about the true solution. Furthermore, the fact that data come from biological experiments, which are not exact, makes nearly optimal solutions (even nearly optimal with respect to different criteria) be almost as relevant as the actual optimum. It is in this situation where the consensus tree problem (often called supertree) comes into play [86]. Essentially, a consensus method tries to summarize a collection of trees provided as input, returning a single tree [87]. This implies identifying common substructures in the input trees and representing these in the output tree.

Formal Definition Let T be a strictly binary rooted tree; a LISP-like notation will be used to denote the structure of the tree. Thus, (sLR) is a tree with root s and with L and R as subtrees, and (·) is an empty tree. The notation (a) is a shortcut for (a(·)(·)). Let (T) be the set of leaves of T. Each edge e in T defines a bipartition , where S₁ are the leaves in (T) that can be reached from the root passing through e, and S₂ are the remaining leaves. We define Π(T) = {π_T(e) | e ∈ T}.

The consensus tree problem consists of representing a collection of trees {T₁, …, T_m} as a single tree that should be optimal with respect to a certain model. This model can be approached in several ways [87]; for instance, the models described by Gusfield [88] (i.e., tree compatibility problem) and by Day [89] (i.e., strict consensus) focus on finding a tree such that and , respectively; also the model presented by Barthélemy and McMorris [90] (i.e., the median tree) tries to minimize the sum of differences between T and the input trees [i.e., min ].

As a consequence, the meaning of global optimum is different from that of typical CCOPs since it is very dependent on the model selected as well as other metrics, such as the way of evaluating the differences between the trees (i.e., the distance between trees). This is so because the distance d(T, T′) between trees is not standard, and different alternatives can be considered. Perhaps the most typical distance is defined as the number of noncommon bipartitions in Π(T) and Π(T′): This is also termed the partition metric. In any case, alternative metrics can be considered. For example, one can cite edit distance [measured in terms of some edition operations, such as nearest-neighbor interchange (NNI), subtree prune and regraft (SPR), or tree bisection and reconnection (TBR), among others; see ref. 91] or the TreeRank measure [92]. All of these metrics have advantages and drawbacks, so it is not always easy to determine which is the best election.

The fact that the problem admits different formulations is an additional reason that it so interesting. For example, recently, the problem was formulated as a constraint satisfaction problem [93]: Gent et al. presented constraint encoding based on the observation that any rooted tree can be considered as being minimum ultrametric [94] when we label interior nodes with their depth in that tree. This guarantees that any path from the root to a leaf corresponds to a strictly increasing sequence. See refs. 93 and 95 for more details about this encoding.

Solving the CTP Regarding the inference of phylogenetic trees, the use of classical exact techniques can be considered generally inappropriate in this context. Indeed, the use of heuristic techniques in this domain seems much more adequate. These can range from simple constructive heuristics (e.g., greedy agglomerative techniques such as UPGMA [96]) to complex metaheuristics [97] (e.g., evolutionary algorithms [98, 99] or local search [100]). At any rate, it is well known that any heuristic method is going to perform in strict accordance with the amount of problem knowledge it incorporates [9,16]. Gallardo et al. [101] explored this possibility precisely and presented a model for the integration of branch-and-bound techniques [102] and memetic algorithms [13–15]. This model resulted in a synergistic combination yielding better results (experimentally speaking) than those of each of its constituent techniques, as well as classical agglomerative algorithms and other efficient tree construction methods.

Regarding the consensus tree problem, very different methods have been used (e.g., polynomial time algorithms [103], constraint programming (CP) [93,95,104], and evolutionary algorithms (EAs) [99], among others). With the aim of improving the results obtained so far, we are now experimenting with hybrid methods that combine the best of the CP and EA proposals. More specifically, we are evaluating two algorithms: The first is an MA [15] in which we use a CP method for supertree construction based on the method published by Gent et al. [93] as a recombination operator. The results should soon be reported [105].

7.4 CONCLUSIONS

Constrained COPs are ubiquitous and are representative of a plethora of relevant real-world problems. As such, they are also typically difficult to solve and demand the use of flexible cutting-edge optimization technologies for achieving competitive results. As we have shown, the framework of evolutionary computation offers solid ground on which powerful optimizations algorithms for CCOPs can be built via hybridization.

HEAs provide different options for dealing with CCOPs, ranging from the inclusion of constraints as side objectives to the definition of ad hoc operators working within the feasible region, including the use of repairing mechanisms or complex genotype–phenotype mappings. Each of these approaches is suited to different (not necessarily disjoint) optimization scenarios. Hence, they can avail practitioners in different ways, providing them with alternative methods for solving the problem at hand.

It is difficult to provide general design guidelines, since there are many problem specificities to be accounted for. The availability of other heuristics (either classical or not) may suggest the usefulness of performing a direct search in the space of solutions, so that these heuristics can be exploited by the HEA. The particulars of the objective function or the sparseness of valid solutions may dictate whether or not a penalty-based approach is feasible (e.g., nonfeasible solutions could not be evaluated at all, the search algorithm could spend most of the time outside the feasible region). The availability of construction heuristics can in turn suggest the utilization of indirect approaches (e.g., via decoder functions). This approach is sometimes overestimated, in the sense that one has to be careful to provide the HEA with a search landscape that is easy to navigate. Otherwise, the benefits of the heuristic mapping can be counteracted by the erratic search dynamics.

From a global perspective, the record of success of HEAs on CCOPs suggests that these techniques will be used increasingly to solve problems in this domain. It is then expected that the corpus of theoretical knowledge on the deployment of HEAs on CCOPs will grow alongside applications of these techniques to new problems in the area.

Acknowledgments

The authors are partially supported by the Ministry of Science and Technology and FEDER under contract TIN2005-08818-C04-01 (the OPLINK project). The second author is also supported under contract TIN-2007-67134.

REFERENCES

1. L. J. Fogel, A. J. Owens, and M. J. Walsh. Artificial Intelligence Through Simulated Evolution. Wiley, New York, 1966.

2. H.-P. Schwefel. Kybernetische Evolution als Strategie der experimentellen Forschung in der Strömungstechnik. Diplomarbeit, Technische Universität Berlin, Hermann Föttinger–Institut für Strömungstechnik, März, Germany, 1965.

3. J. Holland. Adaptation in Natural and Artificial Systems. University of Michigan Press, Ann Arbor, MI, 1975.

4. I. Rechenberg. Evolutionsstrategie: optimierung technischer Systeme nach Prinzipien der biologischen Evolution. Frommann-Holzboog, Stuttgart, Germany, 1973.

5. S. Kirkpatrick, C. D. Gelatt, Jr., and M. P. Vecchi. Optimization by simulated annealing. Science, 220(4598):671–680, 1983.

6. F. Glover and M. Laguna. Tabu Search. Kluwer Academic, Norwell, MA, 1997.

7. C. Reeves. Hybrid genetic algorithm for bin-packing and related problems. Annals of Operation Research, 63:371–396, 1996.

8. A. P. French, A. C. Robinson, and J. M. Wilson. Using a hybrid genetic-algorithm/branch and bound approach to solve feasibility and optimization integer programming problems. Journal of Heuristics, 7(6):551–564, 2001.

9. D. H. Wolpert and W. G. Macready. No free lunch theorems for optimization. IEEE Transactions on Evolutionary Computation, 1(1):67–82, 1997.

10. W. E. Hart and R. K. Belew. Optimizing an arbitrary function is hard for the genetic algorithm. In R. K. Belew and L. B. Booker, eds., Proceedings of the 4th International Conference on Genetic Algorithms, San Mateo CA. Morgan Kaufmann, San Francisco, CA, 1991, pp. 190–195.

11. L. D. Davis. Handbook of Genetic Algorithms. Van Nostrand Reinhold Computer Library, New York, 1991.

12. P. Moscato. On evolution, search, optimization, genetic algorithms and martial arts: towards memetic algorithms. Technical Report 826. Caltech Concurrent Computation Program, California Institute of Technology, Pasadena, CA, 1989.

13. P. Moscato. Memetic algorithms: a short introduction. In D. Corne, M. Dorigo, and F. Glover, eds., New Ideas in Optimization, McGraw-Hill, Maidenhead, UK, 1999, pp. 219–234.

14. P. Moscato and C. Cotta. A gentle introduction to memetic algorithms. In F. Glover and G. Kochenberger, eds., Handbook of Metaheuristics, Kluwer Academic, Norwell, MA, 2003, pp. 105–144.

15. P. Moscato, C. Cotta, and A. S. Mendes. Memetic algorithms. In G. C. Onwubolu and B. V. Babu, eds., New Optimization Techniques in Engineering. Springer-Verlag, Berlin, 2004, pp. 53–85.

16. J. Culberson. On the futility of blind search: an algorithmic view of “no free lunch.” Evolutionary Computation, 6(2):109–127, 1998.

17. E. C. Freuder and R. J. Wallace. Partial constraint satisfaction. Artificial Intelligence, 58:21–70, 1992.

18. A. E. Eiben and J. E. Smith. Introduction to Evolutionary Computating. Natural Computing Series. Springer-Verlag, New York, 2003.

19. P. C. Chu and J. E. Beasley. A genetic algorithm for the multidimensional knapsack problem. Journal of Heuristics, 4(1):63–86, 1998.

20. C. Cotta. Protein structure prediction using evolutionary algorithms hybridized with backtracking. In J. Mira and J.R. Álvarez, eds., Artificial Neural Nets Problem Solving Methods, vol. 2687 of Lecture Notes in Computer Science. Springer-Verlag, New York, 2003, pp. 321–328.

21. C. Cotta and J. M. Troya. Genetic forma recombination in permutation flowshop problems. Evolutionary Computation, 6(1):25–44, 1998.

22. C. Cotta and J. M. Troya. A hybrid genetic algorithm for the 0–1 multiple knapsack problem. In G. D. Smith, N. C. Steele, and R. F. Albrecht, eds., Artificial Neural Nets and Genetic Algorithms 3, Springer-Verlag, New York, 1998, pp. 251–255.

23. C. Cotta and A. J. Fernández. A hybrid GRASP: evolutionary algorithm approach to Golomb ruler search. In Xin Yao et al., eds., Parallel Problem Solving from Nature VIII, vol. 3242 of Lecture Notes in Computer Science. Springer-Verlag, New York, 2004, pp. 481–490.

24. E. Falkenauer. The lavish ordering genetic algorithm. In Proceedings of the 2nd Metaheuristics International Conference (MIC'97), Sophia-Antipolis, France, 1997, pp. 249–256.

25. J. Gottlieb and G. R. Raidl. The effects of locality on the dynamics of decoder-based evolutionary search. In L. D. Whitley et al., eds., Proceedings of the 2000 Genetic and Evolutionary Computation Conference, Las Vegas, NV. Morgan Kaufmann, San Francisco, CA, 2000, pp. 283–290.

26. J. Gottlieb, B. A. Julstrom, F. Rothlauf, and G. R. Raidl. Prüfer numbers: a poor representation of spanning trees for evolutionary search. In L. Spector et al., eds., Proceedings of the 2001 Genetic and Evolutionary Computation Conference, San Francisco, CA. Morgan Kaufmann, San Francisco, CA, 2001, pp. 343–350.

27. W. C. Babcock. Intermodulation interference in radio systems. Bell Systems Technical Journal, pp. 63–73, 1953.

28. G. S. Bloom and S. W. Golomb. Applications of numbered undirected graphs. Proceedings of the IEEE, 65(4):562–570, 1977.

29. B. Feeney. Determining optimum and near-optimum Golomb rulers using genetic algorithms. Master's thesis, Computer Science, University College Cork, UK, Oct. 2003.

30. W. T. Rankin. Optimal Golomb rulers: an exhaustive parallel search implementation. Master's thesis, Electrical Engineering Department, Duke University, Durham, NC, Dec. 1993.

31. A. Dollas, W. T. Rankin, and D. McCracken. A new algorithm for Golomb ruler derivation and proof of the 19 mark ruler. IEEE Transactions on Information Theory, 44:379–382, 1998.

32. M. Garry, D. Vanderschel, et al. In search of the optimal 20, 21 & 22 mark Golomb rulers. GVANT project. http://members.aol.com/golomb20/index.html, 1999.

33. J. B. Shearer. Golomb ruler table. Mathematics Department, IBM Research. http://www.research.ibm.com/people/s/shearer/grtab.html, 2001.

34. W. Schneider. Golomb rulers. MATHEWS: the archive of recreational mathematics. http://www.wschnei.de/number-theory/golomb-rulers.html, 2002.

35. P. Mirchandani and R. Francis. Discrete Location Theory. Wiley-Interscience, New York, 1990.

36. S. W. Soliday, A. Homaifar, and G. L. Lebby. Genetic algorithm approach to the search for Golomb rulers. In L. J. Eshelman, ed., Proceedings of the 6th International Conference on Genetic Algorithms (ICGA'95), Pittsburgh, PA. Morgan Kaufmann, San Francisco, CA, 1995, pp. 528–535.

37. J. B. Shearer. Some new optimum Golomb rulers. IEEE Transactions on Information Theory, 36:183–184, Jan. 1990.

38. B. M. Smith and T. Walsh. Modelling the Golomb ruler problem. Presented at the Workshop on Non-binary Constraints (IJCAI'99), Stockholm, Sweden, 1999.

39. P. Galinier, B. Jaumard, R. Morales, and G. Pesant. A constraint-based approach to the Golomb ruler problem. Presented at the 3rd International Workshop on Integration of AI and OR Techniques (CP-AI-OR'01), 2001.

40. S. Prestwich. Trading completeness for scalability: hybrid search for cliques and rulers. In Proceedings of the 3rd International Workshop on the Integration of AI and OR Techniques in Constraint Programming for Combinatorial Optimization Problems (CPAIOR'01), Ashford, UK, 2001, pp. 159–174.

41. S Koziel and Z. Michalewicz. A decoder-based evolutionary algorithm for constrained parameter optimization problems. In T. Bäeck, A. E. Eiben, M. Schoenauer, and H.-P. Schwefel, eds., Parallel Problem Solving from Nature V, vol. 1498 of Lecture Notes in Computer Science. Springer-Verlag, New York, 1998, pp. 231–240.

42. F. B. Pereira, J. Tavares, and E. Costa. Golomb rulers: The advantage of evolution. In F. Moura-Pires and S. Abreu, eds., Progress in Artificial Intelligence, 11th Portuguese Conference on Artificial Intelligence, vol. 2902 of Lecture Notes in Computer Science, Springer-Verlag, New York, 2003, pp. 29–42.

43. J. Bean. Genetic algorithms and random keys for sequencing and optimization. ORSA Journal on Computing, 6:154–160, 1994.

44. M. G. C. Resende and C. C. Ribeiro. Greedy randomized adaptive search procedures. In F. Glover and G. Kochenberger, eds., Handbook of Metaheuristics, Kluwer Academic, Norwell, MA, 2003, pp. 219–249.

45. I. Dotú and P. Van Hentenryck. A simple hybrid evolutionary algorithm for finding Golomb rulers. In D.W. Corne et al., eds., Proceedings of the 2005 Congress on Evolutionary Computation (CEC'05), Edinburgh, UK, vol. 3. IEEE Press, Piscataway, NJ, 2005, pp. 2018–2023.

46. C. Cotta and A. J. Fernández. Analyzing fitness landscapes for the optimal Golomb ruler problem. In J. Gottlieb and G. R. Raidl, eds., Evolutionary Computation in Combinatorial Optimization, vol. 3248 of Lecture Notes in Computer Science. Springer-Verlag, New York, 2005, pp. 68–79.

47. C. Cotta, I. Dotú, A. J. Fernández, and P. Van Hentenryck. A memetic approach to Golomb rulers. In T. P. Runarsson et al., eds., Parallel Problem Solving from Nature IX, vol. 4193 of Lecture Notes in Computer Science. Springer-Verlag, New York, 2006, pp. 252–261.

48. C. Cotta, I. Dotú, A. J. Fernández, and P. Van Hentenryck. Local search-based hybrid algorithms for finding Golomb rulers. Constraints, 12(3):263–291, 2007.

49. T. A. Feo and M. G. C. Resende. Greedy randomized adaptive search procedures. Journal of Global Optimization, 6:109–133, 1995.

50. F. Glover. A template for scatter search and path relinking. In Jin-Kao Hao et al., eds., Selected Papers of the 3rd European Conference on Artificial Evolution (AE'97), Nîmes, France, vol. 1363 of Lecture Notes in Computer Science. Springer-Verlag, New York, 1997, pp. 1–51.

51. M. Laguna and R. Martí. Scatter Search: Methodology and Implementations in C. Kluwer Academic, Norwell, MA, 2003.

52. F. Glover. Tabu search: part I. ORSA Journal of Computing, 1(3):190–206, 1989.

53. F. Glover. Tabu search: part II. ORSA Journal of Computing, 2(1):4–31, 1989.

54. A. K. Jain, N. M. Murty, and P. J. Flynn. Data clustering: a review. ACM Computing Surveys, 31(3):264–323, 1999.

55. M. Gardner. The fantastic combinations of John Conway's new solitaire game. Scientific American, 223:120–123, 1970.

56. M. Gardner. On cellular automata, self-reproduction, the garden of Eden and the game of “life.” Scientific American, 224:112–117, 1971.

57. E. R. Berlekamp, J. H. Conway, and R. K. Guy. Winning Ways for Your Mathematical Plays, vol. 2 of Games in Particular. Academic Press, London, 1982.

58. M. Gardner. Wheels, Life, and Other Mathematical Amusements. W.H. Freeman, New York, 1983.

59. J. Larrosa and E. Morancho. Solving “still life” with soft constraints and bucket elimination. In Rossi [106], pp. 466–479.

60. J. Larrosa, E. Morancho, and D. Niso. On the practical use of variable elimination in constraint optimization problems: “still life” as a case study. Journal of Artificial Intelligence Research, 23:421–440, 2005.

61. R. Bosch and M. Trick. Constraint programming and hybrid formulations for three life designs. In Proceedings of the 4th International Workshop on Integration of AI and OR Techniques in Constraint Programming for Combinatorial Optimization Problems (CP-AI-OR), Le Croisic, France, 2002, pp. 77–91.

62. B. M. Smith. A dual graph translation of a problem in “life.” In P. Van Hentenryck, ed., Principles and Practice of Constraint Programming (CP'02), Ithaca, NY, vol. 2470 of Lecture Notes in Computer Science. Springer-Verlag, New York, 2002, pp. 402–414.

63. R. Dechter. Bucket elimination: a unifying framework for reasoning. Artificial Intelligence, 113(1–2):41–85, 1999.

64. K. C. K. Cheng and R. H. C. Yap. Ad-hoc global constraints for life. In P. van Beek, ed., Principles and Practice of Constraint Programming (CP'05), Sitges, Spain, vol. 3709 of Lecture Notes in Computer Science. Springer-Verlag, New York, 2005, pp. 182–195.

65. K. C. K. Cheng and R. H. C. Yap. Applying ad-hoc global constraints with the case constraint to still-life. Constraints, 11:91–114, 2006.

66. J. E. Gallardo, C. Cotta, and A. J. Fernández. A memetic algorithm with bucket elimination for the still life problem. In J. Gottlieb and G. Raidl, eds., Evolutionary Computation in Combinatorial Optimization, Budapest, Hungary vol. 3906 of Lecture Notes in Computer Science. Springer-Verlag, New York, 2006, pp. 73–85.

67. J. E. Gallardo, C. Cotta, and A. J. Fernández. A multi-level memetic/exact hybrid algorithm for the still life problem. In T. P. Runarsson et al., eds., Parallel Problem Solving from Nature IX, Reykjavik, Iceland, vol. 4193 of Lecture Notes in Computer Science. Springer-Verlag, New York, 2006, pp. 212–221.

68. R. Dechter. Mini-buckets: a general scheme for generating approximations in automated reasoning. In Proceedings of the 15th International Joint Conference on Artificial Intelligence, 1997, pp. 1297–1303.

69. W. Harvey and T. Winterer. Solving the MOLR and social golfers problems. In P. van Beek, ed., Proceedings of the 11th International Conference on Principles and Practice of Constraint Programming, Sitges, Spain, vol. 3709 of Lecture Notes in Computer Science. Springer-Verlag, New York, 2005, pp. 286–300.

70. N. Barnier and P. Brisset. Solving Kirkman's schoolgirl problem in a few seconds. Constraints, 10(1):7–21, 2005.

71. C. Cotta, I. Dotú, A. J. Fernández, and P. Van Hentenryck. Scheduling social golfers with memetic evolutionary programming. In F. Almeida et al., eds., Hybrid Metaheuristics, vol. 4030 of Lecture Notes in Computer Science. Springer-Verlag, New York, 2006, pp. 150–161.

72. T. Fahle, S. Schamberger, and M. Sellmann. Symmetry breaking. In T. Walsh, ed., Proceedings of the 7th International Conference on Principles and Practice of Constraint Programming, Paphos, Cyprus, vol. 2239 of Lecture Notes in Computer Science. Springer-Verlag, New York, 2001, pp. 93–107.

73. B. M. Smith. Reducing symmetry in a combinatorial design problem. In Proceedings of the 3rd International Workshop on the Integration of AI and OR Techniques in Constraint Programming for Combinatorial Optimization Problems, Ashford, UK, 2001, pp. 351–359.

74. M. Sellmann and W. Harvey. Heuristic constraint propagation. In P. Van Hentenryck, ed., Proceedings of the 8th International Conference on Principles and Practice of Constraint Programming, Ithaca, NY, vol. 2470 of Lecture Notes in Computer Science. Springer-Verlag, New York, 2002, pp. 738–743.

75. A. Ramani and I. L. Markov. Automatically exploiting symmetries in constraint programming. In B. Faltings, A. Petcu, F. Fages, and F. Rossi, eds., Recent Advances in Constraints, Joint ERCIM/CoLogNet International Workshop on Constraint Solving and Constraint Logic Programming, (CSCLP'04), Lausanne, Switzerland, vol. 3419 of Lecture Notes in Computer Science, Revised Selected and Invited Papers. Springer-Verlag, New York, 2005, pp. 98–112.

76. S. D. Prestwich and A. Roli. Symmetry breaking and local search spaces. In R. Barták and M. Milano, eds., Proceedings of the 2nd International Conference on the Integration of AI and OR Techniques in Constraint Programming for Combinatorial Optimization Problems, Prague, Czech Republic, vol. 3524 of Lecture Notes in Computer Science. Springer-Verlag, New York, 2005, pp. 273–287.

77. T. Mancini and M. Cadoli. Detecting and breaking symmetries by reasoning on problem specifications. In J.-D. Zucker and L. Saitta, eds., International Symposium on Abstraction, Reformulation and Approximation (SARA'05), Airth Castle, Scotland, UK, vol. 3607 of Lecture Notes in Computer Science. Springer-Verlag, New York, 2005, pp. 165–181.

78. M. Sellmann and P. Van Hentenryck. Structural symmetry breaking. In L. Pack Kaelbling and A. Saffiotti, eds., Proceedings of the 19th International Joint Conference on Artificial Intelligence (IJCAI'05). Professional Book Center, Edinburgh, UK, 2005, pp. 298–303.

79. I. P. Gent and I. Lynce. A SAT encoding for the social golfer problem. Presented at the IJCAI'05 Workshop on Modelling and Solving Problems with Constraints, Edinburgh, UK, July 2005.

80. A. M. Frisch, B. Hnich, Z. Kiziltan, I. Miguel, and T. Walsh. Global constraints for lexicographic orderings. In P. Van Hentenryck, ed., Proceedings of the 8th International Conference on Principles and Practice of Constraint Programming, Ithaca, NY, vol. 2470 of Lecture Notes in Computer Science. Springer-Verlag, New York, 2002, pp. 93–108.

81. I. Dotú and P. Van Hentenryck. Scheduling social golfers locally. In R. Barták and M. Milano, eds., Proceedings of the International Conference on Integration of AI and OR Techniques in Constraint Programming for Combinatorial Optimization Problems 2005, Prague, Czech Republic, vol. 3524 of Lecture Notes in Computer Science. Springer-Verlag, New York, 2005, pp. 155–167.

82. J. Hein. A new method that simultaneously aligns and reconstructs ancestral sequences for any number of homologous sequences, when the phylogeny is given. Molecular Biology and Evolution, 6:649–668, 1989.

83. B. Rost and C. Sander. Prediction of protein secondary structure at better than 70% accuracy. Journal of Molecular Biology, 232:584–599, 1993.

84. C.-K. Ong, S. Nee, A. Rambaut, H.-U. Bernard, and P. H. Harvey. Elucidating the population histories and transmission dynamics of papillomaviruses using phylogenetic trees. Journal of Molecular Evolution, 44:199–206, 1997.

85. J. Kim and T. Warnow. Tutorial on phylogenetic tree estimation. In T. Lengauer et al., eds., Proceedings of the 7th International Conference on Intelligent Systems for Molecular Biology, Heidelberg, Germany. American Association for Artificial Intelligence Press, Merlo Park, CA, 1999, pp. 118–129.

86. O. R. P. Bininda-Emonds, ed. Phylogenetic Supertrees: Combining Information to Reveal the Tree of Life. Computational Biology Series. Kluwer Academic, Boston, 2004.

87. D. Bryant. A classification of consensus methods for phylogenetics. In M. Janowitz et al., eds., Bioconsensus, DIMACS-AMS, 2003, pp. 163–184.

88. D. Gusfield. Efficient algorithms for inferring evolutionary trees. Networks, 21:19–28, 1991.

89. W. H. E. Day. Optimal algorithms for comparing trees with labeled leaves. Journal of Classification, 2:7–28, 1985.

90. J.-P. Barthélemy and F. R. McMorris. The median procedure for n-trees. Journal of Classification, 3:329–334, 1986.

91. B. L. Allen and M. Steel. Subtree transfer operations and their induced metrics on evolutionary trees. Annals of Combinatorics, 5:1–15, 2001.

92. J. T. L. Wang, H. Shan, D. Shasha, and W. H. Piel. Treerank: A similarity measure for nearest neighbor searching in phylogenetic databases. In Proceedings of the 15th International Conference on Scientific and Statistical Database Management, Cambridge MA. IEEE Press, Piscataway, NJ, 2003, pp. 171–180.

93. I. P. Gent, P. Prosser, B. M. Smith, and W. Wei. Supertree construction with constraint programming. In Rossi [106], pp. 837–841.

94. B. Y. Wu, K.-M. Chao, and C. Y. Tang. Approximation and exact algorithms for constructing minimum ultrametric trees from distance matrices. Journal of Combinatorial Optimization, 3(2):199–211, 1999.

95. P. Prosser. Supertree construction with constraint programming: recent progress and new challenges. In Workshop on Constraint Based Methods for Bioinformatics, (WCB'06), 2006, pp. 75–82.

96. R. R. Sokal and C. D. Michener. A statistical method for evaluating systematic relationships. University of Kansas Science Bulletin, 38:1409–1438, 1958.

97. A. A. Andreatta and C. C. Ribeiro. Heuristics for the phylogeny problem. Journal of Heuristics, 8:429–447, 2002.

98. C. Cotta and P. Moscato. Inferring phylogenetic trees using evolutionary algorithms. In J. J. Merelo et al., eds., Parallel Problem Solving from Nature VII, volume 2439 of Lecture Notes in Computer Science. Springer-Verlag, New York, 2002, pp. 720–729.

99. C. Cotta. On the application of evolutionary algorithms to the consensus tree problem. In G.R. Raidl and J. Gottlieb, eds., Evolutionary Computation in Combinatorial Optimization, vol. 3448 of Lecture Notes in Computer Science. Springer-Verlag, New York, 2005, pp. 58–67.

100. D. Barker. LVB: parsimony and simulated annealing in the search for phylogenetic trees. Bioinformatics, 20:274–275, 2004.

101. J. E. Gallardo, C. Cotta, and A. J. Fernández. Reconstructing phylogenies with memetic algorithms and branch-and-bound. In S. Bandyopadhyay, U. Maulik, and J. Tsong-Li Wang, eds., Analysis of Biological Data: A Soft Computing Approach. World Scientific, Hackensack, NJ, 2007, pp. 59–84.

102. E. L. Lawler and D. E. Wood. Branch and bounds methods: a survey. Operations Research, 4(4):669–719, 1966.

103. P. Daniel and C. Semple. A class of general supertree methods for nested taxa. SIAM Journal of Discrete Mathematics, 19(2):463–480, 2005.

104. A. Ozäygen. Phylogenetic supertree construction using constraint programming. Master's thesis, Graduate School of Natural and Applied Sciences, Çankaya University, Ankara, Turkey, 2006.

105. C. Cotta, A. J. Fernández, and A. Gutiérrez. On the hybridization of complete and incomplete methods for the consensus tree problem. Manuscript in preparation, 2008.

106. F. Rossi, ed. Proceedings of the 9th International Conference on Principles and Practice of Constraint Programming, Kinsale, UK, vol. 2833 of Lecture Notes in Computer Science. Springer-Verlag, New York, 2003.