This chapter describes the applications of nonlinear effects in guided wave devices, especially the channel and rib waveguide structure, so that the converted lightwave beam can be coupled with optical transmission systems to generate phase conjugation for compensation of distorted data pulses or as a bispectrum photonic preprocessing or in a fiber ring laser to generate mode-locked pulse sequences. We also illustrate the bispectrum property of optical multibound solitons described in Chapter 4.

9.2 Nonlinear Effects on Optical Waveguides and Photonic Signal Processing

9.2.1 Introductory Remarks

With increasing demand for high capacity, communication networks are facing several challenges, especially in signal processing at the physical layer at ultrahigh speed. When the processing speed is over that of the electronic limit or requires massive parallel and high-speed operations, the processing in the optical domain offers significant advantages. Thus, all-optical signal processing is a promising technology for future optical communication networks. An advanced optical network requires a variety of signal processing functions including optical regeneration, wavelength conversion, optical switching, and signal monitoring. An attractive way to realize these processing functions in transparent and high-speed mode is to exploit the third-order nonlinearity in optical waveguides, particularly parametric processes.

Nonlinearity is a fundamental property of optical waveguides including channel, rib-integrated structures, or circular fibers. The origin of nonlinearity comes from the third-order nonlinear polarization in optical transmission media [1]. It is responsible for various phenomena such as self-phase modulation (SPM), cross-phase modulation (XPM), and four-wave mixing (FWM) effects. In these effects, the parametric FWM process is of special interest because it offers several possibilities for signal processing applications [2–16]. To implement all-optical signal processing functions, highly nonlinear optical waveguides are required where the field of the guided waves is concentrated in its core region, hence efficient nonlinear effects. Therefore, the highly nonlinear fibers (HNLFs) are commonly employed for this purpose because the nonlinear coefficient of HNLF is about 10-fold higher than that of standard transmission fibers. The third-order nonlinearity of conventional fibers is often very small to prevent degradation of the transmission signal from nonlinear distortion. Recently, nonlinear chalcogenite and tellurite glass waveguides have emerged as a promising device for ultra-high-speed photonic processing [2,17]. Because of their geometries, these waveguides are called planar waveguides. A planar waveguide can confine a high intensity of light within an area comparable to the wavelength of light, over a short distance of a few centimeters. Hence, they are very compact for signal processing.

In this chapter we demonstrate a number of important applications in optical signal processing using third-order nonlinearity, especially parametric FWM processes by simulation. This section is organized as follows: Section 9.2.2 gives us a mathematical review of third-order nonlinearity in optical waveguides. We particularly focus on the parametric process FWM. The basic propagation equations that describe propagation of optical signal as well as interactions between optical waves in optical waveguides, are also given in this section. Then a MATLAB^® model of nonlinear waveguides is developed and integrated into the Simulink^® platform as described in Section 9.2.3 enabling our investigation of the parametric processes in nonlinear waveguides. This model is used as a functional block in all-optical signal-processing applications. System applications and performance evaluations based on parametric processes are demonstrated in Section 9.2.4. Besides important applications such as optical amplification, ultra-high-speed switching, and distortion compensation, we also demonstrated the potential of a triple-correlation as high-order spectrum estimation for ultrasensitive optical receivers based on FWM as given in Sections 9.3.4 through 9.3.6.

9.2.2 Third-Order Nonlinearity and Parametric Four-Wave Mixing Process

9.2.2.1 Nonlinear Wave Equation

In optical waveguides including optical fibers, the third-order nonlinearity is of special importance because it is responsible for all nonlinear effects. The confinement of lightwaves and their propagation in optical waveguides are generally governed by the nonlinear wave equation (NLE) that can be derived from the Maxwell’s equations under the coupling of the nonlinear polarization. The nonlinear wave propagation in nonlinear waveguide in the time-spatial domain in vector form can be expressed as [1] (see also Appendix A for further details):

where is the electric field vector of the lightwave; is the vacuum permeability assuming a nonmagnetic waveguiding medium; c is the speed of light in a vacuum; , are, respectively, the linear and nonlinear polarization vectors that are formed as

whereis the third-order susceptibility. Thus, the linear and nonlinear coupling effects in optical waveguides can be described by (9.1). The second term on the right-hand side is responsible for nonlinear processes including interaction between optical waves through the third-order susceptibility.

In most telecommunication applications, only the complex envelope of an optical signal is considered in analysis because bandwidth of the optical signal is much smaller than the optical carrier frequency. To model the evolution of the light propagation in optical waveguides, it requires that Equation (1.9) be further modified and simplified by some assumptions that are valid in most telecommunication applications [1]. Hence, the electrical field can be written as

where A(z, t) is the slowly varying complex envelope propagating along z in the waveguide, and k is the wave number. After some algebra using a method of separating variables, the following equation for propagation in the optical waveguide is obtained as

where the effect of propagation constant β around ω₀ is the Taylor-series expanded, and g(t) is the nonlinear response function including the electronic and nuclear contributions. For the optical pulses wide enough to contain many optical cycles, Equation (5.9) can be simplified as

where a frame of reference moving with the pulse at the group velocity v_g is used by making the transformation ; and A is the total complex envelope of propagation waves; a, b_k are the linear loss and dispersion coefficients, respectively; is the nonlinear coefficient of the guided wave structure; and the first moment of the nonlinear response function is defined as

Equation (9.6) is the basic propagation equation, commonly known as the nonlinear Schrödinger equation (NLSE) that is very useful for investigating the evolution of the amplitude of the optical signal and the phase of the lightwave carrier under the effect of third-order nonlinearity in optical waveguides. The left-hand side (LHS) in (9.6) contains all linear terms, while all nonlinear terms are contained on the right-hand side (RHS). In this equation, the first term on the RHS is responsible for the intensity-dependent refractive index effects including FWM.

9.2.2.2 Four-Wave Mixing Coupled-Wave Equations

Four-wave mixing (FWM) is a parametric process through the third-order susceptibility. In the FWM process, the superposition and generation of the propagating of the waves with different amplitudes A_k, frequencies ω_k, and wave numbers k_k through the waveguide can be represented as

By ignoring the linear and scattering effects and with the introduction of (9.8) into Equation (9.6), the NLSE can be separated into coupled differential equations, each of which is responsible for one distinct wave in the waveguide:

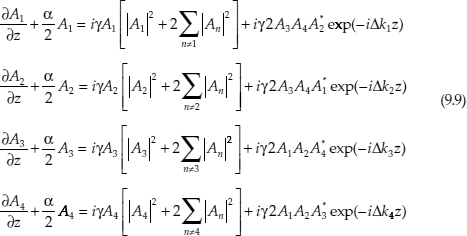
where is the wave vector mismatch. The equation system (9.9) thus describes the interaction between different waves in nonlinear waveguides. The interaction represented by the last term in (9.9) can generate new waves. For three waves with different frequencies, a fourth wave can be generated at frequency. The waves at frequencies and are called pump waves, whereas the wave at frequency is the signal and generated wave at is called the idler wave as shown in Figure 9.1a. If all three waves have the same frequency, the interaction is called a degenerate FWM with the new wave at the same frequency. If only two of the three waves are at the same frequency (), the process is called partly degenerate FWM, which is important for some applications like the wavelength converter and parametric amplifier.

9.2.2.3 Phase Matching

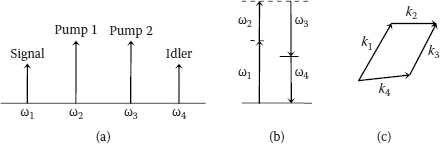
FIGURE 9.1
(a) Position and notation of the distinct waves, (b) diagram of energy conservation, and (c) diagram of momentum conservation in four-wave mixing.

In parametric nonlinear processes such as FWM, the energy conservation and momentum conservation must be satisfied to obtain a high efficiency of the energy transfer as shown in Figure 9.1a. The phase matching condition for the new wave requires

During propagation in optical waveguides, the relative phase difference between four involved waves is determined by [3,5]

where relates to the initial phase and the nonlinear phase shift during propagation. An approximation of the phase-matching condition can be given as follows [4]:

where P_k is the power of the waves, and k is the phase mismatch parameter. Thus, the FWM process has maximum efficiency for k = 0. The mismatch comes from the frequency dependence of the refractive index and the dispersion of optical waveguides. Depending on the dispersion profile of the nonlinear waveguides, it is very important in selection of pump wavelengths to ensure that the phase mismatch parameter is minimized.

9.2.3 Transmission Models and Nonlinear Guided Wave Devices

To model the parametric FWM process between multiwaves, the basic propagation equations described in Section 9.2 are used. There are two approaches to simulate the interaction between waves. The first approach, named the separating channel technique, is to use the coupled equations system (9.9) in which the interactions between different waves are obviously modeled by certain coupling terms in each coupled equation. Thus, each optical wave considered as one separated channel is represented by a phasor. The coupled equations system is then solved to obtain the solutions of the FWM process. The outputs of the nonlinear waveguide are also represented by separated phasors; hence, the desired signal can be extracted without using a filter.

The second or alternating approach is to use the propagation equation, Equation (6.9) that allows us to simulate all evolutionary effects of the optical waves in the nonlinear waveguides. In this technique a total field is used instead of individual waves. The superimposed complex envelope A is represented by only one phasor, which is the summation of individual complex amplitudes of different waves given as

where ω₀ is the defined angular central frequency, A_n, ω_n are the complex envelope and the carrier frequency of individual waves, respectively. Hence, various waves at different frequencies are combined into only a total signal vector that facilitates integration of the nonlinear waveguide model into the Simulink platform. Equation (6.9) can be numerically solved by the split-step Fourier method (SSFM). The Simulink block representing the nonlinear waveguide is implemented with an embedded MATLAB program. Because only complex envelopes of the guided waves are considered in the simulation, each different optical wave is shifted by a frequency difference between the central frequency and the frequency of the wave to allocate the wave in the frequency band of the total field. Then the summation of individual waves, which is equivalent to the combination process at an optical coupler, is performed prior to entering the block of nonlinear waveguide as depicted in Figure 9.3. The output of a nonlinear waveguide will be selected by an optical bandpass filter (BPF). In this way, the model of nonlinear waveguide can be easily connected to other Simulink blocks available in the platform for simulation of optical fiber communication systems [18].

9.2.4 System Applications of Third-Order Parametric Nonlinearity in Optical Signal Processing

In this section, a range of signal processing applications are demonstrated through simulations that use the model of a nonlinear waveguide to model the wave-mixing process.

9.2.4.1 Parametric Amplifiers

One of the important applications of the nonlinearity is parametric amplification. The optical parametric amplifiers (OPAs) offer a wide gain bandwidth, high differential gain and optional wavelength conversion, and operation at any wavelength [4–7]. These important features of OPAs are obtained because the parametric gain process does not rely on energy transitions between energy states, but it is based on highly efficient FWM in which two photons at one or two pump wavelengths interact with a signal photon. The fourth photon, the idler, is formed with a phase such that the phase difference between the pump photons and the signal and idler photons satisfies the phase matching condition (9.10). The schematic of the fiber-based parametric amplifier (Table 9.1) is shown in Figures 9.2 and 9.3.

TABLE 9.1
Critical Parameters of the Parametric Amplifier in 40 Gb/s System

RZ 40 Gb/s Transmitter

λ_s = 1520 nm – 1600 nm, λ₀ = 1559 nm

Modulation: RZ-OOK, P_s = 0.01 mW (peak), B_r = 40 Gb/s

Parametric Amplifier

Pump source: P_p = 1 W (after EDFA), λ_p = 1560.07 nm

HNLF: L_f = 500 m, D = 0.02 ps/km/nm, S = 0.09 ps/nm²/km, α = 0.5 dB/km, A_eff = 12 μm², γ = 13 1/W/km

BPF: Δλ_BPF = 0.64 nm

Receiver

Bandwidth B_e = 28 GHz, i_eq = 20 pA/Hz^1/2, i_d = 10 nA

Note: RZ-OOK (return to zero-on-off keying), EDFA (erbium-doped fiber amplifier), HNLF (high nonlinear fiber), BPF (band pass filter).

FIGURE 9.2
Typical Simulink setup of the parametric amplifier using the model of nonlinear waveguide.

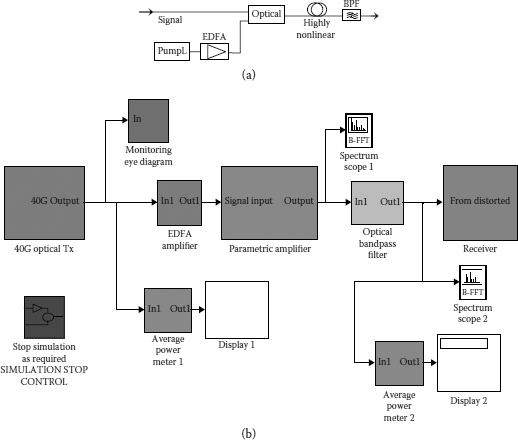
FIGURE 9.3
(a) A typical setup of an optical parametric amplifier; (b) Simulink model of optical parametric amplifier.

For a parametric amplifier using one pump source, from the coupled equations (9.9) with A₁ = A₂ = A_p, A₃ = A_s, and A₄ = A_i, it is possible to derive three coupled equations for complex field amplitude of the three waves A_p,s,i:

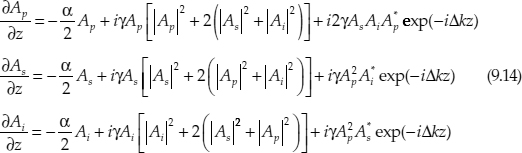
The analytical solution of these coupled equations determines the gain of the amplifier [1,3]:

with L the length of the highly nonlinear fiber/waveguide, P_p the pump power, and g the parametric gain coefficient:

where the phase mismatch Δk can be approximated by extending the propagation constant in a Taylor series around ω₀:

Here, is the slope of the dispersion factor evaluated at the zero-dispersion of the guided wave component (i.e., at the optical wavelength, ).

Figure 9.4b shows the Simulink^® setup of the 40 Gb/s return to zero (RZ) transmission system using the parametric amplifier. The setup contains a 40 Gb/s optical RZ transmitter, an optical receiver for monitoring, a parametric amplifier block, and a bandpass filter that filters the desired signal from the total field output of the amplifier. Details of the parametric amplifier block can be seen in Figure 9.3. The block setup of a parametric amplifier consists of a continuous-wave (CW) pump laser source, an optical coupler to combine the signal and the pump, and a highly nonlinear fiber block that contains the embedded MATLAB^® model for nonlinear propagation. The important simulation parameters of the system are listed in Table 9.2.

Figure 9.5 shows the signals before and after the amplifier in the time domain. The time trace indicates the amplitude fluctuation of the amplified signal as a noisy source from the wave-mixing process. Their corresponding spectra are shown in Figure 9.6. The noise floor of the output spectrum of amplifier shows the gain profile of OPA. Simulated dependence of OPA gain on the wavelength difference between the signal and the pump is shown in Figure 9.7 together with theoretical gain using (9.15). The plot shows agreement between theoretical and simulated results. The peak gain is achieved at the phase-matched condition where the linear phase mismatch is compensated for by the nonlinear phase shift.

9.2.4.2 Wavelength Conversion and Nonlinear Phase Conjugation

In addition to the signal amplification in a parametric amplifier, the idler is generated after the wave-mixing process. Therefore, this process can also be applied to wavelength conversion. Due to very fast response of the third-order nonlinearity in optical waveguides, the wavelength conversion based on this effect is transparent to the modulation format and the bit rate of signals. For a flat wideband converter, which is a key device in wavelength-division multiplexing (WDM) networks, a short-length HNLF with a low dispersion slope is required in design. By a suitable selection of the pump wavelength, the wavelength converter can be optimized to obtain a bandwidth of 200 nm [7]. Therefore, the wavelength conversion between bands such as C and L bands can be performed in WDM networks. Figure 9.7 shows an example of the wavelength conversion for four WDM channels at the C-band. The important parameters of the wavelength converter are shown in Table 9.2. The WDM signals are converted into the L-band with the conversion efficiency of –12 dB.

FIGURE 9.4
Time traces of the 40 Gb/s signal before (a) and after (b) the parametric amplifier.

TABLE 9.2
Critical Parameters of the Parametric Amplifier in 40 Gb/s Transmission System

RZ 40 Gb/s Signal

λ₀ = 1559 nm, λ_s = {1531.12, 1537.4, 1543.73, 1550.12} nm

P_s = 1 mW (peak), B_r = 40 Gb/s

Parametric Amplifier

L pump source: P_p = 100 mW (after EDFA), λ_p = 1560.07 nm

HNLF: L_f = 200 m, D = 0.02 ps/km/nm, S = 0.03 ps/nm²/km, α = 0.5 dB/km, A_eff = 12 μm², γ = 13 1/W/km

BPF: Δλ_BPF = 0.64 nm, λ_i = {1587.91, 1581.21, 1574.58, 1567.98} nm

FIGURE 9.5
Optical spectra at the input (red, lower) and the output (black, higher) of the optical parametric amplifiers.

FIGURE 9.6
Calculated and simulated gain of the optical parametric amplifier at P_p = 30 dBm.

FIGURE 9.7
(a) The wavelength conversion of four wavelength-division multiplexing channels. (b) Eye diagram of the converted 40 Gb/s signal after bandpass filter.

Another important application with the same setup is the nonlinear phase conjugation (NPC). A phase conjugated replica of the signal wave can be generated by the FWM process. From Equation (9.8), the idler wave is approximately given in case of degenerate FWM for simplification: or with the signal wave. Thus, the idler field is a complex conjugate of the signal field. In appropriate conditions, optical distortions can be compensated by using NPC, and optical pulses propagating in the fiber link can be recovered. The basic principle of distortion compensation with NPC refers to spectral inversion. When an optical pulse propagates in an optical fiber, its shape will be spread in time and distorted by the group velocity dispersion. The phase-conjugated replica of the pulse is generated in the middle point of the transmission link by the nonlinear effect. On the other hand, the pulse is spectrally inverted where spectral components in the lower-frequency range are shifted to the higher-frequency range and vice versa. If the pulse propagates in the second part of the link with the same manner in the first part, it is inversely distorted again and can cancel the distortion in the first part to recover the pulse shape at the end of the transmission link. With using NPC for distortion compensation, a 40% to 50% increase in transmission distance compared to a conventional transmission link can be obtained [8–11]. Figure 9.8 shows the setup of a long-haul 40 Gb/s transmission system demonstrating the distortion compensation using NPC. The fiber transmission link of the system is divided into two sections by an NPC based on the parametric amplifier. Each section consists of five spans with 100 km standard single-mode fiber (SSMF) in each span. Figure 9.9a shows the eye diagram of the signal after propagating through the first fiber section. After the parametric amplifier at the midpoint of the link, the idler signal, a phase-conjugated replica of the original signal, is filtered for transmission in the next section. The signal in the second section suffers the same dispersion as in the first section. At the output of the transmission system the optical signal is regenerated as shown in Figure 9.9b. Due to the change in the wavelength of the signal in NPC, a tunable dispersion compensator can be required to compensate the residual dispersion after transmission in real system. The parameters of the transmission system with NPC are given in Tables 9.3 and 9.4.

FIGURE 9.8
Simulink setup of a long-haul 40 Gb/s transmission system using nonlinear phase conjugation for distortion compensation.

FIGURE 9.9
Eye diagrams of the 40 Gb/s signal at the end (a) of the first section and (b) of the transmission link.

TABLE 9.3
Critical Parameters of the Long-Haul Transmission System Using Nonlinear Phase Conjugation (NPC) for Distortion Compensation

RZ 40 Gb/s Transmitter

λ_s = 1547 nm, λ₀ = 1559 nm

Modulation: RZ-OOK, P_s = 1 mW (peak), B_r = 40 Gb/s

Fiber transmission link

SMF: L_SMF = 100 km, D_SMF = 17 ps/nm/km, α = 0.2 dB/km

EDFA: Gain = 20 dB, NF = 5 dB

Number of spans: 10 (5 in each section), L_link = 1000 km

NPC based on OPA

Pump source: P_p = 1 W (after EDFA), λ_p = 1560.07 nm

HNLF: L_f = 500 m, D = 0.02 ps/km/nm, S = 0.09 ps/nm²/km, α = 0.5 dB/km, A_eff = 12 μm², γ = 13 1/W/km

BPF: Δλ_BPF = 0.64 nm

Receiver

Bandwidth: B_e = 28GHz, i_eq = 20 pA/Hz^1/2, i_d = 10 nA.

Note: SMF (single mode fiber), OPA (optical parametric amplifier).

9.2.4.3 High-Speed Optical Switching

When the pump is an intensity-modulated signal instead of the CW signal, the gain of the OPA is also modulated due to its exponential dependence on the pump power in a phase-matched condition. The width of gain profile in the time domain is inversely proportional to the product of the gain slope (S_p) or the nonlinear coefficient and the length of the nonlinear waveguide (L) [3]. Therefore, an OPA with high gain or large S_pL operates as an optical switch with an ultrahigh bandwidth, which is very important in some signal-processing applications such as pulse compression or short-pulse generation [12,13]. A Simulink setup for a 40 GHz short-pulse generator is built with the configuration as shown in Figure 9.10. In this setup, the input signal is a CW source with low power and the pump is amplitude modulated by a Mach–Zehnder intensity modulator (MZIM), which is driven by a radio-frequency (RF) sinusoidal wave at 40 GHz. The waveform of the modulated pump is shown in Figure 9.11a. Important parameters of the FWM-based short-pulse generator are shown in Table 9.5. Figure 9.11b shows the generated short-pulse sequence with the pulse width of 2.6 ps at the signal wavelength after the optical BPF.

TABLE 9.4
Parameters of the 40 GHz Short-Pulse Generator

Short-Pulse Generator

Signal: P_s = 0.7 mW, λ_s = 1535 nm, λ₀ = 1559 nm

Pump source: P_p = 1 W (peak), λ_p = 1560.07 nm, f_m = 40 GHz

HNLF: L_f = 500 m, D = 0.02 ps/km/nm, S = 0.03 ps/nm²/km

α = 0.5 dB/km, A_eff = 12 μm², γ = 13 1/W/km

BPF: Δλ_BPF = 3.2 nm

FIGURE 9.10
Simulink setup of the 40 GHz short-pulse generator.

FIGURE 9.11
Time traces of (a) the sinusoidal amplitude modulated pump, and (b) the generated short-pulse sequence (Inset: the pulse spectrum).

TABLE 9.5
Important Parameters of the Four-Wave Mixing (FWM) Based Optical Time-Division Multiplexing (OTDM) Demultiplexer Using a Nonlinear Waveguide

OTDM Transmitter

MLL: P₀ = 1 mW, T_p = 2.5 ps, f_m = 40 GHz

Modulation formats: OOK and DQPSK; OTDM multiplexer: 4 × 40 GSymbols/s

FWM-Based Demultiplexer

Pumped control: P_p = 500 mW, T_p = 2.5 ps, f_m = 40 GHz, λ_p = 1556.55 nm

Input signal: P_s = 10 mW (after EDFA), λ_s = 1548.51 nm

Waveguide: L_w = 7 cm, D_w = 28 ps/km/nm, S_w = 0.003 ps/nm²/km

α = 0.5 dB/cm, γ = 10⁴ 1/W/km

BPF: Δλ_BPF = 0.64 nm

Note: MLL (mode locked laser), QPSK (quadrature phase shift keying).

Another important application of the optical switch based on the FWM process is the demultiplexer, a key component in ultra-high-speed optical time-division multiplexing (OTDM) systems. OTDM is a key technology for Tb/s Ethernet transmission, which can meet the increasing demand of traffic in future optical networks. A typical scheme of the OTDM demultiplexer in which the pump is a mode-locked laser (MLL) to generate short pulses for control is shown in Figure 9.12a. The working principle of the FWM-based demultiplexing is described as follows: The control pulses generated from a MLL at the tributary rate are pumped and copropagated with the OTDM signal through the nonlinear waveguide. Mixing processes between the control pulses and the OTDM signal during propagation through the nonlinear waveguide converts the desired tributary channel to a new idler wavelength. Then the demultiplexed signal at the idler wavelength is extracted by a bandpass filter before going to a receiver as shown in Figure 9.12a.

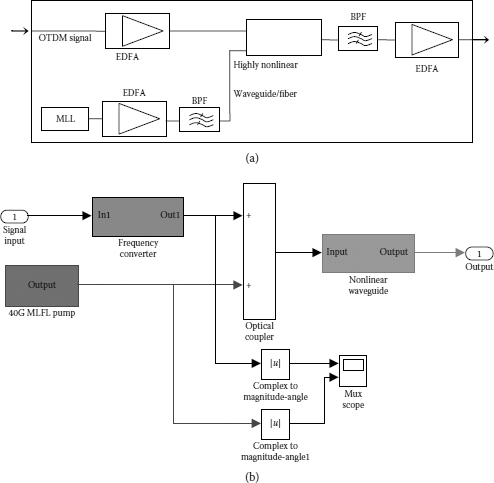
FIGURE 9.12
(a) A typical setup of the four-wave mixing–based optical time-division multiplexing (OTDM) demultiplexer. (b) Simulink model of the OTDM demultiplexer.

FIGURE 9.13
Spectra at the outputs (a) of nonlinear waveguide and (b) of bandpass filter.

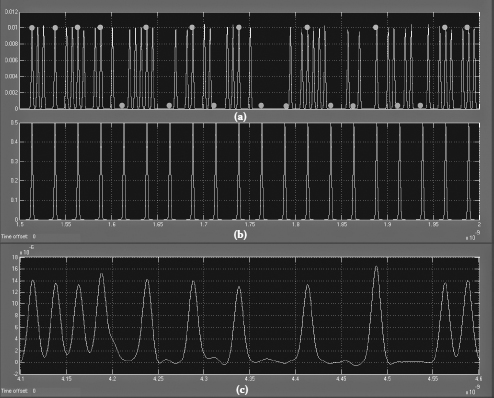
FIGURE 9.14
Time traces of (a) the 160 Gb/s optical time-division multiplexing signal, (b) the control signal, and (c) the 40 Gb/s demultiplexed signal.

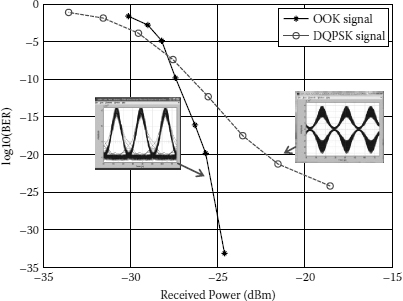
FIGURE 9.15
Simulated performance of the demultiplexed signals for 160 Gb/s on-off keying and 320 Gb/s differential quadrature phase shift keying/optical time-division multiplexing (DQPSK-OTDM) systems (Insets: eye diagrams at the receiver).

Using HNLF is relatively popular in structures of the OTDM demultiplexer [6,14]. However, its stability, especially the walk-off problem, is still a serious obstacle. Recently, planar nonlinear waveguides have emerged as promising devices for ultra-high-speed photonic processing [15,16]. These nonlinear waveguides offer a lot of advantages such as no free-carrier absorption, stable at room temperature, no requirement of quasi-phase matching, and the possibility of dispersion engineering. With the same operational principle, planar waveguide-based OTDM demultiplexers are very compact and suitable for photonic integrated solutions. Figure 9.12b shows the Simulink setup of the FWM-based demultiplexer of the on-off keying (OOK) 40 Gb/s signal from the 160 Gb/s OTDM signal using a highly nonlinear waveguide instead of HNLF. Important parameters of the OTDM system in Table 9.4 are used in the simulation. Figure 9.13a shows the spectrum at the output of the nonlinear waveguide. Then the demultiplexed signal is extracted by the bandpass filter as shown in Figure 9.13b. Figure 9.14 shows the time traces of the 160 Gb/s OTDM signal, the control signal, and the 40 Gb/s demultiplexed signal, respectively. The dots in Figure 9.14a indicate the time slots of the desired tributary signal in the OTDM signal. The developed model of the OTDM demultiplexer can be applied not only to the conventional OOK format but also to advanced modulation formats such as the differential quadrature phase shift keying (DQPSK), which increases the data load of the OTDM system without increase in bandwidth of the signal. By using available blocks developed for the DQPSK system [18], a Simulink model of the DQPSK-OTDM system is also set up for demonstration. The bit-rate of the OTDM system is doubled to 320 Gb/s with the same pulse repetition rate. Figure 9.15 shows the simulated performance of the demultiplexer in both 160 Gb/s OOK- and 320 Gb/s DQPSK-OTDM systems. The bit error rate (BER) curve in the case of the DQPSK-OTDM signal shows a low error floor that may result from the influence of nonlinear effects on phase-modulated signals in the waveguide.

9.2.4.4 Triple Correlation

One promising application exploiting the nonlinearity is implementation of triple correlation in the optical domain. Triple correlation is a higher-order correlation technique, and its Fourier transform called bispectrum is very important in signal processing, especially in signal recovery [19,20]. The triple correlation of a signal can be defined as

where, are time-delay variables. To implement the triple correlation in the optical domain, the product of three signals including different delayed versions of the original signal need to be generated and then detected by an optical photodiode to perform the integral operation. From the representation of the nonlinear polarization vector (see Equation 9.3), this triple product can be generated by the nonlinearity. One way to generate the triple correlation is based on third-harmonic generation (THG) where the generated new wave containing the triple product is at the frequency of three times the original carrier frequency. Thus, if the signal wavelength is in the 1550 nm band, the new wave needs to be detected at around 517 nm. The triple-optical autocorrelation based on single-stage THG has been demonstrated in direct optical pulse shape measurement [21]. However, this way is hard to obtain high efficiency in the wave-mixing process due to the difficulty of phase matching between three signals. Moreover, the triple-product wave is in 517 nm where wideband photodetectors are not available for high-speed communication applications. Therefore, a possible alternative to generate the triple product is based on other nonlinear interactions such as FWM. From (9.9), the fourth wave is proportional to the product of three waves If A₁ and A₂ are the delayed versions of the signal A₃, the mixing of three waves results in the fourth wave A₄_, which is obviously the triple product of three signals. Dk is the phase mismatching and z is the propagation direction. As mentioned in Section 9.3, all three waves can take the same frequency; however, these waves should propagate into different directions to possibly distinguish the new generated wave in a diverse propagation direction that requires a strict arrangement of the signals in spatial domain. An alternative way we propose is to convert the three signals into different frequencies (ω₁, ω₂_, and ω₃). Then the triple-product wave can be extracted at the frequency which is still in the 1550 nm band.

Figure 9.15a shows the Simulink model for the triple correlation based on FWM in nonlinear waveguide (see Simulink model in Figure 9.17 ). The structural block consists of two variable delay lines to generate delayed versions of the original signal as shown in Figure 9.16 and frequency converters to convert the signal into three different waves before combining at the optical coupler to launch into the nonlinear waveguide (see Simulink model in Figure 9.17). Then the fourth wave signal generated by FWM is extracted by the passband filter. To verify the triple-product based on FWM, another model shown in Figure 9.16b to estimate the triple product by using (9.18) is also implemented for comparison. The integration of the generated triple-product signal is then performed at the photodetector in the optical receiver to estimate the triple correlation of the signal. A repetitive signal, which is a dual-pulse sequence with unequal amplitude, is generated for investigation. Important parameters of the setup are shown in Table 9.6. Table 9.6 shows the waveform of the dual-pulse signal and the spectrum at the output of the nonlinear waveguide. The wavelength spacing between three waves is unequal to reduce the noise from other mixing processes. The triple-product waveforms estimated by theory and FWM process are shown in Table 9.6.

FIGURE 9.16
(a) Simulink setup of the four-wave mixing-based triple-product generation. (b) Simulink setup of the theory-based triple-product generation.

FIGURE 9.17
The variation in time domain of the time delay (slightly darker), the original signal (dark), and the delayed signal (light).

TABLE 9.6
Important Parameters of the Four-Wave Mixing (FWM) Based Optical Time-Division Multiplexing (OTDM) Demultiplexer Using a Nonlinear Waveguide

Signal Generator

Single-pulse: P₀ = 100 mW, T_p = 2.5 ps, f_m = 10 GHz

Dual-pulse: P₁ = 100 mW, P₂ = 2/3P₁, T_p = 2.5 ps, f_m = 10 GHz

FWM based triple-product generator

Original signal: λ_s1 = 1550 nm, λ_s1 = 1552.52 nm

Delayed t₁ signal: λ_s2 = 1552.52 nm

Delayed t₂ signal: λ_s3 = 1554.13 nm

Waveguide: L_w = 7 cm, D_w = 28 ps/km/nm, S_w = 0.003 ps/nm²/km

α = 0.5 dB/cm, g = 10⁴ 1/W/km

BPF: Δλ_BPF = 0.64 nm

In case of the estimation based on FWM, the triple-product signal is contaminated by the noise generated from other mixing processes as indicated in Table 9.6. The pulse sequence and its spectrum at the output of the NPC are shown in Figures 9.18a and b, respectively. Figure 9.19 shows the triple correlations of the signal after processing at the receiver in both cases based on theory and FWM. The triple correlation is represented by the three-dimensional plot that is displayed by the image. The x and y axes of the image represent the time-delay variables (τ₁ and τ₂) in terms of samples with the step-size of, where T_m is the pulse period. The intensity of the triple correlation is represented by colors with scale specified by the color bar. Although the FWM-based triple correlation result is noisy, the triple-correlation pattern is still distinguishable as compared to the theory. Another signal pattern of the single pulse that is simpler has been also investigated as shown in Figures 19.20 and 9.21.

FIGURE 9.18
(a) Time trace of the dual-pulse sequence for investigation. (b) Spectrum at the output of the nonlinear waveguide.

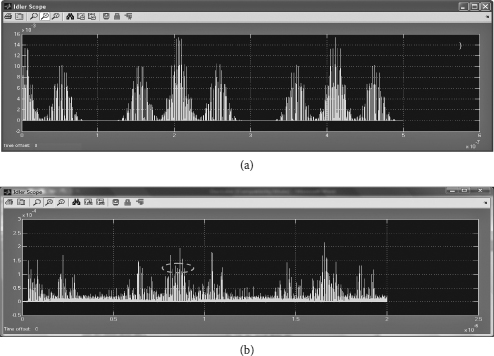
FIGURE 9.19
Generated triple-product waves in time domain of the dual-pulse signal based on (a) theory, and (b) four-wave mixing in nonlinear waveguide.

FIGURE 9.20
Triple correlation of the dual-pulse signal based on (a) theoretical estimation, and (b) four-wave mixing in nonlinear waveguide.

9.2.5 Application of Nonlinear Photonics in Advanced Telecommunications

This section looks at the uses of nonlinear effects and applications in modern optical communications networks in which 100 Gb/s optical Ethernet is expected to be deployed.

Typical performance of a photonic signal preprocessor employing no linear four-wave mixing is given, and that of an advanced processing of such received signals in the electronic domain processed by a digital triple correlation system. At least 10 dB improvement is achieved on the receiver sensitivity.

Regarding the nonlinear effects, the nonlinearity of the optical fibers hinders and limits the maximum level of the total average power of all the multiplexed channels for maximizing the transmission distance. These are due to the change of the refractive index of the guided medium as a function of the intensity of the guided waves. This in turn creates the phase changes and hence different group delays, and then distortion. Furthermore, other associate nonlinear effects such as the four-wave mixing, Raman scattering, Brillouin scattering, intermodulation have also created jittering and distortion of the received pulse sequences after a long transmission distance.

FIGURE 9.21
Triple correlation of the single-pulse signal based on (a) theoretical estimation, (b) four-wave mixing in nonlinear waveguide (Inset: the single-pulse pattern).

However, recently we have been able to use to our advantage these nonlinear optical effects as a preprocessing element before the optical receiver to improve its sensitivity. A higher-order spectrum technique is employed with the triple correlation implemented in the optical domain via the use of the degenerate four-wave mixing effects in a high nonlinear optical waveguide. This may add additional optical elements and filtering in the processor and hence complicate the receiver structure. We can overcome this by bringing this nonlinear higher-order spectrum processing (see schematic diagram in Figure 9.22) to after the opto-electronic conversion and in the digital processing domain after a coherent receiving and electronic amplification subsystem is used.

In this section, we illustrate some uses of nonlinear effects and nonlinear processing algorithms for improving the sensitivity of optical receivers employing nonlinear processing at the front end of the photodetector and nonlinear processing algorithm in the electronic domain.

The spectral distribution of the FWM and the simulated spectral conversion can be achieved [22–26]. There is degeneracy of the frequencies of the waves so that efficient conversion can be achieved by satisfying the conservation of momentum. This can be detailed in another paper in the special session of this workshop [2]. The detected phase states and bispectral properties are depicted in Figure 9.23 in which the phases can be distinguished based on the diagonal spectral lines. Under noisy conditions these spectral distributions can be observed in Figure 9.24.

Alternating to the optical processing described above, a nonlinear processing technique using a high-order spectrum technique can be implemented in the electronic domain. This is implemented after the ADC, which samples the incoming electronic signals produced by the coherent optical receiver as shown in Figure 9.25 [27]. The operation of a third-order spectrum analysis is based on the combined interference of three signals (in this case the complex signals produced at the output of the analog-to-digital converter, ADC), two of which are the delayed version of the original. Then the amplitude and phase distribution of the complex signals are obtained in three-dimensional graphs that allow us to determine the signal and noise power and the phase distribution. These distributions allow us to perform several functions necessary for evaluation of the performance of optical transmission systems. Simultaneously, the processed signals allow us to monitor the health of the transmission systems such as the effects due to nonlinear effects, the distortion due to chromatic dispersion of the fiber transmission lines, the noises contributed by inline amplifiers, and so forth. A typical curve that compares the performance of this innovative processing with convention detection techniques is shown in Figure 9.25. If we project the error rate of the receivers employing conventional techniques and our high-order spectral receiver employing digital signal processing techniques at a bit error rate of, then at least 1000 times lower than digital receiver without using this type of processor. This is equivalent to at least one unit improvement on the quality factor of the eye opening. In turn, this is equivalent to about 10 dB in the signal-to-noise ratio.

FIGURE 9.22
A high-order spectral optical receiver and electronic processing.

FIGURE 9.23
Input waveform with phase changes at the transitions (a,b), triple correlation and bispectrum (c–h) of both phase and amplitude.

FIGURE 9.24
Effect of Gaussian noise on the bispectrum (a,c) amplitude distribution in two dim (b,d) phase spectral distribution.

These results are very exciting for network and system operators as significant improvement of the receiver sensitivity can be achieved, and this allows significant flexibility in the operation and management of the transmission systems and networks. Simultaneously, the monitored signals produced by the high-order spectral techniques can be used to determine the distortion and noises of the transmission line and thus the management of the tuning of the operating parameters of the transmitter, the number of wavelength channels, and the receiver or inline optical amplifiers.

FIGURE 9.25
Error estimation version detection level of the high-order spectrum processor.

The effect of additive white Gaussian noise on the bispectrum magnitude is shown in Figure 9.24, the sequence of figures are as indicated in Figure 9.23. The uncorrupted bispectrum magnitude is shown in Figure 9.23a, while Figures 9.23b, 9.23c, and 9.23d were generated using signal-to-noise ratios of 10 dB, 3 dB, and 0 dB, respectively. This provides a method of monitoring the integrity of a channel and illustrates another attractive attribute of the bispectrum. It is noted that the bispectrum phase is more sensitive to Gaussian white noise than is the magnitude and quickly becomes indistinguishable below 6 dB.

The algorithm employing the nonlinear processing (e.g., optical preprocessing or electronic processing of the triple correlation and bispectrum) will involve hardware and soft implementation. From the point of view of industry, it needs to deliver to the market at the right time for systems and networks operating in the Tera-bits/s speed. One can thus be facing the following dilemma:

• The optical preprocessing requires an efficient nonlinear optical waveguide that must be in an integrated structure whereby efficient coupling and interaction can be achieved. If not then the gain of about 3 dB in signal-to-noise ratio would be defeated by this loss. Furthermore, the integration of the linear optical waveguiding section and a nonlinear optical waveguide is not matched due to differences in the waveguide structures of both regions. For a linear waveguide structure to be efficient for coupling with circular optical fibers, silica on silicon would be best suited due to the small refractive index difference and the technology of burying such waveguides to form an embedded structure whose optical spot size would match that of a single guided mode fiber. This silica on silicon would not match an efficient nonlinear waveguide made by As₂S₃ on silicon.

• On the other hand, if electronic processing is employed then it requires an ultrafast analog to digital converter (ADC) and then fast electronic signal processors. Currently a 56 GSamples/s ADC is available from Fujitsu as shown in Figure 9.26. It is noted that the data output samples of the ADC are structured in parallel forms with the referenced clock rate of 1.75 GHz. Thus, all processing of the digital samples must be in parallel form, and parallel processing algorithms must be structured in parallel. This is the most challenging problem we must overcome in the near future.

• An application-specific integrated circuit (ASIC) must also be designed for this processor.

FIGURE 9.26
Plane view of the Fujitsu analog-to-digital converter operating at 56 GSamples/s: (a) integrated view and (b) operation schematic.

• Hard decisions must be made as is fitting of such ASIC and associated optical and opto-electronic components into international standard compatible size. Thus, all designs and components must meet this requirement.

• Finally the laboratory and field testing must be demonstrated for market delivery.

These challenges will be met and we are currently progressing toward the final target for the delivery of such sensitive receivers for 100 Gb/s optical Internet.

9.2.6 Remarks

In this section we demonstrated a range of signal processing applications exploiting the parametric process in nonlinear waveguides. A brief mathematical description of the parametric process through third-order nonlinearity has been reviewed. A Simulink model of nonlinear waveguide has been developed to simulate interaction of multiwaves in optical waveguides including optical fibers. Based on the developed Simulink modeling platform, a range of signal processing applications exploiting parametric FWM processes has been investigated through simulation. With a CW pump source, the applications such as parametric amplifier, wavelength converter, and optical phase conjugator have been implemented for demonstration. The ultra-high-speed optical switching can be implemented by using an intensity-modulated pump to apply in the short-pulse generator and the OTDM demultiplexer. Moreover, the FWM process has been proposed to estimate the triple correlation that is very important in signal processing. The simulation results showed the possibility of the FWM-based triple correlation using the nonlinear waveguide with different pulse patterns. Although the triple-correlation is contaminated by noise from other FWM processes, it is possible to distinguish it. The wavelength positions as well as the power of three delayed signals need to be optimized to obtain the best results.

Furthermore, we also addressed the important issues of nonlinearity and its uses in optical transmission systems, the management of networks if the signals that indicate the health of the transmission system are available. It is no doubt that the nonlinear phenomena play several important roles in the distortion effects of signals transmitted but also allow us to improve the transmission quality of the signals. This has been briefly described in this paper on the optical processing using four-wave mixing effects and nonlinear signal processing using high-order spectral analysis and processing in the electronic domain. This ultra-high-speed optical preprocessing and electronic triple correlation and bispectrum receivers are the first system using nonlinear processing for 100 Gb/s optical Internet.

9.3 Nonlinear Photonic Preprocessing and Bispectrum Optical Receivers

In this section, we present the processing of optical signals before the optoelectronic detection in the optical domain in a nonlinear optical waveguide as an NL (NL) signal processing technique for the digital optical receiving system for long-haul optically amplified fiber transmission systems. The algorithm implemented is a high-order spectrum (HOS) technique in which the original signals and two delayed versions are correlated via the four-wave mixing or third harmonic conversion process. The optical receivers employing a higher-order spectral photonic preprocessor and very large scale integration (VLSI) electronic system for the electronic decoding and evaluation of the bit error rate of the transmission system are presented. A photonic signal preprocessing system is developed to generate the triple correlation via the third harmonic conversion in an NL optical waveguide. It is employed as the photonic preprocessor to generate the essential part of a triple correlator. The performance of an optical receiver incorporating the HOS processor is given for the long-haul phase-modulated fiber transmission.

9.3.1 Introductory Remarks

Recently, tremendous efforts have been pushing for reaching higher transmission bit rates and longer haul for optical fiber communication systems [29–32]. The bit rate can reach several hundreds of Gb/s to the Tb/s. In this extremely high-speed operational region, the limits of electronic speed processors have been surpassed, and optical processing is assumed to play an important part of the optical receiving circuitry. Novel processing techniques are required in order to minimize the bottlenecks of electronic processing and noises and distortion due to the impairment of the transmission medium and the linear and NL distortion effects.

This paper deals with the photonic processing of optically modulated signals prior to the electronic receiver for long-haul optically amplified transmission systems. NL optical waveguides in planar or channel structures are studied and employed as a third harmonic converter so as to generate a triple product of the original optical waves and its two delayed copies. The triple product is then detected by an opto-electronic receiver. Then the detected current would be electronically sampled and digitally processed to obtain the bispectrum of the data sequence, and a recovery algorithm is used to recover the data sequence. The generic structures of such high-order spectral optical receivers are shown in Figure 9.27. For the nonlinear photonic processor (Figure 9.27a), the optical signals at the input are delayed and then coupled to a nonlinear photonic device in which the nonlinear conversion process is implemented via the uses of third harmonic conversion or degenerate four-wave mixing. In the nonlinear digital processor (see Figure 9.27b) the optical signals are detected coherently and then sampled and processed using the nonlinear triple correlation and decoding algorithm.

FIGURE 9.27
Generic structure of high-order spectrum optical receiver, (a) photonic preprocessor, (b) nonlinear digital signal processing in electronic domain.

We propose and simulate this NL optical preprocessor optical receiver under the MATLAB/Simulink platform for differentially coded phase shift keying, the DQPSK modulation scheme.

9.3.2 Bispectrum Optical Receiver

Figure 9.27 shows the structure of a bispectrum optical receiver in which there are three main sections: an all-optical preprocessor, an optoelectronic detection, and amplification including an ADC to generate sampled values of the triple correlated product.

9.3.3 Triple Correlation and Bispectra

9.3.3.1 Definition

The power spectrum is the Fourier transform of the autocorrelation of a signal. The bispectrum is the Fourier transform of the triple correlation of a signal. Thus, both the phase and amplitude information of the signals is embedded in the triple-correlated product.

While autocorrelation and its frequency domain power spectrum does not contain the phase information of a signal, the triple correlation contains both, due to the definition of the triple correlation:

where is the continuous time domain signals to be recovered. are the delay time intervals. For the special case where or, the triple correlation is proportional with the autocorrelation. It means that the amplitude information is also contained in the triple correlation. The benefit of holding phase and amplitude information is that it gives a potential to recover the signal from its triple correlation. In practice, the delays τ₁ and τ₂ indicate the path difference between the three optical waveguides. These delay times are corresponding to the frequency regions in the spectral domain. Thus, a different time interval would determine the frequency lines in the bispectrum.

9.3.3.2 Gaussian Noise Rejection

Given a deterministic sampled signal, the sampled version of the continuous signals, are corrupted by Gaussian noise, with n the sampled time index. The observed signal takes the form. The polyspectra of any Gaussian process is zero for any order greater than two [34]. The bispectrum is the third-order polyspectrum and offers a significant advantage for signal processing over the second-order polyspectrum, commonly known as the power spectrum, which is corrupted by Gaussian noise. Theoretically speaking, the bispectral analysis allows us to extract a non-Gaussian signal from the corrupting affects of Gaussian noise.

Thus, for a signal arriving at the optical receiver, the steps to recover the amplitude and phase of the lightwave modulated signals are [27] as follows:

• Estimate the bispectrum of S(n) based on observations of Y(n).

• From the amplitude and phase bispectra form an estimate of the amplitude and phase distribution in a one-dimensional frequency of the Fourier transform of S(n). This forms the constituents of the signal S(n) in the frequency domain.

• Recover the original signal S(n) by taking the inverse Fourier transform.

This type of receiver is termed the bispectral optical receiver.

9.3.3.3 Encoding of Phase Information

The bispectra contain almost complete information about the original signal (magnitude and phase). If the original signal is real and finite, it can be reconstructed except for a shift a. Equivalently, the Fourier transform can be determined except for a linear shift factor of. By determining two adjacent pulses any differential phase information will be readily available [28]. In other words, the bispectra, hence the triple correlation, contain the phase information of the original signal allowing it to pass through the square law photodiode that would otherwise destroy this information. The encoded phase information can then be recovered up to a linear phase term, thus necessitating a differential coding scheme.

9.3.3.4 Eliminating Gaussian Noise

For any processes that have zero mean and the symmetrical probability density function (pdf), their third-order cummulant are equaled to zero. Therefore, in a triple correlation, those symmetrical processes are eliminated. Gaussian noise is assumed to affect to signal quality. Mathematically, the third cummulant is defined as

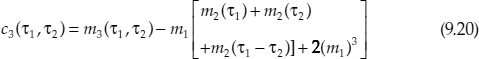
where m_k is the k^th order moment of the signal. Thus, for the zero mean and symmetrical pdf, its third-order cummulant becomes zero [29]. Theoretically, considering the signal as, where is an additive Gaussian noise, the triple correlation of will reject Gaussian noise affecting the [30,31].

FIGURE 9.28
Generic structure of an optical preprocessing receiver employing bispectrum processing technique.

9.3.4 Bispectral Optical Structures

Figure 9.28 shows the generic and detailed structure of the bispectral optical receiver, respectively, which consists of (1) an all-optical preprocessor front end followed by (2) a photodetector and electronic amplifier to transfer the detected electronic current to voltage level appropriate for sampling by an analog to digital converter, and thus the signals at this stage are in sampled form; (3) the sampled triple correlation product is then transformed to the Fourier domain using the fast Fourier transform (FFT). The product at this stage is the row of the matrix of the bispectral amplitude and phase plane (see Figure 9.29). A number of parallel structures may be required if passive delay paths are used. (4) A recovery algorithm is used to derive the one-dimensional distribution of the amplitude and phase as a function of the frequency that are the essential parameters required for taking the inverse Fourier transform to recover the time domain signals.

9.3.4.1 Principles

The physical process of mixing the three waves to generate the fourth wave whose amplitude and phase are proportional to the product of the three input waves is well known in literatures of NL optics.

FIGURE 9.29
Parallel structures of photonic preprocessing to generate triple correlation product in the optical domain.

This process requires

• Highly NL medium so as to efficiently convert the energy of the three waves to that of the fourth wave

• Phase-matching conditions of the three input waves of the same frequency (wavelength) to satisfy the conservation of momentum

9.3.4.2 Technological Implementation

9.3.4.2.1 Nonlinear (NL) Optical Waveguides

In order to satisfy the condition of four-wave mixing we will be using

• A rib-waveguide for guiding whose NL refractive index coefficient is about 100,000 times greater than that of silica. The material used in this waveguide is a chalcogenide glass type (e.g., AS₂S₃) or TeO₂. The three waves are guided in this waveguide structure. Their optical fields are overlapped. The cross section of the waveguide is in the order of 4 mm × 0.4 mm.

• The waveguide cross section is designed such that the dispersion is “flat” over the spectral range of the input waves, ideally from 1520 nm to 1565 nm. This can be done by adjusting the thickness of the rib structure.

9.3.4.2.2 Mixing and Integrating

The fourth wave generated from the FWM waveguide is then detected by the photodetector that acts as an integrating device. Thus, the output of this detector is the triple correlation product in the electronic domain that we are looking for.

9.3.4.2.3 Equalization and Filtering

If equalization or filtering is required, then these functional blocks can be implemented in the bispectral domain as shown in Figure 9.28. Figure 9.29 shows the parallel structures of the bispectral receiver so as to obtain all rows of the bispectral matrix. The components of the structure are almost similar except the delay time of the optical preprocessor.

9.3.4.2.4 Four-Wave Mixing (FWM) in Highly Nonlinear Media

In the NL channel waveguide fabricated using TeO₂ (tellurium oxide) on silica the interaction of the three waves, one original and two delayed beams, happens via the electronic processes with highly NL coefficient [χ3] will convert to the fourth wave.

When the three waves are copropagating, the conservation of the momentum of the three waves and the fourth wave is satisfied to produce efficient FWM. Phase matching can also be satisfied by one forward wave and two backward propagating waves (delayed version of the first wave), leading to almost 100% conversion efficiency to generate the fourth wave.

The interaction of the three waves via electronic process and the gives rise to the polarization vector P that couples to the electric field density of the lightwaves and then to the NL Schrödinger wave equation. By solving and modeling this wave equation with the FWM term on the right-hand side of the equation one can obtain the wave output (the fourth wave) at the output of the NL waveguide section.

9.3.4.2.5 Third Harmonic Conversion

Third harmonic conversion may happen but at extremely low efficiency, at least one thousand times less than that of FWM due to the nonmatching of the effective refractive indices of the guided modes at 1550 nm (fundamental wave) and 517 nm (third harmonic wave).

Note: The common term for this process is the matching of the dispersion characteristics (i.e., k/omega with omega the radial frequency of the waves at 1550 nm and 517 nm) versus the thickness of the waveguide.

9.3.4.2.6 Conservation of Momentum

The conservation of momentum and thus the phase matching condition for the FWM is satisfied without much difficulty as the wavelengths of the three input waves are the same. The optical NL channel waveguide is to be designed such that there is mismatching of the third harmonic conversion and is most efficient for FWM. It is considered that a single polarized mode, either traverse electric (TE) or traverse magnetic (TM) will be used to achieve efficient FWM. Thus, the dimension of the channel waveguide would be estimated at about 0.4 mm (height) × 4 mm (width).

9.3.4.2.7 Estimate of Optical Power Required for Four-Wave Mixing

In order to achieve the most efficient FWM process the NL coefficient n₂, which is proportional to χ⁽³⁾ by a constant (8n/3, with n the refractive index of the medium or approximately the effective refractive index of the guided mode). This NL coefficient is then multiplied by the intensity of the guided waves to give an estimate of the phase change and estimation of the efficiency of the FWM. With the cross section estimated in (9.3) and the well confinement of the guided mode, the effective area of the guided waves is very close to the cross-sectional area. Thus, an average power of the guide waves would be about 3 to 5 mW or about 6 dBm.

With the practical data of the loss of the linear section (section of multimode interference and delay split, similar to array waveguide grating technology) estimated at 3 dB, the input power of the three waves required for efficient FWM is about 10 dBm (maximum).

9.3.5 Mathematical Principles of Four-Wave Mixing and the Wave Equations

9.3.5.1 The Phenomena of Four-Wave Mixing

The origin of the FWM comes from the parametric processes that lie in the NL responses of bound electrons of a material to applied optical fields. More specifically the polarization induced in the medium is not linear in the applied field but contains NL terms whose magnitude is governed by the NL susceptibilities [32–34]. The first-, second-, and third-order parametric processes can occur due to these NL susceptibilities [χ¹χ² χ³]. The coefficient χ³ is responsible for the FWM that is exploited in this work. Simultaneously with this FWM, there is also a possibility of generating third harmonic waves with mixing the three waves and parametric amplification. The third harmonic generation is normally very small due to the phase mismatching of the guided wave number (the momentum vector) between the fundamental waves and the third harmonic waves. FWM in a guided wave medium such as single-mode optical fibers have been extensively studied due to its efficient mixing to give the fourth wave [35,36]. The exploitation of the FWM process has not been extensively exploited yet in channel optical waveguides. In this work, we demonstrate this theoretically and experimentally (and investigated for optical signal processing for the bispectrum analyzer).

The three lightwaves are mixed to generate the polarization vector due to the NL third-order susceptibility given as

where is the permittivity in the vacuum; are the electric field components of the lightwaves; is the total field entering the NL waveguide, and is the third-order susceptibility of the NL medium. is the product of the three total optical fields of the three optical waves that give the triple product of the waves required for the bispectrum receiver in which the NL waveguide acts as a multiplier of the three waves considered as the pump waves in this section. The mathematical analysis of the coupling equations via the wave equation is complicated but straightforward. Let ω₁, ω₂, ω₃, and ω₄ be the angular frequencies of the four waves of the FWM process and linearly polarized along the horizontal direction y of the channel waveguides and propagating along the z-direction. The total electric field vector of the four waves is given by

The propagation constant can be obtained by with n_eff,i the effective index of the ith guided waves E_i (i = 1,…4) a which can be either, TE or TM polarized guided mode propagating along the channel NL optical waveguide and all four waves are assumed propagating along the same direction. Substituting (9.22) into (9.21), we have

where P_i (i = 1,2..4) consists of a large number of terms involving the product of three electric fields of the optical guided waves, for example, the term P₄ can be expressed as

The first four terms of Equation (24.9) represents the self-phase modulation (SPM) and cross-phase modulation effects (XPM) that are dependent on the intensity of the waves. The remaining terms results into FWM. Thus, the question is which terms are the most effective components resulting from the parametric mixing process? The effectiveness of the parametric coupling depends on the phase-matching terms governed by or a similar quantity.

It is obvious that significant FWM would occur if the phase matching is satisfied. This requires the matching of both the frequency as well as the wave vectors as given in (9.24). From (9.24) we can see that the term corresponds to the case in which three waves are mixed to give the fourth wave whose frequency is three times that of the original wave. This is the third harmonic generation. However, the matching of the wave vector would not normally be satisfied due to the dispersion effect. Furthermore, the propagation constants of the guided modes at different wavelength of the four wave mixing process would not be matched due to the dispersion characteristics of the optical waveguide. This would only allow a minute conversion to the third harmonic waves.

The conservation of momentum derived from the wave vectors of the four waves requires that

The effective refractive indices of the guided modes of the three waves E₁, E₂, and E₃ must be the same at their frequencies so as to achieve the most efficient conversion. This condition is automatically satisfied provided that the NL waveguide is designed such that it supports only a single polarized mode TE or TM and with minimum dispersion difference within the band of the signals.

9.3.5.2 Coupled Equations and Conversion Efficiency

To derive the wave equations to represent the propagation of the three waves to generate the fourth wave, we can resort to the Maxwell equations. It is lengthy to write down all the steps involved in this derivation so we summarize the standard steps usually employed to derive the wave equations as follows: First add the NL polarization vector given in (9.21) into the electric field density vector D. Then taking the curl of the Maxwell first equation and use the second equation of the Maxwell four equations and substituting the electric field density vector and using the fourth equation, one would then come up with the vectorial wave equation.

For the FWM process occurring during the interaction of the three waves along the propagation direction of the NL optical channel waveguide, the evolution of the amplitudes, A₁ through A₄, of the four waves, E₁ to E₄, is given by (only A₁ term is given)

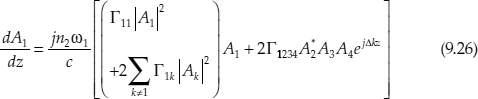
where the wave vector mismatch Δk is given in (9.25), and the * denotes the complex conjugation. Note that the coefficient n₂ in Equation 9.26 is the NL coefficient related to the nonlinear susceptibility coefficient, defined as

9.3.5.3 Evolution of FWM along the NL Waveguide Section

Once the fourth wave is generated, the interaction of the four waves along the section of the waveguide continues happening, thus the NL Schrödinger equation must be used to investigate the evolution of the waves. The NLSE is well known and presented in Bartelt et al. [34] and given for the temporal amplitude of the waves as

This makes the four equations complicated and only numerical simulations can offer the evolution of the complex amplitude and the power of the fourth wave at the output of the NL waveguide. This takes into account the dispersion of the waveguide and material of the waveguide under chromatic dispersion.

9.3.6 Transmission and Detection

9.3.6.1 Optical Transmission Route and Simulation Platform

Shown in Figure 9.30 is the schematic of the transmission link over a total length of 700 km with sections from Melbourne City (of Victoria, Australia) to Gippsland, the inland section in Victoria of Australia, an undersea section of more than 300 km crossing the Bass Strait to George Town of Tasmania and then inland transmission to Hobart of Tasmania—the Gippsland/George Town Link (see Figure 9.30). Other inland sections in Victoria and Tasmania of Australia are structured with optical fibers and lumped optical amplifiers (Er:doped fiber amplifiers, EDFA). Raman-distributed optical amplification (ROA) is used by pump sources located at both ends of the Melbourne, Victoria, to Hobart of Tasmania link including the 300 km undersea section. The undersea section of nearly 300 km consists of only the transmission and dispersion compensating fibers, no active subsystems are included. Only Raman amplification is used with pump sources located at both sides of the section and installed inland. This 300 km distance is fairly long, and only the Raman distributed gain is used. Simulink models of the transmission system include the optical transmitter, the transmission line, and the bispectrum optical receiver.

9.3.6.2 Four-Wave Mixing and Bispectrum Receiving

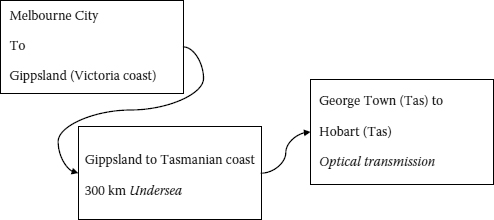
FIGURE 9.30
The transmission link including inland and undersea sections between Melbourne (Victoria) and Hobart (Tasmania) of Australia.

We also integrated into the MATLAB Simulink of the transmission system so that would enable us to investigate the NL parametric conversion system very close to practice. The spectra of the optical signals before and after this amplification are shown in Figures 9.31 and 9.32. The temporal distribution of the pulses at the input and output are also shown in Figures 9.33(a) and (b), respectively, indicating the conversion efficiency. This indicates the performance of the bispectrum optical receiver.

9.3.6.3 Performance

We implement the models for both techniques for binary phase shift keying modulation format for serving as a guideline for phase modulation optical transmission systems using nonlinear preprocessing. We note the following:

1. The arbitrary white Gaussian noise (AWGN) block in the Simulink platform can be set in different operating modes. This block then accepts the signal input and assumes the sampling rate of the input signal, then estimates the noise variance based on Gaussian distribution and the specified signal-to-noise ratio (SNR). This is then superimposed on the amplitude of the sampled value. Thus, we believe at that stage, the noise is contributed evenly across the entire band of the sampled time (converted to spectral band).

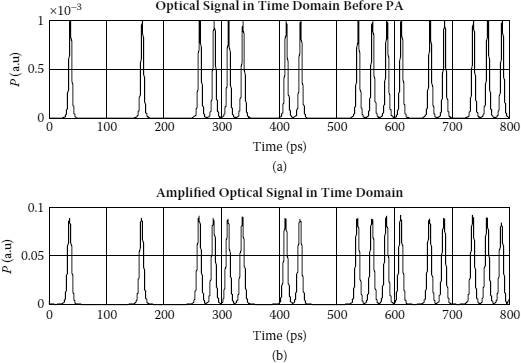
FIGURE 9.31
Time traces of the optical signal (a) before and (b) after the parametric amplifier.

2. The ideal curve SNR versus BER plotted in the graph provided is calculated using the commonly used formula in several textbooks on communication theory. This is evaluated based on the geometrical distribution of the phase states and then the noise distribution over those states. That means that all the modulation and demodulation are assumed to be perfect. However, in the digital system simulation, the signals must be sampled. This is even more complicated when a carrier is embedded in the signal, especially when the phase shift keying modulation format is used.

3. We thus reset the models of (1) AWGN in a complete binary phase shift keying (BPSK) modulation format with both the ideal coherent modulator and demodulator and any necessary filtering required and (2) AWGN blocks with the coherent modulator and demodulator incorporating the triple correlator and necessary signal processing block. This is done in order to make a fair comparison between the two pressing systems.

4. In our former model, the AWGN block was being used incorrectly in that it was being used in the SNR mode that applies the noise power over the entire bandwidth of the channel, which of course is larger than the data bandwidth, meaning that the amount of noise in the data band was a fraction of the total noise applied. We accept that this was an unfair comparison to the theoretical curve that is given against E_b/N₀ as defined in Mendel [37].

FIGURE 9.32
Corresponding spectra of the optical signal (a) before and (b) after the parametric amplifier.

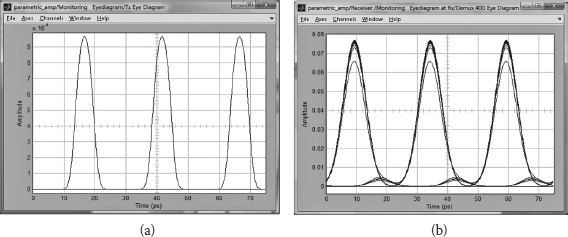
FIGURE 9.33
(a) Input data sequence. (b) Detected sequence processed using triple-correlation nonlinear photonic processing and recovery scheme bispectrum receiver.

5. In the current model, we provide a fair comparison noise added to the modulated signal using the AWGN block in the E_b/N₀ mode (E₀ is the energy per bit and N₀ is the noise contained within the bit period) with the symbol period set to the carrier period, in effect this set the carrier-to-noise ratio (CNR). Also the triple correlation receiver was modified a little from the original—namely, the addition on the bispectrum product (BP) filter and some tweaking of the triple correlation delays this result in the BER curve shown in Figure 9.34. Also an ideal homodyne receiver model was constructed with noise added and measured in the same method as the triple correlation model. This provided a benchmark against which to compare the triple correlation receiver.

6. We can compare the simulated BER values with the theoretical limit set by

• By relating the CNR to E_b/N₀ so

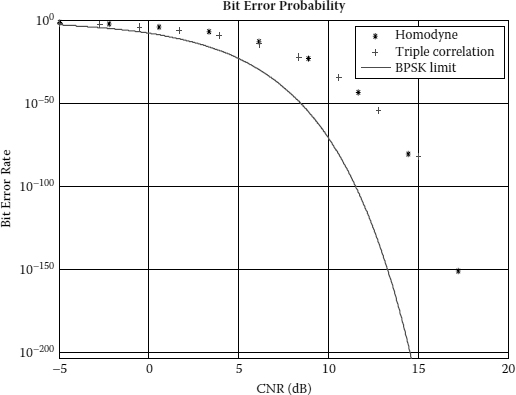
FIGURE 9.34
BER versus carrier—noise ratio for nonlinear triple correlation, ideal binary phase shift keying (BPSK) under coherent detection and ideal BPSK limit.

where channel bandwidth B_W is 1600 Hz set by the sampling rate; f_s is the symbol rate, in our case a symbol is one carrier period (100 Hz) as we are adding noise to the carrier. These frequencies are set at the normalized level so as to scale to wherever the spectral regions would be of interest. As can be seen in Figure 9.34 the triple correlation receiver matches the performance of the ideal homodyne case and closely approaches the theoretical limit of BPSK (approximately 3 dB at BER of 10^–10). As discussed the principal benefit from the triple correlation over the ideal homodyne case will be the characterization of the noise of the channel that is achieved by analysis of the regions of symmetry in the two-dimensional bispectrum. Finally, we still expect possible performance improvement when symbol identification is performed directly from the triple correlation matrix as opposed to the traditional method that involves recovering the pulse shape first. It is not possible at this stage to model the effect of the direct method.

As a demonstration of the triple correlation we would like to insert here the spectra of the bound solitons described in Chapter 4. Figure 9.35 shows a description of power spectrum regions (a) and its corresponding bispectrum regions (b). Figure 9.36 shows the triple correlations in contour plot view of various bound soliton states: (a) single soliton, (b) dual-bound solitons, (c) triple-bound solitons, and (d) quadruple-bound solitons, respectively. The insets show the temporal waveforms in logarithm scale showing the enhancement of the pedestal in higher-order multibound solitons. Furthermore Figures 9.37 9a), (b), (c) and (d) show the magnitude bispectra in logarithm scale of different multibound soliton states: single soliton, dual-bound solitons, triple-bound solitons, and quadruple-bound solitons, respectively.

FIGURE 9.35
A description of (a) power spectrum regions and (b) bispectrum regions for explanation.

FIGURE 9.36
Triple correlations in contour plot view of various bound soliton states: (a) single soliton, (b) dual-bound solitons, (c) triple-bound solitons, and (d) quadruple-bound solitons, respectively (Insets: the temporal waveforms in logarithm scale showing the enhancement of the pedestal in higher-order multibound solitons).

FIGURE 9.37
The magnitude bispectra in logarithm scale of different multibound soliton states: (a) single soliton, (b) dual-bound solitons, (c) triple-bound solitons, and (d) quadruple-bound solitons, respectively.

9.3.6.4 Remarks

This section demonstrates the employment of an NL optical waveguide and associated NL effects such as parametric amplification, four-wave mixing, and third harmonic generation for the implementation of the triple correlation, and the bispectrum creation and signal recovery techniques to reconstruct the data sequence transmitted over a long haul optically amplified fiber transmission link.

9.4 Bispectrum of Multibound Solitons

9.4.1 Bispectrum

In signal processing, the power spectrum estimation showing the distribution of power in the frequency domain is a useful and popular tool to analyze or characterize a signal or process, however the phase information between frequency components is suppressed in the power spectrum. Therefore, it is necessarily useful to exploit higher-order spectra known as multidimensional spectra instead of the power spectrum in some cases, especially in nonlinear processes or systems [1,2]. Different from the power spectrum, the Fourier transform of the autocorrelation, multidimensional spectra are known as Fourier transforms of high-order correlation functions, hence they provide us not only the magnitude information but also the phase information.

In particular, the two-dimensional spectrum also called the bispectrum is by definition the Fourier transform of the triple correlation or the third-order statistics [2]. For a signal x(t) its triple-correlation function C₃ is defined as

where τ₁, τ₂ are the time-delay variables. Thus, the bispectrum can be estimated through the Fourier transform of C₃ as follows:

where F{} is the Fourier transform, and f₁, f₂ are the frequency variables. From the definitions (9.31) and (9.32), both the triple correlation and the bispectrum are represented in a three-dimensional graph with two variables of time and frequency, respectively. Figure 9.35 shows the regions of the power spectrum and bispectrum, respectively, and their relationship. The cut-off frequencies are determined by the intersection between the noise and spectral lines of the signal. These frequencies also determine the distinct areas basically bounded by a hexagon in the bispectrum. The area inside the hexagon shows the relationship between frequency components of the signal only, otherwise the area outside shows the relationship between the signal components and noise. Due to a two-dimensional representation in the bispectrum, the variation of the signal and the interaction between signal components can be easily identified.

Because of unique features of the bispectrum, it is really useful in characterizing the non-Gaussian or nonlinear processes and is applicable in many various fields such as signal processing [37], biomedicine [37], and image reconstruction [37]. Extension of a number of representation dimensions makes the bispectrum become more easily and significantly a representation of different types of signals and differentiation of various processes, especially nonlinear processes such as doubling and chaos. Multidimensional spectra are proposed as a useful tool to analyze the behaviors of signals generated from these systems such as multibound solitons, especially transition states in the formation process of multibound solitons.

9.4.2 Various States of Bound Solitons

For multibound solitons, the optical power spectrum is modulated with the appearance of main lobes and sublobes due to the phase relationship between bound pulses as demonstrated in Chapter 3. Therefore, various multibound states generated from the FM mode-locked fiber laser can be distinguished by the optical power spectrum analysis. However, as a result the bispectrum of each multibound soliton state obviously exhibits a distinct structure for characterization. In this section, various multibound solitons in steady state obtained from simulation are used to estimate their bispectra. Moreover, some interesting information of the multibound solitons (MBS) can be obtained from the bispectrum.

First, the triple correlations of various multibound solitons are estimated as shown in Figure 9.36. The triple correlation of a pulse can be represented by the elliptical contour lines corresponding to its magnitude as shown in Figure 9.36a. Depending on the number of solitons in the bound state, the triple correlation of the multibound soliton is represented by the layers of elliptical contour lines bounded in a hexagon as shown in Figures 9.36b through 9.2d. The quality and symmetry of pulses can be reflected by the uniformity of the ellipsis in the same layer. In the triple correlation, the presence of pedestals, which is commonly characterized by the high dynamic range autocorrelation measurement [6], can be easily observed by the contour lines outside the hexagon. When the gain is enhanced in the cavity for the higher multibound state, the pulses are not only shortened but also possibly degraded by the increase in pedestal energy, which is proportional to the level of the lines outside the hexagon area.

The Fourier transform of the triple correlations results in the bispectra of multibound solitons, which consist of the magnitude and the phase representations. Figure 9.37 shows the magnitude in contour plot view of different multibound soliton states with a π phase difference that circulates stably in the FM mode-locked fiber laser cavity. In the single soliton state only, the magnitude bispectrum contour is only closed contour lines inside the area bounded by the hexagon as shown in Figure 9.37a. While the bispectra of higher-order bound solitons from dual- to quadruple-bound states exhibit a periodic structure inside this area as shown in Figures 9.37b through 9.37d. Depending on the number of pulses in a bound states, the periodic structures of both phase and magnitude spectra can vary correspondingly. When the number of pulses in a bound state increases, the periodic structure of its bispectra is more sophisticated because of the interactive relationship between sidelobes or various frequency components. Moreover, the hexagonal area in the bispectrum that is broader at a higher-order bound state reflects the bandwidth of the signal that is broadened by the pulse compression due to the enhancement of the gain or power in the fiber cavity. Similar to the observation in the triple correlation, the stability of the bound states also exhibits obviously in the bispectrum. A lower stability of higher-order bound states is shown by the blurred contour lines inside the hexagon and the enhancement of the contour ridges outside the hexagon.

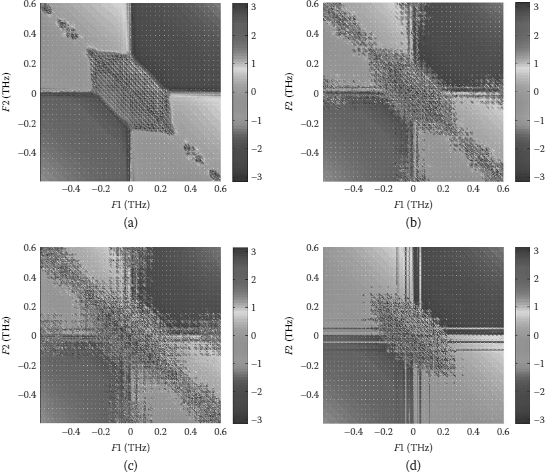
FIGURE 9.38
The phase bispectra of different multibound soliton states: (a) single soliton, (b) dual-bound solitons, (c) triple-bound solitons, and (d) quadruple-bound solitons, respectively.

The phase bispectra provide additional information about the status and quality of the bound state. Figure 9.38 shows the phase bispectra of various soliton states from the single pulse to quadruple pulse. For the phase bispectrum, periodic phase variation of a stable state in the frequency domain is easily exhibited in two dimensions. The sharply periodic structure of the phase bispectrum inside the hexagon with two distinct regions that are complex conjugates of each other and separated by the line f₁ = –f₂ as shown in Figure 9.38a indicates high stability of the single soliton state. On the other hand, the periodic structure of the stable multibound state is corrupted by the change in operating conditions of the multibound state such as gain, the noise level in the fiber cavity. At a higher-order bound soliton state, the phase variation in the bispectrum is more blurred in the hexagon, however two conjugate regions can still be obviously identified.

9.4.3 Transitions in Multibound Soliton Formation

One of the important advantages of the bispectrum representation is to differentiate the linear and nonlinear responses or processes; therefore, it is especially useful in analyzing the transition processes from the noise to the steady state or from the unstable state to the stable. In transition processes of multibound solitons, the signal experiences strong fluctuations in phase and magnitude like a chaotic state before reaching a new steady state. Therefore, the average bispectrum of these processes also exhibits clearly the variation in terms of both phase and magnitude, which can be used to analyze multibound solitons at this stage. One of the most important transition processes is the formation of multibound solitons from the noise in the fiber cavity that has been numerically investigated in Chapter 3. The evolution of the signal from the noise into the multibound solitons can be split into three stages in which the first stage is the process that the noise builds up into the pulses, yet the amplitude and phase of the signal fluctuate strongly during circulating inside the cavity like a chaotic state. In order to analyze this stage, the bispectrum is averaged over the first 1000 round-trips in the evolution of the multibound soliton formation that was simulated in Chapter 3. Figure 9.39 shows the magnitude and phase bispectra of the dual-bound soliton and the triple-bound soliton evolutions, respectively. For the case of the dual-bound soliton, the bispectra in Figures 9.39a and 9.39b show nonperiodic structure in a hexagon with a small area that corresponds to the rapid variation of magnitude and phase of the signal from round-trip to round-trip. In particular, the phase structure shows a uniform distribution indicating an independence of the frequency components in the signal envelope because the signal behavior in this stage is similar to a chaotic state. While the magnitude bispectrum for the case of the triple-bound soliton shows the closed contours in a low- frequency region with the phase bispectrum having a periodic structure due to the existence of two dominant short pulses in this first stage. However, the state of these two pulses is unstable, as expressed by the ridges in the hexagon of the magnitude bispectrum and the unclarity of two distinct regions in phase structure of the bispectrum.

The second stage in the next 1000 round-trips is the process that the built-up pulses interact and bind together to form the multibound solitons. For the evolution of the dual-bound soliton, therefore the elliptical contours in magnitude bispectra and the periodic structure in phase bispectra in this stage appear obviously because of the presence of periodic components as shown in Figures 9.40a and 9.40b. The structure of closed contours in magnitude bispectra becomes finer and extended due to the appearance of three solitons in the evolution of the triple-bound soliton as shown in Figure 9.40c. However, the bound state in this stage is unstable during circulating in the cavity because the operating conditions such as gain factor are not optimized. Hence, the contamination in phase bispecta still exists, and the structure of ridges is dominant in the hexagon of the magnitude spectra. The transition process between different bound states due to the change in operating conditions behaves similar to the evolution in this stage, which is easily identified by the bispectral representation. When the fluctuations of multibound solitons occurs, the periodic lines of bispectrum at that process are commonly varied and smeared, before another periodic structure of the bispectrum is formed when a new stable state is established.

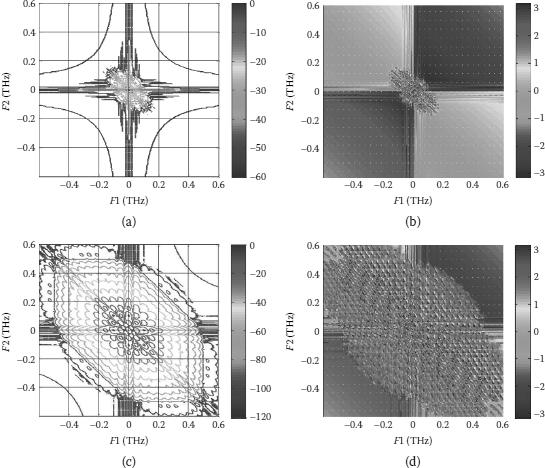
FIGURE 9.39
Magnitude and phase bispectra averaged over 1000 round-trips of evolution of the signal at the first stage in formation process from the noise of various multibound solitons: (a,b) dual-bound soliton and (c,d) triple-bound soliton.

The last stage in the evolution of multibound solitons is the process in which the pulses do self-adjustments until multibound solitons reach a steady state after the gain of the cavity is optimally adjusted. Although there is still the existence of small fluctuations of the phase and amplitude in this process, the pulses in bound states are well defined in a periodic evolution. Therefore, the magnitude bispectra in both the dual- and the triple-bound solitons show the periodic structure with the closed elliptical contours dominant in the hexagon as shown in Figures 9.41a and 9.41c. Figures 9.41b and 9.41d show the phase bispectra with a periodic relationship between frequency components of pulses and two clearly distinct conjugate regions separated by the diagonal f₁ = –f₂. On the other hand, the periodic structure in the bispectra is progressively widened until a stable final state during transition from the unstable to the stable states.

FIGURE 9.40
Magnitude and phase bispectra averaged over 1000 round-trips of evolution of the signal at the second stage in formation process of various multibound solitons: (a,b) dual-bound soliton and (c,d) triple-bound soliton.

Another state of multipulse in the fiber cavity can be obtained when the gain factor is not optimized for a higher multibound soliton state. Therefore, the magnitude and the phase fluctuate strongly during circulation in the cavity. Nonuniformity and deviation of the phase difference between pulses from the value of the π result in collision of pulses in this state and formation of new pulses. Figure 9.42 shows both the magnitude and the phase bispectra of this state averaged over 2000 round-trips. The presence of both the closed contours and the ridges in a jumble indicate the presence of a multipulsing operation and its dynamic state with the rapid variation in time due to the collision and the interaction of pulses in the cavity. The chaotic states as indicated by the uniform distribution of the phase bispectrum observed in Figure 9.42b.

FIGURE 9.41
Magnitude and phase bispectra averaged over the last 1000 round-trips of evolution of the signal at the third stage in formation process of various multibound solitons: (a,b) dual-bound soliton and (c,d) triple-bound soliton.

FIGURE 9.42
(a) Magnitude spectrum and (b) phase bispectra averaged over 2000 round-trips of the unstable multipulse state in the frequency modulation fiber ring cavity.

9.5 Summary

In this chapter, a number of nonlinear wave propagation equations that describe the evolution as well as the parametric interaction of multioptical waves in nonlinear waveguides are developed for photonic signal processing. A range of signal processing applications based on the parametric conversion process of third-order nonlinearity are demonstrated by simulation, such as high-order spectrum analysis for ultrasensitive receivers, time division demultiplexing, amplification and wavelength conversion, and phase conjugation. Models of nonlinear waveguides are integrated into the MATLAB Simulink platform for processing performance simulations. The FWM is the central nonlinear physical process.

Furthermore, nonlinear effects in active mode-locked fiber lasers are described. A laser model including a gain media, a bandpass filter, optical fiber, and intensity modulator are introduced to investigate the performance of the laser under nonlinear effects. Lasers in both working conditions, nondetuning and detuning, are studied. We find that the nonlinear effects compress the pulse through the self-phase modulation (SPM) effect. However, there is a trade-off between pulse shortening and a large detuning range. A laser with a shorter pulse has a narrower detuning range and vice versa.

References

1. G. P. Agrawal, Nonlinear Fiber Optics, Academic Press, New York, 2004.

2. F. Luan et al., Dispersion Engineered As2S3 Planar Waveguides for Broadband Four-Wave Mixing Based Wavelength Conversion of 40 Gb/s Signals, Opt. Express, 17, 3514–3520, 2009.

3. M. E. Marhic et al., Broadband Fiber Optical Parametric Amplifiers, Opt. Lett., 21, 573–575, 1996.

4. R. H. Stolen et al., Parametric Amplification and Frequency Conversion in Optical Fibers, IEEE J. Selected Topics in Quantum Electron., 18, 1062–1072, 1982.

5. J. Hansryd et al., Fiber-Based Optical Parametric Amplifiers and Their Applications, IEEE J. Selected Topics in Quantum Electron., 8(3), 506–520, 2002.

6. P. O. Hedekvist et al., Fiber Four-Wave Mixing Demultiplexing with Inherent Parametric Amplification, J. Lightwave Technol., 19, 977–981, July 2001.

7. M. C. Ho et al., 200-nm-Bandwidth Fiber Optical Amplifier Combining Parametric and Raman Gain, IEEE J. Lightwave Technol., 19, 977–981, July 2001.

8. R. M. Jopson et al., Compensation of Fiber Chromatic Dispersion by Spectral Inversion, Electron. Lett., 29(7), 576–578,

9. S. L. Jansen et al., Long-Haul DWDM Transmission Systems Employing Optical Phase Conjugation, IEEE J. Selected Topics Quantum Electron., 12, 505–520, 2006.

10. S. Watanabe et al., Simultaneous Wavelength Conversion and Optical Phase Conjugation of 200 Gb/s (5 × 40 Gb/s) WDM Signal Using a Highly Nonlinear Fiber Four-Wave Mixer, in Proceedings of ECOC ’97, 1997, pp. 1–4.

11. S. Radic et al., Wavelength Division Multiplexed Transmission over Standard Single Mode Fiber Using Polarization Insensitive Signal Conjugation in Highly Nonlinear Optical Fiber, in Proceedings of OFC ’03, Atlanta, Georgia, 2003, Paper PD12.

12. T. Yamamoto et al., Active Optical Pulse Compression with a Gain of 29 dB by Using Four-Wave Mixing in an Optical Fiber, IEEE Photonics Technol. Lett., 9, 1595–1597, December 1997.

13. J. Hansryd et al., Wavelength Tunable 40 GHz Pulse Source Based on Fiber Optical Parametric Amplifier, Electron. Lett., 37, 584–585, April 2001.

14. H. C. H. Mulvad et al., 1.28 Tbit/s Single-Polarization Serial OOK Optical Data Generation and Demultiplexing, Electron. Lett., 45(5), 280–281, February 2009.

15. M. D. Pelusi et al., Applications of Highly-Nonlinear Chalcogenide Glass Devices Tailored for High-Speed All-Optical Signal Processing, IEEE J. Selected Topics in Quantum Electron., 14, 529–539, 2008.

16. T. D. Vo et al., Photonic Chip Based 1.28 Tbaud Transmitter Optimization and Receiver OTDM Demultiplexing, Proceedings of OFC 2010, San Diego, 2010, Paper PDPC5.

17. M. Steve et al., Very Low Reactively Ion Etched Tellurium Dioxide Planar Rib Waveguides for Linear and Nonlinear Optics, Opt. Express, 17, 17645–17651, 2009.

18. L. N. Binh, Optical Fiber Communications Systems: Theory and Practice with MATLAB and Simulink Models, CRC Press, Boca Raton, FL, 2010.

19. C. L. Nikias and J. M. Mendel, Signal Processing with Higher-Order Spectra, IEEE Sig. Proc. Mag., 10(3), 10–37, 1993.

20. G. Sundaramoorthy et al., Bispectral Reconstruction of Signals in Noise: Amplitude Reconstruction Issues, IEEE Trans. Acoustics, Speech and Signal Proc., 38(7), 1297–1306, July 1990.

21. T. M. Liu et al., Triple-Optical Autocorrelation for Direct Optical Pulse-Shape Measurement, App. Phys. Lett., 81(8), 1402–1404, 2002.

22. J. K. Yang and D. J. Kaup, Stability and Evolution of Solitary Waves in Perturbed Generalized Nonlinear Schrödinger Equations, Siam J. Appl. Math., 60, 967–989, 2000.

23. J. C. Bronski, Nonlinear Scattering and Analyticity Properties of Solitons , J. Nonlinear Sci., 8, 161–182, 1998.

24. G. P. Agrawal, Applications of Nonlinear Fiber Optics, Academic Press, Arlington, MA, 2001.

25. G. P. Agrawal, Fiber-Optic Communication Systems, 3rd ed., Wiley-Interscience, New York, 2002.

26. G. P. Agrawal, Nonlinear Fiber Optics, Springer, Berlin, 2001.

27. A. Hasegawa and F. Tappert, Transmission of Stationary Nonlinear Optical Pulses in Dispersive Dielectric Fibers. I. Anomalous Dispersion, Appl. Phys. Lett., 23, 142–144, 1973.

28. C. T. Seaton, Xu Mai, G. I. Stegeman, and H. G. Winful, Nonlinear Guided Wave Applications, Opt. Eng., 24, 593–599, 1985.

29. G. I. Stegeman, E. M. Wright, N. Finlayson, R. Zanoni, and C. T. Seaton, Third Order NL Integrated Optics, IEEE J. Lightwave Technol., 6, 953–970, 1988.

30. G. I. Stegeman and R. H. Stolen, Waveguides and Fibers for Nonlinear Optics, J. Opt. Soc. Am. B, 6, 652–662, 1989.

31. K. Hayata and M. Koshiba, Full Vectorial Analysis of Nonlinear Optical Waveguides, J. Opt. Soc. Am. B, 5, 2494–2501, 1988.

32. D. R. Brillinger, Introduction to Polyspectra, Ann. Math. Stat., 36, 1351–1374, 1965.

33. G. Sundaramoorthy, M. R. Raghuveer, and S. A. Dianat, Bispectral Reconstruction of Signals in Noise: Amplitude Reconstruction Issues, IEEE Trans. Acoustics, Speech and Sig. Proc., 38(7), 1297–1306, July 1990.

34. H. Bartelt, A. W. Lohmann, and B. Wirnitzer, Phase and Amplitude Recovery from Bispectra, Appl. Opt., 23, 3121–3129, 1984.

35. Chrysostomos L. Nikias et al., Signal Processing with Higher-Order Spectra, IEEE Signal Proc. Mag., 10(3), July 1993.

36. B. M. Sadler et al., Acousto-optic Estimation of Correlations and Spectra Using Triple Correlations and Bispectra, Opt. Eng., 31(10), 1992.

37. J. M. Mendel, Tutorial on High-Order Statistic (Spectra) in Signal Processing and System Theory: Theoretical Results and Some Applications, Proc. IEEE, 79(3), 1991.

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 9 Nonlinear Photonic Signal Processing Using Third-Order Nonlinearity: Le Nguyen Binh

Create new playlist

Sign In

Sign Up

9

Nonlinear Photonic Signal Processing Using Third-Order Nonlinearity

Le Nguyen Binh

CONTENTS

9.1 Introduction

9.2 Nonlinear Effects on Optical Waveguides and Photonic Signal Processing

9.2.1 Introductory Remarks

9.2.2 Third-Order Nonlinearity and Parametric Four-Wave Mixing Process

9.2.2.1 Nonlinear Wave Equation

9.2.2.2 Four-Wave Mixing Coupled-Wave Equations

9.2.2.3 Phase Matching

9.2.3 Transmission Models and Nonlinear Guided Wave Devices

9.2.4 System Applications of Third-Order Parametric Nonlinearity in Optical Signal Processing

9.2.4.1 Parametric Amplifiers

9.2.4.2 Wavelength Conversion and Nonlinear Phase Conjugation

9.2.4.3 High-Speed Optical Switching

9.2.4.4 Triple Correlation

9.2.5 Application of Nonlinear Photonics in Advanced Telecommunications

9.2.6 Remarks

9.3 Nonlinear Photonic Preprocessing and Bispectrum Optical Receivers

9.3.1 Introductory Remarks

9.3.2 Bispectrum Optical Receiver

9.3.3 Triple Correlation and Bispectra

9.3.3.1 Definition

9.3.3.2 Gaussian Noise Rejection

9.3.3.3 Encoding of Phase Information

9.3.3.4 Eliminating Gaussian Noise

9.3.4 Bispectral Optical Structures

9.3.4.1 Principles

9.3.4.2 Technological Implementation

9.3.4.2.1 Nonlinear (NL) Optical Waveguides

9.3.4.2.2 Mixing and Integrating

9.3.4.2.3 Equalization and Filtering

9.3.4.2.4 Four-Wave Mixing (FWM) in Highly Nonlinear Media

9.3.4.2.5 Third Harmonic Conversion

9.3.4.2.6 Conservation of Momentum

9.3.4.2.7 Estimate of Optical Power Required for Four-Wave Mixing

9.3.5 Mathematical Principles of Four-Wave Mixing and the Wave Equations

9.3.5.1 The Phenomena of Four-Wave Mixing

9.3.5.2 Coupled Equations and Conversion Efficiency

9.3.5.3 Evolution of FWM along the NL Waveguide Section

9.3.6 Transmission and Detection

9.3.6.1 Optical Transmission Route and Simulation Platform

9.3.6.2 Four-Wave Mixing and Bispectrum Receiving

9.3.6.3 Performance

9.3.6.4 Remarks

9.4 Bispectrum of Multibound Solitons

9.4.1 Bispectrum

9.4.2 Various States of Bound Solitons

9.4.3 Transitions in Multibound Soliton Formation

9.5 Summary

References

Table of Contents for
9 Nonlinear Photonic Signal Processing Using Third-Order Nonlinearity: Le Nguyen Binh