Since K. Ikeda first showed that the transmission of a passive nonlinear optical cavity could exhibit multistability and chaos in response to a constant incident light [1], extensive studies on the dynamic property of both the passive and active nonlinear optical cavities have been carried out. It has been shown that period-doubling bifurcation and the period-doubling route to chaos are generic features of light traversing a nonlinear cavity. However, the majority of the researches have been focused on the continuous-wave operation of the cavities [2]. As a matter of fact, apart from the continuous-wave (CW) operation, short-pulse operation of the cavities is also available. Moreover, determined by the cavity parameters, various types of solitons can even be formed in a nonlinear cavity. Solitons as a special nonlinear wave that can propagate long distance in dispersive materials without distorting their shapes have been found in a wide range of physical systems in thermodynamics, plasma physics, condensed matter physics, and optics. As solitons are a nonlinear wave packet intrinsically stable against perturbations, it would be of interest to investigate the dynamical features of the cavities and their manifestations under the ultrashort pulse operation, in particular when the ultrashort pulse is itself an optical soliton.

Soliton operation has been obtained in various ultrashort pulse mode-locked fiber lasers [3–10], as well as in the mode-locked bulk solid-state lasers [11,12]. In the case of a fiber laser, except for the cavity components necessary for achieving mode locking and for laser output, its cavity is mainly made up of optical fibers. Due to the small core size of the single-mode fibers and the long propagating distance, strong nonlinear phase shift can be accumulated when an ultrashort pulse propagates in the fiber laser cavity. Therefore, a mode-locked pulse could be easily shaped into an optical soliton in a fiber laser. It has been shown that despite the actions of the other discrete cavity components, the average dynamics of the formed solitons in a fiber laser is well described by the nonlinear Schrödinger equation (NLSE), a paradigm equation that has been extensively investigated. A soliton formed in a laser is inherently different from those formed in a single-mode fiber as in a laser a soliton also experiences loss and gain. It has been shown both experimentally and numerically that under certain conditions, the solitons formed in a fiber laser could exhibit deterministic dynamics [13–22], such as the soliton period-doubling bifurcations, soliton intermittency, and soliton quasi-periodicity. Moreover, the appearance of the soliton deterministic dynamics is independent of the concrete laser cavity design, showing that it is a general feature of the system.

In this chapter we describe the deterministic dynamics of solitons in fiber lasers. Our discussions are mainly focused on fiber soliton lasers passively mode locked by the nonlinear polarization rotation (NPR) technique. In the fiber lasers the scalar solitons are normally formed. We also investigated the vector soliton dynamics in fiber laser mode locked by the semiconductor saturable absorber mirrors (SESAMs) and the dissipative solitons dynamics in fiber lasers with normal cavity dispersion. The chapter is organized as follows: Section 6.2 presents the general theoretical background for NPR mode locking and soliton generation in fiber lasers. Section 6.3 reviews the deterministic dynamics of various solitons in different fiber lasers, which is followed by the corresponding numerical simulations in Section 6.4. Furthermore, this section describes the cavity-induced modulation instability effect and its relation to the soliton deterministic dynamics. We show that the various forms of the soliton deterministic dynamics observed could be related to the cavity-induced soliton modulation instability effect. Namely, their physical origin could be traced back to the self-induced nonlinear resonant wave coupling in the laser cavity. Section 6.5 presents our conclusion.

6.2 Solution Generation in Fiber Lasers

Solution formation in anomalous dispersion cavity fiber lasers is mainly due to the natural balance between the cavity dispersion and the fiber nonlinear optical Kerr effect. An optical pulse can be routinely generated in a fiber laser by various mode-locking techniques. In terms of the passive mode locking these include the nonlinear optical loop mirror method [23], figure-eight cavity method [24], NPR technique [25], and SESAM method [26]. Among the various passive mode-locking techniques, the NPR technique is widely used. The technique exploits the nonlinear birefringence of the single-mode optical fibers for the generation of an artificial saturable absorber effect in the laser cavity. It is the artificial saturable absorber effect that initiates a self-started mode locking in the laser. To explain the operation principle of the technique, it is to note that generally the polarization state of light passing through a piece of birefringent fiber varies linearly with the fiber birefringence and length. However, when the light intensity is strong, the nonlinear optical Kerr effect of the fiber introduces an extra change to the light polarization. As the extra polarization change is proportional to the light intensity, if a polarizer is placed behind the fiber, then through appropriately selecting the orientation of the polarizer, an effect with the feature that light with higher intensity experiences larger transmission through the polarizer could be obtained. Such an effect is known as an artificial saturable absorber effect. Incorporating such an artificial saturable absorber effect in a fiber laser is equivalent to inserting a saturable absorber in the laser cavity. Under the effect of a saturable absorber, the operation of a laser can automatically become mode locked. In the NPR mode-locked fiber laser, a nonlinear phase shift is required to achieve mode locking. If the nonlinear phase modulation of the pulse could balance the pulse width broadening caused by the cavity dispersion, a soliton is then formed in the laser.

6.2.1 Pulse Propagation in Single-Mode Fibers

When an optical pulse propagates in a birefringent single-mode fiber, not only would the fiber dispersion broaden the pulse width, but also the pulses along different polarizations will have different group velocities, which broadens the pulse width or even splits the pulse. As there exist two polarization components, the nonlinear fiber Kerr effect will not only generate self-phase modulation (SPM) of each component, but also generate cross-phase modulations (XPM) between the two polarization components. The coherent coupling between the two polarization components also generates degenerated four-wave mixing (FWM), whose strength is related to the strength of the linear fiber birefringence [27].

In a fiber laser system, one of the essential components is the active medium, which generally is rare earth ions doped fiber. When an optical pulse propagates in the rare earth ions doped fibers, the effect of light amplification must be considered. A fiber amplifier is characterized by its small signal gain, gain bandwidth, gain saturation, and noise figure. Therefore, to precisely describe pulse evolution in a fiber laser, it is necessary to consider the cavity dispersion, fiber nonlinearity (SPM and XPM), fiber birefringence, FWM, gain and loss, gain dispersion effects, and so on.

Optical pulse propagation in fiber segments in a fiber laser can be described by the extended Ginzburg–Landau equation (GLE) [28]:

where A_x and A_y are the two normalized slowly varying pulse envelopes along the slow and the fast axes, A_x* and A_y* are their conjugates, respectively. is the wave-number difference, and is the inverse group-velocity difference. The equations are written in the coordinate system that moves with the average group velocity. The GLE is nonintegrable, but numerical simulations are available for studying the pulse dynamics in such fiber lasers.

The last two terms in the right part of Equation (1.6) correspond to the gain and the gain dispersion effects when an optical pulse propagates in the active fiber segments of a fiber laser. g is the peak gain coefficient; Ω_g is the gain bandwidth. When the gain saturation results from light along both polarizations, the saturated gain coefficient is calculated by

where g₀ is the small signal gain, and E_s is the saturation energy. Typical values of E_s for erbium-doped fibers are about 10 μJ. As the pulse energies are normally much smaller than the saturation energy E_s, gain saturation is negligible over the duration of a single pulse. However, in the case of a pulsed fiber laser, the pulse circulates in the laser cavity. The average power of the light will saturate the gain and determine the saturated gain value.

6.2.2 Cavity Transmission of Nonlinear Polarization Rotation Mode-Locked Fiber Lasers

Apart from the pulse propagation in various fiber segments, cavity boundary condition is another intrinsic feature that needs to be considered for soliton generation in fiber lasers. A fiber laser mode locked with the NPR technique can always be equivalently simplified into the three parts as shown in Figure 6.1 where a polarization controller P1 is at the beginning of the fiber and an analyzer at the end of the fiber, and the fiber is a weakly birefringence fiber. The two principal polarization axes of the birefringent fiber are x (horizontal) and y (vertical) axes and we consider that the birefringent axes of the different segments of fibers are the same. The fast axis of P1 and the transmission axis of the analyzer have an angle of θ and φ to the y-axis of the fiber polarization, respectively.

FIGURE 6.1
Equivalent physically simplified laser cavity for fiber lasers using the nonlinear polarization rotation (NPR) mode-locking technique.

Briefly speaking, the pulse evolution in the fiber laser starts with an arbitrary weak pulse, and it circulates in the laser cavity until a steady pulse evolution state is established. Whenever the pulse encounters an individual intracavity component except the fiber segments, the Jones matrix of the component is multiplied to the optical field of the pulse.

Starting from a linearly polarized weak pulse F_n, two polarization components are obtained when F_n travels through P1:

where is the phase shift between the wave components in the two orthogonal birefringent axes x and y.

Then the two polarization components propagate in the fiber segments, which is governed by the coupled GLEs as shown in previous section.

The light propagates along the laser cavity and finally projects on the transmission axis of the analyzer:

where and are the two orthogonal polarization components of the light after propagation in all the fiber segments.

The intensity transmission T of light through the setup is [29]

where Φ_F is the phase delay generated between the two light polarization components when they traverse the birefringent fiber. The phase delay actually consists of two parts: a linear phase delay ΔΦ_l raised because of the linear birefringence of the fiber, this part always exists; and a nonlinear part ΔΦ_nl generated by the nonlinear effects of the fiber. If the light intensity is weak, the nonlinear part becomes zero. Hence, one can divide the light transmission into the linear transmission and the nonlinear transmission. The linear intensity transmission can be written as

Once the orientations of the polarizer and analyzer with respect to the fiber polarization principal axes are fixed, the linear transmission of the setup is a sinusoidal function of the linear phase delay between the two polarization components. Although the relative orientation between the polarizer and the analyzer could be arbitrarily selected, in order to possibly achieve a stable mode-locked operation, it is preferred to choose the relative orientation between the polarizer and the analyzer as 90 degrees, as under such a selection the linear transmission is possible to set to zero.

To illustrate the effect of the nonlinear polarization rotation on the intensity transmission, we assume that the nonlinear fiber birefringence only introduces a small extra phase delay ΔΦ_nl. Then the intensity transmission can be written as

The nonlinear phase delay introduces a transmission change relative to the value of the linear transmission T_l. The change is not only the nonlinear phase delay ΔΦ_nl; therefore, the light intensity dependent, but also the orientation of the polarizer, as well as the linear phase delay are dependent. As a result, in order to generate an artificial saturable absorber effect by the nonlinear fiber birefringent effect, it is necessary to appropriately select the combination of all these parameters.

It is instructive to consider a special case to illustrate it. Consider that the polarizer and the P1 are set orthogonally. In this case the linear intensity transmission is

Therefore, the maximum linear intensity transmission is limited by. The intensity transmission under the existence of a nonlinear phase delay ΔΦ_nl is

The orientation of the polarizer determines the projection of light on the two polarization axes of the fiber and, therefore, determines whether a positive ΔΦ_nl or a negative ΔΦ_nl would be generated. Assuming that a negative ΔΦ_nl is generated, then further depending on the linear phase delay, either an increase or decrease in the intensity transmission could be caused by the nonlinear polarization rotation. The magnitude of ΔΦ_nl is always proportional to the intensity of light. This means that with the increase of the light intensity, either an increase or a decrease in the transmission could be generated, which is purely determined by the linear phase delay selection.

Strictly speaking, the nonlinear phase delay between the two polarization components of an optical pulse traversing a piece of birefringent fiber can only be determined by numerically solving the coupled GLEs (Equation 6.1). However, in the case of CW light propagation and ignoring the effect of energy exchange between the two polarization components, this can be calculated explicitly as [28]

where P₀ is the power of the light, and L is the length of the fiber. Using the nonlinear phase delay, the intensity transmission can be written as [30]

where. As far as κ > 0, a saturable absorber effect can be obtained. Based on the formula one could estimate the optimum selection for the θ value so that the strongest saturable absorber effect could be achieved [31]. In this case it occurs at θ = 27.7°.

In practice it is difficult to set the linear phase delay just within the range where the saturable absorption effect is achieved. Therefore, a polarization controller is normally inserted in the setup to efficiently control the value of the linear phase delay ΔΦ_l. Mathematically, this is equivalent to adding a variable linear phase delay bias term in the intensity transmission formula. Hence, the intensity transmission can be further written as

where Φ_pc is the phase delay bias introduced by the polarization controller, and it is continuously tunable. With the insertion of a polarization controller in the setup, it is always possible to achieve an artificial saturable absorber effect through changing the linear birefringence of the fiber.

In summary, the soliton generation in fiber lasers should be the stable pulse propagation that can both fulfill pulse propagation in fiber segments as described by Equation (1.6) and the cavity transmission as indicated by Equation (6.12).

6.3 Deterministic Dynamics of Solitons in Fiber Lasers

6.3.1 Experimental Configuration

We have experimentally investigated deterministic soliton dynamics in passive mode-locked fiber lasers with various cavity design and cavity parameters. Figure 6.2 shows a typical fiber laser we used. The fiber laser has a ring cavity composed of a segment of the erbium-doped fiber used as the laser gain medium. The erbium fiber is pumped by a high-power Fiber Raman Laser source (BWC-FL-1480-1) of wavelength 1480 nm. The pump light is coupled into the cavity through a fiber wavelength division multiplexer (WDM). A fiber pigtailed isolator is inserted in the cavity to force the unidirectional operation of the cavity. We used the NPR technique for the self-started mode locking of the laser. To this end, two polarization controllers, one consisting of two quarter-wave plates and the other two quarter-wave plates and one half-wave plate, are used to adjust the polarization of the light. A cubic polarization beam splitter is used to output the laser pulses and set the polarization at the position of the cavity. The polarization controllers and the beam splitter are mounted on a 7-cm-long fiber bench. The soliton output of the laser is monitored with an optical spectrum analyzer (Ando AQ-6315B), a 26.5 GHz radio-frequency (RF) spectrum analyzer (Agilent E4407B ESA-E series), and a 350 MHz oscilloscope (Agilent 54641A) together with a 5 GHz photodetector. A commercial optical autocorrelator (Autocorrelator Pulsescope) was used to measure the soliton pulse width.

FIGURE 6.2
The experimental setup: quarter-wave plate; : half-wave plate; BS: beam splitter; WDM: wavelength-division multiplexer; EDF: erbium-doped fiber; OSA: optical spectrum analyzer; PD: photodetector; Osci.: oscilloscope; SA: rf spectrum analyzer.

In our experiments we used optical fibers with various parameters, such as different fiber group velocity dispersion (GVD), different lengths, and different doping concentrations of the gain fiber. The purpose of using fibers of different properties and lengths is to change the laser cavity parameters, so possibly different soliton dynamics in the cavity could be observed. Experimentally we found that with the appropriate selection on the orientations of the waveplates, self-started mode locking of the fiber lasers could always be achieved, and as far as the cavity nonlinearity is not too strong, stable soliton operation of the fiber lasers can always be observed. Such stable soliton operation of the fiber lasers has been extensively investigated and reported previously [29]. However, we also found that when the peak power of the formed solitons reached a certain high level in a fiber laser, deterministic dynamics of the optical solitons could also be observed.

6.3.2 Soliton Deterministic Dynamics

Suggested by the average soliton theory of lasers [32], it is generally believed that the output of the fiber soliton lasers is a uniform soliton pulse train. However, Kim et al. found theoretically that depending on the strength of the fiber birefringence and the alignment of the polarizer with the fast- and slow-polarization axes of the fiber, the output pulse train of a fiber laser mode locked with the NPR technique could exhibit periodic fluctuations in pulse intensity and polarization [33,34]. Nevertheless, the nonuniformity of the pulse train could be diminished by aligning the polarizer with either the fast or slow axis of the fiber. We had also experimentally investigated the output property of a fiber soliton ring laser passively mode locked by the NPR technique [35] and found that the soliton pulse nonuniformity is in fact an intrinsic feature of the laser, whose appearance is independent on the orientation of the polarizer in the cavity but closely related to the pump power. Based on numerical simulations we showed that depending on the linear cavity phase delay bias, the nonlinear polarization switching effect could play an important role on the soliton dynamics of the lasers. When the linear cavity phase delay bias is set close to the nonlinear polarization switching point and the pump power is strong, the soliton pulse peak intensity could increase to so high that the generated NPR cross over the nonlinear polarization switching point and, consequently, drive the laser cavity from the positive feedback regime to the negative feedback regime. Eventually the competition between the soliton pulses with the linear waves in the cavity such as the dispersive waves or CW laser emission then causes the amplitude of the soliton pulses to vary periodically. There are two methods to suppress the periodical intensity fluctuations: one is to reduce the pump power so that the peak intensity of the solitons is below the polarization switch threshold; the other is to increase the polarization switching power of a laser. However, the latter method needs to appropriately adjust the linear phase delay bias of the cavity.

Experimentally, lasers of the same cavity configuration but with different cavity lengths, different fiber birefringence, and different fiber dispersion properties have been set up and investigated [13,15,17,19,20]. In all lasers if the pump power is set beyond the mode-locking threshold, and the linear cavity phase delay is appropriately selected, self-started mode locking can always be obtained. However, depending on the laser parameter selection, deterministic dynamics of the solitons may not necessarily appear. In the following we summarize the typical soliton deterministic dynamics of the lasers observed.

6.3.3 Period-Doubling Bifurcation and Period-Doubling Route to Chaos of Single-Pulse Solitons

Provided that the orientations of the polarization controllers are appropriately set, self-started soliton operation of the lasers is automatically obtained by simply increasing the pump power beyond the mode-locking threshold. Multiple solitons are initially obtained. However, by decreasing the pump power, the state with only one soliton existing in the cavity can always be achieved. Starting from a stable soliton operation state, experimentally it was noticed that turning the orientation of one of the quarter-wave plates to one direction, which theoretically corresponds to shifting the linear cavity phase delay bias away from the nonlinear polarization switching point, the peak power of the soliton pulse formed in the cavity increases. Consequently, the strength of nonlinear interaction of the soliton pulses with the cavity components such as the optical fiber and the gain medium increases. To a certain level of the nonlinear interaction, it was observed that the output soliton intensity pattern of the laser experiences period-doubling bifurcations and a period-doubling route to chaos. Figure 6.3 shows as an example an experimentally observed period-doubling route to chaos. The results were obtained with fixed linear cavity phase delay bias but increasing pump power. At a relatively weak pump power, a stable soliton pulse train with uniform pulse intensity was obtained. The pulses repeat themselves with the cavity fundamental repetition rate (Figure 6.3a). We experimentally measured the laser output power when it is operating in such a state. With a pump power of about 26 mW, an average output power of about 140 μW was obtained, which illustrates that the single soliton pulse energy is about 8.05 pJ. Carefully increasing the pump power further, the intensity of the soliton pulse becomes no longer uniform, but alternates between two values (Figure 6.3b). Although the round-trip time of the solitons circulating in the cavity is still the same, the pulse energy returns only every two round-trips, forming a period-doubled state as compared with that of Figure 6.3a. Further slightly increasing the pump power, a period-quadrupled state then appears (Figure 6.3c). Eventually the process ends up with a chaotic soliton pulse energy variation state (Figure 6.3d).

FIGURE 6.3
Period-doubling bifurcation to chaos of the soliton trains. (a) Period 1 state; (b) Period 2 state; (c) Period 4 state; (d) chaotic state. From (a) to (d) the pump intensity is increased.

With fixed pump power all the states shown are stable. Provided there are no great disturbances, they can last for several hours. It was also confirmed experimentally by combined use of the autocorrelator (PulseScope, scan range varies from 50 fs to 50 ps) and a high-speed oscilloscope (Agilent 86100A 50 GHz) that there is only one soliton in the cavity. Limited by the resolution of our autocorrelator, the measured autocorrelation traces show no unusual features of the soliton pulses and thus give no evidence of the behavior of period-doubling bifurcations, which is similar to that observed by G. Sucha et al. [36]. In all states the average soliton duration measured was about 316 ± 10 fs. The experimental results demonstrate that contrary to the general understanding to the mode-locked lasers, after one round-trip the mode-locked pulse does not return to its original value but does it in every two or four cavity round-trips in the stable periodic states. Depending on the strength of the nonlinear interaction between the pulse and the cavity components, the pulse could never return back to its original state in the chaotic state. To exclude any possibility of artificial digital sampling effect of the oscilloscope, we checked the pulse intensity alternation of the various periodic states by using a high-speed sampling oscilloscope (Agilent 86100A 50 GHz). Figure 6.4 shows the result corresponding to a Period 2 state. In obtaining the figure we used the soliton pulse as the trigger for the oscilloscope and a high oscilloscope resolution of 50 ps/division. Due to the high scan speed of the oscilloscope we could clearly see that the individual soliton pulse trace on the screen now becomes broader. Therefore, no sampling problem exists. Triggered by different pulses the oscilloscope traces formed have two distinct peak intensities, indicating that the solitons in the laser output have two different pulse energies.

FIGURE 6.4
Oscilloscope traces of a period-two state of the laser emission.

The optical spectra of the solitons corresponding to the Period 1 and Period 2 states are shown in Figures 6.5a and 6.5b, respectively. While the spectral curve shown in Figure 6.5a is smooth, the spectral curve shown in Figure 6.5b exhibits clear modulations. The spectral curve shown in Figure 6.5a possesses typical features of the soliton spectra of the passive mode-locked fiber lasers, characterized by the existence of sidebands superposing on the soliton spectrum. As in a Period 1 state solitons are identical in the soliton train, the spectrum shown in Figure 6.5a is also the optical spectrum of each individual soliton. In contrast, the optical spectrum shown in Figure 6.5b is an average of the spectra of two different solitons, each with different energy and frequency chirps. Based on Figure 6.5b it is to conclude that after a period-doubling bifurcation, the solitons possess different frequency properties as that of the solitons before bifurcation.

We also measured the intensity modulation of the soliton train with an RF spectrum analyzer. If period doubling does occur, there should appear a new frequency component in the RF spectrum locating exactly at the half of the fundamental cavity repetition rate position. Figure 6.6 shows the RF spectra of the laser output measured. As expected, after a period-doubling bifurcation a new frequency component of about 8.7 MHz appears in the spectrum. The amplitude of the new frequency component is quite strong compared to the fundamental frequency component, which vividly suggests that the soliton peak intensity alternates between two values with large difference. When period quadrupling occurs, in the RF spectrum we found that the amplitude of the new frequency component decreased; however, the frequency components corresponding to the period quadrupling were too weak to be clearly distinguished from the background noise.

FIGURE 6.5
Optical spectra of the laser measured in the states of (a) Period 1 and (b) Period 2.

FIGURE 6.6
Radio-frequency spectra corresponding to (a) Period 1 and (b) Period 2 states.

It is to be noted that if the linear cavity phase delay bias is selected close to the nonlinear polarization switching point of the cavity, although the single soliton operation of the laser can still be obtained, because the peak intensity of the soliton pulses is limited by the nonlinear polarization switching power, which is weak under the linear cavity phase delay bias selection, no matter how strong the pump power is, no period-doubling bifurcation could be observed. There exists a threshold for the occurrence of the period-doubling bifurcation. Only when the linear cavity phase delay bias, which determines the stable soliton peak intensity, is appropriately set so that the stable soliton peak intensity exceeds a certain value, can period-doubling bifurcation be achieved. The experimental result further confirms that the appearance of the period-doubling bifurcations and period-doubling route to chaos is soliton pulse intensity dependent, and it is a nonlinear dynamic feature of the laser. One thing confirmed in our experiment is that for the occurrence of the effect, the soliton pulse energy or peak power must be strong. It is to imagine that in this case the nonlinear interaction between light and the gain medium, light and the nonlinear laser cavity will also become strong. It is well known that as a result of strong nonlinear interaction between light and gain medium in the laser cavity, a laser operating in the CW or Q-switched mode can exhibit a period-doubling route to chaos. Our experimental result now further demonstrated that this phenomenon could even appear in a mode-locked soliton laser. Finally, we point out that Côté and van Driel reported period doubling of a femtosecond Ti:sapphire laser by total mode locking of the TEM₀₀ and TEM₀₁ modes in an effective confocal cavity [37]. They believe that the gain saturation is a likely mechanism to support the transverse mode locking and the period doubling. However, in our laser there only exists one transverse mode of the fiber due to the characteristics of the single-mode fibers.

6.3.4 Period Doubling and Quadrupling of Bound Solitons

The full route of soliton period-doubling bifurcation to chaos was only observed under appropriately selected laser cavity parameters. In most cases only one or two soliton period-doubling bifurcations could be obtained. A common feature of all soliton fiber lasers is the multiple soliton generation under strong pumping. And in the steady states all the solitons generated have identical properties, a result of the soliton energy quantization effect [38]. Interaction between the multiple solitons has been extensively investigated previously. It was found that various modes of the multiple soliton operation could be formed [39]. A special situation also experimentally observed is that under appropriate laser cavity conditions, the solitons in the cavity could automatically bind together and form states of bound solitons [40,41]. Depending on the strength of the soliton binding, a certain state of the bound solitons can even become the only stable state in a laser. In such a state the bound solitons as an entity exhibit features that are in close similarity to those of the single pulse solitons [40,42,43]. It was speculated that such a state of bound solitons could even be regarded as a new form of multipulse solitons in the lasers [44]. We found experimentally that period-doubling bifurcations could also occur on these bound solitons. Like the conventional single-pulse solitons, the bound solitons as an entity can exhibit complicated deterministic dynamics.

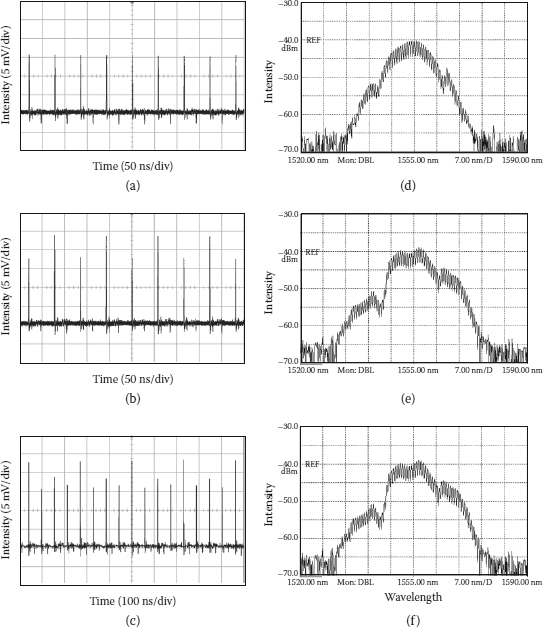
FIGURE 6.7
Oscilloscope traces and corresponding spectra of period-doubling bifurcations of a bound-soliton pulse train. (a,d) Period 1 state; (b,e) period-doubled state; and (c,f) period-quadrupled state.

Figures 6.7a, 6.7b, and 6.7c show, for example, an experimentally observed period-doubling bifurcation route of a state of bound solitons. In the current case several solitons are tightly bound and move together at the cavity fundamental repetition frequency. When the peak intensity of the bound solitons is strong, the total intensity of the bound solitons exhibits the period-doubling bifurcation. The response time of the photodetector used in our experiment is about 140 ps, which can clearly resolve the pulse train but not the intensity profile of the bound solitons. Therefore, the measured oscilloscope traces shown in Figure 6.7 have no distinctions to those of the period-doubling bifurcations of the single-pulse solitons [13]. Figures 6.7d, 6.7e, and 6.7f are the simultaneously measured optical spectra corresponding to Figures 6.7a through 6.7c. Clear optical spectral modulations exist on the spectra, which show that more than one soliton are actually in the cavity and they are closely spaced. The oscillating peaks of the optical spectra have a peak separation of 0.7 nm. Assuming that the central wavelength of the soliton pulse is 1550 nm, based on the Fourier transformation, the solitons have a peak separation of about 11.5 ps in the time domain. The bound soliton nature of the state is also confirmed by the simultaneous autocorrelation trace measurement as shown in Figure 6.8. Limited by our autocorrelator resolution, the measured autocorrelation traces show no distinguishable features among different period-doubled states. The measured single soliton duration of the state is about 326 ± 12 fs, and the soliton separation between neighboring solitons is about 11.8 ps, which agrees with the 0.70 nm period of optical spectral modulation within the experimental errors. The soliton separations under different period-doubled states are also the same. From the autocorrelation traces it is shown that there are at least three solitons with the same soliton separations binding together in the bound-soliton state. Due to the limited scan range of our autocorrelator we could not identify how many solitons are actually in the state. Nevertheless, it is confirmed that all the solitons in the state are equally spaced, and the bound soliton as an entity exhibits period-doubling bifurcations. We note that the state of bound solitons shown in Figure 6.7 is the only pulse pattern existing in the cavity, which is confirmed by the combined monitoring of the autocorrelation trace and a high-speed oscilloscope trace.

Figures 6.7a, 6.7b, and 6.7c are obtained with continuously increased pump power while keeping all the other cavity parameters fixed. The chaotic state of the bound solitons could be obtained with further increasing pump power from the state in Figure 6.7c. However, the chaotic state was not stable. It quickly evolved into a chaotic state of the single-pulse soliton. The change of the laser emission from a chaotic state of bound solitons to that of single-pulse solitons was experimentally identified by the change of the optical spectra. It was observed that whenever the bound-soliton became chaotic, the modulations on the optical spectrum, which is a direct indication of close soliton separation in the time domain, disappeared, and subsequently the optical spectrum had exactly the same profile as that of the chaotic state of the single-pulse solitons. Considering that in a chaotic state the energy of solitons varies randomly, which may affect the binding energy between the solitons and destroy their binding, this result seems also plausible. The states of period-doubled and quadrupled-bound solitons are stable. Nevertheless, compared with those states of the single-pulse solitons [13], they are more sensitive to the environment perturbations. Analyzing the optical spectra of the period-doubled bound solitons, it is found that the overall spectral profile in each state is similar to those of the single-pulse soliton undergoing the period doubling, except that it is now modulated [13]. The feature of the optical spectra indicates that the individual solitons within a bound-soliton are still the same as the single-pulse soliton of the laser.

FIGURE 6.8
A typical measured autocorrelation trace of the bound soliton.

RF spectra of the bound-soliton pulse train also disclose different period-doubled states. The emergence of a new frequency component at the position of half of the fundamental cavity repetition frequency clearly shows that the repetition rate of the bound solitons is doubled. The amplitude of the new frequency component is nearly half of that of the fundamental frequency component, which vividly suggests that the total peak intensity of the bound solitons alternates between two values with a large difference. The same as observed in [13], the new frequency component corresponding to the period-quadrupling is not distinguishable from the background noise. Limited by the resolution of our measurement system, the detailed intensity variations of each of the solitons under period-doubling bifurcations could not be resolved. There are two possible ways for a two-pulse bound soliton exhibiting a period-doubling intensity pattern. Either the two solitons simultaneously experience the period doubling, or only one soliton experiences the period doubling while the other remains stable. With more solitons binding together the process could become more complicated.

Experimentally, we also observed period-doubling bifurcations of bound solitons with different soliton separations. Bound solitons with different pulse separations can be easily distinguished by their optical spectra, as different spectral modulation periods correspond to different pulse separations in the time domain. This experimental result suggests that the appearance of the phenomenon should be a generic feature of the laser, which is independent of the concrete property of the optical pulses. The period-doubling route to chaos is a well-known nonlinear dynamic phenomenon widely investigated. The period-doubling route to chaos of the CW and the Q-switched lasers as a result of strong nonlinear interaction between the light field and the gain medium have already been reported [45,46]. Except that the laser modes are phase locked, physically the interaction between the light and the gain medium in a mode-locked laser is still the same. Therefore, it is not surprising that under the existence of strong mode-locked pulses, the period-doubling route to chaos on the pulse repetition rate could still be obtained. Nevertheless, it was a little bit unexpected that a bound-soliton can exhibit period-doubling bifurcations as intuitively the dynamic bifurcation of the laser state could easily damage the binding between the solitons. In our experiment a dispersion-managed laser cavity was used. The purpose of using a dispersion-managed cavity is to possibly make the energy of the formed solitons strong, so an average strong nonlinear interaction between the pulses with the cavity components could be achieved.

6.3.5 Period Doubling of Multiple Solitons

It is well known that a passive mode-locked fiber laser can operate with multiple solitons in a cavity, and depending on the soliton interaction, the multiple solitons can either form a soliton bunch or randomly distribute with stable relative soliton separations [47]. With more than two solitons coexisting in a cavity, soliton interaction cannot be ignored. In the previous section we reported the period-doubling bifurcation of bound solitons. In that case two or more solitons coexist in the cavity. However, because the solitons are strongly coupled, the formed state of bound solitons actually behaves like a single pulse soliton. No difference in their period-doubling bifurcations was observed to those of the single pulse soliton. Different from the case of the bound solitons, the solitons are now distributed far apart in the cavity with stable relative separations. We show that even with multiple solitons coexisting in a fiber cavity, and there is obviously gain-competition between them, period-doubling bifurcation can still occur in the laser, and specifically, each soliton in the cavity experiences period-doubling bifurcation. However, the intensity variation of the individual solitons is not necessarily synchronized.

FIGURE 6.9
(a) Oscilloscope trace and (b) optical spectrum of a period-one state of the randomly distributed multiple solitons (four solitons in the cavity).

Figure 6.9 shows, for example, a typical state of the multiple soliton operation observed in a fiber laser. The laser has a cavity round-trip time of about 38 ns. It is to see that four solitons coexist in the cavity and locate far apart from each other. In the case of current soliton operation, all solitons have the same pulse height in the oscilloscope trace, indicating that after every cavity round-trip the energy of each soliton returns to its previous value. Such a multiple soliton operation has also been reported by other authors, which is a typical case of the conventional soliton fiber laser operation [6]. Changing the orientation of one of the waveplates in the laser cavity, which corresponds to shifting the linear cavity phase delay bias away from the cavity polarization switching point, and therefore increasing the formed soliton peak power [29], period-doubling bifurcation occurs in the laser. Figure 6.10 shows a case of the period-doubled state of the laser with two solitons coexisting in the cavity. Comparing with the oscilloscope trace shown in Figure 6.9, the pulse height of each soliton in the oscilloscope returns to its value after every two cavity round-trips. It is obvious that each individual soliton in the cavity experiences the period-doubling bifurcation, suggesting that each of them has the same bifurcation threshold and behaves identically in the cavity. For the sake of completeness, we have also shown in Figures 6.9b and 6.10b the corresponding optical spectrum of the solitons. As the solitons have large separations in the cavity, the spectrum of the multiple solitons is the same as that of the single soliton. Again it is to see that after the period-doubling bifurcation, extra spectral structures appear on the soliton spectrum, indicating the existence of dynamical sideband generation [18].

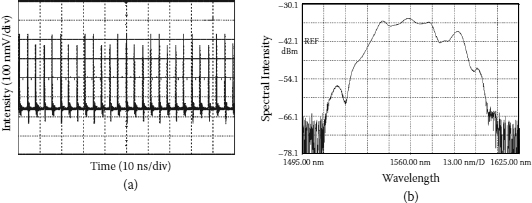
FIGURE 6.10
(a) Oscilloscope trace and (b) optical spectrum of a period-doubled multiple-soliton state (two solitons in the cavity).

As there are only two solitons in the cavity, it is difficult to judge from the oscilloscope trace whether the intensity variations of the solitons are synchronized or not. To clarify, we show in Figure 6.11a another period-doubled state of the multiple solitons, where six pulses randomly scattered in the cavity. Again after the period-doubling bifurcation, the period of each pulse in the cavity becomes doubled, but it is now clear to see that the intensity variation of the pulses is not all synchronized. In the same cavity round-trip some pulses are in their high-power state while the others are in their low-power state. Note that one pulse in the oscilloscope trace has significantly larger pulse height than the others. It is actually due to that two solitons are too close in the cavity that our detector cannot resolve them. Therefore, in the oscilloscope trace they appear as one pulse. It is to point out that due to the opposite intensity variation of the two solitons in the current state, the total pulse height of them in the oscilloscope exhibits no change. It is only an experimental artificial appearance. In the experiment we also obtained a state as shown in Figure 6.11b, where the strong pulse in the oscilloscope trace also exhibits period doubling, indicating that the two solitons that form the pulse have synchronized intensity variation. Using the commercial autocorrelator, we measured the soliton pulse width of our laser, which is about 1.54 ps if a Gaussian pulse shape is assumed.

FIGURE 6.11
Oscilloscope traces of period-doubled multiple-soliton states. (The higher pulses with nearly twice intensity are caused by two closely spaced solitons.): (a) period doubling under moderate intensity excitation, (b) period doubling with high intensity.

It was shown that even under the existence of multiple solitons in the cavity the laser still can experience period-doubling bifurcation. In particular, each soliton in the cavity exhibits the same period-doubling bifurcation. However, the detailed intensity variation of the solitons could be unsynchronized, indicating that their period doubling is actually not related.

6.3.6 Period Doubling of Dispersion-Managed Solitons at around Zero Cavity Dispersion

Although a dispersion-managed cavity consists of fibers with either positive or negative dispersion, and on average the pulse peak power is lower than that of the pulses formed in the equivalent uniform dispersion cavity, as far as the net cavity GVD is negative and large, conventional solitary waves (solitons with clear sidebands) could still be formed in the lasers. Furthermore, in the regime of near-zero net cavity GVD a different type of solitary wave known as the dispersion-managed solitons [48] could also be formed. Comparing with the conventional solitons formed in a laser, the dispersion-managed solitons are characterized by that their optical spectra have a Gaussian profile without spectral sidebands. Dispersion-managed solitons in the fiber transmission lines have been extensively investigated [48–53]. It was shown that such a soliton could even exist in a system with positive near-zero net GVD [49–52].

It is well known that cavity dispersion is wavelength related, and the central wavelength of the mode-locked pulses shifts with the experimental conditions. It is difficult to accurately determine the net cavity dispersion under various laser mode-locking states. However, one can roughly estimate the dispersion of a laser cavity by simply accumulating the dispersion of each cavity component, and then fine-tune it through cutting back the single mode fiber (SMF) length.

We also investigated the period-doubling bifurcation of the dispersion-managed solitons. After having obtained a uniform dispersion-managed soliton pulse train as shown in Figure 6.12a, we then carefully tuned one of the waveplates to the direction that causes the pulse peak power to increase while keeping all other laser parameters unchanged. Physically this action corresponds to shift the linear cavity phase delay bias to the direction that causes the peak power of the optical pulse to be clamped at a higher level by the cavity [14]. To a certain level of the pulse peak power, it was observed that the dispersion-managed solitons exhibited period-doubling bifurcation as shown in Figure 6.12b. Obviously, in a Period 2 state the pulse intensity returned to its original value by every two cavity round-trips. Figure 6.13b shows the optical spectrum of the dispersion-managed solitons corresponding to Figure 6.12b. The fundamental repetition rate of the laser is 21.3 MHz. Limited by the resolution of our autocorrelator, the autocorrelation trace measured under a period-doubled state has no obvious difference to that of the uniform soliton pulse train. However, the optical spectrum of the state shows clear modulation as compared with that of the Period 1 state (Figure 6.13a). The measured optical spectrum is an average of the pulse spectra. As in the period-doubled state the laser emits alternately between two mode-locked pulse states, it is expected that the resultant spectrum is different from that of the Period 1 state. Monitored by a high-speed sampling oscilloscope, we confirmed experimentally that in the state shown there is only one soliton pulse propagating in the cavity.

FIGURE 6.12
Oscilloscope traces of the dispersion-managed solitons: (a) Period 1 state and (b) period-doubled state.

FIGURE 6.13
Dispersion-managed solitons of the laser: (a) optical spectrum of the Period 1 state and (b) optical spectrum of the period-doubled state.

Figure 6.14 further shows the RF spectra of the laser outputs. Obviously, in the period-doubled state a new frequency component appears at half of the cavity repetition rate, while there is no such frequency component in the case of the Period 1 state.

6.3.7 Period Doubling of Gain-Guided Solitons in Fiber Lasers with Large Net Normal Dispersion

Although dynamics of the lasers with large positive cavity dispersion is still determined by the extended GLE, the formed soliton pulses in these lasers have distinct features from those of the solitons formed in lasers with negative cavity dispersion. While the solitons formed in the latter are dominantly a result of the balanced interaction between the cavity negative dispersion and the fiber nonlinear Kerr effect, the solitons formed in lasers with positive cavity dispersion are due to the spectral filtering of the limited gain bandwidth and the cavity nonlinearity. To highlight their differences solitons formed in fiber lasers with positive cavity dispersion were also called gain-guided solitons (GGSs) [54]. The GGSs belong to the family of dissipative solitons [55]. They are a localized, stable chirped nonlinear wave. It was found that the GGSs could also exhibit deterministic dynamics despite the fact that GGSs have large chirp and broad pulse width.

FIGURE 6.14
Radio-frequency spectrum of the dispersion-managed solitons: (a) Period 1 state and (b) period-doubled state.

GGSs are characterized by their steep spectral edges and pump-power-dependent spectral bandwidth. They could be easily obtained in a mode-locked fiber laser with large positive cavity dispersion. To observe period-doubling bifurcation of GGSs, one starts from a stable GGS operation state. If the saturable absorption strength of the cavity is gradually increased, this could be done through shifting the linear cavity phase delay bias away from the polarization switching point [29] of the laser, the peak power of the mode-locked pulses increases. Note that accompanying the increase of the saturable absorption strength, the pump power should also be carefully increased in order to maintain the stable GGS operation. To a certain point of the pulse peak power it could be observed that some spectral spikes suddenly appear on the long wavelength side of the soliton spectrum as shown in Figure 6.15a. However, the appearance of the soliton spikes does not affect the stable GGS operation. Figures 6.15b and 6.15c show the oscilloscope trace and the RF spectrum measured immediately after the appearance of the spectral spikes. Obviously, the laser still emitted uniform pulses. The laser cavity length was about 4.5 m, which matched the soliton repetition rate of 44.8 MHz shown in Figure 6.15c. Based on autocorrelation measurements, the GGSs of the laser have pulse duration of about 3.18 ps if a Gaussian pulse profile is assumed. After the spectral spikes are obtained, if the pump power is further increased but with all other laser operation conditions fixed, a period-doubling bifurcation of the GGS is then observed, as shown in Figures 6.15d through 6.15f. Associated with the period-doubling bifurcation, more spectral spikes appear on the soliton spectrum (Figure 6.15d). The period doubling of the soliton is clearly visible on the oscilloscope trace, where after every two cavity round-trips the pulse energy returned, and on the RF spectrum, where a new spectral component appears at the position of half-cavity fundamental repetition frequency. The above process is stable and repeatable in a laser. Nevertheless, in our experiments no further period-doubling bifurcation but a noise-like state was observed when the pump power was further increased.

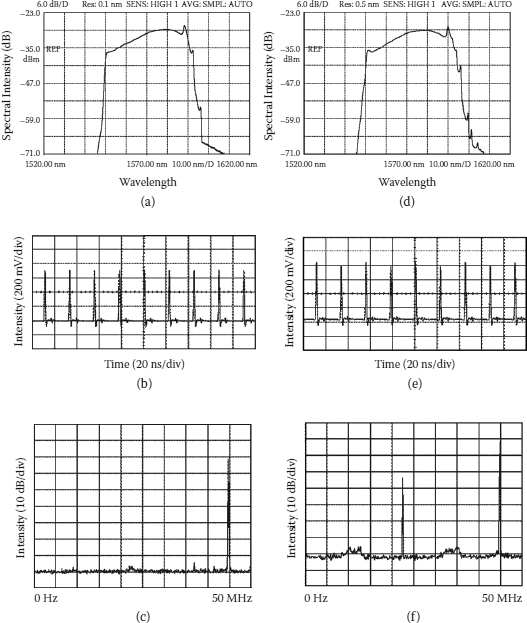
FIGURE 6.15
Period 1 doubling of gain-guided solitons in the laser: (a,d) optical spectrum, (b,e) oscilloscope trace, and (c,f) radio frequency (RF) spectrum.

6.3.8 Period Doubling of Vector Solitons in a Fiber Laser

A characteristic of the NPR mode-locked fiber lasers is that a polarizer is inserted in the laser cavity for the generation of an artificial saturable absorption effect in the cavity [56]. As the intracavity polarizer fixes light polarization at the cavity position, solitons formed in the lasers are considered as scalar solitons.

Due to technical limitation in fabricating perfectly circular cross-sectional core fibers and random mechanical stresses, in practice a single-mode fiber always supports two polarization eigenmodes, or in other words, possesses weak birefringence. It has been shown that without a polarizer in the cavity, solitons formed in a fiber laser could exhibit complicated polarization dynamics. S. T. Cundiff et al. demonstrated the formation of vector solitons in a fiber laser mode locked with a semiconductor saturable absorber mirror (SESAM) [57]. A vector soliton differs from a scalar soliton in that it consists of two orthogonal polarization components, and the two polarization components are nonlinearly coupled. Depending on the features of their coupling there are different types of vector solitons, the Polarization–locked vector solitons (PLVSs), the group velocity locked vector solitons (GVLVSs), and the polarization rotating vector solitons.

A vector soliton fiber laser can also exhibit deterministic dynamics. Using a similar cavity configuration as reported in [58], we have first experimentally observed period-doubling bifurcation of a vector soliton fiber laser. Briefly, the vector soliton fiber laser has a ring cavity with a length of about 9.40 m, which consists of 2.63 m erbium-doped fiber (StockerYale EDF-1480-T6) and all other fibers used are the standard single-mode fibers (SMFs). With the help of a three-port polarization independent circulator, an SESAM is introduced in the ring cavity of the laser. A 1480 nm Raman fiber laser with maximum output of 220 mW is used to pump the laser. The backward pump scheme is adopted to avoid the CW overdriving of the SESAM by the residual pump strength. The laser outputs through a 10% fiber coupler. A fiber-based polarization controller is inserted in the cavity to control the cavity birefringence. The SESAM used has a saturable absorption of 8%, and a recovery time of 2 ps.

As no explicit polarization discrimination components are used in the cavity, and all the fibers used have weak birefringence, vector solitons are easily obtained in the laser by simply increasing the pump power above the mode-locking threshold. Determined by the detailed laser operation conditions, various types of vector solitons, such as the PLVS, incoherently coupled vector soliton, and polarization rotating vector solitons are obtained in the fiber laser. In particular, it is found that the polarization rotation of the formed polarization rotating vector solitons could be locked to the laser cavity round-trip time or a multiple of it [58].

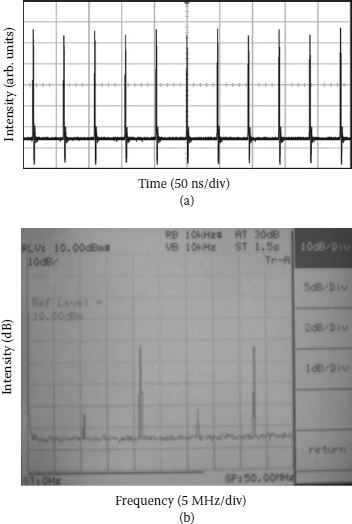
FIGURE 6.16
The (a) oscilloscope trace and (b) corresponding radio-frequency spectrum of direct intensity period doubling.

In the parameter regime of a polarization rotation locked vector soliton, a state of the period-doubling of the vector solitons, as shown in Figure 6.16a, is also observed. The vector soliton output of the fiber laser is directly monitored by a photodetector with 2 GHz bandwidth. Although the pulse intensity difference between two adjacent cavity round-trips is weak, intensity period-doubling of the soliton pulse train is evident. The RF spectrum of the laser emission is also measured, as shown in Figure 6.16b. A weak but clearly visible frequency component appears at the position of half of the cavity fundamental repetition frequency. Measured after passing through an external polarizer, a polarization rotation state with polarization rotation locked to twice of the cavity round-trip time would have the same result as shown in Figure 6.16. However, such a state is not a period-doubled state as the pulse intensity alternation observed on the oscilloscope trace is due to the polarization rotation of the vector soliton. The period doubling shown in Figure 6.16 is formed due to the intrinsic dynamic feature of the laser.

FIGURE 6.17
Period doubling of multiple vector solitons: (a) two vector solitons and (b) eight vector solitons.

After the period-doubling state is achieved, keeping all other laser operation parameters fixed but increasing the pump power the number of vector solitons circulating in the cavity increases. The new vector solitons generated exhibit the same period-doubling feature. Figures 6.17a and 6.17b show, for example, the cases where two vector solitons and eight vector solitons coexist in the cavity, respectively. Period-doubling of the vector solitons can be clearly identified. Decreasing pump power reduces the number of vector solitons in the cavity. Varying pump power could also change the soliton pulse intensity within a small range. However, no Period 1 state could be obtained by simply decreasing the pump power. Period 1 state could be obtained only if the cavity birefringence is changed. Similarly, after a Period 1 state is obtained, the period-doubling state could not be obtained by simply increasing the pump strength. Experimentally it is found that in a period-doubled state the polarization rotation of the vector solitons is locked to twice that of the cavity round-trip time.

6.4 Numerical Simulations on the Soliton Deterministic Dynamics in Fiber Lasers

6.4.1 Round-Trip Model of the Soliton Fiber Lasers

The soliton propagation in a fiber laser is characterized by the soliton circulation in the nonlinear ring cavity and the periodical interaction with the cavity components. Therefore, in order to simulate the soliton dynamics, in particular to gain an insight into the deterministic dynamics of the various types of solitons in the mode-locked fiber lasers, a round-trip model is used to simulate the soliton evolution in the lasers. Concretely, we start a simulation with an arbitrarily small light pulse and let it circulate in the cavity. We follow the pulse circulation in the laser cavity. Whenever the pulse encounters a discrete cavity component, for example, the cavity output coupler, the action of the cavity component on the light pulse is considered by multiplying the transfer-matrix of the discrete cavity component to the pulse. The pulse propagation in the fiber segments of the cavity is described by Equation (6.1). After one round of circulation in the cavity, the result of the previous round of calculation is then used as the input of the next round of calculation until a steady state is reached, which is denoted as a stable soliton state of the laser.

The round-trip model has several advantages. The calculation is made following the pulse propagation in the cavity. Therefore, the detailed pulse evolution within one cavity round-trip can be studied. Within each step of calculation the pulse’s variation is always small, even if the change of a pulse within one cavity round-trip is big. As there is no limitation on the pulse change within one cavity round-trip, dynamical process of soliton evolution, such as the process of new soliton generation in the cavity, soliton interaction, soliton collapse, and so forth can be investigated. In addition, the effect of discrete cavity components on the soliton, the influence of the dispersive waves, and the different order of the cavity components on the soliton property are automatically included in the calculation.

The soliton operation of a fiber laser is simulated using exactly the laser cavity parameters whenever they are known. Numerically we found that independent of the concrete laser cavity design, as far as the intensity of the formed soliton is strong, soliton quasi-periodicity and period-doubling bifurcations could always be obtained. Under certain laser designs, soliton intermittency could also be numerically observed. Nevertheless, in order to obtain a full period-doubling route to chaos, the cavity parameters such as the fiber dispersion and fiber lengths must be appropriately selected.

6.4.2 Deterministic Dynamics of Solitons in Different Fiber Lasers

Based on the round-trip model the soliton operation of the passive mode-locked fiber ring lasers mode locked with the nonlinear polarization rotation technique were numerically simulated. Properties of the soliton pulses formed in the lasers, influence of different laser cavity parameters on the soliton properties, as well as the intrinsic laser cavity effect on the soliton operation were numerically studied. In all of the numerical simulations, if it is not explicitly pointed out, the same simulation parameters as the following were used. The fiber nonlinearity: γ = 3 W^–1m^–1; fiber dispersion: –12.8 ps²/km for the erbium-doped fiber, –23 ps²/km for the single-mode fiber, –2.6 ps²/km for the dispersion-shifted fiber; fiber beat length: L_b = L/2; the orientation of the intracavity polarizer to the fiber fast birefringent axis: Ψ = 0.152π; gain saturation energy: E_sat = 300 pJ; gain bandwidth: Ω_g = 16 nm; laser cavity length: L = 6 m, and the orientations of the polarizer and the analyzer with the fast axis of the birefringent fiber: θ = π/8 and φ = π/2 + π/8.

6.4.3 Period-Doubling Route to Chaos of the Single-Pulse Solitons

Through properly choosing the linear cavity phase delay bias, which corresponds in the experiment to appropriately selecting the orientations of the polarization controllers, soliton operation can always be obtained in our simulations. With a fixed linear cavity phase delay bias but different values of gain, as long as the generated peak power of the soliton pulse is weaker than that of the polarization switching power of the cavity [29], a stable uniform soliton pulse train can always be obtained. Figure 6.18a shows the soliton profiles of the laser under different gain coefficients when the linear cavity phase delay bias is fixed at δϕ = 1.2π. Figure 6.18b is the corresponding soliton spectra. The exact soliton parameters, such as the pulse width and peak power, are determined by the laser parameter settings and the laser operation condition such as the gain value. Under a larger pump power the solitons generated have higher peak power and narrower pulse width. With the current linear cavity phase delay bias selection, the nonlinear polarization switching (NPS) threshold of the cavity is low. Therefore, the maximum peak power of the solitons reachable is clamped by the nonlinear polarization switching effect. Once the soliton peak is clamped, further increasing the gain, instead of further increasing the soliton peak power, a new soliton is generated, and consequently a multiple soliton operation state of the laser can be obtained. As a laser operating in the state has weak linear cavity loss, mode locking can be easily achieved. Therefore, in practice a laser will always start the soliton operation from the state. However, our numerical simulations show that no soliton period-doubling bifurcation could occur at such a linear cavity phase delay bias as the soliton peak power is weak.

FIGURE 6.18
Soliton profiles (a) and the corresponding optical spectra (b) when the linear cavity phase delay bias is set as δϕ = 1.2π.

When the linear cavity phase delay bias is chosen as δϕ = 1.6π, which corresponds to lifting the nonlinear polarization switching threshold of the cavity higher so that the soliton pulse formed could have higher peak power, stable soliton operation can still be obtained. As now the soliton peak power can reach a very high value under strong pumping, it is observed that when the peak power of the soliton increases to a certain value, period-doubling bifurcations and period-doubling route to chaos of the solitons as observed in the experiments automatically appear. Figure 6.19 shows, for example, a numerically calculated period-doubling route to chaos of a laser. When the gain coefficient was set at G = 800, a stable and uniform high-intensity soliton train is obtained (Figure 6.19a). Increasing the value of G and keeping all the other parameters fixed, the soliton repetition period in the cavity is then doubled at G = 850 (Figure 6.19b). At G = 902 it doubles again (Figure 6.19c) and further doubles at G = 908 (Figure 6.19d). Eventually the soliton repetition in the laser becomes chaotic (Figure 6.19e). Figures 6.19f through 6.19j show the corresponding optical spectra of the solitons in Figures 6.19a through 6.19e. Associated with the soliton intensity variation the soliton spectrum also exhibits period-doubling changes. Figure 6.20 further shows the soliton spectral variation within one period of the Period 4 state. In this state after every four cavity round-trips the soliton intensity and profile return to the original value and shape. From Figure 6.20, see that the soliton spectrum in each round-trip is different. Corresponding to the soliton of the highest peak power, the soliton spectrum (Figure 6.20a) also exhibits the strongest sidebands and spectral modulations, indicating the existence of strong nonlinear self-phase modulation (SPM) on the pulse. The change from one soliton operation state to the other is abrupt. At the bifurcation point when the gain coefficient is slightly increased, the soliton quickly jumps to another state with the doubled periodicity, exhibiting the universal characteristic of the period-doubling bifurcation and route to chaos of the nonlinear dynamics systems.

The appearance of the period-doubling bifurcation is independent of the concrete laser cavity design. Under different cavity parameter settings, as far as the soliton peak power is unlimited by the nonlinear polarization switching effect of the cavity, we could always obtain the phenomenon in our simulations. Even the period-doubling route to chaos of a Period 3 state, which in terms of the nonlinear dynamics theory is known as a periodic window within the chaotic regime, has also been numerically revealed. However, it is to point out that due to the coexistence of other effects in the laser, for example, the soliton peak nonuniformity [35] and soliton collapse [59], in order to obtain a full period-doubling route to chaos in a laser, the cavity parameters must be appropriately selected. In some of our numerical simulations frequently only certain period-doubling bifurcations, for example, the Period 1 to Period 2 bifurcation and then to chaos, or the Period 1 to chaotic state, could be obtained. If the linear cavity phase delay bias is not set large enough, the nonlinear polarization switching effect could also limit the peak power of the solitons. Consequently, only bifurcations to a certain periodic state, for example, the Period 4 state, could be reached. Further increase of the gain would cause the generation of a new soliton rather than the further bifurcation to chaos, which clearly shows the direct relation of the period-doubling bifurcation to the soliton peak power.

FIGURE 6.19
Soliton pulse evolution and the corresponding optical spectra numerically calculated under different pump strengths. The linear cavity phase delay bias is set as df = 1.6π. (a,f) Period 1 soliton state, G = 800; (b,g) Period 2 soliton state, G = 850; (c,h) Period 4 soliton state, G = 902; (d,i) Period 8 soliton state, G = 908; (e,j) chaotic soliton state, G = 915.

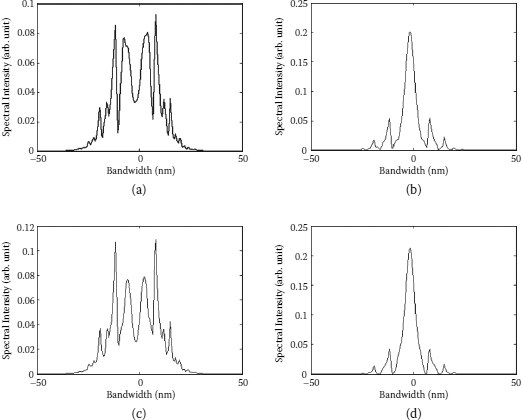
FIGURE 6.20
Soliton spectral variation within one Period 4 state [soliton evolves from (a) to (d)].

Previous studies on the synchronously pumped passive ring cavities have also revealed a period-doubling cascade to chaos in the sequence of pulses emerging from the cavities [60,61]. It was shown that the bifurcations and route to chaos of the system were caused by the repetitive interference between the input pulse and the pulse that has completed a round-trip in the cavity. As the pulse traveling in the cavity suffers nonlinear phase shift, which itself is pulse intensity dependent, the transmission of the cavity is a nonlinear function of the pulse intensity. It is an intrinsic property of such a nonlinear cavity that under larger nonlinear phase shift of the pulse, its output exhibits the period-doubling route to chaos [2]. We note that a similar repetitive interference process exists in the fiber soliton lasers. Due to the birefringence of the laser cavity, the pulse propagation in the laser actually includes two orthogonal polarization components. Although there are nonlinear couplings between the two orthogonally polarized pulses as can be seen from Equation (6.1), after one round-trip they experience different linear and nonlinear phase shifts. The interference between them at the intracavity polarizer results in that the effective cavity transmission is a nonlinear function of the soliton intensity. Based on the studies on the synchronously pumped passive ring cavities, it is therefore to imagine that under strong soliton peak intensity, the period-doubling bifurcation and route to chaos could also appear in the lasers. Our numerical simulation shows that the effect could only occur in the fiber lasers when the linear cavity phase delay bias is set away from the nonlinear polarization switching point. In this case the soliton peak power is unclamped by the cavity and can increase to a very high value with the increase of the pump strength. A high soliton peak power generates a large nonlinear phase shift difference between the two polarization components, which causes the intrinsic instability of the system.

In order to obtain a full route to chaos, the cavity parameters such as the fiber dispersion and fiber lengths must be appropriately selected. In one of our numerical simulations even the period-doubling route to chaos of a Period 3 state, which in the nonlinear dynamics theory is known as a periodic window within the chaotic regime, was also obtained as shown in Figure 6.21.

6.4.4 Period-Doubling Route to Chaos of the Bound Solitons

Period-doubling bifurcations and route to chaos have also been numerically revealed for the bound solitons. Figure 6.22 shows, for example, one of such results obtained. In calculating the state we used the same laser parameters as those for obtaining the single-pulse soliton period-doubling route to chaos, only the pump strength and initial state are different. Figure 6.22a shows that two solitons coexist in the cavity and bind together. Note that due to the close separation between the solitons, their optical spectra have strong intensity modulations, but from round to round the modulation patterns do not change, which indicates that the phase difference between the solitons is fixed as well. The binding nature of the solitons is represented by the fixed soliton separation and phase difference even under the existence of soliton interaction between them. Increasing pump strength from the state of Figure 6.22a, both solitons experience simultaneously period-doubling bifurcations and route to chaos. Associated with the soliton period doubling, the soliton separation between the bound solitons also changes slightly. However, after the period-doubling bifurcation the soliton separation then remains constant again. This soliton separation change suggests that the dynamic bifurcation of the system could affect the soliton interaction.

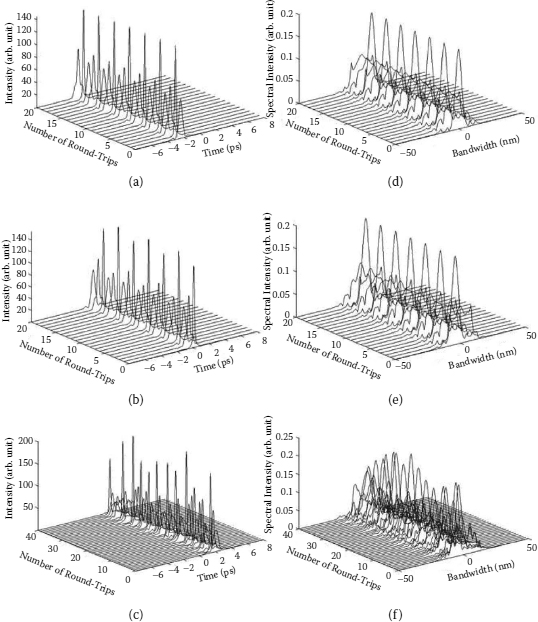
FIGURE 6.21
Soliton profiles and corresponding optical spectra numerically calculated. (a,d) State of Period 3, G = 730; (b,e) state of Period 6, G = 735; (c,f) chaotic state, G = 750.

6.4.5 Period Doubling of Multiple Solitons

As shown previously, multiple soliton formation in the fiber lasers is a result of the cavity pulse peak clamping effect [29]. Therefore, through appropriately setting the linear cavity phase delay bias and the pumping strength, randomly distributed multiple solitons can be numerically easily obtained. The maximum achievable soliton pulse peak power is also determined by the setting of the linear cavity phase delay bias. If the linear cavity phase delay bias is set too close to the cavity polarization switching point, only low peak power of the solitons could be obtained. In this case increasing the pumping strength except that the number of the solitons in the cavity will increase, no period-doubling bifurcation of the solitons could be observed. Therefore, to obtain the soliton period-doubling bifurcation it is necessary to set the linear cavity phase delay bias away from the polarization switching point. Numerically we find that with current simulation parameters only when the linear cavity phase delay bias is larger than 1.4π, the phenomenon of soliton period doubling could be achieved. In our simulation we fixed it as δφ = 1.5π. Depending on the initial state and pump strength, either synchronous or asynchronous period doubled evolutions are obtained. Figures 6.23a and 6.23b show the typical numerical results, where two solitons have a separation of 64 ps in cavity. Figure 6.23a shows that both solitons are period-doubled and have exactly the same intensity evolution with the cavity round-trips, while Figure 6.23b shows a case where the solitons have unsynchronized pulse intensity evolution with the cavity round-trips. Numerically we also obtained states of period-doubling of multiple solitons with more than two solitons and confirmed all of the experimental observations.

FIGURE 6.22
Period-doubling route to chaos of the bound solitons. (a,e) State of stable bound solitons, G = 1149; (b,f) state of Period 2 of the bound solitons, G = 1300; (c,g) state of Period 4 of the bound solitons, G = 1353; and (d,h) chaotic state of the bound solitons, G = 1358.

FIGURE 6.23
Calculated pulse intensity evolution with the cavity round-trips of the period-doubled solitons: (a) synchronous evolution and (b) asynchronous evolution.

6.4.6 Period Doubling of Dispersion-Managed Solitons

The cavity of a mode-locked fiber laser is a nonlinear cavity. Therefore, it is expected that when the intensity of the pulse circulating in the fiber ring laser has strong peak power, the laser output could exhibit similar nonlinear dynamical behaviors. Furthermore, as the occurrence of the period doubling is a property of the nonlinear laser cavity, no matter whether the pulse circulating in it is a conventional soliton or a dispersion-managed soliton, the same cavity dynamics should be observed.

Figure 6.24 shows, for example, the numerically calculated dispersion-managed soliton for the positive near-zero cavity dispersion case. The optical spectrum of the dispersion-managed soliton shown in Figure 6.24a has a Gaussian-like spectral profile and no obvious sidebands, which agrees with the experimental observation. Figure 6.24b shows the corresponding temporal pulse profile. Again it is closer to the Gaussian shape than the sech² form. Our numerical results clearly show that the dispersion-managed soliton could be formed in lasers with positive near-zero cavity dispersion just as experimentally observed.

After a Gaussian-like stable uniform pulse train is obtained, with all the other simulation parameters fixed but the small signal gain coefficient is increased, a period-doubled state as shown in Figure 6.24c is then observed, which shows that, like the conventional solitons, the dispersion-managed solitons can experience the period-doubling bifurcation as well. With our current laser cavity design only a Period 2 state could be obtained. If the pump strength is further increased, a new dispersion-managed soliton is generated instead of a further period-doubling of the pulse [62]. Similar results were also obtained when the net cavity dispersion is set negative near zero or zero.

6.4.7 Period Doubling of the Gain-Guided Solitons

The period-doubling bifurcation of the GGSs could also be numerically simulated. Figure 6.25 shows, for example, a numerically calculated period doubling of a GGS when the pump strength was selected as G = 4300. Figure 6.25a shows the evolution of the calculated GGS with the cavity round-trips. Period doubling of the pulse is evidenced by the pulse returning to its previous parameters at every two cavity round-trips. Figure 6.25b shows the optical spectra of the soliton in two adjacent round-trips and the averaged one. Clear differences between them are visible. However, no obvious spectral spikes were obtained. We believe the absence of the spectral spikes could be caused by the parabolic gain profile approximation used in our simulations. From the experimental results the spikes appeared only on the edges of the spectrum, but where the parabolic gain profile artificially introduced large losses. Nevertheless, the numerical simulations have reasonably reproduced the essential features of the soliton period-doubling bifurcation (e.g., the simulated spectra have a flat and smooth top, and the spectral variations between the Period 1 and period-doubled states only occur on the edges of the spectrum, which are in agreement with the experimental observations and different from those of the soliton period doubling observed in fiber lasers of negative cavity dispersion) [13].

Figure 6.26 shows a comparison between the evolutions of the GGSs in cavity before and after the period-doubling bifurcation was numerically calculated. Figures 6.26a and 6.26b show the pulse evolution in the time domain along the cavity; Figures 6.26c and 6.26d show the corresponding pulse width variation along the cavity; Figures 6.26e and 6.26f show the evolution of the pulse spectrum corresponding to Figures 6.26a and 6.26b, respectively. We note that Figure 6.26 has shown pulse evolution in two cavity round-trips in order to display the period-doubling effect. With all other parameters fixed, the Period 1 state could be obtained in a large pump strength range. In a Period 1 state the chirped GGS is compressed in the SMF segments. The stronger the pump strength, the larger is the chirp accumulated in the EDF, and consequently, narrower pulse and higher pulse peak power is obtained in the SMF. After that the pulse peak power is beyond a certain value, period doubling of the pulse occurs. Numerically we found that in a period-doubled state, the GGS may be dechirped to a transform-limited pulse in the SMF, and remain the shortest pulse width until entering the EDF as shown in Figure 6.26d. However, a pedestal also associates with the compressed pulse, which could be understood as a result of the pulse breaking.

FIGURE 6.24
Numerical simulations of the dispersion-managed soliton in the positive near-zero net cavity group velocity dispersion regime: (a) optical spectrum and (b) temporal profile of a dispersion-managed soliton: small signal gain coefficient g₀ = 520; (c) a period-doubled state: small signal gain coefficient g₀ = 550.

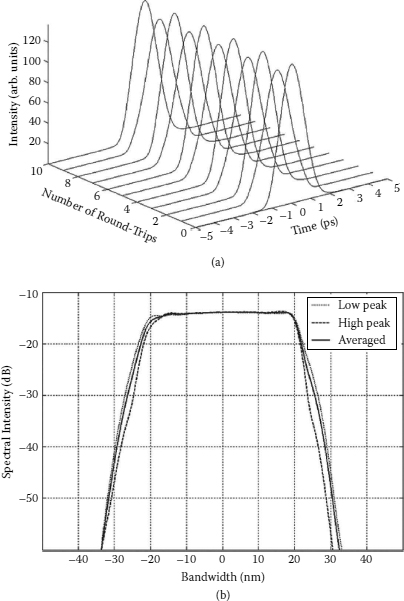
FIGURE 6.25
Period doubling of the gain-guided solitons numerically calculated. (a) Soliton evolution with the cavity round-trips. (b) Optical spectra of the soliton in two adjacent round-trips and their average.

FIGURE 6.26
Comparison between the soliton evolutions in cavity before and after the period-doubling bifurcation. (a,b) Pulse evolution in time domain; (c,d) pulse width evolution; and (e,f) optical spectrum evolution in double cavity length.

6.4.8 Period Doubling of Vector Solitons

Due to the existence of a polarizer in the cavity, which fixes the polarization of light in the position of the cavity, solitons formed in fiber lasers mode locked with the NPR technique are considered as scalar solitons. In fiber lasers if there are no polarization-dependent components in the cavity, vector solitons could be formed. The formed vector solitons have two coupled orthogonal polarization components. Numerical simulations have shown that the vector solitons can also exhibit period-doubling bifurcations as observed in the experiments.

Similarly, in the experiments where in order to obtain vector soliton operation of a fiber laser instead of the NPR mode locking but a polarization-insensitive SESAM was used, to numerically simulate the features of vector solitons formed in a fiber laser, the effect of a real saturable absorber is considered. Figure 6.27 shows the results of simulations obtained under different net cavity birefringence but the same other laser parameters. Numerically it is found that when the cavity birefringence is selected as L_b = L/0.4, where L is the cavity length, a Period 1 vector soliton state is obtained. When the cavity birefringence is selected as L_b = L/0.09, a period-doubled vector soliton is then obtained. Figures 6.27a and 6.27b show the calculated vector soliton evolution with the cavity round-trips. The soliton period-doubling of the state shown in Figure 6.27a in comparison with that shown in Figure 6.27b is evident. Figure 6.27c/Figure 6.27e, and Figure 6.27d/Figure 6.27f show further the evolution of the vector soliton components, of the period-doubled vector soliton and the period-one vector soliton, respectively. Each component of the period-doubled vector soliton also exhibits period doubling. However, the pulse intensity variation between the two orthogonal polarization components is antiphase. It is because of this antiphase pulse intensity evolution of the period-doubled vector soliton, only a weak period-doubling could be observed on the vector soliton intensity evolution, as shown in Figure 6.27a. The result agrees with our experimental observations of Figure 6.16a.

6.4.9 Cavity-Induced Soliton Modulation Instability Effect

Modulation instability (MI) is a well-known phenomenon that destabilizes strong CW propagation in dispersive media. In optics, Tai et al. first reported the experimental observation of MI in light propagation in single-mode fibers [63]. They found that MI is physically a special case of four-wave mixing where the phase-matching condition is self-generated by the nonlinear refractive index change and the anomalous dispersion of the fibers. Soliton propagation in single-mode fibers is intrinsically stable against MI. However, it was theoretically shown that if dispersion of a fiber is periodically varied or the intensity of a solitary wave is periodically modulated, MI of solitons could still occur [64,65]. MI establishes resonant energy exchange between the soliton and dispersive waves, which results in a new type of spectral sideband generation on the soliton spectrum. Soliton propagation in a laser cavity experiences periodically fiber dispersion and soliton energy variations. It is to be expected that under certain conditions such a soliton MI could appear.

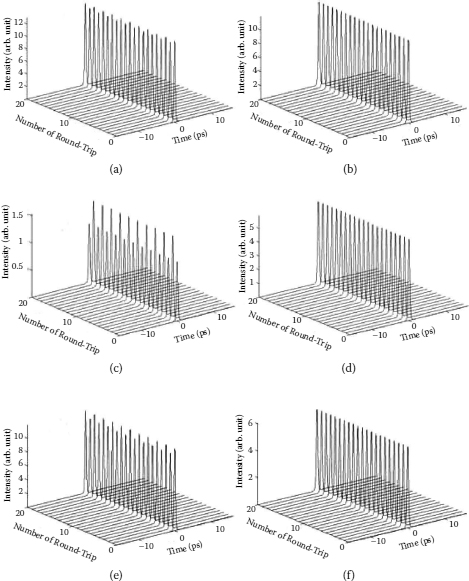
FIGURE 6.27
Numerically simulated results of period-doubling/Period 1 of (a,b) the vector soliton, (c,d) the vector soliton along the horizontal birefringent axis, and (e,f) the vector soliton along the vertical birefringent axis with the cavity round-trips.

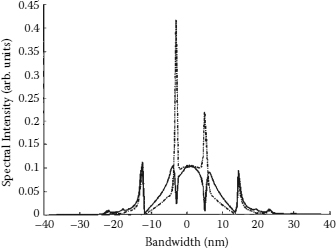
FIGURE 6.28
Comparison between soliton spectra of adjacent round-trips in the Period 2 state.

We point out that MI is an intrinsic feature of the solitons formed in a laser. The development of MI leads to strong resonant wave coupling between the soliton and dispersive waves, which further leads to the dynamic instability of the soliton. We believe that it is the dynamic instability of a soliton that ultimately limits the performance of a soliton laser. MI of a soliton in lasers is characterized by the formation of a new set of spectral sidebands on the soliton spectrum.

Figure 6.28 shows a case of the soliton spectra numerically calculated for a Period 2 soliton state. In the soliton Period 1 state the soliton spectrum has only the Kelly sidebands. The Kelly sidebands are generated by the constructive interference between the soliton and the dispersion waves in the cavity, whose positions are almost fixed for a fiber laser once its cavity parameters are fixed. We note that the formation of Kelly sidebands is a linear effect. However, after the soliton experienced a period-doubling bifurcation, it is observed that apart from the Kelly sidebands a new set of spectral sidebands also appears on the soliton spectrum. Positions of the new spectral sidebands vary with the laser cavity detuning. At certain particular cavity detuning settings, or when the new sidebands appear at certain positions on the soliton spectrum, the soliton period-doubling bifurcation occurs, while at the other positions the soliton quasi-periodicity effect is observed. Carefully checking the soliton spectral evolution within one cavity round-trip, it is further identified that in a soliton Period 2 state, while in one cavity round-trip the new sideband is a spectral spike, in the subsequent cavity round-trip the new spectrum will become a spectral dip, and vice versa, which indicates that the new spectral sidebands are formed due to a parametric wave interaction process.

FIGURE 6.29
Comparison between soliton spectra of adjacent round-trips in the Period 3 state.

Figure 6.29 shows a comparison between the soliton spectra of the adjacent cavity round-trips of a Period 3 state. Due to that the soliton period in the state is three cavity lengths the variation of the extra sidebands between two adjacent round-trips is not exactly opposite, but 2π/3 out of phase.

Based on the new spectral sideband formation and their relation to the observed soliton dynamics, we speculate that the appearance of the deterministic soliton dynamics is related to the cavity-induced soliton modulation instability. Independent of the cavity dispersion, soliton propagation in the cavity experiences a periodic intensity variation, which causes a phase matching of the soliton with certain particular frequencies of weak light or dispersive waves. Energy exchange between the soliton pulse and the phase-matched dispersive waves could be built up. When the phase difference between the soliton and the dispersive waves within one cavity round-trip is 2π, then a soliton Period 2 state is formed. As energy exchange between the soliton and weak light depends on their phase difference, within half of the period energy flows from the soliton to the dispersive waves, while in the other half period it then flows reversely, resulting in a soliton Period 2 state. In the case that the phase difference between the soliton and dispersive waves is not a multiple of 2π but an arbitrary value, the quasi-periodicity state occurs. This could be why the quasi-periodic soliton operation state could be experimentally easily observed, while the period-doubling and period-doubling route to chaos could only be observed under certain special laser conditions.

6.5 Conclusions

In conclusion, we investigated both experimentally and numerically the deterministic dynamics of solitons formed in passive mode-locked fiber lasers. We have shown experimentally that under strong soliton strength, deterministic soliton dynamics, these are the soliton period-doubling bifurcations and soliton period-doubling route to chaos, could appear. In particular, the deterministic soliton dynamics is independent of the number of solitons in the cavity and the types of soliton formed. We observed the period-doubling route to chaos on the soliton repetition rate of both the single pulse soliton and the bound solitons; on the conventional solitons formed in anomalous dispersion cavity fiber lasers, or on the dispersion-managed solitons generated in around net zero dispersion fiber lasers, or on the gain-guided solitons generated in normal dispersion fiber lasers. Period doubling of vector solitons was also experimentally observed. Based on the coupled extended GLEs and the round-trip model, we numerically simulated the soliton operation of various fiber lasers and successfully reproduced all the observed soliton deterministic dynamics experimentally observed. Moreover, based on results of both experimental studies and numerical simulations, we found that the appearance of these soliton dynamics could be related to the cavity-induced soliton modulation instability effect. We speculate that the cavity-induced modulation instability is also responsible for the deterministic dynamics of the nonlinear cavity under CW operation.

References

1. K. Ikeda, Multiple-Value Stationary State and Its Instability of the Transmitted Light by a Ring Cavity System, Opt. Commun., 30, 257–261, 1979.

2. K. Ikeda, H. Daido, and O. Akimoto, Optical Turbulence: Chaotic Behavior of Transmitted Light from a Ring Cavity, Phys. Rev. Lett., 45, 709–712, 1980.

3. D. U. Noske, N. Pandit, and J. R. Taylor, Subpicosecond Soliton Pulse Formation from Self-Mode-Locked Erbium Fiber Laser Using Intensity Dependent Polarization Rotation, Electron. Lett., 28, 1391–1393, 1992.

4. V. J. Matsas, T. P. Newson, D. J. Richardson, and D. N. Payne, Self-Starting Passive Mode-Locked Fiber Ring Soliton Laser Exploiting Nonlinear Polarization Rotation, Electron. Lett., 28, 1391–1393, 1992.

5. I. N. Duling III, All-Fiber Ring Soliton Laser Mode Locked with a Nonlinear Mirror, Opt. Lett., 16, 539–541, 1991.

6. D. J. Richardson, R. I. Laming, D. N. Payne, M. W. Phillips, and V. J. Matsas, 320fs Soliton Generation with Passively Mode-Locked Erbium Fiber Laser, Electron. Lett., 27, 730–732, 1991.

7. B. C. Collings, K. Bergman, S. T. Cundiff, S. Tsuda, J. N. Kutz, J. E. Cunningham, W. Y. Jan, M. Koch, and W. H. Knox, Short Cavity Erbium/Ytterbium Fiber Lasers Mode-Locked with a Saturable Bragg Reflector, IEEE J. Select Topics in Quantum Electron., 3, 1065–1075, 1997.

8. S. Gray and A. B. Grudinin, Soliton Fiber Laser with a Hybrid Saturable Absorber, Opt. Lett., 21, 207–209, 1996.

9. D. J. Jones, H. A. Haus, and E. P. Ippen, Subpicosecond Solitons in an Actively Mode-Locked Fiber Laser, Opt. Lett., 21, 1818–1820, 1996.

10. R. P. Davey, N. Langford, and A. I. Ferguson, Interacting Solitons in Erbium Fiber Laser, Electron. Lett., 27, 1257–1259, 1991.

11. Y. P. Tong, P. M. W. French, J. R. Taylor, and J. O. Fujimoto, All-Solid-State Femtosecond Source in the Near Infrared, Opt. Commun., 136, 235–238, 1997.

12. A. M. Kowalevicz, Jr., A. Tucay Zare, F. Kartner, J. G. Fujimoto, S. Dewald, U. Morgner, V. Scheuer, and G. Angelow, Generation of 150-nJ Pulses from a Multiple-Pass Cavity Kerr-Lens Mode-Locked Ti:Al₂O₃ Oscillator, Opt. Lett., 28, 1597–1599, 2003.

13. L. M. Zhao, D. Y. Tang, F. Lin, and B. Zhao, Observation of Period-Doubling Bifurcations in a Femtosecond Fiber Soliton Laser with Dispersion Management Cavity, Opt. Express, 12, 4573–4578, 2004.

14. D. Y. Tang, L. M. Zhao, and F. Lin, Numerical Studies of Routes to Chaos in Passively Mode Locked Fiber Soliton Ring Lasers with Dispersion-Managed Cavity, Europhys. Lett., 71(1), 56–62, 2005.

15. L. M. Zhao, D. Y. Tang, and B. Zhao, Period-Doubling and Quadrupling of Bound Solitons in a Passively Mode-Locked Fiber Laser, Opt. Commun., 252, 167–172, 2005.

16. L. M. Zhao, D. Y. Tang, and A. Q. Liu, Chaotic Dynamics of a Passively Mode-Locked Soliton Fiber Ring Laser, Chaos, 16, 013128, 2006.

17. L. M. Zhao, D. Y. Tang, T. H. Cheng, and C. Lu, Period-Doubling of Multiple Solitons in a Passively Mode-Locked Fiber Laser, Opt. Commun., 273, 554–559, 2007.

18. D. Y. Tang, J. Wu, L. M. Zhao, and L. J. Qian, Dynamic Sideband Generation in Soliton Fiber Lasers, Opt. Commun., 275, 213–216, 2007.

19. L. M. Zhao, D. Y. Tang, T. H. Cheng, H. Y. Tam, C. Lu, and S. C. Wen, Period-Doubling of Dispersion-Managed Solitons in an Erbium-Doped Fiber Laser at around Zero Dispersion, Opt. Commun., 278, 428–433, 2007.

20. L. M. Zhao, D. Y. Tang, Wu, H. Zhang, Period-Doubling of Gain-Guided Solitons in Fiber Lasers of Large Net Normal Dispersion, Opt. Commun., 281, 3557–3560, 2008.

21. L. M. Zhao, D. Y. Tang, H. Zhang, X Wu, C. Lu, and H. Y. Tam, Period-Doubling of Vector Solitons in a Ring Fiber Laser, Opt. Commun., 281, 5614–5617, 2008.

22. D. Y. Tang, L. M. Zhao, Wu, and H. Zhang, Soliton Modulation Instability in Fiber Lasers, Phys. Rev. A, 80, 023806, 2009.

23. F. Ö. Ilday, F. W. Wise, and T. Sosnowski, High-Energy Femtosecond Stretched-Pulse Fiber Laser with a Nonlinear Optical Loop Mirror, Opt. Lett., 27, 1531–1533, 2002.

24. M. J. Guy, D. U. Noske, and J. R. Taylor, Generation of Femtosecond Soliton Pulses by Passive Mode Locking of an Ytterbium-Erbium Figure-of-Eight Fiber Laser, Opt. Lett., 18, 1447–1449, 1993.

25. D. Y. Tang, W. S. Man, H. Y. Tam, and M. S. Demokan, Modulational Instability in a Fiber Soliton Ring Laser Induced by Periodic Dispersion Variation, Phys. Rev. A, 61, 023804, 2000.

26. L. M. Zhao, D. Y. Tang, H. Zhang, Wu, and N. Xiang, Soliton Trapping in Fiber Lasers, Opt. Express, 16, 9528–9533, 2008.

27. C. R. Menyuk, Nonlinear Pulse Propagation in Birefringent Optical Fibers IEEE Journal of Quantum Electronics, 23, 174–176, 1987.

28. G. P. Agrawal, Nonlinear Fiber Optics, 4th ed., Academic Press, Boston, 2007.

29. D. Y. Tang, L. M. Zhao, B. Zhao, and A. Q. Liu, Mechanism of Multisoliton Formation and Soliton Energy Quantization in Passively Mode-Locked Fiber Lasers, Phys. Rev. A, 72, 043816, 2005.

30. M. Hofer, M. H. Ober, F. Haberl, and M. E. Fermann, Characterization of Ultrashort Pulse Formation in Passively Mode-Locked Fiber Lasers, IEEE J. Quantum Electron., QE-28, 720–728, 1992.

31. R. P. Davey, N. Langford, and A. I. Ferguson, Role of Polarization Rotation in the Modelocking of an Erbium Fiber Laser, Electron. Lett., 29, 758–760, 1993.

32. S. M. J. Kelly, K. Smith, K. J. Blow, and N. J. Doran, Average Soliton Dynamics of a High-Gain Erbium Fiber Laser, Opt. Lett., 16, 1337–1339, 1991.

33. A. D. Kim, J. N. Kutz, and D. J. Muraki, Pulse-Train Uniformity in Optical Fiber Lasers Passively Mode-Locked by Nonlinear Polarization Rotation, IEEE J. Quantum Electron., 36, 465–471, 2000.

34. K. M. Spaulding, D. H. Yong, A. D. Kim, and J. N. Kutz, Nonlinear Dynamics of Mode-Locking Optical Fiber Ring Lasers, J. Opt. Soc. Am. B, 19, 1045–1054, 2002.

35. B. Zhao, D. Y. Tang, L. M. Zhao, and P. Shum, Pulse-Train Nonuniformity in a Fiber Soliton Ring Laser Mode-Locked by Using the Nonlinear Polarization Rotation Technique, Phys. Rev. A, 69, 043808, 2004.

36. G. Sucha, S. R. Bolton, S. Weiss, and D. S. Chemla, Period Doubling and Quasi-Periodicity in Additive-Pulse Mode-Locked Lasers, Opt. Lett., 20, 1794–1796, 1995.

37. D. Côté and H. M. van Driel, Period Doubling of a Femtosecond Ti:Sapphire Laser by Total Mode Locking, Opt. Lett., 23, 715–717, 1998.

38. A. B. Grudinin, D. J. Richardson, and D. N. Payne, Energy Quantization in Figure Eight Fiber Laser, Electron. Lett., 28, 67–68, 1992.

39. D. J. Richardson, R. I. Laming, D. N. Payne, V. J. Matsas, and M. W. Phillips, Characterization of a Self-Starting, Passively Mode-Locked Fiber Ring Laser That Exploits Nonlinear Polarization Evolution, Electron. Lett., 27, 1451, 1991.

40. D. Y. Tang, W. S. Man, H. Y. Tam, and P. D. Drummond, Observation of Bound States of Solitons in a Passively Mode-Locked Fiber Laser, Phys. Rev. A, 64, 033814, 2001.

41. Ph. Grelu, F. Belhache, F. Gutty, and J.-M. Soto-Crespo, Soliton Pairs in a Fiber Laser: from Anomalous to Normal Average Dispersion Regime, Opt. Lett., 27, 966, 2002.

42. B. Zhao, D. Y. Tang, P. Shum, Y. D. Gong, C. Lu, W. S. Man, and H. Y. Tam, Energy Quantization of Twin-Pulse Solitons in a Passively Mode-Locked Fiber Ring Laser, Appl. Phys. B, 77, 585, 2003.

43. B. Zhao, D. Y. Tang, P. Shum, W. S. Man, H. Y. Tam, Y. D. Gong, and C. Lu, Passive Harmonic Mode Locking of Twin-Pulse Solitons in an Erbium-Doped Fiber Ring Laser, Opt. Commun., 229, 363, 2004.

44. D. Y. Tang, B. Zhao, D. Y. Shen, C. Lu, W. S. Man, and H. Y. Tam, Compound Pulse Solitons in a Fiber Ring Laser, Phys. Rev. A, 68, 013816, 2003.

45. C. O. Weiss and H. King, Oscillation Period Doubling Chaos in a Laser, 59-61, Opt. Commun., 44, 59, 1982.

46. D. Y. Tang, S. P. Ng, L. J. Qin, and L. Meng, Deterministic Chaos in a Diode-Pumped NdYAG Laser Passively Q Switched by a Cr 4+: YAG Crystal, Opt. Lett., 28, 325, 2003.

47. D. Y. Tang, B. Zhao, L. M. Zhao, and H. Y. Tam, Soliton Interaction in a Fiber Ring Laser, Phys. Rev. E, 72, 016616, 2005.

48. N. J. Smith, F. M. Knox, N. J. Doran, K. J. Blow, and I. Bennion, Enhanced Power Solitons in Optical Fibres with Periodic Dispersion Management, Electron. Lett., 32, 54–55, 1996.

49. J. H. B. Nijhof, N. J. Doran, W. Forysiak, and F. M. Knox, Stable Soliton-Like Propagation in Dispersion Managed Systems with Net Anomalous, Zero and Normal Dispersion, Electron. Lett., 33, 1726–1727, 1997.

50. J. N. Kutz and S. G. Evangelides, Jr., Dispersion-Managed Breathers with Average Normal Dispersion, Opt. Lett., 23, 685–687, 1998.

51. J. H. B. Nijhof, W. Forysiak, and N. J. Doran, Dispersion-Managed Solitons in the Normal Dispersion Regime: A Physical Interpretation, Opt. Lett., 23, 1674–1676, 1998.

52. Y. Chen and H. A. Haus, Dispersion-Managed Solitons in the Net Positive Dispersion Regime, J. Opt. Soc. Am. B, 16, 24–30, 1999.

53. V. S. Grigoryan, R. -M. Mu, G. M. Carter, and C. R. Menyuk, Experimental Demonstration of Long-Distance Dispersion-Managed Soliton Propagation at Zero Average Dispersion, IEEE Photonics Technol. Lett., 12, 45–46, 2000.

54. L. M. Zhao, D. Y. Tang, T. H. Cheng, and C. Lu, Gain-Guided Solitons in Dispersion-Managed Fiber Lasers with Large Net Cavity Dispersion, Opt. Lett., 31, 2957–2959, 2006.

55. N. Akhmediev and A. Ankiewicz (Eds.), Dissipative Solitons: Lecture Notes in Physics, V. 661, Springer, Heidelberg, 2005.

56. H. A. Haus, J. G. Fujimoto, and E. P. Ippen, Analytic Theory of Additive Pulse and Kerr Lens Mode Locking, IEEE J. Quantum Electron., 28, 2086–2096, 1992.

57. S. T. Cundiff, B. C. Collings, and W. H. Knox, Polarization Locking in an Isotropic, Modelocked Soliton Er/Yb Fiber Laser, Opt. Express, 1, 12–20, 1997.

58. L. M. Zhao, D. Y. Tang, H. Zhang, and H. Wu, Polarization Rotation Locking of Vector Solitons in a Fiber Ring Laser, Optics Express, 16 (4), 10053–10058, 2008.

59. A. I. Chernykh and S. K. Turitsyn, Soliton and Collapse Regimes of Pulse Generation in Passively Mode-Locking Laser Systems, Opt. Lett., 12, 1011, 1987.

60. H. Nakatsuka, S. Asaka, H. Itoh, K. Ikeda, and M. Matsuoka, Observation to Chaos in All-Optical Bistabe System, Phys. Rev. Lett., 50, 109, 1983.

61. G. Steinmeyer, A. Buchholz, M. Hansel, M. Heuer, A. Schwache, and F. Mitschke, Dynamical Pulse Shaping in a Nonlinear Resonator, Phys. Rev. A, 52, 830, 1995.

62. F. Ilday, J. Buckley, and F. Wise, Period-Doubling Route to Multiple-Pulsing in Femtosecond Fiber Lasers, Proc. of Conf. on Nonlinear Guided Waves and Their Applications, Section Optical Amplifiers (MD), Paper MD9, Canada, March 28, 2004.

63. K. Tai, A. Hasegawa, and A. Tomita, Observation of Modulational Instability in Optical Fibers, Phys. Rev. Lett., 56, 135–138, 1986.

64. F. Matera, A. Mecozzi, M. Romagnoli, and M. Settembre, Sideband Instability Induced by Periodic Power Variation in Long-Distance Fiber Links, Opt. Lett., 18, 1499–1501, 1993.

65. N. J. Smith and N. J. Doran, Modulation Instabilities in Fibers with Periodic Dispersion Management, Opt. Lett., 21, 570–572, 1996.

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for
6 Deterministic Dynamics of Solitons in Passive Mode-Locked Fiber Lasers: Tang Ding Yuan and L. M. Zhao

6

Deterministic Dynamics of Solitons in Passive Mode-Locked Fiber Lasers

Tang Ding Yuan and L. M. Zhao

CONTENTS

6.1 Introduction

6.2 Solution Generation in Fiber Lasers

6.2.1 Pulse Propagation in Single-Mode Fibers

6.2.2 Cavity Transmission of Nonlinear Polarization Rotation Mode-Locked Fiber Lasers

6.3 Deterministic Dynamics of Solitons in Fiber Lasers

6.3.1 Experimental Configuration

6.3.2 Soliton Deterministic Dynamics

6.3.3 Period-Doubling Bifurcation and Period-Doubling Route to Chaos of Single-Pulse Solitons

6.3.4 Period Doubling and Quadrupling of Bound Solitons

6.3.5 Period Doubling of Multiple Solitons

6.3.6 Period Doubling of Dispersion-Managed Solitons at around Zero Cavity Dispersion

6.3.7 Period Doubling of Gain-Guided Solitons in Fiber Lasers with Large Net Normal Dispersion

6.3.8 Period Doubling of Vector Solitons in a Fiber Laser

6.4 Numerical Simulations on the Soliton Deterministic Dynamics in Fiber Lasers

6.4.1 Round-Trip Model of the Soliton Fiber Lasers

6.4.2 Deterministic Dynamics of Solitons in Different Fiber Lasers

6.4.3 Period-Doubling Route to Chaos of the Single-Pulse Solitons

6.4.4 Period-Doubling Route to Chaos of the Bound Solitons

6.4.5 Period Doubling of Multiple Solitons

6.4.6 Period Doubling of Dispersion-Managed Solitons

6.4.7 Period Doubling of the Gain-Guided Solitons

6.4.8 Period Doubling of Vector Solitons

6.4.9 Cavity-Induced Soliton Modulation Instability Effect

6.5 Conclusions

References

Table of Contents for 6 Deterministic Dynamics of Solitons in Passive Mode-Locked Fiber Lasers: Tang Ding Yuan and L. M. Zhao

Create new playlist

Sign In

Sign Up

6

Deterministic Dynamics of Solitons in Passive Mode-Locked Fiber Lasers

Tang Ding Yuan and L. M. Zhao

CONTENTS

6.1 Introduction

6.2 Solution Generation in Fiber Lasers

6.2.1 Pulse Propagation in Single-Mode Fibers

6.2.2 Cavity Transmission of Nonlinear Polarization Rotation Mode-Locked Fiber Lasers

6.3 Deterministic Dynamics of Solitons in Fiber Lasers

6.3.1 Experimental Configuration

6.3.2 Soliton Deterministic Dynamics

6.3.3 Period-Doubling Bifurcation and Period-Doubling Route to Chaos of Single-Pulse Solitons

6.3.4 Period Doubling and Quadrupling of Bound Solitons

6.3.5 Period Doubling of Multiple Solitons

6.3.6 Period Doubling of Dispersion-Managed Solitons at around Zero Cavity Dispersion

6.3.7 Period Doubling of Gain-Guided Solitons in Fiber Lasers with Large Net Normal Dispersion

6.3.8 Period Doubling of Vector Solitons in a Fiber Laser

6.4 Numerical Simulations on the Soliton Deterministic Dynamics in Fiber Lasers

6.4.1 Round-Trip Model of the Soliton Fiber Lasers

6.4.2 Deterministic Dynamics of Solitons in Different Fiber Lasers

6.4.3 Period-Doubling Route to Chaos of the Single-Pulse Solitons

6.4.4 Period-Doubling Route to Chaos of the Bound Solitons

6.4.5 Period Doubling of Multiple Solitons

6.4.6 Period Doubling of Dispersion-Managed Solitons

6.4.7 Period Doubling of the Gain-Guided Solitons

6.4.8 Period Doubling of Vector Solitons

6.4.9 Cavity-Induced Soliton Modulation Instability Effect

6.5 Conclusions

References

Table of Contents for
6 Deterministic Dynamics of Solitons in Passive Mode-Locked Fiber Lasers: Tang Ding Yuan and L. M. Zhao