CHAPTER 6
Serial Implementation
In this chapter, we turn the ideas of the previous two chapters into a simulation library in C++. We introduce a library with a generic, modular architecture, capable of accommodating wide varieties of models and products. We also instantiate a small number of models and products, where the calculation code is mainly a translation in C++ of the mathematics in the previous chapters.
Other publications cover the design and development of financial libraries, the best to our knowledge being Joshi's [74] and Schlogl's [75]. Our purpose is not to build a complete financial library, but to introduce the generic design of valuation libraries and establish a baseline for our work on parallelism and differentiation in the following chapters. In particular, we only cover simulation. Calibration is introduced in Chapter 13. We don't implement interest rate markets, model hierarchies, or algorithms other than simulation.
6.1 THE TEMPLATE SIMULATION ALGORITHM
Object Oriented Design (OOD) reigned supreme for decades over the software development community and gave birth to popular programming languages like Java, C#, and C++. OOD lost traction in the past decade in favor of the more intellectually satisfying functional programming; see for instance the excellent [23], and the more efficient meta-programming, see for instance [76].
The main criticisms toward OOD are the run-time overhead of dynamic polymorphism, and the presence of mutable state causing race conditions in multi-threaded programs. While we don't disagree and generally prefer functional code and static polymorphism, we also like OOD architectures in relevant situations. We believe a simulation library is one of them. C++ is a multi-paradigm language, and OOD is one of its many facets. We believe that OOD is ideally suited to a modular architecture where models, products, and random number generators may be mixed and matched at run time.
Products, models, and random number generators are defined and discussed in detail in the previous two chapters. The previous chapter also articulated the detail of the steps involved in a simulation. We reiterate these steps here in software development words.
In the previous chapters, we assumed that the payoff ![]() of a product was a scalar function of the scenario. We extend it here to a vector function, allowing a single product to represent
of a product was a scalar function of the scenario. We extend it here to a vector function, allowing a single product to represent ![]() payoffs. Each payoff is not necessarily a separate cash-flow, but rather a separate aggregate of the cash-flows. This allows us to represent multiple products in one, like a barrier option together with its European counterpart, or a portfolio of many European options of different strikes and maturities. This allows us to evaluate the
payoffs. Each payoff is not necessarily a separate cash-flow, but rather a separate aggregate of the cash-flows. This allows us to represent multiple products in one, like a barrier option together with its European counterpart, or a portfolio of many European options of different strikes and maturities. This allows us to evaluate the ![]() payoffs together, in particular, with the same set of simulated scenarios, resulting in a performance improvement. The rest of the algorithm scrupulously follows the previous chapter.
payoffs together, in particular, with the same set of simulated scenarios, resulting in a performance improvement. The rest of the algorithm scrupulously follows the previous chapter.
- Initialization phase
- The product advertises its timeline
 and the definition of the samples
and the definition of the samples  s for the event date
s for the event date 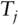 s: the number of market observations on the event date, along with their natures and maturities.
s: the number of market observations on the event date, along with their natures and maturities. - The model initializes itself to simulate scenarios over the product timeline, knowing what market observations it is required to simulate. Among other initialization steps, the model establishes its own simulation timeline. After initialization, the model knows the dimension of the simulation
 , how many random numbers it consumes to generate one path.
, how many random numbers it consumes to generate one path. - The model advertises
 and the RNG initializes itself so as to generate
and the RNG initializes itself so as to generate  random numbers repeatedly during the simulation phase.
random numbers repeatedly during the simulation phase.
- The product advertises its timeline
- Simulation phase Simulate and evaluate
 paths. For every path
paths. For every path  :
:
- The RNG generates a new Gaussian vector
 in dimension
in dimension 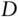 .1
.1 - The model consumes
 to simulate the scenario
to simulate the scenario  .
. - The product runs its payoff function over the path to compute
 , which is now a vector in dimension
, which is now a vector in dimension  .
.
- The RNG generates a new Gaussian vector
- Aggregation phase The algorithm returns the
 matrix of all the
matrix of all the  s so client code may aggregate it to compute values (averages), standard errors (standard deviations over
s so client code may aggregate it to compute values (averages), standard errors (standard deviations over  ), quantiles, and so forth.
), quantiles, and so forth.
This summary is sufficient to design the base classes and the simulation algorithm. The code of this section is in mcBase.h in our repository.
Scenarios
We start with the scenarios, which are the objects that models and products communicate to one another. Scenarios are collections of samples:

Why the template? The full answer will be given in Part III. The short answer is that we template our code for the number type. We use a template type in place of doubles to represent real numbers. AAD is almost noninvasive, in the sense that it doesn't require any modification in the differentiated code, except for the representation of its numbers. AAD works with numbers represented with a custom type. It would be messy to code with that custom type in place of doubles. It is a much better practice to template code on the number representation type, so that the code may be instantiated with doubles for evaluation, or with the AAD number type for differentiation.
Our code is therefore templated in the number type, but not all of it. Once again, the full answer will be given in Chapter 12. The short answer is that inactive code, the code that doesn't depend on the parameters, is best left untemplated so it runs without unnecessary AAD overhead.
A sample is the collection of market observations on an event date for the evaluation of the payoff: the numeraire if the event date is a payment date, and collections of forwards, discounts, and libors, fixed on the event date:

This sample definition accommodates a wide class of single underlying price, rate, or price/rate hybrid models and products. In order to deal with other model or product types, like credit, the definition of the sample must be extended with additional observations, like credit spreads or credit events. It can also be extended to accommodate multi-underlying and multi-currency models and products with collections of forwards for every underlying and collections of rates (discounts and libors) for every currency, like this:

Although we are not implementing these extensions here, it is worth noting that the range of admissible models and products can be easily extended with a straightforward modification of the definition of samples.
Together with the Sample, which stores the simulated market observations, we have the SampleDef, which specifies the definition of these observations:

Time is an alias for double, the number of years from today. A SampleDef contains the definition of a Sample, the number and nature of the market observations on a given event date: whether the sample requires a numeraire, the maturities of the forwards and discounts in the sample, and the specification (start date, end date and index) of the Libor observations. The sizes of the vectors forwardsMats, discountMats, and liborDefs also tell how many forwards, discounts, and Libors are simulated on this event date.
It is the responsibility of the product to determine the sample definition, and the responsibility of the model to simulate samples in accordance with their definition.
A Sample is initialized from its SampleDef. We split initialization into two different functions: one that allocates memory, and one that initializes values. Following the discussion of the Section 3.11 of our multi-threaded programming Chapter 3, we always separate allocation and initialization. Memory must be allocated initially, before simulations start and certainly before the execution of concurrent code, whereas, in some circumstances, it may be necessary to conduct initialization during the simulation phase.

To give default values is not necessary but may be convenient. The standard library algorithm ![]() is self-explanatory. Finally, we provide free functions to batch allocate and initialize a collection of samples:
is self-explanatory. Finally, we provide free functions to batch allocate and initialize a collection of samples:

The code is final and will not be modified in the rest of the publication.
Base classes
From the description of the steps involved in a simulation, we know exactly what is the responsibility of models, products, and RNGs. This is enough information to develop abstract base classes:

The base Product class defines the product's contract, and directly follows a product's responsibilities in the sequential steps of a simulation: a product knows its timeline, and the definition of the samples on the event dates. It advertises this information with its accessors ![]() and
and ![]() . We commented earlier that a product could encompass a number
. We commented earlier that a product could encompass a number ![]() of payoffs. Its accessor
of payoffs. Its accessor ![]() advertises the names of the
advertises the names of the ![]() payoffs, so client code knows which is which. Note that the accessors return information by const reference. This way, a product may store the information and make it available to client code, instead of having to regenerate it every time on demand.
payoffs, so client code knows which is which. Note that the accessors return information by const reference. This way, a product may store the information and make it available to client code, instead of having to regenerate it every time on demand.
The const method ![]() is the main responsibility of a product in a simulation: compute the
is the main responsibility of a product in a simulation: compute the ![]() payoffs from a given scenario
payoffs from a given scenario ![]() , what we denoted
, what we denoted ![]() in the previous chapters. The
in the previous chapters. The ![]() payoffs are returned in a preallocated vector to minimize allocations.
payoffs are returned in a preallocated vector to minimize allocations.
Finally, ![]() implements the virtual copy constructor idiom. When an object is manipulated with a pointer or reference on its base class, C++ does not provide any means to make copies of the object and obtain clones, new objects of the same concrete type, with a copy of all the data members. Generic code, which manipulates objects with polymorphic base class pointers, cannot make copies, which substantially restricts its possibilities. In the absence of a native language solution, the development community worked out the virtual copy constructor solution, now a well-established idiom: a pure virtual method
implements the virtual copy constructor idiom. When an object is manipulated with a pointer or reference on its base class, C++ does not provide any means to make copies of the object and obtain clones, new objects of the same concrete type, with a copy of all the data members. Generic code, which manipulates objects with polymorphic base class pointers, cannot make copies, which substantially restricts its possibilities. In the absence of a native language solution, the development community worked out the virtual copy constructor solution, now a well-established idiom: a pure virtual method ![]() , which contract is to return a copy of the invoking object through a (smart) pointer on its base class. The actual copy happens in the derived classes, where concrete types are known, and
, which contract is to return a copy of the invoking object through a (smart) pointer on its base class. The actual copy happens in the derived classes, where concrete types are known, and ![]() is overridden to invoke the copy constructor of the concrete class. We will further clarify this point when we develop concrete products (and models and RNGs, where this idiom is also implemented).
is overridden to invoke the copy constructor of the concrete class. We will further clarify this point when we develop concrete products (and models and RNGs, where this idiom is also implemented).
The product class is final, but the model base class will need a minor upgrade for AAD in Part III. It is written in a similar manner:

A model initializes itself to perform simulations, knowing the timeline and scenario definition from the product. We separate memory allocation as usual, so we have two initialization methods: ![]() and
and ![]() . The first method only allocates working memory. The second method conducts the actual initialization. This is where a model initializes its simulation timeline, as explained on page 195, and pre-calculates some scenario independent results. After a model is initialized, it knows the dimension
. The first method only allocates working memory. The second method conducts the actual initialization. This is where a model initializes its simulation timeline, as explained on page 195, and pre-calculates some scenario independent results. After a model is initialized, it knows the dimension ![]() of the simulation, how many random numbers it needs to simulate a scenario. It advertises
of the simulation, how many random numbers it needs to simulate a scenario. It advertises ![]() with its const method
with its const method ![]() so that the RNG can initialize itself, too.
so that the RNG can initialize itself, too.
The const method ![]() is the principal responsibility of a model in a simulation: to generate a scenario in accordance with the product's event dates and sample definitions, which the model knows from the initialization step. The process consumes a Gaussian vector in dimension
is the principal responsibility of a model in a simulation: to generate a scenario in accordance with the product's event dates and sample definitions, which the model knows from the initialization step. The process consumes a Gaussian vector in dimension ![]() . The result is returned in a preallocated vector or preallocated samples.
. The result is returned in a preallocated vector or preallocated samples.
Models implement the virtual copy constructor idiom in their const method ![]() .
.
The next three methods are something new. Different models have different parameters: in Black and Scholes, the parameters are the spot price, and time dependent rates, dividends, and volatilities (which could be represented with vectors, although we will implement a simplified version of Black and Scholes where all the parameters are scalar). In Dupire's model, it is a two-dimensional local volatility surface (which we represent with a bi-linearly interpolated matrix). In LGM (which we don't implement), it is a volatility curve and a mean reversion curve (which could be represented with two interpolated vectors). The parameters of different models are different in nature, dimension, and number.
Our generic algorithms manipulate models by base class pointers. They have no knowledge of the concrete model they are manipulating. Risk is the sensitivity to model parameters, so risk algorithms must access and manipulate the parameters. This is why it is a part of a model's contract to expose its parameters in a flat vector of pointers to its internal parameters, so client code not only can read, but also modify the parameters of a generic model with the non const accessor ![]() . Models also expose the names of their parameters, in the same way that products advertise the names of their payoffs, so client code knows what parameters in the vector correspond to what. Finally, the number of parameters in a model can be accessed with a call to
. Models also expose the names of their parameters, in the same way that products advertise the names of their payoffs, so client code knows what parameters in the vector correspond to what. Finally, the number of parameters in a model can be accessed with a call to ![]() but, since
but, since ![]() is not const, it would be considered a mutable call, which is of course not the case. This is why models offer a non-virtual method, written directly on the base class, to provide the number of parameters. The method is const and encapsulates ugly const casts so client code doesn't have to.
is not const, it would be considered a mutable call, which is of course not the case. This is why models offer a non-virtual method, written directly on the base class, to provide the number of parameters. The method is const and encapsulates ugly const casts so client code doesn't have to.
Finally, the base RNG class is as follows for now. We need nothing else for serial simulations, but parallel simulations will require a major extension to the base and concrete RNGs.

For now, the RNGs contract should be self-explanatory: an RNG is initialized with a simulation dimension ![]() ; it delivers either uniform or standard Gaussian vectors in dimension
; it delivers either uniform or standard Gaussian vectors in dimension ![]() in sequence, returning them in preallocated vectors. It also implements the virtual copy constructor idiom and advertises its dimension.
in sequence, returning them in preallocated vectors. It also implements the virtual copy constructor idiom and advertises its dimension.
An important note is that the methods ![]() and
and ![]() are not const, since generators typically update their internal state when they compute a new set of numbers, as we have seen in the previous chapter with mrg32k3a and Sobol. This is in contrast to models and products, who respectively generate scenarios and compute payoffs without modification of internal state. It follows that models and products are thread safe after they are initialized, whereas RNGs are mutable objects. This comment affects the code of the next chapter.
are not const, since generators typically update their internal state when they compute a new set of numbers, as we have seen in the previous chapter with mrg32k3a and Sobol. This is in contrast to models and products, who respectively generate scenarios and compute payoffs without modification of internal state. It follows that models and products are thread safe after they are initialized, whereas RNGs are mutable objects. This comment affects the code of the next chapter.
Template algorithm
We have everything we need to code the Monte-Carlo algorithm, with a literal translation in C++ of the steps recalled in the beginning of this chapter.

This generic Monte-Carlo simulation algorithm implements its successive steps with calls to the (pure virtual) methods of our product, model, and RNG base classes. We haven't yet implemented any model, product, or RNG, or written a concrete implementation of any of their methods. We wrote the skeleton of an algorithm in terms of generic steps, which concrete implementation belongs to the overridden methods of derived classes. Our generic algorithm never addresses concrete models, products, or RNGs; it only calls the interface defined in their base class. In GOF [25] terms,2 this idiom is called a template pattern. Our generic simulation algorithm is a template algorithm.
The template code is remarkably short, and most of it deals with initialization and the preallocation of working memory. The actual simulations are implemented in the lines 31 to 40 and iterate over three lines of code 35, 37, and 39, excluding comments: generate a Gaussian vector, consume it to generate a scenario, compute the payoff over the scenario, repeat. But, of course, it is all the initializations that make the computation efficient: we will see that a lot of the work is performed there so that the repeated code only conducts fast calculations in the most efficient possible way.
In order to run this code, of course, we need concrete models, products, and RNGs. We start with the number generators.
6.2 RANDOM NUMBER GENERATORS
MRG32k3a
L'Ecuyer's random generator is coded in mrg32k3a.h in accordance with the algorithm on page 201. The file gaussians.h, referenced on the second line, contains an implementation of Moro's [66] inverse cumulative Gaussian ![]() . The implementation in mrg32k3a.h mainly translates in C++ the steps of the algorithm on page 201, with the incorporation of the important antithetic optimization, discussed on page 202.
. The implementation in mrg32k3a.h mainly translates in C++ the steps of the algorithm on page 201, with the incorporation of the important antithetic optimization, discussed on page 202.



The method ![]() implements the recursions on page 201. The constructor records the seeds, so the method
implements the recursions on page 201. The constructor records the seeds, so the method ![]() factory resets the state of the generator.
factory resets the state of the generator.
Note the virtual copy constructor in action. Generic client code calls the virtual ![]() method to copy an RNG manipulated by base class pointer. The implementation of
method to copy an RNG manipulated by base class pointer. The implementation of ![]() is overridden in the concrete class. The implementation therefore knows that the RNG is an mrg32k3a, and easily makes a copy of itself with a call to its (default) copy constructor. The copy is stored on the heap and returned by base class (unique) pointer. The unique pointer on the concrete class implicitly and silently converts to a unique pointer of the base class when the method returns.
is overridden in the concrete class. The implementation therefore knows that the RNG is an mrg32k3a, and easily makes a copy of itself with a call to its (default) copy constructor. The copy is stored on the heap and returned by base class (unique) pointer. The unique pointer on the concrete class implicitly and silently converts to a unique pointer of the base class when the method returns.
The override ![]() records the dimension, and allocates space for the caching of uniform and Gaussian numbers for the implementation of the antithetic logic. The antithetic logic itself is implemented in the overrides
records the dimension, and allocates space for the caching of uniform and Gaussian numbers for the implementation of the antithetic logic. The antithetic logic itself is implemented in the overrides ![]() and
and ![]() , which return the next (respectively uniform or Gaussian) random vector in dimension
, which return the next (respectively uniform or Gaussian) random vector in dimension ![]() . The indicator
. The indicator ![]() starts
starts ![]() and flicks at every every call to
and flicks at every every call to ![]() or
or ![]() . When
. When ![]() is
is ![]() , a new random vector is generated by
, a new random vector is generated by ![]() repeated calls to
repeated calls to ![]() for uniforms or
for uniforms or ![]() for Gaussians (encapsulated in the standard algorithm
for Gaussians (encapsulated in the standard algorithm ![]() ). Before the random vector is returned, a copy is cached in the generator, so on the next call to
). Before the random vector is returned, a copy is cached in the generator, so on the next call to ![]() or
or ![]() , with
, with ![]() now
now ![]() , no new numbers are generated; instead, a negation of the previously cached vector (
, no new numbers are generated; instead, a negation of the previously cached vector (![]() for uniforms,
for uniforms, ![]() for Gaussians) is returned, effectively producing two random vectors for the price of one, cutting in half the overhead of random number generation and Gaussian transformation.
for Gaussians) is returned, effectively producing two random vectors for the price of one, cutting in half the overhead of random number generation and Gaussian transformation.
Sobol
Our implementation of the Sobol sequence uses the ![]() direction numbers found by Joe and Kuo in 2003. The numbers are listed in sobol.cpp:
direction numbers found by Joe and Kuo in 2003. The numbers are listed in sobol.cpp:

It follows that our implementation is limited to dimension 1,111. The application crashes in a higher dimension. When a higher dimension is desired, for example, for the purpose of xVA or regulatory calculations, mrg32k3a may be used instead. The construction of mrg32k3a numbers almost matches the speed of Sobol, thanks to the antithetic optimization (not recommended with Sobol, since it would interfere with the naturally low discrepancy), but its convergence order is lower, together with accuracy and stability. Alternative sets of direction numbers in dimension up to 21,201 are found on Joe and Kuo's page. Jaeckel [63] delivers code that generates direction numbers on demand (with virtually no overhead) in dimension up to 8,129,334 (!)
The implementation of the sequence in sobol.h is a direct translation of the recursion on page 206:


6.3 CONCRETE PRODUCTS
We have introduced a generic, professional simulation environment with support for a wide variety of models and products. Professionally developed model hierarchies and product representations fit in this environment as long as they implement the Product and Model interfaces.
In the chapters that follow, we will extend this environment for parallel simulation and constant time differentiation, working on the template algorithm without modification of models or products. It follows that models and products interfaced with our environment automatically benefit from parallelism and AAD.3
In the rest of this chapter, we implement a few examples of concrete models and products so we can run concrete simulations. But those concrete implementations are meant for demonstration only; they do not constitute professional code suitable for production.
Concrete products, in particular, are sketchy, and for good reason. It is not best practice to represent products and cash-flows with dedicated C++ code in modern financial systems. The correct, generic, versatile representation of products and cash-flows is with a scripting library, where all cash-flows are represented in a consistent manner, products are created and customized at run time, and client code may inspect and manipulate cash-flows in many ways, including aggregation, compression, or decoration. Well-designed scripting libraries offer all these facilities, and much more, without significant overhead. Scripting is a keystone of modern financial systems. It is also a demanding topic, which we address in detail in a dedicated publication [11]. Of course, scripted products implement the Product interface and seamlessly connect to our simulation library, including parallelism and AAD.
This being said, we need a few simple examples to effectively run simulations. All the demonstration products are listed in mcPrd.h in our repository. We start with a simple European call.
European call
All the concrete products implement the same pattern: they build their timeline and defline (definition of the samples on event dates, for lack of a better word) on construction, and evaluate payoffs against scenarios in their const ![]() override, reading market observations on the scenario in accordance with the definition of the samples. They also expose the number of the name of their different payoffs, advertise their timeline and defline with const accessors, and implement the virtual copy constructor idiom in the same manner as RNGs.
override, reading market observations on the scenario in accordance with the definition of the samples. They also expose the number of the name of their different payoffs, advertise their timeline and defline with const accessors, and implement the virtual copy constructor idiom in the same manner as RNGs.


This class illustrates some key notions covered in Chapter 4. It represents a call option of strike ![]() that pays
that pays ![]() on the settlement date
on the settlement date ![]() if exercised on the exercise date
if exercised on the exercise date ![]() . The holder exercises if
. The holder exercises if ![]() , in which case the present value at
, in which case the present value at ![]() is:
is:
so that it may be modeled as a single cash-flow on the exercise date:
The product holds its strike, exercise, and settlement date, as well as timeline and defline, and exposes them to client code. This is a single payoff product, so the vector of results filled by ![]() and the vector of labels exposed in
and the vector of labels exposed in ![]() are of dimension 1. The label, which identifies the product as “call K
are of dimension 1. The label, which identifies the product as “call K ![]()
![]() ,” is initialized on lines 45–60 in the constructor, along with the timeline and the defline.
,” is initialized on lines 45–60 in the constructor, along with the timeline and the defline.
The timeline ![]() is initialized on line 29. The defline is initialized on lines 31–43, with the definition of the sample on the exercise date: the forward and discount to the settlement date. We modeled the option as a single cash-flow on the exercise date, hence,
is initialized on line 29. The defline is initialized on lines 31–43, with the definition of the sample on the exercise date: the forward and discount to the settlement date. We modeled the option as a single cash-flow on the exercise date, hence, ![]() is considered a payment date and must include the numeraire.
is considered a payment date and must include the numeraire.
The payoff, computed in ![]() , was defined in Chapter 4 as the sum of the numeraire deflated cash-flows. In this case, the payoff is:
, was defined in Chapter 4 as the sum of the numeraire deflated cash-flows. In this case, the payoff is:

Note how the definition of the timeline and defline in the constructor synchronizes with the computation of the payoff in the ![]() override. The timeline is set as vector with a unique entry myTimeline[0] = exerciseDate, so the model's contract is to generate paths with a single sample path[0], observed on the exercise date. It follows that the vector myDefline also has a unique entry myDefline[0] that specifies the market sample on the exercise date: what observations the model simulates. The numeraire property on the sample is set to true so the model simulates the numeraire on the exercise date in path[0].numeraire. The forwardMats and discountMats vectors on the sample definition are set to the unique entries forwardMats[0] = settlementDate and discountMats[0] = settlementDate. It follows that the model's contract is simulate
override. The timeline is set as vector with a unique entry myTimeline[0] = exerciseDate, so the model's contract is to generate paths with a single sample path[0], observed on the exercise date. It follows that the vector myDefline also has a unique entry myDefline[0] that specifies the market sample on the exercise date: what observations the model simulates. The numeraire property on the sample is set to true so the model simulates the numeraire on the exercise date in path[0].numeraire. The forwardMats and discountMats vectors on the sample definition are set to the unique entries forwardMats[0] = settlementDate and discountMats[0] = settlementDate. It follows that the model's contract is simulate ![]() on path[0].forwards[0], and
on path[0].forwards[0], and ![]() on path[0].discounts[0], in addition to the numeraire. The product doesn't require any other market observation to compute its payoff; in particular, the vector liborDefs on the sample definition is left empty, so the model doesn't need to simulate Libors. The product knows all this because it is in control of the timeline and defline and trusts the model to fulfill its contract. Therefore, in its
on path[0].discounts[0], in addition to the numeraire. The product doesn't require any other market observation to compute its payoff; in particular, the vector liborDefs on the sample definition is left empty, so the model doesn't need to simulate Libors. The product knows all this because it is in control of the timeline and defline and trusts the model to fulfill its contract. Therefore, in its ![]() override, it knows that path[0].numeraire is
override, it knows that path[0].numeraire is ![]() , paths[0].forwards[0] is
, paths[0].forwards[0] is ![]() , and path[0].discounts[0] is
, and path[0].discounts[0] is ![]() , and confidently implements the payoff equation above on lines 112–114.
, and confidently implements the payoff equation above on lines 112–114.
Barrier option
Next, we define a discretely monitored barrier option, more precisely an up-and-out call. We dropped the separate settlement date for simplicity. We define the up-and-out call and the corresponding European call together in the same product with two different payoffs, so we can evaluate them simultaneously against a shared set of scenarios.



This code follows the same pattern as the European option. The timeline is the set of barrier monitoring dates plus maturity, built on lines 36–54 in the constructor. All samples include the spot ![]() , and the sample on maturity includes the numeraire, too. We have two payoffs: the barrier and the European, with two corresponding labels.
, and the sample on maturity includes the numeraire, too. We have two payoffs: the barrier and the European, with two corresponding labels.
The payoff implements the smooth barrier technique to mitigate the instability of Monte-Carlo risk sensitivities with discontinuous cash-flows. Smoothing is the approximation of a discontinuous cash-flow by a close continuous one. We apply a smoothing spread ![]() (in percentage of
(in percentage of ![]() ) so the barrier dies above
) so the barrier dies above ![]() , lives below
, lives below ![]() , and in between loses a part of the notional interpolated between 1 at
, and in between loses a part of the notional interpolated between 1 at ![]() and 0 and
and 0 and ![]() and continues with the remaining notional. See our presentation [77] for an introduction to smoothing or Bergomi's [78] for an insightful discussion. We differentiate this code in Part III so we must apply smoothing to obtain correct, stable risks (as option traders always do). Note that smoothing is the responsibility of the product, not the model, because it consists in a modification of the payoff.
and continues with the remaining notional. See our presentation [77] for an introduction to smoothing or Bergomi's [78] for an insightful discussion. We differentiate this code in Part III so we must apply smoothing to obtain correct, stable risks (as option traders always do). Note that smoothing is the responsibility of the product, not the model, because it consists in a modification of the payoff.
Like in the European option, the timeline and samples are defined in the constructor. The timeline is the union of the barrier monitoring schedule, today's date, and the maturity date. The sample on all event dates is defined as the spot, that is, the forward with maturity the same event date. So the product knows, when it accepts the path simulated by the model in its ![]() override, that path[j].forwards[0] is the spot observed on
override, that path[j].forwards[0] is the spot observed on ![]() . In addition, the numeraire property on the sample definition is set to true on maturity only, so the product knows to read
. In addition, the numeraire property on the sample definition is set to true on maturity only, so the product knows to read ![]() on path.back().numeraire, where
on path.back().numeraire, where ![]() accesses the last entry of a STL vector, so path.back().forwards[0] is the spot at maturity. This is how the product confidently calculates the payoff of the barrier on line 163 and the corresponding European on line 159. It knows that (provided the model fulfills its contract) the correct observations are in the right places on the scenario.
accesses the last entry of a STL vector, so path.back().forwards[0] is the spot at maturity. This is how the product confidently calculates the payoff of the barrier on line 163 and the corresponding European on line 159. It knows that (provided the model fulfills its contract) the correct observations are in the right places on the scenario.
We shall not further comment on this correspondence between the definition of the timeline and defline on one side, and the computation of the payoff on the other side. This is a fundamental element of generic design in our simulation library. When a product sets the timeline and the sample definitions, it specifies what goes where on the path. To populate the path correctly, and in accordance with these instructions, is the model's responsibility, so the timeline and defline are communicated to the model on initialization. The product computes payoffs accordingly, reading the correct simulated observations in the right places on the scenario in accordance with its own specifications. The specifications in the product's constructor, and the computations in its ![]() override, must always remain synchronized, otherwise the product is incorrectly implemented and the simulations evaluate it incorrectly.
override, must always remain synchronized, otherwise the product is incorrectly implemented and the simulations evaluate it incorrectly.
European portfolio
To demonstrate the simultaneous pricing of many different payoffs in a single product, we develop a product class for a portfolio of European options of different strikes and maturities.


It is very clumsy to code product portfolios as separate products. What we should code is a single portfolio class that aggregates a collection of products of any type into a single product.
This is possible, but it would take substantial effort. The portfolio's timeline is the union of its product's timelines, and the portfolio's samples are unions of its product's samples. But a product reads market variables on its own scenario to compute its payoff, not an aggregated scenario. Some clumsy, prone-to-error, inefficient boilerplate indexation code would have to be written so that timelines and samples may be aggregated in a way that keeps track of what belongs to whom. In contrast, aggregation is natural with scripted products.
The code above is therefore only for demonstration. We use it to check the calibration of Dupire's model in Chapter 13 by repricing a large number of European options, simultaneously and in a time virtually constant in the number of options. The simulations are shared, so only the (insignificant) computation of payoffs is linear in the number of options. In Chapter 14, we use this code to demonstrate the production of itemized risk reports (one risk report for every product in the book) with AAD, in almost constant time.
Contingent floater
Although our framework supports interest rate models, we are not implementing one in this publication, but we demonstrate the rate infrastructure with a basic hybrid product that pays Libor coupons, plus a spread, over a floating schedule, but only in those periods where the performance of some asset is positive.
The product is structured as a bond that also pays a redemption of 100% of the notional at maturity. The payoff of this contingent bond is:

where ![]() is the number of coupons and
is the number of coupons and ![]() is payment period. We smooth the digital indicators with a call spread, as is market practice, similarly to the smoothing we applied to the barrier, referring again to [77] for a quick introduction to smoothing. The resulting code is:
is payment period. We smooth the digital indicators with a call spread, as is market practice, similarly to the smoothing we applied to the barrier, referring again to [77] for a quick introduction to smoothing. The resulting code is:



6.4 CONCRETE MODELS
Finally, we implement two concrete models: Black-Scholes and Dupire. Contrary to the concrete products, which we only developed for demonstration, the model code is correct and professional, although somewhat simplified. We take the opportunity to demonstrate a few patterns for the efficient implementation of simulation models.
The implementations remain simplified compared to a production environment. We don't implement linear models or model hierarchies (although we do implement an IVS in Chapter 13) and store the initial market conditions as parameters in the dynamic models. The initial market conditions are simplified to the extreme: Black and Scholes is implemented with constant rate, dividend yield, and volatility, and Dupire is implemented with zero rates and dividends. We simplified the representation of the current market, which is not directly relevant for the purpose of this publication, and focused on the implementation of the simulated dynamics.
The main methods implemented in the models are overrides of ![]() , where the model accepts the definition of the scenario, so it knows what to simulate and initializes itself accordingly; and
, where the model accepts the definition of the scenario, so it knows what to simulate and initializes itself accordingly; and ![]() , where the model simulates a scenario, in accordance with its definition, consuming a random vector in the process. Remember that initialization is split in two methods, memory allocations being gathered in a separate
, where the model simulates a scenario, in accordance with its definition, consuming a random vector in the process. Remember that initialization is split in two methods, memory allocations being gathered in a separate ![]() override.
override.
Black and Scholes's model
Black and Scholes's model is implemented in mcMdlBs.h in our repository.
In order to illustrate the change of numeraire technique covered in length in Chapter 4, we implement the Black-Scholes model under the risk-neutral measure, or the spot measure, see page 163, at the client code's choice. Depending on the selected measure, the model implements different dynamics, and populates scenarios with the corresponding numeraire. The simulation under both measures results in the same price at convergence for all products, all the necessary logic remaining strictly encapsulated in the model, without any modification of the template algorithm or products.






In the constructor line 59, the model initializes its parameters: spot, volatility, rate, dividend. Note that the constructor is templated so a model that represent numbers with a type T can be initialized with numbers of another type U. The model also initializes a vector of four pointers on its four parameters, which it advertises in its method ![]() , line 119. It also initializes a vector of four strings in the same order “spot,” “vol,” “rate,” “div” and advertises it with
, line 119. It also initializes a vector of four strings in the same order “spot,” “vol,” “rate,” “div” and advertises it with ![]() , line 125, so client code knows what pointer refers to what parameter. The pointers are set in the private method
, line 125, so client code knows what pointer refers to what parameter. The pointers are set in the private method ![]() on line 86.
on line 86.
The virtual copy constructor idiom is implemented in ![]() on line 130, where the model makes a copy of itself as usual. This copies all the data members, including the vector of pointers to parameters (myParameters), which are copied by value, so the pointers in the cloned model still point on the parameters of the original model. For this reason, the cloned model must reset its pointers to its own parameters to finalize cloning. This is why we made
on line 130, where the model makes a copy of itself as usual. This copies all the data members, including the vector of pointers to parameters (myParameters), which are copied by value, so the pointers in the cloned model still point on the parameters of the original model. For this reason, the cloned model must reset its pointers to its own parameters to finalize cloning. This is why we made ![]() a separate method.
a separate method.
A model's primary responsibility is to simulate scenarios and override ![]() on line 320, which accepts a random vector and consumes it to produce a scenario in accordance with the timeline and sample definitions of the product. From the discussion on page 195, Black and Scholes is best simulated with the transitional scheme:
on line 320, which accepts a random vector and consumes it to produce a scenario in accordance with the timeline and sample definitions of the product. From the discussion on page 195, Black and Scholes is best simulated with the transitional scheme:

under the risk-neutral measure, with large steps over the event dates.4 With constant parameters, the forward factors are:
and ![]() . The
. The ![]() s are the standard independent Gaussian numbers consumed in the simulation. We derived the dynamics under the spot measure on page 163, and the corresponding transitional scheme is:
s are the standard independent Gaussian numbers consumed in the simulation. We derived the dynamics under the spot measure on page 163, and the corresponding transitional scheme is:

As the path of ![]() over the timeline is generated, the model's mapping
over the timeline is generated, the model's mapping ![]() is applied to produce the samples
is applied to produce the samples ![]() as discussed in depth in the previous chapter. The mapping is implemented in the private method
as discussed in depth in the previous chapter. The mapping is implemented in the private method ![]() , line 283. The definition of samples on the event dates
, line 283. The definition of samples on the event dates ![]() s was communicated along with the timeline on initialization, and the model took a reference myDefline (line 158) so it knows what to set on the samples. If timeline[j].numeraire is true, the model sets the correct numeraire
s was communicated along with the timeline on initialization, and the model took a reference myDefline (line 158) so it knows what to set on the samples. If timeline[j].numeraire is true, the model sets the correct numeraire ![]() on path[j].numeraire:
on path[j].numeraire: ![]() under the risk-neutral measure or the spot with reinvested dividends, as explained on page 163, under the spot measure.5 The mapping
under the risk-neutral measure or the spot with reinvested dividends, as explained on page 163, under the spot measure.5 The mapping ![]() also sets the forwards
also sets the forwards ![]() on paths[j].forwards[k], with the maturities
on paths[j].forwards[k], with the maturities ![]() specified on (*myDefline)[j].forwardMats[k]. The forward factors
specified on (*myDefline)[j].forwardMats[k]. The forward factors ![]() are deterministic in this model, so they are not computed during the simulation. The are pre-calculated in
are deterministic in this model, so they are not computed during the simulation. The are pre-calculated in ![]() and stored in the model's working memory, where they're picked when needed for the simulation of the scenario. The same applies to discounts and Libors, which are also deterministic in this model.
and stored in the model's working memory, where they're picked when needed for the simulation of the scenario. The same applies to discounts and Libors, which are also deterministic in this model.
Note how this mechanics naturally articulates with that of products and permits a clear separation of models and products together with a synchronization through the timeline and the definition of samples.
The simulation is implemented in ![]() line 320, the event date loop on lines 342–354 implementing the transitional scheme, including the mapping with a call to
line 320, the event date loop on lines 342–354 implementing the transitional scheme, including the mapping with a call to ![]() on line 351. Lines 330–340 apply the same treatment to today's date, which is special, because it may or may not be an event date.
on line 351. Lines 330–340 apply the same treatment to today's date, which is special, because it may or may not be an event date.
At this point, we state a key rule for the efficient implementation of simulation models:
Perform as much work as possible on initialization and as little as possible during simulations.
Initialization only occurs once. Simulations are repeated a large number of times. We must conduct all the administrative work, including allocation of working memory, on initialization. This is done in ![]() , line 140. But there is more. We can often pre-calculate parts of the computations occurring during simulation. The amount of computations moved to initialization time is a major determinant of the simulation's performance.
, line 140. But there is more. We can often pre-calculate parts of the computations occurring during simulation. The amount of computations moved to initialization time is a major determinant of the simulation's performance.
In the Black and Scholes model, a vast number of amounts in the simulation scheme and the mapping are deterministic, independent on random numbers, and may therefore be pre-calculated: the expectations, variances, and standard deviations for the Gaussian scheme, as well as the forward factors, and the deterministic discounts and libors for the mapping. For the numeraire, it is also deterministic under the risk-neutral measure, but not under the spot measure. In this case,

and we pre-calculate ![]() so we only multiply by the spot
so we only multiply by the spot ![]() during simulations. The method
during simulations. The method ![]() on line 190 implements all these pre-calculations and stores them in the model's working memory. The memory is preallocated in
on line 190 implements all these pre-calculations and stores them in the model's working memory. The memory is preallocated in ![]() .
.
The code is not short, but the core functionality, the simulation in ![]() , including mapping in
, including mapping in ![]() , takes around 50 lines, including many comments. Most computations are conducted in the initialization phase, in
, takes around 50 lines, including many comments. Most computations are conducted in the initialization phase, in ![]() and
and ![]() (150 lines), as should be expected from an efficient implementation.
(150 lines), as should be expected from an efficient implementation.
Dupire's model
To demonstrate the library with a more ambitious concrete model, we implement Dupire's local volatility model (although with zero rates and dividends) in mcMdlDupire.h:

The local volatility function ![]() is meant to be calibrated – using Dupire's famous formula – to the market prices of European options. We will discuss, code, and differentiate Dupire's calibration in Chapter 13. For now, we focus on the simulation. We take the local volatility as a given matrix, with spots in rows and times in columns, and bi-linearly interpolate it in the simulation scheme. As discussed on page 195 of the previous chapter, a transitional scheme is not appropriate for Dupire's model, where transition probabilities are unknown, and we implement the log-Euler scheme instead:
is meant to be calibrated – using Dupire's famous formula – to the market prices of European options. We will discuss, code, and differentiate Dupire's calibration in Chapter 13. For now, we focus on the simulation. We take the local volatility as a given matrix, with spots in rows and times in columns, and bi-linearly interpolate it in the simulation scheme. As discussed on page 195 of the previous chapter, a transitional scheme is not appropriate for Dupire's model, where transition probabilities are unknown, and we implement the log-Euler scheme instead:

where ![]() is bi-linearly interpolated spot and time over the local volatility matrix, keeping extrapolation flat. In addition, as discussed on page 195, we cannot accurately simulate over long time steps with this scheme. The simulation timeline cannot only consist of the product's event dates. We must insert additional time steps so that the space between them does not exceed a specified maximum
is bi-linearly interpolated spot and time over the local volatility matrix, keeping extrapolation flat. In addition, as discussed on page 195, we cannot accurately simulate over long time steps with this scheme. The simulation timeline cannot only consist of the product's event dates. We must insert additional time steps so that the space between them does not exceed a specified maximum ![]() .
.
It is clear that a lot of CPU time is spent in the interpolation. Bi-linear interpolation is expensive, and we have one in the innermost loop in the algorithm, in every simulation, on every time step. This is something we must optimize with pre-calculations. We therefore pre-interpolate volatilities in time on initialization, so we only conduct one-dimensional interpolations in spot in the simulation. We also pre-calculate the ![]() s and their square roots.
s and their square roots.
Finally, we refer to our cache efficiency comments from Chapter 1. We will be interpolating in spot at simulation time, so our pre-interpolated in time volatilities must be stored in time major to be localized in memory in spot space, even though the matrix as a model parameter is spot major in our specification: ![]() not
not ![]() .
.
Having discussed the challenges and the solutions specific to Dupire's model, we list the code below. The model mainly follows the same pattern as Black and Scholes, somewhat simplified in the absence of rates and dividends, the only differences coming for the local volatility matrix and its interpolation. We reuse our matrix class from Chapter 1 in the file matrix.h. We also need a few utility functions. One is for linear interpolation (with hard-coded flat extrapolation):
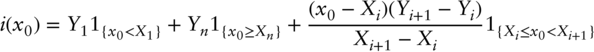
The code is in interp.h file in our repository and listed below.

We coded the function generically, STL style. The ![]() s and the
s and the ![]() s are passed through iterators, the type T of
s are passed through iterators, the type T of ![]() is templated, and the return type is deduced on instantiation. To code this algorithm generically is not only best practice, it is also convenient for our client code, where we will be using it with different types and different kinds of containers.
is templated, and the return type is deduced on instantiation. To code this algorithm generically is not only best practice, it is also convenient for our client code, where we will be using it with different types and different kinds of containers.
The return type is auto, with a trailing syntax that specifies it:
all of which is specialized C++11 syntax meaning “raw type of the elements referenced by the iterator yBegin, with references removed,” or more simply the “type of the ![]() s.” The reason for the complications is that the
s.” The reason for the complications is that the ![]() s are passed by iterator.
s are passed by iterator.
We need another utility function to fill a schedule with additional time steps so the spacing would not exceed a given amount. That is how we produce a simulation timeline out of the product timeline, as explained on page 195. The following code is in utility.h:

The routine takes the product timeline, adds some specified points that we may want on the timeline, fills the schedule so that maxDx is not exceeded, and does not add points distant by less than minDx from existing. It is coded in a generic manner, in the sense that it doesn't specify the type of the containers or the type of the elements, although the code is mostly boilerplate.
The code for the model itself is listed below. It is very similar to the Black and Scholes code, the differences being extensively described above.





Note that the local volatilities are stored in the templated number type, whereas their labels (spots for rows and times for columns) are stored in native types (doubles and times, which is another name for a double in our implementation). Similarly, all the computations related to timelines use native types. We will see in Part III that those amounts are inactive; they don't contribute to the production of differentials. It is a strong optimization to leave them out of differentiation logic. A practical means of doing this is store them as native number types. The details will be given in Chapter 12. The RNGs are untemplated for the same reason.
The simulation timeline is computed in ![]() , where we build the simulation timeline from the product's event dates, and insert additional steps, keeping track of which time steps on the simulation are original event dates and which are not, so we only apply the mapping
, where we build the simulation timeline from the product's event dates, and insert additional steps, keeping track of which time steps on the simulation are original event dates and which are not, so we only apply the mapping ![]() on the event dates, as explained on page 195. Local volatilities are interpolated in time over the simulation timeline on initialization, and in spot during simulations in
on the event dates, as explained on page 195. Local volatilities are interpolated in time over the simulation timeline on initialization, and in spot during simulations in ![]() .
.
Dupire has a large number of parameters: all the cells in the volatility matrix, making it an ideal model for the demonstration of AAD. The constructor carefully labels all the parameters so client code can identify every local volatility with the corresponding spot and time.
6.5 USER INTERFACE
We have everything we need to run the library and price concrete products with concrete models. One of the benefits of a generic architecture is that we can mix and match models and products at run time. A particularly convenient user interface is one that stores models and products in memory, by name, and exports a function that takes the name of a model, the name of a product, and executes the simulation.
The code to do this is in store.h in our repository. It uses hash maps, a classic, efficient data structure for storing and retrieving labeled data. Hash maps are standard C++11. The data structure is called unordered_map, it is defined in the header <unordered_map> and its interface is virtually identical to the classic C++ map data structure.6

We have a global model store that stores models by unique pointer under string labels, and another global product store for products. We implement functions to create and store models, one function per model type, and a unique function to retrieve a model from the map:

When a model is stored under the same name as a model previously stored, the store destroys the previous model and removes it from memory. We have the exact same pattern for products:

Even though this is not implemented to keep the code short, this is the ideal place to conduct some sanity checks: are spots and times sorted in the specification of local volatility? Is volatility strictly positive? A violation could cause the program to crash or return irrelevant results.
Finally, in main.h, we have the higher level functions in the library:

The first overload of ![]() accepts a model, a product, and some numerical parameters as arguments, runs the simulations, averages the results for all payoffs in the product, and returns them along with the payoff labels.7
accepts a model, a product, and some numerical parameters as arguments, runs the simulations, averages the results for all payoffs in the product, and returns them along with the payoff labels.7
The second overload picks a model and a product in the store by name and runs the first overload. It is the most convenient entry point into the simulation library.
Note that those functions have a boolean parameter “parallel” for calling ![]() in place of
in place of ![]() . The template algorithm
. The template algorithm ![]() is the parallel version built in the next chapter.
is the parallel version built in the next chapter.
The functions can be executed on the console with some test data, although it is most convenient to export them to Excel. We have included in our online repository a folder xlCpp that contains a tutorial and some necessary files to export C++ functions to Excel. The tutorial teaches this technology within a couple of hours, skipping many details. A detailed discussion can be found in Dalton's dedicated [79].
The code in our repository is set up to build an xll. Open the xll in Excel, like any other file, and the exported functions appear along Excel's native functions. In particular, xPutBlackScholes, xPutDupire, xPutEuropean, xPutBarrier, xPutContingent, xPutEuropeans, and xValue are the exported counterparts of the functions in store.h and main.h listed above.
Readers can easily build the xll or use the prebuilt one from our repository (they may need to install the included redistributables on a machine without a Visual Studio installation) and price all the products in all the models with various parameters. We detail below some results for the barrier option in Dupire. Barriers in Dupire are best priced with FDM, very accurately and in a fraction of a millisecond. However, many contexts don't allow FDM and the purpose of this book is to accelerate Monte-Carlo as much as possible. The test below is therefore our baseline, which we accelerate with parallelism and AAD in the rest of the book.
Finally, the spreadsheet xlTest.xlsx in the repository is set up to work with the functions of the library in a convenient Excel environment, and, among other things, reproduce all the results and charts in the publication. The xll must be loaded in Excel for the spreadsheet to work.
6.6 RESULTS
We set Dupire's model with a local volatility matrix of 60 times and 30 spots, monthly in time up to 5y, and every 5 points in spot (currently 100), from 50 to 200. We set local volatility to 15% everywhere for now8 so our Dupire is really a Black-Scholes. We value a 3y 120 European call, with and without a knock-out barrier 150, simulating and monitoring the barrier over 156 weekly time steps. The theoretical value of the European option is known from the Black and Scholes formula, around 4.04. For the discrete barrier, we use the result of a simulation with 5M paths as a benchmark, where Sobol and mrg32k3a agree to the second decimal at 1.20.9 We simulate with Sobol and mrg32k3a, resetting mrg32k3a seeds in between simulations to produce a visual glimpse of the standard error. Results are shown in the charts below.


These confirm that convergence is slow with Monte-Carlo: it takes a large number of paths, at least 100,000, to obtain results accurate within the second decimal. Sobol converges faster and in a more reliable manner, with estimates within ![]() of the benchmark with 100,000 paths or more. Although Sobol errors may be as large with a small number of paths, its convergence speed is visibly superior.
of the benchmark with 100,000 paths or more. Although Sobol errors may be as large with a small number of paths, its convergence speed is visibly superior.
On our iMac Pro, it takes around 3 seconds with 500,000 paths to obtain an accurate price (for the European and the barrier simultaneously, as discussed on page 234) with either mrg32k3a or Sobol. Both return 1.20 for the barrier, correct to the second decimal. Sobol returns 4.04 for the European, correct to the second decimal. Results obtained with mrg32k3a depend on the seeds; with ![]() we got 4.00.
we got 4.00.
In the context of a European or barrier option in Dupire's model, results of a comparable accuracy could be obtained with one-dimensional FDM, with 150 nodes in spot and 100 nodes in time, in less than a millisecond. In this instance, FDM is around 3,000 times faster than Sobol MC. We reiterate, however, that FDM is only viable in specific contexts with low dimension, Monte-Carlo being the only choice in a vast majority of practical situations. The purpose of the parallel simulations of the next chapter, and the constant time differentiation of Part III, is to bring FDM performance to Monte-Carlo simulations.
This example constitutes the baseline to measure the improvements of the next chapter and the performance of AAD in Part III. The timing of our serial Monte-Carlo, in this example, is around 6 microseconds per path. We shall revisit this example with the parallel implementation of the next chapter, and the AAD instrumentation of Part III.
