Products and cash-flows

We therefore define a financial product as a collection of cash-flows paid over a given schedule. The payment schedule can be either discrete, in which case the product is a set of cash-flows paid on dates , or continuous, in which case the product is a continuous set of cash-flows paid over the time interval , being the payment date of the last cash-flow, called the product's maturity.

Valuation is linear, so the value of a product at a time is the sum of the values of its subsequent cash-flows: .

Cash-flows may be deterministic, linear in underlying asset prices, optional, or exotic. In its most general form, a cash-flow paid at time is a -measurable random variable. This means that it may depend on the state of the market on and before its payment date , and is fully determined at . Formally, is a functional of the path (which we also call scenario) and denote:

where is the “state of the market” at time (which we call sample): the values at time of the market variables that affect the cash-flow.

A European call of strike and maturity on some underlying asset pays one cash-flow:

at maturity. A call up and out on a barrier also pays one cash-flow but it is contingent on not breaching the barrier before maturity:

The floating leg of an interest rate swap (IRS) pays Libor coupons over a discrete schedule; for instance, a quarterly floating leg pays 40 cash-flows:

where is the Libor rate of matuirty fixed at .¹

Scenarios

A cash-flow paid at time depends on the scenario, generally defined as the evolution of the market up to the maturity, but its specific meaning depends on the cash-flow: for a European call, the scenario is the underlying asset price at maturity. For a barrier option, it is the continuous path of the underlying price series from now to maturity. For an interest rate swap (IRS), the scenario is the discrete set of Libor fixings on the floating schedule. Cash-flows don't depend on the complete state of the world market at all times in . Depending on the particular cash-flow, the scenario is specified by two characteristics:

1. The subset of of dates where the state of the market affects the cash-flow, called timeline. For a European call, the timeline is the maturity date: . For a barrier, it is the entire interval .

   A product's timeline is the union of its cash-flows timelines. The dates in the timeline are called event dates; they are the contractual dates where something meaningful happens to determine the cash-flows, in reference to the state of the market on those dates: the exercise of a call, the monitoring of a barrier, the fixing of a Libor, or the payment of a cash-flow. For the floating leg of an IRS, the timeline is the discrete set of fixing and payment dates on the floating schedule.

2. The nature of the sample for every event date on the timeline. For a European call or a barrier option, this is the underlying asset price on time . For a floating leg cash-flow, it is the Libor of a given maturity fixed at . In general, a sample for the event date 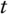is a collection of market variables (asset prices, rates,…) observed at time . It is the snapshot of the fraction of the market at time that is useful for the determination of the cash-flows. In principle, its dimension could be infinite or even continuous. The dimension and contents of different samples on the timeline may be different from one another.

   The time sample for a product is the union of the time samples of its cash-flows. The collection of all the samples across the timeline is called scenario, and denoted .

The scenario is therefore a multidimensional, and sometimes continuous, collection of samples over a timeline. The timeline, and the nature and the dimension of its samples, depend on the product. The cash-flows are a function(al) of the scenario, more precisely, of the scenario before the payment date:

Underlying assets

The notions of products, cash-flows, timelines, samples, and scenarios are the building blocks of the product side of a generic financial library (the other sides being models, discussed next, and algorithms that articulate the two to produce values and risk, like the Monte-Carlo simulations of the next chapter). We illustrate these notions with a few examples, starting with the underlying assets. Underlying assets, like stocks or currencies, are not exactly financial products, but they can be modeled as financial products with the introduction of a holding horizon . A stock is not a financial product, but the strategy of buying the stock and holding it to some horizon is one.

A stock without dividends, with value at time , can be assimilated, given a holding horizon , to a financial product with a single cash-flow on the horizon date . The timeline is therefore the singleton and the scenario is .

With a discrete schedule of dividends paid on times , a stock is modeled as a schedule of cash-flows , plus a final cash-flow . The timeline is the set of ex-dividend dates before horizon , plus the horizon date , and the scenario is .

A stock or stock index with a continuous dividend yield is modeled as a continuous schedule of cash-flows and a final cash-flow . The timeline is the interval ; the scenario is .

A foreign currency, which is economically identical to a stock with dividend yield the foreign short rate, is modeled as a financial product in the same way.

In interest rate markets, the notion of “underlying assets” is typically associated with zero-coupon bonds, although they are not directly traded instruments. The zero-coupon bond of maturity is a financial product that pays a unique cash-flow of one monetary unit at time . Its timeline is . Its cash-flow is deterministic and independent of a scenario.

The value of a zero-coupon bond of maturity at a time , denoted , acts as a conversion rate between payments at and , the value at of a cash-flow known at (-measurable) and paid at being . For this reason, zero-coupon bond prices are also called discount factors. Evidently, .

The collection of discount factors of all maturities at time is called the discount curve at . The discount curve is part of the market state at . Discount factors are market primitives and may be part of samples in a scenario. What discount maturities are included in what samples depends on the product and its cash-flows. In general, a cash-flow doesn't depend on the whole collection of discount factors on an event date , but on a smaller number of discounts of a specific set of maturities . The set of discount maturities in the sample is part of the product-specific definition of the scenario.

Finally, the discount curve can be expressed in price units, discount factors, or in rate units,

is called discount rate of maturity . The quantity:

is called instantaneous forward rate (IFR).² It follows immediately that:

and the short rate at time is defined as .

Linear transactions

A forward contract with strike and maturity on an underlying asset is a financial product paying a unique cash-flow at date . Its timeline is the singleton and the time sample is the scalar .

On a date , the unique strike such that the value of the corresponding forward contract is 0 is called the forward price of and denoted . Forward prices are part of the market state at time , and it is best, in order to accommodate a wide range of products and models, to consider forwards as market primitives and parts of samples in the scenario. In this case, we don't need spot prices in the samples, since .

What forwards of what maturities are part of the samples depends on the exact nature of the cash-flows, same as discount factors. For instance, a forward contract depends on the sample so in this case, .

In interest rate markets, a forward rate agreement (FRA) pays on date ,³ where is the Libor rate fixed at for maturity . The FRA's timeline is the union of its fixing and payment dates and its dependency is on the sample on the fixing date . Why is on the timeline without a sample will be clarified when we move on to pricing, and realize that we are missing “something” on the payment dates samples.

On a date , the unique strike such that the value of the corresponding FRA is 0 is called forward rate, or forward Libor, and denoted . We consider forward Libors as market primitives and part of samples in the scenario. Spot Libors are therefore not necessary, since .⁴

What forward Libors of what start and end dates and what index are included in the samples is something specified from the nature of the cash-flows. For instance, a FRA of maturity on a 3m Libor (“3m” referring both to the Libor's duration and to its index) pays on time . Its timeline is , and it is determined by the time sample . It follows that , one Libor being defined, in addition to its fixing date, by two dates and an index.

Since the cash-flow is known at time and paid later, we can equivalently model this FRA as the cash-flow:

paid at time . We used the discount factor to convert an amount paid in 3m into an amount paid immediately. This allows to reduce the timeline to the singleton but increases the sample to include the discount factor: . In this case, and .

An interest rate swap (IRS) is a financial product that exchanges a fixed leg for a floating leg. The payment schedules of both legs share a common start date and end date but they typically have different periods and , hence a different number of coupons and . In a receiver swap, the fixed leg pays the coupons on dates and the floating leg pays the coupons on dates . A payer swap pays the opposite coupons. The timeline of an IRS is the union of the fixed and floating schedules. The scenario that determines an IRS is the sequence of Libor fixings over the floating schedule.

The fixed coupon such that the value of the swap is 0 on a date is called “par swap rate,” or sometimes “forward swap rate.” Par swap rates are not market primitives; we will see shortly that they are expressed in a simple, universal, and model-independent manner from forward Libors and discount factors.

Forward contracts, FRAs, and IRS are all examples of a particular type of financial products called linear products. Linear products are defined as schedules of linear cash-flows. Linear cash-flows are often defined as linear functions of the scenario, although this definition is approximate and in some cases incorrect. The definition of linear cash-flows is related to valuation, as we will see shortly.

European options

Traditionally, European options are those that depend on a single observation of an underlying market variable on a single event date. We go with this definition for now, although it is somewhat blurry in our context. We will correctly define European products later, when we move on to valuation.

For now, a cash-flow is called European if it depends on a single observation, on a single event date, of a single market variable: where is a scalar market variable. The timeline of a European cash-flow is a singleton , called “maturity,” “expiry,” or “exercise date” depending on the product. The cash-flow is a function (not a functional) of the scalar .

When , the cash-flow is a European call. When , it is a European put. More generally, any smooth function can be written as:

This is known as Carr-Madan's formula [28] and shows that all European cash-flows are combinations of calls and puts. Carr-Madan's formula is demonstrated with simple calculus and remains valid when is discontinuous, as long as derivatives are read in the distributional sense of Laurent Schwartz.

A European call (respectively put) on a Libor is called a caplet (floorlet). A succession of caplets (floorlets) over a floating schedule is called a cap (floor).

A cash-settled swaption pays a single cash-flow on its exercise date :

for a payer swaption, or replace the right-hand side with for a receiver swaption, where is the par swap rate on the exercise date. A swaption's cash-flow is a function of the par swap rate, which is not a market primitive, but an aggregate of a number of discount factors and forward Libors as we will see shortly. A swaption may therefore appear not stricto sensu European.⁵ We will revisit swaptions shortly.

A financial product is called European if all its cash-flows are European (European products may also include multiple European cash-flows on the same date, on different underlying variables). All the linear products we introduced previously are European products. Nonlinear European products are called European options.

Path-dependent exotics

Cash-flows that are not linear or European depend on multidimensional samples on multiple event dates, in a nonlinear manner. Products that involve such cash-flows are collectively known as exotics. Cash-flows that depend nonlinearly on multidimensional samples are called “basket options.” Those depending on multiple samples prior to their payment dates are called “path-dependent.” When a party holds the contractual right to cancel, redefine, or alter cash-flows in any way, the product is said to be “callable” or “early exerciseable.” Those categories are not mutually exclusive.

The timeline of path-dependent cash-flows includes, by definition, multiple event dates. A textbook example is a barrier option⁶ on some underlying asset . A barrier delivers the cash-flow of a European call or put at maturity, but only when the underlying asset price remained below (up and out) or above (down and out) a predefined level called barrier and denoted , at all times before maturity. The cash-flow of an up-and-out call, for example, is:

where . Its timeline is therefore the continuous interval and it is a functional of the continuous scenario . Many other variations exist, like knock-in barriers, which pay only if the barrier was breached, American digitals, which pay a different amount depending on whether the barrier was breached or not, double barriers (those with a down barrier and an up barrier, sometimes called corridors), and all the imaginable combinations of these.

One important variation for Monte-Carlo simulations is the discretely monitored barrier. In this case, the payment is subject to not breaching (knock-out) or breaching (knock-in) the barrier over a discrete timeline, irrespective of what happens in between the observation dates. The timeline is the discrete union of the monitoring schedule with the fixing and payment dates of the cash-flow. The scenario is the spot price on the event dates in the timeline.

American options and cancellable products

Moving on to callable products, we introduce the two most common types of early exerciseable transactions, American options and cancellable products.

American options are those exerciseable at any time before maturity into a cash-flow for an American call or for an American put. The party who holds the right to exercise does so on the first occasion when the exercise cash-flow exceeds the continuation value of the option (the value immediately after if not exercised). An American option's payment schedule and its timeline are therefore both the continuous interval and its cash-flows are defined by:

where tracks whether the option is still alive and defines the exercise cash-flow. We have a product which cash-flow at depends on the product's value on and before . We have seen that the product's value at time is the sum of the values at of all the cash-flows paid after . Hence, values depend on cash-flows and cash-flows depend on values. In addition, the continuation value depends not only on the state of the market at , but also on the option pricing model.

American options therefore involve an undesirable coupling between the product and the model and a recursive relationship between values and cash-flows.

Cancellable products are those where a party has the right to cancel all the subsequent cash-flows on a set of exercise dates. A cancellable product's timeline is the union of the timeline of its non-callable counterpart with the exercise dates. When the non-callable product pays the cash-flows on times , the callable product's cash-flows are defined with:

where is 1 before cancellation and 0 thereafter, hence and is updated on exercise dates with:

where is the time value of all subsequent cancellable cash-flows. Again, cash-flows depend on future values in a recursive manner, and the definition of the cash-flows depends on the model. This is a defining characteristic of callable products; it is what makes them special and the reason why they require special modeling.

In the somewhat simplified case of a cancelable product with one exercise date, sometimes called “one-time callable,” the cash-flows are the cash-flows of the non-callable counterpart before the exercise date , and:

after the exercise date, so the cash-flows are still dependent on a future value, but this is the future value of the non-callable counterpart, not the value of the callable product itself. The recursive relationship is gone, but the dependency on a future value and a model remains.

For instance, a physically settled swaption is the right to enter the underlying swap, or, equivalently, the right to cancel its cash-flows. It is therefore a one-time callable swap, which pays the cash-flows of the underlying swap, provided its present value on the exercise date is positive:

We will see shortly that is an explicit function of the forward Libors on the exercise date with maturities the start and end dates on the floating schedule, and the discount factors to the payment dates of both legs. It follows that:

All these discounts and forward Libors are therefore included in the swaption's sample on the exercise date: , , and:

so:

Seen from this angle, the swaption is no longer a callable product, but fits the definition of path-dependent products. We will see shortly that we can also consider it a European option that delivers the present value of the underlying swap on the exercise date.

Turning callables into path-dependents

Callable products are therefore those whose cash-flows depend on the future values of themselves, and/or the future values of financial products other than primary market variables. How algorithms deal with them depends on the algorithm. We will see shortly that finite difference methods (FDM) cope with callable features in a native and natural manner. On the contrary, Monte-Carlo naturally handles path dependency, but doesn't know future transaction values and cannot handle callable features. In order to price a callable transaction with Monte-Carlo, we must first transform the transaction into an equivalent path-dependent, like we just did for a swaption.

In general, unlike for the swaption, we don't have an analytic expression of the future values, so we must somehow estimate them as a function of the market:

where is called a proxy function and the sample is the set of market variables on it accepts as arguments, which must be included in the scenario in order to use the proxy.⁷ Using proxies, the cash-flows of the American option simplify into:

and the cash-flows of an early cancellable transaction simplify into:

In both cases, the explicit dependency on future values vanished and the modified cash-flows fit the definition of classic path-dependents. The injection of proxies effectively turns callables into path-dependents.

It is also noticeable that proxies only appear in exercise indicators. On an exercise date, the set of sample values that cause early exercise is called the exercise region. The border of the exercise region is called the exercise boundary. The problem of finding effective proxies boils down to the estimation of exercise boundaries.

In the context of FDM, exercise boundaries are directly estimated on the FDM grid, as we will see shortly. In the context of Monte-Carlo, proxies are estimated by regression over pre-simulations, with an algorithm known as the least squares method or LSM, pioneered by Carriere in [13] and Longstaff and Schwartz in [14]. Proxies obtained with LSM are called regression proxies. The LSM algorithm is the established best practice for pricing callables with Monte-Carlo since the early 2000s. We briefly introduce it in the next chapter.

CVA

Finally, it is important to understand that counterparty value adjustment (CVA), along with most other value adjustments (xVA) and other bank-wise regulatory calculations, can be modeled as a financial product. This is crucial, because it follows that the models we develop for financial products are also suitable for these calculations. CVA is a real option a bank gives away whenever it trades with a defaultable counterparty. If the counterparty defaults on a future date when the net sum of all ongoing transactions with that counterparty (called netting set) is positive, the bank loses the positive value of the netting set. This is a one-way street, hence, really an option: if , the liquidator will insist that the bank refunds its value. CVA is therefore a zero-strike put, contingent to default, on the entire netting set, consisting itself in thousands of transactions, each one of which is a financial product in its own right, perhaps exotic or hybrid. The difficulty of computing CVA in a practical manner, and in reasonable time, is directly related to the high dimension of the “underlying” netting set.

In its simplest form, an uncollateralized CVA, defined in a discrete manner and without recursion, is modeled as a financial product that pays, over an exposure schedule , where and , the payment date of the last cash-flow in the netting set, the cash-flows:

where is the proportion defaulted between and .⁸

The cash-flows of a CVA therefore depend on the future values of the netting set, so everything we said about callable products applies to CVA, too.⁹ In addition, CVA cannot be valued with FDM due to its high dimension, so proxies are necessary there, too.¹⁰

In addition, CVA depends on credit, so the scenarios must be enlarged to incorporate credit variables and credit events, something we are not doing in this publication. The future values of the netting set typically depend on a vast number of market variables from different asset classes: stocks, rates, currencies, etc. CVA is therefore a hybrid option, which valuation necessitates a hybrid model (essentially, an assembly of multiple models driving the different underlying markets, brought together and made consistent and arbitrage-free; see [7]).

Due to the dimension of the model and the size of the market samples, Monte-Carlo is the only practical means of pricing CVA. To generate high-dimensional market samples in reasonable time may be challenging; see [7]. The netting set's timeline, which is the union of the timelines of all the transactions, is typically dense, further slowing down evaluation, unless compression techniques, introduced in [30] and [11], are implemented. A reasonably fast generation of scenarios is not enough. To evaluate the large number of cash-flows in the netting set in every scenario is another bottleneck. Our publication dedicated to scripting [11] covers general, efficient means of representing and manipulating cash-flows, which helps with the aggregation and compression of the cash-flows, as well as a fast evaluation over the generated scenarios.

It follows that even though CVA may be seen as another financial product and evaluated in a hybrid platform, it remains that its size raises specific problems when we wish to price it in a practical manner and in reasonable time. Although this publication covers major ground for the efficient management of CVA, including generic simulation, parallelism, and AAD, it does not cover all the pieces, in particular, the representation and manipulation of cash-flows, the application of regression proxies, and some important algorithms specifically designed for the acceleration of xVA and explained in [31].

The Asset Pricing Theorem

We state the fundamental asset pricing theorem here, referring to the original articles or textbooks for demonstrations. In the absence of arbitrage, and in complete markets (both of which we assume in all that follows):

1. Financial cash-flows can be replicated by self-financing strategies.

   A self-financing strategy is a dynamic trading strategy over a time interval, without injection or withdrawal of cash or assets (hence, self financing), that consists in holding, at time , the underlying assets that constitute the market, of prices , in the amounts .

   A self-financing strategy is specified by the vector process . The vector , the amounts of assets held at time , must be -measurable, which means that they are determined at time 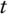, from the state of the market on a before , but not after.¹²

   It follows from this definition that the value series of a self-financing strategy is an adapted process satisfying:

   

   with . One trivial, yet important, self-financing strategy is leave compounding at the short rate on a bank account. This strategy is traditionally called “bank account,” and its value, denoted , is of course:

   

   What the theorem says is that for any financial cash-flow (defined as a -measurable variable) paid at time , there exists a self-financing strategy such that the value of the strategy replicates the cash-flow at time with probability 1:¹³

   

   The amounts of assets held in the replication strategy are called replication coefficients, hedge coefficients, or just “deltas.”

   The value of the cash flow at a time is the value of the replicating strategy.

2. There exists a unique probability measure, equivalent to the “real” probability measure,¹⁴ denoted and called risk-neutral measure, such that the discounted values of all financial cash-flows are martingales under :
   
   for any .

   One consequence is that the value processes of all cash-flows have a drift equal to under .¹⁵ It is also the case for financial products, in between the payment of cash-flows (the value of a product dropping by the cash-flow on a payment date).

   Another consequence is the fundamental pricing formula:

   
3. The value is a function of the market state on and before , including the current values of the underlying assets in the current market. The replication strategy, the amounts of underlying assets to trade at time to replicate a cash-flow , are the derivative sensitivities of to these underlying prices:
   
4. More generally, the drift of the value process of any self-financing strategy under is , and conversely, any adapted process with drift , under is the value process of a self-financing strategy, and therefore, the price series of a tradable asset.

This theorem guarantees that the market risk of financial products can be covered with trading strategies, justifies the universal practice of measuring risk by taking derivatives of transaction values to current market prices, and provides a general pricing formula for all financial products.

Later work precised, confirmed, and extended this fundamental theorem. For instance, it was no earlier than 2009 that it was finally demonstrated, indisputably and in the most general case, that derivative sensitivities effectively always correspond to hedge coefficients. The demonstration is due to Dupire, who had to develop a new branch of stochastic mathematics, called “stochastic functional calculus,” to obtain this result [34].

Pricing with a numeraire

Another extension, extremely useful for analytic calculations and numerical implementations, including Monte-Carlo, was introduced in 1995 by El-Karoui, Geman, and Rochet [35]. The bank account is not the only choice of numeraire: any (strictly positive) self-financing strategy may be used as numeraire, including positive financial cash-flows and products, before payment.

For every such choice of a numeraire , there exists a unique probability measure , equivalent to , such that all asset values (in between payments) in terms of are martingales under :

where . In particular, the value of a cash-flow paid at time satisfies:

and with without loss of generality:¹⁶

Remembering that cash-flows are defined as functionals of scenarios:

and that product values are the sum of the values of their cash-flow, it follows that the value of any financial product with cash-flows paid on dates satisfies:¹⁷

We augment the definition of scenarios and samples¹⁸ to include the numeraire on payment dates, so that:

The functional of the scenario, including the numeraire on payment dates, is called payoff, and we get the classic result that the value of a financial product is its expected payoff:

Forward measures

Besides the bank account , a number of useful numeraires have been widely used in investment banks and universities to resolve analytic and numerical problems. We will see a few in this chapter, and demonstrate a simple change of numeraire in the code of Chapter 6.

For now, we introduce a particularly useful family of numeraires: the zero-coupon bonds. A zero-coupon bond of maturity satisfies the criteria of a numeraire. The associated martingale measure is called forward measure for a reason that will be made apparent shortly. The forward measure is often denoted and expectations taken under this measure are denoted .

One of the multiple benefits of forward measures is that they provide the means to price linear products directly and independently of a model.

Forward prices and forward contracts Let us revisit a forward contract of maturity and strike on an asset , and price it under the measure. From the fundamental pricing formula, we immediately get:

since . Solving for in the strike to find the forward price , we get:

Forwards of maturity are expectations under the martingale measure associated with the zero-coupon bond of maturity , hence its name “forward measure.” It also follows that forwards of maturity are martingales under , in particular:

These formulas are not particularly helpful for pricing, since today's forwards trade in the market. We know their prices. Where they are helpful is the other way around: the forwards that trade on the market today imply the means of forward-neutral measures.

Another trivial consequence is that the value of a forward contract is . Setting , we get the time value of an asset delivered at time :

Forward rates and FRAs The same can be said of FRAs in interest rate markets. A FRA over the period pays a cash-flow on date , hence, we value it under :

Solving in , we find that the forward Libor is the forward-neutral expectation of the Libor:

and a martingale under . Today's Libor curve implicitly defines the expected values of future Libors under the forward-neutral measures for their end dates. In addition, the value of a FRA is . Setting , we see that the time value of a paid at is:

Forward discount factors and instantaneous forward rates Consider now a product that delivers a zero-coupon bond of maturity at a time . Its value is obviously . From the valuation formula under , we get:

We know, now, that forward-neutral expectations are forwards. It follows that the forward price of maturity of the zero-coupon bond of maturity satisfies:

In addition, the value series of a forward discount factor of maturities is a martingale under . It follows that today's discount curve fixes the forward-neutral expectations of future discount factors.

The amount

is called forward discount rate, and effectively corresponds to the rate of a loan from to that may be locked at time by selling zero-coupon bonds of maturity and buying zero-coupon bonds of maturity for the same total price.

Denoting and considering the limit case where , we get the time instantaneous forward rate of maturity :

which we had defined before, only now we can see where this definition comes from and why the short (discount) rate is effectively .

Forward bank account Another example is the bank account . is a martingale under , therefore:

Since forward-neutral expectations are forwards, it follows that is the forward value of the bank account at time for the maturity . In particular, we have today's value of bank account forwards of all maturities:

Interest rate swaps It immediately follows from what precedes that the value on an IRS (a receiver swap in this instance) is:

and, solving for in to get the par swap rate , we get:

This formula is universal and model independent, which implies that the par swap rate is a redundant market primitive, hence, not directly included in scenarios. The denominator is called the annuity of the fixed leg. The annuity is a combination of zero-coupon bonds, hence, a tradable asset, with time value:

On the par swap rate formula, we recognize that is the value at time of the floating leg in terms of the annuity:

It follows that is a martingale under the martingale measure associated with the annuity.

Also note that the formula of the value of a (receiver, in this instance) IRS can be rearranged into:

Swaption pricing A physically settled payer swaption (right to enter the underlying payer swap) of strike on the exercise date is the value, if positive, of the underlying swap on the exercise date:

We can therefore price it under the annuity-neutral measure:

where the payoff is that of a standard put (for a payer swaption, it is a call) on the swap rate, which itself is a martingale. This is the theoretical basis for pricing swaptions under models like Black-Scholes [22] or SABR [36]. These established market practices therefore implicitly, and correctly, manage swaptions under the annuity-neutral measure. Assuming a constant volatility as in Black and Scholes's specification, is given by Black and Scholes' formula [22]. Assuming is a stochastic volatility martingale as in SABR's specification, is given by Hagan's formula [36].

Natural numeraires We demonstrated that forward prices , observed at with maturity , are martingales under the forward measure associated with the zero bond of maturity , the maturity date of the forward. This zero bond and forward measure are respectively called the natural numeraire and the natural measure of the forward .

In particular, the spot price on time coincides with its forward . Its natural numeraire is therefore the zero bond of maturity , and its natural measure is . Forwards are expectations of asset prices under their natural measure.

This is true of all asset prices. In particular, the forward price of the bank account on time is its expectation under its natural measure .

The forward discount factor:

is a martingale under . Therefore:

The natural measure of the discount factor , observed at time with maturity , is therefore . The expectation of a discount factor under its natural measure is the corresponding forward discount factor observed today. Its natural numeraire is the zero bond of maturity .

A forward Libor observed at time with maturities is a martingale under its natural measure , associated with its natural numeraire, the zero bond of maturity . In particular, a spot Libor observed at with maturity coincides with the forward on the fixing date. It follows that the expectation of a Libor under its natural measure is the forward Libor. Its natural numeraire is the zero bond of maturity the Libor's payment date.

Finally, we have seen that the par rate of a given swap, paid over the annuity of the swap's fixed leg, is a martingale under . is therefore the swap rate's natural measure, and the fixed leg's annuity is its natural numeraire.

Every observation of a market variable fixed at time admits a natural measure, such that conditional expectations of under the natural measure are, by definition, the forward values observed at time of the cash-flow at time . It follows that those forward values are martingales under 's natural measure. The numeraire associated to the natural measure of an observation is called its natural numeraire. The notion of natural numeraire and measure depends on the nature of the market variables, and we have seen that prices, Libors, discounts, bank accounts, and swap rates define their natural measures in a different way. In addition, natural measures relate to observations: two observations on different dates of the same variable have different natural measures and numeraires.

In economic terms, the observation of a market variable always expresses the value of an asset in terms of a unit. This unit is the observation's natural numeraire. The market price of an Apple share on 30 September 2025 expresses the value of a fraction of Apple in terms of 30/09/25 USD. Its natural numeraire is the USD denominated zero bond of maturity 30/09/25.

In formal terms, the natural numeraire of an observation is the numeraire such that under any complete and arbitrage-free probabilistic specification with correct initial values, corresponds to the forward price observed at of the cash-flow . This is rather abstract, but in practical terms, for a given observation of a market variable, it is generally quite clear what its natural numeraire and measure are. In particular, for the market variables that populate market samples:

1. The natural measure for a forward price is , including spot prices with natural measure .
2. It directly follows that the natural measure for a discount factor , or the bank account observed at , is also .
3. The natural measure for a forward Libor is , including spot Libors 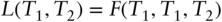with natural measure .

Constant Maturity Swaps We computed the values of all the linear transactions introduced earlier: forward contracts, FRAs, IRS, without specifying a model, directly, as a function of the forward prices, forward rates, and discount factors trading on the current market. This is a defining characteristic of linear products: linear products are financial products whose value depends on the current market, independently of a model. It follows that today's value of linear products is the same in any arbitrage-free model that respects today's market. We just saw that forwards are expectations under natural measures, so we have a clean definition of linear products:

Linear products are those whose value depends on expectations, but not distributions. It follows that the value of any linear product is a linear combination of the present values of a number of forward contracts, hence the name “linear” products.

This (correct) definition of linear products conflicts with the (approximate but widely accepted) one of products where cash-flows are linear functions of scenarios. Consider a cash-flow , linear in the market variable fixed on . We now know that its value satisfies:

When is 's natural measure, is its forward, therefore:

and it follows that the cash-flow is indeed a linear one. When this is not the case, and 's natural measure :

The difference between the two expectations and is called convexity adjustment and can be calculated with Girsanov's theorem, but only under dynamic assumptions on the future behavior of , in particular its volatility. It follows that the cash-flow is not a linear one, but a European one (because it depends on a single variable on a single date).

To see that clearly on an example, a Libor is a linear cash-flow when paid at . Its value is then:

as seen earlier. When paid at , its value is:

and:

Ignoring discount basis and assimilating:

the cash-flow paid at is equivalent to a payment, under the underlying Libor's natural numeraire, of:

which clearly identifies the cash-flow as a nonlinear quadratic function of the underlying Libor. Its linearity was only apparent. It is actually a European cash-flow. Under a simple model a la Bachelier [37] with Gaussian first increments with annual standard deviation , its value is:

(where we skipped trivial calculation steps). In a more general, non-Gaussian context, we can statically replicate this cash-flow, like any European cash-flow written on a Libor, with combinations of caps and floors, by an application of Carr-Madan's formula.

This is the cash-flow of a well-known, actively traded financial product called “Libor in arrears.” More generally, an actively traded family of financial products, called constant maturity swaps or CMS, pay cash-flows linked to libor or swap rates, over schedules different than their natural numeraire, resulting in nonlinear products, which value depends on volatility and dynamic assumptions. Like Libor in arrears, swap-based CMS are statically replicated with combinations of swaptions, with techniques similar to Carr-Madan's, as explained in [38].

Nonlinear products, like swaptions or CMS, cannot be valued out of the underlying market alone. Their value depends on volatility assumptions, and more generally, dynamic assumptions of how the market is going to evolve. This is the purpose of derivatives models.

Linear models

Linear models refer to what we have been calling so far “today's market.” They contain all the underlying asset prices, including dividend and repo curves, all the discount and Libor curves, and other variables that define the current state of the market. They “know,” among other things, the forward prices and discount factors of all maturities , as well as forward Libors of all maturities and , for all Libor indices.

Linear markets achieve this capability by interpolation of the available market information: spots, futures, par swap rates, basis and currency swaps, and so forth. This is not as easy as it may sound, especially since the multiplication of basis and discount curves in 2008–2011. To properly construct a linear market is a sophisticated, challenging exercise that occupies some of the greatest minds in the industry. We refer to [39] for a review of linear markets, including a presentation of the difficulties and the sophisticated solutions implemented in modern systems.

Mathematically, linear markets, who know all forwards, define the expectations of the s under their respective natural measures, but they know nothing else of their distribution , because they have no knowledge of their future dynamics. This transpires in the notations: linear markets know all the for all maturities , but nothing of the when . Linear markets are initial value conditions. They are the modern counterpart of the “initial spot ” found in traditional literature.

Why then do we call them linear models and discuss them in the model section here? We have defined a model by its ability to assign a probability distribution to a scenario. Linear models assign probability 1 to the forward scenario where every market variable lands, on its event date, on its forward value seen from today, which we have seen is its expectation under its natural measure :

This “probability distribution” of the scenario obviously respects initial conditions, and is trivially arbitrage-free, the discounted price series of all assets being (constant) martingales between payments. This is actually the simplest possible arbitrage-free model consistent with today's market.

It follows that the price of any financial product defined by its payoff and scenario in the linear model is:

which may explain why those models are called linear, although:

so the linearity of linear models is an approximate notion.

We priced a number of linear products in the linear model in Section 4.2, although we did not call it linear model at the time. The value in the linear model is called the intrinsic value of the product. For European options, this definition coincides with the traditional definition. For instance, for a European call, . Our definition extends the notion of intrinsic value to all financial products. The difference between the actual value and the intrinsic value is called time value: . Linear products are those whose time value is zero.²¹ The intrinsic value prices the linear part of a product and is independent of volatility or dynamic assumptions. The time value prices the nonlinear part of a product and depends on volatility and other dynamic assumptions.

From a practical point of view, pricing in a linear model is extremely fast, usually a fraction of a millisecond, because it takes a unique scenario. It is also very accurate because no numerical algorithm is involved. Linear models are suitable for Monte-Carlo simulations; in particular they fit the simulation model interface we build in Chapter 6, albeit in a trivial manner, since they generate only one scenario: the forward scenario . Generic, well-designed valuation systems price linear products (and the intrinsic value of other products, an interesting information in its own right) as a simulation in a single scenario.

More sophisticated models used for the valuation of nonlinear transactions can also price linear products, as a special case of options or exotics. Provided that the models respect today's market, the prices coincide with the linear model, but with lower speed and accuracy. Finally, note that those more sophisticated models coincide with linear models, not only for linear products, but for all products, when their volatility parameters are set to zero.²² Therefore linear models are also zero-volatility arbitrage-free dynamic models.

European models

Moving one step up to European models, we discuss those models appropriate for the pricing of European products, but not exotics.

We have seen that a European cash-flow of maturity is a combination of calls and puts on the same market variables, same maturity, and same payment date, as demonstrated by Carr-Madan's formula. It follows that a dynamic model is not necessary for the valuation of European cash-flows; all we need are the call prices of all strikes for the maturity .²³ European models, by definition, “know” these prices in the same way linear models “know” forward prices: by interpolation of available market data, in this case, the prices of calls and puts that trade on today's market.²⁴

Linear models generally interpolate discount factors not in price, but in rate. Similarly, options are typically interpolated not in their price , but in their Black-Scholes implied volatility , defined by:

where is Black and Scholes's formula [22]. We call implied volatility curve, or IVC, the continuous collection of Black-Scholes implied volatilities of a given maturity. An IVC of maturity , combined with a linear model for the forward and discount in Black and Scholes's formula, can price all European cash-flows of maturity . It follows that an interpolated collection of IVCs for all maturities , called implied volatility surface or IVS, can price all European cash-flows, hence, all European products.²⁵ In case a European product includes European cash-flows on different underlying assets, we need multiple IVS, one per underlying asset, although, in the interest of clarity, we just call IVS the collection of all call prices on all underlying assets.

European models, or IVS are we call them now, therefore build on the information contained in linear models, and inject additional information in the form of a continuous, bi-dimensional surface of Black-Scholes implied volatilities. We have seen that linear models define the expectations of the observations in a scenario under their natural measure. European models, or IVS as we call them now, define the marginal distributions of these observations under their natural measure. To see this, we apply the valuation formula to a call of strike , maturity :

Differentiating twice on both sides against the strike (in the sense of Laurent Schwartz's distributions,²⁶ we obtain:

where is the natural numeraire for the observation , and the normalized distribution is the price of the Dirac mass of in , called Arrow-Debreu security. The call prices of all strikes for a maturity are equivalent to the natural probability distribution of the underlying observation.²⁷ Hence, the IVS, which knows the call prices of all strikes and maturities on all relevant assets, also knows the marginal probability distributions of all the market variables in the scenario, called marginal distributions.

Because the IVS delegates forwards to the linear model, the means of the natural distributions s are the forwards of the observations . It follows that the IVS respects today's market and produces arbitrage-free marginal distributions. It does not produce arbitrage-free joint distributions between underlying asset prices on different dates, but, for European products, all that matters are the marginal distributions of the s.

The price of a European cash-flow paid on the natural payment date of an underlying observation is , the integral of the cash-flow's payoff against the distribution of its underlying observation specified in the IVS. In practice, this integral may be evaluated by numerical integration. Chapter 4 of Numerical Recipes [20] covers some efficient procedures and provides source code. Numerical integration consists in the approximation:

where the weights and the knots are carefully chosen by the numerical integration scheme. To price a European product, we may price all its cash-flows and sum them up, or we can price it all together with the help of a change of variable (assuming a discrete schedule of cash-flows and a discrete scenario here to simplify notations, although everything applies in the continuous case too):

where is the cumulative probability distribution of , known to the IVS, as well as its inverse. The value of the product is the sum of the values of its cash-flows:

The payoff function of the product is the sum of the payoff functions of its cash-flows, hence:

where, again, the weights and the knots are determined by the numerical integration routine, we used the property of European cash-flows where they each depend on exactly one , and the definition of should be clear for the context.

A numerical integration is typically extremely fast, of millisecond order, and very accurate, in particular compared to Monte-Carlo. This procedure can also price linear products (although slower and less accurately than linear models). But it cannot correctly price exotics.

The IVS correctly values European products because it knows the (natural) marginal distributions of all the observations in a scenario, but it knows nothing of their joint distribution, including the dependence of different underlying assets on the same date, or the dependence of the same underlying asset on different dates. The mathematical mapping of a number of marginal distributions into a single joint distribution is called a copula and there exists infinitely many copulas that join the same set of marginals into different joint distributions.

A defining characteristic of European products, and a better definition than the one stated earlier, is that these products depend on marginal distributions, but not on copulas (in the same way that linear products only depend on expectations but not distributions). European cash-flows are those whose payoff can be written as a function of one observation, under the natural numeraire of the observation. It follows that a defining characterization of non-European exotics is that they do depend on copulas. To see that on a simple example, consider the twice-monitored digital barrier that pays $1 if two fixings of the underlying asset price on two given dates and are both below a barrier :

Then:

In this formula, the terms and are European digitals that only depend on marginal distributions, but the term

clearly refers to their dependence.

To price this exotic with the IVS would result in a random and incorrect value. Random because the implementation of the IVS implicitly and arbitrarily chooses a copula: in our numerical integration the same quantiles were sampled simultaneously for all the marginal distributions. And incorrect because a random copula almost certainly results in an arbitrageable joint distributions, even when the marginal distributions are arbitrage-free.

Linear models define the expectations of underlying variables and correctly price linear products. European models inject additional marginal distributions around these expectations, and correctly price the time value of European products, in addition to linear products. The purpose of dynamic models is to produce an arbitrage-free, credible copula between the marginal distributions of the IVS, so as to correctly price not only linear and European products, but also exotics.

Dynamic models

To directly specify the copula is a perilous and probably impossible task. The copula must be specified in a way to produce an arbitrage-free, credible joint distribution, and it is unclear how this can be done, working directly on distributions.

To achieve this, dynamic models specify an arbitrage-free stochastic dynamic for the underlying market variables. They fit expectations by respecting the initial values given by the linear model. They fit marginal distributions by calibration to the IVS.²⁸ And they inject copulas, implicitly, with a credible, realistic, and arbitrage-free stochastic dynamics.

All dynamic models calibrated to the IVS produce the same marginals as the IVS, hence the same values for all European transactions. But models also implicitly specify a copula between these marginal distributions. It follows that two different models (say, one with local volatility and one with both stochastic and local volatility) both calibrated perfectly to the same IVS (which in this case is feasible) produce the same marginals but different copulas. It follows that they assign the exact same value for Europeans (modulo calibration and numerical error) but a potentially very different one for exotics. The sensitivity to the copula is a measure of model risk. It may be estimated by pricing an exotic or exotic book with different models calibrated to the same IVS. The price dispersion measures “how exotic is this particular exotic.”

For example, it was discovered by Dupire in [45] that a variance swap, which pays the realized statistical variance of an underlying asset price over a period, can be perfectly replicated by a combination of Europeans and a self-financing strategy, irrespective of any dynamic assumption. This theory is the basis of the VIX index published by the CBOE and widely considered as a primary measure of market nervousness. The details are explained, for instance, in the fourth part of [46]. It follows that the variance swap is completely insensitive to copulas, and priced identically (modulo numerical errors) in different models, as long as they calibrate to the same IVS.

As another example, Peter Carr's well-known static replication of barrier options [47] shows that (under some pretty strong assumptions) simple barrier options are also replicated by combinations of European options and trading strategies. It follows that barriers like down-and-out calls are not that exotic (with the barrier on the strike, the value of a down-and-out call is even linear in the underlying asset price in all continuous models) and their price in different models calibrated to the same IVS is very similar.

On the contrary, tight double no touches (options that pay $1 if the underlying asset price remains in tight corridor at all times for a period) have high volga (second derivative to volatility) and are therefore very sensitive to stochastic volatility. A stochastic volatility model may price such products orders of magnitude higher than models without stochastic volatility, calibrated to the same IVS. It follows that double no touches are very exotic products, with a massive dependency on copulas, and material model risk. Financial institutions should always classify exotics in accordance to model risk, since this is one of the most difficult risks to cover.

The authors of dynamic models generally deliver exact or approximate closed-form solutions for European options, which helps calibration.²⁹ More sophisticated models like Heston's stochastic volatility model [42] don't offer analytic formulas but can value Europeans very quickly with numerical integrals; see the dedicated chapters of [6]. In the simplest models like Black Scholes and, some exotics like barrier options also admit closed-form solutions. But in a vast majority of contexts, the pricing of an exotic necessitates a numerical algorithm. The ultra-efficient FDM, briefly introduced later in this chapter, can be applied in a limited number of situations, other contexts requiring the slower, but almost universally applicable, Monte-Carlo algorithm covered in more detail in the rest of this publication.

Note that the different types of models introduced in this chapter form a hierarchy: linear models are self-contained and correctly, accurately, and efficiently price all linear products. European models (IVS) depend on linear models, so they also correctly price linear products. They are also implemented with accurate and efficient numerical integration algorithms, although not as fast or as accurate as linear models. But they correctly price European products in addition to linear products. Dynamic models depend on linear models for their initial conditions, and on IVS for their calibration. Mainly implemented with Monte-Carlo, they are many orders of magnitude slower and less accurate than European models. But they may value exotics in addition to pricing European and linear products, and they do so consistently with European and linear models. Hybrid models are assemblies of single underlying dynamic models, typically joined with a correlation matrix and made consistent and arbitrage-free by drift adjustments in their various components: for example, the risk-neutral drift of underlying assets that don't pay dividends is the short rate. When a stochastic price model is coupled with a stochastic rate model, the drift of the price process is the short rate produced by the rate model. Another example is that in a multi-currency context, the risk-neutral drift of assets denominated in a foreign currency must incorporate a convexity adjustment known as the quanto adjustment. See [27] for details. It follows that in a hybrid model, each (sub-) model is the same exotic model used for single underlying exotics, and that hybrid models value those exotics consistently with exotic models, hence, also, consistently with IVS and linear models. Hybrid models are slower than exotic models, but they can value hybrids and conduct bank-wide regulatory calculations.

This hierarchy is fundamental. The intrinsic value of Europeans, exotics, and hybrids is produced in the exact same model that prices linear products. Calibration guarantees that the European part of exotic products is valued consistently with the IVS used for the management of Europeans. Hybrids and institution-wide regulatory calculations are conducted in assemblies of the same exotic models that are used to manage exotics. Not only does this provide consistent risk management across an investment bank's trading book, it also satisfies the regulator's justified insistence that regulatory calculations, like credit counterparty risk (CCR), revalue transactions over simulated scenarios in a manner absolutely consistent with front office pricing.

We don't implement a model hierarchy in this publication (actually, we don't implement interest rate models at all, not even linear ones, and keep the initial state as parameters in exotic models for simplicity) because that would double the size of the book and because it is not the primary topic here. Model hierarchies, and the consistency they offer, are nonetheless an extremely important subject in modern finance, and something we intend to address in a forthcoming publication.

The rest of this chapter briefly describes some of the most popular dynamic models. Our introduction is brief and without much detail, with the exception of Dupire's model [12], which we use as the main example to demonstrate parallel simulations and AAD, and which is therefore covered in depth in the rest of this publication. We recommend the three volumes of Andersen and Piterbarg's [6] for a deep and broad review of many financial models.

The Black and Scholes model

The Black and Scholes (BS) model [22] is a single underlying price model on an underlying asset , like a stock, currency, or index, whose value today is . BS copes with a deterministic short rate , which, in a model hierarchy, should be set to the IFR to respect today's market.

The model also allows a deterministic dividend yield . To hold a dividend-paying asset is not a self-financing strategy. What is a self-financing strategy is to hold the asset and reinvest dividends into more units of the asset. Denoting the number of assets held at time , and it follows from the reinvestment of the dividend paid at that:

so and the value of the strategy is:

It follows that

and that the drift of is the drift of plus . Under the risk-neutral measure, associated with the numeraire , the value of the self-financing strategy has a drift ; hence the risk-neutral drift of the price series is:

The defining assumption of the Black and Scholes model is that asset prices are diffusions with a deterministic volatility . It follows that the risk-neutral process of is:

where is a standard Brownian motion under .

Change of numeraire

Models can be equivalently rewritten under different measures, associated with different numeraires than the classic bank account. A wise choice of numeraire may simplify analytic calculations and improve the efficiency of numerical algorithms. We demonstrate this technique in the simple case of the Black and Scholes model, although it applies in a vast number of more sophisticated contexts; see [35] for some classic applications.

Forward measure First, we note that with deterministic interest rates, all forward-neutral measures are identical and coincide with the risk-neutral measure. To see this, we price a cash-flow paid at date under the risk-neutral measure:

where we moved the deterministic out of the expectation. Repeating the exercise under the forward measure , we get:

Trivially:

and it follows that , for any -measurable variable . Hence, by definition, the two measures coincide. This is all true for any maturity . Hence, all measures coincide with the risk-neutral measure and are therefore identical.

It follows that forwards are also risk-neutral expectations in this case:

and that all forwards of all maturities are martingales under . In addition, the volatility of a forward is:

so the risk-neutral dynamics of all forwards is simply:

Applying Ito's lemma to the logarithm, we get:

and it follows that for all times :

Hence, the distribution of conditional to is:

where and is a standard Gaussian variable.

Spot measure An algorithm implementing the model under the risk-neutral measure must track the spot price and the bank account numeraire .³⁰ Alternatively, we can equivalently rewrite the model using the underlying asset itself as a numeraire, something known in literature as “spot measure,” so we no longer need to additionally track the numeraire, the underlying asset being the numeraire.

With dividends, however, the asset price does not qualify as a numeraire. We fix a horizon on or after the last date of interest in our working context, a technique known as “terminal measure.” We consider the present value of a forward of maturity :

where we dropped the reference to the fixed horizon to simplify notations, and trivially qualifies as numeraire. We call spot measure the associated measure , even though is not exactly the spot price of .

Pricing a -measurable cash-flow under the spot measure:

and comparing with the risk-neutral measure:

(where we moved the deterministic bank account out of the expectation) implies that for any -measurable variable ,

It follows that the Radon-Nikodym derivative of the spot-neutral to the risk-neutral measure, conditional to , is:

where

is an exponential martingale under with volatility . Therefore, by Girsanov's theorem:

is a standard Brownian motion under , and we get the dynamics of the forward (any forward) under the spot measure:

Hence, the distribution of conditional to under the spot measure is:

where we note that the only difference with the risk-neutral measure is the sign of the left term in the exponential.

The Black and Scholes formula

Having investigated some fundamental properties of the Black and Scholes model, we can easily derive the analytic formula for call options (the formula for puts following from the call–put parity):

and

where we used the notation to refer to a standard Gaussian variable or the cumulative normal distribution, which is clear from context, and the traditional and notations.

One singular beauty in the Black and Scholes formula is that it exposes the hedge coefficients, too. In principle, and are functions of and so the differentiation of the formula could be a painful, if trivial, exercise. Noting that an option price is homogeneous in the forward and strike (an option on assets for times the strike is like options on one asset for the strike price), it follows by Euler's theorem that the price is the sum of its derivatives, hence:³¹

It follows that the replication strategy at time is hold forwards and borrow an amount of cash, the value of the replication portfolio being trivially given by Black and Scholes's formula. It follows that the formula does not only express a price: it expresses the replication strategy, of which the price is a byproduct.

Dupire's model

The Black and Scholes model, despite its simplicity, remains a strong reference in the theory and practice of option trading, and not only because of its historical importance or its remarkable analytic tractability. The Black and Scholes model remains a keystone derivatives risk management instrument, useful in many important ways besides converting prices to volatilities and back. To appreciate the robustness of the model and its relevance for risk management, see the recent [48].

But the model suffers from one major flaw: the same assumption of a deterministic volatility that gave it such remarkable analytic tractability prevents it from correctly calibrating to option markets. It should be clear that with a single time-dependent free parameter , the model may hope to hit, at best, one option price (one strike) per maturity. It follows that the implied volatility (obtained by solving in volatility so Black and Scholes's price corresponds to the market price) may be different for different strikes, a phenomenon commonly known as “smile,” the curve of implied volatility as a function of the strike generally rising away from the money on both sides,³² looking like a smile (with a bit of imagination).

In the early 1990s, Bruno Dupire worked out the simplest possible extension of the Black and Scholes model that can be calibrated to option prices of all strikes and maturities. Like most ground-breaking ideas, Dupire's specification looks trivial after the fact: make volatility a function of the underlying asset price. This is called local volatility and presented here under , with zero rates and dividends for simplicity:

To calibrate Dupire's model means to solve for all strikes and maturities, in the local volatility surface . We are calibrating a continuous, two-dimensional local volatility surface, to a continuous, two-dimensional IVS. Intuitively, we could find a unique, perfect fit. Dupire's formula [12] confirms the intuition and even provides an explicit formula for as a function of today's options prices .

We discuss, demonstrate, implement in code, and apply Dupire's formula to risk management in Chapter 13. Dupire's formula is widely considered one of the three most important formulas in finance (the other two being Black and Scholes and Heath-Jarrow-Morton [49], which we introduce shortly). Dupire's model, or its stochastic volatility extensions by Dupire himself [50] and [45] and Bergomi [51], power almost all modern exotic risk management platforms.

Stochastic volatility models

The milestone stochastic volatility models, where volatility itself is a random process, were developed in 1987 by Hull and White [52], 1993 by Heston [42], and 2002 by Hagan [36]. They gained traction in the early 2000s, when the industry realized that “options are hedged with options,” and that stochastic volatility is necessary to measure the consequences on valuation and risk management; see [46].

We briefly introduce Hagan's SABR, which specification is simpler than Heston, although both models produce a similar behavior and mainly differ in their implementation. Heston's model and its implementation are explained in detail in the first volume of [6].

SABR is written directly under a forward or annuity measure, depending on context³³ where the forward is a martingale. With the addition of stochastic volatility, it implements the following dynamics:

The first line is a trivial extension of Black and Scholes with a power coefficient. The rest specifies the dynamics of volatility. The first thing to note is that this model is incomplete, in the sense that two sources of risk, represented by the two Brownian motions, cannot be hedged by trading one underlying forward. In addition, the initial value is undefined.³⁴ It follows that we can't apply the asset pricing theorem unless we complete the model by calibration. After we calibrate to hit the market price of some option ,³⁵ the model is complete (because we now have two hedge instruments: the forward and the option), with well-defined initial conditions and an arbitrage-free dynamics (the forward is a martingale, and so is the numeraire deflated option price, by construction, because ).

A strong dependency on calibration is a defining characteristic of stochastic volatility models. Calibration is always a concern, but stochastic volatility models, unless calibrated, are ill-defined and fundamentally incorrect. The purpose of these models is to measure the impact of hedging with options on values and risk, hence the strong reliance on the initial values of options.

The parameters (volatility of volatility), (an additional local volatility parameter), and (correlation between the forward and its volatility) are the free parameters of SABR. Note that the acronym SABR comes from the initials of its parameters: Sigma-Alpha-Beta-Rho.

Hagan produced a closed-form approximation for European options under the SABR dynamics using small noise expansion techniques. The result is a very precise approximation. It may be found in the original paper, a number of textbooks, or Wikipedia's SABR article. Hagan's solution involves steps specific to the SABR model and is not easily reusable. For a general presentation of expansion techniques and applications outside SABR, see Andreasen and Huge's [53].

Stochastic volatility is covered in a vast amount of literature, including Lipton's textbook [54], Gatheral's lecture notes [43], and Bergomi's recent [51]. It is also covered in detail in the lecture notes [46].

Interest rate models

The Heath-Jarrow-Morton framework Despite several early attempts to implement models a la Black and Scholes in the interest rate world, it was not before 1992 and the ground-breaking work of Heath, Jarrow, and Morton (HJM, [49]) that a consistent, general, and correct theoretical framework was established for modeling stochastic interest rates.

In interest rate markets, the “underlying asset” is the collection of zero-coupon bonds of all maturities, their value at time being the continuous curve . Ignoring stochastic basis for now, the state of the model at time is the entire discount curve, or, equivalently, the instantaneous forward rate (IFR) curve, introduced earlier:

Under the risk-neutral measure, the drift of all discount factors must be the short rate :

where is the volatility of discount factors, it is conventionally negative, so that Brownian increments that positively affect rates, negatively affect bonds, and we introduced a one-factor version (one Brownian motion) for simplicity, although the original paper works with the general multifactor case, where equations remain essentially unchanged with matrices in place of scalars.

The celebrated Heath-Jarrow-Morton formula gives the dynamics of the IFR under the risk-neutral measure:

where where is the volatility of the IFR's increments (not returns). From the definition of the IFR it immediately follows that:

and that

is a martingale under . Further, we prove below that:

is a standard Brownian motion under , and the HJM formula immediately follows.

Pricing a -measurable cash-flow under :

and comparing with the risk-neutral measure:

implies that for any -measurable variable ,

It follows that the Radon-Nikodym derivative of to , conditional to , is:

where:

is an exponential martingale under ³⁶ with volatility, the volatility of the zero-coupon bond of maturity .³⁷ Therefore, by Girsanov's theorem:

is a standard Brownian motion under , which completes the demonstration.

When is deterministic, the distributions of the IFRs are Gaussian and those of the discounts are log-normal. This model, despite being subject to a single Brownian motion, is generally non-Markov. This means that there exists no deterministic relationship between and or between and when . The Markov dimension of the model is infinite: its state at time is the whole discount or forward curve and it cannot be reduced without loss of information.

Infinite dimension does not lend itself to an effective practical implementation. Therefore, HJM remains to date the theoretical reference for stochastic interest rate modeling, but what is effectively implemented in modern systems, for the risk management of interest rate exotics, are variations and extensions purposely developed for algorithmic tractability. The most successful variations, developed shortly after HJM and still in activity today with substantial upgrades, are the Libor Market Model (LMM) of Brace, Gatarek, and Musiela (BGM, [29]) and Markov versions of HJM, independently established by many researchers in the mid-1990s, most prominently Cheyette [55].

Markov specification of HJM LMM resolved the infinite dimension problem by implementing what is essentially a discrete version of HJM. Another, diametrically opposite approach is to specify HJM in a way to lower its Markov dimension. In its one-factor Gaussian form presented here, HJM is Markov in dimension one if (and only if) for any couple of maturities , there exists a deterministic function such that:

When this is the case, all the forward rates at time are deduced from one another, so when we know one, for example, the short rate , we know them them all, and it follows that the state of the model at time is contained in one scalar variable, for example , so the Markov dimension of the model is, by definition, one. This would allow to model interest rate curves in the same way we model asset prices, with one-dimensional dynamics, and apply the efficient algorithms designed for these, FDM whenever possible, low-dimension Monte-Carlo simulations otherwise.

Although this is somewhat outside of our scope, we demonstrate here how this is achieved, because this is an interesting exercise, and because it sheds light on why HJM was infinite dimensional to start with, even in its one-factor form.

Integrating the HJM formula (and dropping the subscript on the IFR volatility) we find:

The left-hand side is a deterministic, known risk-neutral expectation and does not matter for our purpose. The right-hand side is the unknown, stochastic part of the IFR, a centred Gaussian variable. The stochastic parts of two IFRs of maturities and are:

and we see why the model is non-Markov: the random increments affect the IFRs with different weights and , and it is, in general, impossible to retro-engineer their aggregated impact on one out of their aggregated impact on the other . The model is Markov if and only if one is somehow a deterministic function of the other. Since both are centered Gaussian variables, if such function exists, it has to be linear:

This must be true for all times , so we can differentiate the equation in :

For this equation to be satisfied irrespective of the Brownian path, the derivative in of the right-hand side's left term must be zero, so is not a function of after all, and the equation simplifies into:

which implies that for any , and for any triplet :

It follows that there must exist a function such that

in particular:

and denoting , we find that the model is Markov if and only if:

This requirement restricts the specification of HJM to a so-called separable volatility specification, because is the product of a function of only : and a function of only : . It is also clear that the dimension of the free parameters in HJM is reduced by an order of magnitude from a two-dimensional surface to two curves and . The resulting model is orders of magnitude more tractable in a practical implementation, but its ability to calibrate to the market prices of interest rate options is limited due to the small number of free parameters.³⁹

In addition, going back to the integral form of the IFR and setting , we find the integral form of the short rate:

Injecting the Markov volatility form, differentiating, and rearranging, we quickly find the dynamics of the short rate (we make a constant here to simplify the equations):

where is deterministic. The short rate follows a mean-reverting process a la Vasicek (1977) [56], so one of this model's many names is “extended Vasicek.” It is also widely known as Hull and White's interest rate model [57], although, like Vasicek whose work precedes HJM by 15 years, Hull and White postulated a Markov dynamic for the short rate and worked their way up to the dynamics of the curve, not the other way around. We shall call this model by another of its popular names, Linear Gauss Markov (LGM). Its parameters are , the volatility of the first differences (not returns) of the short rate, and its mean-reversion (even though we kept constant to simplify the presentation, it doesn't have to be).

It is more convenient to work with the variable , which dynamics is the same as but drops the reference to today's forwards in the drift:

where . The following results may be found with simple (if somewhat painful) calculus.

1. All forward rates at time are a deterministic function of . This is the whole point of the model, of course, but it so happens that this function is explicit:
   
2. It follows that all discount factors at time are also a deterministic function of :
   
3. Finally, forward Libors at time are a deterministic function of :
   
   This formula correctly incorporates Libor basis, but keeps it constant.

These formulas, called reconstruction formulas, are a fundamental part of the model, because they map a path of its state variable to a scenario of market samples . Contrary to the other models we introduced so far, the LGM dynamics is not directly written on market variables, so the scenario is not modeled directly, but implicitly, as its samples are deduced from with the reconstruction formulas.

Remember that the purpose of this model, like any model, is to specify the joint distribution of the market observations in the scenario. In an interest rate context, these observations are the values on the event dates of forward discounts and Libors, as well as the numeraire on payment dates. What LGM models is its internal state variable , which joint distribution on event dates is a multidimensional Gaussian distribution, with known expectations and a known covariance matrix (although we are not calculating them here). The discounts and Libors on the event date are modeled implicitly as known functions of the state variable on the same event date. But this is not the case for the risk-neutral numeraire . From its definition:

it appears clearly that is a functional of the continuous path of over but not of . Of more concern is that is not a function of a discrete path of . It would follow that, in order to fulfill its purpose and specify the distribution of the scenario, the model would need to track the numeraire, in addition to its state variable, on event dates, somewhat defeating the benefit of the one-dimensional Markov specification, and damaging the speed and accuracy of algorithms. This comment is not limited to LGM and concerns all interest rate models. The risk-neutral measure is generally not the wisest choice for their implementation.

The solution is to change the numeraire, of course, and use one numeraire where is a known function of . We have seen that this is the case for zero-coupon bonds. In order to use the same numeraire for all cash-flows, we must use a bond of a longer maturity than the financial product we are working with. The preferred maturity is generally the payment date of the last coupon, and the related probability is known as the terminal measure.

When we demonstrated the Heath-Jarrow-Morton formula page 169, we proved that:

is a standard Brownian motion under . In LGM:

hence, the dynamics of the state variable under the terminal measure is:

the rest of the model, in particular, the reconstruction formulas, being unmodified by the change of measure.

Finally, an exact closed-form solution for coupon bond options was derived in this model by El Karoui and Rochet in 1989 [58]. The formula can be applied to price a swaption by turning the underlying swap into a coupon bond, although the exercise is less trivial with Libor basis. It also applies to caplets and floorlets, considered as single-period swaptions, hence to caps and floors.

LGM is a fundamental interest rate model, and, to a large extent, the Black (and Scholes) of the interest rate world. Like Black, LGM is simple, Gaussian, and analytic. Like Black, LGM can be implemented in very fast algorithms, thanks to its one-factor Markov dimension and Gaussian transition probabilities. And like Black, LGM was one of the first operational models in its field, and provided a solid, if somewhat limited, basis for trading the first interest rate exotics.

The fundamental result, that HJM is Markov if and only if its volatility structure is separable, was independently found by multiple researchers in the mid-1990s, including Cheyette in 1992 [55] and Ritchken and Sankarasubramanian in 1995 [59]. Cheyette, in particular, derived the result in a very general context, not only in a multifactor framework, but also with a non-deterministic volatility. Cheyette demonstrated that reconstruction formulas hold with local and even stochastic volatility, as long as it remains separable, even though any other specification than Gaussian increases the Markov dimension of the model.

A general formulation of dynamic models

The purpose of a model, dynamic or not, is to specify the distribution of the scenario , a collection of market observations on a collection of event dates, which definition is independent of the model. How models fulfill this purpose is down to their internal mechanics and depends on the specific model. Dynamic models are those that determine the distribution of the scenario, implicitly, with the specification of a stochastic dynamics. Some models, like Black and Scholes, directly specify the dynamics of market variables. But this is not always the case. Other models, like LGM, specify the dynamics of some internal state variables, together with a mapping from state to market, which we called reconstruction formulas.

More generally, dynamic models define the stochastic dynamics of an internal state and specify a mapping from state to market variables. A model is the sum of the dynamics and the mapping. Both may be subject to parameters, like Black and Scholes's volatility, Dupire's bi-dimensional local volatility surface, or LGM's time-dependent volatility and mean-reversion.

More formally, a dynamic model defines by specifying the dynamics of an internal state vector and a mapping:

from a path of to the market samples over a scenario's timeline, including the numeraire on payment dates. Note that we have a mapping from to , not one from to for every event date . This would be generally desirable, but not always possible. For example, we have seen that the risk-neutral numeraire in LGM is a functional of but not a function of . Particular models may have time-wise mappings, but in general, it is a path-wise mapping. This is a detail, but one that affects the architecture of simulation libraries.

We restrict the presentation to diffusive models, in which the state vector follows, under , a multidimensional diffusion of the type:

The size of the state vector is called the Markov dimension of the model. It may be as low as one, but we also introduced models where it may be large (LMM), or infinite and even continuous (HJM). We carefully distinguish the Markov dimension: the size of the state vector ; and the number of factors: the size of the Brownian Motion . It is always the case that , and, in many cases, is vastly superior to .

The drift is a vector-valued function of the state vector and time, which components are the risk-neutral drifts of the components of (called state variables) each as a function of the entire state vector . The volatility matrix is an matrix that represents the (instantaneous) covariance of the state variables. Since is a standard Brownian Motion of dimension , its components are independent; hence, the covariance of is , which also means that is a square root (in matrix terms) of the covariance matrix of .

The specification of and , along with the parameters of the mapping , constitute the parameter set of the model. The model parameters are either set in reference to initial values (today's spot and forward prices, discounts, or rates), estimated (correlation) or calibrated (typically, volatilities) to match the market prices of a number of active (generally, European) instruments. Derivatives of product values to model parameters are the risk sensitivities, which effective production is a topic of Part III.

Finally, the combination of the dynamics of and the mapping must guarantee that ratios of asset prices to the numeraire are martingales, and that initial values correspond to today's market prices. This guarantees that the model is arbitrage-free and respects today's market. Practically, it also ensures that the model correctly prices linear instruments. When, in addition, the model is correctly calibrated, it also correctly prices European instruments. Dynamic models also implicitly specify the joint distribution of the scenario, allowing them to price exotics, including hybrids and xVA, provided that the model correctly specifies the joint dynamics of all the relevant market variables.

Finite Difference Methods

We have seen that, with the exception of a small number of particularly simple cases, dynamic models cannot price exotics analytically. Numerical methods must be invoked. There exist essentially two families of generic numerical methods for pricing with dynamic models: finite difference methods (FDM) and Monte-Carlo simulations. Other methods exist, but they are generally niche and only work in specific contexts like Fourier transforms, or they are inefficient, like binomial or trinomial trees, which can be seen as less stable and less efficient versions of FDM.

We briefly introduce FDM now, and explore Monte-Carlo in detail in the next chapters. We shall not discuss FDM further thereafter, and refer to the dedicated chapters in Andersen and Piterbarg's book [6] or Andreasen's lecture notes [60].

For the purpose of this brief introduction to FDM, we disregard interest rates and work under the risk-neutral measure, where, in this case, all the discount factors, and the numeraire, are constant equal to one, and cash-flows and payoffs are the same thing. Let us start with a European transaction with a single cash-flow of maturity with a one-factor, one-state-variable dynamic model, with a time-wise mapping :

From the Markov property of , we know that . From Feynman-Kac's theorem, we know that is the solution of the partial differential equation (PDE):

(where the subscripts denote partial derivatives) with the boundary condition:

(the value at maturity is the payoff).

The solution of this PDE may be approached as follows: consider a grid of , say evenly spaced times and evenly spaced s ranging from, say, the expectation minus five standard deviations at maturity to the expectation plus five standard deviations at maturity.⁴¹

Now we have a grid where each node represents a scenario where . We are going to populate this grid with the corresponding future values of the transaction. First, we apply the boundary condition, which populates . Then, we approximate the PDE with finite differences over the nodes in the grid in place of the continuous derivatives, which permits to propagate values backwards in time and populate the grid entirely. The node (where is the position of in the grid) is today's value.

Unfortunately, it does not work that easily. We left out the details of the back-propagation process. What do we do exactly once we know the values at to find the values at ? We could compute the derivatives in over the known grid at , and apply time differences to produce the grid at . This is known as an explicit scheme and is notoriously unstable. An implicit scheme must be applied instead, where finite differences are computed over the unknown grid at . This boils down to a tri-diagonal system of equations, something that is solvable efficiently in linear time. Numerical Recipes [20] provides the code of an efficient routine for this purpose. Even better, we can populate the grid at with a mix (say, half–half) of the explicit and the implicit solutions, something known as the Crank-Nicolson (CN) scheme. CN not only guarantees the stability of the numerical solution (as long as it is at least 50% implicit), but also its convergence with order .

The complexity of FDM is linear in both the size of the grid and the size of the time grid. Linear complexity combined with quadratic convergence makes FDM the most efficient valuation method ever invented.

Of course, FDM is not only adequate for European profiles. The back-propagation equation is independent of the transaction. The cash flows only intervene through boundary conditions. We can incorporate many types of cash-flows by manipulating boundaries and without modification of back-propagation. For instance:

• We can have multiple European cash flows by applying the boundary:
  
  (where we used the C style “+=” notation) after we solved the grid for .
• We can implement a barrier with the boundary condition that is 0 above or below the barrier. The FDM will even correctly value a continuous barrier with a minor modification of the back-propagation scheme. For this reason, FDM is the method of choice for barrier options.
• Since we are populating the different scenarios on the grid with the future values of the transaction, we can easily incorporate early exercise at time with payoff with the boundary:
  
  again, to be applied after we solved the grid for . We can also determine exercise regions:
  
  and exercise boundaries. FDM can even correctly propagate the exercise between consecutive time steps as a continuous exercise; therefore it is adequate (actually, it is the method of choice) for American options.

What we cannot easily incorporate is general path dependence that cannot be interpreted as a boundary. For instance, the payoff of an Asian option (option on average) cannot be interpreted as a boundary. Because of that path-dependence, the future price of an Asian option is not a function of time and spot only, but also of the running average up to that time. Hence, the Markov dimension of the PDE is two in this case, although the Markov dimension of the model is still one. In general, FDM can handle path-dependency, but at the cost of an increase in dimension, something that FDM does not handle that well.

The major challenge with FDM is that its complexity grows exponentially with dimension for a fixed convergence. As the Markov dimension of the PDE grows to , the number of nodes to process grows to to maintain a numerical error in . If we have 100 steps in each direction, we have 10,000 nodes to process in dimension 1. A modern computer does that in a fraction of a millisecond. In dimension 2, we have 1M nodes, something a modern computer also handles easily. But we are no longer talking milliseconds. In dimension 3, this is 100M nodes. Now we are talking seconds. In dimension 4, it is 10BN nodes we have to process for a single valuation. We may be talking talking minutes. In addition to an exponentially growing complexity, dimension more than one creates difficulties in the treatment of the cross-derivatives, and the solutions (known as Craig-Sneyd's scheme and friends) further increase complexity.

We will see that Monte-Carlo simulations, which have a much lower convergence order of in the number of simulations and a much higher complexity per scenario, still win because of their linear complexity in the Markov dimension of the model (not of the PDE, which dimension is at least equal to that of the model). FDM is not practical in dimension 4 or higher. That pretty much disqualifies it in the context of general path-dependent transactions and many models of practical relevance. Cheyette's Markov interest rate model with two factors, for example, is of dimension two with a deterministic volatility, but five otherwise. Hence, FDM is out for multi-factor interest rate models, too. More generally, the growing complexity of the exotic transactions in the decade 1998–2008, causing models to grow in sophistication to follow-up, increased the Markov dimension in most pricing contexts, disqualifying FDM and leaving the much slower and less accurate Monte-Carlo as the only solution. This is without even mentioning the hybrid models used for regulatory calculations, the dimension of which routinely stands in the hundreds.

One specific area in modern financial markets where FDM remains relevant is the so-called first-generation foreign exchange exotics. These are short-term (typically less than 6 months) barrier options (all sort of barriers, one touch, double no touch, knock-in, reverse knock-out, and so forth) written on currency exchange rates. These exotics trade in high volumes on specialized OTC⁴² markets. The short maturity permits to neglect the impact of stochastic rates and keep dimension low, and FDM is ideal for barriers, as mentioned earlier.

Lipton's masterclass [61] provides an overview of forex exotics and analyses models with local volatility, stochastic volatility, and jumps in relation to those markets. One leading model is the so-called SLV (stochastic and local volatility) model defined by:

with Heston's specification for the stochastic volatility, although other specifications are possible; see [51]. This is a two-factor, two-state-variable model suitable for FDM. The model is calibrated with Dupire's second formula (see [50]) implemented in the form of a forward FDM (see [44]), and it values barriers with backward FDM. Pricing takes a few s of a second, remarkably for a model of such sophistication.

It is, however, Monte-Carlo that accounts for the vast majority of valuation contexts of practical relevance in modern finance. But this is only because Monte-Carlo is the only viable method in such high dimension. Researchers settled for Monte-Carlo despite its slow convergence and CPU-demanding operation. Monte-Carlo is a fallback in a context where the superior FDM is no longer relevant.

For this reason, a computationally efficient implementation of Monte-Carlo simulations, including parallelism, and the differentiation of results, is a critical objective in modern finance. To give an idea of the time scales involved, it takes around one second to compute the full risk against 1,600 local volatilities of a barrier option in Dupire's local volatility model, with FDM, 100 time steps, 150 spot steps, by bumping, on a single modern CPU. To get a similar accuracy with Monte-Carlo takes at least 100,000 simulations over 200 time steps, and the full bump risk on a single core takes about half an hour, around 2,000 times slower than FDM. With parallelism and AAD, FDM risk time is reduced under of a second (on a quad core laptop). In relative terms, this is a fantastic 100+ speed-up. In absolute terms, 1 second or of a second does not make much difference. With Monte-Carlo, parallelism and AAD reduce the time spent on the risk report from half an hour to half a second (on a quad core laptop or a quarter of a second on an octo-core workstation), without loss of accuracy. The difference this makes for investment banks and their trading desks is massive. This is the difference between a real-time risk report on a trader's workstation or an overnight computation in a data center.

The purpose of the techniques described in the rest of this publication is to bring the performance of FDM to Monte-Carlo simulations.