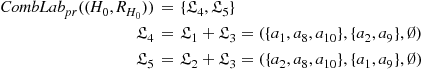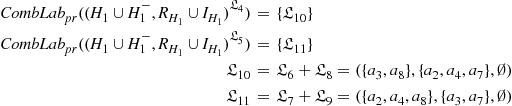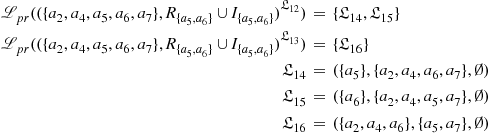An Approach for Static Argumentation Frameworks
Abstract
Currently, except some classes of argumentation frameworks (with special topologies or fixed parameters, such as acyclic, symmetric, and bounded tree-width, etc.) that have been clearly identified as tractable, for a generic argumentation framework, how to efficiently compute its semantics is still a challenging problem. Based on fundamental theories presented in the previous two chapters, in this chapter, we first propose a decomposition-based approach, and then conduct an empirical investigation. Given a generic argumentation framework, it is firstly decomposed into a set of sub-frameworks that are located in a number of layers. Then, the semantics of an argumentation framework are computed incrementally, from the lowest layer in which each sub-framework is not restricted by other sub-frameworks, to the highest layer in which each sub-framework is most restricted by the sub-frameworks located in the lower layers. In each iteration, the semantics of each sub-framework is computed locally, while the combination of semantics of a set of sub-frameworks is performed in two dimensions: horizontally and vertically. The average results show that when the ratio of the number of edges to the number of nodes of a defeat graph is less than 1.5:1, the decomposition-based approach is obviously efficient.
Keywords
computational complexity; decomposition; labelling-based computation; local tractability; semantics combination; strongly connected components
6.1 Introduction
As introduced in Chapter 1, due to the fact that many natural questions regarding argument acceptability are computationally intractable [1], how to efficiently compute the semantics of an argumentation framework is still an open problem.
Since the tractability of an argumentation framework is closely related to its structure [1], it is intuitively feasible to develop efficient computation methods by taking advantage of the special topologies of argumentation frameworks. Indeed, some tractable classes of argumentation frameworks have been clearly identified so far, including acyclic argumentation frameworks [2], symmetric argumentation frameworks [3], and bounded tree-width argumentation frameworks [1,4], etc. However, for an argumentation framework that may not belong to any tractable class, how to efficiently compute its semantics is still unexplored.
In this chapter, inspired by the local tractability of an argumentation framework, we introduce an incremental approach to compute the semantics of a static argumentation framework. The basic idea is as follows:
The existing proof theories and algorithms [2,5–12] all treat argumentation frameworks as monolithic entities1. As a result, the tractability of various parts of a generic argumentation framework (called local tractability) has not been exploited. So, if it is feasible to decompose an argumentation framework into a set of sub-frameworks and compute the semantics of each sub-framework locally, then the local tractability could be exploited.
According to this intuitive observation, we naturally have the following hypothesis:
Given a generic argumentation framework, if we consider its topology as a whole, it may not belong to any tractable class. However, if we decompose it into a set of sub-frameworks, some of them may be tractable, while others might not, but have smaller sizes. This idea could be illustrated by the following example.
Example 6.1
Let 
be an argumentation framework, in which 
. For 
is shown in Figure 6.1(1).
According to [4], the tree-width of 
(with increasing 
) cannot be bounded by a constant. Meanwhile, 
is neither acyclic nor symmetric. So, 
may not belong to any tractable class. However, after we decompose 
into two sub-frameworks 
and 
, it holds that the former is symmetric, and the latter is acyclic. So, if it is feasible to compute the semantics of the two sub-frameworks locally and combine them to form the semantics of 
, then the overall time complexity of computation will be reduced.
Based on the above idea, we hope that the semantics of an argumentation framework could be computed by means of: (i) decomposing the argumentation framework into a set of sub-frameworks; (ii) computing the semantics of each sub-framework locally; and (iii) combining the semantics of a set of sub-frameworks to form the semantics of the original argumentation framework, such that:
(a) the local tractability of the argumentation framework could be exploited to some extent; and
(b) the size of each intractable sub-framework could be made as small as possible.
In order to exploit the local tractability of an argumentation framework, we need to identify tractable fragments. In this book, for simplicity, we only consider acyclic fragments, while the handling of other classes of fragments is left to future work.
6.2 Decomposing an Argumentation Framework: A Layered Approach
In order to enable the incremental computation of argumentation semantics, we need to decompose an argumentation framework in a general way such that there exists a partial order among different sub-frameworks with respect to the dependent relation. As explained in Example 4.3, this requirement might not be satisfied, if an argumentation framework is decomposed in an arbitrary manner. In this example, it turns out that all sub-frameworks are interdependent. The basic reason behind it is that some arguments in these sub-frameworks are in single strongly connected components (SCCs). Now, a natural question arises: is there a partial order among different SCCs? According to graph theory, the answer is positive. Meanwhile, since the set of SCCs of an argumentation framework can be obtained by a polynomial time algorithm [14], it is intuitively feasible to decompose an argumentation framework based on its SCCs.
6.2.1 Strongly Connected Components of an Argumentation Framework
The notion of strongly connected components (SCCs) of an argumentation framework is directly from graph theory, and has been reformulated in [15].
Definition 6.1
Strongly connected components
Given an argumentation framework 
, the set of strongly connected components of 
(denoted as 
) are the equivalence classes of nodes under the relation of path-equivalence between nodes, which, denoted as 
, is defined as follows:
, and
, if and only if there is a path from 
to 
and a path from 
to 
.According to graph theory, an important property of SCCs is that every directed graph corresponds to a directed acyclic graph of its SCCs. In other words, if we shrink each SCC down to a single meta-node, and draw an edge from one meta-node to another if there is an edge (in the same direction) between their respective components, then the resulting condensation graph must be a directed acyclic graph [16].
Example 6.2
Let 
be an argumentation framework, where:
According to Definition 6.1, 
is decomposed into eight SCCs: 
, i.e., 
(Figure 6.2(a)). The corresponding condensation graph (Figure 6.2(b)) is acyclic.
and its condensation graph.6.2.2 A Decomposition Approach Based on SCCs
Since there exists a partial order among different SCCs, a simple approach to decompose an argumentation framework is to use each SCC to induce a sub-framework. However, for each acyclic sub-framework (which is polynomial time tractable), it is induced by the union of a set of SCCs, each of which contains a single argument. Let us consider again the argumentation framework 
in Example 6.1, the sub-framework induced by the set 
is composed of five SCCs, each of which only contains a single argument. For a SCC containing a single argument which does not self-attack, we call it a trivial SCC. Otherwise, it is non-trivial.
Definition 6.2
Trivial/non-trivial SCCs
Let 
be an argumentation framework, and 
be the set of SCCs of 
. For all 
, if there is only one argument (say 
) in 
and the only argument does not self-attack, i.e., 
, then we call 
a trivial SCC, else a non-trivial SCC.
With the notion of trivial SCCs, acyclic sub-frameworks could be constructed by using the unions of trivial SCCs, as long as the partial order of dependence relation among different sub-frameworks is preserved. Meanwhile, since the sub-framework induced by each non-trivial SCC contains cycles, it might be intractable. So, we simply use a single non-trivial SCC to induce a sub-framework.
Besides the considerations for constructing sub-frameworks, when decomposing an argumentation framework, we need also to consider how to organize the sub-frameworks, such that their semantics can be computed incrementally. According to the partial order over the set of SCCs, it is natural to adopt a layered approach. The basic idea is that the sub-frameworks in the same layer can be handled simultaneously, while the sub-frameworks in a given layer are only dependent on the sub-frameworks in the lower layers. And, in the lowest layer, all sub-frameworks are independent.
In order to realize a layered decomposition approach, given the set of SCCs of an argumentation framework, we assign to each SCC a natural number, called the level of the SCC, indicating the order of computing the status of arguments in this SCC, such that:
(i) each non-trivial SCC is used to induce a sub-framework, and
(ii) the union of a set of trivial SCCs is used to induce an acyclic sub-framework, under the condition that the partial order among different sub-frameworks is preserved.
Formally, the notion of the level of a SCC is defined as follows.
Definition 6.3
Level of a SCC
Let 
be the set of SCCs of an argumentation framework 
. For all 
, the level of 
is a function 
. Recursively, 
is defined as follows:
has no parent, then 
;
is non-trivial, 
;
is trivial, 
is a non-trivial parent of 
is a trivial parent of 
.In Definition 6.3, the first item indicates that if 
has no parent, then 
is located in a layer such that the status computation of arguments in 
is independent of the status computation of any arguments in other SCCs.
The second item indicates that if 
has some parents, then there are two possible cases:
• First, if 
is non-trivial, then 
is located in a layer such that the status of arguments in 
is computed after the status of arguments in every parent of 
has been computed.
• Second, if 
is trivial, then 
is located in the layer such that the status of arguments in 
is computed after the status of arguments in every non-trivial parent2 of 
has been computed, and the status of arguments in every trivial parent of 
, whose level is not higher than that of any non-trivial parent of 
(when there exist some non-trivial parents of 
), has been computed. In this way, the status of arguments in some trivial SCCs that have the same level can be computed together within a sub-framework, which, induced by the union of these trivial SCCs, is acyclic.
After all SCCs of an argumentation framework are assigned with specific levels, they can be easily decomposed into layers.
Definition 6.4
Layer of SCCs
Let 
be the set of SCCs of an argumentation framework 
, and 
.3 Then, 
can be decomposed into 
layers, denoted as 
, and 
, respectively, in which
(6.1)
Furthermore, let 
and 
(
) denote the set of trivial, and non-trivial SCCs of Layer 
, respectively. Then, it holds that:
(6.2)
Example 6.3
According to Figure 6.2 and Definition 6.3, it holds that 
, and 
. These SCCs are partitioned into three layers (as shown in Figure 6.3):
, and 
.
, and 
.
, and 
.
.In each layer 
, we use every non-trivial SCC to induce a sub-framework that contains cycles, and the union of all trivial SCCs to induce an acyclic sub-framework.
Formally, let 
be the union of the set of trivial SCCs in Layer 
. For every 
is used to induce a sub-framework 
.
The above formulation shows that given an argumentation framework, it can be decomposed into a set of sub-frameworks located in a number of layers.
Definition 6.5
A decomposition of an argumentation framework
Formally, a decomposition of an argumentation framework 
, denoted as 
, is defined as a tuple:
(6.3)
In Formula (6.3), 
.
Example 6.4
Continue Example 6.3. According to Definition 6.5, 
is decomposed into a set of sub-frameworks located in three layers (Figure 6.4):
, where
.
.
.
.Now, let us verify the following dependence relations between different sub-frameworks in a decomposition. First, each sub-framework is not dependent on any other sub-frameworks in the same layer. Second, the sub-frameworks in a given layer are only dependent on the sub-frameworks in lower layers. Third, no two sub-frameworks are dependent on each other. Formally, we have the following proposition.
Proposition 6.1
Let 
be an argumentation framework. Let 
and 
be subsets of 
, in which 
, and 
. In a decomposition of 
(Definition 6.5), it holds that:
, then 
is not dependent on 
;
is dependent on 
, then 
.
is dependent on 
, then it is not the case that 
is dependent on 
.Proof
(a) Assume that 
is dependent on 
. It follows that there exist two SCCs 
, such that 
, and 
is a parent of 
. Since 
and 
are in the same layer, it holds that 
. According to Definition 6.3, both 
and 
are trivial SCCs. It follows that 
and 
should belong to a unique sub-framework, and therefore 
. Contradiction.
(b) Since 
is dependent on 
, according to Definition 4.2, there exist 
and 
, such that there is a path from 
to 
with respect to 
. So, there exist two SCCs 
and 
, such that 
, and 
(according to Definition 6.3). Hence, 
is in a layer higher than that of 
, and as a result 
is in a layer higher than that of 
. Since P is in Layer 
and Q is in Layer 
, it holds that 
.
(c) Assume that 
is also dependent on 
. It follows that there exist 
and 
, such that there are a path from 
to 
and a path from 
to 
, with respect to 
. Since there is a path from 
to 
with respect to 
, there exist two SCCs 
and 
, such that 
, and 
is a parent of 
. So, compared to 
is not located in a higher layer (so 
). Meanwhile, since there is a path from 
to 
with respect to 
, there exist two SCCs 
and 
, such that 
, and 
is a parent of 
. It follows that compared to 
is not located in a higher layer (so 
). As a result, 
and 
are in the same layer (
). According to the proof of the item (a), 
is not dependent on 
. Contradiction.
6.3 An Incremental Approach to Compute Argumentation Semantics
Given an argumentation framework, after it is decomposed into a set of sub-frameworks located in a number of layers, the computation of argumentation semantics proceeds incrementally, from the lowest layer (Layer 0) in which each sub-framework is not restricted by other sub-frameworks, to the highest layer (Layer 
) in which each sub-framework is most restricted by the sub-frameworks located in the lower layers. In this chapter, we focus on the labelling-based approach.
6.3.1 The Computation of Layer 
(
)
The computation of a layer may include the following steps:
(1) Constructing partially labelled sub-frameworks in Layer 
(
),
(2) Computing the labellings of each sub-framework in Layer 
(
),
(3) Horizontally combining the labellings of Layer 
(
), and
(4) Vertically combining the labellings of layers from 0 to 
(
).
6.3.1.1 Constructing Partially Labelled Sub-Frameworks in Layer i (
)
As presented in Section 4.3, given a sub-framework, if its set of conditioning arguments is not empty, then before computing the labellings of this sub-framework, we need to assign the status of the conditioning arguments externally and obtain a partially labelled sub-framework. Now, for all 
is not empty. So, the status of arguments in 
could only be evaluated in the sub-frameworks that are not dependent on 
.
According to Proposition 6.1, the sub-frameworks in a given layer are only dependent on the sub-frameworks in lower layers. So, given a sub-framework 
, the arguments in 
are contained in a single sub-framework induced by the whole set of arguments located in layers from 0 to 
(called the multi-layer sub-framework, or briefly MLSF, of layers from 0 to 
). Formally, we have the following definition and proposition.
Definition 6.6
MLSF of layers from 0 to 
Let 
be an argumentation framework, and 
be a set of SCCs of 
. The MLSF of layers from 0 to 
, is denoted as 
(since 
and 
are empty, they are omitted), in which 
is defined as follows:
(6.4)
Proposition 6.2
Based on Definitions 6.5 and 6.6, let 
be a sub-framework of 
. It holds that 
.
Proof
According to Formula 2.1 in Chapter 2, 
, such that 
. So, for every SCC 
, if 
, such that 
, then there exists a SCC 
, such that 
is a parent of 
. According to Definition 6.3, 
. If 
, then 
and 
are trivial SCCs (otherwise, 
and therefore 
). According to Definition 6.5, the union of all trivial SCCs in a layer is used to induce a unique sub-framework. It turns out that 
is included in 
. So, 
, such that 
. Contradiction. As a result, 
, i.e., 
is located in a layer between 0 to 
. According to Formula (6.4) in Definition 6.6, all SCCs located in the layers from 0 to 
are included in 
. It follows that 
.
Let 
be a labeling of 
under a given semantics 
.4 Since 
, according to Definition 4.3, 
is a partially labelled sub-framework.
6.3.1.2 Computing the Labellings of Each Sub-Framework in Layer i (
)
In Layer 0, each sub-framework is independent. Its labellings are computed according to the definitions of various kinds of labellings presented in Section 2.3.2.
In Layer 
, when 
, each sub-framework is dependent on the sub-frameworks in lower layers. As formulated in Section 6.3.1.1, before computing the semantics of each sub-framework in this layer, a set of partially labelled sub-frameworks are constructed according to the labellings of the MLSF of layers from 0 to 
. Then, for each partially labelled sub-framework, its labellings are computed according to Definition 4.6 in Chapter 4.
6.3.1.3 Horizontally Combining the Labellings of Layer i (
)
After the labellings of all sub-frameworks in a layer are computed, we hope that they could be combined to form the labellings of the sub-framework induced by the whole set of arguments in this layer. This process is called the horizontal combination of argumentation semantics. For convenience, the sub-framework induced by the whole set of arguments of a layer is called the whole-layer sub-framework (or briefly HLSF) of this layer. Formally, we have the following definition.
Definition 6.7
HLSF of Layer 
Let 
be an argumentation framework, and 
be a set of SCCs of 
. The HLSF of Layer 
, is denoted as 
, in which 
is defined as follows:
(6.5)
When 
is an independent sub-framework.
When 
, according to Proposition 6.2, it is easy to infer that 
is a subset of 
. Let 
be the set of labellings of 
under a given semantics 
. For every 
in 
, it holds that 
is a partially labelled HLSF of Layer 
.
Then, the labellings of an independent HLSF or a partially labelled HLSF are obtained by means of semantics combination.
Definition 6.8
Combined labellings of Layer 
Let 
be the set of sub-frameworks of 
within Layer 
, in which 
and 
. Let 
be a semantics.
First, the combined labellings of Layer 0, denoted as 
, is defined as follows:
Second, for every 
in 
, the combined labellings of Layer 
, denoted as 
, is defined as follows:
6.3.1.4 Vertically Combining the Labellings of Layers from 0 to i (
)
After we get the labellings of the HLSF of Layer 
(
) and the labellings of the MLSF of layers from 0 to 
(initially, when 
, the MLSF of layers from 0 to 
is equal to the HLSF of Layer 0), we hope that they could be combined to form the labellings of the MLSF of layers from 0 to 
. This process is called a vertical combination of argumentation semantics of layers from 0 to 
. Formally, we have the following definition.
Definition 6.9
Combined labellings of layers from 0 to 
Let 
be a semantics. Let 
be an argumentation framework, 
be the MLSF of layers from 0 to 
, and 
be the HLSF of Layer 
. The set of combined labellings of 
, denoted as 
, is defined as follows:
After introducing the incremental approach for computing argumentation semantics, it is necessary to verify that this approach is correct. In the next subsection, we will explain the soundness and completeness of semantic combination, which ensure the correctness of the incremental approach. Then, in Section 6.3.3, we will further explain the process and the correctness of the incremental approach by an example.
6.3.2 Soundness and Completeness of Semantic Combination
Whether the combined labellings are the labellings under a given semantics depends on the soundness and completeness of the semantic combination in all layers. According to theories presented in Chapter 5, we directly have the following propositions.
The first proposition is for the vertical semantics combination.
Proposition 6.3
Let 
be a semantics. Let 
be an argumentation framework, 
be the MLSF of layers from 0 to 
, and 
be the HLSF of Layer 
. The vertical combination of argumentation semantics of layers from 0 to 
is sound and complete. Formally, it holds that:
The second is for the horizontal semantic combination.
be a semantics. Let 
be an argumentation framework. Let 
be the HLSF of Layer 
. Let 
be the MLSF of layers from 0 to 
. The horizontal combination of argumentation semantics is sound and complete. Specifically, it holds that:
; and
, it holds that 
.6.3.3 An Illustrating Example
In order to further illustrate the process of the incremental approach, let us consider the following example. In this example, we only consider the computation under preferred semantics.
Example 6.5
According to the decomposition of 
in Example 6.4, the computation proceeds from Layer 0 to Layer 2.
In Layer 0, there are the following two steps of computation.
Step 0_1: Computing the preferred labellings of each independent sub-framework. According to Example 6.4, we have 
. According to Definition 2.18 in Chapter 2, it holds that:
Step 0_2: Horizontally combining the labellings of Layer 0. By combining the set of preferred labellings of 
and the set of preferred labellings of 
, we obtain the set of combined labellings of 
, the HLSF of Layer 0:
According to Proposition 6.4, 
.
In Layer 1, there are the following four steps of computation.
Step 1_1: Constructing partially labelled sub-frameworks in Layer 1. According to Example 6.4, 
. When 
(the MLSF of layers from 0 to 
is equal to the HLSF of Layer 0). Since 
has two labellings, we obtain four partially labelled sub-frameworks as follows (Figure 6.5):
Step 1_2: Computing the labellings of each partially labelled sub-framework in Layer 1. According to Definition 4.6 in Chapter 4, it holds that:
Step 1_3: Horizontally combining the semantics of Layer 1. The HLSF of Layer 1 is 
, in which the set of conditioning arguments is 
. The corresponding two partially labelled sub-frameworks are 
and 
(Figure 6.6). According to Definition 6.8, it holds that:
According to Proposition 6.4, we have 
, and 
.
Step 1_4: Vertically combining the semantics of layers from 0 to 1. According to Example 6.3 and Formula 6.4 in Definition 6.6, 
. So, the MLSF of layers from 0 to 1 is 
. According to Definition 6.9, it holds that:
According to Proposition 6.3, 
.
Finally, in Layer 2, there are also four steps of computation.
Step 2_1: Constructing partially labelled sub-frameworks in Layer 2. According to Example 6.4, 
. Since 
has two labellings, we obtain two partially labelled sub-frameworks as follows (Figure 6.7).
Step 2_2: Computing the semantics of each partially labelled sub-framework in Layer 2. According to Definition 4.6 in Chapter 4, it holds that:
Step 2_3: Horizontally combining the semantics of Layer 2. Since there is only one sub-framework in this layer, the semantics combination is trivial. Let 
be the HLSF of Layer 2. 
. It is obvious that
Step 2_4: Vertically combining the semantics of layers from 0 to 
. The MLSF of layers from 0 to 2 is 
. According to Definition 6.9, it holds that:
Since 
, the set of combined extensions of 
is 
. According to Proposition 6.3, 
.
within Layer 1.
within Layer 1.
within Layer 2.6.4 Empirical Evaluation
In this section, for simplicity and without loss of generality, we only focus on evaluating the performance of our decomposition-based algorithm for computing preferred labellings of an argumentation framework. The algorithm is composed of the following two components.
The first component is responsible for decomposing argumentation frameworks. Given an argumentation framework 
, it is partitioned into a set of SCCs (by using Tarjan’s algorithm [14]). Then, each SCC is assigned with a level (according to Definition 6.3), decomposition of 
is obtained.
The second component is responsible for the incremental computation of preferred labellings. Besides the combination of labellings (as formulated in Section 5.3), the core of this component is to compute the preferred labellings of each sub-framework. Given an independent sub-framework 
of 
, its preferred labellings are computed directly by the MC algorithm; given a partially labelled sub-framework 
of 
, in which 
, its preferred labellings are computed by Algorithm 4.1 in Chapter 4.
The algorithm was implemented in Java, and tested on a machine with an Intel CPU running at 1.86 GHz and 1.98 GB RAM. Since the performance of the algorithms for computing the labellings of an argumentation framework is highly related to its topology and edge density, we tried the following three configurations:
• The nodes of argumentation frameworks range from 100 to 200, and the ratio of the number of edges to the number of nodes is 1:1.
• The nodes of argumentation frameworks range from 15 to 25, and the ratios of the number of edges to the number of nodes are respectively 1.5:1 and 2:1.
• The nodes of argumentation frameworks range from 8 to 12, and the ratios of the number of edges to the number of nodes are respectively 3:1, 4:1 and 5:1.
In the test, for each assignment of the number of nodes and the ratio of the number of edges to the number of nodes, the program was executed 20 times. In each time, an argumentation framework was generated at random,5 and then its preferred labellings were computed by using the MC algorithm and our decomposition-based algorithm (or briefly, our algorithm), respectively. Table 6.1 shows the average results of the number of SCCs and the execution time of the two approaches.
In this table, “#nodes”, “#SCCS” and “#timeout” denote, respectively, the number of nodes of an argumentation framework, the number of SCCs, and the number of timeouts (when the time for computing the preferred labellings of an argumentation framework is over 30 minutes) among the 20 times of execution.6 When the average time shown in Table 6.1 was computed, only the cases without timeouts were considered. For instance, when #nodes = 180 and the ratio of #edges to #nodes is 1:1, there are four timeouts. According to the corresponding records in Table 6.3, the average time of the MC algorithm is: 
; the average time of our algorithm is: 
.
Note that in our decomposition-based algorithm, the execution time includes the time for generating a set of SCCs, for constructing a set of sub-frameworks, and for generating and combining the preferred labellings of all sub-frameworks. Compared to the time for generating preferred labellings, the time for computing a set of SCCs is negligible. Table 6.2 shows that the average time for computing the SCCs of argumentation frameworks in all cases is less than 2 milliseconds.7
From Table 6.1, we found that when the ratio of the number of edges to the number of nodes is around 1.5:1, our decomposition-based algorithm is very efficient. With the increase of the ratios of the number of edges to the number of nodes, the ratios of the number of SCCs to the number of nodes decrease. Meanwhile, the execution time of the two algorithms increases, and the computational advantage of our algorithm becomes more and more indistinct.
Now, let us have a close look at the detailed results of the individual cases of computation. Table 6.3 shows the cases when #nodes = 180 and the ratio of the number of edges to the number of nodes is 1:1. In this table, #undec denotes the maximal number of arguments that are labelled UNDEC in a preferred labelling of a given argumentation framework; #lab denotes the number of preferred labellings of a given argumentation framework; “
” indicates the number of arguments in trivial SCCs of Layer 
; “
” indicates the number of non-trivial SCCs in Layer 
and the number of arguments in each non-trivial SCC. For instance, in Record 1 of Table 6.3, “Tri[0(111), 1(2), 2(25), 4(16)]” denotes that the number of arguments in trivial SCCs of Layers 0, 1, 2 and 4 is respectively 111, 2, 25 and 16; “Non[0(1+1), 1(15), 3(9)]” denotes that there are two non-trivial SCCs (each of which contains one argument) in Layer 0, one non-trivial SCC (which contains 15 arguments) in Layer 1, and one non-trivial SCC (which contains 9 arguments) in Layer 3. For simplicity, when there are no trivial (or non-trivial) SCCs in a given layer, the corresponding item is omitted.
.
From Table 6.3, we found that the execution time of our decomposition-based algorithm is very low (no more than 0.031 seconds) in all cases, while the execution time of the MC algorithm fluctuates from 0.015 seconds to more than 30 minutes. What are the basic reasons behind this phenomenon? Intuitively, we may observe that the time complexity of the MC algorithm is closely related to the number of arguments that are labelled UNDEC and the number of preferred labellings. Please look at Records 2, 4, 11, 13, 15 and 18 in Table 6.3: in Record 2, #undec = 21 and the execution time is more than 30 minutes; in Record 13, #undec = 9 and the execution time is 3.485 seconds; in Record 15, #undec = 4 and the execution time is more than 30 minutes; in Records 4, 11 and 18, all argumentation frameworks have two preferred labellings. Theoretically, according to the MC algorithm for generating preferred labellings, when the number of UNDEC-labelled arguments is bigger, it takes more time to perform transition steps. Meanwhile, when an argumentation framework has more preferred labellings, the time for finding and comparing candidate labellings tends to increase.
To see the specific topologies of the argumentation frameworks that have more UNDEC-labelled arguments and/or more preferred labellings, let us consider the cases when #nodes = 15 and the ratio of the number of edges to the number of nodes is 1.5:1 (Table 6.4).
According to Record 1 in Table 6.4, the number of UNDEC-labelled arguments is 8, and the execution times of our algorithm and MC algorithm are, respectively, 9.016 seconds and 10.062 seconds. The corresponding argumentation framework is illustrated in Figure 6.8(a). This argumentation framework has only one preferred labelling 
. According to the topology of this argumentation framework, we found that the UNDEC-labelled arguments are related to some odd-length cycles. In this example, there are three odd-length cycles 
and 
, which are the fundamental reason that the related arguments are undecided under preferred semantics. Meanwhile, we observed that there is a non-trivial SCC whose size is 12 in this argumentation framework. This is why the execution time of our algorithm is close to that of the MC algorithm. In other words, the efficiency of our algorithm is highly limited by the size of the maximal SCC of an argumentation framework.
Figure 6.8 Argumentation frameworks with respect to Records 1, 6 and 14 in Table 6.4.
The argumentation framework with respect to Record 6, as shown in Figure 6.8(b), is interesting. It has only one non-trivial SCC, which is an odd-length cycle containing only one argument. However, from the unique preferred labelling 
, we observed that when the arguments in acyclic fragments are affected by some arguments from odd-length cycles, they might also become undecided under preferred semantics and consume more computation time.
Finally, as illustrated in Figure 6.8(c), the argumentation framework with respect to Record 14 has four non-trivial SCCs and three preferred labellings: 
and 
. The execution time of the MC algorithm for this argumentation framework is 183.031 seconds. This example shows again that the number of UNDEC-labelled arguments and the number of labellings are closely related to the time complexity of the MC algorithm. This problem could be effectively coped with by our decomposition-based algorithm.
According to the above results, we may come to the following conclusions:
• When the ratio of the number of edges to the number of nodes of an argumentation framework is about 1:1, the execution time of our algorithm is very low and stable.
• When the ratio of the number of edges to the number of nodes of an argumentation framework is no more than 1.5:1, the execution time of our algorithm is obviously better than the MC algorithm.
• When the ratio of the number of edges to the number of nodes of an argumentation framework is bigger than 4:1, the difference between our algorithm and the existing one is not apparent.
• Two factors that affect the time complexity of the MC algorithm for computing preferred labellings are the number of UNDEC-labelled arguments in a labelling and the number of preferred labellings. Our decomposition-based approach could effectively cope with this problem.
6.5 Conclusions
In this chapter, we have introduced an approach for incrementally computing the semantics of a static argumentation framework, and then performed an empirical investigation.
The decomposition-based approach is realized by exploiting the notion of strongly connected components of a directed graph. Given an argumentation framework (which is regarded as a directed graph), it is firstly decomposed into a set of SCCs, and then into a set of sub-frameworks located in a number of layers. According to the decomposition, under some typical semantics (admissible, complete, grounded, preferred), the semantics of the argumentation framework are computed incrementally from the lowest layer in which each sub-framework is not restricted by other sub-frameworks, to the highest layer in which each sub-framework is most restricted by the sub-frameworks located in the lower layers. The empirical results showed that when the defeat graphs of argumentation frameworks are sparse (more specifically, when the ratio of the number of edges to the number of nodes of a defeat graph is less than 1.5:1), the efficiency of the decomposition-based approach is apparent.
It should be noticed that the efficiency of the decomposition-based approach is highly limited by the maximal SCC of an argumentation framework. In [17], we present a further solution by exploiting the most skeptically rejected arguments of an argumentation framework. Given an argumentation framework, its grounded labelling is first generated. Then, the attacks between the undecided arguments and the rejected arguments are removed. It turns out that the modified argumentation framework has the same preferred labellings as the original argumentation framework, but the maximal SCC in it could be much smaller than that of the original argumentation framework. Empirical results show that this new method dramatically reduces the computation time for some sparse argumentation frameworks (when the ratio of the number of edges to the number of nodes of an AF is between 1:1 and 1.8:1).
Besides the decomposition-based approach presented in this chapter, some other work for efficiently computing the semantics of a static argumentation framework mainly consist of the following three lines.
The first line of work is on identifying tractable classes of argumentation frameworks with special structures [1], and developing efficient algorithms for some classes of argumentation frameworks with fixed parameters, such as bounded tree-width [4] and bounded clique-width [18], etc. And, in [19], Dvořák et al proposed a generic approach for solving hard problems in the area of argumentation in a “complexity-sensitive” way. The corresponding empirical results showed that their approach significantly outperforms existing systems developed for hard argumentation problems (i.e., problems under the preferred, semi-stable or stage semantics).
The second line of work is on decomposition-based computation of extensions [15,20]. In [15], Baroni et al proposed a SCC-recursive scheme for argumentation semantics, based on decomposition along the strongly connected components of an argumentation framework. Meanwhile, they pointed out, at the end of the paper, that “it is worth investigating the development of efficient and incremental algorithms based on local computation at the level of strongly connected components”. In line with Baroni et al’s proposal, Baumann et al developed splitting-based algorithms for the computation of extensions. Their experimental results showed an average improvement by 50% and by 54% for preferred and stable semantics respectively, compared to Modgil and Caminada’s algorithms [6].
The third line of work is to develop specific algorithms to improve the efficiency of computing the status of arguments. For instance, in [21], Nofal et al presented a case study on experimental algorithms in the context of an instance of extended argumentation frameworks, and analysed the efficiency of three different algorithms for deciding the acceptability of an argument with respect to a set of arguments; in [22], they proposed a more efficient algorithm for enumerating all preferred extensions, by utilizing further labels8 to improve labels’ transitions.
The approach proposed in this chapter is related to the above three lines of work, but differs from them in the following ways. Firstly, while the first and third lines of work treat argumentation frameworks as monolithic entities and therefore have not considered the local tractability of a generic argumentation framework, our decomposition-based approach takes advantage of the local tractability of acyclic fragments. Secondly, the similarity between our work and the second line of work is the idea of incremental computation of argumentation semantics. However, the existing works have not considered how to exploit the tractability of some sub-frameworks with special topologies (in this book acyclic sub-frameworks). Thirdly, the layered approach for decomposing an argumentation framework and combining argumentation semantics has not been introduced in the existing literature.
References
1. Dunne P. Computational properties of argument systems satisfying graph-theoretic constraints. Artificial Intelligence. 2007;171(10–15):701–729.
2. Dung P, Kowalski R, Toni F. Dialectic proof procedures for assumption-based, admissible argumentation. Artificial Intelligence. 2006;170(2):114–159.
3. Coste-Marquis S, Devred C, Marquis P. Symmetric argumentation frameworks. In: Proceedings of the Eighth European Conferences on Symbolic and Quantitative Approaches to Reasoning with Uncertainty. 2005;317–328.
4. Dvořák W, Pichler R, Woltran S. Towards fixed-parameter tractable algorithms for argumentation. In: Proceedings of the 12th International Conference on the Principles of Knowledge Representation and Reasoning. 2010;112–122.
5. Cayrol C, Doutre S, Mengin J. On decision problems related to the preferred semantics for argumentation frameworks. Journal of Logic and Computation. 2003;13(3):377–403.
6. Modgil S, Caminada M. Proof theories and algorithms for abstract argumentation frameworks. Argumentation in Artificial Intelligence 2009;105–129.
7. Dung P, Thang P. A sound and complete dialectical proof procedure for sceptical preferred argumentation. In: Proceedings of an LPNMR Workshop on Argumentation and Non-Monotonic Reasoning. 2007;49–63.
8. Dung P, Mancarella P, Toni F. Computing ideal sceptical argumentation. Artificial Intelligence. 2007;171(10–15):642–674.
9. Egly U, Gaggl S, Woltran S. Aspartix: Implementing argumentation frameworks using answer-set programming. In: Proceedings of the 24th International Conference on Logic Programming. 2009;734–738.
10. Nieves J, Cortés U, Osorio M. Preferred extensions as stable models. Theory and Practice of Logic Programming. 2008;8(4):527–543.
11. Wakaki T, Nitta K. Computing argumentation semantics in answer set programming. In: Proceedings of the 22nd Annual Conference of the Japanese Society for Artificial Intelligence. 2008;254–269.
12. Kim E, Ordyniak S, Szeider S. Algorithms and complexity results for persuasive argumentation. Artificial Intelligence. 2011;175(9–10):1722–1736.
13. Coste-Marquis S, Devred C, Lagasquie-Schiex M, Marquis P. On the merging of dung’s argumentation systems. Artificial Intelligence. 2007;171(10–15):730–753.
14. Tarjan R. Depth-first search and linear graph algorithms. SIAM Journal on Computing. 1972;1(2):146–160.
15. Baroni P, Giacomin M, Guida G. Scc-recursiveness: a general schema for argumentation semantics. Artificial Intelligence. 2005;168(1–2):162–210.
16. Dasgupta S, Papadimitriou CH, Vazirani UV. Algorithms. McGraw-Hill 2006.
17. Liao B, Lei L, Dai J. Computing preferred labellings by exploiting SCCs and most sceptically rejected arguments. In: Proceedings of Second International Workshop on Theory and Applications of Formal Argumentation. 2013.
18. Dvořák W, Szeider S, Woltran S. Reasoning in argumentation frameworks of bounded clique-width. In: Proceedings of the Third International Conference on Computational Models of Argument. 2010;219–230.
19. Dvořák W, Järvisalo M, Wallner JP, Woltran S. Complexity-sensitive decision procedures for abstract argumentation. In: Proceedings of the 13th International Conference on the Principles of Knowledge Representation and Reasoning. 2012;54–64.
20. Baumann R, Brewka G, Wong R. Splitting argumentation frameworks: an empirical evaluation. In: Proceedings of the First International Workshop on Theory and Applications of Formal Argumentation. 2011;17–31.
21. Nofal S, Dunne P, Atkinson K. Towards experimental algorithms for abstract argumentation. In: Proceedings of the Fourth International Conference on Computational Models of Argument. 2012;217–228.
22. Nofal S, Dunne P, Atkinson K. On preferred extension enumeration in abstract argumentation. In: Proceedings of the Fourth International Conference on Computational Models of Argument. 2012;205–216.
1In some existing literature [13,15], argumentation frameworks are not treated as monolithic entities. However, their work is not focused on developing efficient methods to compute argumentation semantics.
2Here, the term trivial parent (non-trivial parent) stands for a parent of a SCC that is trivial (respectively, non-trivial).
3Throughout this chapter, without explicit explanation, we use 
to stand for 
, i.e., the highest level of a layered decomposition of an argumentation framework.
4In a layered computation approach, the labellings of an argumentation framework are computed incrementally from Layer 0 to Layer 
. So, before computing the labellings of each sub-framework in Layer 
, the (combined) labellings of the sub-framework induced by the MLSF of layers from 0 to 
have been obtained.
5The basic idea of generating a random graph is as follows: Given a set of arguments 
and a ratio 
, select at random two nodes 
and 
from the set, if the edge 
has not been generated, then 
is generated, until the number of edges is equal to a given value (
).
6Since in many cases, the execution time might last very long, to make the test easier, when the time for computing the preferred labellings of an argumentation framework is over 30 minutes, we stopped the execution by setting a break in the program.
7The data of Table 6.2 were generated in another test. Given an assignment of edge density (ration = 1:1, 1.5:1, 2:1, 3:1, 4:1, 5:1) and the number of nodes (
), the program for computing SCCs was executed 100 times. In each time, an argumentation framework with given edge density and size was generated at random, and the set of SCCs of the argumentation framework was computed.
8Besides applying the labels IN, OUT and UNDEC, they introduced the use of MUST-OUT and IGNORED, in which the MUST-OUT label identifies arguments that attack IN arguments. The IGNORED label designates arguments which might not be included in a preferred extension because they might not be defended by any IN argument.