CHAPTER
6

Evaluating Limits Numerically

In This Chapter

• Three easy methods for finding limits
• Limits and asymptotes
• Finding limits at infinity
• Trig and exponential limit theorems

Now you know what a limit is, when a limit exists, and when it doesn’t. However, the question of how to actually evaluate limits remains. In Chapter 5 we approximated limits by plugging in x values insanely close to the number we were approaching, but that got tedious quickly. As soon as you have to raise numbers like 2.999999 to various exponents, it becomes clear that you either need a better way or a giant bottle of aspirin.

Good news: there are lots of better ways, and this chapter will lead you through all of the major processes to evaluate limits and the important limit theorems you should memorize. For those of you who were uncomfortable with math turning a little conceptual and philosophical there for a little bit, don’t worry—we’re back to comfortable, familiar, soft, fuzzy, and predictable math techniques and formulas.

All of that theory you learned in the last chapter will resurface to some degree in Chapter 7, when we discuss continuity of functions, so keep it fresh in your mind. A lot of our discussion about limits will get hazy quickly when you move on to derivatives and integrals as the book progresses. Make sure you come back and review these early topics often throughout your calculus course to keep them fresh in your brain.

The Major Methods

The vast majority of limits can be evaluated by using one of three techniques: substitution, factoring, and the conjugate method. Usually, only one of these techniques will work on a given limit problem, so you should try one method at a time until you find one that works. Because I am efficient (understand, by that I mean extremely lazy) I always try the easiest method first, and only move on to more complicated methods if I absolutely have to. As such, I’ll present the methods from easiest to hardest.

Substitution Method

Prepare yourself—you’re going to weep with uncontrollable joy when I tell you this. Many limits can be evaluated simply by plugging the x value you’re approaching into the function. The fancy term for this is the substitution method (or the direct substitution method).

Example 1: Evaluate .

Solution: In order to evaluate the limit, simply plug the number you’re approaching (4) in for the variable:

4² – 4 + 2 = 16 – 2 = 14

According to the substitution method, . That was too easy! Just to make sure it actually worked, let’s check the answer by looking at the graph of y = x² – x + 2 in Figure 6.1.

Figure 6.1

Use the graph of y + x² –x + 2 to visually verify the limit at x = 4.

As we approach x = 4 from either the left or the right, the function clearly heads toward a height of 14, which, as we know, guarantees that the general limit exists and is 14. It worked! Huzzah!

If every limit problem in the world could be solved using substitution, there would probably be no need for mathematically induced antidepressants. However (and there’s always a however, isn’t there?), sometimes substitution cannot be used. In such cases, you should resort to the next method of evaluating limits: factoring.

Factoring Method

Consider the function . How would you find the limit of f(x) as x approaches –3? Well, if you try to use substitution to find the limit, bad things happen:

What kind of an answer is ? A gross one, that’s for sure. Remember that we can’t have 0 in the denominator of a fraction; that’s not allowed. If you recall, in the last chapter we called this an “indeterminate form,” which means the answer can be anything. Clearly, then, the limit is not , but that answer does tell us two things:

1. You must use a different method to find the limit, because …

2. … the function likely has a hole at the x value you substituted into the function, and you need to determine the height of that hole.

The best alternative to substitution is the factoring method, which works just beautifully in this case. In the next example, we’ll find this troubling limit.

Example 2: Evaluate using the factoring method.

Solution: To begin the factoring method, factor! It makes sense, because the numerator is the difference of perfect squares and factors very happily:

Now both the top and bottom of the fraction contain (x + 3), so you can cancel those terms out to get the much simpler limit expression of:

Now you can use the substitution method to finish:

–3 – 3 = –6

So .

Conjugate Method

If substitution and factoring don’t work, you have one last bastion of hope when evaluating limits, but this final method is very limited in its scope and power. In fact, it is most useful for limits that contain radicals, as its power comes from the use of the conjugate. The conjugate of a binomial expression (i.e., an expression with two terms) is the same expression with the opposite middle sign. For example, the conjugate of is .

The true power of conjugate pairs is displayed when you multiply them together. The product of two conjugates containing radicals will, itself, contain no radical expressions! In other words, multiplying by a conjugate can eliminate square roots:

You should use the conjugate method whenever you have a limit problem containing radicals for which substitution does not work—always try substitution first. However, if substitution results in an illegal value , you’ll know to employ the conjugate method, which we’ll use to solve the next example.

Example 3: Evaluate .

Solution: If you try the substitution method, you get , indicating that you’ll need another method to find the limit because the function probably has a hole at x = 5. The function itself contains a radical and a number being subtracted from it—the fingerprint of a problem needing the conjugate method. To start, multiply both the numerator and denominator by the conjugate of the radical expression :

Multiply the numerators and denominators as you would any pair of binomials—i.e., (a + b)(c + d) = ac + ad + bc + bd—and all of the radical expressions will disappear from the numerator. Do not actually multiply the nonconjugate pair together. You’ll see why in a second:

Here’s the neat trick: the numerator and denominator now contain the same term (x – 5) so you can cancel that term and then finish the problem with the substitution method:

What If Nothing Works?

If none of the three techniques we have discussed works on the problem at hand, you’re not out of hope. Don’t forget we have an alternative (albeit tedious, mechanical, and unexciting—like most television sitcoms) method of finding limits. If all else fails, substitute a number insanely close to the number for which you are evaluating, as we did in Chapter 5.

Let me also play the part of the soothsayer for a moment. For maximum effect, read the next sentences in a creepy fortune-teller voice. “I see something in your future, yes, off in the distance. A promised method, a shortcut, a new way to evaluate limits that makes hard things easy. I’m getting a French name … L’Hôpital’s Rule … and an unlucky number … 13. Chapter 13. Look for it in Chapter 13.”

Limits and Infinity

There is a deep relationship between limits and infinity. At first they thought they were “just friends,” and then one would occasionally catch the other in a sidelong glance with eyes that spoke volumes. Without going into the long history, now they’re inseparable, and without their storybook relationship, there’d be no vertical or horizontal asymptotes.

Vertical Asymptotes

You already know that a limit does not exist if a function increases or decreases infinitely, such as at a vertical asymptote. You may be wondering if it’s possible to tell if a function is doing just that without having to draw the graph, and the answer is yes. Just as a substitution result of typically means a hole exists on the graph, a result of indicates a vertical asymptote. To be more specific, you don’t have to get 5 in the numerator—any nonzero number divided by 0 indicates that the function is increasing or decreasing without bound, meaning no limit exists.

Example 4: At what value(s) of x does no limit exist for

Solution: Begin by factoring the expression, because knowing what x values cause a 0 in the denominator is key:

At x = –5, the function should have a hole, as substituting in that value results in . You can use the factoring method to actually find that limit:

However, you’re supposed to determine where the limit doesn’t exist, so let’s look at the other distressing x-value: x = 5. If you substitute that into f(x), you get . This result, any number (other than 0) divided by 0, indicates the presence of a vertical asymptote at x = 5, so does not exist because f will either increase or decrease infinitely there.

If substitution results in , that does not guarantee that a hole exists in the function. You can only be sure there’s a hole there if a limit exists, as was the case with x = –5 in this example.

Example 5: Calculate all values of c for which or − ∞.

Solution: This problem looks like a spilled bowl of alphabet soup, doesn’t it? Don’t let all of the unknowns in there discourage you. Although r, s, v, and w don’t look like numbers, that’s all they are. You don’t know their values, but don’t let that bother you. Think of them as little boxes, hidden inside each of which is a plain old harmless number.

Because the limit of the function is either ∞ or –∞, technically that limit doesn’t exist because the rational function either increases or decreases without bound near that value of c. This happens at a vertical asymptote.

In other words, this question is actually wondering, “At what x-values does this function have a vertical asymptote?” Begin by setting the denominator equal to zero and solving. Remember, the x-values you’re looking for will cause the denominator to equal 0 but not the numerator.

Now you know the denominator equals 0 whenever or . Why use a c there instead of an x? The question wants specific x-values that cause a vertical asymptote, and it names those values c, so you should do the same. One thing left to consider: these strange c-values won’t actually represent vertical asymptotes if their values also cause the numerator to equal 0.

Your next step is to find out when the numerator equals 0 to specifically avoid those values. You’ll need to set the numerator equal to 0 and solve using the factoring method.

Believe it or not, you’re finished! The answer isn’t all that satisfying, but here goes nothing. The function will increase or decrease without bound for c-values and , as long as those values are neither equal to 0 nor equal to 3.

Horizontal Asymptotes

Vertical asymptotes are caused by a function’s values increasing or decreasing infinitely as that function gets closer and closer to a fixed x-value; so, if a function has a vertical asymptote at x = c, we can write or − ∞. Horizontal asymptotes have a lot of the same components, but everything is reversed. One minor exception: a function can cross a horizontal asymptote (but not a vertical asymptote), because horizontal asymptotes only deal with the “end behavior” of the function, the intended heights of the function at the far right and left ends of the graph.

A horizontal asymptote is the height that a function tries to, but cannot, reach as the function’s x-values get infinitely positive or negative. In Figure 6.2, f(x) approaches a height of 5 as x gets infinitely positive and a height of –1 as f(x) becomes infinitely negative.

Figure 6.2

The graph of f(x) has different horizontal asymptotes as x gets infinitively positive and negative. A rational function won’t look like this—it will have (at most) one horizontal asymptote.

This is written as: or .

These are called limits at infinity, since you are not approaching a fixed number, as you do with typical limits. However, the limit still exists because the function clearly intends to reach the limiting height indicated by the horizontal asymptote, although it never actually reaches it.

Evaluating limits at infinity is a bit different from evaluating standard limits; substitution, factoring, and the conjugate methods won’t work, so you need an alternative method. Although L’Hôpital’s Rule works quite nicely, you won’t learn that until Chapter 13. In the meantime, you can evaluate these limits simply by comparing the highest exponents in their numerators and denominators.

Let’s say we calculate , where r(x) is defined as a fraction whose numerator, n(x), and denominator, d(x), are simply polynomials. Compare the degrees (highest exponents) of n(x) and d(x):

• If the degree of the numerator is higher, then = ∞ or − ∞(i.e., there is no limit because the function increases or decreases infinitely).
• If the degree of the denominator is higher, then .
• If the degrees are equal, then is equal to the leading coefficient of n(x) divided by the leading coefficient of d(x).

Remember, these guidelines only apply to limits at infinity.

Example 6: Evaluate .

Solution: This is a limit at infinity, so you should compare the degrees of the numerator and denominator. They are both 3, so the limit is equal to the leading coefficient of the numerator (5) divided by the leading coefficient of the denominator (8), so .

Now that you’ve got the basics down, let’s turn the difficulty up a notch.

Example 7: Given the function g(x) as defined here, assume that . what is the value of a – f?

Solution: Remember, as with Example 5, all of the letters except for g and x (in other words a, b, c, d, e, and f) are just numbers.

Although there are letters all over the place in this fraction, you do have a few numbers to work with. Specifically, a couple of 2s, the exponents in the numerator and denominator. That means, as ugly as they are, the expressions in both parts of the fraction are just quadratics.

A fraction where the degrees of the numerator and denominator are equal? Sounds familiar! When those degrees are equal, the limit as x approaches infinity is equal to the leading coefficient of the numerator (a) divided by the leading coefficient of the denominator (f). The problem tells you that the limit is equal to .

Okay, that’s a start, but you need more information to move forward. Luckily, the problem provides that information. It tells you that a + f = 12. Now you have two equations that explain the relationship between a and f; you have a system of equations that you can solve by substitution. Solve the linear equation for a by subtracting f from both sides:

Because a has the same value as 12 – f, you can replace a with 12 – f in the other equation, the proportion you created earlier:

Finally! An equation with just one variable. Solve this for f by cross-multiplying.

Now that you know the value of f, you can find the corresponding value of a. Just use that equation you used to solve for a only a few moments ago:

That was a lot of work, but now we can finally answer the question posed by the problem. If a + f = 12, what is the value of a – f?

Special Limit Theorems

The five following special limits are not special because of the way they make you feel all giddy inside. By “special,” I mean they can’t be evaluated by the means we’ve discussed so far, yet you’ll see them frequently and should probably memorize them, even though that stinks. Now that we’re on the same page, so to speak, here they are with no further ado:

• 

This formula is only true when you approach 0, so don’t use this under any other circumstances. The α can be any quantity.

• 

As with the first special limit, this formula is only true when approaching 0. Sometimes, you’ll also see this formula written as ; the limit is still 0 either way.

• 

If any real number is divided by x, and we let that x get infinitely large, the result is 0. Think about that—it makes sense. What is 4 divided by 900 kajillion? Who knows, but it’s definitely very, very small. So small, in fact, that it’s basically 0.

• 

This basically says that 1 plus an extremely small number, when raised to an extremely high power, is exactly equal to Euler’s number (2.71828 …). You will see this very infrequently, but it’s important to recognize it when you do.

• 

This is another specialty trigonometric limit that pops up now and again. Tuck it into the folds of your brain in case it shows up on a test.

Example 8: Evaluate .

Solution: This is the first special limit formula, but notice that the value inside sine must match the denominator for that formula to work; therefore, we need a 3x in the denominator instead of just x. The trick is to multiply the top and bottom by 3 (because that’s really the same thing as multiplying by 1—you’re not changing the expression’s value):

You can evaluate the limits of the factors separately and multiply the results together for the final answer:

Evaluating Limits Graphically

Throughout this chapter, you have focused on computational methods to calculate limits. Before you move on, it’s time to reinforce everything you’ve learned by calculating limits graphically. Why do this? It may help you determine whether or not you understand what finite and infinite limits actually mean. Sometimes it’s easy to fall into a “computational trap,” where you get so focused on the step-by-step algorithms of calculus that you forget how the techniques connect to reality.

Example 9: Given the graph of f(x) in Figure 6.3, evaluate the following limits:

(a)

(b)

(c)

(d)

Figure 6.3

The graph of f(x). Assume that the dotted lines are asymptotes.

Solution:

(a) As you approach x = 0 from the right and the left, the graph approaches the hole at point (0,1). Because the graph intends to reach a height of 1, .

(b) Trace your finger along the graph from right to left. As the graph heads off toward –∞ at its left edge, it is trying to reach a height of 4. The horizontal asymptote at that height will prevent it from ever reaching y = 4, but that does not change the limit: .

(c) As you approach x = 1 from the left and the right, the graph intends to reach (and actually does reach) a height of –1. Thus, .

(d) Whether you approach x = 2 from the left or the right, the graph plummets, decreasing without bound. Therefore, the limit does not exist, because .

Technology Focus: Calculating Limits

Most calculus courses these days allow you to use a graphing calculator or other technology tool, at least some of the time. The tools vary widely in their functionality, but the process we’ll explore here works the same for all calculators (except for a few tricks I included for Texas Instruments calculator owners).

How can you use graphing calculators to check your homework on limit problems? Well, calculators don’t mind plugging really small, annoying numbers into expressions—and we love them for their embrace of the mundane.

Back in Example 3, you applied the conjugate method to calculate a fairly complicated limit:

The problem asks you to calculate a limit as x approaches 5, so plug an x-value very close to 5 into the fraction, such as x = 5.0001:

I don’t know about you, but I can’t calculate off the top of my head, let alone subtract 4 from it and then divide it by 0.0001. Your calculator, however, is more than happy to do the work for you:

Figure 6.4

Your calculator may be able to express mathematical expressions that look like this, or your screen might look more like Figure 6.5.

Your digital buddy reports an approximate limit of 0.124999805, which is very close to 0.125, or .

By the way, the calculator screen in Figure 6.4 formats mathematics very neatly. The fractions and the square roots look just like they do in a regular math book. However, your calculator doesn’t need to be so fancy to get the correct answer. You just need to use parentheses carefully, as demonstrated in Figure 6.5.

Figure 6.5

This screen isn’t formatted as neatly, but you still get the same answer.

So, your calculator can help you check answers for problems that approach a finite limit, in this case x = 5. What about limits at infinity?

In Example 6, you calculated a limit as x approaches infinity of a rational function:

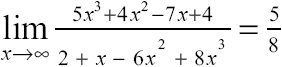
Near that problem, in a “Critical Point” sidebar, I insisted that if a rational function has a limit as x approaches ∞, then it has the same limit as x approaches –∞. Let’s use your calculator to make sure I’m not lying to you and verify that the limit as x approaches –∞ is the same: .

Replace x in the rational function with a really large negative number, something like x = –10,000. The result should come back close to 0.625, the decimal equivalent of :

Figure 6.6

There are a lot of zeros on this screen, so it’s pretty confusing. If only there were a better way ….

The final result, .6249031227, proves that I’m not a liar (at least not about asymptotes). The limit as x approaches –∞ is . Let’s be honest, though. That was a lot of typing, which leaves a lot of places to make mistakes. Luckily, there is a shortcut!

Your calculator probably lets you store values of variables in memory. On the Texas Instruments family of calculators, the button tells the calculator to store a number as a variable. For example, you could set A = –10,000 by typing (Pressing the green button allows you to access the green letters above the buttons, and the green letter A appears above the button.) Your screen should look like Figure 6.7. If you own a different calculator, check the manual for more information and instructions.

Figure 6.7

This set of keystrokes sets the variable A equal to –10,000 in your calculator’s memory. From now on, whenever it sees “A,” it thinks “–10,000.”

Now that you have stored –10,000 as A, you can type the rational expression using A, which is much easier on the eyes; the result is the same.

Figure 6.8

This is the same calculation as Figure 6.5, but this time the value –10,000 is represented by A.

The Least You Need to Know

• Most limits can be evaluated via the substitution, factoring, or conjugate methods.
• If a function f(x) has a vertical asymptote x = c, then or − ∞.
• If a rational function f(x) has a horizontal asymptote y = L, then (as long as there are no radicals in there).
• There are five common limits that defy our techniques and must be memorized.