CHAPTER
19

Final Exam

In This Chapter

• Measuring your understanding of all major calculus topics
• Practicing your skills
• Determining where you need more practice

Nothing helps you understand math like good old-fashioned practice, and that’s the purpose of this chapter. You can use it however you like, but I suggest one of the following three strategies:

1. As you finish reading each chapter, skip back here and work on the practice problems from that chapter.

2. If you’re using this book as a refresher for a class you’ve already taken, complete this test before you start reading the book. Then, go back and read the chapters containing problems you missed. After you’ve reviewed those topics, try these problems again.

3. Save this chapter until the end, and use it to see how much you remember of each topic when you haven’t seen it for a while.

Because these problems are just meant for practice, and not meant to teach new concepts, only the answers are given at the end of the chapter, usually without explanation or justification (unlike the problems in the “You’ve Got Problems” sidebars throughout the book). However, these practice problems are designed to mirror those examples, so you can always go back and review if you forgot something or need extra practice.

Are you ready? There’s a lot of practice ahead of you—as some problems have multiple parts, there are actually more than 100 practice problems in this chapter! (But no one said you have to do them all at one sitting.)

Chapter 2

1. Put the linear equation in standard form: –3(x + 2y) – 4y + 8 = x – 1.

2. Determine the equation of the line that passes through the point (–5,3) and has slope ; write the equation in standard form.

3. Calculate the slope of the line that passes through points (2,–3) and (–5,–8).

4. Line n passes through the point (2,–1) and is perpendicular to the line 3x – 5y = 2. Write the equation of n in standard form.

5. Simplify the expression .

6. Factor the expression completely: 32x² – 98y².

7. Solve the equation 2x² – 16x = 22 by completing the square.

8. Solve the equation by factoring: x² – 256 = 0.

9. Solve the equation using the quadratic formula: 3x² + 4x + 1.

Chapter 3

10.

11. Determine what kind of symmetry, if any, is evident in the graph of y = x⁵ – x³ + x – 5.

12. Find the inverse function, f^–1(x), if f(x) = 5x – 3; verify that f(x) and are inverses by demonstrating that .

13. Given the graph of function j(x) and a table of values for the following function k(x), calculate j ^–1(k(2)). Assume that j(x) has inverse function j ^–1(x); also assume that all points indicated on the graph of j(x) have integer coordinates.

14. Put the parametric equations x = 2t + 6, into rectangular form.

Chapter 4

15. If calculate cscθ and cotθ.

16. Evaluate using a coterminal angle and the unit circle.

17. Factor and simplify the trigonometric expression 1 – tan⁴θ.

18. Solve the equation and provide all solutions on the interval [0,2π).

20. Given f(x) as defined here, calculate .

21. Evaluate the limits on the graph:

(a)

(b)

(c)

(d)

Chapter 6

22. Evaluate the limits using substitution:

(a)

(b)

23. Evaluate the limits using the factoring method:

(a)

(b)

24. Evaluate using the conjugate method.

25. Evaluate the limit of as x approaches each value for which g(x) is undefined.

26. Evaluate the following limits:

(a)

(b)

(c)

(d)

27. Given h(x) = tan x, evaluate the following limits:

(a)

(b)

Chapter 7

28. Determine whether or not the function f(x), as defined here, is continuous at x = 4:

29. Find the value of c that makes the function g(x) everywhere continuous:

30. Find all the x-values for which the function is discontinuous and classify each instance of discontinuity.

31. Does the Intermediate Value Theorem guarantee the following function values for f(x) = 3x² – 12x + 4 on the closed interval [0,5]? Why or why not?

(a) 10

(b) 20

33. Determine g  ′(1) if g(x) = 3x² – 8x + 2 using the alternative formula for the difference quotient.

(b) (3x² + 4)(9x – 5)

(c)

(d) (x² – 7x + 2)¹⁰

(e)

35. Given the function h(x) = 3x⁴ – 9x² + 2, calculate the following values:

(a) The average rate of change of h(x) on the x-interval [–1,3]

(b) The instantaneous rate of change of h(x) when x = 2

36. Given f(x) = tan (cos x), calculate .

37. Assume functions j(x) and k(x) are continuous and differentiable for all real numbers. The following table lists values of the functions and their derivatives for specific x-values.

Given this information, calculate the following:

(a)

(b)

Chapter 10

38. Identify the equation of the tangent line to f(x) = x² sin x when x = π. Hint: use the Product Rule to differentiate f(x).

39. Calculate the slope of the tangent line to the graph of x² – 7xy – 4y² + y – 9 = 0 at the point (–3,0).

40. Calculate the slope of the normal line to the graph of j(x) = tan x cos x when x = 0.

41. Given g(x) = x³ – 4, evaluate (g ^–1)′(–3).

42. If h(x) = –2x³ – 5x + 3, calculate (h ^–1)′(–1).

43. Given the parametric equations x = cosθ and y = 2θ, determine

Chapter 11

44. If f(x) = x³ – 16x, find f  ′(x), determine its critical numbers, and determine if f(x) changes direction at each.

45. If some function g(x) has derivative , use a wiggle graph to determine the interval(s) on which g(x) is decreasing.

46. What are the absolute maximum and minimum values of 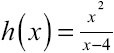on the closed interval [–4,3]?

47. On what interval is f(x) = x³ – 8x² + 9x – 12 concave up?

48. Use the Second Derivative Test to classify the relative extrema of the function .

Based on this information, answer the following questions:

(a) At what time(s) is the fish 3.5 inches left of the treasure chest?

(b) What is the speed of the fish at t = 4.2 seconds?

(c) What is the fish’s average velocity between t = 0 and t = 5?

(d) On what interval(s) does the fish have positive acceleration between t = 0 and t = 2 seconds?

50. Nick throws a baseball straight up from an initial height of 3 feet, with a velocity of 25 ft/sec. Given this information, answer the following questions:

(a) What is the velocity of the ball t = 1 second after Nick throws it?

(b) When does the ball reach its maximum height?

(c) What is the maximum height of the ball?

(d) Assuming no one catches the throw, how long does the ball remain in the air before it hits the ground?

Chapter 13

51. Given x₀ = 0, apply Newton’s Method to calculate x₁ and approximate the root of f(x) = e³x – 2.

52. Evaluate .

53. Given the function f(x) = 6x² – 2x + 3, find the x-value that satisfies the Mean Value Theorem on the interval [–1,1].

54. Erin and Sara are coworkers and exit their office at precisely the same time, 5 P.M. Erin walks due south from the office at a constant speed of 3.5 miles per hour. Sara bikes due west at a constant speed of 12 miles per hour. At what rate is the distance between Erin and Sara increasing at exactly 5:15 P.M.?

55. A farmer owns a plot of land whose western boundary is a river. He wishes to design a rectangular pasture but will only use fence for three of its sides, trusting the river to define the remaining side of the pasture, as illustrated here.

What are the dimensions of the largest pasture he can create using 2,500 feet of fence?

Chapter 14

56. Approximate the area under the curve on the interval [4,8] using the following:

(a) Right sums with n = 8 rectangles

(b) Midpoint sums with n = 4 rectangles

(c) Trapezoidal Rule with n = 4 trapezoids

(d) Simpson’s Rule with n = 6 subintervals

59. Calculate the area beneath the curve on the interval [4,8] using a definite interval.

60. Calculate the derivative: .

61. Integrate using u-substitution:

(a)

(b)

(c)

Chapter 16

62. Calculate the area between the functions .

63. Calculate the value guaranteed by the Mean Value Theorem for Integration on the function on the interval [0,1].

64. The velocity of a particle moving horizontally along the x-axis is modeled by the equation v(t) = t³ – 7t + 6, measured in inches per second. Use this information to answer the following questions:

(a) What is the total displacement of the particle between t = 0 and t = 3?

(b) What total distance does the particle travel between t = 0 and t = 3?

65. Given , evaluate the following:

(a) f(1)

(b) f  ′(1)

66. Write an integral expression representing the length of each graph segment described here, and then use a computational tool (such as a graphing calculator) to compute each integral:

(a) f(x) = tan x, between

(b) The parametric curve defined by x = e2t and y = ln (4t + 2) on the t-interval [0,3]

Chapter 17

67. Solve the differential equation x²dy = –2dx.

68. A popular new song is predicted to sell at a rate of million purchases per day. In fact, it sells 1.85 million copies by the end of the first day alone! Use this information to answer the following questions:

(a) What equation, y(t), models the sales of this CD? Note: calculate C accurate to four decimal places.

(b) Approximately how many songs will have been sold exactly 730 days (2 years) after release? Note: round your answer to four decimal places.

69. By ignoring any standards of cleanliness, and choosing to live a life of squalor, you have inadvertently invented a new kind of chemical weapon forged out of soggy Cheetos, stagnant milk-filled cereal bowls, and a chocolate Easter bunny of indeterminate age.

Here’s the downside. The government has quarantined you inside your filthy house until the nasty mixture disintegrates a bit. In a truly disturbing development, they’ve determined that (like nuclear waste), your food weapon has a half-life, and they’re reasonably sure the half-life is four days.

Assuming this is true, how long will it take the 3,000 grams of dangerous procrastination-produced glop to decay to a safer (but equally stinky) 10 grams?

71. Draw the slope field for by calculating slopes at each point indicated in the following coordinate plane:

Sketch the specific solution to the differential equation that contains the point (0,1).

72. If you begin at the point and proceed units to the right along a line with slope , what are the coordinates of your destination?

73. Use Euler’s Method with three steps of width to approximate if , given that the solution graph passes through (–1,1).

4. 5x + 3y = 7

5.

6. 2(4x + 7y)(4x – 7y)

7.

8. x = –16 or x = 16

9. x = –1 or x = –

Chapter 3

10. –3

11. no symmetry

12.

13. 5

14.

Chapter 4

15.

16.

17. sec²θ(1 + tanθ)(1 – tanθ)

18.

Chapter 5

19. –16

20. –1

21a. does not exist because , but ∞ is not a finite number

21b. 4

21c. does not exist because

21d. 0

Chapter 6

22a.

22b. 4a² – 6a + 1

23a.

23b.

24.

25. does not exist

26a.

26b. , which means it does not exist

26c. 0

26d. : split the two terms into separate limits, apply factoring and substitution methods, and add the results

27a. –1, because

27b. does not exist, because the graph of y = tan x has a vertical asymptote at x = π/2 (see Figure 4.4)

Chapter 7

28. Because is continuous at x = 4

29. c = 2

30. (infinite discontinuity) and x = 7 (point discontinuity)

31a. yes, because f(0) = 4, f(5) = 19, and 4 ≤ 10 ≤ 19

31b. no, because 20 does not fall between the function values of the endpoints f(0) = 4 and f(5) = 19

Chapter 8

32. f  ′(x) = 3x² – 2, f  ′(–3) = 25

33. g′(1) = –2

Chapter 9

34a.

34b. 81x² – 30x + 36

34c.

34d. 10  (x² – 7x + 2)⁹ (2x – 7)

34e. . Note: use the Product Rule and take the derivative of (2x – 3)⁴ with the Chain Rule

35a. 42

35b. 60

36.

37a. Apply the Chain Rule:

37b. Apply the Quotient Rule:

Chapter 10

38. y = –π²x ^{+ π3}. Note: f(π) = 0 and f  ′(π) = – π²

39.

40. j ′(x) = –tan x sin x + cos x sec2 x, so j ′(0) = 0 + 1 = 1, which means tangent and normal slopes are both 1 (as 1 is the reciprocal of itself)

41.

42.

43.

45. g(x) decreases on (–4,–3) and (1,5)

46. maximum = 0, minimum = –9

47.

48. is a relative minimum because is a relative maximum because g"(–6) = –23 < 0.

Chapter 12

49a. t = 0.2596, t = 1.3756, and t = 1.7194 seconds

49b.

49c. 0.6739 in/sec

49d. (0,0.3962) and (1.1746,1.9670)

50a. v(t) = s′(t) = –32t + 25, so
v(1) = –32(1) + 25 = –7 ft/sec (the ball is falling at a rate of 7 ft/sec, so this tells you the ball has already reached its maximum height before t = 1)

50b. v(t) = 0 when –32t + 25 = 0, or

50c. maximum height: s(0.78125) ≈ 12.7656 feet

50d. Solve equation –16t² + 25t + 3 = 0 for t and select only the positive solution: t ≈ 1.674 seconds.

Chapter 13

51.

52.

53. x = 0

54. After 15 minutes, Erin has traveled miles and Sara has traveled miles, so allow those to be the lengths of two sides of the right triangle illustrated here:

Apply the Pythagorean Theorem to determine that the length D of the hypotenuse, the distance between them, is 3.125 miles and then differentiate the Pythagorean Theorem with respect to t:

Solve for to get 12.5 miles per hour.

55. w = 625 feet, l = 2500 – 2(625) = 1250 feet. Note: pasture perimeter is 2w + l = 2500 so l = 2500 – 2w, plug this into the primary equation A = lw to get A = (2500 – 2w)w and optimize

Chapter 14

56a.

56b.

56c.

56d.

Chapter 15

57.

58.

59.

60. 3y ² cos y³

61a. .

61b.

61c.

Chapter 16

62.

63.

64a.

64b.

65a.

65b.

66a. . Note: you may need to enter sec⁴ x as (1/cos(x))⁴

66b.

Chapter 17

67.

68a. . Note: and y(1) = 1.85, so you need to solve the equation 1.85 = for C

68b. y(730) ≈ 4.5831, so 4,583,100 copies sold in two years

69. 32.915 days. Note: y(t) = 3000e ^–0.173287t

Chapter 18

70. 3.01667. Note: linear approximation is

72.

73. . Note: the coordinates of the three steps are ,