10
The Erlang Multirate Loss Model With Batched Poisson Arrivals
In this chapter we consider multirate loss models of batched Poisson arriving calls with fixed bandwidth requirements and fixed bandwidth allocation during service. In the batched Poisson process, simultaneous call‐arrivals (batches) occur at time‐points which follow a negative exponential distribution. A batched Poisson process can model overflow traffic.
10.1 The Erlang Multirate Loss Model with Batched Poisson Arrivals
10.1.1 The Service System
In the Erlang multirate loss model with batched Poisson arrivals (BP‐EMLM) we consider a link of capacity C b.u. that accommodates K different service‐classes under the CS policy. Calls of all service‐classes arrive in the link according to a batched Poisson process.
In the batched Poisson process, one basic principle of random arrivals, according to which no simultaneous arrivals occur (Figure 10.1a), is abolished, while another basic principle of random arrivals, according to which arrivals (the batches) occur at time‐points following a negative exponential distribution, is kept (Figure 10.1b) [1–4]. The batched Poisson process is important not only because in several applications calls arrive as batches (groups), but also because it can represent, in an approximate way, arrival processes that are more “peaked” and “bursty” (expressed by the peakedness factor ![]() ) than the Poisson process. The peakedness factor,
) than the Poisson process. The peakedness factor, ![]() , is the ratio of the variance over the mean of the number of arrivals: if
, is the ratio of the variance over the mean of the number of arrivals: if ![]() , the arrival process is Poisson, if
, the arrival process is Poisson, if ![]() , the arrival process is quasi‐random (see Chapter 6), and if
, the arrival process is quasi‐random (see Chapter 6), and if ![]() , the process is more peaked and bursty than Poisson. For example, batched Poisson processes are used to model overflow traffic (where
, the process is more peaked and bursty than Poisson. For example, batched Poisson processes are used to model overflow traffic (where ![]() ) [3].
) [3].

Figure 10.1 Call arrivals according to (a) a Poisson process and (b) a batched Poisson process.
Calls of service‐class ![]() require
require ![]() b.u. to be serviced and have an exponentially distributed service time with mean
b.u. to be serviced and have an exponentially distributed service time with mean ![]() . Calls arrive to the link according to a batched Poisson process with arrival rate
. Calls arrive to the link according to a batched Poisson process with arrival rate ![]() and batch size distribution
and batch size distribution ![]() , where
, where ![]() denotes the probability that there are
denotes the probability that there are ![]() calls in an arriving batch of service‐class
calls in an arriving batch of service‐class ![]() .
.
The batch blocking discipline adopted in the BP‐EMLM is partial batch blocking. According to the partial batch blocking discipline, a part of the entire batch (one or more calls) is accepted in the link while the rest of it is discarded when the available link bandwidth is not enough to accommodate the entire batch. More precisely, if an arriving batch of service‐class ![]() contains
contains ![]() calls and the available link bandwidth is
calls and the available link bandwidth is ![]() b.u., where
b.u., where ![]() , then
, then ![]() calls will be accepted in the link (where
calls will be accepted in the link (where ![]() is the largest integer not exceeding
is the largest integer not exceeding ![]() ) and the other
) and the other ![]() calls will be blocked and lost. The complete batch blocking discipline, where the whole batch is blocked and lost, even if only one call of the batch cannot be accepted in the system, is not covered here since it results in complex and inefficient formulas for the calculation of the various performance measures [25–7].
calls will be blocked and lost. The complete batch blocking discipline, where the whole batch is blocked and lost, even if only one call of the batch cannot be accepted in the system, is not covered here since it results in complex and inefficient formulas for the calculation of the various performance measures [25–7].
Let ![]() be the number of in‐service calls of service‐class
be the number of in‐service calls of service‐class ![]() in the steady state and
in the steady state and ![]() ,
, ![]() . Due to the CS policy, the set
. Due to the CS policy, the set ![]() of the state space is given by (I.36). In terms of
of the state space is given by (I.36). In terms of ![]() and due to the partial batch blocking discipline (where each call is treated separately to the other calls of a batch), the CAC is identical to that of the EMLM (see Section 1.2.1).
and due to the partial batch blocking discipline (where each call is treated separately to the other calls of a batch), the CAC is identical to that of the EMLM (see Section 1.2.1).
10.1.2 The Analytical Model
10.1.2.1 Steady State Probabilities
In order to analyze the service system, the first target is to determine the PFS of the steady state probability ![]() . In the classical EMLM, the PFS of (1.30) is determined as a consequence of the LB between adjacent states. In the BP‐EMLM, the notion of LB as described in the EMLM does not hold; this is shown by the following example.
. In the classical EMLM, the PFS of (1.30) is determined as a consequence of the LB between adjacent states. In the BP‐EMLM, the notion of LB as described in the EMLM does not hold; this is shown by the following example.
Based on (10.2) and (10.3), we have the following local flow balance equation across the level ![]() for service‐class
for service‐class ![]() calls:
calls:

The following lemma establishes the sufficiency of the flow balance across the levels ![]() for ensuring GB for state
for ensuring GB for state ![]() [ 3]:
[ 3]:
Lemma 10.1
If ![]() satisfies
satisfies ![]() for
for ![]() and all
and all ![]() , then
, then ![]() also satisfies the GB equations.
also satisfies the GB equations.
Proof:
Consider a state ![]() and the difference
and the difference ![]() which is interpreted as follows (after some simplifications), regarding arrivals from service‐class
which is interpreted as follows (after some simplifications), regarding arrivals from service‐class ![]() :
:

Similarly, we may write, regarding departures from service‐class ![]() :
:

By equating (10.7) and (10.8) and rearranging the terms, we have (for service‐class ![]() ):
):

Summing (10.9) over all ![]()
![]() yields the GB equation for state
yields the GB equation for state ![]() :
:

Q.E.D.
Example 10.3
Consider a link of capacity ![]() b.u. that accommodates only calls of a single service‐class
b.u. that accommodates only calls of a single service‐class ![]() which require
which require ![]() b.u. Let the batch arrival rate be
b.u. Let the batch arrival rate be ![]() and the call service rate be
and the call service rate be ![]() . Consider states
. Consider states ![]() and
and ![]() . The purpose of this example is to show the GB equation of state
. The purpose of this example is to show the GB equation of state ![]() . To this end, determine the differences
. To this end, determine the differences ![]() and
and ![]() based on ( 10.2) and ( 10.3), respectively. Present graphically the GB equation of state
based on ( 10.2) and ( 10.3), respectively. Present graphically the GB equation of state ![]() .
.
The difference ![]() can be written as:
can be written as:


Similarly, the difference ![]() is written as:
is written as:
By equating (10.11) and (10.12) and rearranging the terms (in the form ![]() , we have:
, we have:

The purpose of Figure 10.3 is to represent (10.13) graphically (the GB equation of state (2)).

Figure 10.3 Graphical representation of 10.13 (Example 10.3).
The PFS that satisfies (10.6) and (10.10) is given by [ 3]:

where ![]() is the normalization constant,
is the normalization constant, ![]() ,
, ![]() is the state space of the system,
is the state space of the system, ![]() , and
, and

where ![]() is the offered traffic‐load (in erl).
is the offered traffic‐load (in erl).
An important batch size distribution is the geometric distribution, which is memoryless and a discrete equivalent of the exponential distribution. If calls of service‐class k arrive in batches of size ![]() , where
, where ![]() is geometrically distributed with parameter
is geometrically distributed with parameter ![]() , i.e.,
, i.e., ![]() with
with ![]() , then we have in (10.15),
, then we have in (10.15), ![]() . In that case, the average batch size for service‐class
. In that case, the average batch size for service‐class ![]() batches will be
batches will be ![]() .
.
Example 10.4
Consider a link of ![]() b.u. The link accommodates calls of
b.u. The link accommodates calls of ![]() service‐classes whose calls require
service‐classes whose calls require ![]() b.u. and
b.u. and ![]() b.u., respectively. Let
b.u., respectively. Let ![]() . Assuming that the batch size distribution is geometrically distributed with parameters
. Assuming that the batch size distribution is geometrically distributed with parameters ![]() and
and ![]() , calculate the values of
, calculate the values of ![]() and the corresponding values of
and the corresponding values of ![]() based on the GB equations of ( 10.10).
based on the GB equations of ( 10.10).
The state space ![]() of this system consists of six states of the form
of this system consists of six states of the form ![]() , namely (0,0), (0,1), (1,0), (1,1), (2,0), and (3,0). The GB equation, according to ( 10.10), for state (0,0) is:
, namely (0,0), (0,1), (1,0), (1,1), (2,0), and (3,0). The GB equation, according to ( 10.10), for state (0,0) is:


Similarly, the rest GB equations are:
The solution of this linear system is:
Based on the values of ![]() , we have:
, we have:
The existence of a PFS for the steady‐state probabilities leads to an accurate recursive formula for the calculation of the unnormalized link occupancy distribution, ![]() [ 3]:
[ 3]:

where ![]() is the largest integer less than or equal to
is the largest integer less than or equal to ![]() and
and ![]() is the complementary batch size distribution given by
is the complementary batch size distribution given by ![]() .
.
The proof of (10.16) is similar to the proof of (1.39) and therefore is omitted.
If calls of service‐class ![]() arrive in batches of size
arrive in batches of size ![]() , where
, where ![]() is given by the geometric distribution with parameter
is given by the geometric distribution with parameter ![]() (for all
(for all ![]() ) then the BP‐EMLM coincides with the model proposed by Delbrouck in [8], as shown in [ 1] and [ 3]. More precisely, since
) then the BP‐EMLM coincides with the model proposed by Delbrouck in [8], as shown in [ 1] and [ 3]. More precisely, since ![]() , ( 10.16) takes the form:
, ( 10.16) takes the form:

If ![]() for
for ![]() and
and ![]() for
for ![]() , for all service‐classes, then we have a Poisson process and the EMLM results (i.e., the Kaufman–Roberts recursion of (1.39)).
, for all service‐classes, then we have a Poisson process and the EMLM results (i.e., the Kaufman–Roberts recursion of (1.39)).
10.1.2.2 TC Probabilities, CBP, Utilization, and Mean Number of In‐service Calls
The following performance measures can be determined based on ( 10.16):
- The TC probabilities of service‐class
 , via the formula:
(10.18)where
, via the formula:
(10.18)where
 is the normalization constant.
is the normalization constant. - The CBP (or CC probabilities) of service‐class
 , via the formula:
(10.19)where
, via the formula:
(10.19)where
 denotes the average size of service
denotes the average size of service  arriving batches and is given by
arriving batches and is given by  . In the case of the geometric distribution,
. In the case of the geometric distribution,  ).
). - The mean number of in‐service calls of service‐class
 , via (1.56), where the values of
, via (1.56), where the values of  can be determined via:
(10.20)
can be determined via:
(10.20)
where
 and
and  if
if  .
.Note that (10.20) is an intermediate result for the proof of ( 10.16) [ 3]. Indeed, by multiplying both sides of ( 10.20) with
 and taking the sum over all service‐classes, we have ( 10.16).
and taking the sum over all service‐classes, we have ( 10.16). - The link utilization,
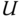 , via (1.54).
, via (1.54).
Example 10.5
In this example we present the difference between TC and CC probabilities. Consider a link of capacity ![]() b.u. that accommodates calls of two services with requirements
b.u. that accommodates calls of two services with requirements ![]() and
and ![]() b.u., respectively. In Figure 10.4 we assume that the link has 6 b.u. available for new calls. At the first time‐point, a call of service‐class 2 arrives. This call is accepted and the available link bandwidth reduces to 4 b.u. At the second time‐point, a batch of service‐class 1 arrives consisting of five calls. One out of these calls is blocked and lost. This type of blocking has to do with CC probability (one blocking event, see the CC probability calculation in Figure 10.4). At the third time‐point, we assume that there is available bandwidth to accept the whole batch of service‐class 1 (two calls) while at the fourth time‐point we assume that the whole batch of service‐class 2 (two calls) is discarded. This type of blocking has to do with both TC probability (one blocking event, see the TC probability calculation in Figure 10.4) and CC probability (two blocking events, see the CC probability calculation in Figure 10.4). At the fourth to sixth time‐points, the comments are similar and thus they are omitted. According to Figure 10.4, the calculation of both CC and TC probabilities gives higher CC probabilities, an expected result since calls arrive following a batched Poisson process.
b.u., respectively. In Figure 10.4 we assume that the link has 6 b.u. available for new calls. At the first time‐point, a call of service‐class 2 arrives. This call is accepted and the available link bandwidth reduces to 4 b.u. At the second time‐point, a batch of service‐class 1 arrives consisting of five calls. One out of these calls is blocked and lost. This type of blocking has to do with CC probability (one blocking event, see the CC probability calculation in Figure 10.4). At the third time‐point, we assume that there is available bandwidth to accept the whole batch of service‐class 1 (two calls) while at the fourth time‐point we assume that the whole batch of service‐class 2 (two calls) is discarded. This type of blocking has to do with both TC probability (one blocking event, see the TC probability calculation in Figure 10.4) and CC probability (two blocking events, see the CC probability calculation in Figure 10.4). At the fourth to sixth time‐points, the comments are similar and thus they are omitted. According to Figure 10.4, the calculation of both CC and TC probabilities gives higher CC probabilities, an expected result since calls arrive following a batched Poisson process.

Figure 10.4 Difference between CC and TC probabilities (Example 10.5).
Example 10.6
Consider again Example 10.4 (![]() ).
).
- Calculate the state probabilities
 by applying (10.17).
by applying (10.17). - Calculate the TC and CC probabilities as well as the link utilization via (10.18), (10.19)–( 10.20), and (1.54), respectively. Compare the obtained results with those of the EMLM.
- Starting with
 , we recursively calculate
, we recursively calculate  for
for 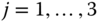 :
: 








The normalization constant is:
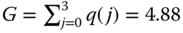 .
.The state probabilities (link occupancy distribution) are:



- TC probabilities:


To determine the CC probabilities, we should initially determine the values of
 and
and  .
.












Based on the above we have:


Utilization:
 b.u.
b.u.The corresponding CBP and link utilization results in the EMLM are:


 b.u.
b.u.
10.2 The Erlang Multirate Loss Model with Batched Poisson Arrivals under the BR Policy
10.2.1 The Service System
In the Erlang multirate loss model with batched Poisson arrivals under the BR policy (BP‐EMLM/BR) a new service‐class ![]() call is accepted in the link if, after its acceptance, the link has at least
call is accepted in the link if, after its acceptance, the link has at least ![]() b.u. available to serve calls of other service‐classes.
b.u. available to serve calls of other service‐classes.
In terms of the system state‐space ![]() and due to the partial batch blocking discipline, the CAC is identical to that of the EMLM/BR (see Section 1.3.2.2).
and due to the partial batch blocking discipline, the CAC is identical to that of the EMLM/BR (see Section 1.3.2.2).
10.2.2 The Analytical Model
10.2.2.1 Link Occupancy Distribution
In the BP‐EMLM/BR, the unnormalized values of the link occupancy distribution, ![]() , can be calculated in an approximate way according to either the Roberts method (see Section 1.3.2.2) or the Stasiak–Glabowski method (see Section 1.3.2.3). Herein we present the first method. Both methods have been investigated in [9], where the conclusions show that (i) both methods provide satisfactory results compared to simulation results, (ii) the Roberts method is preferable when only two service‐classes exist in the link or when the offered traffic‐load is low, and (iii) the Stasiak–Glabowski method can be considered when equalization of blocking probabilities is required, whereas it is preferable when more than two services exist and the offered traffic‐load is high.
, can be calculated in an approximate way according to either the Roberts method (see Section 1.3.2.2) or the Stasiak–Glabowski method (see Section 1.3.2.3). Herein we present the first method. Both methods have been investigated in [9], where the conclusions show that (i) both methods provide satisfactory results compared to simulation results, (ii) the Roberts method is preferable when only two service‐classes exist in the link or when the offered traffic‐load is low, and (iii) the Stasiak–Glabowski method can be considered when equalization of blocking probabilities is required, whereas it is preferable when more than two services exist and the offered traffic‐load is high.
Based on Roberts method, ( 10.16) takes the form [ 9]:

where ![]() is determined via (1.65).
is determined via (1.65).
10.2.2.2 TC Probabilities, CBP, Utilization, and Mean Number of In‐service Calls
The following performance measures can be determined based on (10.21):
- The TC probabilities of service‐class
 , via the formula:
(10.22)where
, via the formula:
(10.22)where
 is the normalization constant.
is the normalization constant. - The CBP (or CC probabilities) of service‐class
 , via ( 10.19).
, via ( 10.19). - The mean number of in‐service calls of service‐class
 , via (1.56), where the values of
, via (1.56), where the values of  can be determined via:
(10.23)
can be determined via:
(10.23)
- The link utilization,
 , via (1.54).
, via (1.54).
Example 10.7
Consider again Example 10.4 (![]() ) and assume the BR parameters
) and assume the BR parameters ![]() .
.
- Calculate the state probabilities
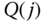 by applying ( 10.21).
by applying ( 10.21). - Calculate the TC and CC probabilities as well as the link utilization via ( 10.12), ( 10.19)–( 10.20), (10.23), and (1.54), respectively. Compare the results obtained with those of the EMLM/BR.
- Starting with
 , we recursively calculate
, we recursively calculate  for
for  :
: 








The normalization constant is:
 .
.The state probabilities (link occupancy distribution) are:



- TC probabilities are:




To determine the CC probabilities, we should initially determine the values of
 and
and  .
.












Based on the above we have:


Utilization:
 b.u.
b.u.The corresponding CBP and link utilization results in the EMLM/BR are:
 and
and  b.u.
b.u.
Example 10.8
Consider a link of capacity ![]() b.u. that accommodates two service‐classes whose calls require
b.u. that accommodates two service‐classes whose calls require ![]() b.u. and
b.u. and ![]() b.u., respectively. Consider also the following sets of BR parameters: (i)
b.u., respectively. Consider also the following sets of BR parameters: (i) ![]() and
and ![]() , (ii)
, (ii) ![]() and
and ![]() , and (iii)
, and (iii) ![]() and
and ![]() . The third set equalizes the TC probabilities of both service‐classes, since
. The third set equalizes the TC probabilities of both service‐classes, since ![]() . The batch size of both service‐classes follows the geometric distribution with parameters
. The batch size of both service‐classes follows the geometric distribution with parameters ![]() and
and ![]() . The call service time is exponentially distributed with mean
. The call service time is exponentially distributed with mean ![]() . The values of the offered traffic are
. The values of the offered traffic are ![]() erl and
erl and ![]() erl. In the first column of Tables 10.1–10.9,
erl. In the first column of Tables 10.1–10.9, ![]() remains constant while
remains constant while ![]() decreases by 0.2. As a reference, Table 10.1 shows the analytical results of TC and CC probabilities (for both service‐classes) in the case of the BP‐EMLM (CS policy). In Tables 10.2–10.4, for each set of BR parameters and for both service‐classes, we present the analytical and simulation results for the TC probabilities in the BP‐EMLM/BR. The corresponding results for the CC probabilities are presented in Tables 10.5–10.7. Table 10.8 presents the analytical results of the link utilization for both the BP‐EMLM and the BP‐EMLM/BR as well as the corresponding simulation results only for the BP‐EMLM/BR. All simulation results are mean values of seven runs with 95% confidence interval.
decreases by 0.2. As a reference, Table 10.1 shows the analytical results of TC and CC probabilities (for both service‐classes) in the case of the BP‐EMLM (CS policy). In Tables 10.2–10.4, for each set of BR parameters and for both service‐classes, we present the analytical and simulation results for the TC probabilities in the BP‐EMLM/BR. The corresponding results for the CC probabilities are presented in Tables 10.5–10.7. Table 10.8 presents the analytical results of the link utilization for both the BP‐EMLM and the BP‐EMLM/BR as well as the corresponding simulation results only for the BP‐EMLM/BR. All simulation results are mean values of seven runs with 95% confidence interval.
According to the results of Tables 10.1–10.8 we observe that:
- The BR policy is not fair to calls of service‐class 1 because the decrease of TC and CC probabilities of service‐class 2 is less significant compared to the increase of TC and CC probabilities of service‐class 1. This results in the decrease of the link utilization; compare the link utilization results of Table 10.8 (BR policy).
- The Roberts method provides quite satisfactory results compared to simulation results.
- Although the third set of BR parameters achieves the TC probabilities equalization, the same set cannot achieve the CC probabilities equalization (see Table 10.7). According to ( 10.19), which holds in the BP‐EMLM/BR, the calculation of CC probabilities depends on the offered traffic‐load rather than on the BR parameters. For a certain offered traffic‐load one can find the BR parameters which almost equalize the CC probabilities. When the offered traffic‐load changes, then a new set of BR parameters is needed. To show this, we present in Table 10.9 the BR parameters that almost equalize the CC probabilities of the service‐classes.
Table 10.1 Analytical results of TC and CC probabilities and link utilization for the BP‐EMLM (Example 10.8).
| TC probabilities (%) (analyt. results) | CC probabilities (%) (analyt. results) | |||
| Service‐class 1 | Service‐class 2 | Service‐class 1 | Service‐class 2 | |
| 2.0 | 2.52 | 25.56 | 3.14 | 47.84 |
| 1.8 | 2.20 | 22.99 | 2.74 | 45.17 |
| 1.6 | 1.88 | 20.32 | 2.35 | 42.26 |
| 1.4 | 1.57 | 17.54 | 1.96 | 39.08 |
| 1.2 | 1.26 | 14.69 | 1.58 | 35.62 |
| 1.0 | 0.97 | 11.79 | 1.22 | 31.85 |
| 0.8 | 0.70 | 8.92 | 0.88 | 27.76 |
| 0.6 | 0.46 | 6.16 | 0.58 | 23.38 |
Table 10.2 Analytical and simulation results of the TC probabilities for the BP‐EMLM/BR (![]() ) (Example 10.8).
) (Example 10.8).
| TC probabilities (%) | Simulation (%) | |||
| Service‐class 1 | Service‐class 2 | Service‐class 1 | Service‐class 2 | |
| 2.0 | 8.27 | 24.44 | 7.46 |
24.82 |
| 1.8 | 7.23 | 21.98 | 6.50 |
22.32 |
| 1.6 | 6.20 | 19.42 | 5.56 |
19.61 |
| 1.4 | 5.18 | 16.76 | 4.75 |
16.80 |
| 1.2 | 4.18 | 14.04 | 3.83 |
14.27 |
| 1.0 | 3.22 | 11.27 | 2.95 |
11.35 |
| 0.8 | 2.33 | 8.53 | 2.12 |
8.68 |
| 0.6 | 1.53 | 5.89 | 1.40 |
6.26 |
Table 10.3 Analytical and simulation results of the TC probabilities for the BP‐EMLM/BR (![]() ) (Example 10.8).
) (Example 10.8).
| TC probabilities (%) | Simulation (%) | |||
| Service‐class 1 | Service‐class 2 | Service‐class 1 | Service‐class 2 | |
| 2.0 | 13.88 | 23.24 | 14.90 |
24.05 |
| 1.8 | 12.24 | 20.87 | 13.10 |
21.55 |
| 1.6 | 10.58 | 18.40 | 11.16 |
19.16 |
| 1.4 | 8.93 | 15.86 | 9.54 |
16.45 |
| 1.2 | 7.30 | 13.25 | 7.65 |
13.94 |
| 1.0 | 5.71 | 10.62 | 6.07 |
10.98 |
| 0.8 | 4.19 | 8.03 | 4.35 |
8.46 |
| 0.6 | 2.81 | 5.53 | 2.93 |
5.82 |
Table 10.4 Analytical and simulation results of the equalized TC probabilities for the BP‐EMLM/BR (![]() ) (Example 10.8).
) (Example 10.8).
| Analytical results ‐ Equalised TC probabilities (%) | |||
| Simulation (%) | |||
| Service‐class 1 | Service‐class 2 | ||
| 2.0 | 21.40 | 22.32 |
22.30 |
| 1.8 | 19.12 | 19.87 |
19.89 |
| 1.6 | 16.78 | 17.39 |
17.42 |
| 1.4 | 14.37 | 14.80 |
14.79 |
| 1.2 | 11.94 | 12.35 |
12.38 |
| 1.0 | 9.51 | 9.80 |
9.78 |
| 0.8 | 7.13 | 7.35 |
7.38 |
| 0.6 | 4.88 | 5.04 |
5.05 |
Table 10.5 Analytical and simulation results of the CC probabilities for the BP‐EMLM/BR (![]() ) (Example 10.8).
) (Example 10.8).
| Analytical results (%) | Simulation (%) | |||
| Service‐class 1 | Service‐class 2 | Service‐class 1 | Service‐class 2 | |
| 2.0 | 8.74 | 47.06 | 8.23 |
47.06 |
| 1.8 | 7.65 | 44.45 | 7.17 |
44.41 |
| 1.6 | 6.56 | 41.61 | 6.13 |
41.77 |
| 1.4 | 5.49 | 38.51 | 5.23 |
38.39 |
| 1.2 | 4.43 | 35.13 | 4.22 |
35.16 |
| 1.0 | 3.42 | 31.44 | 3.25 |
31.61 |
| 0.8 | 2.48 | 27.46 | 2.33 |
27.48 |
| 0.6 | 1.63 | 23.17 | 1.56 |
23.49 |
Table 10.6 Analytical and simulation results of the CC probabilities for the BP‐EMLM/BR (![]() ) (Example 10.8).
) (Example 10.8).
| Analytical results (%) | Simulation (%) | |||
| Service‐class 1 | Service‐class 2 | Service‐class 1 | Service‐class 2 | |
| 2.0 | 14.36 | 46.22 | 15.57 |
46.50 |
| 1.8 | 12.69 | 43.66 | 13.68 |
43.80 |
| 1.6 | 10.99 | 40.88 | 11.71 |
41.12 |
| 1.4 | 9.29 | 37.84 | 10.02 |
37.93 |
| 1.2 | 7.60 | 34.54 | 8.05 |
34.77 |
| 1.0 | 5.96 | 30.95 | 6.41 |
31.10 |
| 0.8 | 4.39 | 27.06 | 4.60 |
27.28 |
| 0.6 | 2.95 | 22.88 | 3.11 |
23.18 |
Table 10.7 Analytical and simulation results of the CC probabilities for the BP‐EMLM/BR (![]() ) (Example 10.8).
) (Example 10.8).
| Analytical results (%) | Simulation (%) | |||
| Service‐class 1 | Service‐class 2 | Service‐class 1 | Service‐class 2 | |
| 2.0 | 22.16 | 44.93 | 22.97 |
45.13 |
| 1.8 | 19.82 | 42.42 | 20.37 |
42.54 |
| 1.6 | 17.41 | 39.69 | 17.86 |
39.89 |
| 1.4 | 14.93 | 36.75 | 15.36 |
36.71 |
| 1.2 | 12.42 | 33.55 | 12.58 |
33.54 |
| 1.0 | 9.91 | 30.08 | 10.23 |
30.05 |
| 0.8 | 7.44 | 26.35 | 7.58 |
26.36 |
| 0.6 | 5.11 | 22.35 | 5.32 |
22.47 |
Table 10.8 Analytical results of the link utilization for the BP‐EMLM and analytical and simulation results of the link utilization for the BP‐EMLM/BR (Example 10.8).
| BP‐EMLM | BP‐EMLM/BR ( |
BP‐EMLM/BR ( |
BP‐EMLM/BR ( |
||||
| Analytical | Simulation | Analytical | Simulation | Analytical | simulation | ||
| 2.0 | 37.14 | 36.82 | 36.82 |
36.52 | 36.17 |
36.16 | 35.77 |
| 1.8 | 35.84 | 35.54 | 35.42 |
35.25 | 34.95 |
34.90 | 34.62 |
| 1.6 | 34.38 | 34.10 | 34.06 |
33.83 | 33.58 |
33.48 | 33.33 |
| 1.4 | 32.72 | 32.47 | 32.38 |
32.22 | 32.05 |
31.89 | 31.74 |
| 1.2 | 30.84 | 30.63 | 30.62 |
30.40 | 30.20 |
30.09 | 29.97 |
| 1.0 | 28.70 | 28.52 | 28.58 |
28.33 | 28.22 |
28.04 | 28.00 |
| 0.8 | 26.26 | 26.12 | 26.12 |
25.96 | 25.87 |
25.71 | 25.66 |
| 0.6 | 23.46 | 23.36 | 23.36 |
23.24 | 23.22 |
23.04 | 23.03 |
Table 10.9 Offered traffic‐load versus CC probabilities equalization and the corresponding BR parameters in the BP‐EMLM/BR (Example 10.8).
| CC probabilities (%) | BR parameter |
||
| Service‐class 1 | Service‐class 2 | ||
| 2.0 | 42.22 | 42.33 | 22 |
| 1.8 | 38.68 | 39.87 | 22 |
| 1.6 | 37.05 | 36.86 | 23 |
| 1.4 | 32.87 | 34.05 | 23 |
| 1.2 | 30.38 | 30.66 | 24 |
| 1.0 | 27.07 | 27.37 | 25 |
| 0.8 | 24.22 | 23.81 | 27 |
| 0.6 | 19.88 | 20.15 | 29 |
10.3 The Erlang Multirate Loss Model with Batched Poisson Arrivals under the Threshold Policy
10.3.1 The Service System
In the Erlang multirate loss model with batched Poisson arrivals under the TH policy (BP‐EMLM/TH) we adopt the following TH‐type CAC to each individual call upon a batch arrival of service‐class ![]() :
:
- Due to the TH policy, the number of in‐service calls of service‐class
 , should be less than a threshold
, should be less than a threshold  , otherwise the new call cannot be accepted in the link.
, otherwise the new call cannot be accepted in the link. - If constraint (a) is met, then if
 , the call is accepted in the system, otherwise the call is blocked and lost (due to link bandwidth unavailability).
, the call is accepted in the system, otherwise the call is blocked and lost (due to link bandwidth unavailability).
10.3.2 The Analytical Model
10.3.2.1 Steady State Probabilities
In order to analyze the service system, the first target is to determine the PFS of the steady state probability ![]() . Following the analysis of Section 10.1.2.1, it is easy to verify that the GB equation of ( 10.10) does hold for a state
. Following the analysis of Section 10.1.2.1, it is easy to verify that the GB equation of ( 10.10) does hold for a state ![]() , where
, where ![]() . It can also be proved that the PFS of the BP‐EMLM/TH is given by (10.14) and ( 10.15), where ( 10.15) holds for
. It can also be proved that the PFS of the BP‐EMLM/TH is given by (10.14) and ( 10.15), where ( 10.15) holds for ![]() [10].
[10].
Example 10.9
Consider again Example 10.4 (![]() ). By assuming that
). By assuming that ![]() , calculate the values of
, calculate the values of ![]() and the corresponding values of
and the corresponding values of ![]() based on the GB equations of ( 10.10).
based on the GB equations of ( 10.10).
The state space ![]() of this system consists of five states of the form
of this system consists of five states of the form ![]() , namely (0,0), (0,1), (1,0), (1,1), and (2,0). The GB equations, according to ( 10.10), are:
, namely (0,0), (0,1), (1,0), (1,1), and (2,0). The GB equations, according to ( 10.10), are:
The solution of this linear system is:
Based on the values of ![]() , we have:
, we have:
To rely on ( 10.14) and ( 10.15) for determining the TC and CC probabilities or link utilization, state space enumeration and processing are required. To circumvent this problem, which is quite complex for many service‐classes and large capacity links, we present the following three‐step convolution algorithm by modifying the convolution algorithm of [11]:


10.3.2.2 TC Probabilities, CBP, Utilization, and Mean Number of In‐service Calls
The following performance measures can be determined based on (10.25)–(10.28):
- The TC probabilities of service‐class
 , via the formula:
(10.29)
, via the formula:
(10.29)
The first sum in (10.29) refers to states
 where there is not enough bandwidth for service‐class
where there is not enough bandwidth for service‐class  calls. The other term refers to states
calls. The other term refers to states  , where available link bandwidth exists, but nevertheless blocking occurs due to the TH policy. The normalization constant
, where available link bandwidth exists, but nevertheless blocking occurs due to the TH policy. The normalization constant  in the second term of ( 10.29) refers to the value used in (10.28).
in the second term of ( 10.29) refers to the value used in (10.28). - The CBP (or CC probabilities) of service‐class
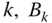 , via the formula ( 10.19).
, via the formula ( 10.19). - The mean number of in‐service calls of service‐class
 , via (1.56), where the values of
, via (1.56), where the values of  can be determined via:
(10.30)
can be determined via:
(10.30)
where
 and
and  if
if  .
.The nominator of (10.30) shows the “transfer” of the population of service‐class
 calls from the previous states
calls from the previous states  to state
to state  due to an arrival of a service‐class
due to an arrival of a service‐class  batch. The normalization constant
batch. The normalization constant  refers to the value used in (10.28).
refers to the value used in (10.28). - The link utilization,
 , via (1.54).
, via (1.54).
Example 10.10
Consider again Example 10.9 (![]() ).
).
- Apply the convolution algorithm to determine the values of
 .
. - Calculate the TC and CC probabilities as well as the link utilization via ( 10.29), ( 10.19), and (1.54), respectively.
- The convolution algorithm is:
- Step 1: Service‐class 1
 erl,
erl,  b.u.,
b.u.,  . For
. For  , we have:
, we have: 


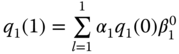




Therefore
 and the normalized values of
and the normalized values of  are:
are: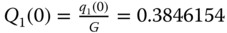


Service‐class 2
 erl,
erl,  b.u.,
b.u.,  . For
. For  , we have:
, we have:




Therefore
 and the normalized values of
and the normalized values of  are:
are:

- Step 2: This step also includes step 3 of the algorithm.
Based on (10.26)–(10.28) the normalized values of
 are given by:
are given by:



Since

we have the same values with those of Example 10.9:




- Step 1: Service‐class 1
- TC probabilities:





To determine the CC probabilities, we determine the values of
 and
and  :
:












Based on the above we have:


Utilization:
 b.u.
b.u.
Example 10.11
Consider a link of ![]() b.u. that accommodates two service‐classes. The batch size of both service‐classes follows the geometric distribution with parameters
b.u. that accommodates two service‐classes. The batch size of both service‐classes follows the geometric distribution with parameters ![]() and
and ![]() . Calls of service‐class 1 require
. Calls of service‐class 1 require ![]() b.u. and have a threshold parameter at
b.u. and have a threshold parameter at ![]() calls. The corresponding values for service‐class 2 are
calls. The corresponding values for service‐class 2 are ![]() b.u. and
b.u. and ![]() calls. The service time is exponentially distributed with mean
calls. The service time is exponentially distributed with mean ![]() . Let
. Let ![]() erl and
erl and ![]() erl. Provide analytical results of the TC and CC probabilities for the BP‐EMLM/TH, the BP‐EMLM, and the BP‐EMLM/BR. Let the BR parameters be
erl. Provide analytical results of the TC and CC probabilities for the BP‐EMLM/TH, the BP‐EMLM, and the BP‐EMLM/BR. Let the BR parameters be ![]() b.u. and
b.u. and ![]() b.u.
b.u.
On the ![]() ‐axis of Figures 10.5–10.8 the offered traffic load of service‐classes 1 and 2 increases in steps of 1.0 and 0.1 erl, respectively. So, point 1 refers to
‐axis of Figures 10.5–10.8 the offered traffic load of service‐classes 1 and 2 increases in steps of 1.0 and 0.1 erl, respectively. So, point 1 refers to ![]() , while point 10 refers to
, while point 10 refers to ![]() . All figures show that (i) the TH policy clearly affects the congestion probabilities of both service‐classes, thus it gives the opportunity for a fine TC and CC control aiming at guaranteeing certain QoS to each service‐class, and (ii) the BP‐EMLM and the BP‐EMLM/BR fail to approximate the results obtained from the BP‐EMLM/TH.
. All figures show that (i) the TH policy clearly affects the congestion probabilities of both service‐classes, thus it gives the opportunity for a fine TC and CC control aiming at guaranteeing certain QoS to each service‐class, and (ii) the BP‐EMLM and the BP‐EMLM/BR fail to approximate the results obtained from the BP‐EMLM/TH.

Figure 10.5 TC probabilities of service‐class 1 (Example 10.11).

Figure 10.6 CC probabilities of service‐class 1 (Example 10.11).

Figure 10.7 TC probabilities of service‐class 2 (Example 10.11).

Figure 10.8 CC probabilities of service‐class 2 (Example 10.11).
10.4 Applications
An interesting application of the BP‐EMLM has been proposed in [12] for the calculation of various performance measures, including call blocking and handover failure probabilities in a LEO mobile satellite system (MSS). In [ 12], a LEO‐MSS of ![]() contiguous “satellite‐fixed” cells is considered, each having a fixed capacity of
contiguous “satellite‐fixed” cells is considered, each having a fixed capacity of ![]() channels. Moreover, each cell is modeled as a rectangle of length
channels. Moreover, each cell is modeled as a rectangle of length ![]() (e.g.,
(e.g., ![]() km in the case of the iridium LEO‐MSS [13]) that forms a strip of contiguous coverage on the region of the Earth. Next, a few common assumptions are made. LEO satellite orbits are polar and circular. MUs are uniformly distributed on the Earth surface, while they are considered as fixed. This assumption is valid as long as the rotation of the Earth and the speed of a MU are negligible compared to the subsatellite point speed on the Earth [14]. Moreover, either beam handovers, within a particular footprint, or handovers between adjacent satellites of the same orbit plane may occur. The system of these
km in the case of the iridium LEO‐MSS [13]) that forms a strip of contiguous coverage on the region of the Earth. Next, a few common assumptions are made. LEO satellite orbits are polar and circular. MUs are uniformly distributed on the Earth surface, while they are considered as fixed. This assumption is valid as long as the rotation of the Earth and the speed of a MU are negligible compared to the subsatellite point speed on the Earth [14]. Moreover, either beam handovers, within a particular footprint, or handovers between adjacent satellites of the same orbit plane may occur. The system of these ![]() cells accommodates MUs that generate calls of
cells accommodates MUs that generate calls of ![]() service‐classes with different QoS requirements. Each service‐class
service‐classes with different QoS requirements. Each service‐class ![]() call requires a fixed number of
call requires a fixed number of ![]() channels for its whole duration in the system. New service‐class
channels for its whole duration in the system. New service‐class ![]() calls arrive in the system according to a batched Poisson process with arrival rate
calls arrive in the system according to a batched Poisson process with arrival rate ![]() and batch size distribution
and batch size distribution ![]() . Due to the uniform MUs distribution, new calls may arrive in any cell with equal probability. The cell that a new call originates is the source cell. Due to the call arrival process of new service‐class
. Due to the uniform MUs distribution, new calls may arrive in any cell with equal probability. The cell that a new call originates is the source cell. Due to the call arrival process of new service‐class ![]() calls, we model the arrival process of handover calls of service‐class
calls, we model the arrival process of handover calls of service‐class ![]() via a batched Poisson process with arrival rate
via a batched Poisson process with arrival rate ![]() and batch size distribution
and batch size distribution ![]() . The arrival of handover calls in a cell is as follows. Handover calls cross the source cell's boundaries to the adjacent right cell having a constant velocity of
. The arrival of handover calls in a cell is as follows. Handover calls cross the source cell's boundaries to the adjacent right cell having a constant velocity of ![]() , where
, where ![]() (approx. 26600 km/h in the iridium constellation) is the subsatellite point speed. An in‐service call that departs from the last cell (cell
(approx. 26600 km/h in the iridium constellation) is the subsatellite point speed. An in‐service call that departs from the last cell (cell ![]() ) will request a handover in cell 1, thus having a continuous cellular network (Figure 10.9).
) will request a handover in cell 1, thus having a continuous cellular network (Figure 10.9).

Figure 10.9 A rectangular cell model for the LEO‐MSS network.
Based on the above, let ![]() be the dwell time of a call in a cell (i.e., the time that a call remains in the cell). Then,
be the dwell time of a call in a cell (i.e., the time that a call remains in the cell). Then, ![]() is (i) uniformly distributed in
is (i) uniformly distributed in ![]() for new calls in their source cell and (ii) deterministically equal to
for new calls in their source cell and (ii) deterministically equal to ![]() for handover calls that traverse any adjacent cell from border to border. Based on (ii),
for handover calls that traverse any adjacent cell from border to border. Based on (ii), ![]() expresses the interarrival time for all handovers subsequent to the first one. As far as the duration of a service‐class
expresses the interarrival time for all handovers subsequent to the first one. As far as the duration of a service‐class ![]() call (new or handover) in the system and the channel holding time in a cell are concerned, they are exponentially distributed with mean
call (new or handover) in the system and the channel holding time in a cell are concerned, they are exponentially distributed with mean ![]() and
and ![]() , respectively.
, respectively.
To determine formulas for the handover arrival rate ![]() and the channel holding time with mean
and the channel holding time with mean ![]() of service‐class
of service‐class ![]() calls, we define:
calls, we define:
- The parameter
 as the ratio between the mean duration of a service‐class
as the ratio between the mean duration of a service‐class  call in the system and the dwell time of a call in a cell [ 14]:
(10.31)
call in the system and the dwell time of a call in a cell [ 14]:
(10.31)
- The time
 as the interval from the arrival of a new service‐class
as the interval from the arrival of a new service‐class  call in the source cell to the instant of the first handover.
call in the source cell to the instant of the first handover.  is uniformly distributed in
is uniformly distributed in  with pdf
with pdf  [15]:
(10.32)
[15]:
(10.32)
- The probabilities
 and
and  express the handover probability for a service‐class
express the handover probability for a service‐class  call in the source and in a transit cell, respectively. These probabilities are different due to the different distances covered by a MU in the source cell and in the transit cells. More precisely,
call in the source and in a transit cell, respectively. These probabilities are different due to the different distances covered by a MU in the source cell and in the transit cells. More precisely,  is defined as:
(10.33)
is defined as:
(10.33)
where
 is the service‐class
is the service‐class  call duration time (exponentially distributed with mean
call duration time (exponentially distributed with mean  ).
).The residual service time of a service‐class
 call after a successful handover request has the same pdf as
call after a successful handover request has the same pdf as  (due to the memoryless property of the exponential distribution). It follows then that
(due to the memoryless property of the exponential distribution). It follows then that  can be expressed by:(10.34)
can be expressed by:(10.34)
The handover arrival rate ![]() can be related to
can be related to ![]() by assuming that in each cell there exists a flow equilibrium between MUs entering and leaving the cell. In that case, we may write the following flow equilibrium equation (MUs entering the cell = MUs leaving the cell):
by assuming that in each cell there exists a flow equilibrium between MUs entering and leaving the cell. In that case, we may write the following flow equilibrium equation (MUs entering the cell = MUs leaving the cell):
where ![]() refers to the CBP of new service‐class
refers to the CBP of new service‐class ![]() calls in the source cell and
calls in the source cell and ![]() refers to the handover failure probability of service‐class
refers to the handover failure probability of service‐class ![]() calls in transit cells. The LHS of (10.35) refers to new and handover service‐class
calls in transit cells. The LHS of (10.35) refers to new and handover service‐class ![]() calls that are accepted in the cell with probability
calls that are accepted in the cell with probability ![]() and
and ![]() , respectively. The RHS of ( 10.35) refers to (i) service‐class
, respectively. The RHS of ( 10.35) refers to (i) service‐class ![]() calls that are handed over to the transit cell (depicted by
calls that are handed over to the transit cell (depicted by ![]() ), (ii) new calls that complete their service in the source cell without requesting a handover (depicted by
), (ii) new calls that complete their service in the source cell without requesting a handover (depicted by ![]() ), and (iii) handover calls that do not handover to the transit cell (depicted by
), and (iii) handover calls that do not handover to the transit cell (depicted by ![]() ).
).
Equation ( 10.35) can be rewritten as:

To derive a formula for the channel holding time of service‐class ![]() calls, note that channels are occupied in a cell by either new or handover calls. Furthermore, channels are occupied either until the end of service of a call or until a call is handed over to a transit cell. Since the channel holding time is expressed as
calls, note that channels are occupied in a cell by either new or handover calls. Furthermore, channels are occupied either until the end of service of a call or until a call is handed over to a transit cell. Since the channel holding time is expressed as ![]() in the case of the source cell and
in the case of the source cell and ![]() in the case of a transit cell, then the mean value of
in the case of a transit cell, then the mean value of ![]() for
for ![]() is given by:
is given by:
Now let ![]() and
and ![]() be the probabilities that a channel is occupied by a new and a handover service‐class
be the probabilities that a channel is occupied by a new and a handover service‐class ![]() call, respectively. Then:
call, respectively. Then:

Based on (10.37) and (10.38), the channel holding time of service‐class ![]() calls (either new or handover) is approximated by an exponential distribution whose mean
calls (either new or handover) is approximated by an exponential distribution whose mean ![]() is the weighted sum of ( 10.37) (for
is the weighted sum of ( 10.37) (for ![]() ) multiplied by the corresponding probabilities
) multiplied by the corresponding probabilities ![]() (for
(for ![]() ) and
) and ![]() (for
(for ![]() ):
):

Having determined the various input traffic parameters, we can analyze the LEO‐MSS via the BP‐EMLM assuming that each cell is modeled as a multirate loss system, where all calls compete for the available channels under the CS policy. To facilitate the description of the analytical model in [ 12], we distinguish new from handover calls and assume that each cell accommodates calls of ![]() service‐classes. A service‐class
service‐classes. A service‐class ![]() is new if
is new if ![]() and handover if
and handover if ![]() .
.
10.5 Further Reading
Due to the close relationship between the models of this chapter and the EMLM, the EMLM/BR, and the EMLM/TH, the interested reader may refer to the corresponding section of Chapter 1 . In addition, due to the fact that the BP‐EMLM can be used for the analysis of overflow traffic, it may be a candidate analytical model for various multirate loss systems that carry overflow traffic (e.g., [16–19]). Other extensions of the BP‐EMLM that show the applicability of the model in wireless networks appear in [20–22]. In [ 20], the BP‐EMLM is used for the CBP determination in the X2 link of LTE networks. In [21], the BP‐EMLM is extended to include multiple access interference, both the notion of local (soft) and hard blocking, the user's activity, as well as interference cancellation for the calculation of congestion probabilities in CDMA networks. An extension of [ 21] that incorporates the BP‐EMLM/BR is proposed in [ 22].
References
- 1 E. van Doorn and F. Panken, Blocking probabilities in a loss system with arrivals in geometrically distributed batches and heterogeneous service requirements. IEEE/ACM Transactions on Networking, 1(6):664–667, December 1993.
- 2 G. Choundhury, K. Leung and W. Whitt, Resource‐sharing models with state‐dependent arrivals of batches, in Computations with Markov Chains, W.J. Stewart (ed.), Kluwer, Boston, pp. 255–282, 1995.
- 3 J. Kaufman and K. Rege, Blocking in a shared resource environment with batched Poisson arrival processes. Performance Evaluation, 24(4):249–263, February 1996.
- 4 J. Morrison, Blocking probabilities for multiple class batched Poisson arrivals to a shared resource. Performance Evaluation, 25(2):131–150, April 1996.
- 5 G. Choundhury, K. Leung and W. Whitt, An inversion algorithm to compute blocking probabilities in loss networks with state‐dependent rates. IEEE/ACM Transactions on Networking, 3(5):585–601, October 1995.
- 6 K. Kawanichi, Y. Takahashi and T. Takenaka, Trunk reservation effects on multi‐server system with batch arrivals of loss and delay customers. IEICE Transactions on Communications, E83‐B(1):20–29, January 2000.
- 7 P. Ezhilchelvan and I. Mitrani, Multi‐class resource sharing with batch arrivals and complete blocking. Proceeding of the International Conference on Quantitative Evaluation of Systems (QEST), Lecture Notes in Computer Science, Vol. 10503, Springer, 2017.
- 8 L. Delbrouck, On the steady state distribution in a service facility with different peakedness factors and capacity requirements. IEEE Transactions on Communications, 31(11):1209–1211, November 1983.
- 9 I. Moscholios and M. Logothetis, The Erlang multirate loss model with batched Poisson arrival processes under the bandwidth reservation policy. Computer Communications, 33(Supplement 1):S167–S179, November 2010.
- 10 I. Moscholios, V. Vassilakis and P. Sarigiannidis, Performance modelling of a multirate loss system with batched Poisson arrivals under a probabilistic threshold policy. IET Networks, 7(4):242–247, July 2018.
- 11 V. Iversen, The exact evaluation of multi‐service loss system with access control. Teleteknik [English edn], 31(2):56–61, August 1987.
- 12 I.D. Moscholios, V.G. Vassilakis, P.G. Sarigiannidis, N.C. Sagias and M.D. Logothetis, An analytical framework in LEO mobile satellite systems servicing batched Poisson traffic. IET Communications, 12(1):18–25, January 2018.
- 13 M. Benslama, W. Kiamouche and H. Batatia, Connections management strategies, in Satellite Cellular Networks, John Wiley, 2015.
- 14 G. Maral, J. Restrepo, E. Del Re, R. Fantacci and G. Giambene, Performance analysis for a guaranteed handover service in an LEO constellation with a satellite‐fixed cell system. IEEE Transactions on Vehicular Technology, 47(4):1200–1214, November 1998.
- 15 E. Del Re, R. Fantacci and G. Giambene, Performance analysis of dynamic channel allocation technique for satellite mobile cellular networks. International Journal of Satellite Communications, 12(1):25–32, January/February 1994.
- 16 Q. Huang, K. Ko and V. Iversen, Performance modeling for heterogeneous wireless networks with multiservice overflow traffic. Proceedings of IEEE Globecom, Honolulu, USA, December 2009.
- 17 X. Yu and H. Zhu, An efficient method for loss performance modeling of hierarchical heterogeneous wireless networks. International Journal of Communication Systems, 27(6):956–968, June 2014.
- 18 M. Glabowski, S. Hanczewski and M. Stasiak, Modelling of cellular networks with traffic overflow. Mathematical Problems in Engineering, 2015, Article ID 286490, 15 pages.
- 19 M. Glabowski, A. Kaliszan and M. Stasiak, Modelling overflow systems with distributed secondary resources. Computer Networks, 108:171–183, October 2016.
- 20 I. Widjaja and H. Roche, Sizing X2 bandwidth for Inter‐connected eNBs. Proceedings of IEEE VTC Fall, Anchorage, Alaska, USA, pp. 1–5, September 2009.
- 21 I. Moscholios, G. Kallos, V. Vassilakis and M. Logothetis, Congestion probabilities in CDMA‐based networks supporting batched Poisson input traffic. Wireless Personal Communications, 79(2):1163–1186, November 2014.
- 22 I. Moscholios, V. Vassilakis, G. Kallos and M. Logothetis, Performance analysis of CDMA‐based networks with interference cancellation, for batched Poisson traffic under the bandwidth reservation policy. Proceedings of the 13th International Conference Telecommunications, ConTEL, Graz, Austria, July 2015.
