Chapter 2

Introduction to Rotating Electrical Machines

2.1. Introduction

Rotating electrical machines are electromechanical energy converters. Their economic importance is considerable because they provide almost all the electrical energy. In addition, electrical motors, usually associated with power electronics static converters, play an ever-increasing part in all industrial areas as well as in day to day life.

These machines are made of two distinct parts, one fixed (the stator) and the other one, mobile (the rotor). Those two parts are mainly constituted of ferromagnetic materials whose high permeability enables us to lead the field lines; they are separated by an air space (the air-gap) and carry a set of conductors (the windings) usually made of copper, a material chosen for its good electric conductivity. Those two armatures have different and complementary roles, illustrated by the terms of “field system” and of “armature” which are allotted to them.

2.2. Main notations

2.2.1. Vectors

– {v}: voltages of the phases vector (dimension n);

– {i}: currents of the phase vector (dimension n);

– {ψ}: fluxes per phase vector (dimension n);

as well as matrix:

– {R}: diagonal matrix of the resistances of the phases (dimensions n x n);

– {L}: inductance matrix or coupling matrix (dimensions n x n).

It should be noticed that the inductance matrix is naturally symmetrical because M_ij = M_ji.

2.3. Principle of the electromechanical energy conversion

First let us see how it is possible to produce electric energy by moving conductors within a magnetic field: let's consider conductor (C) set in an area where a flux density B appears (Figure 2.1).

Let us assume that this conductor is submitted to a basic movement dl during a time dt. The conductor will trace a surface dS through which the flux (or “flux-cutting”) will be noted dΦ.It is known that, under such circumstances, an electromotive force of module appears at the terminals of conductor (C). If this conductor is connected to an external impedance, a current i will flow within (C) and lead to the production of an instantaneous electrical power P_i = e i. The movement of the conductor requiring a mechanical power P_m, a conversion of mechanical energy into electrical energy is therefore achieved.

On the contrary if a current i is injected into (C), a force F which will tend to move it will be applied to it, consequently producing a work and therefore a mechanical power P_m (Figure 2.2). A conversion of electrical energy into mechanical energy is then achieved.

Bear in mind that the situation described in Figure 2.2 (field applied directly on the conductors) is rarely encountered in electromechanical converters. Conductors are usually set in slots, as represented in Figure 2.3a. The magnetic field is then canalized in teeth made of a highly permeable ferromagnetic material. At the conductors level (in the slot), the values of the flux density are small because the corresponding flux is a leakage flux. Consequently, as long as the currents do not exceed their nominal value, the electromagnetic force the conductors are submitted to is not important. The main force is indeed located on the slots sides because of the discontinuity of magnetic permeability.

However it can be shown that the real armature (coils, slots, teeth) may be replaced by an equivalent smooth armature (Figure 2.3b) where the conductors would be set down on the surface and would be of a thickness ε. Thickness ε is often made to tend towards zero in order to replace the real current by equivalent superficial currents.

This equivalence enables us to calculate force F, as suggested in Figure 2.2, but obviously doesn't make it possible to determine the local effects due to the slot. The representation in Figure 2.2 is therefore useful for emphasizing in a qualitative way the phenomena of electromechanical conversion. The example given in Figure 2.2 shows that electromechanical conversion result from the action of magnetic fields in relative movement with one another. This highlights the complementary roles played by the armatures.

Considering this, it can be noted that only a relative movement between these armatures, which can be placed indiscriminately at the stator or at the rotor of the machine, is necessary.

In most cases, the machines used for electromechanical energy conversion are cylindrical. Indeed, this geometry is particularly convenient, as the example in Figure 2.4 shows.

A conductor, carrying a current i directed longitudinally, is fixed to a rotor of circular section (radius R) and of length L. It is placed in a radial field (flux density B) which generates a tangential force creating a torque Γ_e = BiLR which, if the rotor has a speed Ω, will work and produce a mechanical power ΓΩ.

2.4. Continuous energy conversion

In most applications, electrical rotating machines are designed for “continuous energy conversion”. This means that it is desirable for the power produced to have an average value different from zero. For example in the hypothesis of a motor working mode, the average mechanical power Pm produced is given by:

where T is the functioning period of the machine (one turn, for example). If it is admitted that speed Ω is constant (functioning in a stationary mode), this expression leads to:

[2.1]

This concept is usually expressed as follows: a machine achieves a continuous energy conversion when the average value of the instantaneous torque is different from zero. This is an important notion which will then enable us to clarify some principles of the construction and of the power supply of electrical machines.

2.5. Non-salient and salient poles

The inductor has to generate a series of “north” poles and “south” poles along the air-gap. This can be achieved in two different ways: in the first method, the conductors are set inside the slots hollowed out along the field spool, the latter being indiscriminately stator or rotor, and are then connected with one another at the extremities of the machine (those connections are called “end windings”) so as to generate the desired pole alternation (Figure 2.5).

In this case the dimensions of the slots are generally considered to be negligible compared to the other geometrical parameters of the machine, which enables us to admit that the air-gap has a constant thickness. It is then referred to as “non-salient air-gap”, and by extension “non-salient pole machine”.

The other approach consists of using (Figure 2.6) windings around salient poles, with the direction it is wound imposing the name of the pole. In this case they will be referred to as “salient poles inductor” and “salient poles machine”, and the air-gap cannot be considered to be constant.

2.6. Notion of pole pitch

The armatures of an electrical machine generate a series of p “north” poles and p “south” poles, p being the number of pairs of poles along the air-gap, whether the machine is a salient pole one or a non-salient pole one. The pole pitch τ_p is defined by central angle π/p. The “double pole pitch” is therefore the central angle 2π/p through which consecutive “north” pole and “south” pole are seen. This emphasizes the existence of two different periods: the “mechanical period”, which corresponds to one revolution of the rotor, and the “electrical period”, which corresponds to the double pole pitch.

If Figure 2.7 which represents a tetrapolar machine is considered, it is clear that the position of a point P located along the air-gap, can be marked by two distinct angles of same origin: the “mechanical angle” Θ and the “electrical angle” θ with the expression:

[2.2]

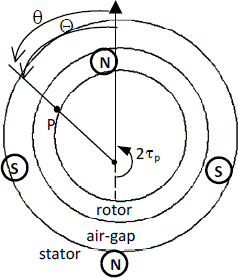
Figure 2.8 shows the distribution of the flux density along the air-gap.

2.7. Stator/rotor coupling: the “basic machine”

In order to attempt an approach of the principles of a “good conversion” of electromechanical energy in machines, we shall consider an elementary structure which shall be called a “basic machine” (Figure 2.9).

The structure is made of a cylindrical ferromagnetic rotor and stator with a circular section, coaxial and a length L. In each one two diametral slots of negligible dimensions have been hollowed out and carry two coils with respectively n_r and n_s turns. The radius of the rotor is named R, and the air-gap thickness e; it is assumed that R >> e, which enables us to consider in what follows that R + e ≈R.

Considering θ ξ the angle made by the axes of the two coils and ξ the angle spotting the position of a point P of the air-gap in relation to the axis of the rotor coil. In order to express the mutual inductance in the two coils, we can assume, for instance, that the rotor coil is supplied by a current i_r and calculate the flux induced in the stator coil which is assumed to be without any power supply.

If the permeability of the iron is assumed to be infinite, and since the air-gap is assumed to be small, it can be stated that field H_f in the iron is zero and that the lines of field H_e in the air-gap are radial. Since they change direction following the plan of the rotor coil (see Figure 2.9), it is arbitrarily set down that:

If Ampere's theorem is applied on a contour (γ) including two crossings of the air-gap located on each side of the rotor coil, we get:

thus the module of H_e:

and therefore

The variation of H_e = B_e/μ₀ in terms of ξis shown in Figure 2.10.

Considering the calculation hypotheses, the flux density within the iron is indeterminate. In order to calculate the flux in a stator turn, we shall consider the half-cylinder of length L located in the air-gap as close to the stator as possible and leaning on the turn (Figure 2.11).

Calling dφ the flux through an elementary surface ds of the cylinder, seen under the central angle dξ, leads to:

The total flux in the n_s turns of the stator coil is then:

Mutual inductance M between the two coils is defined by:

with:

This inductance varies in terms of θ, as shown in Figure 2.12.

The Fourier series of this wave is:

[2.3]

with:

Expression [2.3] highlights the fundamental M₀ cos θ, corresponding to k = 0, and the “space harmonics” obtained for k ≠ 0. In order to show the respective roles of the fundamental and space harmonics, we shall now assume that the machine is made of three identical stator coils shifted 2π/3 in space in comparison to the previous machine (Figure 2.13). Let us assume these coils are supplied by a 3-phase balanced current system and the rotor coil by a DC current.

Let us calculate, for example, the torque resulting from the interaction of the rotor coil with the stator coil “1” travelled by current i₁:

where B_e is the air-gap normal flux density generated by the rotor current. Thus:

Γ₁ can be written as follows:

with:

The variation of ε (“square wave”) is given by Figure 2.14, and its Fourier series is written:

Naming Г₁ Г₂ and Г₃ the torque contributions of the rotor coil with each of the stator coils, the global electromagnetic torque Г_e is worth:

If we set down, for example:

the resolution of the torque in Fourier series leads to:

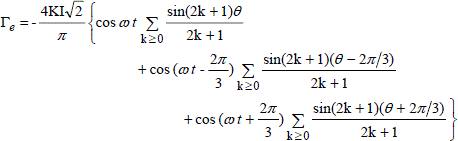
Let us assume that the rotor speed is ω, it is possible to write:

If this expression of θ is transferred into the expression of the torque, we obtain:

On the one hand this expression shows a constant term:

[2.4]

which corresponds to the average value of the instantaneous torque produced by the machine, and on the other hand, time related sinusoidal terms or “torque harmonics”.

Since these harmonics have a zero average value, they will not lead to continuous energy conversion, but only to losses and vibrations. This calculation therefore shows that if a machine is supplied by sinusoidal currents it is important to reduce the space harmonics as much as possible in order to obtain mutual inductances as near as possible to sinusoidal functions of the relative positions of the coils. This can be obtained by distributing the conductors into several slots, as shown in Figure 2.15.

In the example under consideration, the n_r rotor turns are distributed equally in ten slots, which gives n_r/5 conductors per slot, each with a current i_r travelled through them.

Applying Ampere's theorem to the contour γ₁, the embraced Ampere-turns are equal to , leading to an air-gap field worth:

If contour γ₂ is used, the Ampere-turns change to ,hence the new field value:

Likewise contour γ₃ would have led to a field:

The flux being conservative, the magnetic field H varies “in steps” between and (Figure 2.16).

Determination of mutual inductance M between the rotor and phase 1 of the stator requires a calculation of the magnetic flux travelling through the stator coil. This requires the integration of the field (see previous calculation). Each of the “steps” of H will therefore lead to a variation of M with a slope proportional to the value of H. We obtain the variation of M in relation to θ qualitatively, represented in Figure 2.16.

Thus a sinusoidal approximation of inductance M(0) for a sufficiently large number of slots can be admitted. In such conditions it will be quite possible to overlook the space harmonics, at least in a first approximation. In this case, the machines are said to have “a sinusoidal repartition of amperes-turns”.

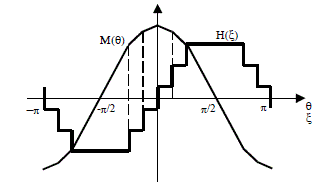
Note that a similar calculation would show that a machine devoid of space harmonics and supplied by non-sinusoidal currents would have a torque with a constant term linked to the fundamental component of current and torque harmonics caused by current harmonics. This explains the fact than when designing static converters, intended to supply sinusoidal distribution rotating machines, considerable attention is paid to the reduction of the harmonics of the output currents.

2.8. Losses within the machines

Rotating machines provide a conversion during which energy takes various successive forms: electric, electromagnetic and mechanical. This process is, at each step, accompanied by energy losses of various natures, which are usually classified as follows.

2.8.1. Losses due to Joule effect (or “Joule losses”)

These are due to the circulation of currents through conductors having a non-zero resistance. In order to reduce them, good conductive materials are used (usually copper, but sometimes aluminum for low cost machines). The frequency of the currents can have an influence upon these losses through the skin effect.

2.8.2. Electromagnetic losses (or “iron losses”)

These are linked to the behavior of ferromagnetic materials submitted to alternating fields. They gather, on the one hand hysteresis losses, and on the other hand losses due to the eddy currents. In order to reduce them, soft materials are used (materials with a narrow hysteresis cycle) in thin laminated steel, insulated from one another. Those losses mainly vary according to the frequency and the amplitude of the fields.

2.8.3. Mechanical losses

Gathered under this term are all of the energy losses caused by machine rotation: friction of the axes on the bearings, ventilation and air movement in the air-gap, etc. These losses are functions of the rotation speed of the machine. They are often represented by a losses torque with polynomial expression in terms of the speed (Γ_p = a₀ + a₁Ω + a₂Ω² + …, where a₀, a₁, a₂ are constants).

All these losses cause the production of heat within the machine, and therefore an increase in temperature with a risk of deterioration. That is why machines include cooling devices in order to extract the calories as they are produced: fans at the shaft ends, or driven by auxiliary motors, hollow conductors through which a coolant fluid runs, etc.

2.9. Nominal values

The previous considerations (power losses, temperature rises, cooling, etc.) bring about the definition of “nominal values” of a given machine. This is a set of quantities (power, voltages, currents, torque, speed, etc.) which the considered machine is likely to bear for an indeterminate time. Those values lead to a thermal equilibrium corresponding to the maximum temperature the machine can bear. This equilibrium is reached when the cooling devices extract the calorific energy exactly due to the losses within the machine.

It can be noted, in this connection, that those quantities can be exceeded during a limited time e.g. in transients like the starting of motors. This is possible because the thermal time constants (from several minutes to a few hours) are noticeably bigger than the mechanical time constants (usually about a few seconds) and electrical time constants (several dozen milliseconds) of the machines.

2.10. General sign covenant

Throughout this book, except for some specific cases which will be specified, we shall consider machines as motors: the mechanical power is considered to be positive when it is produced, and the electrical power is positive when it is absorbed. As a consequence, the various coils and windings shall a priori be considered as receivers.

2.11. Establishment of matricial equations

In this section, we shall establish a general process to translate the problem into equations for electrical machines, and a general expression of the electromagnetic torque. The approach consists of an overall writing of electrical equations in instantaneous quantities (voltages, currents, flux). A machine shall be considered as a set of coils (rotor and stator coils) the self inductances and mutual inductances of which constitute coupling matrices. The expression of the magnetic co-energy in relation to those coupling matrices and to instantaneous currents will enable us to establish a general expression of the electromagnetic torque and to examine the possibility of continuous energy conversion.

2.11.1. Working assumptions

Later in this section we shall consider a machine made of n coils with 2p poles at the stator and at the rotor. We shall neglect saturation and hysteresis phenomena, as well as induced eddy currents in the ferromagnetic parts.

2.11.2. Expression of the instantaneous torque

Let us consider the stator phase I, with R_i its electrical resistance, v_i the voltage applied between its terminals and Ψ_i the total flux through it. The following general equation can be written:

For all n phases of the machine:

[2.5]

with:

The instantaneous power P_i absorbed by the entire circuit is:

[2.6]

The first term of the right-hand member represents the Joule losses while the second represents (see [equation 1.31]) the sum of the “accumulated power” in the electromagnetic field and the converted mechanical power Γ_eΩ.

In a linear state, the global expression of the flux is written:

with:

L_i is the self inductance of phase i, and M_ij, the mutual inductance between phases i and j.

The electromagnetic torque is then obtained from equation [1.37].

[2.7]

This expression of the torque instantaneous value shall enable us to seek the main structures of machines likely to lead to a continuous energy conversion, that is to say the ones producing an average value of Γ_e different from zero.

The inductance matrix {} is broken up in four sub-matrices:

[_s] and [_r] respectively group together the stator and rotor inductances, [_sr] and [_rs] group together the stator-rotor and rotor-stator mutual inductances; keep in mind that the last two sub-matrices are the transposed matrices of one another. We shall now analyze the influence of the structure (non-salient or salient poles) of the machines on the instantaneous electromagnetic torque Γ_e, and, more specifically on the possibility of achieving a continuous energy conversion.

2.11.3. Continuous energy conversion in cylindrical machines

2.11.3.1. Instantaneous torque in cylindrical machines

In a cylindrical machine, the influence of the slots can, in a first approximation, be overlooked, and the air-gap can be considered to be constant. In such conditions the reluctance of the magnetic circuits of stator and rotor phases is independent of the stator-rotor position; it shall thus be the same for the inductances of those phases. It can be deduced that:

thus:

If this expression is transferred into the equation of the instantaneous electromagnetic torque, we obtain:

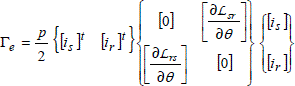
which leads to:

Since , the two terms of the above expression are equal, and it can then be written indiscriminately:

[2.8a]

or:

[2.8b]

2.11.3.2. Periodicities and angular frequencies

We shall now consider that all rotor currents have the angular frequency ω_r, and the stator currents, the angular frequency ω_s. The stator-rotor mutual inductances depend on θ = pΘ, and, if the machine is assumed to be “well built” (that is to say with a sinusoidal distribution of the Ampere-turns), this dependence will be sinusoidal. The period of variation of those mutual inductances will therefore be the “electrical period” or double pole pitch, which leads to an angular frequency pΩ.

Torque Г_e is the product of three periodical functions; hence a non-zero average value needs the algebraic sum of the angular frequencies to be equal to zero. It is deduced that:

[2.9]

Now let us see what can be deduced from this expression, in analyzing first the special case when one of the terms of this expression is zero.

2.11.3.2.1. Case of ω_r = 0 (rotor supplied by a DC current)

In this case:

[2.10]

which corresponds to the functioning of a synchronous machine (rotation speed proportional to the stator angular frequency); this will be studied in Chapter 3.

2.11.3.2.2. Case of ω_s = 0 (stator supplied by a DC current)

In that case:

[2.11]

This expression corresponds to so-called “inverted” synchronous machines (field system at the stator side and the armature at the rotor side), but also to DC machines. The currents in the rotor of the latter are AC currents and are mechanically rectified by the brush-commutator system (Chapter 5).

2.11.3.2.3. Case of Ω= 0 (stationary machine)

If Ω= 0, we obviously get ω_s = ω_r. The stator and rotor angular frequencies will then have to be equal. We shall see that the asynchronous machine (Chapter 4) provides this condition, leading to an initial non-zero torque. The DC machine also respects this expression with ω_s = ω_r = 0 at a zero speed.

2.11.3.2.4. General case

If none of the three variables (ω_s, ω_r, Ω) are zero, equation [2.9] leads to:

[2.12]

This equation corresponds to the functioning of the asynchronous machine, whether it is an induction machine or a “doubly fed” machine (Chapter 4).

2.11.4. Continuous energy conversion in salient pole machines

2.11.4.1. Salient pole machine torque

When one of the two spools (rotor or stator) has salient poles (Figure 2.6), it is not possible to consider the air-gap as constant. For example, let us consider the case of rotor salience (Figure 2.6b): since the stator is cylindrical, the magnetic circuit of the rotor coil has a geometry independent from the stator-rotor position; its reluctance, and as a consequence, its inductance shall be independent from Θ, and therefore from θ. On the contrary, it is clear that as far as the magnetic circuit of the stator phases is concerned, the air-gap, and therefore the reluctance, are extremely dependent from relative rotor-stator position, which generates a variation of the stator inductances in relation to Θ, and therefore to θ.

So, for a machine with a salient rotor, matrix [_s] is a function of Θ, whereas [_r] is not. This leads to an inductance matrix derivative in terms of the position:

Bringing this expression into the equation of the electromagnetic torque leads to an extra term (with regards to the non-salient machine torque) called “salience torque” or “reluctance torque”:

[2.13]

An identical reasoning would show that for a salient stator machine (Figure 2.6a), it is matrix [_r] which is a function of Θ, and this leads to a salience torque as follows:

[2.14]

2.11.4.2. Periodicities and angular frequencies

In the previous sections, the inductances variation period in terms of Θ is the polar pitch (and not the double polar pitch, as for rotor-stator mutuals). Therefore, when in the case of rotor salience, has a 2pΩ angular frequency. also has an angular frequency of 2pΩ in the case of a stator salience.

2.11.4.3. Continuous energy conversion

Expressions [2.13] and [2.14] show that in order to obtain a non-zero average value of Г_s it would be advisable to have:

or:

We can deduce that the machines for which it is useful to have salient rotors are the synchronous machines, which will be studied in Chapter 3. In the same way, DC machines (Chapter 5), as well as “inverted” synchronous machines (Chapter 3) can have stator salient poles. On the contrary, asynchronous machines need a non-salient air-gap, that is to say they cannot have any salient pole either at the stator or at the rotor.

2.12. Mechanical equation

Electrical machines have a mechanical interaction with their environment (charge in the case of a motor, driving mechanism in the case of a generator). This is characterized by the dynamics equation applied to rotating solids. In the case of a motor it can be written as:

[2.15]

where Г is the torque of the electrical machine, Г_c that of the charge, and J the moment of inertia of the whole of the rotating parts. This equation is often called the “mechanical equation” of the rotating machines.

2.13. Conclusion

The matricial formalism introduced in this chapter will later allow the translation into equations of synchronous, asynchronous and DC machines: the analysis of the physical structure of each machine will lead to writing the coupling matrices, and knowing the power supply will enable us to write the current and voltage expressions. Bear in mind that since the equations are written with instantaneous values, the supply by static converters giving out non-sinusoidal currents can be taken into account. The instantaneous electromagnetic torque expression (equation [2.7]) shall be used in the following chapters in order to characterize the electromagnetic energy conversion in each machine.