7
Vibration Damping of Structures Using Active Constrained Layer Damping
7.1 Introduction
The performance characteristics of Active Constrained Layer Damping (ACLD) are presented. The ACLD consists of a viscoelastic damping layer that is sandwiched between two layers of piezoelectric sensor and actuator. The composite ACLD when bonded to a vibrating structure acts as a smart treatment whose shear deformation can be controlled and tuned to the structural response in order to enhance the energy dissipation mechanism and improve the vibration damping characteristics.
Particular emphasis is placed on studying the performance of ACLD treatments that are provided with sensing layers of different spatial distributions. The effect of varying the controller gains and the operating temperature on the ACLD performance is determined for beams, plates, and shells. Comparisons with the performance of conventional passive constrained layer damping (PCLD) are also presented.
7.2 Motivation for Using Passive and Active Constrained Layer Damping
In this section, a control theory perspective is presented to motivate the need for ACLD as an effective means for controlling the structural vibrations. In order to illustrate such effectiveness, several structural configurations are considered as displayed in Figure 7.1. The considered configurations include: an undamped structure, a structure treated with an unconstrained damping layer, a structure treated with a constrained damping layer, and a structure treated with ACLD. For the purpose of illustrating the basic features of these configurations, the base structure is assumed without a loss of generality to be a rod undergoing longitudinal vibrations.

Figure 7.1 Configurations of structures treated with various passive and active constrained layer damping treatments. (a) untreated structure, (b) structure with unconstrained damping layer, (c) structure with passive constrained damping layer, and (d) structure with active constrained damping layer
The considered rod is assumed to be mounted in a fixed‐free configuration and made of aluminum with width of 0.025 m, thickness of 0.025 m, and length of 1 m. Also, it is assumed that the viscoelastic material (VEM) treatment is a full treatment with a width of 0.025 m, thickness = 0.025 m, and density of 1100 kg m−3. The storage modulus and loss factor of the VEM are predicted by Golla–Hughes–McTavish model (GHM) model with one mini‐oscillator with E0 = 15.3MPa, α1 = 39, ζ1 = 1, ω1 = 19, 058rad/s. Furthermore, the VEM is constrained by an aluminum constraining layer that is 0.025 m wide and 0.0025 m thick. For simplicity purposes, the structural system is modeled by one finite element model.
7.2.1 Base Structure
Consider the dynamics of the untreated plain rod shown in Figure 7.2. The equation of motion of the single element undamped rod is given by:

Figure 7.2 Untreated plain rod.
where ![]() , and {FT} = F. Note that ρs, As, L, Es and are the density, area, length, and Young's modulus of the rod.
, and {FT} = F. Note that ρs, As, L, Es and are the density, area, length, and Young's modulus of the rod.
In the Laplace domain, Eq. (7.1) leads to the transfer function between deflection u1 and force F as follows:

The transfer function has no zeros, that is, the roots of the numerator, but has two poles, that is, the roots of the denominator, which are located at:

where s denotes the Laplace complex number.
Figure 7.3 shows a display of the pole‐zero map of the undamped rod. The poles are designated by × and are located on the imaginary axis where the damping ratio is zero.

Figure 7.3 Pole‐zero map of a plain untreated rod.
For this undamped rod, the frequency and time response characteristics are shown in Figure 7.4.

Figure 7.4 Frequency and time response of a plain untreated rod.
7.2.2 Structure Treated with Unconstrained Passive Layer Damping
Consider the dynamics of a rod treated with an unconstrained layer damping as shown in Figure 7.5. The equation of motion of the single element of the rod is given in Chapter 4 by:

Figure 7.5 A rod treated with unconstrained layer damping.
where ![]() and
and ![]() . Also, u1 and z denote the deflection of the rod and internal degree of freedom of the VEM, respectively. Note that ρi, Ai, L, and Ei define the density, area, length, and Young's modulus of the rod (i = s) and VEM (i = v). Also,
. Also, u1 and z denote the deflection of the rod and internal degree of freedom of the VEM, respectively. Note that ρi, Ai, L, and Ei define the density, area, length, and Young's modulus of the rod (i = s) and VEM (i = v). Also, ![]() and the GHM model of the VEM is given by:
and the GHM model of the VEM is given by:

As in the Laplace domain, Eq. (7.1) leads to the transfer function between deflection u1 and force F as follows:

The transfer function has two zeros, that is, the roots of the numerator, at – ω1. These two repeated roots depend only on the parameters of the GHM model of the VEM. However, the transfer function has four poles, that is, the roots of the denominator. The locations of these poles depend on the interaction between the parameters of the rod and the VEM.
Figure 7.6a shows a display of the pole‐zero map of the rod with unconstrained layer damping. The poles are designated “×” and the zeros are designated “o.” The figure displays clearly two sets of pairs of poles. The first set of poles appears to be located on the imaginary axis defining the poles of the structure. The second set of poles consists of distinct negative real numbers defining the poles of the VEM. These VEM poles sandwich the two repeated zeros of the VEM as indicated clearly in Figure 7.6a.

Figure 7.6 Pole‐zero map of a rod treated with unconstrained layer damping. (a) Full view, (b) Close‐up view.
Note that the poles and the zeros of the VEM appear on the real axis as the damping ratio of the GHM mini‐oscillator model is selected to be equal to 1, that is, ζ = 1 or critically damped.
A closer look at the two poles of the rod, as displayed in Figure 7.6b, indicates that these two poles are actually not lying on the imaginary axis, but are located inside the left hand side of pole‐zero map. The migration of these poles from the imaginary axis has resulted from the interaction of the parameters of the rod and the VEM. However, the extent of migration is very limited as indicated by the resulting damping ratio, which is ζ = 0.002 51. Such a very low damping ratio suggests the ineffectiveness of unconstrained layer damping in enhancing the damping characteristics of structures. This fact emphasizes the findings reported in Chapters 4 and 6. The natural frequency of the pole is 7450 rad s−1 (i.e., 1186.3 Hz), which matches that predicted by the frequency response characteristics shown in Figure 7.7.

Figure 7.7 Frequency and time response of a rod treated with unconstrained layer damping.
For this configuration of a rod treated with unconstrained layer damping, the corresponding frequency and time response characteristics are shown in Figure 7.7. The results displayed in Figure 7.7 indicate that use of the unconstrained layer damping has introduced light damping of the rod vibration in comparison with the characteristics displayed in Figure 7.4 for the undamped rod.
7.2.3 Structure Treated with Constrained Passive Layer Damping
Consider the dynamics of a rod treated with a constrained layer damping as shown in Figure 7.8. The equation of motion of the single element of the rod is given in Chapter 4 by Eq. (4.50):

Figure 7.8 Rod treated with a passive constrained layer damping.
where ![]() and {Ft} = {0 F 0}T with
and {Ft} = {0 F 0}T with ![]() denoting the deflection of the constraining layer, deflection of the rod, and internal degree of freedom of the VEM, respectively. The matrices [Mt], [Ct], and [Kt] are described in Section 4.2.4.2 of Chapter 4. Equation (7.8) can be written in the following state‐space representation as:
denoting the deflection of the constraining layer, deflection of the rod, and internal degree of freedom of the VEM, respectively. The matrices [Mt], [Ct], and [Kt] are described in Section 4.2.4.2 of Chapter 4. Equation (7.8) can be written in the following state‐space representation as:
where 
 and u = F.
and u = F.
In the Laplace domain, Eq. (7.9) reduces to:
Then, the transfer function between the rod deflection u3 and the applied force F is given by:

where C = measurement matrix = [0 1 0], N(s) = numerator, and D(s) = denominator.
Figure 7.9 shows a display of the pole‐zero map of the rod with constrained layer damping. The poles are designated by “×” and the zeros are designated by “o.” The figure displays clearly two sets of poles and zeros. The first set of four complex poles is located near the imaginary axis and sandwiching two closely placed complex zeros. The second set of negative real poles sandwiching two negative real zeros. The first set of poles/zeros are related to the rod structural system whereas the second set of poles/zeros defines the dynamics of the VEM with its internal degrees of freedom (DOF).

Figure 7.9 Pole‐zero map of a rod treated with a passive constrained layer damping. (a) Full view and (b) close‐up view.
In Figure 7.9b, a close‐up view of the pole‐zero map indicates clearly that the dominant pole of the rod system is located such that the damping ratio ζ = 0.00524 and a natural frequency of 7510 rad s−1 (i.e., 1196 Hz). This pole coincides with the first natural frequency of the rod system as is confirmed by the frequency and time response characteristics shown in Figure 7.10.

Figure 7.10 Frequency and time response characteristics of a rod treated with a passive constrained layer damping.
Furthermore, the pole‐zero map of Figure 7.9b also displays complex poles, which are located in the s‐plane such that the damping ratio ζ = 0.0857 and a natural frequency of 32,700 rad s−1 (i.e., 5220 Hz). These poles coincide with the second natural frequency of the rod system as is confirmed by the frequency and time response characteristics shown in Figure 7.10.
It is important to note that the low damping ratio (ζ = 0.00524) of the first mode is evident in the sharpness of the resonance of the frequency response and in the low decay of the vibration in the time response displayed in Figure 7.10. Also, the higher damping ratio (ζ = 0.0857) of the second mode is manifested clearly by the flatness of the resonance of the frequency response and by the very fast decay of vibration in the time response displayed in Figure 7.10.
Comparison between the obtained characteristics of rods treated with unconstrained and constrained layer damping indicates that constraining the VEM has significantly enhanced the damping ratio. For the considered examples, the damping ratio of the first mode has increased from 0.002 51 with unconstrained layer damping to almost double the (ζ = 0.005 24) when using constrained layer damping. Also, with constrained layer damping, high damping ratios are obtained for higher order modes as it is predicted that the damping ratio for the second mode reaches ζ = 0.0857, which is 20‐fold that of the first mode.
7.2.4 Structure Treated with Active Constrained Passive Layer Damping
Consider the dynamics of a rod treated with an active constrained layer damping as shown in Figure 7.11. The equation of motion of the single element of the rod is given in Chapter 4:
where ![]() , {Ce} = [0 1 0]T, and {Cc} = [1 0 0]T. Also, Fe and Fc denote the external and control forces, respectively. The matrices [Mt], [Ct], and [Kt] are as described in Section 4.2.4.2 of Chapter 4.
, {Ce} = [0 1 0]T, and {Cc} = [1 0 0]T. Also, Fe and Fc denote the external and control forces, respectively. The matrices [Mt], [Ct], and [Kt] are as described in Section 4.2.4.2 of Chapter 4.

Figure 7.11 Rod treated with active constrained layer damping.
The control force Fc can be generated using the following control law:
where KG is the proportional control gain and KGkr is the derivative control gain. In this form, kr is the ratio between the derivative and proportional control gains.
Putting Eq. (7.12) into the state‐space representation, gives:
where 
 and
and  .
.
In the Laplace domain, Eq. (7.14) reduces to:
Figure 7.12 shows a display of the block diagram of the ACLD/rod system that translates the interactions between Eqs. (7.12) and (7.15).
![Block diagram of an ACLD/rod system treated with active constrained layer damping, from a Be to a circle, to (sI –A)–1, to [C̅e]T, to –KG (1 + krs), to B, and back to the circle.](http://images-20200215.ebookreading.net/1/4/4/9781118481929/9781118481929__active-and-passive__9781118481929__images__c07f012.gif)
Figure 7.12 Block diagram of a rod treated with active constrained layer damping.
Then, the transfer function between the rod deflection u3 and the applied force Fe is given by:

where Nc(s) and Dc(s) are the numerator and denominator of the closed‐loop system. Also, ![]() is given by:
is given by: ![]() .
.
The performance of the closed‐loop system is governed by the denominator of the transfer function u3/F, that is, by the roots of its characteristics equation:
For a given value of kr, Eq. (7.17) can be reduced to the following form:
where N/D is denoted as the open‐loop transfer function.
Equation (7.18) can be rewritten to take one of the following two forms:
when the Gain = 0, the roots of the characteristics equation has roots equal to the roots of the denominator D = 0; that is, poles of the open‐loop transfer function.
when the Gain = ∞, the roots of the characteristics equation has roots equal to the roots of the denominator N = 0, that is, zeros of the open‐loop transfer function.
Hence, by varying the gain from 0 to ∞, the roots of the characteristics equation of the closed‐loop system start from the poles of the open‐loop transfer function and end at the zeros of the open‐loop transfer function. A plot of the loci of the roots of the characteristics equation of the closed‐loop system is denoted the “root locus” plot.
Figure 7.13 displays the root locus plot of the roots of the characteristics equation of the closed‐loop system of the ACLD/rod.

Figure 7.13 Root locus of a rod treated with active constrained layer damping with kr = 0.01.
Note that, when the Gain = 0, the roots of the characteristics equation of the closed‐loop system of the ACLD/rod coincide with those of a rod treated with PCLD, which is shown in Figure 7.9.
The importance of the “roots locus” plot lies in its display of a map of all the roots of the closed‐loop system of the rod/ACLD for different values of the gain. Hence, by varying the gain, it is possible to place the roots of the system at desirable locations that may have favorable damping characteristics. These locations can be different from the poles of the rod/PCLD system. As a matter of fact, these locations can extend over a wider range between the poles and zeros of the rod/PCLD system. This enables placement of the roots of the rod/ACLD at locations where higher damping and stability of the closed‐loop system can be achieved. In this manner, the performance of the rod/ACLD can be significantly enhanced over that of the rod/PCLD.
For example, the observed low damping ratio of the first mode of the rod treated with PCLD ζ = 0.005 24 can be improved to 0.0841, as indicated in the close‐up view of the root locus plot shown in Figure 7.14, by selecting the gain to be 9.5E4 N m−1. Higher values of the gain can still result in better performance but increasing the gain beyond 2.85E5 N m−1 can destabilize the second mode of vibration as the roots start crossing the imaginary axis into the positive side of the s‐plane.

Figure 7.14 Close‐up view of the root locus of a rod treated with active constrained layer damping with kr = 0.01.
The resulting performance characteristics in the frequency and time domains are shown in Figure 7.15. The displayed performance of the rod/ACLD system is compared with the corresponding performance of rod/PCLD system and plain rod.

Figure 7.15 Frequency and time response of a rod treated with active constrained layer damping with Gain = 9.5E4 N m−1 and kr = 0.01.
The figure indicates that the use of the ACLD treatment has significantly improved the damping characteristics of the first mode but has not affected the second mode. This is manifested clearly, in the frequency domain, as the behavior with the ACLD coincides with that with the PCLD treatment. Also, in the time domain, the high frequency components lie on top of each other between 0 and 0.75 ms, whereas the low frequency component with the ACLD is seen to die out very fast as the damping ratio is increased dramatically with the addition of the active control.
Table 7.1 summarizes the main features of the considered basic configurations of the undamped structure, a structure treated with an unconstrained damping layer, a structure treated with a constrained damping layer, and a structure treated with ACLD.
Table 7.1 Features of damping configurations.
| Features | Plain rod | Rod with unconstrained layer damping | Rod/PCLD | Rod/ACLD |
| Poles | Imaginary | Complex with small real part | Complex with larger real part | Complex with much higher real part |
| zeros | None | Sandwiched between the poles | Sandwiched between the poles | Sandwiched between the poles |
| Damping Ratio | zero | Very Low | larger | Much higher |
| Stability | Limited stability | Always stable | Always stable | Can be unstable at high control gains |
7.3 Active Constrained Layer Damping for Beams
7.3.1 Introduction
PCLD treatments have been successfully utilized, as a simple and reliable means, for damping out the vibration of a wide variety of flexible structures (Cremer, et al., 1988). However, for effective performance over a broad range of temperatures and frequencies, the weight of PCLD treatments can pose serious limitations to their use in applications where weight is critically important.
It is therefore the purpose of this section to elaborate on the concepts presented in Section 7.2 by considering ACLD treatments (Baz, 1993, 1996; Baz and Ro 1993a,b, 1994) as a viable alternative to PCLD treatments. ACLD combines the attractive attributes of both passive and active controls to achieve optimal vibration damping. In particular, it provides an effective means for augmenting the simplicity and reliability of passive damping with the low weight and high efficiency of active controls to attain high damping characteristics over broad frequency bands. Such characteristics are particularly suitable for damping the vibration of critical systems such as rotorcraft blades where damping‐to‐weight ratio is very important.
In this chapter, the emphasis is placed on developing distributed‐parameter and finite element models to describe the behavior of structures treated with ACLD treatment. The finite element method (FEM) models, in particular, are intended to enhance the practicality of predicting the behavior of structures such as beams, plates, and shells that are subject to a wide variety of boundary conditions and are partially treated with multi‐patches of ACLD treatments. The models will also allow the prediction of the ACLD performance when specific modes are targeted with proper spatial shaping of the sensing layer.
7.3.2 Concept of Active Constrained Layer Damping
The ACLD, as shown in Figure 7.16, consists of a conventional PCLD, which is augmented with active control means to control the strain of the constrained layer, in response to the structural vibrations. The viscoelastic damping layer is sandwiched between two piezoelectric layers. The three‐layer composite ACLD when bonded to the beam acts as a “smart” constraining layer damping treatment with built‐in sensing and actuation capabilities. The effect of interaction between the sensor and the actuator on the operation of the ACLD can best be understood by considering the motion experienced by the beam during a typical vibration cycle.

Figure 7.16 Concept of active constrained layer damping treatment.
In Figure 7.16a, as the beam moves downward under the action of an external moment Me, the sensor is subjected to tensile stresses that generate a positive voltage Vs by the direct piezoelectric effect. This voltage is amplified, its polarity is reversed, and the resulting voltage Vc is fed back to activate the piezoelectric constraining layer, which shrinks by virtue of the reverse piezoelectric effect. The shrinkage results in a shear deformation angle γa, in the viscoelastic layer, which is larger than the angle γp developed by a conventional passive constraining.
Similarly, Figure 7.16b describes the operation of the ACLD during the upward motion of the beam. During this part of the vibration cycle, the top part of the beam as well as the piezoelectric sensor experiences compressive stresses and a negative voltage is generated by the sensor. Direct feedback of the sensor signal to the active constraining layer makes it extend and increase the shear deformation angle to γa compared to γp for the conventional constraining layer. The increase of the shear deformation of the viscoelastic layer, during the entire vibration cycle, is accompanied with an increase in the energy dissipated.
Furthermore, the shrinkage (or expansion) of the piezoelectric layer during the upward motion (or during the downward motion) produces a bending moment Mc on the beam, which tends to bring the beam back to its equilibrium position and counterbalance the effect of the external moment Me. Therefore, the dual effect of the enhanced energy dissipation and the additional restoring bending moment will quickly damp out the vibration of the flexible beam. This dual effect, which does not exist in conventional constrained damping layers, significantly contributes to the damping effectiveness of the smart ACLD. In this manner, the smart ACLD consists of a conventional PCLD, which is augmented with the described dual effect to actively control the strain of the constrained layer, in response to the structural vibrations. With appropriate strain control strategy, the shear deformation of the viscoelastic damping layer can be increased, the energy dissipation mechanism can be enhanced and the vibration can be damped out. One possible strategy is the direct feedback of the sensor voltage to power the active constraining layer. Another strategy will rely on feeding back both the sensor voltage and its derivative to obtain proportional and derivative control action. With such a strategy additional damping can be imparted to the vibrating beam system and the versatility of active controls can be utilized to considerably improve the damping characteristics of the ACLD.
In this manner, the ACLD provides a practical means for controlling the vibration of massive structures with currently available piezoelectric actuators without the need for excessively large actuation voltages. This is due to the fact that the ACLD properly utilizes the piezoelectric actuator to control the shear in the soft viscoelastic core, which is a task compatible with the low control authority capabilities of the currently available piezoelectric materials.
Figure 7.17 shows different configurations of ACLD treatment that differ in the arrangement of the sensors. The first configuration shown in Figure 7.17a, is the classical three‐layer ACLD treatment that includes a VEM sandwiched between a piezo‐constraining layer and a piezo‐sensor layer.

Figure 7.17 Different configurations of active constrained layer damping treatment. (a) Classical ACLD, (b) self‐sensing ACLD, and (c) ACLD with discrete sensor.
Figure 7.17b shows a two‐layer ACLD treatment with the piezo‐constraining layer acting simultaneously as an actuator and a sensor. This layer is called a “self‐sensing piezo‐layer,” which ensures collocated sensor/actuator arrangement and when controlled properly guarantees global stability as discussed in Chapter 6 (Ro and Baz 2002).
In the third configuration of Figure 7.17c, the two‐layer ACLD is provided with a discrete sensor to complete the control loop. The discrete sensor can be an accelerometer or a strain gage that is placed as close as possible to the treatment in order to approximate the case of collocated sensor/actuator arrangement.
7.3.3 Finite Element Modeling of a Beam/ACLD Assembly
A finite element model is developed in this section to describe the behavior of beams with ACLD treatments. The model extends the studies of Trompette et al. (1978), Rao (1976) used to analyze the dynamics of PCLD treatments. It accounts for the behavior of the distributed and spatially shaped piezoelectric sensor (Miller and Hubbard 1987) and the distributed piezoelectric actuator (Crawley and de Luis 1987). Appropriate control laws are considered to control the interaction between the piezo‐sensor and actuator in order to achieve enhanced vibration control characteristics.
The emphasis is placed, in this section, on the development of a model for Bernoulli–Euler beams that are treated with multi‐patches of ACLD layers in order to demonstrate the feasibility and merits of the ACLD concept. ACLD treatments with uniform and spatially shaped sensors are considered in following analyses in order to investigate the potential of targeting specific modes with the shaped sensors.
7.3.3.1 The Model
Figure 7.18 shows a schematic drawing of the ACLD treatment of a sandwiched beam divided into N finite elements. It is assumed that the shear strains, in the piezoelectric sensor/actuator layers and in the base beam, are negligible.

Figure 7.18 Schematic drawing of a deflected beam treated with ACLD treatment.
It is also assumed that the transverse displacements w of all points on any cross section of the sandwiched beam are considered to be equal. Furthermore, the piezoelectric sensor/actuator layers and the base beam are assumed to be elastic and to dissipate no energy, whereas the core is assumed to be linearly viscoelastic. In addition, the piezoelectric sensor and the base beam are considered to be perfectly bonded together such that they can be reduced to a single equivalent layer. Accordingly, the original four‐layer sandwiched beam reduces to an equivalent three‐layer beam. Hence, the modeling approach presented in Section 4.3 for beams treated with PCLD can be extended to account for the effect of the piezo‐sensing and actuation.
The piezo‐sensor can take the general, uniform, or linear shapes shown in Figures 7.19a–c, respectively.

Figure 7.19 Shaped, uniform, and linearly varying sensors.
The complete description of the beam/ACLD assembly model includes:
Potential Energy
This remains as described by Eq. (4.60) as follows:
where u1, u3, w, and w,x denote the axial displacement of the constraining layer, axial displacement of the beam, as well as the transverse and rotational deflections of beam, respectively. Also, γ defines the shear strain of the VEM given by Eq. (4.58). Note that EiAi and EiIi denote the longitudinal and flexural rigidity of the ith layer. Also, G2A2 denotes the shear rigidity of the VEM with G2 defining its shear modulus.
Kinetic Energy
This is also as given by Eq. (4.62) as follows:
with ρi denoting the density of the ith layer.
Piezo‐Control Forces and Moments
- Piezo‐Actuator. The strain εp induced in the piezoelectric actuator is given by (Crawley and de Luis 1987):
where d31 is the piezoelectric strain constant resulting from the application of the voltage Vc across the piezo‐actuator layer. In Eq. (7.23), Vc is assumed constant over the length of the beam element. The voltage Vc is generated from the proper manipulation of the piezo‐sensor voltage Vs.
- Piezo‐Sensor. The strain εs induced in the piezo‐sensor is proportional to the beam curvature (w,xx) and is given by:
where h is the distance from the beam neutral axis to the sensor surface.
The induced strain εs integrated over the entire length of the sensor due to its distributed nature, generates an output voltage Vs given by (Appendix 7.A):
where fi(x) is a spatial distribution function that defines the shaping of the sensor over the ith element. For uniform sensor fi(x) = 1 and for a linearly shaped sensor fi(x) = 1 − x/L as shown in Figure 7.19c. In Eq. (7.25), the sensor is extended between elements is and if. Also, ![]() is the electromechanical coupling factor, g31 is the piezoelectric voltage constant and C is the capacitance of the sensor, which is given by:
is the electromechanical coupling factor, g31 is the piezoelectric voltage constant and C is the capacitance of the sensor, which is given by:
where A is the sensor surface area and K3t is the dimensionless dielectric constant.
- Control Law. The manipulation of the piezo‐sensor voltage Vs to generate the actuator voltage Vc is governed by the following proportional and derivative control law:

where Kp and Kd are the proportional and derivative control gains, respectively.
- Control Forces and Moments. The vector {Fc} of the control forces and moments generated by the piezo‐constraining layer on the treated beam element can be expressed in the following matrix form:
where Fpj, Fpk, Mpj, and Mpk denote the control forces and moments generated at nodes j and k, which are given by:
For a uniform sensor
and
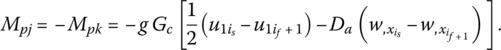
For a shaped sensor

and

where ![]() ,
,  is the distance between a neutral axis of entire sandwiched beam and piezo‐actuator, and p is the d/dt operator. Also, Gc = (KP + Kd p) denotes the controller gain.
is the distance between a neutral axis of entire sandwiched beam and piezo‐actuator, and p is the d/dt operator. Also, Gc = (KP + Kd p) denotes the controller gain.
7.3.3.2 Equations of Motion
The stiffness matrix [Ki], the mass matrix [Mi], and the control force vector {Fc} are combined to describe the dynamics of the ACLD‐treated beam element as follows:
The effect of the proportional and derivative control actions on the performance of the assembled closed‐loop system, given by Eq. (7.31), is determined by computing the eigenvalues (i.e., natural frequencies and damping ratios) of the closed‐loop system and comparing these eigenvalues with those of the open‐loop system. Note that {Δi} denotes the nodal deflection vector of the ith element that is bounded between nodes j and k. The nodal deflection vector {Δi} is given by:
Also, stiffness matrix [Ki] and the mass matrix [Mi] are extracted from the potential energy (PE) and the kinetic energy (KE) such that:
Solution
The equation of motion of the beam/ACLD system, which is divided into N finite elements, is as given in Sections 4.3 and 7.3.3 as follows:
where ![]() , {Ce}1 × 4N = [0 0 .........0 1 0]T, and {CC}1 × 4N = [0 0 .. … 0 1]T.
, {Ce}1 × 4N = [0 0 .........0 1 0]T, and {CC}1 × 4N = [0 0 .. … 0 1]T.
Also, Fe and Fc denote the external and control forces, respectively. The matrices [Mt], [Ct], and [Kt] are as described in Section 4.3.3 of Chapter 4.
The first natural frequencies of the open‐loop beam/ACLD system are listed in Table 7.4 along with comparisons with the predictions obtained by ANSYS. Close agreement is evident between the predictions of the FEM and ANSYS models.
Table 7.4 Comparison between the natural frequencies of the beam/ACLD system as predicted by FEM and ANSYS.
| Mode | 1 | 2 | 3 |
| FEM (Hz) | 48.88 | 248.4 | 668.78 |
| ANSYS (Hz) | 46.35 | 253.52 | 677.49 |
The control force Fc is generated using the following velocity feedback control law:
where Kv is the derivative control gain.
Combining Eqs. (7.34) and (7.35) yields the following state‐space representation:
State Equations:
and
Output:
where 
 , C = [01 × 4N 01 × (4N − 1)1 ], D = 0, and u = Fc.
, C = [01 × 4N 01 × (4N − 1)1 ], D = 0, and u = Fc.
The root locus of the system can be plotted using the following MATLAB command:
Figure 7.20 displays the root locus of the system. The figure indicates the locations of the first three poles of the system that also coincide with the predictions of the FEM.

Figure 7.20 Root locus plot of beam/ACLD system.
For maximum closed‐loop damping, the velocity feedback gain is selected to be 7.4 as displayed in Figure 7.20.
The frequency response of the beam/ACLD system is shown in Figure 7.21a. The corresponding control voltage is also displayed in Figure 7.21b.

Figure 7.21 Frequency response and control voltage of the beam/ACLD system.
The displayed results indicate that the amplitude of vibration at the first mode is attenuated from 3.22E‐5m for the uncontrolled case to 9.93E‐6m when the system is controlled by a 38.15 control volts.
Solution
Figure 7.23a displays the finite element mesh of the beam/ACLD assembly. Also, Figures 7.23b through 7.23d show the modes and mode shapes of the first three natural frequencies of the assembly. Table 7.7 lists a comparison between the natural frequencies of the beam/ACLD assembly as obtained by the finite element model and ANSYS predictions.
Table 7.7 Comparison between the natural frequencies of the beam/ACLD assembly as obtained by the finite element model and ANSYS predictions.
| Method | Mode 1 | Mode 2 | Mode 3 | Mode 4 |
| ANSYS | 22.85 Hz | 143.10 Hz | 400.53 Hz | 784.70 Hz |
| MATLAB | 21.80 Hz | 136.50 Hz | 383.30 Hz | 754.90 Hz |

Figure 7.23 Finite element model and mode shapes of the beam/ACLD assembly. (a) Finite Element Mesh, (b) Mode 1 – 22.85 Hz, (c) Mode 2 – 143.10 Hz, and (d) Mode 3 – 400.53 Hz.
Figure 7.24 displays the frequency response characteristics of the beam/ACLD with a uniform sensor when the proportional (P) and derivative (D) control gains Kp = 700 N m−1 and kr = 0.15 where kr = Kd/Kp. The figure displays also the response of the beam/PCLD for comparison purposes.

Figure 7.24 Frequency response of beam/ACLD system with uniform sensor.
The displayed response indicates that the use of the ACLD has resulted in reducing the maximum amplitude of vibration at the first mode from 0.0724 to 0.002 42 m and required a control voltage of 78.87 V.
In Figure 7.25, the time response characteristics of the beam/ACLD with uniform sensor are displayed for proportional‐derivative (PD) control gains Kp = 700 N m−1 and kr = 0.15 where kr = Kd/Kp. The figure displays also the response of the beam/PCLD for comparison purposes.

Figure 7.25 Time response of beam/ACLD system with uniform sensor.
The displayed response indicates that the use of the ACLD has also resulted in reducing the maximum amplitude of vibration to 0.0298 μm in about 0.1 s. Such a fast attenuation is achieved with a maximum control voltage of only 0.5 V.
Figures 7.26 and 7.27 display the frequency and time response characteristics of the beam/ACLD with a linearly shaped sensor using the same proportional (P) and derivative (D) control gains as those used with the uniform sensor. The figures also display the response of the beam/PCLD for comparison purposes.

Figure 7.26 Frequency response of beam/ACLD system with linearly shaped sensor.

Figure 7.27 Time response of beam with ACLD treatment with linearly shaped sensor.
The displayed frequency response emphasizes that the use of the ACLD has attenuated the maximum amplitude of vibration at the first mode to 0.0178 m with a control voltage of 336.3 V. Also, the displayed time response suggests that using the ACLD has reduced the maximum amplitude of vibration to 0.476 μm in about 0.1 s. Such a fast attenuation is achieved with a maximum control voltage of only 1.0 V.
Table 7.8 summarizes comparisons between the performance characteristics of the ACLD with uniform and linearly shaped sensors at the first mode of vibration. It can be seen that the use of ACLD with a shaped sensor has resulted in significant attenuation in the amplitudes of vibration and required lower voltage to achieve such attenuation as compared to the case of uniform shaped sensor.
Table 7.8 Comparison between ACLD with uniform and linearly shaped sensors.
| Sensor type | Sensor shape | Measured parameter | Frequency response | Time response | ||
| Max. amplitude (m) | Max. volt | Max. amplitude (μm) | Max. volt | |||
| Uniform |  |
w,x(L) | 0.002 42 | 78.873 | 0.0585 | 0.5 |
| Linearly Shaped |  |
w(L)/L | 0.001E‐3 | 4.76 | 0.0217 | 0.5 |
7.3.4 Distributed‐Parameter Modeling of a Beam/ACLD Assembly
7.3.4.1 Overview
This section focuses on developing a distributed‐parameter model (DPM) using Hamilton's principle to describe the dynamics of beams that are fully treated with ACLD (Baz 1997a,b). The variational formulation, being energy‐based, is much simpler to employ than the classical force equilibrium‐based shear models (Mead and Markus 1969; DiTaranto 1965). Furthermore, the variational formulation provides directly the boundary conditions associated with the ACLD treatment.
For the active control purposes, the variational model provides also direct means for devising a globally stable boundary control strategy that is compatible with the operating nature of the ACLD treatments. In this manner, the instability problems associated with the simple proportional and/or derivative controllers are completely avoided. More importantly, as the control strategy is based on a DPM, the classical spillover problems resulting from using “truncated” finite element models are eliminated. Accordingly, the devised boundary controller enables the control of all the modes of vibration of the ACLD‐treated structures.
7.3.4.2 The Energies and Work Done on the Beam/ACLD Assembly
The potential and kinetic energies as well as the external work done by the piezoelectric actuator and external loads, as described in Section 7.2.3, are recast as follows:
Potential Energy
Equation (7.21) is rewritten to include only the conservative component of the energy associated with the VEM as follows:

where ![]() denotes the shear storage modulus of the VEM. Also, K1 = E1A1, K3 = E3A3, and Dt = (E1I1 + E3I3).
denotes the shear storage modulus of the VEM. Also, K1 = E1A1, K3 = E3A3, and Dt = (E1I1 + E3I3).
Kinetic Energy
Equation (7.22) is simplified to only include the contribution of the transverse motion to the kinetic energy as the components associated with the longitudinal motions can be assumed negligible. Hence, Eq. (7.22) reduces to:

where ![]() .
.
External Work Done
The different components that account for the work done by the non‐conservative loads include:
- Work done W1 by piezoelectric control forces. This is given by

where εp denotes the piezo‐strain that is induced in the piezoelectric actuator and given by Eq. (7.23). This strain εp is assumed constant over the entire length of the constraining layer in order to maintain and emphasize the simplicity and practicality of the ACLD treatment.
- Work W2 dissipated in the viscoelastic core. This is given by
where τd is the dissipative shear stress developed by the viscoelastic core. It is given by:
where η, ω, and i denote the loss factor of the viscoelastic core, the frequency and ![]() , respectively. In Eq. (7.41), the behavior of the viscoelastic core is modeled using the common complex modulus approach, which is a frequency domain‐based method.
, respectively. In Eq. (7.41), the behavior of the viscoelastic core is modeled using the common complex modulus approach, which is a frequency domain‐based method.
7.3.4.3 The Distributed‐Parameter Model
The equations and boundary conditions governing the operation of the beam/ACLD assembly are obtained by applying Hamilton's principle (Meirovitch 2010):

where δ(.) denotes the first variation in the quantity inside the parentheses.
The resulting equations of the beam/ACLD assembly are:
and
where ![]() is the complex modulus of the VEM.
is the complex modulus of the VEM.
For a cantilevered beam, Hamilton's principle yields the following boundary conditions:
At x = L:
and
At x = L:
Equations (7.43) and (7.44) give:
and
where z = (u1 − u3) and g = G2/h2[(K1 + K3)/(K1K3)].
Combining Eqs. (7.45) and (7.49) yields:

or,
where ![]() and
and  . Note that g and Y are defined as the shear parameter and geometrical factors, respectively, as introduced by DiTaranto (1973).
. Note that g and Y are defined as the shear parameter and geometrical factors, respectively, as introduced by DiTaranto (1973).
Differentiating Eq. (7.51) partially with respect to x, substituting into Eq. (7.22), and rearranging the terms yields a sixth order partial differential equation describing the dynamics of the beam/ACLD assembly as follows:
The associated boundary conditions given by Eqs. (7.46) and (7.47) simplify to:
At x = 0:
and
At x = L:
Further simplification of the boundary conditions can be obtained by using Eq. (7.51) and its spatial derivative with respect to x to yield:
At x = 0:
and
At x = L:
It is important here to note that the sixth order partial differential equation describing the beam/ACLD system, given by Eq. (7.52) is the same as that describing a beam treated with conventional PCLD as obtained by Mead and Markus (1969). However, the boundary condition given by Eq. (7.56) is modified to account for the control action generated by the strain εp induced by the active constraining layer at the free end of the beam (i.e., at x = L). Therefore, the particular nature of operation of the beam/ACLD system implies the existence of boundary control action εp.
7.3.4.4 Globally Stable Boundary Control Strategy
The globally stable control strategy presented in this section aims at ensuring that the total energy En = PE + KE of the beam/ACLD system is maintained as a strictly non‐increasing function of time.
The total energy En is given by:
Differentiating the total energy expression given by Eq. (7.57) with respect to the time and using Eqs. (7.52) through (7.54), yielding:
Equation (7.58) indicates that the second term is strictly negative, hence a globally stable boundary controller with a continuously decreasing energy norm (i.e., ![]() ) is obtained when the control action εp takes the following form:
) is obtained when the control action εp takes the following form:
where Kg is the gain of the boundary controller. This form of a controller makes the rate of change of the total energy of the entire assembly strictly negative.
Equation (7.59) indicates that the control action is a velocity feedback of the longitudinal displacement of the piezoelectric constraining layer. It is important also here to note that when the active control action εp ceases or fails to operate for one reason or another (i.e., when εp = 0), the beam system remains globally stable as indicated by Eq. (7.58). Such inherent stability is attributed to the second term in the equation that quantifies the contribution of the Passive Constrained Layer Treatment (PCLD).
7.3.4.5 Implementation of the Globally Stable Boundary Control Strategy
The boundary control strategy can be implemented in one of the following two ways:
- in terms of the longitudinal displacement u1 of the piezo‐actuator by using Eq. (7.57) as follows:
where s is the Laplace complex number.
- in terms of the longitudinal displacement u3 of the base beam by using Eqs. (7.47) and (7.48), in order to relate u3 to u1 as follows:
Eliminating u1 between Eqs. (7.60) and (7.61) gives the control action εp in terms of u3 as follows:

7.3.4.6 Response of the Beam/ACLD Assembly
The response w of the beam/ACLD assembly can be determined by solving Eq. (7.52) using the classical separation of variables method such that:
where W(x) and T(t) denote spatial and temporal functions. Substituting Eq. (7.63) into Eq. (7.52) and setting ![]() yields the following characteristic equation:
yields the following characteristic equation:

where λ is a differential operator with respect to x. Let ±δi with i = 1,…,3 be the roots of the characteristics of the equation, then the spatial function W(x) can be written as:
where the coefficients Ci's are to be determined from the boundary conditions given by Eqs. (7.55) and (7.56).
Solution
Note that when the beam/ACLD system is excited by a transverse end load F, the boundary condition at x = L, Eq. (7.56), must be modified to:
At x = L:
Accordingly, the transverse deflection W(x) of beam can be determined using Eq. (7.65) subjected to the boundary conditions (7.55) and (7.56) after including the modifications imposed by Eq. (7.66).
Figure 7.28 displays a comparison between the frequency response characteristics of the open‐loop beam/ACLD system (i.e., KD = 0) as predicted by the FEM and DPM approaches.

Figure 7.28 Frequency response and control voltage of beam with PCLD treatment when KD = 0.
It can be seen that there is close agreement between the two approaches.
Table 7.9 lists also a comparison between the first three natural frequencies of the beam/ACLD system as computed using the FEM, ANSYS, and DPM approaches when KD = 0.
Table 7.9 Comparison between the natural frequencies of the beam/ACLD system as predicted by FEM, ANSYS, and DPM.
| Mode | 1 | 2 | 3 |
| FEM (Hz) | 48.88 | 248.4 | 668.78 |
| ANSYS (Hz) | 46.35 | 253.52 | 677.49 |
| DPM –(Hz) | 47.00 | 256.00 | 683.00 |
It is evident that the predictions of the DPM are very close to those of the ANSYS model.
Figure 7.29 displays the compliance and control voltage characteristics of the beam/ACLD system for control gain KD = 7.4 along with a comparison of the corresponding characteristics of the beam/PCLD system, that is, KD = 0.

Figure 7.29 Frequency response (a) and control voltage (b) of beam with ACLD treatment when KD = 7.5.
Note that there are discrepancies between the predictions of the DPM and the FEM of the closed‐loop response characteristics of the bean/ACLD system. These discrepancies can be attributed to the fact that in the DPM, the control action is a linear force due to the strain εp applied to the constraining layer whereas in the FEM, the control action is a moment due to the piezo‐strain applied to the entire assembly.
The energy dissipated in the beam/ACLD system is given by Eqs. (7.40) and (7.41) as:

where the shear strain γ can be determined from Eq. (7.51) as follows:

Figure 7.30 shows the corresponding energy dissipation of the beam/ACLD system in comparison with the corresponding characteristics of the beam/PCLD system, that is, KP = 0. It is evident that the energy dissipation with the ACLD becomes higher than that of the PCLD particularly at high frequencies.

Figure 7.30 Energy dissipation of beam/ACLD system when Kp = 7.4.
Table 7.10 summarizes the performance characteristics of the beam/ACLD as compared with that of the beam/PCLD system.
Table 7.10 Performance of beam/ACLD assembly at different control gains.
| Mode | Uncontrolled | KD = 7.4 | |||||
| Frequency (Hz) | Amplitude (μm) | Energy dissipated (μJ) | Frequency (Hz) | Amplitude (μm) | Energy dissipated (μJ) | Volts (V) | |
| 1 | 47 | 187.4 | 187.8 | 42 | 0.1823 | 0.124 | 64.28 |
| 2 | 256 | 5.366 | 5.231 | 262 | 1.626 | 3.729 | 32.98 |
| 3 | 683 | 1.181 | 1.121 | 702 | 0.903 | 7.030 | 47.21 |
7.4 Active Constrained Layer Damping for Plates
A finite element model is developed in Section 4.7 to describe the behavior of plates with PCLD treatments. The effect of the control forces and moments generated by the active constrained layer are presented in this section.
7.4.1 Control Forces and Moments Generated by the Active Constraining Layer
7.4.1.1 The In‐Plane Piezoelectric Forces
These in‐plane forces (Fpx, Fpy, and Fpxy) at the jth node, are given by:
with Kp and Kd denoting the proportional and derivative control gains. Also, p and Vs denote the operator d/dt and the sensor voltage. The constants d31 and d32 define the piezoelectric strain constants in the x and y directions. Also, [B1p] and [D1p] are given by (Section 4.8):
where

where Nu1 and Nv1 define the axial shape functions, respectively. Also, E1 and ν1 denoting Young's modulus and Poisson's ratio of the piezoelectric constraining layer, respectively.
7.4.1.2 The Piezoelectric Moments
These piezoelectric moments {Mpi} due to the bending of the piezoelectric constraining layer are given by:
where ![]() .
.
7.4.1.3 Piezoelectric Sensor
The voltage, Vs, developed by the piezo‐sensor is obtained from (Appendix 7.A, and Lee, 1987):
where

Also, h is the distance from the plate neutral plane to the sensor surface and b(x, y) is a distribution shape function of the sensor [b (x,y) = 1 for a uniform sensor]. The sensor is extended between elements isx and ifx in the x direction and isy and ify in the y direction. Also, ![]() is the electromechanical coupling factor, g31 is the piezoelectric voltage constant and C is the capacitance of the sensor that is given by:
is the electromechanical coupling factor, g31 is the piezoelectric voltage constant and C is the capacitance of the sensor that is given by:
where A is the sensor surface area and k3t is the dielectric constant.
Note also that ![]() ,
, ![]() , and [Nw] define the in‐plane and transverse shape functions, respectively, as defined in Section 4.8.
, and [Nw] define the in‐plane and transverse shape functions, respectively, as defined in Section 4.8.
7.4.1.4 Control Voltage to Piezoelectric Constraining Layer
The voltage VA applied to the piezoelectric constraining layer is given by:
7.4.2 Equations of Motion
The dynamics of the ACLD‐treated plate element is described by the following equation of motion:
where [Mi] and [Ki] denote the mass and stiffness matrices of the plate/ACLD element given in Appendix 7.A. The vector {Fc} is the vector of control forces and moments generated by the piezo‐constraining layers on the treated plate element. It is expressed as follows:
where
Solution
Figure 7.32 displays the modes and mode shapes of the plate/ACLD patches.

Figure 7.32 Modes and modes shapes of a cantilever plate treated with two ACLD Patches.
The frequency response of the plate tip and the corresponding control voltage are displayed in Figure 7.33 when the ACLD patches are controlled with a velocity feedback that has a gain K = 1 Ns m−1. Also displayed in the figure, for comparison purposes, is the response of the plate when K = 0 that corresponds to the open‐loop condition. In this case, it is evident that the controller effectiveness is only limited to higher order modes.

Figure 7.33 Frequency response and control voltage of the plate with ACLD patches when K = 0 (open‐loop) and 10 Ns m−1 (closed‐loop).
When the controller gain is increased to K = 1000 Ns m−1, the resulting plate response and the control voltage are shown in Figure 7.34. The effectiveness of the controller, in this case, in attenuating the vibration is clear over a wide frequency band and is extended to the low frequency modes. Note that the maximum control voltage required in this case is only 13.37 V.

Figure 7.34 Frequency response and control voltage of the plate with ACLD patches when K = 0 (open‐loop) and 1000 Ns m−1 (closed‐loop).
Table 7.11 summarizes the performance characteristics of the plate/ACLD patches, at the first mode of vibration, for different control gains.
Table 7.11 Performance of plate/ACLD patches for different control gains in the frequency domain.
| Control gain | Maximum deflection (m) | Maximum control voltage (V) |
| 0 | 0.007 47 | 0 |
| 10 | 0.003 27 | 4.047 |
| 1000 | 0.000 54 | 13.37 |
The time response of the plate tip and the corresponding control voltage are displayed in Figure 7.35 when the ACLD patches are controlled with a velocity feedback that has a gain K = 1 Ns m−1. The displayed characteristics are computed when the plate is subjected, at its mid tip point, to a transient force of 1 N for a duration of 0.01 s. The closed‐loop response is compared also with that of the open‐loop, that is, when K = 0.

Figure 7.35 Time response and control voltage of the plate with ACLD patches when K = 0 (open‐loop) and 10 Ns m−1 (closed‐loop).
The obtained comparison indicates that the damping ratio is increased from 0.00196 for the open loop to 0.00710 for the closed‐loop condition. Note that this 3.5‐times increase in the damping ratio is achieved with only 0.158 V.
When the controller gain is increased to K = 1000 Ns m−1, the resulting plate time response and the control voltage are shown in Figure 7.36. Such an increase in the control gain results in increasing the damping ratio from 0.001 96 for the open loop to 0.051 for the closed‐loop condition. Note that this 25‐times increase of the damping ratio is achieved with only 1.424 V.

Figure 7.36 Time response and control voltage of the plate with ACLD patches when K = 0 (open‐loop) and 1000 Ns m−1 (closed‐loop).
Table 7.12 summarizes the closed‐loop damping ratio and control voltage of the plate/ACLD patches, for different control gains in comparison with the corresponding characteristics of the open‐loop system.
Table 7.12 Performance of plate/ACLD patches for different control gains in the time domain.
| Control gain | Closed‐loop damping ratio (ζ) | Maximum control voltage (V) |
| 0 | 0.001 96 | 0 |
| 10 | 0.007 10 | 0.158 |
| 1000 | 0.051 00 | 1.424 |
7.5 Active Constrained Layer Damping for Shells
A finite element model is developed in Section 4.8 to describe the behavior of shells with PCLD treatments. The effect of the control forces and moments generated by the active constrained layer are presented in this section.
7.5.1 Control Forces and Moments Generated by the Active Constraining Layer
Figure 7.37 shows a schematic drawing of a quadrilateral element of a cylindrical shell treated with an ACLD treatment.
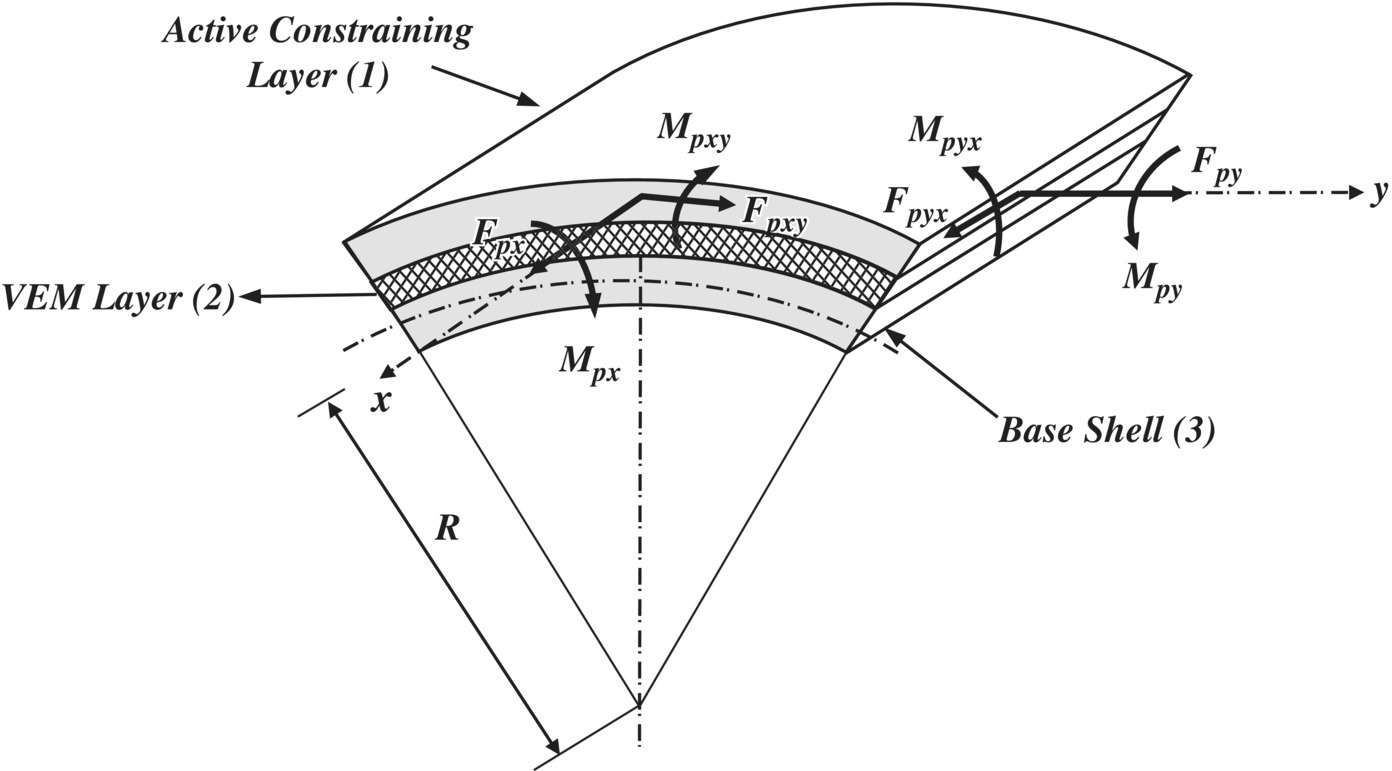
Figure 7.37 Piezoelectric forces and moments on a cylindrical shell element treated with active constrained layer damping treatment (ACLD).
The in‐plane piezoelectric forces (Fpx, Fpy, and Fpxy) and the associated control moments ({Mpx}, {Mpy}, and {Mpxy}) due to the bending of the piezoelectric constraining layer are given by Eqs. (7.69) and (7.71), respectively, as in the case of the quadrilateral plate element described in Section 7.4.
Similarly, the voltage generated by the piezoelectric sensor and the voltage applied to the piezoelectric constraining layer are given by Eqs. (7.72) and (7.75), respectively.
7.5.2 Equations of Motion
The dynamics of the ACLD‐treated plate element is described by the following equation of motion:
where [Mi] and [Ki] denote the mass and stiffness matrices of the plate/ACLD element given in Appendix 7.A. The vector {Fc} is the vector of control forces and moments generated by the piezo‐constraining layers on the treated shell element are as given by Eqs. (7.77) and (7.78).
Solution
Figure 7.39a displays the frequency response of the shell/ACLD assembly, as predicted by the FEM approach from Sections 4.7 and 7.5, when using a proportional control gain KP = 1.5E6 Nm m−1. The corresponding control voltage is shown in Figure 7.39b. The effectiveness of the controller is very limited at the first and second modes (60 and 62 Hz). These modes and corresponding mode shapes are displayed in Table 4.12.

Figure 7.39 Frequency response (a) and control voltage (b) of the shell/ACLD assembly when KP = 1.5E6 Nm m−1.
The effectiveness of the controller becomes more apparent at the 125 Hz mode and higher.
The associated control voltage reaches 11 V at the first mode (60 Hz) and attains a maximum value of 24 V at the 119 Hz mode.
Increasing the control gain KP to 3E6 Nm m−1 considerably improves the performance of the controller as can be seen in the frequency response displayed in Figure 7.40a. The effectiveness of the controller becomes evident at the 62 Hz mode as well at the higher order modes.

Figure 7.40 Frequency response (a) and control voltage (b) of the shell/ACLD assembly when KP = 3E6 Nm m−1.
In this case, the control voltage increases by 30 V at the first mode (60 Hz) and attains a maximum value of 120 V at the 119 Hz mode.
Figure 7.41 displays the ANSYS finite element model of the shell/ACLD assembly. The ANSYS model is used to predict the time response characteristics of the assembly at different control gains.

Figure 7.41 ANSYS finite element model of the shell/ACLD assembly.
Figure 7.42a shows the time response of the shell/ACLD assembly when using a proportional control gain KP = 1.5E6 Nm m−1. The corresponding control voltage is shown in Figure 7.42b. The effectiveness of the controller is limited as it has only attenuated the first and second modes (60 and 62 Hz) but the 119 and 120 Hz modes are still dominating the response.

Figure 7.42 Time response and control voltage of the shell/ACLD assembly when KP = 1.5E6 Nm m−1.
A peak control voltage of 18 V is observed with this control gain.
Figure 7.43a shows the time response of the shell/ACLD assembly when the proportional control gain KP is increased to 3E6 Nm m−1. The corresponding control voltage is shown in Figure 7.43b. The effectiveness of the controller has improved considerably as demonstrated by the significant attenuation of the 119 and 120 Hz modes of vibrations. In this case, the peak control voltage required reaches 40 V.

Figure 7.43 Time response (a) and control voltage (b) of the shell/ACLD assembly when KP = 3E6 Nm m−1.
Table 7.14 summarizes the performance of the shell/ACLD assembly for different control gains as compared with that of the shell/PCLD assembly. The performance is quantified by the maximum deflection and control voltage at the different modes of vibration.
Table 7.14 Performance of shell/ACLD patches for different control gains in the frequency domain.
| Mode (Hz) | Maximum deflection (μm) | Maximum control voltage (V) | ||||||
| 60 | 62 | 120 | 125 | 60 | 62 | 120 | 125 | |
| Gain = 0 | 2.51 | 4.66 | 5.86 | 2.44 | 0 | 0 | 0 | 0 |
| Gain = 1.5E6 | 2.11 | 3.29 | 1.51 | 0.12 | 3.16 | 4.95 | 2.27 | 0.18 |
| Gain = 3.0E6 | 1.85 | 2.45 | 2.00 | 0.11 | 5.55 | 7.34 | 6.01 | 0.32 |
7.6 Summary
This chapter has presented the utilization of active control as an effective means for enhancing the damping characteristics of conventional PCLD treatments. The resulting ACLD treatment is applied to attenuate the vibration of various structural members including: rods, beams, plates, and shells. The performance characteristics of the ACLD are predicted using the finite element models developed in Chapters 4 and 6 after integrating these with the appropriate equations for piezoelectric sensors and control actuators. The obtained predictions are validated also against the predictions of the commercial finite element package ANSYS.
References
- Baz A., “Active constrained laer damping”, Proceedings of DAMPING '93 Conference, San Francisco, CA, Wright Laboratory Document no. WL‐TR‐93‐3105, pp. IBB 1–23, 1993.
- Baz A., Active Constrained Layer Damping, US Patent 5,485,053, filed October 15 1993 and issued January 16 1996.
- Baz, A. (1997a). Dynamic boundary control of beams using active constrained layer damping. Mechanical Systems and Signal Processing 88 (6): 811–825.
- Baz, A. (1997b). Boundary control of beams using active constrained layer damping. ASME Journal of Vibration and Acoustics 119 (2): 166–172.
- Baz A. and Ro J., “Partial treatment of flexible beams with active constrained layer damping”, Proceedings of the American Society of Mechanical Engineers, No. AMD‐ Vol. 167, pp. 61–80, 1993a.
- Baz A. and Ro J., “Finite element modeling and performance of active constrained layer damping” (ed. L. Meirovitch), Proceedings of the Ninth VPI & SU Conference on Dynamics & Control of Large Structures, Blacksburg, VA, pp. 345–358, 1993b.
- Baz, A. and Ro, J. (1994). Actively‐controlled constrained layer damping. Sound & Vibration Magazine 26 (3): 18–21.
- Crawley, E. and De Luis, J. (1987). Use of piezoelectric actuators as elements in intelligent structures. Journal of AIAA 25: 1373–1385.
- Cremer, L., Heckel, M., and Ungar, E. (1988). Structure‐Borne Sound: Structural Vibrations and Sound Radiation at Audio Frequencies, 2e. Berlin: Springer‐Verlag.
- DiTaranto, R.A. (1965). Theory of vibratory bending for elastic and viscoelastic layered finite length beams. ASME Journal of Applied Mechanics 87: 881–886.
- DiTaranto, R.A. (1973). Static analysis of a laminated beam. Journal of Engineering For Industry, Transactions on ASME, Series B 95 (3): 755–761.
- Lee C. K., “Piezoelectric laminates for torsional and bending modal control: theory and experiment,” Ph.D. dissertation, Cornell University, Ithaca, NY, 1987.
- Mead, D. and Markus, S. (1969). The forced vibration of a three layer damped sandwich beam with arbitrary boundary conditions. Journal of Sound and Vibration 10: 163–175.
- Meirovitch, L. (2010). Fundamentals of Vibrations, 1e. Long Grove, IL: Waveland Press Inc.
- Miller S. and Hubbard J. Jr., “Observability of a Bernoulli–Euler Beam using PVF2 as a distributed sensor” (ed. L. Meirovitch), Proceedings of the Seventh Conference on Dynamics & Control of Large Structures, VPI & SU, Blacksburg, VA, pp. 375–390, 1987.
- Rao, D.K. (1976). Static response of stiff‐cored Unsymmetric sandwich beams. ASME Journal of Engineering for Industry 98: 391–396.
- Ro, J. and Baz, A. (2002). Vibration control of plates using self‐sensing active constrained layer damping networks. Journal of Vibration and Control 8 (8): 833–845.
- Trompette, P., Boillot, D., and Ravanel, M.A. (1978). The effect of boundary conditions on the vibration of a Viscoelastically damped cantilever beam. Journal of Sound and Vibration 60 (3): 345–350.
7.A Piezoelectric Sensor Basic Equations
7.A.1 Basic Equations
Piezoelectric films bonded to vibrating structures are used to monitor its vibration. Figure 7.A.1 shows a typical arrangement of the sensor when bonded to a beam.

Figure 7.A.1 Piezoelectric sensor.
The constitutive equations of the piezo‐sensor are:
and
where S1, T1, E3, and D3 are the mechanical strain, mechanical stress, electrical field, and electric displacement, respectively. Also, ![]() , and
, and ![]() denote the compliance, piezo‐strain constant, and permittivity.
denote the compliance, piezo‐strain constant, and permittivity.
Eliminating the stress T1 from Eqs. (7.A.1) and (7.A.2) yields:

where ![]() is the electromechanical coupling factor
is the electromechanical coupling factor  .
.
For short‐circuit conditions (E3 = 0), then:
where e31 is the piezo‐stress constant and S1 is given by:
From Eqs. (7.A.4) and (7.A.5), the electric displacement D3 at the sensor/beam interface (z = h) is given by:
and the associated charge Q is:
7.A.2 Basic Sensor Configurations
Two configurations are considered here. These include the uniform and linearly shaped configurations shown in Figure 7.A.2.

Figure 7.A.2 Uniform and linearly shaped sensors. (a) Uniform and (b) linearly shaped.
For the uniform sensor, the width b(x) is constant = b and the developed charge Q is:
For the linearly shaped sensor, the width b(x) = b(1 − x/L) and the corresponding charge Q is:
For a cantilevered beam, w(0) = 0 and w,x(0) = 0, then:
Hence, the uniform sensor will monitor the angular deflection of the free end of the beam while the shaped sensor will generate a charge proportional to the transverse deflection of the free end.
7.A.3 Output Voltage of Sensor
The output voltage V of the sensor can be computed as follows:
where C denotes the capacitance of the sensor given by:
where ε33, As, and hs denote the permittivity, sensor surface area, and sensor thickness, respectively.
Combining Eqs. (7.A.7), (7.A.11), and (7.A.12) gives:

where g31 = d31/ε33= piezoelectric voltage constant. Also, b(x) is a spatial distribution function that defines the width shaping of the sensor over the beam. For uniform sensor b(x) = 1 and for a linearly shaped sensor b (x) = (1 − x/L).
Problems
- 7.1 Consider a mass = 100 kg supported on a VEM that is modeled on the following GHM model with one mini‐oscillator such that its stiffness is given by:

that is, Ko = 100, α1 = 7, ζ1 = 1, and ω1 = 1000 (see Problem 4.1). Determine the state‐space representation of the system. Plot the root locus of the system when the control law relies on:
- a position sensor with Fc = − kgy, where y = [1 0 0 0]{Δ}.
- a velocity sensor with Fc = − kgy, where y = [0 0 1 0]{Δ}.
with kg = control gain and
 where x and z are the DOF of the mass and the internal DOF of the VEM. Note that Fc is the control force as shown in Figure P7.1.
where x and z are the DOF of the mass and the internal DOF of the VEM. Note that Fc is the control force as shown in Figure P7.1.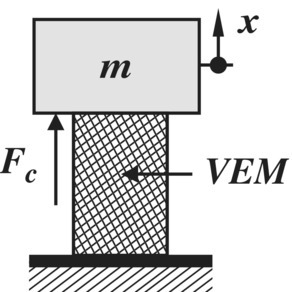
Figure P7.1 Mass supported on a VEM.
Identify the poles and zeros of the structure and of the VEM. Also determine the maximum possible damping ratio of the closed‐loop system when the controller is provided with position or velocity sensor.
- 7.2 Consider the three‐layer composite rod that is mounted in a cantilevered configuration as shown in Figure P7.2. The rod consists of a base structure treated with a VEM layer that is constrained by an active piezoelectric constraining layer. The assembly experiences longitudinal vibration along the x direction.

Figure P7.2 Cantilever rod treated with ACLD.
Derive expression for a globally stable boundary controller that ensures that the piezoelectric strain εp is generated to keep the rate of the total energy of the assembly
 strictly negative where En is given by:
strictly negative where En is given by:
where T and U denote the kinetic and PE of the assembly such that:

and

where hi, Ei, mi, and ui denote the thickness, Young's modulus, mass per unit length, and deflection of the ith layer (i = 1,…,3, such that 1 = piezo‐layer, 2 = VEM layer, and 3 = base structure). Also, b and L denote the width and length of the rod, respectively. The shear storage modulus and shear strain of the VEM are G′ and γ, respectively, with γ = (u1 − u3)/h2.
Using Hamilton's principle show first that the equations of motion and the boundary conditions of the assembly are given by:

and

subject to the boundary conditions:
- at x = 0: u1, x = εP and u3, x = 0
- at x = L: u1 = 0 and u3 = 0.
where G* = G′(1 + ηi) with η denoting the loss factor of the VEM.
Using the equations of motion and the boundary conditions show that:

Hence, for
 , show that the globally stable boundary control law is given by:
, show that the globally stable boundary control law is given by:εP = − KG u1,t with KG = control gain > 0
- 7.3 Derive the finite element model for a single element of the cantilevered three‐layer composite rod of Figure P7.2 such that:

Assuming that the VEM is described by a single GHM mini‐oscillator using the modeling approach given by Eq. (7.5) such that:
where

 ,
,  , and
, and  .
.with [M0] and
 are given by:
are given by:
and

where
 nodal deflection vector. The spatial distribution of u1(x) and u3(x) are assumed to be given by the following shape functions:
nodal deflection vector. The spatial distribution of u1(x) and u3(x) are assumed to be given by the following shape functions:
where
 = wave number of piezo‐layer and
= wave number of piezo‐layer and
where
 = wave number of base structure with ω and ρi denote the excitation frequency and density of the ith layer.
= wave number of base structure with ω and ρi denote the excitation frequency and density of the ith layer.Assume that the rod is made of aluminum with width of 0.025 m, thickness of 0.025 m, and length of 1 m. The rod is treated with a constrained damping treatment that has a width of 0.025 m, thickness = 0.025 m, and density of 1100 kg m−3. The storage modulus and loss factor of the VEM are predicted by the GHM model with one mini‐oscillator with E0 = 15.3MPa, α1 = 39, ζ1 = 1, ω1 = 19, 058rad/s. The physical and geometrical properties of the piezoelectric constraining layer are listed in Table 7.15 Physical and geometrical properties of the piezoelectric constraining layer.
Determine the frequency response of the treated rod when subjected to a longitudinal force F = 10 N at its free end. Compare the results with the response of the rod assembly when its finite element is extracted using classical linear shape functions.
Table 7.15 Physical and geometrical properties of the piezoelectric constraining layer.
Length (m) Thickness (m) Width (m) Density (kg m−3) Young's modulus (GPa) d31 (m V−1) k31 g31 (mV N−1) k3t 1.0 0.0025 0.025 7600 63 186E‐12 0.34 116E‐2 1950 - 7.4 Consider a beam mounted in a fixed‐free configuration as shown in Figure P7.3. The beam is made of aluminum with width of 0.025 m, thickness of 0.025 m, and length of 1 m. The beam is treated with an unconstrained damping treatment that has a width of 0.025 m, thickness = 0.025 m, and density of 1100 kg m−3. The storage modulus and loss factor of the VEM are predicted by GHM model with one mini‐oscillator with E0 = 15.3MPa, α1 = 39, ζ1 = 1, ω1 = 19, 058rad/s. For simplicity purposes, the structural system is modeled by one finite element model.

Figure P7.3 Cantilever beam treated with unconstrained VEM treatment.
Plot the pole‐zero map for the treated beam identifying the structural modes and VEM modes. Compare the results with the pole‐zero map of the untreated beam.
Also determine the frequency response of the treated beam when subjected to a transverse force F = 10 N at its free end for a duration of 0.01 s. Compare the results with the response of the untreated beam.
- 7.5 For the beam considered in Problem 7.3, the VEM is constrained by an aluminum constraining layer that is 0.025 m wide and 0.0025 m thick as shown in Figure P7.4.
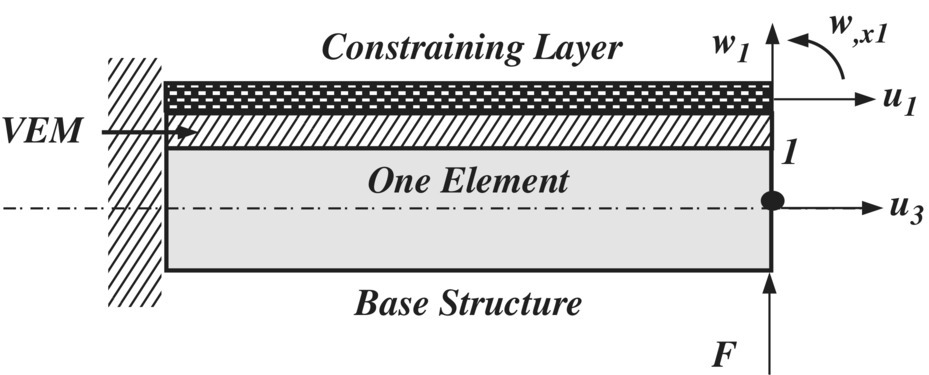
Figure P7.4 Cantilever beam treated with constrained VEM treatment.
Plot the pole‐zero map for the treated beam identifying the structural modes and VEM modes. Compare the results with the pole‐zero map of the untreated beam.
Also determine the time response of the treated beam when subjected to a transverse force F = 10 N at its free end for a duration of 0.01 s. Compare the results with the response of the untreated beam.
- 7.6 Consider the beam system of Example 7.1 that has the physical and geometrical properties listed in Tables 7.2 and 7.3. The beam system is modeled by a single finite element as shown in Figure P7.5. The beam is controlled using a proportional‐derivative (PD) controller such that KG(1 + 0.01s) where KG is the control gain and s is the Laplace complex number. The input to the controller is the transverse deflection of the free end of the beam w1.
Plot the root locus map for the actively treated beam identifying the structural modes and VEM modes for different control gains KG. Select the control gain that ensures the maximum closed‐loop damping ratio.
Also determine the time response of the controlled beam when subjected to a transverse force F = 10 N at its free end for a duration of 0.01 s. Compare the results with the response of the uncontrolled beam. Also plot the associated time history of the control effort.

Figure P7.5 Cantilever beam treated with ACLD treatment with a controller.
- 7.7 For the distributed‐parameter modeling of the beam/ACLD assembly described in Section 7.3.4, develop a globally stable boundary control law if the beam is mounted in a simply‐supported configuration at both of its ends.
Assume the physical and geometrical parameters of the beam/ACLD system with the VEM are the same as those described in Example 7.1.
Determine the compliance and control voltage characteristics of the beam/ACLD system using a velocity feedback controller with a control gain KD = 7.4. Compare these characteristics with those of the beam/PCLD system using the DPM approach outlined in Section 7.3.4. Also, compare the predictions of the DPM against the predictions of the finite element model when the beam is excited by a unit sinusoidal load at its free end.
Also determine the energy dissipation characteristics of the beam/ACLD system as compared with that of the beam/PCLD system.
- 7.8 Consider the aluminum cantilever plate that is fully treated with an ACLD patch placed as shown in Figure P7.6. The dimensions of the plate and the PCLD patches are shown in the figure with h1 = h2 = h3 = 0.005m.
The VEM is modeled using a GHM model with three mini‐oscillators such that:

The parameters αi, ζi, and ωi are listed in Table 4.7. Assume that the constraining layer is made of piezoelectric material (PZT‐4) with d31 = d32 = −123 × 10−12 m V−1 and
 . Determine the frequency response of the plate, at different control gains, when it is excited by a unit force acting at the middle of the free end. Assume a proportional controller that feeds the transverse deflection of the free end back to control the piezoelectric constraining layer.
. Determine the frequency response of the plate, at different control gains, when it is excited by a unit force acting at the middle of the free end. Assume a proportional controller that feeds the transverse deflection of the free end back to control the piezoelectric constraining layer.Also determine the corresponding control effort.

Figure P7.6 Cantilever plate treated with full constrained VEM treatment.
- 7.9 Consider the aluminum cantilever plate that is partially treated with an ACLD patch placed as shown in Figure P7.7. The dimensions of the plate and the PCLD patches are shown in the figure with h1 = h2 = h3 = 0.005m. The physical properties of the VEM and the piezoelectric constraining layers are the same as listed in Problem 7.6.
Determine the frequency response of the plate, at different control gains, when it is excited by a unit force acting at the middle of the free end. Assume a proportional controller that feeds the transverse deflection of the free end back to control the piezoelectric constraining layer.
Also determine the corresponding control effort. Compare the results with the corresponding results obtained when the plate is fully treated with the ACLD treatment as in Problem 7.8.

Figure P7.7 Cantilever plate treated with full constrained VEM treatment.
- 7.10 Consider the clamped‐free shell/ACLD assembly shown in Figure P7.8a. The main physical and geometrical parameters of the shell and PCLD are listed in Table 7.13. The shell has an internal radius R is 0.1016 m. The ACLD treatment consists of two patches as displayed in Figure P7.8b. The patches are bonded 180° apart on the outer surface of the cylinder with each of which subtending an angle of 90° angle at the center of the shell.
Determine the frequency response of the system when excited at the free end by a unit force. Also determine the time response of system when a unit pulse force of duration 0.10 ms is applied at the free end. Compare the response when the response is predicted using ANSYS and the finite element approach outlined in Sections 4.7 and 7.5.
Compare the results with those displayed in Example 7.5 for the partially treated shell/ACLD system.

Figure P7.8 Cantilever shell treated with partial constrained VEM treatment.














