3.3 Number of Newly Acquired Customers and Initial Order Quantity
Companies will always want to acquire as many customers as possible and acquire those customers who will bring large orders for profit maximization. Companies usually perform certain marketing activities to encourage newly acquire customers to buy more the first time and in subsequent purchases. The operation of shipping fees, such as free shipping for large orders or normal shipping fees charged for small orders, is one common way to influence the purchase behavior of potential customers. Lewis [2] examined the data from an online retailing company which experimented with multiple shipping fee schedules for 502 days, including large order size incentives and penalties. The author wanted to examine the effects shipping fees on order incidence, order size, shipping revenues, and customer acquisition simultaneously. Thus, Lewis developed a system of linear regressions to account for the possible correlation among the dependent variables. Among these regressions equations, the author modeled the number of newly acquired customers and the average order size for new customers in the following two equations:
(3.19) ![]()
where ![]() denotes the number of newly acquired customers,
denotes the number of newly acquired customers, ![]() denote the explanatory variables, including shipping, pricing, and customer base terms, and
denote the explanatory variables, including shipping, pricing, and customer base terms, and
(3.20) ![]()
where ![]() denotes the average order size for new customers, and
denotes the average order size for new customers, and ![]() denote the shipping variables and pricing variable. And, to account for the possible correlation between the equations and the possible endogeneity of explanatory variables, the author used three-stage least squares in the estimation and used the lagged values of each quantity as instruments.
denote the shipping variables and pricing variable. And, to account for the possible correlation between the equations and the possible endogeneity of explanatory variables, the author used three-stage least squares in the estimation and used the lagged values of each quantity as instruments.
Besides shipping fees, Villanueva et al. [3] argued that marketing channels influence the customer acquisition process and the value that newly acquired customers will bring to the company. These authors developed two functions to measure how much new customers acquired through different acquisition channels, including WOM and marketing activities, contribute to firm performance. One function is called ‘the value-generating function,’ which links newly acquired customers' contributions to the firm's equity growth, and the other function is called ‘the acquisition response function,’ which expresses the interactions between marketing spending and the number of acquisitions. The authors argued that it was important to incorporate all the indirect effects of each acquisition on customer equity, not just each customer's direct financial contribution to the company. As the estimated variables are treated as potentially endogenous, the authors used a three-variable vector autoregression (VAR) modeling technique:
(3.21) 
where ![]() denotes the number of customers acquired through the firm's marketing actions,
denotes the number of customers acquired through the firm's marketing actions, ![]() denotes the number of customers acquired through WOM, and
denotes the number of customers acquired through WOM, and ![]() denotes the firm's performance. The subscript
denotes the firm's performance. The subscript ![]() denotes time,
denotes time, ![]() denotes the lag order of the model, and
denotes the lag order of the model, and ![]() are white-noise disturbances distributed as N(0, Σ). The direct effects are captured by
are white-noise disturbances distributed as N(0, Σ). The direct effects are captured by ![]() ,
, ![]() ; the feedback effects are captured by
; the feedback effects are captured by ![]() ,
, ![]() ; the cross-effects are captured by
; the cross-effects are captured by ![]() ,
, ![]() ; and the reinforcement effects are captured by
; and the reinforcement effects are captured by ![]() ,
, ![]() ,
, ![]() . The authors used impulse response functions (IRFs) to estimate the long-term effect of an unexpected shock in one variable on the other variables in the system. Dekimpe and Hanssens (2004) give a review of VAR models under the persistence modeling framework and we provide the related introduction in Appendix C.
. The authors used impulse response functions (IRFs) to estimate the long-term effect of an unexpected shock in one variable on the other variables in the system. Dekimpe and Hanssens (2004) give a review of VAR models under the persistence modeling framework and we provide the related introduction in Appendix C.
Both of the previous examples we have discussed deal with cross-sectional time series data, or snapshots of cross-sections of customers that are repeatedly observed over time. There is a great benefit to having cross-sectional time series data – mainly because the effects that are uncovered by the modeling frameworks are persistent over time across customers. However, it might be the case that one of two limitations are present that do not enable you to use cross-sectional time series data. First, it is possible that the data you have is not repeatedly measured over time, that is, it is just cross-sectional. In this case you cannot use a time series modeling framework such as a VAR model. Second, it may be the case that there is no variation over time in any of your key drivers. For instance, if you always charge the same shipping costs over time, repeatedly measuring shipping costs in multiple time periods makes no sense. Thus, we also need to have a method available for instances when we only have cross-sectional data.
When only cross-sectional data are available it is rather straightforward to predict the number of newly acquired customers and the expected initial order quantity. For the number of newly acquired customers, all that we need to do is to determine the expected response probability of each prospect, as outlined in the previous subsection, and aggregate the prediction across all prospects. We can then compare the actual number of acquired customers to the predicted number of acquired customers.
For the initial order quantity we can run a two-stage regression, similar to the two-stage least squares regression as outlined in Reinartz et al. [7] where the acquisition probability is modeled using a probit model and the initial order quantity is modeled as a least squares regression that is conditional on the prospect being acquired. The result of this two-stage model is a prediction of expected initial order quantity conditional on acquisition probability that can be applied to any future prospect.
Thus, regardless of whether the data you have are cross-sectional or cross- sectional time series, this section describes various models that can be used for both number of newly acquired customers and initial order quantity.
3.3.1 Empirical Example: Number of Newly Acquired Customers
Besides being able to predict whether or not we are likely to acquire a prospect as we did in the previous example, we are also interested in determining how well our response probability model does in helping us accurately predict the total number of customers we are likely to acquire and specifically which prospects we are most likely to acquire. Thus, at the end of this example we should be able to do the following:
The information we need for this prediction includes the following list of variables:
| Dependent variable | |
| Acquisition | 1 if the prospect was acquired, 0 otherwise |
| Independent variables | |
| Acq_Expense | Dollars spent on marketing efforts to try and acquire that prospect |
| Acq_Expense_SQ | Square of dollars spent on marketing efforts to try and acquire that prospect |
| Industry | 1 if the prospect is in the B2B industry, 0 otherwise |
| Revenue | Annual sales revenue of the prospect's firm (in millions of dollars) |
| Employees | Number of employees in the prospect's firm |
In this case we only have cross-sectional data, that is, data from a single snapshot in time. Thus, we need to use the estimates we obtained from the response probability model in the first example to help us determine the predicted probability that each prospect will adopt. To do this we use the parameter estimates from the response probability model and values for the x variables to predict whether a customer is likely to be acquired. For a logistic regression we must apply the proper probability function as noted earlier in the chapter (see Equation 3.5)):
![]()
For example, for Customer 9, when we input the statistically significant variables into the Xβ computation we get P[Customer = 9](Acquisition = 1|Xβ) = 0.06 or 6%. Once we do this for each of the customers we can then decide which prospect we believe we are likely to acquire given our acquisition spending and on each prospect's characteristics.
Next, we need to create a cutoff value to determine at which point we are going to divide the prospects into the two groups – predicted to acquire and predicted not to acquire. There is no rule that explicitly tells us what that cutoff number should be. Often by default we select 0.5 since it is equidistant from 0 and 1. However, it is also reasonable to check multiple cutoff values and choose the one that provides the best predictive accuracy for the dataset. By using 0.5 as the cutoff for our example, any prospect whose predicted probability of acquisition is greater than or equal to 0.5 is classified as predicted to acquire, and the rest are predicted as not to acquire. To determine the predictive accuracy we compare the predicted to the actual acquisition values in a 2 × 2 table. For our sample of 500 we get Table 3.3.
Table 3.3 Predicted versus actual acquisition.

As we can see from the table, our in-sample model accurately predicts 90.6% of the prospects who chose not to adopt (183/202) and 91.6% of the prospects who chose to adopt (273/298). This is a significant increase in the predictive capability of a random guess model1 which would be only 58.4% accurate for this dataset. Since our model is significantly better than the best alternative, in this case a random guess model, we determine that the predictive accuracy of the model is good. If there are other benchmark models available for comparison, the ‘best’ model would be the one which provides the highest accuracy of both the prediction to acquire and not to acquire, or in other words the prediction would provide the highest sum of the diagonal. In this case the sum of the diagonal is 456 and it is accurate 91.2% of the time (456/500).
3.3.2 How Do You Implement it?
The implementation of this example was carried out using a SAS Data step and the Freq procedure. First we computed the predicted response probabilities for each prospect using the coefficients from the response probability example and scored the prospects as predicted to acquire (1) if the value was higher than the cutoff (0.5), and predicted not to acquire (0) if the value was lower than the cutoff. Next we ran PROC Freq and created a 2 × 2 table which compared the actual and predicted acquisition values to determine how well our model predicted the number of newly acquired customers.
3.3.3 Empirical Example: Initial order quantity
Many firms have realized that it is not sufficient to merely focus on just trying to acquire as many customers as possible without any concern for the value that the customer is likely to provide. Research in marketing has shown that the initial order value can be a valuable predictor in a customer's future value to the firm – or at the least justify the amount of money that is spent on customer acquisition. Thus, it can be useful to understand the drivers of initial order value and in turn be able to predict each prospect's expected initial order value. At the end of this example we should be able to do the following:
The information we need for this model includes the following list of variables:
| Dependent variables | |
| Acquisition | 1 if the prospect was acquired, 0 otherwise |
| First_Purchase | Dollar value of the first purchase (0 if the customer was not acquired) |
| Independent variables | |
| Lambda(λ) | The computed inverse Mills ratio from the acquisition model |
| Acq_Expense | Dollars spent on marketing efforts to try and acquire that prospect |
| Acq_Expense_SQ | Square of dollars spent on marketing efforts to try and acquire that prospect |
| Industry | 1 if the prospect is in the B2B industry, 0 otherwise |
| Revenue | Annual sales revenue of the prospect's firm (in millions of dollars) |
| Employees | Number of employees in the prospect's firm |
Again, we need to note that we are dealing with cross-sectional data. We see from the data requirement that in order to determine the drivers of initial order quantity we need to have two dependent variables: First_Purchase and Acquisition. This is due to the fact that expected initial order quantity is derived from the following equation:
![]()
This equation shows us that the expected initial order quantity is a function of the probability that the prospect will be acquired multiplied by the expected value of a purchase given that the prospect was acquired. If we were to merely run a regression with First_Purchase as the dependent variable and ignore the probability that the prospect will be acquired, we would get biased estimates due to a potential sample selection bias.
Sample selection bias is a problem that is common in many marketing problems and has to be statistically accounted for in many modeling frameworks. In this case the prospect has a choice of whether or not to be acquired before making a purchase. If we were to ignore this choice we would bias the estimates from the model and we would have fewer precise predictions for the value of First_Purchase. To account for this issue we need to be able to predict the value for both the probability of Acquisition (similar to what we have done for the first empirical example) and the expected value of First_Purchase given that the prospect is expected to be acquired. One important consideration to note is that we cannot just run two models independently since there is likely to be a correlation between the error terms of the two models. Thus, we need to use a modeling framework that can simultaneously estimate the coefficients of the two models, or at least account for the correlation between First_Purchase and Acquisition. To do this we use a two-stage modeling framework similar to that described earlier in this chapter and found in Reinartz et al. [7].
The first model for Acquisition will be set up using the same equation as for the response probability example (see Equation 3.1). The only difference here is that instead of using a logistic regression we will be using a probit model to estimate the coefficients. The main reason for this lies in the error term of the probit model which is distributed normal with a mean of 0 and a standard deviation of 1. The fact that the probit model and the OLS regression model (which we will be using for First_Purchase) are both normally distributed allows us to more easily estimate them in a two-stage framework.
Once we estimate the probit model we need to create a new variable, λ, which will represent the correlation in the error structure across the two equations. This variable, also known as the sample selection correction variable, will then be used as an independent variable in the First_Purchase model to remove the sample selection bias in the estimates. To compute λ we use the following equation, also known as the inverse Mills ratio:
![]()
In this equation ϕ represents the normal probability density function, Φ represents the normal cumulative density function, X represents the value of the variables in the Acquisition model, and β represents the coefficients derived from the estimation of the Acquisition model.
Finally, we want to estimate a regression model for First_Purchase and include the variable ρ as an additional independent variable. This is done in a straightforward manner with the following equation:
![]()
In this case First_Purchase is the value of the initial order quantity, γ is the matrix of variables used to help explain the value of First_Purchase, α are the coefficients for the independent variables, μ is the coefficient of the inverse Mills ratio, λ is the inverse Mills ratio, and ε is the error term.
When we estimate the two-stage model, we get the following parameter estimates for each of the two equations:

We gain the following insights from the results. We see that λ is positive and significant. We can interpret this to mean that there is a potential selection bias problem since the error term of our selection equation is correlated positively with the error term of our regression equation. We also see that all other variables of the First_Purchase model are significant with the exception of Industry, meaning that we have uncovered many of the drivers of initial order quantity. We find that Acq_Expense is positive with a diminishing return, as noted by the positive coefficient on Acq_Expense and the negative coefficient on Acq_Expense_SQ. We also find that two of the firm characteristic variables are positive (Revenue and Employees) showing that firms with higher annual revenue and firms with more employees tend to have larger initial order quantities.
Our next step is to predict the value of First_Purchase to see how well our model compares to the actual values. We do this by starting with the equation for expected initial order quantity at the beginning of this example:
![]()
In this case Φ is the normal cumulative distribution function (CDF), X is the matrix of independent variable values from the Acquisition equation, β is the vector of parameter estimates from the Acquisition equation, γ is the matrix of independent variables from the First_Purchase equation, α is the vector of parameter estimates from the First_Purchase equation, μ is the parameter estimate for the inverse Mills ratio, and λ is the inverse Mills ratio. Once we have predicted the First_Purchase value for each of the prospects, we want to compare this to the actual value from the database. We do this by computing the mean absolute deviation (MAD) and mean absolute percent error (MAPE). The equations are as follows:
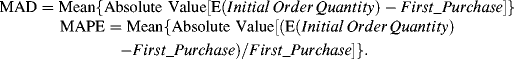
We find for the acquired customers that MAD = 51.96 and MAPE = 18.69%. This means that on average each of our predictions of First_Purchase deviates from the actual value by $51.96 or 18.69% (based on a Mean(First_Purchase) = $372.47). If we were instead to use the mean value of First_Purchase ($372.47) as our prediction for all prospects (this would be the benchmark model case), we would find that MAD = 127.17 and MAPE = 135.48%. Thus, our model does a significantly better job of predicting the value of initial order quantity than the benchmark case.
3.3.4 How Do You Implement it?
In this example we used a two-stage least squares approach with a probit model for acquisition and a least squares regression for the initial order quantity. We used multiple procedures in SAS to implement this model. First we used PROC logistic with a probit link function to estimate the model of customer acquisition. Next we used a SAS Data step to compute the inverse Mills Ratio using the output of the probit model. Finally we ran an OLS regression using PROC Reg and added the inverse Mills ratio as an additional variable. While we did use SAS to implement this modeling framework, programs such as SPSS can be used as well.
