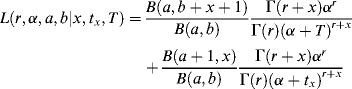4.3 Lifetime Duration
The biggest concern in customer duration modeling is to predict whether customers will repurchase or not in a non-contractual setting, such as in the retailing industry, and whether customers will renew a contract or not in a contractual setting, such as in the telecommunications industry. The estimation of duration is also essential for the calculation of CLV, which is an important metric for customer selection and optimal marketing resource allocation. Logit and probit models are still the most popular and simple modeling methods ever used. The multinomial logit model is another similar method when researchers are to model customers' repurchase choice among several alternatives, such as different stores. To model the timing and occurrence of leaving, survival analysis which models the hazard of lapsing is by nature a suitable modeling method. Survival analysis gives the instantaneous probability of customers lapsing at time t, which is also called the hazard rate, conditional on non-lapsing having occurred. In some cases, researchers consider that a customer's shopping trips occur at discrete-time points, such as days or weeks, and the discrete-time hazard model will be used to model the probability that the purchase event will occur at discrete time t. The proportional hazards model, which does not specify any functional form for the baseline hazard, is another widely used technique in duration data modeling. This model is chosen because of its attractive features, such as the relative risk-type measure of association, no parametric assumptions, and the use of the partial likelihood function. In some circumstances, researchers consider that estimating customers' or firms' choices of contract renewal without accounting for the intrafirm association and potential heterogeneity will provide biased estimates. Random effect models, such as a random intercept model which allows intercepts not to be constant but to follow a distribution, are used in such situations. Besides these traditional statistical methods, methods from machine learning fields, such as NNs or Bayesian network classifiers, have been used to solve the binary classification problem, repurchase or not.
How long customers will stay with the company, or the duration of customers' lifetime, is another important question in customer retention modeling. In non-contractual settings, companies do not directly observe when customers defect and hence cannot decide which customers are more likely to be active or inactive. The negative binomial distribution (NBD)/Pareto model gives the probability that a customer with a particular observed transaction history is still alive at time T since trial. Hazard models, such as proportional hazards models, can also estimate the duration of customers' lifetimes. A newly proposed model, the shifted-beta geometric (sBG) distribution which can fit some flexible function of time to the observed data, is able to project the survivor function beyond the observed time horizon.
In a non-contractual setting, in the catalog retailing industry, Reinartz and Kumar [8] analyzed the profitability of long-life customers (long relationship duration) versus short-life customers (short relationship duration). Since customers in the study were not bound by any contract, these authors did not actually observe when a customer defection occurred and thus did not observe each customer's lifetime duration. As a result, the authors adopted a methodology which predicts the probability that the customer is still actively engaged in the relationship with the firm. In this case they used a NBD/Pareto model. This model was proposed by Schmittlein, Morrison, and Colombo (1987) and further developed by Schmittlein and Peterson (1994). The key result of the NBD/Pareto model is an answer to the question: which individual customers are more likely to represent active or inactive customers? The outcome of the NBD/Pareto model is the probability that a customer with a particular observed transaction history is still alive at time T since the first purchase occurred. Schmittlein and Peterson give the desired probability for ![]() as
as
where
![]()
![]() is the Gauss hypergeometric function;
is the Gauss hypergeometric function; ![]() and
and ![]() are model parameters;
are model parameters; ![]() is the number of purchases since the first purchase;
is the number of purchases since the first purchase; ![]() is the time since the most recent transaction occurred; and
is the time since the most recent transaction occurred; and ![]() is the time since the first purchase occurred. The corresponding probabilities for
is the time since the first purchase occurred. The corresponding probabilities for ![]() and
and ![]() are then derived by Schmittlein and Peterson (1994, p. 65). Given that the outcome of the NBD/Pareto model is a continuous probability estimate, Schmittlein and Peterson's (1994) model is extended by transforming the continuous P(Alive) estimate into a dichotomous alive/dead measure. Knowing a person's ‘time of birth’ and given a specified probability level, the authors can approximate when a customer is deemed to have left the relationship. They can then estimate the lifetime duration from birth
are then derived by Schmittlein and Peterson (1994, p. 65). Given that the outcome of the NBD/Pareto model is a continuous probability estimate, Schmittlein and Peterson's (1994) model is extended by transforming the continuous P(Alive) estimate into a dichotomous alive/dead measure. Knowing a person's ‘time of birth’ and given a specified probability level, the authors can approximate when a customer is deemed to have left the relationship. They can then estimate the lifetime duration from birth ![]() , until the data associated with the cutoff threshold,
, until the data associated with the cutoff threshold, ![]() . A key assumption of this model is that the time when the customer made the purchase is known. The dataset that Reinartz and Kumar [8] used fulfilled this requirement and the observations were not left-censored.
. A key assumption of this model is that the time when the customer made the purchase is known. The dataset that Reinartz and Kumar [8] used fulfilled this requirement and the observations were not left-censored.
Similarly in a paper by Fader, Hardie, and Lee (2005), the authors proposed an alternative to the NBD/Pareto model which requires the same input values (x, t, and T) and generally the same outcome, but is much less computationally burdensome to implement. The model proposed is the beta geometric negative binomial distribution or BG/NBD model. The key benefit of this approach is that it can be implemented using Microsoft Excel.
In a study of retailing stores by Meyer-Waarden [9], one of the basic variables used was customer defection (coded as a binary variable (0/1)). In this case the situation was non-contractual, but the author created a heuristic to use in order to determine which customers should be considered no longer active. A customer was considered no longer a customer when the time between the last purchase in a given store and the end of the observation period was greater than four times the average interpurchase time for that same point of sale. The author included two variables in a proportional hazards model: a positive random variable ![]() that denoted the lifetime and a binary variable for whether the defection event occurs. Thus in the proportional hazards model, the survival function
that denoted the lifetime and a binary variable for whether the defection event occurs. Thus in the proportional hazards model, the survival function ![]() , which denotes the likelihood that the customer will not to have left a given store by time
, which denotes the likelihood that the customer will not to have left a given store by time ![]() , is as follows:
, is as follows:
where ![]() , the probability density function, denotes the likelihood that a customer will defect at moment
, the probability density function, denotes the likelihood that a customer will defect at moment ![]() . It is calculated as the product of the survival function
. It is calculated as the product of the survival function ![]() and the hazard function
and the hazard function ![]() :
:
where ![]() is the hazard function and denotes the likelihood that defection occurs at duration time
is the hazard function and denotes the likelihood that defection occurs at duration time ![]() , given that it has not occurred in the duration time
, given that it has not occurred in the duration time ![]() . It also represents the ratio between
. It also represents the ratio between ![]() and
and![]() :
:
In Bolton [10], ![]() is considered as the conditional likelihood that service termination occurs at duration time
is considered as the conditional likelihood that service termination occurs at duration time ![]() , given that it has not occurred in the duration time
, given that it has not occurred in the duration time ![]() . Bolton [10] denoted
. Bolton [10] denoted ![]() as the hazard rate for a customer
as the hazard rate for a customer ![]() with specific characteristics captured by the vector
with specific characteristics captured by the vector ![]() (such as different levels of overall satisfaction). The hazard rate was assumed to take the form
(such as different levels of overall satisfaction). The hazard rate was assumed to take the form
where ![]() is the baseline hazard function that estimates longitudinal effects and the effects of independent variables on hazard rate. The parameter estimates of the proportional hazards model are obtained by maximizing the partial likelihood which is given by
is the baseline hazard function that estimates longitudinal effects and the effects of independent variables on hazard rate. The parameter estimates of the proportional hazards model are obtained by maximizing the partial likelihood which is given by
The hazard ratios and confidence intervals can be estimated by the maximum likelihood method. The author modeled the lifetime duration for one of the existing stores as
Meyer-Waarden [9] included as explanatory variables dummy variables for loyalty cards, the distance of the household from the stores, and the SOW for each store as the focal store.
While survival analysis is widely used in estimating customers' lifetime duration in contractual settings, Fader and Hardie [11] suggested using a methodology that is able to project the survivor function beyond the observed time horizon. These authors proposed an approach, the sBG distribution, which can fit some flexible function of time to the observed data. Following Fader and Hardie [11], the proposed model is based on two assumptions. First, it assumes that an individual remains a customer of the firm with constant retention probability ![]() . This also means that the duration,
. This also means that the duration, ![]() is characterized by the (shifted) geometric distribution with probability mass function and survivor function
is characterized by the (shifted) geometric distribution with probability mass function and survivor function
Second, heterogeneity in ![]() follows a beta distribution with probability density function (PDF)
follows a beta distribution with probability density function (PDF)
![]()
where ![]() is the beta function. The beta distribution is a flexible distribution that is bounded between zero and one characterizing heterogeneity in the churn probabilities. Based on the value of parameters
is the beta function. The beta distribution is a flexible distribution that is bounded between zero and one characterizing heterogeneity in the churn probabilities. Based on the value of parameters ![]() and
and ![]() , the churn probabilities could be ‘U-shaped,’ homogeneous, ‘J-shaped,’ or ‘reverse-J-shaped.’ To compute the probability that a customer fails to renew his/her contract at the end of period
, the churn probabilities could be ‘U-shaped,’ homogeneous, ‘J-shaped,’ or ‘reverse-J-shaped.’ To compute the probability that a customer fails to renew his/her contract at the end of period ![]() or survives beyond period
or survives beyond period ![]() ,
, ![]() and
and ![]() , the authors took the expectation over the beta distribution that characterizes the cross-sectional heterogeneity in
, the authors took the expectation over the beta distribution that characterizes the cross-sectional heterogeneity in ![]() to arrive at the expressions for a randomly chosen individual:
to arrive at the expressions for a randomly chosen individual:
The sBG probabilities are then calculated by using the following forward recursion formula from ![]()
The authors proposed the sBG distribution as the model for the duration of customer relationships in a discrete-time contractual setting, where transactions can occur only at fixed points in time. This model can be implemented in a simple Excel spreadsheet.
Since the data that researchers have usually have right-censored observations, the Tobit model is a commonly used method in lifetime duration estimation. After correcting the selection bias problem using Heckman's (1979) two-step procedure, Reinartz, Thomas, and Kumar (2005) forecasted the expected relationship duration for each customer with a standard right-censored Tobit model. Thomas [12] also adopted a standard right-censored Tobit model to capture the length of time a customer spends with a firm.
4.3.1 Empirical Example: Lifetime duration
One of the key questions we want to answer with regard to lifetime duration is whether we can determine which customers have the highest likelihood of being active in the future. In a non-contractual setting this means estimating the probability that the customer is currently active given his/her past purchase history. In the case of a contractual setting this means estimating the expected lifetime of the customers who have yet to defect given the historical information about all customers in the past (including those who have already defected). This is often done using an accelerated failure time or proportional hazards model. Since the data provided for this chapter represent a non-contractual setting (i.e., we do not observe customer defection), our goal is to determine the probability that a customer is active given that customer's past purchase history. To do this we need to have information on the transaction behavior of each customer including the timing of the first purchase, the timing of the most recent purchase, and the number of transaction which have occurred during the observation window. In the dataset provided for this chapter we have a detailed description of the transaction history for each customer. We just need to compute the values for each of the three required variables. At the end of this example you should be able to identify the following:
A B2C firm wants to improve its ability to identify customers who are likely to still be actively engaged in a relationship with the firm. A random sample of 500 customers from a single cohort was taken from the customer database. The information we need for our model includes the following list of variables:
| Variables | |
| x | The number of transactions by a given customer over all time periods. Here we assume that it is the sum of the variable Purchase where customers at most made 1 purchase per quarter |
| tx | This is the time of the last transaction, that is, the last quarter where Purchase = 1 |
| T | The total time between the first purchase and the end of the observation window, that is, 12 quarters for all customers |
In this case we do not have a dependent variable since we do not actually observe customer defection. Instead, we use attributes of the customer transaction information to form probabilities of a customer being active. In this case we require the number of transactions a customer has had over the observation window (x). To simplify this case we assume that customers only purchase at most once from any quarter. Thus, when Purchase = 1, we observe one transaction. Second, we require the last time when a customer had a transaction with the firm (tx). In this case it is the last quarter where Purchase = 1. Finally, we require the time when the customer has been a customer. Since this is a cohort of customers who all made their first purchases in quarter 1, they all receive a value of 12 for T.
Once we have created our data table, we use the BG/NBD framework as described by Fader, Hardie, and Lee (2005) to estimate the parameters r, α, a, and b using the following likelihood function:
where B(·) is the beta distribution function, Γ(·) is the gamma distribution function, a and b are the parameters of the beta distribution function, r and α are the parameters of the gamma distribution function, and x, tx, and T are the data from the firm. We estimate the model using Solver in Excel to obtain the parameter estimates for a, b, α, and r. We get the following result:
| Parameter | Estimate |
| R | 126.537 |
| α | 159.864 |
| a | 0.512 |
| b | 3.329 |
| Log-likelihood | −4676.1 |
Once we obtain the parameter estimates from the model we then need to estimate the probability that each customer in the database is still active at the end of the 12th quarter, or P(Alive). To do this we need to construct the equation for P(Alive). Given that we used the BG/NBD framework, it follows that
Using this equation we are able to solve for the probability that each customer is active. We summarize the results in the following table:
| P(Alive) | |
| Minimum | 0.2% |
| Average | 50.1% |
| Maximum | 96.8% |
The results of this table show that the average customer in the database has a 50.1% chance of being active given the purchase histories of all the customers. Given the low minimum (0.2%) and the relatively high maximum (96.8%), the results also show that there is quite a bit of variation in the probability that a customer is active, meaning that it is highly likely that different customers will respond quite differently to retention efforts from the firm given their likelihood of still being actively engaged in a relationship with the firm.
As a result we now know the probability that each customer is active at the end of the 12th quarter. This information can provide significant insights to managers who are charged with determining the optimal amount of resources to spend on retention efforts in the future by only targeting those customers who are likely to still be engaged in a relationship with the firm.
4.3.2 How Do You Implement it?
To implement this example we used the Solver function in Excel. While we did use Excel to estimate the model, many other statistical packages are capable of estimating this model including (but not limited to) MATLAB, GAUSS, and R.