Wheeled Mobile Robotics

Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

Example 3.17

Compute the optimal velocity profile that will result in the shortest traveling time for a given path $x_{p} (u) = cos (u)$ $x_{p} (u) = cos (u)$ , $y_{p} (u) = sin (2 u)$ $y_{p} (u) = sin (2 u)$ where u ∈ [0, 2π] and considering maximal tangential accelerations a_MAXt = 2 m/s² and radial acceleration a_MAXr = 4 m/s².

Compute the schedule u(t) and velocity profiles v(u), v(t).

Solution

To compute the optimal schedule u(t) the algorithm presented in this chapter needs to be implemented. First the TPs need to be computed with the initial conditions given in relations (3.119), (3.123); then the solutions for each TP are simulated using Eq. (3.122). Finally, the time derivative of the schedule is minimized according to Eq. (3.125).

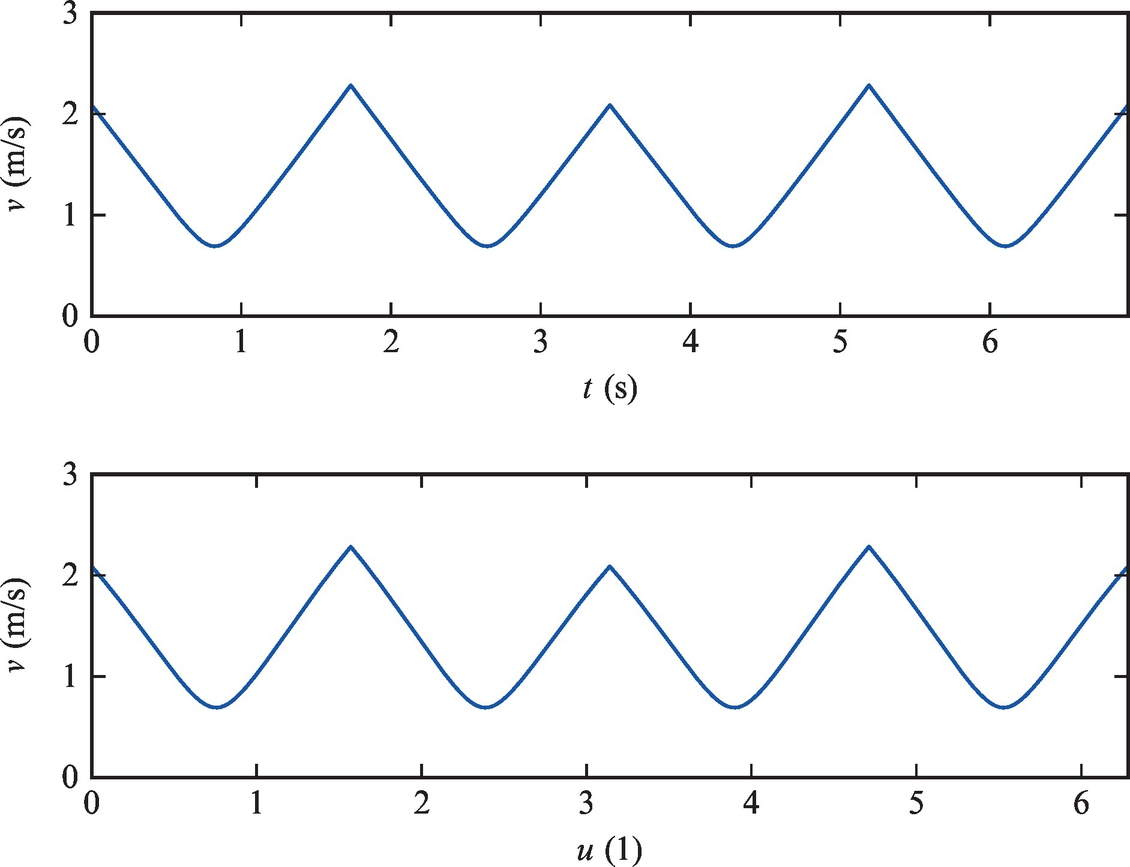
A possible implementation of the solution is given in Listing 3.16 (neglect code clocks that could be evaluated if the variable velCnstr would be set to true). Optimum schedule determination of Example 3.17 is given in Figs. 3.39–3.41. In Fig. 3.39 it can be seen that solution for each TP is integrated up to the point where the acceleration constraints are violated, which is marked with a thin line. The final solution is marked with a thick line.

f03-39-9780128042045 — Fig. 3.39 Optimum schedule determination finding the minimum profile $\dot{u}$ $\dot{u}$ of all the turn points.

f03-40-9780128042045 — Fig. 3.40 Optimum schedule u(t), which is the nonlinear function, although for this case it looks close to linear.

f03-41-9780128042045 — Fig. 3.41 Optimum velocity v(u) and v(t).

Listing 3.16

1 % Define trajectory with function handles

2 x = @(u) cos(u) ; y = @(u) sin(2*u) ; % Path

3 dx = @(u) − sin ( u ) ; dy = @(u) 2*cos(2*u) ; % First derivative

4 ddx = @(u) − cos ( u ) ; ddy = @(u) −4* sin (2* u ) ; % Second derivative

5 v = @(u) sqrt(dx(u) .ˆ2 + dy(u) .ˆ2) ; % Tangential velocity

6 w = @(u) (dx(u) .* ddy(u)− dy ( u ) .* ddx ( u ) ) . / ( dx(u) .ˆ2+dy(u) .ˆ2) ; % Angular vel.

7 kappa = @(u) w(u) ./ v(u) ; % Curvature

9 u = 0:0.001:2*pi; % Time

10 arMax = 4; atMax = 2; % Acceleration constraints

11 vSP = 0 . 2 ; vEP = 0 . 1 ; % Initial and f i n a l velocity requirements

12 uSP = u(1) ; uEP = u(end) ; % Start point and end point

13 uTP = [ ] ; % Turn points

14 for i = 2:length(u)−1 % Determine turn points

15 if a l l (abs(kappa(u( i ) ) ) > abs(kappa(u ( [ i −1, i +1]) ) ) )

16 uTP = [ uTP , u ( i ) ] ;

17 end

18 end

19 up0 = sqrt(arMax ./abs(v(uTP) .*w(uTP) ) ) ; % Derivative in turn points

21 velCnstr = false ; % Enable velocity contraints (disabled)

22 if velCnstr

23 vMax = 1.5* inf ; % Velocity constraints

24 for i = 1:length(uTP) % Make uTP in accordance with velocity constraint

25 vvu = v(uTP( i ) ) ; vvt = vvu*up0( i ) ;

26 if abs( vvt ) > vMax, up0( i ) = abs(vMax/vvu) ; end

27 end

28 % Add requirements for Initial and f i n a l velocity

29 uTP = [uSP, uTP, uEP ] ; up0 = [ vSP/v(uSP) , up0 , vEP/v(uEP) ] ;

30 end

32 Ts = 0.001; % Simulation sampling time

33 N = length(uTP) ; ts = c e l l (1 ,N) ; us = c e l l (1 ,N) ; ups = c e l l (1 ,N) ;

34 for i = 1:N % Loop through a l l turn points

35 uB = uTP( i ) ; upB = up0( i ) ; tB = 0;

36 uF = uTP( i ) ; upF = up0( i ) ; tF = 0;

37 uBs =[]; upBs = [ ] ; tBs = [ ] ; uFs = [ ] ; upFs =[]; tFs = [ ] ; % Storage

38 goB = true ; goF = true ;

40 while goB || goF

41 % Integrate back from the turn point

42 if uB > uSP && goB

43 dxT = dx(uB) ; dyT = dy(uB) ;

44 ddxT = ddx(uB) ; ddyT = ddy(uB) ;

45 vT = v(uB)*upB; wT = w(uB)*upB; kappaT = kappa(uB) ;

46 arT = vT* wT; atT = atMax*sqrt(1 − ( arT / arMax ) ˆ2) ;

48 if velCnstr && abs(vT) > vMax

49 upB = vMax/v(uB) ; upp = 0;

50 else i f abs(arT)− arMax > 0.001

51 arT = arMax ; atT = 0; upp = 0; goB = false ;

52 else

53 atT = − r e a l ( atT ) ;

54 upp = real(− atMax * sqrt(1/(dxTˆ2 + dyTˆ2) − . . .

55 (dxTˆ2 + dyTˆ2)*kappaTˆ2*upBˆ4/arMaxˆ2) − . . .

56 (dxT*ddxT + dyT*ddyT) /(dxTˆ2 + dyTˆ2) * upBˆ2) ;

57 end

59 uBs = [ uBs ; uB ] ; upBs = [ upBs ; upB ] ; tBs = [ tBs ; tB ] ; % Store

60 tB = tB + Ts ;

61 uB = uB − upB * Ts ; % Euler integration

62 upB = upB − upp * Ts ; % Euler integration

63 else

64 goB = false ;

65 end

67 % Integrate forward from the turn point

68 if uF < uEP && goF

69 (dxT = dx(uF) ; dyT = dy(uF) ;

70 (ddxT = ddx(uF) ; ddyT = ddy(uF) ;

71 vT = v(uF)*upF ; wT = w(uF)*upF ; kappaT = kappa(uF) ;

72 arT = vT* wT; atT = atMax*sqrt(1 − ( arT / arMax ) ˆ2) ;

74 if velCnstr && abs(vT) > vMax

75 upF = vMax/v(uF) ; upp = 0;

76 else i f abs(arT)− arMax > 0.001

77 arT = arMax ; atT = 0; upp = 0; goF = false ;

78 else

79 atT = real(atT) ;

80 upp = real(+atMax*sqrt(1/(dxTˆ2 + dyTˆ2) − . . .

81 (dxTˆ2 + dyTˆ2)*kappaTˆ2*upFˆ4/arMaxˆ2) − . . .

82 (dxT*ddxT + dyT*ddyT) /(dxTˆ2 + dyTˆ2) * upFˆ2) ;

83 end

85 uFs = [ uFs ; uF ] ; upFs = [ upFs ; upF ] ; tFs = [ tFs ; tF ] ; % Store

86 tF = tF + Ts ;

87 uF = uF + upF*Ts ; % Euler integration

88 upF = upF + upp*Ts ; % Euler integration

89 else

90 goF = false ;

91 end

92 end

94 ts { i } = [ tBs ; tB +tFs (2:end) ] ;

95 us{ i } = [flipud(uBs) ; uFs (2:end) ] ;

96 ups{ i } = [flipud(upBs) ; upFs (2:end) ] ;

97 end

99 % Find minimum of a l l p r o f i l e s ups (schedule derivative)

100 usOrig = us ;

101 for i = 1:N−1

102 d = ups { i +1} − interp1 ( us{ i } , ups{ i } , us{ i +1}) ;

103 j = find(d (1:end−1) .* d ( 2 : end ) <0, 1) ; % Where ups{i} i s approx. ups{i+1}

104 % Find more exact u where p r o f i l e s ups{i} and ups{i+1} are equal

105 uj = us{ i +1}( j ) + ( us{ i +1}( j +1) − us { i +1}( j ) ) /( d ( j +1) − d ( j ) ) *(0− d ( j ) ) ;

106 rob = interp1( us{ i } , ups{ i } , uj ) ;

107

108 keep = us{ i } < uj ;

109 us{ i } = [ us{ i }( keep ) ; uj ] ; ups{ i } = [ ups{ i }( keep ) ; rob ] ;

110 keep = us{ i +1} > uj ;

111 us{ i +1} = [ uj ; us{ i +1}(keep ) ] ; ups{ i +1} = [ rob ; ups{ i +1}(keep ) ] ;

112 end

113

114 % Construct f i n a l solution p r o f i l e

115 tt = interp1( usOrig {1} , ts {1} , us {1}) ; uu = us {1}; uup = ups {1};

116 for i = 2:N

117 t i = interp1( usOrig{ i } , ts { i } , us{ i }) ;

118 tt = [ tt ; t i + tt (end) − t i (1) ] ;

119 uu = [ uu ; us{ i } + uu(end) − us { i }(1) ] ;

120 uup = [ uup ; ups{ i } ] ;

121 end

122 vv = v(uu) .* uup ;

Example 3.18

Extend Example 3.17 to also include requirements for initial and final velocity, v_SP = 0.2 and v_EP = 0.1 m/s, respectively. Additionally consider that maximum velocity is limited to v_MAX = 1.5 m/s.

Compute the schedule u(t) and velocity profiles v(u), v(t).

Solution

Code from Example 3.17 can be modified to include additional requirements. Requirements for initial and terminal velocities are handled similarly as other TPs. Simply, SP and EP are treated as new TPs whose initial conditions are u_SP = 0, u_EP = 2π, ${\dot{u}}_{SP} = \frac{v_{SP}}{v_{p} (u_{SP)}}$ ${\dot{u}}_{SP} = \frac{v_{SP}}{v_{p} (u_{SP)}}$ , and ${\dot{u}}_{EP} = \frac{v_{EP}}{v_{p} (u_{EP})}$ ${\dot{u}}_{EP} = \frac{v_{EP}}{v_{p} (u_{EP})}$ .

The velocity constraints are taken into account if the variable velCnstr in Listing 3.16 is set to true. Optimum schedule determination of Example 3.18 is shown in Figs. 3.42–3.44.

f03-42-9780128042045 — Fig. 3.42 Optimum schedule determination finding the minimum profile $\dot{u}$ $\dot{u}$ of all the turn points.

f03-43-9780128042045 — Fig. 3.43 Optimum schedule u(t), which is a nonlinear function, although for this case it looks close to linear.

f03-44-9780128042045 — Fig. 3.44 Optimum velocity v(u) and v(t).

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for Wheeled Mobile Robotics

Create new playlist

Sign In

Sign Up

Table of Contents for
Wheeled Mobile Robotics