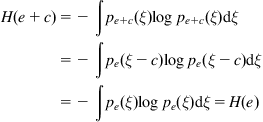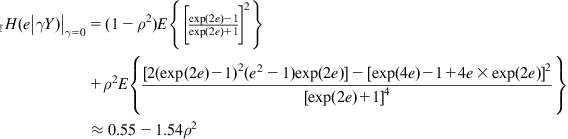Information Theoretic Parameter Estimation
Information theory is closely associated with the estimation theory. For example, the maximum entropy (MaxEnt) principle has been widely used to deal with estimation problems given incomplete knowledge or data. Another example is the Fisher information, which is a central concept in statistical estimation theory. Its inverse yields a fundamental lower bound on the variance of any unbiased estimator, i.e., the well-known Cramer–Rao lower bound (CRLB). An interesting link between information theory and estimation theory was also shown for the Gaussian channel, which relates the derivative of the mutual information with the minimum mean square error (MMSE) [81].
3.1 Traditional Methods for Parameter Estimation
Estimation theory is a branch of statistics and signal processing that deals with estimating the unknown values of parameters based on measured (observed) empirical data. Many estimation methods can be found in the literature. In general, the statistical estimation can be divided into two main categories: point estimation and interval estimation. The point estimation involves the use of empirical data to calculate a single value of an unknown parameter, while the interval estimation is the use of empirical data to calculate an interval of possible values of an unknown parameter. In this book, we only discuss the point estimation. The most common approaches to point estimation include the maximum likelihood (ML), method of moments (MM), MMSE (also known as Bayes least squared error), maximum a posteriori (MAP), and so on. These estimation methods also fall into two categories, namely, classical estimation (ML, MM, etc.) and Bayes estimation (MMSE, MAP, etc.).
3.1.1 Classical Estimation
The general description of the classical estimation is as follows: let the distribution function of population 
be 
, where 
is an unknown (but deterministic) parameter that needs to be estimated. Suppose 
are samples (usually independent and identically distributed, i.i.d.) coming from 
(
are corresponding sample values). Then the goal of estimation is to construct an appropriate statistics 
that serves as an approximation of unknown parameter 
. The statistics 
is called an estimator of 
, and its sample value 
is called the estimated value of 
. Both the samples 
and the parameter 
can be vectors.
The ML estimation and the MM are two prevalent types of classical estimation.
3.1.1.1 ML Estimation
The ML method, proposed by the famous statistician R.A. Fisher, leads to many well-known estimation methods in statistics. The basic idea of ML method is quite simple: the event with greatest probability is most likely to occur. Thus, one should choose the parameter that maximizes the probability of the observed sample data. Assume that 
is a continuous random variable with probability density function (PDF) 
, 
, where 
is an unknown parameter, 
is the set of all possible parameters. The ML estimate of parameter 
is expressed as
(3.1)
where 
is the joint PDF of samples 
. By considering the sample values 
to be fixed “parameters,” this joint PDF is a function of the parameter 
, called the likelihood function, denoted by 
. If samples 
are i.i.d., we have 
. Then the ML estimate of 
becomes
(3.2)
In practice, it is often more convenient to work with the logarithm of the likelihood function (called the log-likelihood function). In this case, we have
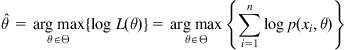(3.3)
An ML estimate is the same regardless of whether we maximize the likelihood or log-likelihood function, since log is a monotone transformation.
In most cases, the ML estimate can be solved by setting the derivative of the log-likelihood function to zero:
(3.4)
For many models, however, there is no closed form solution of ML estimate, and it has to be found numerically using optimization methods.
If the likelihood function involves latent variables in addition to unknown parameter 
and known data observations 
, one can use the expectation–maximization (EM) algorithm to find the ML solution [164,165] (see Appendix E). Typically, the latent variables are included in a likelihood function because either there are missing values among the data or the model can be formulated more simply by assuming the existence of additional unobserved data points.
ML estimators possess a number of attractive properties especially when sample size tends to infinity. In general, they have the following properties:
• Consistency: As the sample size increases, the estimator converges in probability to the true value being estimated.
• Asymptotic normality: As the sample size increases, the distribution of the estimator tends to the Gaussian distribution.
• Efficiency: The estimator achieves the CRLB when the sample size tends to infinity.
3.1.1.2 Method of Moments
The MM uses the sample algebraic moments to approximate the population algebraic moments, and then solves the parameters. Consider a continuous random variable 
, with PDF 
, where 
are 
unknown parameters. By the law of large numbers, the 
-order sample moment 
of 
will converge in probability to the 
-order population moment 
, which is a function of 
, i.e.,
(3.5)
The sample moment 
is a good approximation of the population moment 
, thus one can achieve an estimator of parameters 
(
) by solving the following equations:
(3.6)
The solution of (3.6) is the MM estimator, denoted by 
, 
.
3.1.2 Bayes Estimation
The basic viewpoint of Bayes statistics is that in any statistic reasoning problem, a prior distribution must be prescribed as a basic factor in the reasoning process, besides the availability of empirical data. Unlike classical estimation, the Bayes estimation regards the unknown parameter as a random variable (or random vector) with some prior distribution. In many situations, this prior distribution does not need to be precise, which can be even improper (e.g., uniform distribution on the whole space). Since the unknown parameter is a random variable, in the following we use 
to denote the parameter to be estimated, and 
to denote the observation data 
.
Assume that both the parameter 
and observation 
are continuous random variables with joint PDF
(3.7)
where 
is the marginal PDF of 
(the prior PDF) and 
is the conditional PDF of 
given 
(also known as the likelihood function if considering 
as the function’s variable). By using the Bayes formula, one can obtain the posterior PDF of 
given 
:
(3.8)
Let 
be an estimator of 
(based on the observation 
), and let 
be a loss function that measures the difference between random variables 
and 
. The Bayes risk of 
is defined as the expected loss (the expectation is taken over the joint distribution of 
and 
):
(3.9)
where 
denotes the posterior expected loss (posterior Bayes risk). An estimator is said to be a Bayes estimator if it minimizes the Bayes risk among all estimators. Thus, the Bayes estimator can be obtained by solving the following optimization problem:
(3.10)
where 
denotes all Borel measurable functions 
. Obviously, the Bayes estimator also minimizes the posterior Bayes risk for each 
.
The loss function in Bayes risk is usually a function of the estimation error 
. The common loss functions used for Bayes estimation include:
;
;3. 0–1 loss function: 
, where 
denotes the delta function.1
The squared error loss corresponds to the MSE criterion, which is perhaps the most prevalent risk function in use due to its simplicity and efficiency. With the above loss functions, the Bayes estimates of the unknown parameter are, respectively, the mean, median, and mode2 of the posterior PDF 
, i.e.,
(3.11)
The estimators (a) and (c) in (3.11) are known as the MMSE and MAP estimators. A simple proof of the MMSE estimator is given in Appendix F. It should be noted that if the posterior PDF is symmetric and unimodal (SUM, such as Gaussian distribution), the three Bayes estimators are identical.
The MAP estimate is a mode of the posterior distribution. It is a limit of Bayes estimation under 0–1 loss function. When the prior distribution is uniform (i.e., a constant function), the MAP estimation coincides with the ML estimation. Actually, in this case we have
(3.12)
where (a) comes from the fact that 
is a constant.
Besides the previous common risks, other Bayes risks can be conceived. Important examples include the mean 
-power error [30], Huber’s M-estimation cost [33], and the risk-sensitive cost [38], etc. It has been shown in [24] that if the posterior PDF is symmetric, the posterior mean is an optimal estimate for a large family of Bayes risks, where the loss function is even and convex.
In general, a Bayes estimator is a nonlinear function of the observation. However, if 
and 
are jointly Gaussian, then the MMSE estimator is linear. Suppose 
, 
, with jointly Gaussian PDF
(3.13)
where 
is the covariance matrix:
(3.14)
Then the posterior PDF 
is also Gaussian and has mean (the MMSE estimate)
(3.15)
which is, obviously, a linear function of 
.
There are close relationships between estimation theory and information theory. The concepts and principles in information theory can throw new light on estimation problems and suggest new methods for parameter estimation. In the sequel, we will discuss information theoretic approaches to parameter estimation.
3.2 Information Theoretic Approaches to Classical Estimation
In the literature, there have been many reports on the use of information theory to deal with classical estimation problems (e.g., see [149]). Here, we only give several typical examples.
3.2.1 Entropy Matching Method
Similar to the MM, the entropy matching method obtains the parameter estimator by using the sample entropy (entropy estimator) to approximate the population entropy. Suppose the PDF of population 
is 
(
is an unknown parameter). Then its differential entropy is
(3.16)
At the same time, one can use the sample 
to calculate the sample entropy 
.3 Thus, we can obtain an estimator of parameter 
through solving the following equation:
(3.17)
If there are several parameters, the above equation may have infinite number of solutions, while a unique solution can be achieved by combining the MM. In [166], the entropy matching method was used to estimate parameters of generalized Gaussian distribution (GGD).
3.2.2 Maximum Entropy Method
The maximum entropy method applies the famous MaxEnt principle to parameter estimation. The basic idea is that, subject to the information available, one should choose the parameter 
such that the entropy is as large as possible, or the distribution as nearly uniform as possible. Here, the maximum entropy method refers to a general approach rather than a specific parameter estimation method. In the following, we give three examples of maximum entropy method.
3.2.2.1 Parameter Estimation of Exponential Type Distribution
Assume that the PDF of population 
is of the following form:
(3.18)
where 
, 
, are 
(generalized) characteristic moment functions, 
is an unknown parameter vector to be estimated. Many known probability distributions are special cases of this exponential type distribution. By Theorem 2.2, 
is the maximum entropy distribution satisfying the following constraints:
(3.19)
where 
denotes the population characteristic moment:
(3.20)
As 
is unknown, the population characteristic moments cannot be calculated. We can approximate them using the sample characteristic moments. And then, an estimator of parameter 
can be obtained by solving the following optimization problem:
(3.21)
where 
, 
, are 
sample characteristic moments, i.e.,
(3.22)
According to Theorem 2.2, the estimator of 
satisfies the equations:
(3.23)
If 
, the above estimation method will be equivalent to the MM.
3.2.2.2 Maximum Spacing Estimation
Suppose the distribution function of population 
is 
, and the true value of the unknown parameter 
is 
, then the random variable 
will be distributed over the interval 
, which is a uniform distribution if 
. According to the MaxEnt principle, if the distribution over a finite interval is uniform, the entropy will achieve its maximum. Therefore, the entropy of random variable 
will attain the maximum value if 
. So one can obtain an estimator of the parameter 
by maximizing the sample entropy of 
. Let a sample of population 
be 
, the sample of 
will be 
. Let 
denote the sample entropy of 
, the estimator of parameter 
can be expressed as
(3.24)
If the sample entropy is calculated by using the one-spacing estimation method (see Chapter 4), then we have
(3.25)
where 
is the order statistics of 
. Formula (3.25) is called the maximum spacing estimation of parameter 
.
3.2.2.3 Maximum Equality Estimation
Suppose 
is an i.i.d. sample of population 
with PDF 
. Let 
be the order statistics of 
. Then the random sample divides the real axis into 
subintervals 
, 
, where 
and 
. Each subinterval has the probability:
(3.26)
Since the sample is random and i.i.d., the most reasonable situation is that the probabilities of 
subinterval are equal. Hence, the parameter 
should be chosen in such a way as to maximize the entropy of distribution 
(or to make 
as nearly uniform as possible), i.e.,
(3.27)
The above estimation is called the maximum equality estimation of parameter 
.
It is worth noting that besides parameter estimation, the MaxEnt principle can also be applied to spectral density estimation [48]. The general idea is that the maximum entropy rate stochastic process that satisfies the given constant autocorrelation and variance constraints, is a linear Gauss–Markov process with i.i.d. zero-mean, Gaussian input.
3.2.3 Minimum Divergence Estimation
Let 
be an i.i.d. random sample from a population 
with PDF 
, 
. Let 
be the estimated PDF based on the sample. Let 
be an estimator of 
. Then 
is also an estimator for 
. Then the estimator 
should be chosen so that 
is as close as possible to 
. This can be achieved by minimizing any measure of information divergence, say the KL-divergence
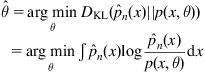(3.28)
or, alternatively,
(3.29)
The estimate 
in (3.28) or (3.29) is called the minimum divergence (MD) estimate of 
. In practice, we usually use (3.28) for parameter estimation, because it can be simplified as
(3.30)
Depending on the estimated PDF 
, the MD estimator may take many different forms. Next, we present three specific examples of MD estimator.
• MD Estimator 1
Without loss of generality, we assume that the sample satisfies 
. Then the distribution function can be estimated as
(3.31)
(3.32)
where 
is the likelihood function. In this case, the MD estimation is exactly the ML estimation.
• MD Estimator 2
Suppose the population 
is distributed over the interval 
, and the sample satisfies 
. It is reasonable to assume that in each subinterval 
, the probability is 
. And hence, the PDF of 
can be estimated as
(3.33)
Substituting (3.33) into (3.30) yields
(3.34)
If 
is a continuous function of 
, then according to the mean value theorem of integral calculus, we have
(3.35)
where 
. Hence, (3.34) can be written as
(3.36)
The above parameter estimation is in form very similar to the ML estimation. However, different from Fisher’s likelihood function, the values of the cost function in (3.36) are taken at 
, which are determined by mean value theorem of integral calculus.
• MD Estimator 3
Assume population 
is distributed over the interval 
, and this interval is divided into 
subintervals 
(
) by 
data 
. The probability of each subinterval is determined by
(3.37)
If 
are given proportions of the population that lie in the 
subintervals (
), then parameter 
should be chosen so as to make 
and 
as close as possible, i.e.,
(3.38)
This is a useful estimation approach, especially when the information available is on proportions in the population, such as proportions of persons in different income intervals or proportions of students in different score intervals.
In the previous MD estimations, the KL-divergence can be substituted by other definitions of divergence. For instance, if using 
-divergence, we have
(3.39)
or
(3.40)
For details on the minimum 
-divergence estimation, the readers can refer to [130].
3.3 Information Theoretic Approaches to Bayes Estimation
The Bayes estimation can also be embedded within the framework of information theory. In particular, some information theoretic measures, such as the entropy and correntropy, can be used instead of the traditional Bayes risks.
3.3.1 Minimum Error Entropy Estimation
In the scenario of Bayes estimation, the minimum error entropy (MEE) estimation aims to minimize the entropy of the estimation error, and hence decrease the uncertainty in estimation. Given two random variables: 
, an unknown parameter to be estimated, and 
, the observation (or measurement), the MEE (with Shannon entropy) estimation of 
based on 
can be formulated as
(3.41)
where 
is the estimation error, 
is an estimator of 
based on 
, 
is a measurable function, 
stands for the collection of all measurable functions 
, and 
denotes the PDF of the estimation error. When (3.41) is compared with (3.9) one concludes that the “loss function” in MEE is 
, which is different from traditional Bayesian risks, like MSE. Indeed one does not need to impose a risk functional in MEE, the risk is directly related to the error PDF. Obviously, other entropy definitions (such as order-
Renyi entropy) can also be used in MEE estimation. This feature is potentially beneficial because the risk is matched to the error distribution.
The early work in MEE estimation can be traced back to the late 1960s when Weidemann and Stear [86] studied the use of error entropy as a criterion function (risk function) for analyzing the performance of sampled data estimation systems. They proved that minimizing the error entropy is equivalent to minimizing the mutual information between the error and the observation, and also proved that the reduced error entropy is upper-bounded by the amount of information obtained by the observation. Minamide [89] extended Weidemann and Stear’s results to a continuous-time estimation system. Tomita et al. applied the MEE criterion to linear Gaussian systems and studied state estimation (Kalman filtering), smoothing, and predicting problems from the information theory viewpoint. In recent years, the MEE became an important criterion in supervised machine learning [64].
In the following, we present some important properties of the MEE criterion, and discuss its relationship to conventional Bayes risks. For simplicity, we assume that the error 
is a scalar (
). The extension to arbitrary dimensions will be straightforward.
3.3.1.1 Some Properties of MEE Criterion
Property 1:
, 
Proof:
This is the shift invariance of the differential entropy. According to the definition of differential entropy, we have
(3.42)
Property 2:
If 
is a random variable independent of the error 
, then 
.
Proof:
According to the properties of differential entropy and the independence condition, we have
(3.43)
Remark:
Property 2 implies that MEE criterion is robust to independent additive noise. Specifically, if error 
contains an independent additive noise 
, i.e., 
, where 
is the true error, then minimizing the contaminated error entropy 
will constrain the true error entropy 
.
Property 3:
Minimizing the error entropy 
is equivalent to minimizing the mutual information between error 
and the observation 
, i.e., 
.
Proof:
As 
, we have
(3.44)
It follows easily that
(3.45)
where (a) comes from the fact that the conditional entropy 
is not related to 
.
Property 4:
The error entropy 
is lower bounded by the conditional entropy 
, and this lower bound is achieved if and only if error 
is independent of the observation 
.
Proof:
By (3.44), we have
(3.46)
where the inequality follows from the fact that 
, with equality if and only if error 
and observation 
are independent.
Remark:
The error entropy can never be smaller than the conditional entropy of the parameter 
given observation 
. This lower bound is achieved if and only if the error contains no information about the observation.
For MEE estimation, there is no explicit expression for the optimal estimate unless some constraints on the posterior PDF are imposed. The next property shows that, if the posterior PDF is SUM, the MEE estimate will be equal to the conditional mean (i.e., the MMSE estimate).
Property 5:
If for any 
, the posterior PDF 
is SUM, then the MEE estimate equals the posterior mean, i.e., 
.
Remark:
Since the posterior PDF is SUM, in the above property the MEE estimate also equals the posterior median or posterior mode. We point out that for order-
Renyi entropy, this property still holds. One may be led to conclude that MEE has no advantage over the MMSE, since they correspond to the same solution for SUM case. However, the risk functional in MEE is still well defined for unimodal but asymmetric distributions, although no general results are known for this class of distributions. But we suspect that the practical advantages of MEE versus MSE reported in the literature [64] are taking advantage of this case. In the context of adaptive filtering, the two criteria may yield much different performance surfaces even if they have the same optimal solution.
Table 3.1 gives a summary of the optimal estimates for several Bayes estimation methods.
Proof:
We prove this property by means of a simple example as follows [94]: suppose 
is a discrete random variable with Bernoulli distribution:
(3.47)
The posterior PDF of 
given 
is (
):
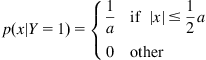
Given an estimator 
, the error PDF will be
(3.48)
Let 
be an unbiased estimator, then 
, and hence 
. Assuming 
(due to symmetry, one can obtain similar results for 
), the error entropy can be calculated as
(3.49)
One can easily verify that the error entropy achieves its minimum value when 
. Clearly, in this example there are infinitely many unbiased MEE estimators.
Property 7 (Score Orthogonality [92]):
Given an MEE estimator 
, the error’s score 
is orthogonal to any measurable function 
of 
, where 
is defined as
(3.50)
where 
denotes the error PDF for estimator 
.
Proof:
Given an MEE estimator 
, 
and
, we have
(3.51)
For 
small enough, 
will be a “small” random variable. According to [167], we have
(3.52)
where 
denotes the higher order terms. Then the derivative of entropy 
with respect to 
at 
is
(3.53)
Combining (3.51) and (3.53) yields
(3.54)
Remark:
If the error is zero-mean Gaussian distributed with variance 
, the score function will be 
. In this case, the score orthogonality condition reduces to 
. This is the well-known orthogonality condition for MMSE estimation.
In MMSE estimation, the orthogonality condition is a necessary and sufficient condition for optimality, and can be used to find the MMSE estimator. In MEE estimation, however, the score orthogonality condition is just a necessary condition for optimality but not a sufficient one. Next, we will present an example to demonstrate that if an estimator satisfies the score orthogonality condition, it can be a local minimum or even a local maximum of 
in a certain direction. Before proceeding, we give a definition.
Definition 3.1
Given an estimator 
, 
is said to be a local minimum (or maximum) of 
in the direction of 
, if and only if 
, such that 
, 
, we have
(3.55)
Example 3.1 [92]
Suppose the joint PDF of 
and 
is the mix-Gaussian density (
):
(3.56)
The MMSE estimation of 
based on 
can be computed as 
. It is easy to check that the estimator 
satisfies the score orthogonality condition.
Now we examine whether the MMSE estimator 
is a local minimum or maximum of the error entropy 
in a certain direction 
. We focus here on the case where 
(linear function). In this case, we have
(3.57)
For the case 
, the error’s entropies 
with respect to different 
and 
values are shown in Figure 3.1, from which we see that the MMSE estimator (
) is a local minimum of the error entropy in the direction of 
for 
and a local maximum for 
. In addition, for the case 
, the error’s entropies 
with respect to different 
and 
values are depicted in Figure 3.2. It can be seen from Figure 3.2 that when 
, 
is a global minimum of 
; while when 
, it becomes a local maximum.
Figure 3.1 Error’s entropy 
with respect to different 
and 
values. Source: Adopted from [92].
Figure 3.2 Error’s entropy 
with respect to different 
and 
values. Source: Adopted from [92].
The local minima or local maxima can also be judged using the second-order derivative of error entropy with respect to 
. For instance, if 
, we can calculate the following second-order derivative using results of [167]:
(3.58)
And hence
(3.59)
which implies that if 
, the MMSE estimator (
) will be a local minimum of the error entropy in the direction of 
, whereas if 
, it becomes a local maximum.
As can be seen from Figure 3.2, if 
, the error entropy 
achieves its global minima at 
. Figure 3.3 depicts the error PDF for 
(MMSE estimator) and 
(linear MEE estimator), where 
. We can see that the MEE solution is in this case not unique but it is much more concentrated (with higher peak) than the MMSE solution, which potentially gives an estimator with much smaller variance. We can also observe that the peaks of the MMSE and MEE error distributions occur at two different error locations, which means that the best parameter sets are different for each case.
Figure 3.3 Error’s PDF 
for 
and 
. Source: Adopted from [92].
3.3.1.2 Relationship to Conventional Bayes Risks
The loss function of MEE criterion is directly related to the error’s PDF, which is much different from the loss functions in conventional Bayes risks, because the user does not need to select the risk functional. To some extent, the error entropy can be viewed as an “adaptive” Bayes risk, in which the loss function is varying with the error distribution, that is, different error distributions correspond to different loss functions. Figure 3.4 shows the loss functions (the lower subplots) of MEE corresponding to three different error PDFs. Notice that the third case provides a risk function that is nonconvex in the space of the errors. This is an unconventional risk function because the role of the weight function is to privilege one solution versus all others in the space of the errors.
There is an important relationship between the MEE criterion and the traditional MSE criterion. The following theorem shows that the MSE is equivalent to the error entropy plus the KL-divergence between the error PDF and any zero-mean Gaussian density.
Theorem 3.1
Let 
denote a Gaussian density, 
, where 
. Then we have
(3.60)
Proof:
Since 
, we have
And hence
(3.61)
It follows easily that 
.
Remark:
The above theorem suggests that the minimization of MSE minimizes both the error entropy 
and the KL-divergence 
. Then the MMSE estimation will decrease the error entropy, and at the same time, make the error distribution close to zero-mean Gaussian distribution. In nonlinear and non-Gaussian estimating systems, the desirable error distribution can be far from Gaussian, while the MSE criterion still makes the error distribution close to zero-mean Gaussian distribution, which may lead to poor estimation performance. Thus, Theorem 3.1 also gives an explanation on why the performance of MMSE estimation may be not good for non-Gaussian samples.
Suppose that the error is zero-mean Gaussian distributed. Then we have 
, where 
. In this case, the MSE criterion is equivalent to the MEE criterion.
From the derivation of Theorem 3.1, let 
, we have
(3.62)
Since 
, then
(3.63)
Inequality (3.63) suggests that, minimizing the MSE is equivalent to minimizing an upper bound of error entropy.
There exists a similar relationship between MEE criterion and a large family of Bayes risks [168]. To prove this fact, we need a lemma.
corresponds to a PDF
and 
satisfy
Theorem 3.2
For any Bayes risk 
, if the loss function 
satisfies 
, then
(3.66)
where 
is the PDF given in (3.64).
Proof:
First, we show that in the PDF 
, 
is a positive number. Since 
satisfies 
and 
, we have 
. Then
(3.67)
where (a) follows from 
. Therefore,
(3.68)
which completes the proof.
Remark:
The condition 
in the theorem is not very restrictive, because for most Bayes risks, the loss function increases rapidly when 
goes to infinity. But for instance, it does not apply to the maximum correntropy (MC) criterion studied next.
3.3.2 MC Estimation
Correntropy is a novel measure of similarity between two random variables [64]. Let 
and 
be two random variables with the same dimensions, the correntropy is
(3.69)
where 
is a translation invariant Mercer kernel. The most popular kernel used in correntropy is the Gaussian kernel:
(3.70)
where 
denotes the kernel size (kernel width). Gaussian kernel 
is a translation invariant kernel that is a function of 
, so it can be rewritten as 
.
Compared with other similarity measures, such as the mean square error, correntropy (with Gaussian kernel) has some nice properties: (i) it is always bounded (
); (ii) it contains all even-order moments of the difference variable for the Gaussian kernel (using a series expansion); (iii) the weights of higher order moments are controlled by kernel size; and (iv) it is a local similarity measure, and is very robust to outliers.
The correntropy function can also be applied to Bayes estimation [169]. Let 
be an unknown parameter to be estimated and 
be the observation. We assume, for simplification, that 
is a scalar random variable (extension to the vector case is straightforward), 
, and 
is a random vector taking values in 
. The MC estimation of 
based on 
is to find a measurable function 
such that the correntropy between 
and 
is maximized, i.e.,
(3.71)
With any translation invariant kernel such as the Gaussian kernel 
, the MC estimator will be
(3.72)
where 
is the estimation error. If 
, 
has posterior PDF 
, then the estimation error has PDF
(3.73)
where 
denotes the distribution function of 
. In this case, we have
(3.74)
The following theorem shows that the MC estimation is a smoothed MAP estimation.
Theorem 3.3
The MC estimator (3.74) can be expressed as
(3.75)
where 
(“
” denotes the convolution operator with respect to 
).
Proof:
One can derive
(3.76)
where 
and (a) comes from the symmetry of 
. It follows easily that
(3.77)
This completes the proof.
Remark:
The function 
can be viewed as a smoothed version (through convolution) of the posterior PDF 
. Thus according to Theorem 3.3, the MC estimation is in essence a smoothed MAP estimation, which is the mode of the smoothed posterior distribution. The kernel size 
plays an important role in the smoothing process by controlling the degree of smoothness. When 
, the Gaussian kernel will approach the Dirac delta function, and the function 
will reduce to the original posterior PDF. In this case, the MC estimation is identical to the MAP estimation. On the other hand, when 
, the second-order moment will dominate the correntropy, and the MC estimation will be equivalent to the MMSE estimation [137].
In the literature of global optimization, the convolution smoothing method [170–172] has been proven very effective in searching the global minima (or maxima). Usually, one can use the convolution of a nonconvex cost function with a suitable smooth function to eliminate local optima, and gradually decrease the degree of smoothness to achieve global optimization. Therefore, we believe that by properly annealing the kernel size, the MC estimation can be used to obtain the global maxima of MAP estimation.
The optimal solution of MC estimation is the mode of the smoothed posterior distribution, which is, obviously, not necessarily unique. The next theorem, however, shows that when kernel size is larger than a certain value, the MC estimation will have a unique optimal solution that lies in a strictly concave region of the smoothed PDF (see [169] for the proof).
Theorem 3.4 [169]
Assume that function 
converges uniformly to 1 as 
. Then there exists an interval 
, 
, such that when kernel size 
is larger than a certain value, the smoothed PDF 
will be strictly concave in 
, and has a unique global maximum lying in this interval for any 
.
In the following, a simple example is presented to illustrate how the kernel size affects the solution of MC estimation. Suppose the joint PDF of 
and 
(
) is the mixture density (
) [169]:
(3.78)
where 
denotes the “clean” PDF and 
denotes the contamination part corresponding to “bad” data or outliers. Let 
, and assume that 
and 
are both jointly Gaussian:
(3.79)
(3.80)
For the case 
, the smoothed posterior PDFs with different kernel sizes are shown in Figure 3.5, from which we observe: (i) when kernel size is small, the smoothed PDFs are nonconcave within the dominant region (say the interval 
), and there may exist local optima or even nonunique optimal solutions; (ii) when kernel size is larger, the smoothed PDFs become concave within the dominant region, and there is a unique optimal solution. Several estimates of 
given 
are listed in Table 3.2. It is evident that when the kernel size is very small, the MC estimate is the same as the MAP estimate; while when the kernel size is very large, the MC estimate is close to the MMSE estimate. In particular, for some kernel sizes (say 
or 
), the MC estimate of 
equals −0.05, which is exactly the MMSE (or MAP) estimate of 
based on the “clean” distribution 
. This result confirms the fact that the MC estimation is much more robust (with respect to outliers) than both MMSE and MAP estimations.
Figure 3.5 Smoothed conditional PDFs given 
. Source: Adopted from [169]).
Given 
3.4 Information Criteria for Model Selection
Information theoretic approaches have also been used to solve the model selection problem. Consider the problem of estimating the parameter 
of a family of models
(3.81)
where the parameter space dimension 
is also unknown. This problem is actually a model structure selection problem, and the value of 
is the structure parameter. There are many approaches to select the space dimension 
. Here, we only discuss several information criteria for selecting the most parsimonious correct model, where the name indicates that they are closely related to or can be derived from information theory.
1. Akaike’s information criterion
The Akaike’s information criterion (AIC) was first developed by Akaike [6,7]. AIC is a measure of the relative goodness of fit of a statistical model. It describes the tradeoff between bias and variance (or between accuracy and complexity) in model construction. In the general case, AIC is defined as
(3.82)
where 
is the maximized value of the likelihood function for the estimated model. To apply AIC in practice, we start with a set of candidate models, and find the models’ corresponding AIC values, and then select the model with the minimum AIC value. Since AIC includes a penalty term 
, it can effectively avoid overfitting. However, the penalty is constant regardless of the number of samples used in the fitting process.
The AIC criterion can be derived from the KL-divergence minimization principle or the equivalent relative entropy maximization principle (see Appendix G for the derivation).
2. Bayesian Information Criterion
The Bayesian information criterion (BIC), also known as the Schwarz criterion, was independently developed by Akaike and by Schwarz in 1978, using Bayesian formalism. Akaike’s version of BIC was often referred to as the ABIC (for “a BIC”) or more casually, as Akaike’s Bayesian Information Criterion. BIC is based, in part, on the likelihood function, and is closely related to AIC criterion. The formula for the BIC is
(3.83)
where 
denotes the number of the observed data (i.e., sample size). The BIC criterion has a form very similar to AIC, and as one can see, the penalty term in BIC is in general larger than in AIC, which means that generally it will provide smaller model sizes.
3. Minimum Description Length Criterion
The minimum description length (MDL) principle was introduced by Rissanen [9]. It is an important principle in information and learning theories. The fundamental idea behind the MDL principle is that any regularity in a given set of data can be used to compress the data, that is, to describe it using fewer symbols than needed to describe the data literally. According to MDL, the best model for a given set of data is the one that leads to the best compression of the data. Because data compression is formally equivalent to a form of probabilistic prediction, MDL methods can be interpreted as searching for a model with good predictive performance on unseen data. The ideal MDL approach requires the estimation of the Kolmogorov complexity, which is noncomputable in general. However, there are nonideal, practical versions of MDL.
From a coding perspective, assume that both sender and receiver know which member 
of the parametric family 
generated a data string 
. Then from a straightforward generalization of Shannon’s Source Coding Theorem to continuous random variables, it follows that the best description length of 
(in an average sense) is simply 
, because on average the code length achieves the entropy lower bound 
. Clearly, minimizing 
is equivalent to maximizing 
. Thus the MDL coincides with the ML in parametric estimation problems. In addition, we have to transmit 
, because the receiver did not know its value in advance. Adding in this cost, we arrive at a code length for the data string 
:
(3.84)
where 
denotes the number of bits for transmitting 
. If we assume that the machine precision is 
for each component of 
and 
is transmitted with a uniform encoder, then the term 
is expressed as
(3.85)
In this case, the MDL takes the form of BIC. An alternative expression of 
is
(3.86)
where 
is a constant related to the number of bits in the exponent of the floating point representation of 
and 
is the optimal precision of 
.
Appendix E: EM Algorithm
An EM algorithm is an iterative method for finding the ML estimate of parameters in statistical models, where the model depends on unobserved latent variables. The EM iteration alternates between performing an expectation (E) step, which calculates the expectation of the log-likelihood evaluated using the current estimate for the parameters, and a maximization (M) step, which computes parameters maximizing the expected log-likelihood found on the E step. These parameter estimates are then used to determine the distribution of the latent variables in the next E step.
Let 
be the observed data, 
be the unobserved data, and 
be a vector of unknown parameters. Further, let 
be the likelihood function, 
be the marginal likelihood function of the observed data, and 
be the conditional density of 
given 
under the current estimate of the parameters 
. The EM algorithm seeks to find the ML estimate of the marginal likelihood by iteratively applying the following two steps
given 
under the current estimate 
:
of the parameters by maximizing this quantity:
continues until 
is sufficiently small.Appendix F: Minimum MSE Estimation
The MMSE estimate 
of 
is obtained by minimizing the following cost:
(F.1)
Since 
, 
, one only needs to minimize 
. Let
(F.2)
Then we get 
.
Appendix G: Derivation of AIC Criterion
The information theoretic KL-divergence plays a crucial role in the derivation of AIC. Suppose that the data are generated from some distribution 
. We consider two candidate models (distributions) to represent 
: 
and 
. If we know 
, then we could evaluate the information lost from using 
to represent 
by calculating the KL-divergence, 
; similarly, the information lost from using 
to represent 
would be found by calculating 
. We would then choose the candidate model minimizing the information loss. If 
is unknown, we can estimate, via AIC, how much more (or less) information is lost by 
than by 
. The estimate is, certainly, only valid asymptotically.
Given a family of density models 
, where 
denotes a 
-dimensional parameter space, 
, and a sequence of independent and identically distributed observations 
, the AIC can be expressed as
(G.1)
where 
is the ML estimate of 
:
(G.2)
Let 
be the unknown true parameter vector. Then
(G.3)
where
(G.4)
Taking the first term in a Taylor expansion of 
, we obtain
(G.5)
where 
is the 
Fisher information matrix. Then we have
(G.6)
Suppose 
can be decomposed into
(G.7)
where 
is some nonsingular matrix. We can derive
(G.8)
According to the statistical properties of the ML estimator, when sample number 
is large enough, we have
(G.9)
Combining (G.9) and (G.7) yields
(G.10)
where 
is the 
identity matrix. From (G.8) and (G.10), we obtain
(G.11)
That is, 
is Chi-Squared distributed with 
degree of freedom. This implies
(G.12)
It follows that
(G.13)
And hence
(G.14)
It has been proved in [173] that
(G.15)
Therefore
(G.16)
Combining (G.16) and (G.14), we have
(G.17)
To minimize the KL-divergence 
, one need to maximize 
, or equivalently, to minimize (in an asymptotical sense) the following objective function
(G.18)
This is exactly the AIC criterion.
1For a discrete variable 
, 
is defined by 
, while for a continuous variable, it is defined as 
, satisfying 
.
2The mode of a continuous probability distribution is the value at which its PDF attains its maximum value.
3Several entropy estimation methods will be presented in Chapter 4.
4Here, 
is actually the maximum entropy density that satisfies the constraint condition 
.