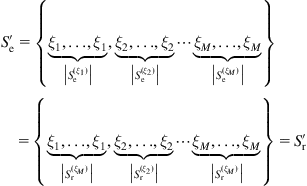
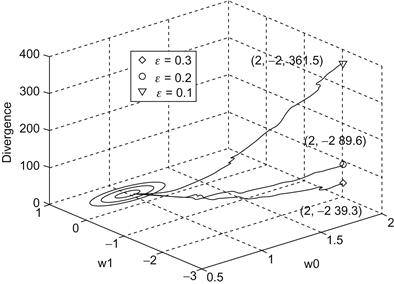
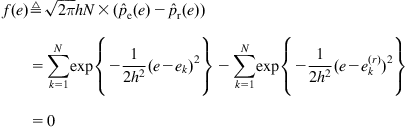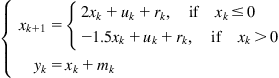System Identification Under Information Divergence Criteria
The fundamental contribution of information theory is to provide a unified framework for dealing with the notion of information in a precise and technical sense. Information, in a technical sense, can be quantified in a unified manner by using the Kullback–Leibler information divergence (KLID). Two information measures, Shannon’s entropy and mutual information are special cases of KL divergence [43]. The use of probability in system identification is also shown to be equivalent to measuring KL divergence between the actual and model distributions. In parameter estimation, the KL divergence for inference is consistent with common statistical approaches, such as the maximum likelihood (ML) estimation. Based on the KL divergence, Akaike derived the well-known Akaike’s information criterion (AIC), which is widely used in the area of model selection. Another important model selection criterion, the minimum description length, first proposed by Rissanen in 1978, is also closely related to the KL divergence. In identification of stationary Gaussian processes, it has been shown that the optimal solution to an approximation problem for Gaussian random variables with the divergence criterion is identical to the main step of the subspace algorithm [123].
There are many definitions of information divergence, but in this chapter our focus is mainly on the KLID. In most cases, the extension to other definitions is straightforward.
5.1 Parameter Identifiability Under KLID Criterion
The identifiability arises in the context of system identification, indicating whether or not the unknown parameter can be uniquely identified from the observation of the system. One would not select a model structure whose parameters cannot be identified, so the problem of identifiability is crucial in the procedures of system identification. There are many concepts of identifiability. Typical examples include Fisher information–based identifiability [216], least squares (LS) identifiability [217], consistency-in-probability identifiability [218], transfer function–based identifiability [219], and spectral density–based identifiability [219]. In the following, we discuss the fundamental problem of system parameter identifiability under KLID criterion.
5.1.1 Definitions and Assumptions
Let ![]() (
(![]() ) be a sequence of observations with joint probability density functions (PDFs)
) be a sequence of observations with joint probability density functions (PDFs) ![]() ,
, ![]() , where
, where ![]() is a
is a ![]() -dimensional column vector,
-dimensional column vector, ![]() is a
is a ![]() -dimensional parameter vector, and
-dimensional parameter vector, and ![]() is the parameter space. Let
is the parameter space. Let ![]() be the true parameter. The KLID between
be the true parameter. The KLID between ![]() and
and ![]() will be
will be
 (5.1)
(5.1)
where ![]() denotes the expectation of the bracketed quantity taken with respect to the actual parameter value
denotes the expectation of the bracketed quantity taken with respect to the actual parameter value ![]() . Based on the KLID, a natural way of parameter identification is to look for a parameter
. Based on the KLID, a natural way of parameter identification is to look for a parameter ![]() , such that the KLID of Eq. (5.1) is minimized, that is,
, such that the KLID of Eq. (5.1) is minimized, that is,
![]() (5.2)
(5.2)
An important question that arises in the context of such identification problem is whether or not the parameter ![]() can be uniquely determined. This is the parameter identifiability problem. Assume
can be uniquely determined. This is the parameter identifiability problem. Assume ![]() lies in
lies in ![]() (hence
(hence ![]() ). The notion of identifiability under KLID criterion can then be defined as follows.
). The notion of identifiability under KLID criterion can then be defined as follows.
5.1.2 Relations with Fisher Information
Fisher information is a classical criterion for parameter identifiability [216]. There are close relationships between KLID (KLIDR)-identifiability and Fisher information.
The Fisher information matrix (FIM) for the family of densities ![]() is given by:
is given by:
 (5.5)
(5.5)
As ![]() , the Fisher information rate matrix (FIRM) is:
, the Fisher information rate matrix (FIRM) is:
![]() (5.6)
(5.6)
5.1.3 Gaussian Process Case
When the observation sequence ![]() is jointly Gaussian distributed, the KLID-identifiability can be easily checked. Consider the following joint Gaussian PDF:
is jointly Gaussian distributed, the KLID-identifiability can be easily checked. Consider the following joint Gaussian PDF:
![]() (5.15)
(5.15)
where ![]() is the mean vector, and
is the mean vector, and ![]() is the
is the ![]() -dimensional covariance matrix. Then we have
-dimensional covariance matrix. Then we have
![]() (5.16)
(5.16)
where ![]() is
is
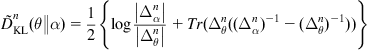 (5.17)
(5.17)
Clearly, for the Gaussian process ![]() , we have
, we have ![]() if and only if
if and only if ![]() and
and ![]() . Denote
. Denote ![]() ,
, ![]() , where
, where ![]() is the ith row and jth column element of
is the ith row and jth column element of ![]() . The element
. The element ![]() is said to be a regular element if and only if
is said to be a regular element if and only if ![]() , i.e., as a function of
, i.e., as a function of ![]() ,
, ![]() is not a constant. In a similar way, we define the regular element of the mean vector
is not a constant. In a similar way, we define the regular element of the mean vector ![]() . Let
. Let ![]() be a column vector containing all the distinct regular elements from
be a column vector containing all the distinct regular elements from ![]() and
and ![]() . We call
. We call ![]() the regular characteristic vector (RCV) of the Gaussian process
the regular characteristic vector (RCV) of the Gaussian process ![]() . Then we have
. Then we have ![]() if and only if
if and only if ![]() . According to Definition 5.1, for the Gaussian process
. According to Definition 5.1, for the Gaussian process ![]() , the parameter set
, the parameter set ![]() is KLID-identifiable at
is KLID-identifiable at ![]() , if and only if
, if and only if ![]() ,
, ![]() ,
, ![]() implies
implies ![]() .
.
Assume that ![]() is an open subset of
is an open subset of ![]() . By Lemma 1 of Ref. [219], the map
. By Lemma 1 of Ref. [219], the map ![]() will be locally one to one at
will be locally one to one at ![]() if the Jacobian of
if the Jacobian of ![]() has full rank
has full rank ![]() at
at ![]() . Therefore, a sufficient condition for
. Therefore, a sufficient condition for ![]() to be locally KLID-identifiable is that
to be locally KLID-identifiable is that
![]() (5.18)
(5.18)
5.1.4 Markov Process Case
Now we focus on situations where the observation sequence is a parameterized Markov process. First, let us define the minimum identifiable horizon (MIH).
1. ![]() : The zero-order strictly stationary Markov process refers to an independent and identically distributed sequence. In this case, we have
: The zero-order strictly stationary Markov process refers to an independent and identically distributed sequence. In this case, we have ![]() , and
, and
 (5.31)
(5.31)
And hence, ![]() , we have
, we have ![]() . It follows that
. It follows that ![]() , and
, and ![]() .
.
![]() (5.32)
(5.32)
By Markovian and stationary properties, one can derive
 (5.33)
(5.33)
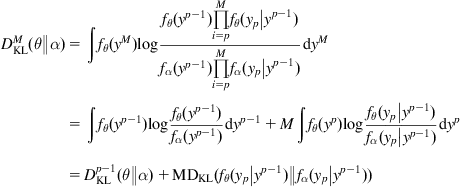 (5.34)
(5.34)
where ![]() is the conditional KLID. And hence,
is the conditional KLID. And hence,
 (5.35)
(5.35)
5.1.5 Asymptotic KLID-Identifiability
In the previous discussions, we assume that the true density ![]() is known. In most practical situations, however, the actual density, and hence the KLID, needs to be estimated using random data drawn from the underlying density. Let
is known. In most practical situations, however, the actual density, and hence the KLID, needs to be estimated using random data drawn from the underlying density. Let ![]() be an independent and identically distributed (i.i.d.) sample drawn from
be an independent and identically distributed (i.i.d.) sample drawn from ![]() . The density estimator for
. The density estimator for ![]() will be a mapping
will be a mapping ![]() [98]:
[98]:
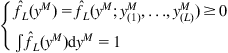 (5.41)
(5.41)
The asymptotic KLID-identifiability is then defined as follows:
![]() (5.42)
(5.42)
where ![]() is the probability of Borel set
is the probability of Borel set ![]() . On the other hand, as
. On the other hand, as ![]() , we have
, we have
![]() (5.43)
(5.43)
Then the event ![]() , and hence
, and hence
![]() (5.44)
(5.44)
By Pinsker’s inequality, we have
 (5.45)
(5.45)
where ![]() is the
is the ![]() -distance (or the total variation). It follows that
-distance (or the total variation). It follows that
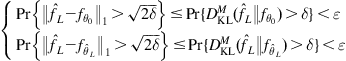 (5.46)
(5.46)
In addition, the following inequality holds:
![]() (5.47)
(5.47)
Then we have
![]() (5.48)
(5.48)
And hence
 (5.49)
(5.49)
For any ![]() , we define the set
, we define the set ![]() , where
, where ![]() is the Euclidean norm. As
is the Euclidean norm. As ![]() is a compact subset in
is a compact subset in ![]() ,
, ![]() must be a compact set too. Meanwhile, by Assumption 5.2, the function
must be a compact set too. Meanwhile, by Assumption 5.2, the function ![]() (
(![]() ) will be a continuous mapping
) will be a continuous mapping ![]() . Thus, a minimum of
. Thus, a minimum of ![]() over the set
over the set ![]() must exist. Denote
must exist. Denote ![]() , it follows easily that
, it follows easily that
![]() (5.50)
(5.50)
If ![]() is KLID-identifiable,
is KLID-identifiable, ![]() ,
, ![]() , we have
, we have ![]() , or equivalently,
, or equivalently, ![]() . It follows that
. It follows that ![]() . Let
. Let ![]() , we have
, we have
 (5.51)
(5.51)
This implies ![]() , and hence
, and hence ![]() .
.
According to Theorem 5.6, if the density estimate ![]() is consistent in KLID in probability (
is consistent in KLID in probability (![]() ), the KLID-identifiability will be a sufficient condition for the asymptotic KLID-identifiability. The next theorem shows that, under certain conditions, the KLID-identifiability will also be a necessary condition for
), the KLID-identifiability will be a sufficient condition for the asymptotic KLID-identifiability. The next theorem shows that, under certain conditions, the KLID-identifiability will also be a necessary condition for ![]() to be asymptotic KLID-identifiable.
to be asymptotic KLID-identifiable.
![]() (5.53)
(5.53)
Suppose ![]() is not KLID-identifiable, then
is not KLID-identifiable, then ![]() ,
, ![]() , such that
, such that ![]() . Let
. Let ![]() , we have (as
, we have (as ![]() is a compact subset, the minimum exists)
is a compact subset, the minimum exists)
 (5.54)
(5.54)
where (a) follows from ![]() . The above result contradicts the condition (2). Therefore,
. The above result contradicts the condition (2). Therefore, ![]() must be KLID-identifiable.
must be KLID-identifiable.
In the following, we consider several specific density estimation methods and discuss the consistency problems of the related parameter estimators.
5.1.5.1 Maximum Likelihood Estimation
The maximum likelihood estimation (MLE) is a popular parameter estimation method and is also an important parametric approach for the density estimation. By MLE, the density estimator is
![]() (5.55)
(5.55)
where ![]() is obtained by maximizing the likelihood function, that is,
is obtained by maximizing the likelihood function, that is,
![]() (5.56)
(5.56)
5.1.5.2 Histogram-Based Estimation
The histogram-based estimation is a common nonparametric method for density estimation. Suppose the i.i.d. samples ![]() take values in a measurable space
take values in a measurable space ![]() . Let
. Let ![]() ,
, ![]() , be a sequence of partitions of
, be a sequence of partitions of ![]() , with
, with ![]() either finite or infinite, such that the
either finite or infinite, such that the ![]() -measure
-measure ![]() for each
for each ![]() . Then the standard histogram density estimator with respect to
. Then the standard histogram density estimator with respect to ![]() and
and ![]() is given by:
is given by:
![]() (5.57)
(5.57)
where ![]() is the standard empirical measure of
is the standard empirical measure of ![]() , i.e.,
, i.e.,
![]() (5.58)
(5.58)
where ![]() is the indicator function.
is the indicator function.
According to Ref. [223], under certain conditions, the density estimator ![]() will converge in reversed order information divergence to the true underlying density
will converge in reversed order information divergence to the true underlying density ![]() , and the expected KLID
, and the expected KLID
![]() (5.59)
(5.59)
Since ![]() , by Markov’s inequality [224], for any
, by Markov’s inequality [224], for any ![]() , we have
, we have
![]() (5.60)
(5.60)
It follows that ![]() ,
, ![]() , and for any
, and for any ![]() and
and ![]() arbitrarily small, there exists an
arbitrarily small, there exists an ![]() such that for
such that for ![]() ,
,
![]() (5.61)
(5.61)
Thus we have ![]() . By Theorem 5.6, the following corollary holds.
. By Theorem 5.6, the following corollary holds.
5.1.5.3 Kernel-Based Estimation
The kernel-based estimation (or kernel density estimation, KDE) is another important nonparametric approach for the density estimation. Given an i.i.d. sample ![]() , the kernel density estimator is
, the kernel density estimator is
 (5.62)
(5.62)
where ![]() is a kernel function satisfying
is a kernel function satisfying ![]() and
and ![]() ,
, ![]() is the kernel width.
is the kernel width.
For the KDE, the following lemma holds (see chapter 9 in Ref. [98] for details).
5.2 Minimum Information Divergence Identification with Reference PDF
Information divergences have been suggested by many authors for the solution of the related problems of system identification. The ML criterion and its extensions (e.g., AIC) can be derived from the KL divergence approach. The information divergence approach is a natural generalization of the LS view. Actually one can think of a “distance” between the actual (empirical) and model distributions of the data, without necessarily introducing the conceptually more demanding concepts of likelihood or posterior. In the following, we introduce a novel system identification approach based on the minimum information divergence criterion.
Apart from conventional methods, the new approach adopts the idea of PDF shaping and uses the divergence between the actual error PDF and a reference (or target) PDF (usually with zero mean and a narrow range) as the identification criterion. As illustrated in Figure 5.1, in this scheme, the model parameters are adjusted such that the error distribution tends to the reference distribution. With KLID, the optimal parameters (or weights) of the model can be expressed as:
![]() (5.65)
(5.65)
where ![]() and
and ![]() denote, respectively, the actual error PDF and the reference PDF. Other information divergence measures such as
denote, respectively, the actual error PDF and the reference PDF. Other information divergence measures such as ![]() -divergence can also be used but are not considered here.
-divergence can also be used but are not considered here.
The above method shapes the error distribution, and can be used to achieve the desired variance or entropy of the error, provided the desired PDF of the error can be achieved. This is expected to be useful in complex signal processing and learning systems. If we choose the ![]() function as the reference PDF, the identification error will be forced to concentrate around the zero with a sharper peak. This coincides with commonsense predictions about system identification.
function as the reference PDF, the identification error will be forced to concentrate around the zero with a sharper peak. This coincides with commonsense predictions about system identification.
It is worth noting that the PDF shaping approaches can be found in other contexts. In the control literature, Karny et al. [225,226] proposed an alternative formulation of stochastic control design problem: the joint distributions of closed-loop variables should be forced to be as close as possible to their desired distributions. This formulation is called the fully probabilistic control. Wang et al. [227–229] designed new algorithms to control the shape of the output PDF of a stochastic dynamic system. In adaptive signal processing literature, Sala-Alvarez et al. [230] proposed a general criterion for the design of adaptive systems in digital communications, called the statistical reference criterion, which imposes a given PDF at the output of an adaptive system.
It is important to remark that the minimum value of the KLID in Eq. (5.65) may not be zero. In fact, all the possible PDFs of the error are, in general, restricted to a certain set of functions ![]() . If the reference PDF is not contained in the possible PDF set, i.e.,
. If the reference PDF is not contained in the possible PDF set, i.e., ![]() , we have
, we have
![]() (5.66)
(5.66)
In this case, the optimal error PDF ![]() , and the reference distribution can never be realized. This is however not a problem of great concern, since our goal is just to make the error distribution closer (not necessarily identical) to the reference distribution.
, and the reference distribution can never be realized. This is however not a problem of great concern, since our goal is just to make the error distribution closer (not necessarily identical) to the reference distribution.
In some special situations, this new identification method is equivalent to the ML identification. Suppose that in Figure 5.1 the noise ![]() is independent of the input
is independent of the input ![]() , and the unknown system can be exactly identified, i.e., the intrinsic error (
, and the unknown system can be exactly identified, i.e., the intrinsic error (![]() ) between the unknown system and the model can be zero. In addition, we assume that the noise PDF
) between the unknown system and the model can be zero. In addition, we assume that the noise PDF ![]() is known. In this case, if setting
is known. In this case, if setting ![]() , we have
, we have
 (5.67)
(5.67)
where (a) comes from the fact that the weight vector minimizing the KLID (when ![]() ) also minimizes the error entropy, and
) also minimizes the error entropy, and ![]() is the likelihood function.
is the likelihood function.
5.2.1 Some Properties
We present in the following some important properties of the minimum KLID criterion with reference PDF (called the KLID criterion for short).
The KLID criterion is much different from the minimum error entropy (MEE) criterion. The MEE criterion does not consider the mean of the error due to its invariance to translation. Under MEE criterion, the estimator makes the error PDF as sharp as possible, and neglects the PDF’s location. Under KLID criterion, however, the estimator makes the actual error PDF and reference PDF as close as possible (in both shape and location).
The KLID criterion is sensitive to the error mean. This can be easily verified: if ![]() and
and ![]() are both Gaussian PDFs with zero mean and unit variance, we have
are both Gaussian PDFs with zero mean and unit variance, we have ![]() ; while if the error mean becomes nonzero,
; while if the error mean becomes nonzero, ![]() , we have
, we have ![]() . The following theorem suggests that, under certain conditions the mean value of the optimal error PDF under KLID criterion is equal to the mean value of the reference PDF.
. The following theorem suggests that, under certain conditions the mean value of the optimal error PDF under KLID criterion is equal to the mean value of the reference PDF.
 (5.68)
(5.68)
where (a), (d), and (e) follow from the shift-invariance of the KLID, (b) is because ![]() is strictly log-concave, and (c) is because
is strictly log-concave, and (c) is because ![]() and
and ![]() are even functions. Therefore,
are even functions. Therefore, ![]() , such that
, such that
![]() (5.69)
(5.69)
This contradicts with ![]() . And hence,
. And hence, ![]() holds.
holds.
On the other hand, the KLID criterion is also closely related to the MEE criterion. The next theorem provides an upper bound on the error entropy under the constraint that the KLID is bounded.
5.2.2 Identification Algorithm
In the following, we derive a stochastic gradient–based identification algorithm under the minimum KLID criterion with a reference PDF. Since the KLID is not symmetric, we use the symmetric version of KLID (also referred to as the J-information divergence):
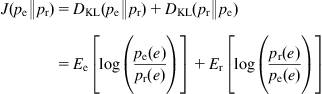 (5.100)
(5.100)
By dropping off the expectation operators ![]() and
and ![]() , and plugging in the estimated PDFs, one may obtain the estimated instantaneous value of J-information divergence:
, and plugging in the estimated PDFs, one may obtain the estimated instantaneous value of J-information divergence:
![]() (5.101)
(5.101)
where ![]() and
and ![]() are
are
 (5.102)
(5.102)
Then a stochastic gradient–based algorithm can be readily derived as follows:
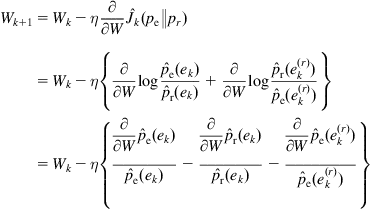 (5.103)
(5.103)
where
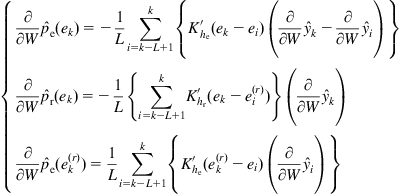 (5.104)
(5.104)
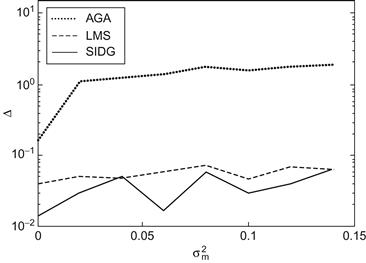
This algorithm is called the stochastic information divergence gradient (SIDG) algorithm [125,126].
In order to achieve an error distribution with zero mean and small entropy, one can choose the ![]() function at zero as the reference PDF. It is, however, worth noting that the
function at zero as the reference PDF. It is, however, worth noting that the ![]() function is not always the best choice. In many situations, the desired error distribution may be far from the
function is not always the best choice. In many situations, the desired error distribution may be far from the ![]() distribution. In practice, the desired error distribution can be estimated from some prior knowledge or preliminary identification results.
distribution. In practice, the desired error distribution can be estimated from some prior knowledge or preliminary identification results.
5.2.4 Adaptive Infinite Impulsive Response Filter with Euclidean Distance Criterion
In Ref. [233], the Euclidean distance criterion (EDC), which can be regarded as a special case of the information divergence criterion with a reference PDF, was successfully applied to develop the global optimization algorithms for adaptive infinite impulsive response (IIR) filters. In the following, we give a brief introduction of this approach.
The EDC for the adaptive IIR filters is defined as the Euclidean distance (or L2 distance) between the error PDF and ![]() function [233]:
function [233]:
![]() (5.110)
(5.110)
The above formula can be expanded as:
![]() (5.111)
(5.111)
where ![]() stands for the parts of this Euclidean distance measure that do not depend on the error distribution. By dropping
stands for the parts of this Euclidean distance measure that do not depend on the error distribution. By dropping ![]() , the EDC can be simplified to
, the EDC can be simplified to
![]() (5.112)
(5.112)
where ![]() is the quadratic information potential of the error.
is the quadratic information potential of the error.
By substituting the kernel density estimator (usually with Gaussian kernel ![]() ) for the error PDF in the integral, one may obtain the empirical EDC:
) for the error PDF in the integral, one may obtain the empirical EDC:
 (5.113)
(5.113)
A gradient-based identification algorithm can then be derived as follows:
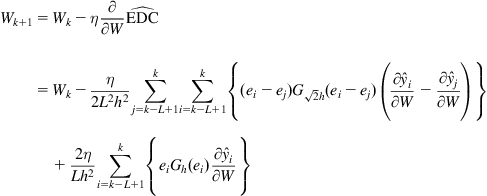 (5.114)
(5.114)
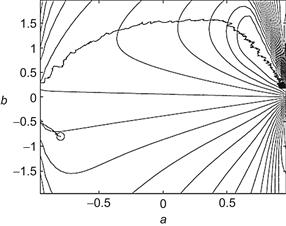
where the gradient ![]() depends on the model structure. Below we derive this gradient for the IIR filters.
depends on the model structure. Below we derive this gradient for the IIR filters.
Let us consider the following IIR filter:
![]() (5.115)
(5.115)
which can be written in the form
![]() (5.116)
(5.116)
where ![]() ,
, ![]() . Then we can derive
. Then we can derive
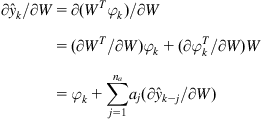 (5.117)
(5.117)
In Eq. (5.117), the parameter gradient is calculated in a recursive manner.



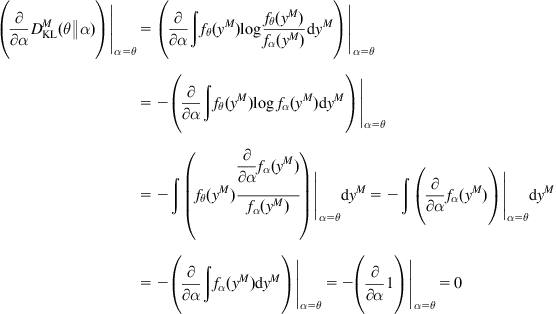
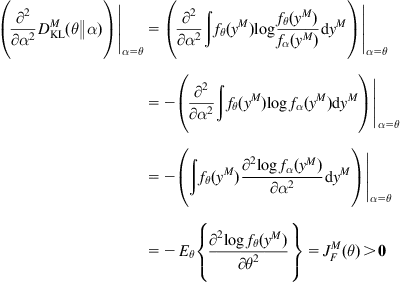




 .
.




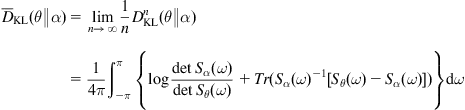






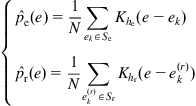



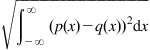 ).
).