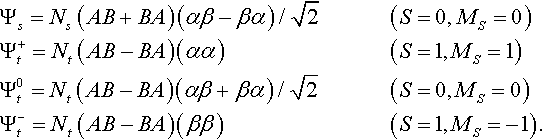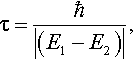1) Introduction

“Reality resists imitation through a model” (Schröinger, 1935)¹

In the early days of quantum mechanics there was much discussion of the ‘reality’ of physical systems and of the ‘completeness’ of theories whose aim was to describe them mathematically. Much effort was expended in devising ‘thought experiments’ to test the validity of quantum mechanics: one such experiment was proposed by Einstein, Podolsky and Rosen [2], whose argument has since been extended and applied to many types of physical system. The EPR paper starts from the premise that “A sufficient condition for the reality of a physical quantity is the possibility of predicting it with certainty, without disturbing the system” and, after considering quantities whose associated operators do not commute, it is concluded that either (i) the description of reality given by quantum mechanics is incomplete; or (ii) that quantities whose operators do not commute can have no simultaneous reality. It is then a short step, by considering a system comprising two subsystems which interact for a short time and then separate, that if (i) is false then (ii) is also false. The final conclusion is that quantum mechanics (and in particular the wavefunction) cannot give a complete description of physical reality.

In 1951, Bohm [3] re-examined the EPR paradox and initiated the search for ‘hidden variables’, new ‘elements of physical reality’ not included among the variables of orthodox quantum mechanics, which might be used to formulate a more complete theory. Bohm took as his ‘model system’ a pair of electron spins, a model containing only six physically measurable quantities (the spin components of the two electrons) and thus amenable to straightforward analysis. His proposals were attacked by von Neumann and others and ultimately ruled out by the work of Bell[4,5], who proved formally that for such a system a hidden-variables interpretation was mathematically untenable. Bell’s work, however, was concerned purely with (i) the hypothetical system of two spins, initially interacting and then separating to a distance at which there was no further interaction; and (ii) with the question of whether or not the EPR paradox might be resolved by introducing hidden variables. Bell’s theorem [4] excludes that possibility; but it must be conceded that the model considered is so remote from the system it sets out to represent (namely “a molecule containing two atoms in a state in which the total spin is zero”) that the applicability of Bell’s analysis to any system encountered in ‘the real world’ is open to question.

Bell recognized very clearly, however, the fundamental problem, restating the views of Einstein [6]: it is the ‘common sense’ requirement that “the result of a measurement on one system be unaffected by operations on a distant system with which it has interacted in the past, that creates the essential difficulty” [4]. And in his second paper [5] he pointed to the possibility of “replacing the arbitrary axioms [concerning hidden variables] .... by some condition of locality, or of separability of distant systems”, suggesting that “an interesting axiom would be that mutually distant systems are independent of one another. However, othodox quantum mechanics apparently denies the possibility of such a separability: the two interacting spins in the EPR model, no matter how far they fly apart, must forever keep their original coupling to total spin zero. The same view has been expressed by d’Espagnat [7] and others, who claim that everything is connected to everything else in the universe. Such conclusions have given rise to the ‘many worlds’ and ‘many minds’ interpretations of quantum mechanics (well presented by, for example, Lockwood [8]), which continue to engage the minds of many philosophers. To the average physicist, however, such interpretations seem to border on science fiction; and one wonders whether such exotic deviations are really necessary (fascinating as they may be) in seeking an escape from the ‘separability/non-separability’ conflict.

The argument is real enough. The idea of non-separability, presented as an inevitable consequence of the axioms of quantum mechanics, appears to have been largely responsible for Einstein’s rejection of the Copenhagen interpretation. But sixty years later it is widely accepted [7] that “non-separability is now one of the most certain general concepts in physics”. One feels that the argument ought to be settled on the basis of orthodox quantum mechanics and that failure to do so may be connected not with the theory but rather with its application: could it not be that the alleged predictions of theory, on which the debate is centred, are simply artefacts arising from the use of drastically oversimplified models? For example, even a cursory inspection of the two-spin model reveals that it does not recognise some of the central features of quantum mechanics. How do we know where the two particles are, if the Hamiltonian contains no spatial variables, so how can we tell when they are ‘distant’? How can their indistinguishability be recognized if we use a wavefunction which does not conform to the Pauli (antisymmetry) principle? And if the (2-electron) model is indeed a non-separable system then at what point can independent observers make measurements on the individual electrons?

The aim of the present work is to reconsider the separability question, using the system referred to by Bohm and Bell but with a more realistic mathematical model: this should include the space and spin variables of all electrons, together with the nuclear coordinates which define the ‘geometry’ of the system. The simplest conceivable system of this type is the hydrogen molecule, to which orthodox quantum mechanics can be applied without difficulty – even with the recognition that the molecule may be in weak interaction with a ‘heat bath’ (i.e. with the rest of the world) and may thus be in an incompletely specified state, rather than a pure state (the isolated molecule singlet ground state). The question to be answered is: If the two hydrogen atoms move apart, at what point does an electron ‘forget’ that in the molecular ground state its spin was coupled to that of the other electron? And the aspects of the problem that seem to require special attention will be (i) the association of a statistical (or ‘density’) operator with the system; (ii) the introduction of ‘reduced’ density operators and, in particular, a function to measure the coupling between the spins of two electrons at different points in space; and (iii) the importance of including electronic and nuclear coordinates in the Hamiltonian operator, which uniquely determines the evolution of the electronic wavefunction as a function of nuclear positions.

2) The system density matrix

First it is necessary to introduce appropriate notation and definitions and to recall some properties of the density operator introduced by von Neumann [10] and Dirac [11]. A general many-electron² wavefunction, for a system in stationary state K, will be written Ψ_K. (q), where q stands for all the required particle variables (space and spin coordinates). Such functions will be assumed orthonormal, so that the scalar product < Ψ_K|Ψ_L > = δKL, and being eigenfunctions of the Hamiltonian operator define a ‘privileged’ basis in the sense that their time evolution is unitary. For a system known to be in state K, the ‘density matrix’ may be represented symbolically by Ψ_KΨ_K^* (also written |Ψ_K > < Ψ_K|) and in reality is an operator, thus, acting on an arbitrary state vector Φ, the result will be ρ_KΦ = Ψ_K(Ψ_K^*Φ), or, in bra-ket notation

${\rho }_K|\mathrm{\Phi }>=|{\mathrm{\Psi }}_K><{\mathrm{\Psi }}_K|\mathrm{\Phi }>=c_K|{\mathrm{\Psi }}_K>(c_K=<{\mathrm{\Psi }}_K|\mathrm{\Phi }>\text{.}$

The number c_K is clearly the ‘component’ of |Φ > in the ‘direction’ |Ψ_K >, when Φ is expanded in the form Φ = Σ_L c_L Ψ_L; and the density operator is therefore a projection operator, with the characteristic property $\left({\rho }_{{}_K}^2={\rho }_K\right)\text{.}$ Thus,

${\rho }_K{\rho }_K=|{\mathrm{\Psi }}_K>\left(<{\mathrm{\Psi }}_K|{\mathrm{\Psi }}_K>\right)<{\mathrm{\Psi }}_K|=|{\mathrm{\Psi }}_K><{\mathrm{\Psi }}_K|={\rho }_K\text{.}$

When the particle variables q are introduced explicitly, ρ_K is represented as an integral operator, ρ_K → ρ_K(q; q′) = Ψ_K(q)Ψ_K^*(q′), whose effect on an arbitrary wavefunction Φ(q) is represented by

${\rho }_K\mathrm{\Phi }\left(q\right)=\mathit{\int }{\rho }_K\left(q;q^{\prime }\right)\mathrm{\Phi }\left(q^{\prime }\right)d{q}^{\prime }\text{.}$

Expectation values of all physical quantities A, B, …, with associated operators Â, $\widehat{B}$, … may then be expressed typically as

$<A>=<{\mathrm{\Psi }}_K|\widehat{A}|{\mathrm{\Psi }}_K>=\mathit{\int }{\mathrm{\Psi }}_K^{*}\left(q\right)\widehat{A}{\mathrm{\Psi }}_K\left(q\right)\mathit{dq}=\mathit{\int }{\left[{\widehat{A}}_{\mathit{\rho K}}\left(q;q^{\prime }\right)\right]}_{q^{\prime }\to q}\mathit{dq}\text{,}$

where q' → q means the primed and unprimed variables are identified after the operation – so that the operator works only on the wavefunction and not on its complex conjugate. The expectation value expression is thus expressed formally as a trace, with q, q' in the role of row and column indices.

Another important operator is the transition operator, ρ_KL = Ψ_KΨ_L^*, connecting two states (Ψ_K, Ψ_L), which is represented by the integral kernel Ψ_K(q)Ψ_L^*(q′). And an off-diagonal matrix element of any operator  may then be expressed as

$A_{\mathit{LK}}=<{\mathrm{\Psi }}_L|\widehat{A}|{\mathrm{\Psi }}_K>={\displaystyle \int {\mathrm{\Psi }}_L^{*}\left(q\right)\widehat{A}{\mathrm{\Psi }}_K\left(q\right)\mathit{dq}}={\displaystyle \int {\left[\widehat{A}{\rho }_{\mathit{KL}}\left(q;q^{\prime }\right)\right]}_{q^{\prime }\to q}\mathit{dq}\text{.}}$

Clearly ρ_K = ρ_KK is the special case L = K of ρ_KL – in which it is immaterial whether the single or double subscript is used.

If a discrete representation is adopted, by expressing all functions {Ψ_K} in terms of a complete set {Φ_K} and collecting any set of expansion coefficients as a column vector c_K, all equations turn into matrix equations, in the usual way; for example, when $\widehat{C}=\widehat{A}\widehat{B}$ there is a corresponding matrix equation C = AB, where the elements of the (infinite) matrices are defined as above.

The density matrices play a special role in statistical mechanics; but also in any situation in which we possess incomplete information about some general system. In that case, the system will not be in a pure state and will thus not be represented by a wavefunction: instead, the ‘mixed state’ must be represented by a density matrix. The density matrix will then refer to an ensemble of identical systems of which a fractional number w_K are in the definite state Ψ_K; and the ensemble density matrix will be

$\rho ={\displaystyle \sum _K{w}_K{\mathrm{\Psi }}_K{\mathrm{\Psi }}_K^{*}\text{.}}$

Since Σ_Kw_K = 1, a system in which all the w_K are equal has ρ = ρ_K – the density matrix for a single system, definitely known to be in state K; but when more than one state is compatible with any given (often limited) knowledge of the system (e.g. that it be in a state with given energy E, without reference to other constants of the motion), the above sum does not reduce to a single term with w_K = 1. The criterion for the possibility of reduction to a pure state (irrespective of the particular representation chosen) is that the density operator be idempotent, ρ² = ρ. When this criterion is not satisfied (e.g. when there are many, equally accessible, states (K) of the same given energy, the ensemble expectation value of any quantity A, with operator Â, will be

$\overline{A}=\mathrm{tr}\rho \widehat{A}={\displaystyle \sum _K{w}_K\left(\mathrm{tr}{\rho }_K\widehat{A}\right)}={\displaystyle \sum _K{w}_K<{\mathrm{\Psi }}_K|\widehat{A}|{\mathrm{\Psi }}_K>}\text{.}$

Evidently a ‘double averaging’ is involved, the quantum mechanical averaging implicit in the expectation value and the ensemble averaging associated with our inability to specify more completely the condition of an individual system. The time-honoured axiom of statistical mechanics (that of ‘equal a priori probabilities and random a priori phases’), whose validity is confirmed by inumerable applications in fields extending from biology to stellar structure, then asserts that the correct density matrix to use will be

$\rho =\left(\frac{1}{g}\right){\displaystyle \sum _K{\rho }_K}\text{,}$

where g is the number of terms in the sum (e.g. the number of distinct terms of precisely specified energy).

3) Reduced density matrices; spin correlation

So far, no assumptions have been made about the precise form of the system of interest – it may be an electron or an arbitrary many-particle system. At this point we specialize to an N-electron molecule, introducing explicitly the variables (space and spin coordinates), collectively x_i = r_i, s_i for electron i. With a small notational change, the wavefunction for state K of the system will be

${\mathrm{\Psi }}_K={\mathrm{\Psi }}_K\left({\mathrm{x}}_1,{\mathrm{x}}_2,\dots {\mathrm{x}}_N\right)={\mathrm{\Psi }}_K\left(\mathrm{x}\right)\text{,}$

the second form (with no subscripts) sometimes being used for brevity. The system density matrix, for pure state K, will then be (adding a superscript ‘sys’ to avoid confusion in what follows) ρ_K^sys(q; q′) = Ψ_K(q)Ψ_K^*(q′) or more fully

${\rho }_K^{\mathrm{sys}}\left(\mathrm{x};{\mathrm{x}}^{\prime }\right)={\mathrm{\Psi }}_K\left({\mathrm{x}}_1,{\mathrm{x}}_2,\dots {\mathrm{x}}_N\right){\mathrm{\Psi }}_K^{*}\left({\mathrm{x}}_1^{\prime },{\mathrm{x}}_2^{\prime },\dots {\mathrm{x}}_N^{\prime }\right)$

– a function of both primed and unprimed variables. The so-called ‘diagonal element’ of the density matrix is obtained simply by removing the primes; and measures the probability density for finding electron 1 at point x₁, electron 2 simultaneously at point x₂, and so on. Since electrons are indistinguishable, the probability of finding volume elements $d{\mathrm{x}}_1,d{\mathrm{x}}_2,\dots {\underset{\dot{}}{\mathrm{x}}}_N$ simultaneously occupied by N particles in any order will be N ! ρ_K^sys(x; x)dx.

Reduced density matrices, introduced by Husimi [9], yield corresponding probability densities for the presence of n(n < N) particles simultaneously in selected volume elements $d{\mathrm{x}}_1,\dots {\underset{\dot{}}{\mathrm{x}}}_n:$ thus, for n = 1, the probability/unit volume of finding an electron (no matter which) at x₁ will be obtained by integrating N ! ρ_K^sys(x; x) over the positions of all N – 1 volume elements dx₂, …dx_N and dividing by (N – 1)! (to avoid multiple counting). The quantity so defined is the ‘one-particle reduced density matrix’: more explicitly, it becomes

$\rho \left(\mathit{KK}|{\mathrm{x}}_1;{\mathrm{x}}_1^{\prime }\right)=N{\displaystyle \int {\mathrm{\Psi }}_K\left({\mathrm{x}}_1,{\mathrm{x}}_2,\dots {\mathrm{x}}_N\right){\mathrm{\Psi }}_K^{*}\left({\mathrm{x}}_1^{\prime },{\mathrm{x}}_2,\dots {\mathrm{x}}_N\right)d{\mathrm{x}}_{2}d{\mathrm{x}}_3\dots d{\mathrm{x}}_N\text{.}}$

The n-particle density matrices are widely used in molecular quantum mechanics (e.g.[10–12], where further references may be found. A well known property of the one-particle density is that it relates matrix elements and expectation values of one-particle operators directly to the density: thus the kinetic energy (in state K) of all N electrons in any given system is expressible as

$<K|{\displaystyle \sum _i\widehat{T}\left(i\right)|K}>={{\displaystyle \int \left[\widehat{T}\left(1\right)\rho \left(\mathit{KK}|{\mathrm{x}}_1;{\mathrm{x}}_1^{\prime }\right)\right]}}_{1^{\prime }\to 1}d{\mathrm{x}}_1\text{,}$

where $\widehat{T}$(i) denotes the kinetic energy operator for the ith particle and the prime is removed after the operation.

The one-electron density matrix gives rise to others, for example P(KK|r₁; r₁′), whose diagonal element gives the probable number of electrons per unit volume (without reference to spin) in the spatial volume element dr₁ at point r₁; and the spin density matrix Q_z(KK|r₁; r₁′), whose diagonal element gives the contribution to the expectation value of the total spin z-component, $<{\widehat{S}}_z>$, associated with the same volume element. These functions are related to ρ(KK|x₁; x₁′) as follows:

$P\left(\mathit{KK}|{\mathrm{r}}_1;{\mathrm{r}}_1^{\prime }\right)={{\displaystyle \int \left[\rho \left(\mathit{KK}|{\mathrm{x}}_1;{\mathrm{x}}_1^{\prime }\right)\right]}}_{s_1^{\prime }=s_1}d{s}_1\text{,}$

$Q_z\left(\mathit{KK}|{\mathrm{r}}_1;{\mathrm{r}}^{\prime }\right)={\displaystyle \int {\left[{\widehat{S}}_z{\left(1\right)}_{\rho }\left(\mathit{KK}|{\mathrm{x}}_1;{\mathrm{x}}_1^{\prime }\right)\right]}_{s_1^{\prime }=s_1}}d{s}_1\text{.}$

It is important to note that, while P is a scalar density, Q_z is one component of a vector density³, the components transverse to the quantization axis being defined in a similar way. Analogous transition densities, in which KK is replaced by KL, are required in discussing transitions between states K and L of the system, but are not needed in the present work.

It will be necessary to discuss also spin correlation: for if spins S(1), S(2),… S(N) are coupled, to a resultant S, then the expectation value of the squared total spin in state K will be

$<K|\mathrm{S}.\mathrm{S}|K>=<K|{\displaystyle \sum _i\mathbf{S}\left(i\right)}\cdot \mathbf{S}\left(i\right)|K>+<K|{\displaystyle \sum _{i\ne j}\mathbf{S}\left(i\right)\cdot \mathbf{S}\left(j\right)}|K>$

and, while the first term involves only a one-electron operator working on the variables x_i, the second term contains the two-electron operator

$\mathbf{S}\left(i\right)\cdot \mathbf{S}\left(j\right)={\widehat{S}}_x\left(i\right){\widehat{S}}_x\left(j\right)+{\widehat{S}}_y\left(i\right){\widehat{S}}_y\left(j\right)+{\widehat{S}}_z\left(i\right){\widehat{S}}_z\left(j\right)\text{.}$

Every 1-electron term in (13) reduces to $\frac{3}{4}$ (i.e. s(s + 1) with s =$\frac{1}{2}$), giving a total $\frac{3}{4}$N. It is the scalar product of the different spins in (13) that describes their coupling to a resultant, with quantum number S; and discussion of the last term in (13) requires knowledge of the two-electron density matrix, which will be denoted by π(KK|x₁, x₂; x₁′, x₂′). This is defined (cf.(9)) by

$\mathrm{\pi }\left(\mathit{KK}|{\mathrm{x}}_1,{\mathrm{x}}_2;{\mathrm{x}}_1^{\prime },{\mathrm{x}}_2^{\prime }\right)=N\left(N-1\right){\displaystyle \int {\mathrm{\Psi }}_K}\left({\mathrm{x}}_1,{\mathrm{x}}_2,\dots {\mathrm{x}}_N\right){\mathrm{\Psi }}_K^{*}\left({\mathrm{x}}_1^{\prime },{\mathrm{x}}_2^{\prime },\dots {\mathrm{x}}_N\right)d{\mathrm{x}}_3\dots d{\mathrm{x}}_N\text{.}$

As in the case of ρ(KK|x₁; x₁′) a number of spatial densities may be derived by spin integration (the best known being the ‘pair density’ which gives the probability of volume elements dr₁, dr₂, at points r₁, r₂, simultaneously holding particles).

A contribution to the expectation value of a spin scalar product may be associated with every pair of volume elements in space through a ‘coupling density’, Q_c, defined by [11]

$Q_c\left(\mathit{KK}|{\mathrm{r}}_1,{\mathrm{r}}_2;{\mathrm{r}}_1^{\prime }{\mathrm{r}}_2^{\prime }\right)={\displaystyle \int [\mathbf{S}\left(1\right)\cdot \mathbf{S}\left(2\right)\mathrm{\pi }{\left(\mathit{KK}|{\mathrm{r}}_1,s_1,{\mathrm{r}}_2,s_2;{\mathrm{r}}_1^{\prime },s_1^{\prime },{\mathrm{r}}_2^{\prime },s_2^{\prime }\right)}_{s_1^{\prime },s_2^{\prime }\to s_1,s_2}}d{s}_{1}d{s}_2\text{.}$

The key property of this function is that the diagonal element, denoted for brevity by Q_c(KK|r₁, r₂), integrated over all positions of points r₁ and r₂ , will give a numerical measure of the spin coupling:

$<{\displaystyle \sum _{i\ne \mathrm{j}}\mathbf{S}\left(i\right)\cdot \mathbf{S}\left(j\right)}>={\displaystyle \int Q_c}(\mathit{KK}|\left({\mathrm{r}}_1,{\mathrm{r}}_2\right)d{\mathrm{r}}_{1}d{\mathrm{r}}_2\text{.}$

This coupling density allows one to give a rather precise meaning to the probable degree of coupling between the spins of electrons occupying different volume elements in space.

The densities introduced in (12) and (16) may be interpreted in terms of the various ‘spinless components’ of the 1- and 2-body density matrices: the latter may be written, for brevity, in the forms

$\rho =P_{\mathrm{\alpha };\mathrm{\alpha }}\left(\mathit{\alpha \alpha }*\right)+P_{\alpha ;\beta }\left(\mathit{\alpha \beta }*\right)+P_{\beta ;\alpha }\left(\mathit{\beta \alpha }*\right)+P_{\beta ;\beta }\left(\mathit{\beta \beta }*\right)\text{,}$

where, for example, the first term stands for P_α;α(r₁; r₁′)α(s₁)α(s₁′); and

$\mathrm{\pi }={\mathrm{\Pi }}_{\mathit{\alpha \alpha };\mathit{\alpha \alpha }}\left(\mathit{\alpha \alpha \alpha }*\alpha *\right)+{\mathrm{\Pi }}_{\mathit{\alpha \alpha };\mathit{\alpha \beta }}\left(\mathit{\alpha \alpha \alpha }*\beta *\right)+\dots +{\mathrm{\Pi }}_{\mathit{\beta \beta };\mathit{\beta \beta }}\left(\mathit{\beta \beta \beta }*\beta *\right)$

where Π_αα;αα(ααα * α *) means Π_αα;αα(r₁, r₂; r₁′, r₂′)(α(s₁)α(s₁)α(s₂)α * (s₁′)α * (s₂′), and so on. For states of definite total spin (quantum numbers S, M_S), only the first and last terms in (18) are non-zero; whereas only 6 of the 16 possible terms are present in (19). The diagonal elements of the spatial components in (18) have an immediate physical significance as probability densities: for example⁴,

$P_{\alpha }\left({\mathrm{r}}_1\right)=P_{\alpha ;\alpha }\left({\mathrm{r}}_1;{\mathrm{r}}_1\right)$

is the probability per unit volume of finding an up-spin electron at point r₁. Similarly, in (19),

${\mathrm{\Pi }}_{\mathit{\alpha \beta }}\left({\mathrm{r}}_1,{\mathrm{r}}_2\right)={\mathrm{\Pi }}_{\mathit{\alpha \beta };\mathit{\alpha \beta }}\left({\mathrm{r}}_1,{\mathrm{r}}_2;{\mathrm{r}}_1,{\mathrm{r}}_2\right)$

is the probability density for finding an up-spin electron at point r₁ and a down-spin electron simultaneously at point r₂.

It is essential to note that the labels on the variables do not refer to the electrons, but rather to points in space, which are chosen by an observer and are physically distinguishable. The Pauli principle has been respected from the start by insisting that |Ψ|² be invariant against any permutation of ‘electron labels’.

On removing the primes in equations (18) and (19) and integrating over spin, one obtains the spinless densities:

$P\left({\mathrm{r}}_1\right)=P_{\alpha }\left({\mathrm{r}}_1\right)+P_{\beta }\left({\mathrm{r}}_1\right)\text{,}$

which is the probability density for finding an electron at r₁, a sum of up-spin and down-spin contributions; while

$\mathrm{\Pi }\left({\mathrm{r}}_1,{\mathrm{r}}_2\right)={\mathrm{\Pi }}_{\mathit{\alpha \alpha }}\left({\mathrm{r}}_1,{\mathrm{r}}_2\right)+{\mathrm{\Pi }}_{\mathit{\alpha \beta }}\left({\mathrm{r}}_1,{\mathrm{r}}_2\right)+{\mathrm{\Pi }}_{\mathit{\beta \alpha }}\left({\mathrm{r}}_1,{\mathrm{r}}_2\right)+{\mathrm{\Pi }}_{\mathit{\beta \beta }}\left({\mathrm{r}}_1,{\mathrm{r}}_2\right)\text{,}$

showing that the pair density is also a sum of contributions from the various spin situations – both up, one up one down, or both down.

The spin density and the coupling density may be presented in a similar way, as follows from the definitions (12) and (16).

5) Dissociation of the hydrogen molecule

The energy curves for the singlet ground state and the first excited triplet state of the hydrogen molecule have well known forms. The singlet curve shows a deep minimum at R ~ 1.4a₀⁶ and then rises to E_h (the energy of two isolated hydrogen atoms) as R → ∞: the triplet curve shows no minimum, falling monotonically to the same asymptotic limit. In general the energies are only approximate (being those of Heitler and London [13]), but at R → ∞ they become exact (for a non-relativistic Born-Oppenheimer Hamiltonian). The main concern here will be with this asymptotic region in which the system approaches dissociation into two subsystems: when, for example, R = 20.0a₀ the separation between the singlet and triplet curves is only 2.69 × 10⁻⁷E_h and the crucial question is then whether the electrons still retain the coupling to S = 0 appropriate to the equilibrium ground state. At this point the integral S_AB, which measures the overlap between the two subsystems is also small (0.962 × 10⁻⁶); and as R increases both quantities diminish exponentially to zero. Nor is it reasonable any longer to regard the ‘molecule’ as an isolated system in a stationary eigenstate; for it is exposed to random fluctuations of the ‘heat bath’ (the rest of the universe!) in which it is embedded. Indeed, between the remote parts of the system there is room for eight more hydrogen atoms! In such a situation, as indicated already, the condition of the system is more correctly represented by means of a mixed-state density operator, not by a single energy eigenfunction.

The validity of using a statistical ensemble to represent an incompletely specified system is fundamental and is not in question. The important question is: which ‘accessible states’ are compatible with our limited information about the system? In the example under discussion there are four states that lie within an energy interval ΔE of the order 10⁻⁷E_h, among which there appears to be no possibility of distinguishing experimentally. The difficulty is clearly connected with the energy-time uncertainty relation, ΔEΔt ~ ħ, which has been extensively discussed, from many points of view (see [14] for a survey). For present purposes it is enough to recall only the simplest approach [15]. One considers the time evolution of a (non-stationary) wavefunction, represented as a sum of two states Ψ₁ and Ψ₂ with time factors exp –iE₁t/ħ and exp –iE₂t/ħ, respectively: the square of the wavefunction then oscillates with period

$\mathrm{\tau }=\frac{\hslash }{\left|\left(E_1-E_2\right)\right|}\text{,}$

which is a ‘characteristic time’ for change of the physical properties of the system. To determine whether a system initially in State 1 is still in State 1 after a certain lapse of time, the energy measurement must be repeated within a time interval Δt, small compared with τ; otherwise there is no guarantee that the same value will be found (i.e. that a transition has not occurred). In the hydrogen molecule example, with R = 20a₀, the characteristic time (which in essence measures the lifetime of the state) turns out to be 0.90 × 10⁻¹⁰ ; and the conclusion is that, when such stringent requirements on state preparation are not fulfilled, all states with energies in the small interval ΔE should be treated on an equal footing in setting up a density operator of the type (6).

First let us discuss the case in which singlet and triplet states are well separated in energy and are represented by eigenstates of the Hamiltonian and the total spin operators Ŝ², Ŝ_z. It is verified immediately (noting that the functions (26) and (29) are normalized to unity on integrating over both variables) that

${\displaystyle \int Q_c\left({\mathrm{r}}_1,{\mathrm{r}}_2\right)d{\mathrm{r}}_{1}d{\mathrm{r}}_2=S\left(S+1\right)-\frac{3}{4}N}$

for all states. It is also informative to consider the origin of the main contributions to the integrals: thus, when volume element dr₁ is in the region of nucleus ‘a’ A(r₁) is large and B(r₁) is small; and the density of spin angular momentum (when nonzero) has the same form as the electron density P(r₁), but with up-spin character in state ‘t+’, down-spin in state ‘t-’. The density of spin coupling, on the other hand, arises mainly when the electrons occupy volume elements dr₁ and dr₂ which are on different centres; this is true for both singlet and triplet coupling and is a crucial embarrasment because it suggests that coupled spins will stay coupled forever, no matter how far apart their parent atoms may move.

It is the non-zero value of the integral in (31), irrespective of the separation of A and B, that violates any principle of locality: it appears as a direct result of applying standard quantum mechanics and seems to imply some kind of ‘action at a distance’ that keeps the two spins coupled. It should be noted, however, that the postulate of Bohm and Bell – that the sytem is “disintegrated by some kind of process that does not change the total angular momentum” – effectively prescribes this result at the outset. It is usually claimed that non-locality is a consequence of quantum mechanics; but, more precisely, it is a consequence of insisting that the system stays forever in its initial spin eigenstate. Let us now remove such restrictions.

On removing the atoms to a considerable distance, such that the singlet and triplet energies fall within a sufficiently small interval, the use of a representative ensemble becomes mandatory. The density matrix (6) then leads to ensemble averaged densities, ${\overline{Q}}_z$ and ${\overline{Q}}_c$, as follows:

${\overline{Q}}_z\left({\mathrm{r}}_1\right)=\frac{1}{4}{Q}_z^s\left({\mathrm{r}}_1\right)+\frac{1}{4}{Q}_z^{t0}\left({\mathrm{r}}_1\right)+\frac{1}{4}{Q}_z^{t,+1}\left({\mathrm{r}}_1\right)+\frac{1}{4}{Q}_z^{t,-1}\left({\mathrm{r}}_1\right)=0$

and

${\overline{Q}}_c\left({\mathrm{r}}_1,{\mathrm{r}}_2\right)=\frac{1}{4}{Q}_c^s\left({\mathrm{r}}_1,{\mathrm{r}}_2\right)+\frac{1}{4}{Q}_c^{t0}\left({\mathrm{r}}_1,{\mathrm{r}}_2\right)+\frac{1}{4}{Q}_c^{t,+1}\left({\mathrm{r}}_1,{\mathrm{r}}_2\right)+\frac{1}{4}{Q}_c^{t,-1}\left({\mathrm{r}}_1,{\mathrm{r}}_2\right)=0$

In other words, as soon as the system breaks into two subsystems any initial spin density will fall to zero, along with any initial spin coupling between the subsystems. The subsystems are then truly independent in the sense that all expectation values for either may be calculated without reference to the other; and that the spin coupling density, which connected the two, is now everywhere zero.

This example clearly shows that the EPR conflict is not between locality and quantum mechanics but is simply between locality and non-locality – both alternatives following from orthodox quantum mechanics, provided the appropriate representative ensemble (pure or mixed) is employed.

6) The general case

A study of the hydrogen molecule hardly provides a sufficient basis for formulating general principles concerning the separation of a system into subsystems. In general one is concerned with the interaction of two subsystems, A and B, in spin states with quantum numbers (S_A, M_A) and (S_B, M_B), whose total spin vectors (S^A,S^B are coupled to a resultant S, yielding a set of states with quantum numbers S,M (M = S, S – 1, … – S). When A and B are close together and their interaction is appreciable, states that differ in S are usually well spaced in energy. The general question to be asked is again: What happens to the spin coupling between the different systems when they Eire pulled apart to a large distance? For the hydrogen molecule, there were only two spins and two possible couplings (S = 0, 1); exact wave functions for the separate subsystems were available; and the 2-electron wavefunction could be written as a product of space and spin factors, the Pauli principle being satisfied by choosing one factor symmetric and the other antisymmetric. In in the general case no such simplifications apply.

Let us now study the general case, postulating the existence of exact eigenfunctions Φ_SA,_MA Φ_SB, _MBfor two quite arbitrary subsystems (many-electron atoms or molecules), with energy eigenvalues E_A, E_B; and suppose all functions to be fully antisymmetric in electron indices. It is then possible to set up spin-coupled linear combinations of the (2S_A + 1)(2S_B + 1) product functions arising from different choices of M_A, M _B : these will be

$\begin{array}{c}{\mathrm{\Phi }}_{S,M}\left({\mathrm{x}}_1,{\mathrm{x}}_2,\dots {\mathrm{x}}_N\right)={\left(-1\right)}^{\left(S_B-S_A-M\right)}{\left(2S+1\right)}^{\frac{1}{2}}{\displaystyle \sum _{M_A,M_B}\left(\begin{array}{ccc}\hfill S_A\hfill & \hfill S_B\hfill & \hfill S\hfill \\ \hfill M_A\hfill & \hfill M_B\hfill & \hfill -M\hfill \end{array}\right)}\\ \times {\mathrm{\Phi }}_{S_A,M_A}\left({\mathrm{x}}_1,{\mathrm{x}}_2,\dots {\mathrm{x}}_{N_A}\right){\mathrm{\Phi }}_{S_B,M_B}\left({\mathrm{x}}_{\overline{1}},{\mathrm{x}}_{\overline{2}},\dots {\mathrm{x}}_{{\overline{N}}_B}\right)\text{,}\end{array}$

where variables with labels 1,2, … N_A refer to electrons of subsystem A, while those with labels $\overline{1},\overline{2},\dots {\overline{N}}_B$$\left(\mathrm{with}\overline{k}=N_A+k\right)$ refer to subsystem B. The round-bracket quantity in (33) is a Wigner 3j symbol.

The vector-coupled function Φ_S,M is not properly antisymmetric against permutations which exchange electrons between the A and B subsystems. But this may be remedied by applying the ‘antisymmetrizer’

$\widehat{A}={\left(N!\right)}^{-1}{\displaystyle \sum _{\widehat{P}}{\in }_{\widehat{P}}}\widehat{P}=\left(N_A!N_B!/N!\right){\widehat{A}}^{\prime }{\widehat{A}}_A{\widehat{A}}_B\text{,}$

where Â_A, Â_B are subsystem antisymmetrizers (which will leave Φ_SA,_MA: Φ_SB,_MAunchanged), while ${\widehat{A}}^{\prime }$ denotes a coset sum of all (multiple) transpositions of variables between subsystem A and subsystem B. On applying the operator (34) to the vector-coupled function (33) we obtain a fully antisymmetric wavefunction

${\mathrm{\Psi }}_{S,M}=K\widehat{A}{\mathrm{\Phi }}_{S,M}\left(K={\left(N!/N_A!N_B!\right)}^{\frac{1}{2}}\right)\text{,}$

where a convenient normalizing factor K has been added.

Expressions for the density functions P(SS|r₁; r₁′) and Π(SS|r₁, r₂; r₁′, r₂′), which (with the usual Hamiltonian) determine the total electronic energy of the system, are available elsewhere [16] and the derivations will not be repeated. Briefly, every function is a finite sum of terms arising from 0,1,2, … N_min (N_min being the smaller of N_A,N_B) electron transpositions between the subsystems, and each term may be written as a functional containing densities for the separate subsystems. Such sums converge rapidly and in discussing molecular interactions it is seldom necessary to go beyond single interchanges. In the present context, where interest is focused on long range interactions, the effects of electron exchange are quite negligible and it is sufficient to consider zero-interchange contributions to all expectation values: this means that (33) in itself provides a satisfactory wavefunction for studying the spin coupling when A and B are remote.

To obtain the spin coupling function Q_c for any given vector-coupled state of the composite system AB, when A and B are remote, we use (33) to evaluate the expectation value of the total spin operator S². Thus,

$<{\mathrm{\Phi }}_{S,M}|{\mathbf{S}}^2|{\mathrm{\Phi }}_{S,M}>=<{\mathrm{\Phi }}_{S,M}|\left({\mathbf{S}}_A^2+{\mathbf{S}}_B^2+2{\mathbf{S}}_A\cdot {\mathbf{S}}_B\right)|{\mathrm{\Phi }}_{S,M}>\text{.}$

The operator ${\mathbf{S}}_A^2={\displaystyle {\sum }_{i=1,N_A}}{\mathbf{S}}^2\left(i\right)$ represents a contribution from the electrons of subsystem A, the contribution from B assuming a similar form with A replaced by B and the summation index running from $\overline{j}=\overline{1}\mathrm{to}{\overline{N}}_B\text{.}$ The first two terms in the expectation value (36) thus arise from the internal spin couplings in the separate subsystems and should reduce to S_A(S_A + 1) and S_B(S_B + 1), respectively. The third contribution arises from the spin coupling between the electrons of different subsystems: to evaluate it one may use the methods of Ref.[17]. Thus,

$\begin{array}{l}<{\mathrm{\Phi }}_{S,M}|{\mathbf{S}}_A\cdot {\mathbf{S}}_B|{\mathrm{\Phi }}_{S,M}>=<{\mathrm{\Phi }}_{S,M}|{\displaystyle \sum _{i=1}^{N_A}{\displaystyle \sum _{\overline{j}=\overline{1}}^{{\overline{N}}_B}\mathbf{S}\left(i\right)\cdot \mathbf{S}\left(\overline{j}\right)}}|{\mathrm{\Phi }}_{S,M}>\\ ={\left(-1\right)}^{\left(S_A+S_B+S\right)}\left\{\begin{array}{rrr}\hfill S_A& \hfill S_B& \hfill S\\ \hfill S_B& \hfill S_A& \hfill 1\end{array}\right\}{\left(\begin{array}{rrr}\hfill S_A& \hfill 1& \hfill S_A\\ \hfill -S_A& \hfill 0& \hfill S_A\end{array}\right)}^{-1}{\left(\begin{array}{rrr}\hfill S_B& \hfill 1& \hfill S_B\\ \hfill -S_B& \hfill 0& \hfill S_B\end{array}\right)}^{-1}\\ \times <{\mathrm{\Phi }}_{S_A,S_A}{\mathrm{\Phi }}_{S_B,S_B}|{\displaystyle \sum _{i,\overline{j}}{\widehat{S}}_z\left(i\right){\widehat{S}}_z\left(\overline{j}\right)|{\mathrm{\Phi }}_{S_A,S_A}{\mathrm{\Phi }}_{S_B,S_B}}>\text{,}\end{array}$

where the scalar product $\mathbf{S}\left(i\right)\cdot \mathbf{S}\left(\overline{j}\right)$ was written in terms of rank-1 sphersical tensor operators $\left({\widehat{S}}_k,k=0,\pm 1\right)$ in order to exploit well known theorems [17]: the matrix element on the right now refers only to ‘standard’ states, with M_A = S_A, M_B = S_B, and is preceded by a Wigner 6j symbol and two 3j symbols.

The matrix element is easily related to the spin densities in subsystems A and B; thus

$\begin{array}{l}<{\mathrm{\Phi }}_{S_A,S_A}|{\displaystyle \sum _i{\widehat{S}}_z\left(i\right)|{\mathrm{\Phi }}_{S_A,S_A}}>={\displaystyle \int {\mathrm{\Phi }}_{S_A,S_A}^{*}{N}_A{\widehat{S}}_z\left(1\right){\mathrm{\Phi }}_{S_A,S_A}}d{\mathrm{r}}_{1}d{s}_{1}d{\mathrm{x}}_2\dots d{\mathrm{x}}_{N_A}\\ ={\displaystyle \int Q_z}\left(S_A|{\mathrm{r}}_1\right)d{\mathrm{r}}_1\text{,}\end{array}$

with a similar expression for the B-factor.

The factor involving the Wigner coefficients may also be put into a simpler form: it is invariant against rotation of the axis of quantization and must therefore be expressible in terms of invariants formed from the total spin operators of the two subsystems. On denoting the numerical factor in (37) by f₁(S_A, S_B, S), it follows easily [16] that

$f_1\left(S_A,S_B,S\right)=\frac{<S,M|{\mathbf{S}}_A\cdot {\mathbf{S}}_B|S,M>}{S_A{S}_B}\text{.}$

The contribution to < S ⋅ S > that arises from electrons belonging to the different subsystems is thus

$<{\mathrm{\Phi }}_{S,M}|{\mathbf{S}}_A\cdot {\mathbf{S}}_B|{\mathrm{\Phi }}_{S,M}>={\displaystyle \int Q_c^{\mathit{AB}}}\left({\mathrm{r}}_1,{\mathrm{r}}_2\right)d{\mathrm{r}}_{1}d{\mathrm{r}}_2\text{,}$

where

$Q_c^{\mathit{AB}}\left({\mathrm{r}}_1,{\mathrm{r}}_2\right)=<S,M|{\mathbf{S}}_A\cdot {\mathbf{S}}_B|S,M>\frac{Q_z\left(S_A|{\mathrm{r}}_1\right)}{S_A}\frac{Q_z\left(S_B|{\mathrm{r}}_1\right)}{S_B}d{\mathrm{r}}_{1}d{\mathrm{r}}_2\text{.}$

The integrations in (40) obviously yield unity, since (41) contains two normalized spin density factors: in fact (40) is a precise analogue of (25) and (28) in the hydrogen molecule example. In any spin eigenstate the coupling density (41) will be nonzero; but the integrations over all space will evidently yield a simple scalar product coupling between the subsystems A and B, however complicated they may be. This result is quite independent of the distance between A and B.

The contributions to < S ⋅ S > that arise from electrons belonging to the same subsystem follow immediately. Thus, for A, the expectation value of ∑ _i ≠ jS(i) ⋅ S(j) (i, j both belonging to the same subsystem) the expectation value becomes

$N_A\left(N_A-1\right){\displaystyle \int {\mathrm{\Phi }}_{S_A,M_A}^{*}}\left({\mathrm{x}}_1,{\mathrm{x}}_2,\dots \right)\mathbf{S}\left(1\right)\cdot \mathbf{S}\left(2\right){\mathrm{\Phi }}_{S_A,M_A}\left({\mathrm{x}}_1,{\mathrm{x}}_2,\dots \right)d{\mathrm{x}}_{1}d{\mathrm{x}}_2\dots d{\mathrm{x}}_{N_A}$

and this is easily seen to be

${\displaystyle \int Q_c^A\left({\mathrm{r}}_1,{\mathrm{r}}_2\right)d{\mathrm{r}}_1}d{\mathrm{r}}_2\text{.}$

There is a similar result for subsystem B and both are independent of M_A, M_B.The vector-coupled state Φ_S,M thus yields ‘internal’ contributions

$<{\mathrm{\Phi }}_{S,M}|{\mathbf{S}}_A\cdot {\mathbf{S}}_A|{\mathrm{\Phi }}_{S,M}>={\displaystyle \int Q_c^A\left({\mathrm{r}}_1,{\mathrm{r}}_2\right)d{\mathrm{r}}_{1}d{\mathrm{r}}_2}=S_A\left(S_A+1\right)\text{,}$

$<{\mathrm{\Phi }}_{S,M}|{\mathbf{S}}_B\cdot {\mathbf{S}}_B|{\mathrm{\Phi }}_{S,M}>={\displaystyle \int Q_c^B\left({\mathrm{r}}_1,{\mathrm{r}}_2\right)d{\mathrm{r}}_{1}d{\mathrm{r}}_2}=S_B\left(S_B+1\right)\text{,}$

which arise from strictly separate coupling functions, one localized in subsystem A and the other in B.

In the absence of any spin coupling beteen the remote fragments, A and B, the expectation value < S² > would be simply S_A(S_A + 1) + S_B(S_B + 1), as if neither subsystem ‘knew’ anything of the other. This would be the ‘common sense’ result. The fact that (40), on the contrary, takes a non-zero value in any state of definite total spin is the ‘action at a distance’ result that Einstein found totally unacceptable.

It is now easy to show that in the long range limit, where the energy curves for the (2S_A + 1) (2S_B + 1) alternative spin couplings approach indefinitely closely, the ensemble-averaged coupling density derived from (41) becomes everywhere zero. The spatial density factors in (41) are in fact quite independent of coupling scheme and the averaging thus concerns only the expectation value < S, M|S_A ⋅ S_B|S, M > over all S, M: the average value of the latter is zero, by simple angular momentum theory, and this establishes that the ensemble-averaged values of the ‘action at a distance term’ (40) and its related spin-coupling density approach zero as A and B separate. It is also possible to estimate a good order of magnitude for the separation of A and B at which the transition from non-locality to locality will take place. The analogue of the squared overlap S_AB² in Section 5 is the quantity [16]

$\begin{array}{l}{S}_{\mathit{AB}}^{\left(1\right)}=\frac{1}{2}{\displaystyle \int P_A\left(S_A{S}_A|{\mathrm{r}}_1,{\mathrm{r}}_1^{\prime }\right)}{P}_B\left(S_B{S}_B|{\mathrm{r}}_1^{\prime },{\mathrm{r}}_1\right)d{\mathrm{r}}_{1}d{\mathrm{r}}_1^{\prime }\\ +2f_1\left(S_A,S_B,S\right){\displaystyle \int Q_{z,A}\left(S_A{S}_A|{\mathrm{r}}_1,{\mathrm{r}}_1^{\prime }\right)d{\mathrm{r}}_1}d{\mathrm{r}}_1^{\prime }{Q}_{z,B}\left(S_B{S}_B|{\mathrm{r}}_1^{\prime },{\mathrm{r}}_1\right)d{\mathrm{r}}_{1}d{\mathrm{r}}_1^{\prime }\text{,}\end{array}$

which contains electron and spin densities for the separate systems in their ground states. For the two hydrogen atoms in Section 5, this single interchange contribution to a generalized overlap correctly reduces to 2S_AB² and at R = 20.0a₀ takes the value 2 × 10⁻¹². A similar discussion, applied in the general case, then suggests that the distance at which (43) assumes a value less than, say, 10⁻¹² will provide a convenient measure of the ‘forgetting distance’ beyond which no spin coupling can persist.

7) Conclusion

The system considered in this paper is, again in the words of Bohm [3], “a molecule containing two atoms in a state in which the total spin is zero and the spin of each atom is $\frac{1}{2}$”: but the restriction to a singlet state and to $\mathrm{spin}‐\frac{1}{2}$ atoms has now been removed. The molecule is dissociated by separating the nuclei to a large distance and the course of the reaction AB → A + B is followed using standard quantum mechanics. In the general case, the wavefunction Ψ for AB is taken to be a spin-coupled antisymmetrized product of two factors Ψ_A, Ψ_B, which are ‘exact’ many-electron wavefunctions for free atoms A and B in states of total spin S_A,S_B, respectively. In the dissociation limit Ψ yields the correct total energy E = E_A + E_B; but it may be any one of (2S_A + 1)(2S_B + 1) accessible states, Ψ_S,M, obtained by coupling the spins S_A, S_Bto a resultant with S = S_A + S_B, S_A + S_B – 1, … |S_A – S_B| and M = S, S – 1, … – S, the energies of such states falling within an interval ΔE which tends to zero.

In this energy regime, the condition of the system is correctly represented not by any one state Ψ _S,Mbut rather by a quantum statistical ensemble in which all the accessible states appear with equal a priori weights and random a priori phases. The appropriate density operator is then

$\rho =\frac{{\displaystyle {\sum }_{S,M}{\mathrm{\Psi }}_{S,M}{\mathrm{\Psi }}_{S,M}^{*}}}{\left(2S_A+1\right)\left(2S_B+1\right)}$

and its use implies the recognition of chaotic mixing of the states whose energies lie within ΔE, which arises from arbitrarily weak interaction with the environment (or ‘heat bath’). In the case considered by Bohm, $S_A=S_B=\frac{1}{2}$ and there are 4 terms in ρ; corresponding to S = 0 (1 term) and S = 1 (3 terms). But for two nitrogen atoms, say, $S_A=S_B=\frac{3}{2}$ and there would be 16 terms – coming from S = 0 (1 term), S = 1 (3 terms), S = 2 (5 terms) and S = 3 (7 terms).

It has been established in Sect.6 that whenever it becomes necessary to employ a mixed (rather than pure) ensemble, with density operator (44), the interatomic spin-coupling density Q_c^AB (r₁,r₂) is everywhere zero and thus yields zero for the expectation value of the spin scalar product S_A ⋅ S_B: there can be no spin coupling between A and B. Two regimes may thus be distinguished:

(i) Well below the dissociation limit the system is well represented by a pure state, the ensemble degenerates into a single term with the same spin (e.g. S = 0) as the initial state, other states being energetically distant and therefore inaccessible under weak (‘heat bath’) perturbations. Throughout this regime the generally accepted conclusion holds: the spin coupling remains that of the molecular ground state, as if each atom ‘remembers’ its coupling to the other – even when A and B are rather distant. Non-locality is thus apparently confirmed. It could hardly be otherwise of course! – because the coupling is imposed at the outset by Bohm’s postulate that the molecule be “disintegrated by some process that does not change the total [spin] angular momentum”.

(ii) In the ‘ΔE’ regime, where use of the mixed ensemble is mandatory, the spin coupling between A and B falls to zero, only the mtraatomic couplings (to S_A and S_B, within atoms A and B, respectively) remaining intact. At this point A and B become completely independent, neither having any ‘recollection’ of any previous coupling in the molecule. Throughout the rest of this regime, as A and B separate to infinity, experiments may be performed separately on the two subsystems and it is guaranteed that the expectation values of all observables will coincide with those for the free atoms.

To summarize: Below the dissociation limit, the system AB will display non-locality; but beyond that limit locality will re-emerge, each of the subsystems (A,B) being restored to its original (free-atom) condition, irrespective of any previous interactions. In other words, locality and non-locality are simply two faces of the same quantum coin.

At this point is seems appropriate to add a few words on the subject of ‘physical reality’ and ‘mathematical models’ – the touchstone for the EPR paper and the 60 years of discussion that followed it. EPR stress that “an element of physical reality cannot be determined by a priori philosophical considerations but must be found by an appeal to results of experiments and measurements”: their approach is thus essentially pragmatic. Between this ‘reality’ and the ‘mathematical models’ we actually use stands the physical theory, in this case quantum mechanics, which operates with the elements of reality and enables one to draw new, and experimentally verifiable, conclusions. When the conclusions are verified the theory is considered ‘correct’ – or at least satisfactory. In fact, however, the theory (in anything approaching a complete form) is almost always impossible to apply, owing to its mathematical complexity; and it is here that the ‘mathematical model’ intrudes. Such a model represents an attempt to simplify the theory, often drastically, by discarding all details not deemed essential for the purpose in hand (e.g. the prediction of some new observable property or the derivation of some relationship among the observables). To construct an adequate model, delicate and highly subjective choices have to be made and the various models proposed aften lead to conflicting conclusions.

It has been argued that the mathematical model first put in concrete form by Bohm and then adopted by Bell and others (as a ‘standard’ formulation of the EPR experiment) does not do full justice to either quantum mechanics or physical reality. The system considered is said to be a molecule i.e. a many-electron system whose particles have masses, charges, positions, velocities and interactions: there is a Hamiltonian, whose associated operator governs the time evolution of the system and determines the energies of the stationary states and their dependence on molecular geometry as the system is dissociated into two fragments; and there are inviolable principles to be respected, notably the Pauli principle for fermions. These are all features of quantum mechanics that cannot be discarded (least of all in discussing a ‘real physical system’) except at the risk of tearing the whole fabric of the theory.

In the usual EPR model, the only variables considered are the six components of the two spins: all the rest has been thrown away. There are no masses, charges, positions, velocities, interactions, nor even particles! – only two disembodied spins. To use the imagery of ‘Schrodinger’s cat’, this is a ‘Lewis Carrol’s Cheshire cat’: the spin without the particle is like the grin without the cat.