Density functional (DF) theory rests on the two theorems of Hohenberg-Kohn (HK) [13]. The first of these states that for systems with a nondegenerate ground state and a given electron-electron interaction there is a one-to-one mapping between the external (local) potential and the ground state wave function as well as the diagonal one-electron density. Therefore the wave function is uniquely determined by the one-electron density, i.e. it is a functional of the density, and so are all properties, being ground state expectation values of the associated operators. In particular also the total energy and its components, such as the kinetic energy, are functionals of the density. The second HK theorem defines a density functional for the energy, E_v[r], for a system with given external potential v. This energy functional will have a minimum for the exact ground state density associated with that external potential.

It has not proven possible to find sufficiently accurate approximations for E_v[r], so that a single Euler-Langrage equation for the density would yield an accurate density and energy. In particular, it is very difficult to find a good density functional for the kinetic energy. Therefore applications of DF theory in chemistry invariably use the one-electron model of Kohn and Sham (KS). They introduced an auxiliary system of noninteracting electrons moving in a local potential called v_s(r). This potential has the property that the occupied KS orbitals give the exact (correlated) electron density of the system. It has been proven that, under certain conditions, such a potential exists, and by HK theorems applied to noninteracting electrons, it must be unique. The important quantities in KS theory may be now defined. Suppose the KS potential v_s(r).is known, then the KS equations

$h_{\mathit{KS}}{\varphi }_i\left(r\right)={\epsilon }_i{\varphi }_i\left(r\right)$

with

$h_{\mathit{KS}}=\left[-\frac{\mathit{1}}{\mathit{2}}{\nabla }^2+v_s\left(r\right)\right]$

give the exact density as

$\rho \left(r\right)={\displaystyle \sum _i^N{\left|{\varphi }_i\left(r\right)\right|}^2}$

Since the KS potential is uniquely determined by the density, the same applies to the solutions of the KS equations. Therefore, the kinetic energy of the electrons described by the KS orbitals is a functional of the density:

$T_s\left[\rho \right]={\displaystyle \sum _i^N〈{\varphi }_i^{*}\left[\rho \left(r\right)\right]\left|-\frac{1}{2}{\nabla }^2\right|{\varphi }_i\left[\rho \left(r\right)\right]〉}$

From these equations, we get the exact total energy of the system:

$E=T_s\left[\rho \right]+{\displaystyle \int \rho \left(r_1\right)v\left(r_1\right)d{r}_1+\frac{1}{2}{\displaystyle \int \frac{\rho \left(r_1\right)\rho \left(r_1\right)}{r_{12}}}d{r}_{1}d{r}_2}+E_{\mathit{xc}}$

Here v is the external potential of the system, in our case always the nuclear potential

$v\left(r_1\right)=V_N\left(r_1\right)={\displaystyle \sum _A\frac{-Z_A}{\left|R_A-r_1\right|}}$

The only unknown quantity in eqn (5) is the exchange-correlation energy E_xc, which is therefore defined by this equation. This quantity plays a crucial role in DF theory. It is, after a KS calculation, the only quantity for which a reliable estimate is needed to obtain a good total energy.

Moreover, it determines also the KS potential itself. It is possible to prove that the KS potential is given by:

$v_s\left(r\right)=v\left(r\right)+{\displaystyle \int \frac{\rho \left(r\text{'}\right)}{\left|r-r\text{'}\right|}\mathit{dr}\text{'}+v_{\mathit{xc}}}\left[\rho \left(r\right)\right]$

where v_xc is the funtional derivative of E_xc

$v_{\mathit{XC}}\left[\rho \left(r\right)\right]=\frac{\partial E_{\mathit{xc}}}{\partial \rho \left(r\right)}$

So the KS equations have the final form:

$h_{\mathit{KS}}{\varphi }_i\left(\mathbf{r}\right)=\left[-\frac{1}{2}{\nabla }^2+V_N+V_C+v_{\mathit{xc}}\left(r\right)\right]{\varphi }_i\left(r\right)={\epsilon }_i{\varphi }_i\left(\mathbf{r}\right)$

where the Coulomb potential is given by

$V_C\left(r\right)={\displaystyle \int \frac{\rho \left(r\text{'}\right)}{\left|r-r\text{'}\right|}}d{r}^{\prime }$

2.2 The generalized SCF model

The solution of the KS problem, expressed by eqn. (9), is similar to the procedure utilized for the HF model, both methods resting on a self consistent field (SCF) solution for the evaluation of the total energy. The SCF equations are built by expanding the ϕ_i in a set of one-electron basis functions:

${\varphi }_i\left(r\right)={\displaystyle \sum _{\mu =1}^m{C}_{\mathit{i\mu }}{\chi }_{\mu }\left(r\right)}$

so that the electron density can be described in terms of these functions and of the corresponding one-body density matrix P

$\rho \left(r\right)={\displaystyle \sum _{\mathit{\mu v}}{P}_{\mathit{\mu v}}{\chi }_{\mu }\left(r\right){\chi }_v\left(r\right)}$

The total SCF energy is:

$E_{\mathit{SCF}}={\displaystyle \sum _{\mathit{\mu v}}{P}_{\mathit{\mu v}}{H}_{\mathit{\mu v}}}+\frac{1}{2}{\displaystyle \sum _{\mathit{\mu v\lambda \sigma }}{P}_{\mathit{\mu v}}{P}_{\mathit{\lambda \sigma }}\left(\mathit{\mu v}|\mathit{\lambda \sigma }\right)}+E_{\mathit{xc}}$

where the Hv_μv are the matrix elements of the one-electron operator

$H^{\mathit{core}}=-\frac{1}{2}{\nabla }^2+V_N$

In a spin unrestricted formalism

$\rho \left(r\right)={\rho }^{\alpha }\left(r\right)+{\rho }^{\beta }\left(r\right);P\left(r\right)=P^{\alpha }\left(r\right)+P^{\beta }\left(r\right)$

and the KS equation (9) is transformed into a secular equation from which the eigenvalues and eigenfunctions are obtained:

$F^{\sigma }{C}^{\sigma }=S{C}^{\sigma }{\epsilon }^{\sigma }$

with the orthonormality conditions

${\left(C^{\sigma }\right)}^{+}S{C}^{\sigma }=I$

where σ refers to either α or β spin. The F^σ are Fock-like matrices, whose elements are

$F_{\mathit{\mu v}}^{\sigma }=\frac{\partial E_{\mathit{SCF}}}{\partial P_{\mathit{\mu v}}^{\sigma }}$

C^σ are the matrices of the molecular orbital coefficients, S is the atomic overlap matrix and ε^σ are diagonal matrices of the KS orbital eigenvalues. Now the difference between HF and KS approaches resides in the term E_xc, which is

$E_{\mathit{xc}}^{\mathit{HF}}=\frac{1}{2}\left({\displaystyle \sum _{\mathit{\mu v\lambda \tau }}{P}_{\mathit{\mu v}}^{\alpha }}{P}_{\mathit{\lambda \tau }}^{\alpha }+P_{\mathit{\mu v}}^{\beta }{P}_{\mathit{\lambda \tau }}^{\beta }\right)\left(\mathit{\mu \lambda }|\mathit{v\tau }\right)$

in HF theory, and

$E_{\mathit{xc}}^{\mathit{KS}}={\displaystyle \int f\left({\rho }^{\alpha }{\rho }^{\beta }\right)}\mathit{dr}$

in KS theory. In most cases the integral (19) cannot be computed analytically and must be obtained by numerical quadrature. This introduces a number of technical problems, which, although resonably well under control in the most recent packages [60-64], suggest the development of grid-free methods [65,66]. Furthermore, many current KS implementations employ various auxiliary fitting or projection techniques to aid in the evaluation of the Coulomb and/or exchange-correlation potential [14,15,19,20]. Although fitting can reduce the computational effort for small systems, this is no longer the case for large molecules. In some particularly efficient procedures, the integrands of eqn (19) can be obtained without evaluation of the Hessians of the densities, even though these appear in eqn (8). As a consequence, the cost of the exchange-correlation part of the electronic calculation scales linearly with the size of the atomic basis set used in the expansion of the molecular orbitals. Of course, the evaluation of the Hessians cannot be avoided when computing analytical gradients, or second derivatives. This task is, however, performed only once in each optimization step.

2.3 Density functionals

The key-problem in KS theory is to determine an analytical form for the E_xc term. The knowledge of the exact expression of the E_xc term leads, through eqn (5), to the exact total energy. Unfortunately, this expression is unknown, and approximations must be used. The most common approach to the problem of the representation of E_xc is to separate the correlation contribution from the exchange counterpart. This distinction is somewhat artificial in the context of DF theory, but the separation between these two terms considerably simplifies the discussion. Let us start with the simplest DF approach to the problem of exchange functional, i.e. the local spin density approximation (LSD), in which the functional for the uniform electron gas of density ρ is integrated over the whole space:

$E_x^{\mathit{LSD}}=A_x{\displaystyle \sum _{\sigma }{\displaystyle \int {\rho }_{\sigma }{\left(r\right)}^{4/3}\mathit{dr}}}$

where

$A_x=-\frac{3}{2}{\left(\frac{3}{4\pi }\right)}^{1/3}$

Such an approach underestimates the exchange energy by about 10%. Starting from eqn (20) several corrections for the nonuniformity of atomic and molecular densities have been proposed. In particular, those based on density gradients have received considerable attention, due to their simplicity. These corrections, collectively referrred to as generalized gradient approximation (GGA), are usually expressed in terms of an enhancement factor over the exchange energy of the uniform electron gas, so that the total exchange energy takes the form:

${\mathrm{E}}_{\mathrm{X}}^{\mathrm{GGA}}={\mathrm{E}}_{\mathrm{X}}^{\mathrm{LSD}}-{\displaystyle \sum _{\sigma }{\displaystyle \int \mathrm{F}\left[\mathrm{x}\right]}{\mathrm{\rho }}_{\sigma }{\left(\mathrm{r}\right)}^{4/3}\mathrm{dr}}$

where x is the dimensionless reduced gradient:

$x=\frac{\left|\nabla {\rho }_{\sigma }\right|}{{\left({\rho }_{\sigma }\right)}^{4/3}}$

A number of semiempirical GGA exchange functionals, which contain parameters obtained by fitting the exchange atomic energies have been proposed. Roughly speaking, these functionals can be divided in two main classes. In the first one, we may group those which can be considered as modifications of the functional proposed by Becke in 1988 [25] (hereafter referred to as B), whose enhancement factor can be expressed as

$F^B\left[x\right]=\frac{b{x}^2}{1+6\mathit{bx}{sinh}^{-1}}$

where b is a constant. In this class we include the functional developed by Perdew and Wang in 1991 (hereafter PW) [46], the so-called CAM family of functionals [17], and the exchange functional of Chermette and co-workers [29].

The other class contains all the functionals which can be expressed as polynomial function of the reduced density gradient. Among them, we can mention those introduced by Becke in 1986 (B86) [22,23], by Perdew and Wang in 1986 (P) [24], by Lacks and Gordon in 1993 (LG) [27] and the very recent functional of Gill (G) [30], either in its original form or in the modified form proposed by Handy. For instance, the enhancement factor of the P functional is:

$F^P={\left[1+a_2{s}^2+a_4{s}^4+a_6{s}^6\right]}^{1/15}$

where

$s=\frac{1}{2{\left(3{\pi }^2\right)}^{1/3}}x$

and a₂, a₄, and a₆ are constants

It is possible to have a rough idea about the performances of the different exchange functionals by computing the total exchange atomic energies for the first and second rows of the periodic table. Standard exchange functionals usually give total atomic exchange energy within 1% of the HF exchange energies, as is well evidenced by the data reported in table I.

All the above mentioned functionals generally provide atomic or molecular properties with a reasonable precision, so that conventional DF methods are claimed to deliver results comparable to those obtained by second-order many body perturbation approaches (MP2). From a purely formal point of view, the reasons for such good performances are not yet evident.

In particular, a number of physical conditions that must be satisfied by an exchange functional have been established, but only few of the current exchange functionals obey to them.

Among others, three conditions are of particular importance. The first constraint is related to the behavior in the small x region, where the GGA exchange functional should reduce to E_X^LSD in order to recover the correct uniform gas limit. The second condition was defined by Levy, who showed that some scaling properties can be satisfied if the asymptotic form of the functional for large x is x^−α, where α ≥ ½ [68,69]. The last condition is the so called “Lieb-Oxford bound” [70], which states that:

$E_x\ge E_{\mathit{xc}}\ge -1.679A_x{\displaystyle \int \rho {\left(r\right)}^{4/3}\mathit{dr}}$

The behavior of some of the most common functionals with respect to these three constraints is reported in table II. The B functional does not obey neither the Levy condition nor the Lieb-Oxford bound, but its numerical performances are better than those provided by the PW functional, which respects all the above mentioned constraints.

This situation is, of course, quite disturbing and some efforts have been done to design an exchange functional which couples a rigourous theoretical formalism with good numerical performances. For instance, we have recently found that some mofidications of the PW exchange functional (hereafter referred to as mPW) induce significant improvements of its numerical results, while retaining the same parameters and correct physical behavior of the original model. Furthermore, the correct asymptotic conditions are less important in the high density (which corresponds to covalent bonds), than in low-density region. This point is of particular importance, since these latter regions are responsible for non-covalent interactions, such as H-bond, van der Waals (vdW) and charge transfer(CT) [39].

The situation is well evidenced by computing the HF and DF differential exchange energy for the He dimers, i.e; the exchange energy of the atom pair minus the exchange energy of the two free atoms. In figure 1 are reported the DF errors, computed with respect to the HF differential exchange energy, for the He pairs. This plot evidences the significant error obtained in the long-range region (d>2.0 Å) by using conventional exchange functionals. In contrast, an improved behavior is obtained by properly designed functionals, like the mPW or the LG one.

Many approximate functionals have been proposed for the remaining part of the total energy, i.e. the correlation energy. The development of an improved local form of this functional is of special interest for large systems because the complexity of the system will be significantly reduced. Recently, a new form of E_c[ρ] based on the functional expansion and the adiabatic connection formulation of DF has been advanced which is a sum of integrals of various powers of the density [37]:

$E_c=C_{1}N+C_2{\displaystyle \int {\rho }^{2/3}\left(r\right)\mathit{dr}+C_3{\displaystyle \int {\rho }^{1/3}\left(r\right)\mathit{dr}}}$

where C_n are constants to be determined and N is the number of electrons in the system. In spite of its accuracy, this functional, called the Liu-Parr (LP) correlation functional, has the fundamental deficiency, that the corresponding correlation potential approaches infinity for all densitites that fall to zero at large values of r. This fact rules out the possibility of applying the LP functional, without truncation, in a KS-SCF procedure.

Starting from eqn (28) and applying the Padé summation approximation, it is possible to define a family of correlation functionals, which has the general form:

$E_c^{\left[m,n\right]}={\displaystyle \int \rho \left(r\right)\frac{p_m\left(\zeta \right)}{q_m\left(\zeta \right)}}\mathit{dr}$

Here, ζ=ρ^− 1/3, the superscripts label the order of the Padé approximant employed, and p_m and q_m are polynomials of order m and n, respectively. The lowest expansions of eqn (29) are:

$E_c^{\left[0,1\right]}={\displaystyle \int \rho \left(r\right)}\frac{a_0}{b_0+b_1\zeta }\mathit{dr}$

$E_c^{\left[1,2\right]}={\displaystyle \int \rho \left(r\right)\left(\frac{a_0+a_1\zeta }{b_0+b_1\zeta +b_2{\zeta }^2}\right)\mathit{dr}}$

Equation (30) is the form proposed by Wigner over sixty years ago [70].

A different approach to the problem of the correlation representation starts from the definition of a local correlation functional with the correct asymptotyc behaviour, which i.e. correctly reproduces the correct uniform gas limit. The most common functional with this characteristic is the Vosko-Wilk-Nuisar (VWN) parametrization of the Monte Carlo results of Ceperly and Alder [45]]. More recently Perdew and Wang proposed an improved local correlation functional [46]:

${\mathrm{E}}_{\mathrm{c}}^{\mathrm{LDA}}=-2\mathrm{a\rho }\left(1+{\mathrm{\alpha }}_1{\mathrm{r}}_{\mathrm{s}}\right)log\left[1+\frac{1}{2\mathrm{a}\left({\mathrm{\beta }}_1{{\mathrm{r}}_{\mathrm{s}}}^{1/2}+{\mathrm{\beta }}_2{\mathrm{r}}_{\mathrm{s}}+{\mathrm{\beta }}_3{\mathrm{r}}_{\mathrm{s}}^3+{\mathrm{\beta }}_4{\mathrm{r}}_{\mathrm{s}}^4\right)}\right.$

where a, α₁ β₁, β₂, β₃ and β₄ are constants, and

$r_s={\left(\frac{3}{4\mathit{\pi \rho }}\right)}^{1/3}$

As for the exchange functionals, local correlation functionals reproduce only in part the total correlation energy and GGA corrections are in order. In particular the correlation functional proposed by Lee, Yang and Parr (LYP) [71] embodies a Wigner-like functional (eqn 30) as the local contribution. The analytical expression of the LYP functional is:

$\begin{array}{l}{E}_c^{\mathit{LYP}}=\frac{4a}{1+d{\rho }^{-1/3}}\frac{{\rho }_{\alpha }{\rho }_{\beta }}{\rho }-2^{11/3}\frac{3}{10}{\left(3{\pi }^2\right)}^{2/3}\mathit{ab\omega }\left(\rho \right){\rho }_{\alpha }{\rho }_{\beta }\left({\rho }_{\alpha }^{8/3}+{\rho }_{\alpha }^{8/3}\right)\\ +\frac{\partial E_c^{\mathit{LYP}}}{\partial \nabla {\rho }_{\alpha }\nabla {\rho }_{\alpha }}\nabla {\rho }_{\alpha }\nabla {\rho }_{\alpha }+\frac{\partial E_c^{\mathit{LYP}}}{\partial \nabla {\rho }_{\alpha }\partial \nabla {\rho }_{\beta }}\nabla {\rho }_{\alpha }\nabla {\rho }_{\beta }+\frac{\partial E_c^{\mathit{LYP}}}{\partial \nabla {\rho }_{\beta }\nabla {\rho }_{\beta }}\nabla {\rho }_{\beta }\nabla {\rho }_{\beta }\end{array}$

where

$\begin{array}{l}\frac{\partial E_c^{\mathit{LYP}}}{\partial \nabla {\rho }_{\alpha }\nabla {\rho }_{\alpha }}=-\mathit{ab\varpi }\left(\rho \right)\left[\frac{1}{9}{\rho }_{\alpha }{\rho }_{\beta }\left\{1-3\delta \left(\rho \right)-\left[\delta \left(\rho \right)-11\right]\frac{{\rho }_{\alpha }}{\rho }\right\}-{\rho }_{\beta }^2\right]\\ \frac{\partial E_c^{\mathit{LYP}}}{\partial \nabla {\rho }_{\alpha }\nabla {\rho }_{\beta }}=-\mathit{ab\varpi }\left(\rho \right)\left\{\frac{1}{9}{\rho }_{\alpha }{\rho }_{\beta }\left[47-7\delta \left(\rho \right)\right]-\frac{4}{3}{\rho }^2\right\}\\ \frac{\partial {\mathrm{E}}_{\mathrm{c}}^{\mathrm{LYP}}}{\partial \nabla {\mathrm{\rho }}_{\mathrm{\beta }}\nabla {\mathrm{\rho }}_{\mathrm{\beta }}}=-\mathrm{ab\varpi }\left(\mathrm{\rho }\right)\left[\frac{1}{9}{\mathrm{\rho }}_{\mathrm{\alpha }}{\mathrm{\rho }}_{\mathrm{\beta }}\left\{1-3\mathrm{\delta }\left(\mathrm{\rho }\right)-\left[\mathrm{\delta }\left(\mathrm{\rho }\right)-11\right]\frac{{\mathrm{\rho }}_{\mathrm{\beta }}}{\mathrm{\rho }}\right\}\right.-{\mathrm{\rho }}_{\mathrm{\alpha }}^2\\ \varpi \left(\rho \right)=\frac{e^{-c{p}^{-1/3}}}{1+\mathit{dp}{p}^{-1/3}}{\rho }^{-11/3}\\ \delta \left(\rho \right)=c{\rho }^{-1/3}\frac{d{\rho }^{-1/3}}{1+d{\rho }^{-1/3}}\end{array}$

and a, b, c, d are constants.

In a similar way, the local PW correlation functional of eqn (32) can be significantly improved by adding a gradient correction. The resulting GGA correlation functional is:

$E_c^{\mathit{PW}91}=E_c^{\mathit{LDA}}+\mathit{\rho H}$

where

$H=\frac{{\beta }^2}{2\alpha }log\left[1+\frac{2\alpha }{\beta }\frac{t^2+A{t}^4}{1+A{t}^2+A^2{t}^4}\right]+C_{c0}\left[C_c-C_{c1}\right]t^2{e}^{-100s^2}\text{;}$

$A=\frac{2\alpha }{\beta }{\left[e^{-2\alpha {\epsilon }_c/{\beta }^2}-1\right]}^{-1}\text{;}$

$C_c=C_1+\frac{C_2+C_3{r}_3+C_4{r}_s^2}{1+C_5{r}_s+C_6{r}_s^2+C_7{r}_s^3}\text{;}$

$t=\frac{\left|\nabla \rho \right|}{2{\left[\frac{4}{\pi }{\left(3{\pi }^2\rho \right)}^{1/3}\right]}^{1/2}}$

${\epsilon }_c=\rho E_c^{\mathit{LDA}}$

and α,β,C_c0, C_c1, C₁, C₂, C₃, C₄, C₅, C₆ and C₇ are constants.

As for the exchange functionals, a set of “minimal” requirements has been established (see table III). In this connection it must be mentioned that the LYP functional does not reach the exact uniform electron gas limit and does not allow for a distintic treatment of parallel and antiparallel spin correlation, but gives vanishing correlation for one-electron systems

Despites its theoretical weakness, the LYP functional is one of the best forms of the correlation functional currently available, generally performing better than the PW functional, especially for molecules containing first-row atoms.

In table IV are reported the total correlation energies for the atoms belonging to the first two rows of the periodic table.

2.4 Adiabatic connection methods

The adiabatic connection formula is at the root of the ACMs. This formula is usually expressed in the form:

$E_{\mathit{xc}}={\displaystyle \underset{0}{\overset{1}{\int }}{U}_{\mathit{xc},\lambda }\mathit{d\lambda }}$

with

$U_{\mathit{xc},\lambda }=〈{\Psi }_{\lambda }\left|V_{\mathit{ee}}\right|{\Psi }_{\lambda }〉-\frac{e^2}{2}{\displaystyle \iint \frac{\rho \left(r\right)\rho \left(r\text{'}\right)}{\left|r-r\text{'}\right|}}\mathit{drdr}\text{'}$

here λ is an electronic coupling strength parameter that switches on the Coulomb repulsion between electrons and U_xc,λ is the corresponding potential energy of exchange and correlation for electron-electron interaction at intermediate coupling strength λ. The integrand of eqn (42) refers explicity to the potential energy only, the kinetic part of the exchange correlation energy being generated, by the λ integration. This formula connects the noninteracting KS reference system (λ = 0) to the fully interacting real system (λ = l), through a continuum of partially interacting systems (0 ≤λ≤ 1), all sharing a common density ρ. Becke showed that the simplest approximation to eqn (42) can be expressed by a two-point formula [48]:

$E_{\mathit{xc}}^{\mathit{ACM}}=\frac{1}{2}\left(E_{\mathit{xc},\lambda =0}+E_{\mathit{xc},\lambda =1}\right)$

An application of eqn (44) is the so called half-and-half (h&h) ACM approach, which is obtained if E_xc,λ = 0 = E_x^HF, the HF exchange, and E_xc,λ = 1 = E_x^LSD, the LSD approximation to exchange, are used. Variants of the h&h method, including GGAs, are defective in several resepects and cannot be considered significant improvements over standard functionals, even if they provide good results for some difficult systems. A more valuable approach has been next obtained by Becke using a three parameter equation [47]:

$E_{\mathit{xc}}^{\mathit{ACM}}=a_{x0}{E}_x^{\mathit{LSD}}+\left(1-a_{x0}\right)E_x^{\mathit{HF}}+a_{x1}\Delta E_x^{\mathit{GGA}}+E_c^{\mathit{LSD}}+a_c\Delta E_c^{\mathit{GGA}}$

where ΔE_x^GGA and ΔE_c^GGA are the generalized gradient contributions to the exchange and correlation contribution, and E_x ^LSD and E_c ^LSD their LSD counterparts. The three semiempirical parameters, a_x0, a_x1 and a_c, have been determined by fitting the heats of formation of a standard set of molecules. Even if the original work uses the Perdew-Wang (PW) correlation functional, the most popular implementation is the so-called B3LYP method, which uses (in a selfconsistent way) the B exchange functional together with the LYP correlation functional:

$E_{\mathit{xc}}^{B3\mathit{LUP}}=a_{x0}{E}_x^{\mathit{LSD}}+\left(1-a_{x0}\right)E_x^{\mathit{HF}}+a_{x1}\Delta E_x^B+E_c^{\mathit{VWN}}+a_c\Delta E_c^{\mathit{LYP}}$

where the LSD contribution to the exchange energy is that of a uniform spinpolarized electron gas and the local correlation component is represented by the VWN parametrization. Since the local (Wigner) part of the LYP correlation functional is not too different from the correlation energy of the uniform electron gas, the last term is usually replaced by:

$\Delta E_c^{\mathit{LYP}}=E_c^{\mathit{LYP}}-E_c^{\mathit{VWN}}$

This protocol is nowadays considered as the most powerful among all the ACM approaches, providing, at a fraction of the computational costs, numerical results close to those obtained by the most refined post-HF methods. On the basis of such an experience, Becke has recently proposed a single-parameter version of his ACM approach [49]:

$\begin{array}{l}{E}_{\mathit{xc}}^{\mathit{ACM}}=a_0{E}_x^{\mathit{HF}}+\left(1-a_0\right)\left(E_x^{\mathit{LSD}}+\Delta E_x^{\mathit{GGA}}\right)+E_c^{\mathit{LSD}}+\Delta E_c^{\mathit{GGA}}=\\ a_0\left(E_x^{\mathit{HF}}-E_x^{\mathit{GGA}}\right)+E_{\mathit{xc}}^{\mathit{GGA}}\end{array}$

where a₀ ranges between 0.28 and 0.16, depending on the choice of the GGA correlation functional. This parameter is, once again, chosen to obtain the best fitting to the experimental data of a standard set of molecules.

Very recently, several authors focused their attention on the theoretical evaluation of the exact mixing coefficients in ACM approaches In particular, Perdew and co-workers argue that the optimum integer value ruling the HF/DF exchange ratio can be determined by the lowest order of the Gorling-Levy perturbation theory which provides an accurate description of the dependence of E_xc,λ upon the coupling constant λ. They showed that the E_xc,λ term has a correct dependence, i.e. it is has the correct value, slope and second derivative at λ = 1, only for a₀ = 1/4 [53].

Following these works, we have introduced a parameter-free version of the B3LYP approach, in which only the HF and the DF exchange contributions are mixed together in the ratio 1/4, while the correlation part is entirely included at the DF level [54]. Starting fron eqn (48), we have defined the B1LYP protocol, which uses the Becke exchange and LYP correlation functionals as:

$\begin{array}{c}{E}_{\mathit{xc}}^{B1\mathit{LYP}}=\frac{1}{4}{E}_x^{\mathit{HF}}+\left(1-\frac{1}{4}\right)\left(E_x^{\mathit{LSD}}+\Delta E^B\right)+E_c^{\mathit{VWN}}+\Delta E_c^{\mathit{LYP}}=\\ \frac{1}{4}{E}_x^{\mathit{HF}}+\frac{3}{4}\left(E_x^{\mathit{LSD}}+\Delta E_x^B\right)+E_c^{\mathit{LYP}}\end{array}$

Note that, while slightly different B3LYP functionals are obtained choosing different fittings for the correlation energy of the free electron gas, this problem completely disappears in the B1LYP model. As is the case for the popular B3LYP protocol, the B1LYP approach has been used in a fully self-consistent way, that is the iterative determination of the KS orbitals is performed by the whole functional including contributions from GGA and HF exchange.

The so called G2 set of molecules is nowadays considered a standard for the validation of new quantum chemical approaches [72]. Table V collects an error statistic for several quantum mechanical approaches concerning the geometric and thermodynamic parameters of 32 molecules belonging to the G2 set, together with dipole moments and harmonic vibrational frequencies.

From these data, it is clear that all the GGA methods provide geometric parameters with comparable accuracies, the error ranging between 0.012 and 0.014 Å. In contrast, a variety of results are obtained for the atomization energies, the BLYP protocol being the less accurate (9.6 kcal/mol) and the mPWPW the most accurate (6.7 kcal/mol) one. In particular, it is remarkable that protocols including exchange functionals with the correct asymptotic behaviour (i.e. LG and mPW) provide thermochemical parameters with a greater precision than those obtained by more conventional exchange functionals (i.e. B and PW).

As concerns the correlation part, the PW functional seems to outperform the LYP functional, the results obtained at the BPW level being better than those provided by the BLYP protocol.The inclusion of some HF exchange induces a significant improvement of the performances. In particular, the mPW3PW protocol performs at least as well as the B3LYP version and should be preferred in view of its improved asymptotic behaviour. In the same vein, a comparison between B1LYP and mPW1PW approaches shows that both models give results close to those provided by 3-parameter ACM methods, thus offering a significant improvement over the underlying GGA functionals (BLYP and mPWPW) without adding any additional parameter. Furthermore, all the ACM methods approach the accuracy of the most refined post-HF methods, such as CCSD[T]. Note, however, that the comparisons offered in table V are quite unfair for some post-HF methods, which would require larger basis sets to give converged results.

The results reported above give some indications about the performances of the different DF protocols. It must be remarked, anyway, that the geometries and harmonic frequencies of the G2 set of molecules are relatively well described by all the most common quantum mechanical methods. There are, however, well known molecular systems which are much more demanding, some of which are considered in the following.

As a first test, we have selected cis-FONO, which has been recently investigated in detail by several other methods [73]. The results collected in table VI unambiguosly show that the B1LYP protocol outperforms the MP2 method concerning both geometries and harmonic vibrational frequencies. In particular, both the average and maximum error on frequencies are nearly half the corresponding B3LYP values. Furthermore, contrary to HF and post-HF computations, at the B1LYP level even the relatively modest 6-311+G(d,p) basis set provides satisfactory results, thus significantly enlarging the dimensions of difficult systems amenable to quantitative studies.

The structures and the hyperfine splittings (hfs) of organic free radicals provide another severe challenge to theoretical chemistry, since they are related to subtle details of the ground state electronic wave function. Here we analyze the dihydronitrosyl radical for which both experimental and refined theoretical results are available in the literature [56-59]. The most relevant physico-chemical observables obtained by different methods for H₂NO are shown in table VII. From these data, it is quite apparent that the B1LYP approach provides results very close to the B3LYP one, concerning both geometric and magnetic parameters. Taking the UQCISD[T] results as a reference rather than experimental values (which involve significant vibrational averaging), both the B1LYP and B3LYP models provide reliable results. The only departure from the reference values concerns a slight underestimation of the isotropic hfs of nitrogen, for which the B1LYP approach offers even some improvement over the B3LYP method (8.3 vs. 7.6 G). As has been already reported in literature, the PW correlation functional provides quite poor isotropic hfs for non-hydrogen atoms and the situation is only slightly improved by adding some HF exchange.

3.2 Non covalent interactions

Van der Waals complexes, such as the dimers of rare-gas atoms, are very difficult to handle in the framework of DF methods. In particular, standard methods, including some ACM approaches, significantly underestimate the stabilities of these complexes. The structural and energetic characteristics of the energy minima of He and Ne dimers, computed by a number of DF methods, are collected in table VIII.

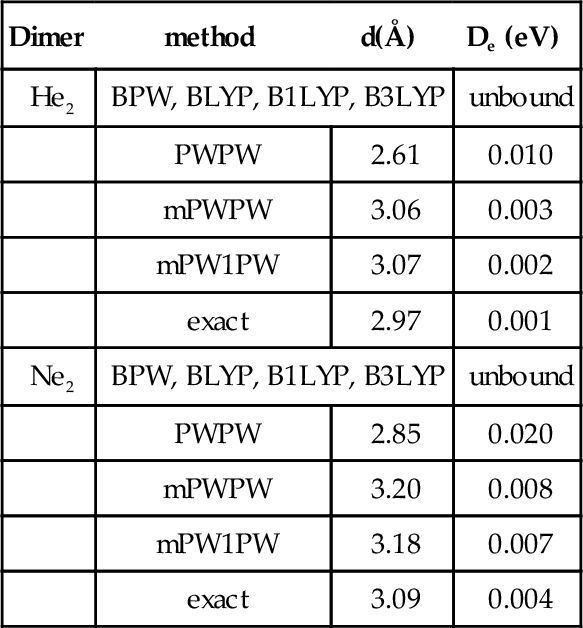
Two limiting situations are evidenced by these data. From the one hand, all the protocols using the B exchange functional predict a vanishing interaction between He atoms, while, from the other hand, a strong interaction is found at the PWPW level. Between these two extremes, the mPWPW conventional DF approach gives much improved results and an even better agreement with the exact values is obtained at the mPW1PW level.

The results are better evidenced in the graphs of figure 2, which represent the potential energy profiles for the He-He interaction, computed by several DF methods. All the plots are comprised between the BPW repulsive curve and the strong attractive curve of the PWPW functional. In the middle, and close to the exact profile, lie both the mPWPW and the mPW1PW plots.

A similar behaviour is obtained for the Ne dimer, where a variety of situations is predicted by standard pure DF approaches, while a good agrement with the “exact” data is found for all the models which include the mPW functional (see table VIII).

An even more stringent test is represented by CT complexes, and in particular those arising from a π–σ type interaction, such as that of ethylene with a halogen molecule. These systems are very difficult to describe either at the post-HF and DF levels. Among the well characterized CT systems, we have focussed our attention on the simple ethylene-chlorine complex. Furthermore, even if several possibile molecular arrangements are possible, the axial-perpendicular structure is the most stable one. So we have limited our attention only to this molecular arrangement, whose main molecular parameters are reported in table IX.

The most striking features in the calculations with the different methods are the chlorine-ethylene distances, which are directly related to the interaction strengths. In this connection, all the GGA methods provide very short intermolecular distances, even if the LGLYP result can be considered a significant improvement over the other GGA values.

The inclusion of some HF exchange increases the distance up to 2.83 Å for the mPW1PW model. This last value is equal to the B3LYP estimate (2.84 Å), but its is not accurate enogh to describe this parameter properly. The best agreement with the reference MP2 value (3.00 Å) is found at the B1LYP level (2.901 Å). In contrast, it must be remarked that all the methods provide geometries for the free molecules (not reported in table IX) which are in good agreement with experimental results.

The trend in the geometrical parameters is reflected in the harmonic frequencies and, in particular, in the stretching of the Cl-Cl bond. In this complex, the intermolecular distance is directly related to the σ–π electron donation from chlorine to ethylene, which weakens the Cl-Cl bond. As a consequence an overestimation of this interaction induces a vey low Cl-Cl stretching frequency. This is the case for the conventional DF approaches, which predict harmonic wave numbers significantly lower than the experimental estimate. In contrast, a better agreement is found at the mPW1PW level, whose value is close to the MP2 prediction (467 vs. 506 cm^− 1, respectively).

In the same table are reported the interaction energies, corrected for both zero point energy (ZPE) and basis set superposition error (BSSE) effects [74]. As expected, these energies show a strong correlation with the intermolecular distances. For instance, the BPW model predicts a strong Cl₂-C₂H₄ interaction (-3.6 kcal/mol), which is reduced to -1.4 kcal/mol at the mPW1PW level. This last value is only sligthly lower than the MP2 estimate (-1.6 kcal/mol) or the experimental findings (between -1.7 and -2.7 kcal/mol).

3.3 Reactivity

As a first test of kinetic predictions we have chose the S_N2 reaction, whose importance in organic chemistry is well evidenced by the accumulation of a large body of experimental and theoretical data [75-80]. From a theoretical point of view, several studies have shown these reactions to be extremely sensitive to the theoretical model used [77,78]. Already the simple Walden inversion:

${\mathrm{Cl}}^{‐}+{\mathrm{CH}}_3\mathrm{Cl}\to {\mathrm{ClCH}}_3+{\mathrm{Cl}}^{‐}$

is difficult to describe by quantum mechanical methods. This reaction is characterized, in the gas-phase, by a double-well energetic profile, with two minima corresponding to the formation of a pre- and post- reaction ion-molecule complex (Cl⁻..CH₃Cl) and with a saddle point (SP) of D_3h symmetry (C1CH₃C1⁻). The most significant quantities are the complexation energy of the ion-molecule complex (ΔE_comp), the activation energy, i.e. the relative energy of the D_3h saddle point with respect to the ion-molecule complex (ΔE^#), and the overall barrier (ΔE_ovr), defined as the difference between these two energies. The geometrical parameters of the ion-molecule complex and of the SP are collected in table X.

The key parameter differentiating the various functionals is the distance between the chloride anion and the carbon of the methyl chloride. Once again, the MP2 results can be considered as the reference data, the distance being 3.270 Å and 2.317 Å for the ionic-complex and for the SP, respectively. All the GGA models lead to a too short distance for the ion-molecule complex and a too long bond length for the Cl-Cl bond in the SP. The inclusion of some HF exchange significantly improves the performances, even if the computed values are still far from the MP2 results.

These geometrical trends are reflected in the computed energetical parameters (see table XI). In particular, an increasing of the Cl-C distance induces a significant stabilization of the SP structure with respect to the minimum. The effect may be so relevant to induce a negative value for ΔE_ovr. This is true for all the conventional DF methods considered in the present paper, as well as all the ACMs which embody the LYP correlation functional. In particular, the B1LYP method predicts an overall barrier of -0.8 kcal/mol. In contrast, the mPW1PW approach predicts a positive, albeit small, value for ΔE_ovr, thus restoring the right trend.

As concerns the other energetical quantities, we found that complexation energies are relatively well reproduced by all the DF methods. A greater sensitivity to the functional used in computations is found, instead, for ΔE^#, whose estimates range between 6.3 (mPWPW) and 10.6 (LGLYP) kcal/mol.

The mechanism of the Diels-Alder (DA) reaction has attracted interest and stimulated debate since its discovery [81]. Both experimental data and quantum-mechanical calculations indicate that the reaction occurs through a concerted mechanism, although, in some cases, stepwise mechanisms involving diradical intermediates are only slightly less favourable [82,83]. In particular, for the reaction between ethylene and butadiene thermochemical estimates indicate that the activation energy for the formation of the biradical intermediate is only slightly higher (by 2.7 kcal/mol) than the barrier governing the concerted mechanism [82,84]. While the QCISD(T) approach reproduces quantitatively this trend, the CAS method overstabilizes biradical species leading to a preference for the stepwise mechanism [85]. Since the effect of dynamical correlation (not taken into account in the CAS model) should be even larger for the addition of H₂CO and H₂CS due to the presence of lone pairs, we will take QCISD(T) results as our references. Then UQCISD(T)/SVP results indicate that the stepwise mechanism is even less likely for H₂CO and H₂CS than for C₂H₄. As a consequence we have concentrated our attention on the concerted mechanism. The experimental activation energy for addition of ethylene to trans-butadiene is 27.5 kcal/mol, which gives an estimated value at OK of 25.1±2 kcal/mol. Adding the zero point correction to bare energy barriers, only QCISD[T], G2 and B3LYP results fall within the error bar of the experimental estimate (see table XII).

The energy barriers and reaction energies for the three prototypical DA reactions are compared in table XII. The most striking aspect of this table is the non negligible effect of basis set extension in post-HF methods and the remarkable agreement between G2 and B3LYP approaches. On the other hand, the HF and MP2 methods are not sufficiently reliable, whereas MP4 results are quite close to QCISD[T] ones. This would allow to avoid the lengthy iterative computations involved in all the variants of the coupled cluster approach, but the huge basis set needed to obtain G2-like results is prohibitive for larger systems.

A better analysis of basis set saturation can be performed by a progressive refinement of the starting SVP basis set. The results obtained for the energy barrier governing addition of H₂CO are shown in figure 5. Very similar trends have been found for addition of C₂H₄ and H₂CS. It is quite apparent that polarization functions on hydrogen atoms are playing a negligible role, whereas the balanced description of π bonds in different stages of formation requires a triple-ζ valence space coupled to double sets of polarization functions on nonhydrogen atoms. The role of f functions, although not completely negligible, is comparatively less important, whereas addition of a third set of polarization functions is essentially useless.

In summary, the smallest basis set suggested for quantitative studies of DA reactions by post-HF methods is of TZ2P quality, possibly with a single set of polarization functions on hydrogen atom. However, coupling these basis set requirements with the need of a refined treatment of correlation (at least MP4) produces a computational model which becomes prohibitive for all, but the smallest prototypical reactions.

The situation is even worse considering that comparison between concerted and stepwise mechanisms requires the use of the even more expensive coupled cluster approaches. In such circumstances we think that a much more viable route is offered by the B3LYP/SVP model, which provides quite reliable results for all the aspects considered in this paragraph [85].

3.5 Molecular properties: NMR chemical shifts

A number of approaches have been proposed for the computation of NMR properties in the framework of DF approaches [86-91]. Here we will make explicit reference to the GIAO model, which appears particularly effective [92,93]. It has been recently pointed out that the MP2 method predicts chemical shifts which are closer to experiment than those obtained using DF approaches, including the B3LYP model [93]. It is so natural to include, as a stringent test, the computation of chemical shieldings. In particular, we have selected some examples in order to investigate the different possible hybridizations of carbon atoms. We have next added the ozone molecule, which is a particularly difficult test for NMR properties [90,92]. The results are collected in table XIII.

Let us first analyze the results for ¹³C. From the data reported in the table, it is apparent that all the computational methods provide reliable results for chemical shieldings of sp³ carbons. For instance the mPW1PW value for the methylic carbon of formaldehyde is 154 ppm, wheras the MP2 value is 163 ppm, both values being close to the experimental finding (153 ppm). In going to sp² carbon atoms, like the carboxylic one in the same molecule, a dramatic change is observed. In particular both MP2 and B3LYP methods fail in predicting the shielding constants, the computed values being 1 and -27 ppm, respectively. In contrast, the mPW1PW approach gives results close to the experimental value. Finally, the chemical shifts of the sp carbon, in CH₂CO, is well reproduced by the mPW1PW model (-10 ppm), which gives values close to MP2 (-11 ppm) and to experiment (-8 ppm). In contrast a dramatic difference is observed for the B3LYP value (-38 ppm).

It must be noted that for chemical shifts of first-row nuclei, and carbon in particular, the inclusion of HF exchange has a small effect. For instance GIAO-BLYP and GIAO-B3LYP chemical shifts have been shown to differ by few ppm [91,93]. So the differences found in the present study can be attributed to the improved asymptotic properties of the underlying GGA functional.

A more demanding test is represented by ozone, since correlation effects play a huge role both on the structure and on the NMR properties of this molecule. The results obtained by the mPW1PW model are compared in table XIII to those obtained by HF and MP2 methods [141]. The most striking feature of these data is the poor performance of the MP2 approach in predicting the shielding constants of both oxygens, concerning absolute values and even signs. In contrast, all the ACM methods, including the mPW1PW one, give the right trend, even if the absolute values are significantly underestimated with respect to the experimental data. It must be emphasized, anyway, that quantitative accuracy cannot be expected from single-determinant calculations in this situation, where the use of multiconfigurational approaches is mandatory [92]. Furthermore, the role played in this case by the neglected current dependency of the exchange correlation functional [86] could be particularly significant.

3.6 Electronic excitation energies

Time-dependent DF theory (TD-DF) provides a formally rigourous extension of Hohenberg-Kohn-Sham DF theory, which is time independent, to the situation where a system, initially in its ground stationary state, is subject to a time-dependent perturbation modifying its external potential, v [95]. A stationary action principle may be derived, analogous to the minimum energy principle of Hohenberg-Kohn theory, and this can be used to derive the time-dependent KS equations [95]. Since the dynamic polarizability describes the response of the dipole moment to a time-dependent electric field, it may be calculated from the response of the charge density obtained from TD-DF. This allows the determination of the electronic excitation spectrum in the usual dipole approximation, because the poles of the dynamic polarizability determine the excitation energies [96]. Here we adopt the implementation of the TD-DF model introduced by Scuseria and co-workers [97] using, on the basis of previous studies [97,98], the 6-31+G(d) basis set of Foresman et al. [99].

There is a growing interest in the application of TD-DF to the calculation of abiabatic excitation energies [96-98, 100, 101]. The results obtained for low excitation energies are usually superior to the those obtained by HF-based methods, like the Random Phase Approximation (RPA) [102], or the Configuation Interaction with Single excitations (CIS) [98, 100, 103]. In addition, given that the time dependent HF (TDHF) scheme can be derived along the same lines as TDDF, Bauemschmitt and Ahlrichs [98] have also included the ACM model in the calculation of energies, showing that the B3LYP functional represents a further improvement over conventional DF methods. In this connection, it has been suggested that the numerical performances of the different functionals strongly depend on their ability to predict reliable molecular ionization potentials (IP) [96]. This points out that, like in ground-state computations, the domain of applicability of TD-DF rests on the development and validation of suitable functionals. We expect that the mPW1PW functional gives results at least comparable with those provided by other ACM approaches, because it provides comparable IP's, but has an improved long range behavior.

In table XIV are collected our mPW1PW results together with HF-based and experimental data from ref. 98. The chosen molecular set, even if limited, is in our opinion quite representative, since it includes π→ π*, σ→ π*and n → π* transitions.

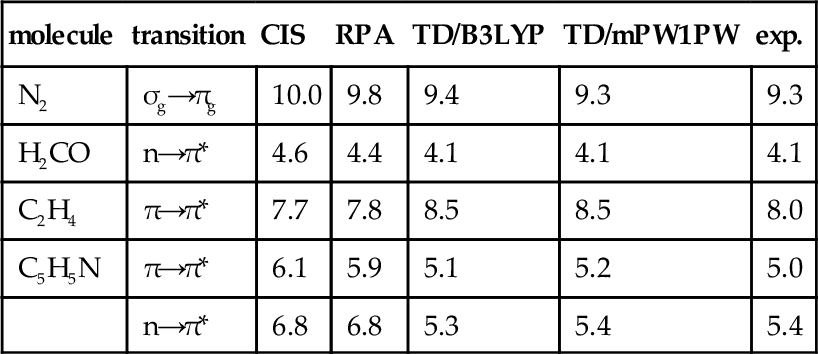
The table shows that reliable results are obtained also in this case by the mPW1PW model, which provides data slightly closer to the experiment than their B3LYP counterparts. An even larger improvement is found with respect to RPA and CIS values. It is interesting to note also that the largest deviation is found for C₂H₄, whose IP is one of the less accurately predicted by the mPW1PW model.