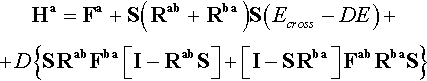The half projected hartree-fock model for determining singlet excited states.
Yves G. Smeyers Instituto de Estructura de la Materia C.S.I.C. Serrano, 113-bis 28006- MADRID Spain.
Abstract
The Half-Projected-Hartree-Fock model (HPHF) which introdudes some electronic correlation effects into the a singlet ground state wave-function is briefly described. Two procedures for determining the HPHF orbitals are described and extended to the direct determination of singlet excited states. The procedure is applied to various examples of interest. The spectroscopic constants of the Li2 molecule lowest singlet excited states are calculated. The optimal geometries of cyclobutanone and 3-cyclopenten-1-one in their singlet (n → π*) excited state are determined. Both molecules are found to exhibit, in their excited state, a pyramidal conformation with the carbonyl oxygen atom pointing outward with respect to the molecular plane. Finally, the HPHF procedure is applied to estimate core excitations in the SF6 molecule.
1 INTRODUCTION
As is well known, the restricted Hartree-Fock model (RHF) has the form of a single Slater determinant built up with doubly occupied orbitals which minimize the total energy [1]. This model may be used without any problem to determine the electronic energy and structure of closed shell molecular systems in their fundamental singlet state. It presents, however, the disadvantage of predicting incorrectly the molecular dissociation into ions instead of neutral atoms, because of the orbital double occupation. Thus, it should not be used for studying chemical reactions which involve bond breaking.
One way to overcome this difficulty is to use different orbitals for different spins (DODS model). This technique introduced, into the Hartree-Fock scheme, gave rise to the unrestricted Hartree-Fock model (UHF), the wave-function being written as an open shell single Slater determinant[2]:
where the spinorbital of different spins, ai, and ![]() , may have different spatial functions:
, may have different spatial functions:
The procedure to obtain the UHF spinorbitals is exactely the same as that for the RHF ones, except that two pseudo-eigenvalue equations have to be solved simultaneously by successive iterations:
and

where Jiq and Kiq are the usual Coulomb and Exchange operators, and the lack or presence of the upper bar means that the operators are constructed with α or β spinorbitals, respectively.
The UHF energy is expected to be lower than the RHF one, but in the case of closed shell systems close to the equilibium geometry, the UHF energy usually coincides with the RHF one. This feature produces a sort of discontinuity in the potential energy curve the internuclear distance when increases.
In addition, the UHF function has the defect of not being an eigenstate of the total spin operator, ![]() , so that it is not a pure spin function but, rather, a superimposition of states of different multiplicities:
, so that it is not a pure spin function but, rather, a superimposition of states of different multiplicities:
As is well known also, this new inconvenient may be overcome by projecting the Slater determinant on the singlet space [3]. The projection can be performed before or after the minimization procedure. The latter (PUHF), however, does not avoid the problem of the discontinuity in the potential energy curve. In addition, it does not furnish a wave-function which corresponds to the energy minimum.
The determination of the spinorbitals after an orthogonal projection gave rise to the projected Hartree-Fock model (PHF), proposed by Lowdin in 1955 [3].
When an DODS Slater determinant of n electron pairs is projected on a spin space of spin quantum number S, its projection takes the form of a linear combination of ![]() Slater determinants:
Slater determinants:
where the Cp are the well known Sanibel coefficients which depend only on the S quantum number and on the number of electron pairs. The second sum runs over the k permutations corresponding to p transpositions, and the first sum runs over all the possible transpositions [4].
The determination of such a wave-function is very involved and has been studied by some authors [5,6]. Notice that the Sanibel coefficients are not variational parameters but constant, this feature is the defect of the model.
On the other hand, a linear combination of only two DODS Slater determinants in which all the α and β spins are interchanged, was shown to produce similar results [7].
Taking advantage of the symmetry properties of the Sanibel coefficients, this linear combination (6) was seen to contain only spin eigenstates with even S quantum number, i.e, singlets, quintuplets, etc..:
Because this new model is equivalent to a projection on half of the spin space, it is called the Half-Projected Hartree-Fock model (HPHF). The corresponding projection operator can be written easily in the following way [8]:
where ![]() is an operator which permutes all the ai and bi functions of a same electron pair.
is an operator which permutes all the ai and bi functions of a same electron pair.
It can be easily verified also that, ![]() is a projection operator which depends only on the parity of the spin number S:
is a projection operator which depends only on the parity of the spin number S:
where ![]() projects on the even spin space; and
projects on the even spin space; and ![]() projects on the odd spin space.
projects on the odd spin space.
Finally, it must be mentioned that the HPHF function is invariant under any unitary transformation applied to the orbitals because all permutations of the spin functions are performed [8].
The HPHF function is indeed not a pure spin function, but, in the ground state the wave function for singlets will not contain any triplet component which is usually the largest contaminant in the DODS function. Furthermore, it may be expected that, in the ground state, the quintuplet contamination will be very small because of its high energy. Different procedures have been developed and applied successfully to small molecular systems [8–11]. A review on this subject is given in Ref.[12].
In addition, the two-determinantal form of the HPHF function suggests the use of this model for the direct determination of the lowest singlet excited states. In this aim, a procedure similar to that for the ground state was developed and successfully applied to small molecular systems [13–16]. In these calculations, the HPHF model was shown to yield much better results than single excitation CI calculations [15].
2 THE HPHF FUNCTION FOR THE SINGLET GROUND STATE
2.1 The Brillouin Theorem
The first attempt to determine the HPHF orbitals was analogous to the procedure used initially for the PHF orbitals [5]. For this purpose, the Brillouin procedure was extended to the PHF scheme. Two sets of occupied orbitals, each of them associated with different spin functions, are written in terms of a limited basis:
In the same way, the virtual orbitals corresponding to the complementary space can be expressed as:
The trial occupied orbitals are then corrected in terms of the virtual ones:
and introduced in the PHF function which is developed in terms of single, double, triple,…, excitations.
where Ψopt are the Slater determinants in which an occupied orbital, ap, has been replaced by a virtual one, at, and so on. The corrections cpt and c′pt are then determined by minimizing the total energy.
The conditions which minimize the energy are obtained by setting the partial derivatives with respect to the corrections equal to zero:
There are as many equations as corrections. These equations are not linear. Their solutions would yield the exact PHF orbitals in the functional space of dimension m, but they are unmanageable.
However, whenever the starting orbitals, aop and bop, are sufficiently close to the solutions, the terms of second and higher order in the corrections may be neglected in (14). As a result, the conditions (14) become linear and nonhomogeneous. The solution of this system will provide new improved orbitals, that may be used to start an iterative process. When selfconsistency is reached, the corrections are zero. The conditions (14) take the form:
These requirements on the matrix elements are precisely the generalized Brillouin conditions for the PHF functions [5]. They are very general and hold also for all the DODS type funtions such as the HPHF function, as well as for the RHF function.
2.2 The Pairing Theorem
Since the HPHF function is invariant under an unitary transformation applied to the orbitals ai or/and bi, both sets may be conveniently transformed so that the orbitals belonging to different electron pairs are orthogonal:
Such orbitals are known as corresponding orbitals [4].
As a result, the overlap between the HPHF function with itself may be expressed as:
where:
2.3 The HPHF Equations
In order to deal with the HPHF equations, it is convenient to define a series of operators analogous to those of the UHF model:
In these expressions, ![]() ,
, ![]() and
and ![]() are the usual monoelectronic coulombic, bielectronic coulombic and exchange operators, respectively.
are the usual monoelectronic coulombic, bielectronic coulombic and exchange operators, respectively. ![]() and
and ![]() are the one-particle density operators expressed in the ai and bi orbital basis:
are the one-particle density operators expressed in the ai and bi orbital basis:
In the same way, ![]() is a cross density operator between both basis sets:
is a cross density operator between both basis sets:
With these definitions, the total HPHF electronic energy may be easily written down:
where EUHF should be the one-DODS-determinant energy and Ecross, the interaction energy between both determinants:
From the energy expression for the HPHF function (23), the pseudoeigen-value equations for the HPHF orbitals may be easily deduced resorting to the Generalized Brillouin Theorem expression [10]. This theorem has been shown to be valid for any MCSCF function [17] and, in particular, for a two determinant SCF function [7,8]:
where Ψ is now the HPHF function for the singlet ground state and is Ψit a HPHF function in which an ai occupied orbital has been replaced by a virtual one at.
This expression may be rewritten in terms of the two DODS functions and, taking into account the idempotency of the operator ![]() (9):
(9):
Developing this last expression in terms of the corresponding orbitals, we have
We can now express this equation in compact form as:
A similar equation may be written for the bi orbitals.
Since ΨHPHF is invariant under an unitary transformation, two canonical sets of ai and bi, which diagonalize the matrix representation of ![]() and
and ![]() operators, may be chosen:
operators, may be chosen:
The expression (26) was developed in Ref. [10], and it is possible to show that it is equivalent to the diagonal of expression given by Smeyers et al. [11,18].
In matrix form, expression (26) may be rewritten as:
where S is the overlap matrix between the basis functions used for expanding the orbitals.
The procedure is carried out by diagonalizing the Ha and Hb matrices in an alternated way just as in the UHF procedure until the convergence is reached.
2.4 Some Applications to Singlet Ground States
Because of the complexity of the PHF function, only very small electronic systems were initially considered. As first example, the electronic energy of some four electron atomic systems was calculated using the Brillouin procedure [8]. For this purpose, a short double zeta STO basis set, 1 s, 1 s’, 2 s and 2 s’, with optimized exponents was used. The energy values obtained are given in Table 1. In the same table, the RHF energy values calculated with the same basis are gathered for comparison. It is seen that the PHF model introduces some electronic correlation in the wave-function. Because of the nature of the basis set formed by only s-type orbitals, only radial correlation is included which account for about 30% of the electronic correlation energy.
Table 1
Electronic energy (in a.u.) for some four electron atomic systems calculated into the RHF, PHF and HPHF approximations.
| RHF | PHF | HPHF | |
| Li− | -7.42655 | -7.44087 | -7.44085 |
| Be | -14.57213 | -14.58556 | -14.58560 |
| B+ | -24.23644 | -24.24959 | -24.24946 |
| C++ | -36.40718 | -36.42013 | -36.41955 |
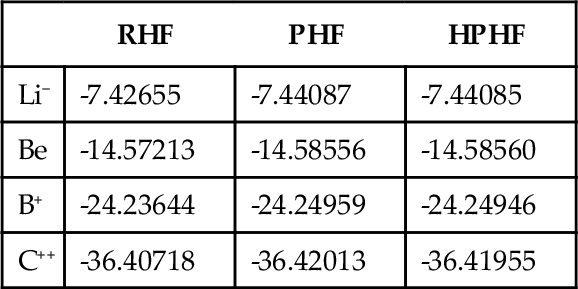
In the same table, the HPHF energy for the same systems obtained with the same basis are also given. It is seen that the HPHF model furnishes energy values very close to the PHF ones with much less work and less computation time.
The HPHF potential energy curve calculated as a function of the nuclear separation in lithium hydride is given in Figure 1. Six STO’s as basis functions, 1 s, 1 s’, 2 s, 2pσ, on the Li atom, and 1 s and 2pσ on the H atom, with adjustable exponents, were used. In the same figure, the RHF potential energy curve obtained in the same conditions is also represented. It is seen that the HPHF curve dissociates correctly into neutral atoms, whereas the RHF ones does it incorrectly into ions. The HPHF model is seen to introduce some alternant correlation effects in the wave-function.

It is interesting to point out that models such as the PHF and HPHF ones, which resort to orthogonal projection are able to open only one electronic shell, i.e., they are able to introduce either radial or alternant correlation [19]. This is the limitation of these models. To introduce simultaneouly both effects non-orthogonal projection operadors have to be used [20].
3 THE HPHF EQUATIONS FOR EXCITED STATES
The two-determinant form of the HPHF function suggests the use of this model to determine singlet excited states. There is indeed no simple method for the direct determination of the singlet excited states analogous to the UHF for the triplet with MS = 1.
The HPHF wave-function for singlet excited states is constructed by simple substitution of an ak or bk occupied orbital by an at or bt orbital of the virtual space in the two determinantal DODS function:
The deduction of the HPHF equations for excited states gives rise to a new challenge, since the excited orbital bt is usually orthogonal to the occupied one ak. As a result, one of the overlap λi in equation (14) could be zero, (or close to zero) which will give rise to singularities.
In order to solve this problem, we adopted a procedure originally developed for biradicals [21]. New cross Fock and density operators are defined:
Finally we have:
and for the energy:
where
With these new definitions, the HPHF equations may be easily written in matrix form as:
A similar expression for the Hob matrix is obtained by interchanging the a and b indices in (35).
The HPHF program structure is similar to that of the standard UHF program except for the presence of additional cross Fock matrices, Fab and Fba. The corresponding orbitals have to be restored at each cycle of the iterative process.
The HPHF procedure was initially applied to excited states with symmetry different from that of the ground state. When the symmetry is the same, special care has to be taken in order to avoid the variational colapsing into the ground state [22].
There are different techniques for avoiding this problem. One way is to orthogonalize the excited orbital bt to the occupied orbital ap of the same shell, at each stage of the iterative procedure:
The HPHF procedure for determining the orbitals of a singlet excited state is remarkably stable and converges very quickly. Usually, twenty iterations yield reasonable values of the total electronic energy.
4 APPLICATIONS
4.1 The Lithium Molecule excited states
In an attempt to check the performance of the HPHF model for determining singlet excited states, most of the excited states of the lithium molecule, L12, were determined as a function of the nuclear separation, and their spectroscopic constants evaluated. In this aim, the standard 6-311G* basis set was used for all of them [15].
In Fig.2, the corresponding potential curves are represented, including that of the C1Σg+ state with identical symmetry as that of the ground state.

Table 2
The equilibrium distances, Re, (in oA), the force constants, ωei (in cm−1) and the anharmonicity constants, ωexe, obtained by using the HPHF and other methods are given for some singlet states of the lithium molecule, together with the experimental values.
| State | Methods | Re | ωe | ωexe |
| X1Σg+ | RHF HPHF MCSCF Exp. | 2.784 2.931 2.692 2.673 | 343.17 259.71 347.1 351.43 | 2.96 1.66 - 2.61 |
| A1Σu+ | HPHF MCSCF Exp. | 3.106 3.13 3.108 | 270.09 254. 255.47 | 1.40 - 1.58 |
| B1 ∏ u | HPHF MCSCF Exp. | 2.884 3.050 2.936 | 325.76 288. 270.12 | 1.46 - 2.67 |
| C1Σg+ | HPHF CCSD | 3.182 3.56 | 256.30 137. | 0.138 - |
| D1 ∏ g | HPHF MCSCF | 3.183 4.161 | 258.19 83. | 1.80 - |

In this table it is seen that the values obtained in the HPHF approach for the spectroscopic constants of Li2 in its first singlet excited state are especially satisfactory when compared with the MCSCF and experimental values. The values for higher excited states are not so good, probably because of the contamination of higher spin states, as well as the use of a basis set built up essentially for the ground state. Finally, it is noticeable that the values found for the ground state are not satisfactory at all, this result is generally observed when using DODS functions, which rise to a too flat potential energy curve.
4.2 Cyclobutanone and Cyclopentenone in their first singlet excited states
As a test for checking the effectiveness of the model, we have applied the procedure and determined the optimal geometries of two relatively large molecules: cyclobutanone and 3-cyclopenten-l-one [16], which are well known in their first (n → π*) excited state [23–26].
To optimize the geometry, we used the Simplex method recently implemented into the HPHF program [27].
4.2.1 Cyclobutanone
Cyclobutanone was considered in both the singlet fundamental and the first excited (n → π*) state [16]. The geometry was fully optimized, at the RHF and HPHF levels, respectively, using a dummy atom at the center of the molecule (X), and the minimal basis set [7 s,3p/2 s,1p] [28].
The following restrictions were imposed during the optimization: (i) the molecule was symmetric with respect to a plane perpendicular to the C2C4C4 molecular plane; (ii) the hydrogen atoms, H4’, and H4” were in this plane, H2’ and H4’ were in the XC2H2” and H4”C4X planes, respectively; (iii) the bond length C – H was the same for all hydrogens, as well as the HCH bond angle.
The optimal geometrical parameters of this molecule in its fundamental singlet and its first excited state are given in Ref. [16], where it is seen that the fundamental singlet state exhibits a planar conformation with the carbonyl oxygen atom lying very approximately in the C2C2C4 plane. In contrast, the excited state (n → π*) shows a pyramidal conformation, with the C1 = O bond pointing outwards and forming a wagging angle of α = 38.66° with its projection in the molecular plane C2C1C4, in very good agreement with the experimental data 41°, 42° and 39° [23–26].
In order to evaluate the energy dependence on the wagging angle, the RHF and HPHF calculations were repeated in both states at some critical values: for the gound state at ± 40°, and for the excited state at 0° with the oxygen atom fixed in the molecular plane.
The most relevant results are given in Table 3, where it is seen that the ground state exhibits a single minimum, whereas the excited state presents a double minimum with an inversion barrier height of 1,362.2 cm−1, in reasonable agreement with the experimental data: 1,940, 1,850, and 1,550 cm−1 [23–25]. In the same table, the mean total spin momentum for < S2 > is given. It is seen that the HPHF method yields practically a pure spin function for the singlet excited state.
Table 3
Main geometry parameters (in °A or degrees), barrier heights (in cm−1), and S2 mean values for cyclobutanone and 3-cylopenten-l-one in their fundamental and lowest singlet excited states.
| Molecules | Parameters • | Planar So (RHF) | Pyramidal S1; (HPHF) |
| Cyclo-butanone | α C1 = O C1-C2 O-C1-C2 Barrier < S2> | 0.0117 1.2791 1.6311 134.48 - 0.0 | ± 38.66 1.5410 1.5058 118.55 1,362.2 0.0885 |
| 3-Cyclo-penten-l-one | α C1 = O C1-C2 O-C1-C2 Barrier < S2 > | 0.003 1.2867 1.6169 126.03 - 0.0 | ± 30.26 1.5233 1.5185 118.265 895.6 0.0803 |

• The UPAC atom numbering is used.
4.2.2 3-Cyclopenten-1-one
In the same way, 3-cyclopenten-l-one was considered in both the singlet fundamental and the first (n → π*) excited states. The geometries were also optimized at RHF and HPHF levels, respectively, using the same basis set [28].
The following restrictions were imposed during the optimization: (i) the molecule was symmetric with respect to a plane perpendicular to the molecular plane C2C1C5. H2' and H5' were in the XC2H2' and H5C5X planes, respectively; (ii) the H3′ and H4′ atoms were in the C3C4X1 plane; (iii) finally, two values for the bond lengths C – H were considered according to the hybridization.
The results are presented in Ref. [16]. As expected, the fundamental singlet state exhibits a planar conformation [23], with the carbonyl oxygen atom lying approximately in the molecular plane. In contrast, the singlet (n → π*) excited state shows a pyramidal conformation, with the C1 = O bond forming an angle of α = 30.26° with the molecular plane, C2C1C5, in very good agreement with the experimental data: 26° and 33° [23,26].
In the same way the energy dependence on the wagging angle was evaluated by performing, RHF and HPHF calculations in both states at some critical values: for the ground state at ± 30°, and for the excited state at 0° with the oxygen atom fixed in the molecular plane.
The main results are given in Table 3, where it is seen that the ground state presents a single minimum, whereas the excited state exhibits a double minimum with an inversion barrier height of 895.6 cm−1 in very good agreement with the experimental data: 966 and 780 cm−1 [23,26].
In the same table 3, the mean total spin momentum is given. It is seen that the HPHF method furnishes practically a pure spin singlet function.
4.3 Core excitations
Finally, the applications of the Half-Projected-Hartree-Fock model have not to be limited to the excitations of the valence electron shell. This model can also be used to study core electron excitations. This aspect is especially interesting, since there are very few efficient methods for such calculations in molecular systems [29,30].
In order to illustate this possibility, the SF6 molecule, for which there exist experimental data has been tested [31]. For this purpose different basis sets for the different excitations have to be used. For 1 s excitations in the central sulfur atom, the standard chlorine atom basis was employed for describing all the sulfur electrons. For the 2 s or 2p excitations in the same atom, the chlorine atom basis was employed for describing the sulfur L and M shells. The corresponding excitation values are given in Table 4.
Table 4
HPHF excitation energies for different states of the SF6 molecule, semi-empirical and experimental values] in a.u.), as well as the mean < S2 > values.
| Core Excitations | Semi-empical calculations | Flexible basis | Experimental | < S2 > |
| 1S → t1u | 91.678 | 91.524 | 91.358 | 0.170 |
| 2 s → t1u | 9.008 | 8.838 | 8.838 | 0.105 |
| 2p → a1g | 6.467 | 6.253 | 6.331 | 0.091 |
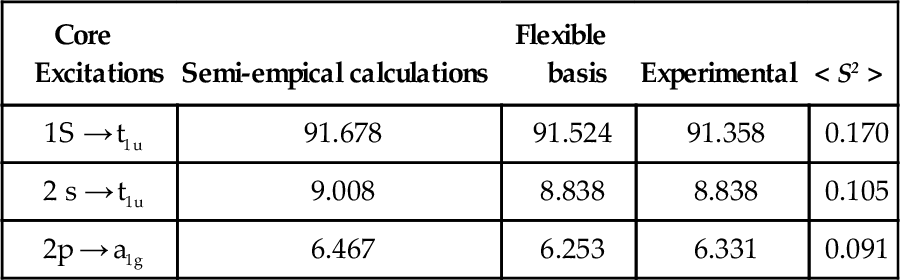
It is seen that the HPHF model reproduces satisfactorily the core excitations in SF6, even better than some semi-empirical procedures [32]. The mean total spin momentum values are seen also to be very small.
5 DISCUSSION AND CONCLUSIONS
Throughout this paper the HPHF model is described and applied to determine the optimal geometry of the first singlet excited state of some molecular systems. The procedure yields only one electronic state in each calculation but it is found to converge quickly. The results are in relatively good agreement with the available experimental data. The procedure permits also the use of different basis sets for the different states.
The model permits to determine spectroscopic constants, as well as to optimize the geometry in the lowest excited singlet state. The theoretical structures, inversion angles and barrier heights obtained for cyclobutanone and tures, inversion angles and barrier heights obtained for cyclobutanone and 3-cyclopenten-l-one compare surprisingly well with the available experimental data.
Finally, the HPHF model permits also to determine core excitation in molecular systems.
It may thus concluded that this procedure can be advantageously used to determine the lowest singlet excited states of large molecules to which more sophisticated methods could not be easily applied.
ACKNOWLEDGEMENTS
The author gratefully acknowledges the Spanish DGICIT for the financial support by the Grant PB96-0882.