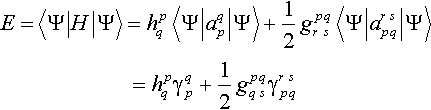Electron correlation at the dawn of the 21st century
Werner Kutzelnigg; Pasquale von Herigonte Lehrstuhl für Theoretische Chemie Ruhr-Universität Bochum, D-44780 Bochum, Germany
Abstract
The history and the present state of the treatment of electron correlation is reviewed. For very small atoms or molecules calculations of higher than spectroscopic accuracy are possible. A detailed account for many-electron methods in terms of one-electron basis sets is given with particular attention to the scaling of computer requirements with the size of the molecule. The problems related to the correlation cusp, especially the slow convergence of a basis expansion, as well as their solutions are discussed. The unphysical scaling with the particle number may be overcome by localized-correlation methods. Finally density functional methods as an alternative to traditional ab-initio methods are reviewed.
1 Introduction
One of us [1] reviewed the situation of electron correlation a quarter of a century ago in a paper with the title ’electron correlation in the seventies’ [2]. At that time most quantum chemists did not care about electron correlation, and standard methods for the large scale treatment of electron correlation, like Møller-Plesset (MP) perturbation theory or coupled-cluster (CC) theory were not yet available. However precursors of these methods such as IEPA (independent electron pair approximation) and CEPA (coupled-electron-pair approximation) had already been developped and were being used, mainly in research groups in Germany [3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13].
A quite spectacular progress has been achieved since then, but electron correlation is still the severest bottleneck on the way to accurate quantum chemical results.
Electron correlation means everything that goes beyond the independent particle model for electrons, i.e. which is due to the correlation of the motion of the individual electrons [14]. There has been some controversy on whether or not electron exchange should be regarded as part of the correlation. (For a recent discussion of this aspect see ref. [15]). We adopt here the view that electron exchange is taken care of by the independent particle model and is not part of the electron correlation.
High accuracy of quantum chemical calculations not only requires a satisfactory treatment of electron correlation, but also relativistic and beyond-Born-Oppenheimer effects need to be considered [16, 17, 18]. These are not in the scope of the present review. We further concentrate on correlation effects on the energy (and on quantities directly derivable from potential energy surfaces) and we ignore correlation effects on properties, which is in important subject at present [19]. We further shall report more on the calculation than on the interpretation of correlation effects.
The correlation problem is more or less solved for systems with up to, say, four electrons. For these, calculations involving all interelectronic coordinates are possible such that one can satisfy all cusp conditions [20] and rapid convergence to numerically exact values is achieved. Sec. 2 of this review will deal with these systems. For medium-sized molecules one knows, in principle, what one should do. However, the computer resources for methods which are routinely available, scale so unfortunately with the size of the molecule and converge so slowly with extension of the orbital basis, that their application is rather limited. We shall review these classical methods of CI (configuraton interaction) type in sec. 3. There seems to be a solution at least to the poor convergence with the size of the basis, namely to use explicitly correlated wave functions, either with linear terms in the electronic coordinates such as in the R12-methods, or by using so called Gaussian geminals. These methods and the related approximation schemes will be the topic of sec. 4. A possible way out of the scaling problem lies in the use of localized-correlation methods, to which we come in sec. 5. Finally sec. 6 is devoted to density functional methods which allow to account for correlation effects in an economic but rather uncontrolled way. An outlook to the future closes this review.
2 Electron correlation in very small atoms and molecules
A very compact and highly accurate wave function for the ground state of the He atom has already been constructed by Hylleraas long ago [21]. He expressed this in terms of the coordinates r1, r2 and r12 with r1 and r2 the distances of the first and second electron from the nucleus, and r12 the distance between the electrons. Thus the cusp conditions [20] could be satisfied. Essentially in the same philosophy Pekeris performed a calculation on the He-ground state [22], that remained an undisputed landmark for quite some time. A progress beyond this was possible when analytic properties of the exact wave function of a three-particle system (one nucleus and two electrons) were taken into account, which were ignored in earlier formulations. The keyword to this is Fock expansion and it requires terms that are logarithmic in the coordinates [23, 24, 25].
Including such terms Frankowski and Pekeris [26] needed only a 246 term wave function to be more accurate that Pekeris in his original work with more than 1000 terms. The performance was even superseded by Morgan and coworkers [27] who obtained the non-relativistic He ground state energy with 13-figure accuracy. One may celebrate this as an example where a careful study of properties of the exact wave function can inspire an improved computational method, had there not been the more recent work by Drake [28, 29, 30, 31], who obtained an even higher accuracy with a rather simple-minded ansatz using a linear combination of two Hylleraas type wave functions with different orbital exponents,
that was rather a result of a fortunate incident, and for which it is hard to give a justification in terms of physical principles. Meanwhile an 18-figure accuracy has been achieved [32, 33, 34] and this does not appear to be the end [35], where the ansatz by Goldman [35] which involves r< and r>, looks particularly promising.
Recently Rychlewski and coworkers [36] have been able to achieve a similar accuracy as Pekeris even with a wave function of Gaussian geminal type
For He 12-figure accuracy was reported [36, 16]. This is surprising since this ansatz neither fulfills the nuclear cusp nor the correlation cusp conditions. Although it is not yet fully understood why this works, some preliminary comments can be made.
It is well understood that expansions in orthogonal functions such as the famous Fourier expansion are extremely sensitive to singularities of the function to be expanded [37, 38]. The cusp singularities of electronic wave functions are at the origin of the slow convergence of CI-like expansions (see sec. 4). Alternatively to Fourier type expansions there are expansions that can best be rationalized as discretized integral transformations [39, 40]. For these the convergence behaviour is much different, in particular there is practically no sensitivity to singularities. The expansion in Gaussian geminals is obviously of this type.
We can mention only briefly, that hardly for He itself, but for the He isoelectronic series relativistic corrections and even QED (quantum electrodynamic) effects become important with increasing Z [41, 42, 43].
The first application of the Hylleraas method to the H2 molecule by James and Coolidge appeared in the first volume of J. Chem. Phys. [44]. The accuracy was later pushed further by Kolos and Wolniewicz, with whose names the theory of the H2 molecule is intimately linked [45, 46]. The first triumph of this group was a slight disagreement with the experimental dissociation energy of Herzberg et al. [47], which made Herzberg reconsider his analysis of the spectra, and confirm the theoretical prediction. The most recent calculations are really spectacular [48, 49]. However, also for H2, Rychlewski et al. [36] using a Gaussian geminal expansion, were able to beat this accuracy. They thus invalidated the common belief, that H2 is a special case insofar as one can use elliptical coordinates and an ansatz for the wave function that satisfies all cusp conditions, and that this is the reason for the much better performance for H2 compared to all other molecules.
The H3+ ion is a two-electron system like He or H2, but it has resisted an accurate quantum chemical treatment much longer. On table 1 one can follow the history of the accuracy achieved for the energy of the H3 ground at its (equilateral triangular) equilibrium geometry with re = 1.65a0. For a while the conventional calculation (of CI type – see sec. 3 – and not including interelectronic coordinates) of Meyer, Botschwina and Burton [50] was a landmark, in particular as to a full potential surface of this system. Microhartree accuracy was only achieved in 1993 [51, 52]. Two years later the accuracy could even be pushed by two more decimal places [53]. At this level of accuracy, non-Born-Oppenheimer effects can no longer be neglected, especially if one wants to compare theoretical and experimental rovibronic spectra [54], but this is not the topic of the present review.
Table 1
Accuracy of the ground state energy of H3+ at the equilateral triangular equilibrium geometry (re = 1.65ao)
Until 1970 -1.3….. Eh
Until 1980 -1.34… Eh
Until 1990 -1.343… Eh
1991/92 -1.343 8 Eh
1993 (Bochum) -1.343 835. Eh
1995 (Poznan) -1.343 835 624 Eh
(after ref. [51])
In the context of H3+ one must mention the Monte-Carlo calculations by Anderson [55]. In fact, these authors were also able to achieve microhartree accuracy for H3 at its equilibrium geometry. However, calculations of this type are extremely demanding as far as computer resources are concerned, and a potential energy surface for H3+ has not been computed by this method.
Interesting 3-electron systems are the Li atom and the H3 ground state surface. H3 is not a bound molecule, but essential for an understanding of the simplest chemical reaction H+H2 → H2+ H. For Li 10-figure accuracy was recently achieved with a generalization of the Hylleraas ansatz [56, 57]. The saddle point of H3 has been evaluated with 7-figure accuracy (i.e. with an error of ~ 10 microhartree) with Monte-Carlo [58] and Gaussian geminals [59] methods, but for the whole surface only conventional calculations of CI-type [60, 61, 62, 63, 64, 65] are available, for which the absolute error is of the order of ~ 1 millihartree. An extension of the MC calculation [58] to a full surface appears to be in progress [66].
As to 4-electron systems there has been special interest in the Be atom and the van-der-Waals interaction in He2. In a paper with 9 authors from 8 groups [67] the exact nonrelativistic energy of the Be ground state was estimated rather than computed. Meanwhile this energy could also be computed with microhartree accuracy [68, 69, 70]. A somewhat disappointing message has been that CCSDT (see sec. 3) is not sufficient and that linked quadruple excitations contribute as much ~ 90 microhartree to the ground state energy of Be [71].
The potential curve of He2, has been a big challenge to quantum chemsitry, since the potential well of the van-der Waals interaction is only 11K, i.e. an extremely small fraction of the total energy. If one uses a method which accounts for the energy of an He atom with an error of, say, 1 millihartree (≈ 300 K) one can hardly expect a reliable result for the interaction energy, unless one can rely on a controlled error compensation.
Two highly accurate calculations are available, one by van Mourik et al. [72, 73] the other by Klopper and Noga [74]. Further recent calculations are those of ref. [75, 76]. These can be compared with a potential curve constructed from experimental and theoretical data by Aziz et al. [77]
3 Many-electron methods in terms of one-electron basis sets
3.1 Full CI
There is a method which allows one to solve – at least in principle – the Schrödinger equation of an n-electron system. The recipe is to choose a basis set of m orbitals or 2m spin orbitals and to construct all possible n-electron determinants from this basis. Their number is ![]() . One expands the Hamiltonian in this basis and diagonalizes it. This is called full CI (CI for configuration interaction). Next one increases the dimension of the orbital basis such that eventually it becomes complete (more precisely complete in the lst Sobolev space [78]) and proceeds until convergence of the lowest eigenvalue(s). In the limit of a complete basis full CI becomes complete CI and virtually exact [79]. Unfortunately this method is completely inpracticable. For large m the number of Slater determinants increases as ~ mn/n!, i.e. exponentially with the electron number n.
. One expands the Hamiltonian in this basis and diagonalizes it. This is called full CI (CI for configuration interaction). Next one increases the dimension of the orbital basis such that eventually it becomes complete (more precisely complete in the lst Sobolev space [78]) and proceeds until convergence of the lowest eigenvalue(s). In the limit of a complete basis full CI becomes complete CI and virtually exact [79]. Unfortunately this method is completely inpracticable. For large m the number of Slater determinants increases as ~ mn/n!, i.e. exponentially with the electron number n.
It is clear that full CI is only possible for relatively small basis sets. In view of this the progress in full CI calculations [83, 84, 85] is rather impressive. The main practical interest in full CI is to use it as benchmark to check the performance of approximations to full CI for the same basis, with the hope that good approximations to full CI can then be used successfully with larger basis sets.
The scaling of the computational effort with the number n of electrons (we shall henceforth simply say n-scaling) is particularly unfortunate for full CI, other current methods scale – as we shall see – as some power nk of n. There is evidence that one does something basically wrong if one uses a method that scales unphysically with the particle number n, where it remains to be seen what is a physical n-scaling. If one compares calculations of related molecules with a different number N of similar atoms, the number n of electrons scales essentially with N such that n-scaling and N-scaling show the same pattern. One is also interested in the scaling with the number m of basis functions. This has a different meaning depending on whether one compares calculations on one system with constant n and varying m, or whether one consider different systems consistently with m essentially proportional to N.
The improvement of the n-scaling will definitely be one of the great challenges to quantum chemistry in the 21st century.
The n-electron wave function is a rather complicated quantity and it contains much more information than is usually needed. In order to evaluate the energy one has – in a modern Fock space notation [86, 87] –
Here apq etc. are excitation operators with respect to an orthonormal spinorbital basis {ψp}, while hqp and grpsq are one- and two-particle matrix elements
with h and g the one- and two-particle parts of the Hamiltonian respectively, and γpq, γprqs and the one- and two-particle density matrices respectively
In the above expressions the Einstein summation convention is implied.
When the one electron basis {ψp} on which our Fock space is built, is finite (of dimension 2m), the Hamiltonian H given by (3) is exactly that of full CI [87]. The eigenfunctions and eigenvalues that one obtains in full CI, are the eigenfunctions and eigenvalues of this Hamiltonian.
3.2 The 2-particle density matrix and the n-representability problem
The number of density matrix elements γprss scales with m4, i.e. it does not directly depend on n. However, since m should be choosen roughly proportional to n, there is a scaling ~ n4. If it were possible to take the γprqs rather than the CI coefficients as variational parameters, we would have got rid of the scaling problem of full CI. Unfortunately the γprqs cannot be regarded as variational parameters, unless one can impose conditions which guarantee that a γ-matrix is derivable from an n-particle wave function. This n-representability problem has played a big role in the late sixties and has been most thoroughly been formulated by Coleman [88, 89]. Unfortunately a simple solution of the n-representability problem which allows one to replace the n-electron wave function Ф by the two-particle density matrix γprqs, in a variational approach has not been found. Note that γpq is not independent of γprqs, but can be derived from this by partial contraction
Although the idea to formulate the n-electron problem in terms of density matrices has been more or less abandoned, it is likely that it will be revived in the future, especially in view of the success and the limitations of the much more simple-minded density functional approaches (see sec. 6). For interpretational purposes the density matrices have always been rather central quantities [90, 91, 92, 93, 94, 95].
The eigenfunctions and eigenvalues of {γqp} are known as natural spinorbitals and their occupation numbers [80], those of {γrpsq} the natural geminals and their occupation numbers.
For typical closed shell atoms or molecules {γqp} is close to idempotent, i.e. its eigenvalues are either close to 1 or to 0. In this case a single determinant Ф built up from the n first natural spin orbitals (with occupation numbers close to 1) is a good first order approximation to the exact Ψ. Then Hartree-Fock theory, in which < Ф|H|Ф > is minimized with respect to variation of the orbitals contained in Ф, is a good first order approximation. In fact, everything not contained in Ф means electron correlation.
For Ф a single Slater determinant all information is contained in its one particle density matrix [96]. For this special case we use ![]() instead of γ.
instead of γ.
If one defines a two-particle cumulant matrix
and analogously higher order cumulants [15, 97, 98], a simple Slater determinant wave function is characterized by vanishing of all cumulants. Obviously the two-particle cumulant describes two-particle correlations etc.. On the basis of cumulants [15] which are (at variance with the k-particle density matrices) extensive (additively separable quantities) a definition of the correlation energy is possible that does not require a single Slater-determinant reference state and the corresponding Hartree-Fock energy. We define
Where the non-correlated energy Enc is of the same form as the Hartree-Fock energy, but with {γqp} the exact one-particle density matrix, which is usually not idempotent. This concept has not yet been applied in practice.
3.3 Many-body perturbation theory
Noting that full CI is – in principle (when the basis limit is reached) – exact but unfeasible (except for very small basis set), and that Hartree-Fock is feasible, but a very crude approximation, some compromise between these two extrema has to be found.
One possibility is to use perturbation theory, truncated at some low order. There are various options for perturbation theory applied to an n-electron system. One of them consists in dividing the Hamiltonian H in the following way into an unperturbed Hamiltonian H0 and a perturbation V
On this partition many-body perturbation theory (MBPT) as developed by Brueckner, Goldstone and others is based [99, 100, 101, 102, 103, 104]. This is also the basis of the Z-dependent perturbation theory of atoms of Layzer and others [105, 106, 107]. Strictly speaking one should distinguish between a perturbation theory in terms of the original Hamiltonian (not projected to a finite one-electron basis) and perturbation theory of the Fock space Hamiltonian in a finite basis, which is equivalent to perturbation theory of the matrix eigenvalue problem of full CI. When one refers to perturbation theory for electron correlation, almost exclusively the latter choice is implied, and we shall only consider this option.
The partition (14) corresponds to treating the bare nuclear Hamiltonian (BNH) as unperturbed and the entire electron interaction as perturbation. It is much better (i.e. leads to better results to low orders and gives a better overall convergence pattern), to include part of the electron interaction in H0. Again there are various possibilities, but the Møller-Plesset partition [108, 109, 110] has turned out to be most convenient. Here
where ![]() qp are density matrices corresponding to a Hartree-Fock reference function Ф, and where
qp are density matrices corresponding to a Hartree-Fock reference function Ф, and where ![]() and
and ![]() are excitation operators with respect to Ф as so-called physical vacuum. These have the property
are excitation operators with respect to Ф as so-called physical vacuum. These have the property
and are related to the apq and aqrps with respect to the genuine vacuum as [111, 97]
For the Møller-Plesset partition the first order perturbation vanishes
If one chooses canonical orbitals, for which fqp is diagonal
the second order energy is simply
with i,j counting spin-orbitals occupied in Ф, a, b virtual spin-orbitals.
Only doubly excited configurations
contribute to E2. Also E3 only requires double excitations, while for the evaluation of E4 triple excitations are needed and so forth.
MP-perturbation theory is formally simple to low orders, but becomes increasingly complicated to higher orders. The most serious drawback is that convergence of MP-PT is by no means guaranteed. Depending on the choice of the basis, divergence can be enforced or avoided [112, 113], which indicates that much that one finds may be an artifact of the matrix representation, that has other singularities – which determine the radius of convergence – than the original Hamiltonian. Anyway even if the MP-PT series converges, convergence may be very slow [114] and one cannot break up the series, unless sophisticated extrapolation methods are used.
Actually only MP2 has become a kind of standard, MP3 is regarded as hardly superior to MP2, while MP4 is occassionally used, but it requires about as much computational effort as the usually much better CCSD(T) method.
Let us also mention that, independent of the partition of H that one chooses, always the Rayleigh-Schrödinger form of PT is used, because – at variance with the Brillouin-Wigner PT – it is extensive (connected). See later.
3.4 Coupled-cluster and related methods
Related to perturbation theory are methods that have been inspired by perturbation theory, but which are essentially non-perturbative. Early attempts on these lines were partial summations of certain classes of diagrams [115] (in a diagrammatic formulation of MBPT), where it was not always clear whether these diagrams were summed because this was formally easy or because these diagrams were regarded as particularly important. More simple-minded but rather effective has been selective CI based on arguments from MP-PT [116].
Noting that to the leading orders of MP-PT only doubly excited configurations Φiajb contribute, one can decide to do better than MP2 or MP3 by including all Φiajb in a CI (i.e. variational) calculation. The number of unknown coefficients scales then as n2m2, i. e. essentially as n4, while the overall computational effort goes as n4m2 i.e. essentially as n6. The scaling is much better than for full CI, but the quality of the result is, of course, much poorer. One can so define a hierarchy of CI methods, called CI-SD, CI-SDT, CISDTQ etc. where S, D, T, Q stands for singly, doubly, triply, quadruply excited configurations. This hierarchy has the advantage over MP-PT that it does converge to full CI if one let the excitation rank go to the number of electrons. This is, however, just what one wants to avoid.
A serious disadvantage of these truncated CI schemes is that they are not extensive (size consistent). This means essentially that the energy of a supersystem consisting of two identical subsystems at large distances computed by CI is not twice the energy of the subsystem. For a system of N He atoms at mutually infinite distance the correlation energy goes for large N not as ~ N but as ~ ![]() [12, 117].
[12, 117].
The size-consistency problem has been removed by using the coupled cluster (CC) ansatz [12, 118, 119, 120, 121, 122, 123, 124, 125]. While in CI one writes the wave function as (in intermediate normalization)
in CC theory the formulation is
If one truncates the CI expansion one gets a result which is variational, but not extensive, one can truncate the CC-expansion (in the exponential) without loosing extensivity. It is then, however, practically impossible to be variational as well [125]. Like for CI one can define CC-SD, CC-SDT, CC-SDTQ etc. The n-scaling of the computational demands is similar to that for the corresponding steps in the CI hierarchy. Like for the CI hierarchy the CC hierarchy also converges to full CI if the excitation rank goes to n, but the convergence is definitely faster.
While CCSD has become a kind of standard, full CCSDT calculations [126, 127, 128] are still too computer-resource demanding that their use is limited to rather small basis sets. Among the simplifications of CCSDT, the CCSD(T) method [129] has become very popular. There single and double substitutions are treated non-perturbativity, but triple substitutions by means of perturbation theory. An alternative to CCSD(T) is CCSD[T] – formerly called CCSD+T(CCSD) – that is probably better [131], although formal arguments are rather in favour of CCSD(T) [130]. While CCSDT scales with n8 (and CCSDTQ with n10), CCSD(T) and CCSD[T] scale only with n7, which matters a lot. CCSD(T) is these days regarded as the best that one can do for sufficiently small molecules. Nevertheless cases have been reported, where CCSD(T) is definitely not enough, e.g. if one wants to evaluate the harmonic vibration frequency of HF with an error of less than 1 cm-1 [131].
Closely related to CC theory (and also to MP-theory) are the IEPA [3, 10, 12] and CEPA [11, 12, 13, 132, 133, 134] methods, that were used in molecular calculations prior even to the large scale studies in terms of MP2. IEPA (independent electron pair approximation) has in common with MP2 that the various electron pairs are decoupled, and MP2 has, in fact, been a first step on the way to IEPA [3, 10, 12]. Unlike in MP2 the various decoupled pairs are treated exactly (in the limitations due to the use of a finite basis) in IEPA. In CEPA (coupled electron pair approximation) the coupling of the pairs is taken into account, but unlike in CCSD, to which CEPA is closely related, some (generally small) indirect couplings are ignored. Although CEPA can be formulated as an approximation to CCSD [11, 12], in practical applications it has turned out that CEPA performs even better than CCSD (although it is cheaper), because apparently effects of triple substitutions are, to some extent simulated in CEPA [135, 136]. IEPA and CEPA share with MP and CC that they are extensive and not variational.
It is often forgotten that the probably first large-scale ab-initio implementation of CCSD by Taylor et al. [120] was based on the CEPA code of Ahlrichs et al. [13]. As to a comparison of CEPA and CC methods see [137]. We come back to an interesting aspect of IEPA and CEPA in sec. 5.
Closely related to CEPA are the method of self-consistency electron pairs (SCEP) [138] and also the coupled-pair functional approach (CPF) [139].
3.5 Multi-configuration-based methods
Most of the effort in coupled-cluster theory has concentrated on systems which are essentially of closed shell type, where the wave function is dominated by a single Slater determinant Ф, such that the wave function can be expanded around this Ф and good convergence is expected.
The situation is much more complicated if to 1st order a single Slater determinant is not sufficient and rather a multiconfiguration reference Ф must be used. A completely satisfactory coupled-cluster theory for this case has not yet been formulated. This has both fundamental and practical reasons.
Among the fundamental reasons is the dilemma that the most straightforward formulation of an extensive theory leads inevitably to the appearance of the intruder problem and that it is hard to eliminate this problem without violating extensivity. In fact extensivity requires a Fock space formulation with a multiplicatively separable wave operator [12, 87]. This means that one formulates the wave operator and an effective Hamiltonian for the full valence space, for all possible particle numbers, i.e. that one uses a so-called valence universal theory. However then one can generally not avoid that external orbitals (i.e. which are not not in the valence space) get energies close to those of valence orbitals and dangerous energy denominators arise. These intruder problems are largely avoided in a state-specific theory limited to a single state, but this means to loose a formulation in Fock space and extensivity is no longer guaranteed. This dilemma has been analysed in detail by Mukherjee, [140, 141] who has also discussed possible solutions, which we can only mention without going into details. One possibility is the use of intermediate Hamiltonians, mainly proposed by Malrieu et al. [142], but see also refs. [143, 144]. Another possibility consists in the use of incomplete model spaces [145, 146, 148], a disadvantage of which is that they can usually not be applied to potential energy surfaces, since for different ranges of geometry different incomplete model spaces must be used. There are further methods in the framework of a state universal theory both for complete and incomplete model spaces [149, 150, 151], which are somewhat intermediate between valence universal and state specific, and which are to some extent based on the projection of a Fock space theory to a Hilbert space for finite particle number. Particularly promising appears the combination of extensivity and a state-specific theory using the recently developed concept of normal ordering (and the corresponding Wick theorem) with respect to a multiconfiguration wave function[15, 97, 98]. On this line there are certainly challenges for the next century.
From a practical point of view one has to decide whether one chooses a contracted [152, 153] or uncontracted excitation scheme. In the latter the number of excitations to include is tremendous, in the former one must find a way how to deal with the so-called excitations with spectator-lines (unless one neglects these, which appears to be justified to some extent). Contracted means that one considers formal single, double etc. excitations with respect to the full MC-SCF wave function Ψ, e.g. aqpΨ, arpsqΨ, uncontracted means that one decomposes Ψ into a sum of Slater determinants and takes the excitations with respect to these.
As long as a satisfactory multireference coupled-cluster theory is missing, there are various options for states that need a zeroth-order multiconfiguration wave function. One possibility is to start from an MC-SCF calculation and to improve this by selected CI. Since the MC-SCF part is basically extensive, while the CI part is not, and since one can hardly go beyond external double excitations, one tends to include as many configurations in the MC-SCF part as possible. However, MC-SCF is usually of CAS (complete active space) [154] type, e.g. like full CI, which restricts the possible size of the active space. Such multireference CI scheme have been very popular for describing excited states, reaction barriers, dissociation processes etc.
Another possibility is to start from MC-SCF and to improve it by means of perturbation theory. The most popular approach on these lines is CASPT2 of Roos et al. [155]. This is almost extensive and one is not obliged to make the active space as large as possible.
One can further try to formulate a generalization of CEPA or rather CPF to a multiconfiguration reference function. On these lines the average coupled pair functional (ACPF) has been derived by Gdanitz and Ahlrichs [157]. A straightforward MC-CEPA method has been proposed by Fink and Staemmler [158]. This is extensive, while ACPF is only approximatively so.
One can finally try to apply single reference CC, but to go to very high excitations, at least selectively [159]. It is hard to avoid a lack of balance in such treatments.
In this context one should also mention the rather old MRD-CI-method of Buenker and Peyerimhoff [160]. There one starts from a multideterminant reference function and improves it by CI with single and double substitution. This method has not been designed for single states, but rather for the computation of various states simultaneously.
4 The convergence with the basis size and the R12 method
All methods discussed in the previous chapter have two difficulties, one – on which we have commtented already – is the convergence with respect to the sophistication of the level of the treatment of electron correlation (with the related n-scaling problem), the other is the convergence with the extension of the one-electron basis. We shall now concentrate on this aspect.
There are actually three types of expansions that one has to worry about
(a) The expansion in a Gaussian basis, which neither allows a correct description near the nuclei nor very far from them.
(b) The expansion of one-electron functions in a basis of eigenfunctions of angular momentum with respect to the atomic centers, i.e. essentially the LCAO expansion
(c) The expansion of the correlation cusp in a one-electron basis.
The expansion (a) is, contrary to what one might have expected, the least problematic. In fact, Gaussian basis sets were introduced, because they lead to simple two-electron integrals. On the other hand one knows that atomic orbitals are more like Slater type, i.e. exponential functions. Gaussians have the wrong behaviour both close to a nucleus and very far from it. The expansion of hydrogenic 1s function in an even-tempered Gaussian basis has been studied analytically [161] and the surprising result was found that the error ∆E of the energy depends on the number m of basis functions as
This is not as good as exponential, but almost as good. For properties other than the energy one gets a similar behaviour but with a different mk-factor in front and a different prefactor of ![]() in the exponential. Even the density at a nucleus has this convergence behaviour, although
in the exponential. Even the density at a nucleus has this convergence behaviour, although ![]() at r = 0 has an error indepent of m and
at r = 0 has an error indepent of m and ![]() at r = 0 diverges with n.
at r = 0 diverges with n.
The expansion (b) has not been studied in a formal way. A rather detailed unpublished investigation of R. Franke and one of the present authors on the H2+ ion has shown numerically [162] that the error of an expansion in atomic s,p,d etc. functions appears to converge exponentially. There is some evidence that this holds for all one-electron problems, especially for Hartree-Fock. It is, for not too large molecules, not too difficult to saturate a basis and to get sufficiently close to the Hartree-Fock limit at least for the energy.
Much more critical is the expansion (c). The simplest case is that of 2-electron atoms such as He ion their 1S ground states. Here it could be shown that for an expansion
the l-increments to the energy go as [163, 164]
This is an extremely slow convergence and is related to the fact that the exact wave function has a correlation cusp [20], i.e. a discontinuous first derivative at r12 → 0, such that
If one includes explicit linear r12-dependent terms in the wave functions and expands only the remainder [165] as in (29), the l-increments of the remainder go essentially as  at leaf at the level of 2nd order perturbation theorty, which is a substantial improvement.
at leaf at the level of 2nd order perturbation theorty, which is a substantial improvement.
It is difficult to derive the asymptotic behaviour of ∆El by purely numerical studies. One of the reasons for this is that for increasing l, the number of terms in the (n, n′)-expansion necesscary to reach convergence increases with l. In practical calculations one rather does the opposite, i.e. one uses smaller n-expansions for larger l, and one gets so the impression of a much faster convergence than that found analytically. Therefore empirical extrapolations [166, 167, 168, 169] to l → ∞ are rather dangerous. Extrapolations based on exact properties are, however, a serious alternative to the use of R12 methods. An interesting approach on these lines is the CBS (complete basis set) extrapolation method of Petersson et al. [170].
One should also mention that the  dependence of ∆El only holds for typical singlet states, for triplet states ∆El goes as
dependence of ∆El only holds for typical singlet states, for triplet states ∆El goes as ![]() and for non-natural-parity singlet states even as
and for non-natural-parity singlet states even as ![]() [164].
[164].
The slow convergence plagues all CI-type calculations. Since in view of the unfortunate scaling of the computational effort with the number of basis functions, one cannot choose very large basis sets, one cannot use CI-type methods if one strives at high accuracy. There are essentially three ways to overcome this problem.
(a) One uses wave functions with explicit linear r12-terms to describe the correlation cusp correctly. The brute-force variant of this approach is known as Hylleraas-CI [171]. It leads to a large number of difficult integrals, even 3- and 4-electron integrals in addition to the 2-electron integrals needed in conventional SCF or CI calculations. Therefore it has so far only been applied to systems with 2 electrons, or slightly beyond this.
(b) It is however possible to use tricks to avoid the difficult integrals, without introducing unacceptable errors. This leads to the R12 methods[172, 173, 174, 175, 176, 177, 178, 179, 180, 181]. The variant MP2-R12 allows one to reach the MP2 basis limit with comparably little effort, and with an increase of the computer time with respect to a conventional MP2-calculation with the same basis by only a factor ~ 5. In the case of CCSD-R12 vs. conventional CCSD the extra computer time for the same basis is only ~ 30% of that of the conventional calculation, but the gain in accuracy is spectacular. The best method available so far is CCSDT1-R12, but also the more approximate CCSD(T)R12 and CCSD[T]-R12 methods [181] can be used.
An essential ingredient of the R12 methods is the systematic introduction of completeness insertions in such a way that (i) 3- and 4-electron integrals don’t arise explicitly, (ii) the results become exact in the limit of a complete one-electron basis, (iii) the basis truncation error decreases much faster with the size of the basis than in conventional calculations, such that much higher accuracy is achieved with less computational effort. The only disadvantage is that no strict upper-bond property holds, but this does not even hold for conventional coupled-cluster calculations. There is no stronger limitation of the size of the system to be computed than for conventional CC calculations. Typical examples of applications of R12-methods were to the Ar-benzene complex [176] or to (H2O)3 [177].
In a systematic study of 10-electron molecules and ions [178] the total energies for CCSD[T]-R12 calculations turned out to agree within less than 1mEh with the experimental non-relativistic energies.
For details on the R12-methods the reader is referred to recent reviews [179, 180] and original papers [172, 173, 174, 175, 176, 177, 178, 181]. The R12-method has been combined successfully with the ACPF approach by Gdanitz [182].
(c) An alternative to the use of linear ri,j-terms as in the R1‘2 method, is the method of Gaussian geminals. Here one introduces correlation factors of the form
With such functions it is not possible to satisfy the correlation cusp exactly, but all integrals that arise, including three and four-electron integrals, can be evaluated in closed form. The convergence of this kind of expansion is much faster than that of a CI It is possibly similar to that of the expansion of 1s hydrogen wave function in a Gaussian basis. The Gaussian geminal method has been implemented e.g. for MP2 and CCSD [183, 184, 185, 186]. A rather difficult practical problem is that of the choice of the optimum non-linear parameters γ. This has so far been inhibited the application of the Gaussian geminal method beyond HF [185] or H2O [186]. The technique of Rychlewski et. al. [36] to optimize non-linear parameters has to the authors’ knowledge not yet been applied in this context.
For Hartree-Fock calculations alternatives to basis expansion methods, e.g. finite elements or finite differences have been used successfully. It does not appear straightforward to use such methods for the treatment of electron correlation, because for the lowest-level treatment of electron correlation, i.e. pair theory, one has a 6-dimensional problem, and this is hard to treat by finite-element or finite difference methods.
5 Localized correlation methods
The scaling with the number of particles is one of the most serious problems for all methods to treat electron correlation. Unfortunate scaling is, however, if one looks carefully, in most cases avoidable, and is a result of uneconomic computer codes.
For a long while it was believed that SCF calculations have to scale with N4, because the rate-determining step is the construction of the two-electron integrals (pq|rs) and their number is proportional to m4 with m the number of basis functions, and m scales with the number N of atoms. Let us henceforth assume that we consider a molecule with N atoms and q basis functions per atom such that m = N ⋅ q, with q constant.
One must be aware that the accuracy of a computation is limited by the number of significant figures with which numbers are stored in the computer. Since one cannot completely avoid small differences of large numbers, one looses a few figures anyway. It is convenient to impose a threshold defining the final accuracy that one wants to have. Quantities, say in a sum, which are smaller than that threshold, don’t contribute and can as well be ignored. It now turns out that the number of (pq|rs) integrals above a given threshold scales – for sufficiently large N— only with m2 (and hence N2) rather than m4, so the majority of the m4 integrals can safely be ignored. A particularly powerful screening of integrals has been proposed and coded by Häser and Ahlrichs [187].
If one goes one step further, one realizes that there are two types of integrals, namely Coulomb-like long range and exchange or hybrid-like short range integrals. One can take advantage of this and evaluate Coulomb type expressions by a multipole expansion. This has been exploited by Almlöf [188] in a formulation for large molecules.
Further progress with the multipole expansion has been achieved recently, which allows linear scaling for the electron interaction. [189, 190, 191].
It has almost been a dogma that post-Hartree-Fock methods (which treat correlation effects) require at least a N5 scaling. The origin of this is that the time-determining step for MP2 (as the simplest post HF method) is an integral transformation from the integrals (pq|rs) over basis functions to integrals over MOs. In fact a classification of MOs into occupied and virtual ones is at the basis of this formulation. The MOs used conventionally are delocalized and this means that all MO integrals have roughly the same order of magnitude, and no prescreening is possible. So although of ~ m4 AO integrals only ~ m2 are non-negligible, one has to take care of ~ m4 MO integrals. The integral transformation, however, is a ~ m5 step.
It is obvious that the problem is the delocalized nature of the MOs. Fortunately it has been known, based on the work of Lennard-Jones [192] and worked out mainly by Edmiston and Ruedenberg [193] and also by Foster and Boys [194], that it is possible to transform the (occupied) MOs to localized orbitals (LMOs) which span the same space, and which are orthogonal to each other, but which are mainly localized in rather restricted areas of space.
LMOs have been used in the IEPA- and CEPA-formulations by Ahlrichs et al. [3, 10, 12, 13], and the main difference in philosophy between the early work of Ahlrichs et al. and Meyer [11], is that the latter has preferred a delocalized formulation in terms of canonical MOs. Nevertheless the question of approximate invariance between a localized and a delocalized description has played an important role to justify the so-called CEPA-2 variant as slightly superior to CEPA-1 [11, 12].
In IEPA, like in MP2, one pair is treated at a time, in CEPA the coupling between the pairs is treated iteratively, with in each iteration cycle again one pair treated at a time. The number of pairs scales as n2 for delocalized MOs, but only as ~ n (for a large enough molecule). Take e.g. a linear chain molecule with one MO per atom, then the diagonal pairs k, k will denominate, followed by pairs k, k + 1, then k, k + 2 etc. such that one can truncate at k, k + v with v fixed, and k variable. The number of pairs to be considered goes then roughly as v ⋅ n. So using localized MO and screening the pairs according to their importance improves the scaling with respect to pairs of canonical MOs. The effort per pair then still goes as m4, which is the number of two-electron integrals that have to be processed. The scaling problem was actually solved in IEPA-PNO or CEPA-PNO, where one expanded the functions for one pair in pair natural orbitals (PNOs), a kind of optimized virtual orbitals for the various pairs. Their number was kept fixed, so the PNOs were a kind of localized virtual MOs, although they are not orthogonal [3, 12, 152]. An extension to infinite systems was recently proposed by Fink and Staemmler [195].
The N-scaling of CEPA was, in fact not bad, although not even the basic two-electron integrals were prescreened (since this was long before prescreening was discovered).
The methods which succeeded CEPA, i. e. essentially the hierarchy of CC methods, were formulated in terms of canonical MOs, hence very frustrating n-dependencies resulted. Only rather recently the advantage of the use of localized MOs were rediscovered and elaborated, mainly by Pulay [1961 and Werner [197].
If one succeeds in transforming not only the occupied but also the virtual MOs to a set of well-localized MOs, such that one can associate q (occupied and virtual) MOs with each atom, then one can argue that for the description of intraatomic correlation only excitations in this q-dimensional (and hence n-independent) subspace need to be considered. For interatomic correlations between a pair of neighboring atoms excitations with the 2q dimensional space of the MOs of the two atoms are necessary, and so forth. Correlations beyond next-nearest neighbors may be regarded as unimportant. The number of pairs of atoms to be considered scales with n, so the overall computational demands should scale with n as well, provided that also takes advantage of fast multipole expansion [190, 191] for the Coulomb interaction.
To arrive at linear scaling with n should be possible, and is one of the big challenges of methodologic quantum chemistry. Werner et al. have at least arrived at a n3-scaling, which is a big progress [197]. Linear scaling has been possible in density functional theory (see sec. 6). An interesting new approach towards linear scaling even for MP2 theory has very recently been formulated by Ayala and Scuseria [198], taking advantage of an idea of Häser and Almlöf [199].
A generalization of the concept of localized MOs is that of extremal pair functions [200]. They may play a role in the future in the context of well-scaling methods. So far the main application of extremal pairs have been in R12-theories in order to avoid near-linear dependencies [179].
Extremal pair functions are defined as linear combinations of a given set of (usually canonical) pair functions, such that they extremize some expectation value, e.g.
With this criterion the extremal pair functions appear as a generalization of the LMOs attributed to Foster and Boys. Restricting the extremal pair functions to the form
one is led to LMOs.
6 Density functional methods
6.1 History
Density functional (DF) [201] methods (for reviews see [202, 203, 204, 205]) were very popular in solid state physics since about 1965, but were hardly applied in chemistry for quite a while (among the applications to structural chemistry see e.g. ref. [206]), before suddenly around 1988 they really conquered chemistry. Even before this the rather good performance in solid theory did not remain unobserved by quantum chemists, but the reluctance to consider density functional methods more seriously had various reasons.
(a) The justification of density functional methods in terms of the Hohenberg-Kohn theorem [207, 208, 209] appeared somewhat unorthodox and had a touch of mystery.
(b) DF methods performed surprisingly well at rather low cost. The results were usually superior to those of Hartree-Fock calculations, i. e. correlation effects were somehow taken care of, but not as accurately as in standard quantum chemical methods.
(c) There appeared to be no way to improve DF calculations systematically, when they were not good enough. The usual DF schemes did not appear to be steps in a hierarchy that eventually lead to an exact theory.
(d) A precursor of DF methods, the X α-scheme [210, 211] had been used in quantum chemistry before, but got a rather bad reputation, mainly due to overselling and the marriage with muffin-tin potentials [212].
(e) The existing DFT-codes of the first generation were numerically often rather inaccurate. Therefore calculations with one code could not be reproduced by another code, using, of course, the same functional. More serrious was that the limited numerical accuracy made the calculation of potential curves rather problematic.
Things changed drastically when independently Becke [213] and Perdew [214] invented new gradient-corrected functionals, which performed much better than the previously used local density functionals and which turned out to be competitive with MP2 at a cost somewhat lower than that of SCF calculations. Various groups implemented DF calculations taking advantage of all the knowhow of traditional quantum chemistry, in particular using expansions in a Gaussian basis, and shortly afterwards DF codes became available in commercial program packages. Also the problems of accurately (and reproduceably) evaluating the exchange correlation functionals were solved [215, 216, 217]. Further the evaluation of energy derivatives became routine [218, 219]. For a black-box user it is now as easy to perform an SCF as a B3LYP calculation. ’B3LYP’ stands for Becke-3-parameter for the exchange part and Lee-Yang-Parr for the corelation part. It is one of the most popular density functionals for use in chemistry and is implemented in the commerical GAUSSIAN program package.
The attitude of most users is pragmatic. One does not worry why DF methods work and uses them as one uses other methods implemented in the same black box. There are quite a few different functionals available and one can choose between them depending on the problem that one wants to solve, where the superiority of one functional over another is usually based on statistical comparison with experiment rather than on formal arguments. This pragmatic attitude is encouraged by the fact that some of the density functionals in current use, contain parameters that were adjusted to fit experimental data. This – in order not to say more – puts DF schemes in the neighborhood of semiempirical methods.
The density functionals which perform best at present, like B3LYP are mixtures of Kohn-Sham type functionals (see later) and Hartree-Fock functionals and exploit the fact that Kohn-Sham type functionals tend to overestimate binding, while Hartree-Fock underestimates it.
The acceptance of DFT by the ab-initio community necessarily implied some change of paradigm. In the ab-initio world it had always been regarded as problematic and even as a kind of cheating if one got good agreement with experiment due to a fortunate cancellation of errors (unless this cancellation was ’controlled’). In DFT one can judge the quality of a functional only from a comparison of the results wit experiment or with some benchmark calculation. There is hence no criterion for the extent of error compensation on which the performance of the functional is based. So the refutation of error cancellation can hardly be maintained. Nevertheless if one wants to get ’the right answer for the right reason’ one should not rely on DFT.
6.2 The Hohenberg-Kohn theorem as a Legendre transformation
The essential problem with DF methods is to understand why they work, or rather which of their features is responsible for the good agreement with experiment in many cases. A systematic improvement but also a guide to scope and limitations rests on the answer to this question. Although some current studies concentrate on this aspect [220, 221, 222, 223], for the majority of people grown up with DF approaches even to ask this question is a kind of sacrilege. The argument often put forward is that density functional theory is exact – in principle – and that deviations from exact results are simply due to the approximations inherent in the used functionals. This argument, usually given with reference to the so-called Hohenberg-Kohn theorem, is rather meaningless and reveals a basic misunderstanding of the situation.
To appreciate what the Hohenberg-Kohn theorem [207] really implies it is useful to formulate it in a language that it is slightly different from that given in most papers in this field. The key reference is that to a study of E. H. Lieb [224, 225], who gave a mathematically rigorous analysis of density functional theory on the basis of the modern theory of convex functionals, in which the concept of a Legendre transformation plays a central role. This concept was, in a related context even been alluded to in a paper [208] contemporary with that of Hohenberg and Kohn. The main concern of Lieb was related to the appropriate definition of the domains of the important functionals E(V) and F(![]() ). In fact Lieb criticized Hohenberg and Kohn for having been somewhat too careless with these domains. Nevertheless we can here only give a nonrigorous presentation of Lieb’s approach, not worrying about the domains of E(V) and F(
). In fact Lieb criticized Hohenberg and Kohn for having been somewhat too careless with these domains. Nevertheless we can here only give a nonrigorous presentation of Lieb’s approach, not worrying about the domains of E(V) and F(![]() ) and other mathematical subtleties. Readers interested in the mathematical details are referred to Lieb’s original paper [225] or to the excellent survey by Eschrig [205].
) and other mathematical subtleties. Readers interested in the mathematical details are referred to Lieb’s original paper [225] or to the excellent survey by Eschrig [205].
Let us consider a family of (exact) Hamiltonians for the same number n of electrons. These Hamiltonians can only differ in the external potential V, we hence have a V-dependent family of Hamiltonians. Let us further assume that V is a continuous set of local (multiplicative) potentials, and that for the whole family of potentials considered, the ground state is non-degenerate (the latter restriction is actually not necessary). The energy E of the ground state is then a functional of V, i.e. E = E(V). It is also clear how one has to proceed to evaluate this functional: one constructs the Hamiltonians H(V), and solves the Schrödinger equations
for the respective ground states. E(V) is even defined if there is no bound ground state, but this possibility causes some problems. For a potential ![]() that only differs infinitesimally from a given potential V the change in E is given by 1st order perturbation theory as
that only differs infinitesimally from a given potential V the change in E is given by 1st order perturbation theory as
where ![]() is the electron density corresponding to ψ(V).
is the electron density corresponding to ψ(V).
It can easily be shown that (for fixed particle number) the functional E(V) is concave [205, 225], i. e. that
The functional derivative of the ground state energy with respect to V is the density
This relation between ![]() and V, together with (40) implies an invertibly unique mapping between V and ρ and suggests a change of variables (where the variables are functions) as is familiar from the Legendre transformation in thermodynamics (change from U(V, T) to H(p,T) with
and V, together with (40) implies an invertibly unique mapping between V and ρ and suggests a change of variables (where the variables are functions) as is familiar from the Legendre transformation in thermodynamics (change from U(V, T) to H(p,T) with  or classical mechanics (change from
or classical mechanics (change from ![]() to H(q,p) with
to H(q,p) with ![]() ). The corresponding change is now
). The corresponding change is now
The functional F(![]() ) is the internal energy, i. e. the total ground state energy minus the interaction of the ground state density with the external potential. It is equal to the sum of the kinetic energy and the electron interaction energy. The internal energy F(
) is the internal energy, i. e. the total ground state energy minus the interaction of the ground state density with the external potential. It is equal to the sum of the kinetic energy and the electron interaction energy. The internal energy F(![]() ) is independent of V and a functional of
) is independent of V and a functional of ![]() only. Hohenberg and Kohn have introduced the functional F(
only. Hohenberg and Kohn have introduced the functional F(![]() ) without seeing that (for appropriately chosen domains) it is just the Legendre transformation of E(V) and have given F(
) without seeing that (for appropriately chosen domains) it is just the Legendre transformation of E(V) and have given F(![]() ) the somewhat unfortunate name ’universal functional of the density’. Of course F(
) the somewhat unfortunate name ’universal functional of the density’. Of course F(![]() ) is a functional of
) is a functional of ![]() in the same sense as E(V) is a functional of V. There is no indication that there should be a simple and direct way to evaluate this functional.
in the same sense as E(V) is a functional of V. There is no indication that there should be a simple and direct way to evaluate this functional.
In spite of the universal nature of F(![]() ), a change of
), a change of ![]() can (we always have the exact expressions in mind) only be caused by a change of V. Only those
can (we always have the exact expressions in mind) only be caused by a change of V. Only those ![]() are admissible as arguments of F, which correspond to the considered V. Although F(
are admissible as arguments of F, which correspond to the considered V. Although F(![]() ) does not explicitly depend on V, it depends parametrically on V, and one finds that
) does not explicitly depend on V, it depends parametrically on V, and one finds that
since the variation of E with respect to variations of ![]() vanishes, provided that
vanishes, provided that ![]() is chosen such that it corresponds to the chosen V. Relation (43) actually allows one to invert the Legendre transformation and to arrive at E(V) starting from F(
is chosen such that it corresponds to the chosen V. Relation (43) actually allows one to invert the Legendre transformation and to arrive at E(V) starting from F(![]() ). This somewhat delicate nature of F(
). This somewhat delicate nature of F(![]() ) must be kept in mind if one really wants to appreciate density functional theory. The role of F(
) must be kept in mind if one really wants to appreciate density functional theory. The role of F(![]() ) is somewhat obscured if one regards E as a functional of
) is somewhat obscured if one regards E as a functional of ![]() . Since E depends both on V and
. Since E depends both on V and ![]() and since we are searching for the
and since we are searching for the ![]() which corresponds t o V the double dependence of E on g and V is somewhat confusing. It can be shown that (for an appropriately chosen domain) F(
which corresponds t o V the double dependence of E on g and V is somewhat confusing. It can be shown that (for an appropriately chosen domain) F(![]() ) + ∫ V
) + ∫ V![]() dτ is convex and hence attains its minimum for the exact
dτ is convex and hence attains its minimum for the exact ![]() , provided, of course, that F(
, provided, of course, that F(![]() ) is the exact (unknown) functional. This is known as the Hohenberg-Kohn variational principle. For a mathematically rigorous fomulation of the Hohenberg-Kohn theorem and especially of the Legendre transformation see [205, 225].
) is the exact (unknown) functional. This is known as the Hohenberg-Kohn variational principle. For a mathematically rigorous fomulation of the Hohenberg-Kohn theorem and especially of the Legendre transformation see [205, 225].
The main problem with F(![]() ) is that it is entirely unknown, that it is at least as complicated as E(V) which is unknown as well, and that there is no way how one should construct F(
) is that it is entirely unknown, that it is at least as complicated as E(V) which is unknown as well, and that there is no way how one should construct F(![]() ). One can formally decompose F(
). One can formally decompose F(![]() ) into three parts
) into three parts
(b) the Coulomb contribution to the electron interaction energy
(c) the remaining contributions to the electron interaction energy, i. e. the exchange and correlation energies.
Of these contributions only (b) happens to be known exactly, while for the other two one can at best best hope to approximate them somehow.
Density functional methods have been used even before the formulation of the Hohenberg-Kohn-theorem. The classical of these methods is the Thomas-Fermi model [226, 227, 228, 229]. It is based on an analysis of the homogeneous electron gas. This is characterized by a single parameter, namely the density ![]() (i. e. the number of electrons per unit volume), which is a constant, i.e. which is independent of the position
(i. e. the number of electrons per unit volume), which is a constant, i.e. which is independent of the position ![]() Other properties, like the density of the kinetic energy, must be expressible in terms of
Other properties, like the density of the kinetic energy, must be expressible in terms of ![]() , the kinetic energy density is e. g. proportional to
, the kinetic energy density is e. g. proportional to ![]() 2/3 and the exchange density to
2/3 and the exchange density to ![]() 1/3. These relations were applied to atomic theory, ignoring that the electron density in an atom is very far from homogeneous. Although various kinds of corrections were added to the simple Thomas-Fermi-model [228, 229], its success was very limited, it could e.g. not account for the shell structure of atoms and not for chemical binding [230]. A careful analysis has shown that the most serious defect of the Thomas-Fermi model lies in the approximation of the kinetic energy as a functional of the density. Even till now no acceptable expression of the kinetic energy as functional of the density has been proposed.
1/3. These relations were applied to atomic theory, ignoring that the electron density in an atom is very far from homogeneous. Although various kinds of corrections were added to the simple Thomas-Fermi-model [228, 229], its success was very limited, it could e.g. not account for the shell structure of atoms and not for chemical binding [230]. A careful analysis has shown that the most serious defect of the Thomas-Fermi model lies in the approximation of the kinetic energy as a functional of the density. Even till now no acceptable expression of the kinetic energy as functional of the density has been proposed.
6.3 Slater-Kohn-Sham type methods
Modern density functional methods, that can be traced back to a paper by Kohn and Sham [231], avoid the evaluation of the kinetic energy as a functional of the density. One rather introduces an artificial non-interacting system – in a modified external potential – with the same density as the considered system and one evaluates the kinetic energy of this system as the kinetic energy of a Slater determinant. So the density functional methods in current use, are strictly speaking not genuine density functional methods.
An ingredient of Kohn-Sham type DF methods is that the modified external potential for the artificial non-interacting system should be local (multiplicative).
Since in DF methods the unknown is the density, only basis sets to describe the density well are required. So much smaller basis sets are sufficient than for the genuine many-body methods described in sec. 6.
If one evaluates the kinetic energy (a) in the indicated way (plus an unkown correction, since the two systems – i. e. the real and the artificial one – only have approximatively the same kinetic energy), the two remaining parts (b) and (c) cause less problems. In fact (b) is a genuine and universal density functional, and (c) is regarded as relatively small, such that it does not matter too much how one approximates this term.
A curious aspect is that the dominant part of the exchange-correlation contribution is the removal of the unphysical self-interaction of the electrons contained in (b). Attempts to leave this out from the very beginning, were not too successful and have become popular only recently.
All essential ingredients of the Kohn-Sham approach were already contained in the much older Xα method of Slater [210]. The main difference is that the Xα method was designed as an approximation to Hartree Fock theory, replacing the (non-local) exact Hartree-Fock exchange by a local approximation, inspired by Thomas-Fermi theory. It was then somewhat surprising that the Xα method performed often much better than the Hartree-Fock method that it was designed to approximate. The origin of this apparent superiority remained rather obscure for a long time. It has to do with the fact that in replacing the exact Hartree-Fock exchange by a local exchange one simulates to some extent the ’left-right-correlation’, that is ignored in the Hartree-Fock approximation. Now one tends to say that Xα should rather be regarded as a density functional theory of Kohn-Sham type. Therefore it appears fair to refer to this class of functionals as of Slater-Kohn-Sham type, and to regard Xα so to say as their ’zeroth generation’. That Xα did not turn out too successful, had less to do with its shortcomings, e.g. that it did not treat exchange and correlation separately, but rather with its somewhat unlucky marriage with the ’muffin-tin approximation’.
Following the paper by Kohn and Sham various types of local exchange-correlation functionals were used successfully in solid state physics and with moderate success in chemistry. A big step in advance, especially as far as chemical applications were concerned, came with the generalized gradient-corrected functionals of Becke [213] and Perdew [214].
Meanwhile one counts three generations of density functional methods, (in addition to Xα as zeroth order) namely
1. Local density (LD) functionals or local spin density (LSD) functionals
2. Generalized gradient-corrected (GGA) functionals
3. Optimized potential method (OPM).
While methods of the first generation were only of limited use for chemical applications, those of the second generation had a large impact on applied quantum chemistry. They were especially successful for transition metal compounds for which traditional quantum chemical methods has serious problems, due to the strong dependence of the correlation energy on the occupancy of the d-shell. Even systems with partially filled f-shells could be treated successfully by DFT [232].
Methods of the third generation have so far mainly been applied to atoms with rather good success, while for molecules they have not yet made the methods of the second generation obsolete. These involve to some extent orbital functionals [233, 234] rather than density functionals, and they are much closer in spirit to quantum chemical ab-initio methods than were the older DF methods. Like in older DF schemes one still insists on a local effective potential, but self-interaction is usually – unlike in the older schemes – eliminated, which makes the remaining exchange and correlation effects much smaller. In fact the bulk of the exchange contribution consists in eliminating the unphysical self interaction, that is characteristic for the older DF approaches.
In the OPM schemes one starts from a Hartree-Fock like exchange energy, but the energy is optimized under the restriction that the effective potential is local. So ’exchange only’ OPM is as close to Hartree-Fock theory as a scheme with a local potential can be.
If one tries to forecast the future of density functional theory, the following statements can be safely made:
1. Density functional calculations with black-box programs will become very popular, and this even for relatively large molecules, since one is now very close to linear scaling [235, 236] of the computational effort with the size of the molecule.
2. On the methodologic side there will be an increased pragmatic attitude, and functionals with adjustable parameters will continue to be proposed, so making the theory to a large extent semiempirical.
3. Simultaneously studies will be continued to understand the physical basis of DF theory better, in particular to understand which are the essential ingredients that make DFT work and whether it is possible to arrive at any desired accuracy. If one is very optimistic one will hope that a hierarchy of density functionals will be found, such that it is also possible to go to the next higher level, if the lower one was not good enough. At present one is very far from this situation. The history of DFT is rich in examples of improvements based on formal arguments which rather deteriorated the agreement with experiment.
4. There are indications that there may be some convergence between traditional attempts to solve the Schrödinger equation by ab-initio methods and the so far very different philosophy of DFT. The two approaches to manyelectron systems have so far almost been orthogonal and there was hardly a communication between them. For DF methods of the third generation this has drastically changed.
If one compares the attempts reviewed in sec. 3.2 to base many-electron quantum mechanics on the two-particle density matrix, i.e. a 2-particle density matrix functional theory with the current density functional theory one realizes that for the former the functional is exactly known, while the full n-representability condition is unknown. For DFT on the other hand, the functional is unknown, but the n representability does not cause problems. Why should one take incomplete information on n-representability as more serious as lack of information on the exact functional? Possibly there was just more reluctance in the two-particle-density matrix functional community to be satisfied with approximate n-representability conditions than in the density functional community to accept approximate density functionals, and that this different attitude was decisive for the historical development.
7 Conclusions
A quarter of a century ago electron correlation was a topic for a small group of specialists, now it is the main challenge on the way to accurate quantum mechanical calculations for atoms, molecules and solids. A corollary of this observation is that Hartree-Fock calculations no longer pose any serious problems, which was not the case some 25 years ago, when it did make sense to worry about the optimum implementation of Hartree-Fock theory.
The main difficulties with electron correlation, that are only partially solved are
(a) the poor convergence with extension of the one-electron basis
(b) the unphysical scaling of the computation effort with the number n of electrons or N of atoms
(c) the lack of a fully satisfactory theory for those situations where a closedshell Slater determinant has to be replaced by a multiconfiguration reference function.
As to problem (a) it is at least understood that the basic difficulty is caused by the correlation cusp and that much better convergence is obtained if one uses wave functions depending explicitly on the interelectronic coordinates. The problem of difficult integrals can be avoided in the R12-methods, or possibly by using Gaussian geminals. One may also think of improved extrapolation techniques based on the known behaviour of the wave function for rij → 0.
The unphysical scaling (b) is one aspect of the fact that in standard quantum chemical computations one actually calculates more than is really needed. If one succeeds in ignoring everything that is irrelevant, one will have got rid of the scaling problem.
Even problem (c) is now being understood in principle, and satisfactory solutions will probably be found.
So far calculations of correlation effects are rather expensive, but hopefully this is going to change. As long as a rigorous improvement of ab-initio methods has not been achieved, it will be hard for these methods to compete with density functional approaches. These have the advantage of being relatively cheap. Even if they are often not exceedingly accurate, the price-performance ratio can hardly be beaten.
At the time of our first review [2] it would hardly have been possible to predict the progress obtained in a quarter of a century. This is a warning as to predictions for the next period of about the same lengths. One has to admit that the past progress was to a large part due to the improvement of computer hardware, and only to a smaller part the merit of theoretical chemists. In the next 25 years or so the progress in methodological development will probably become more important than that of computer technology.
The main challenge as to an improved theory of electron correlation as a basis of accurate numerical quantum chemistry have been mentioned in this review, namely (a) the explicit treatment of the correlation cusp, (b) the formulation of methods that scale with a low power of the number of particles, (c) the consistent combination of MC-SCF-theory for the nondynamic and coupled-cluster methods for the dynamic correlation.
Whether density functional methods will become dominating or whether eventually they will be replaced by genuine many-body methods is hard to predict. Possibly the two approaches will converge to a new simple and rigorous theory of the electronic structure of atoms and molecules.
Although electron correlation is still the main bottleneck toward a rigorous quantum chemistry, one should not forget that for molecules containing heavy elements relativistic effects are not less important [17], while for molecules with lighter atoms adiabatic and even non-adiabatic effects need to be considered [18]. The theory of both types of effects is, fortunately on a good way.
It has been the aim of the present review to concentrate on what we regard as the essential aspects. If we had cared to be complete as to methods that have been proposed to treat electron correlation, we would have had to add other methods, e.g.
(a) Valence bond (VB) approaches. There is a small, but rather convinced community that is in favour of VB [237, 238] as an alternative selection of configurations in a CI type formalism with a more complicated but also more compact structure with less variational parameters. The problems characteristic for CI, such as slow convergence with the basis size related to the correlation cusp are also shared by VB.
(b) So-called fully numerical methods [239, 240] of the type finite differences (FD) or finite elements (FE). Such methods perform very well for onedimensional problems where they are among the most accurate ones. For multidimensional problems there are serious difficulties. Since correlation in an arbitrary molecule is at least a 6D problem much progress is needed for FD or FE to become competitive.
(c) Monte-Carlo (MC) type methods. We have mentioned such methods in the context of H3. Monte-Carlo calculations have also been performed for somewhat larger small molecules [241, 242]. For recent reviews see [243, 244, 245]. That the big breakthrough of such methods has not yet come, is due to two difficulties, the node-problem and the different time scales for core and valence-electrons. For multiboson systems where the node-problem does not arise and where there is no shell structure, MC methods perform very well. If these problems will be overcome, MC methods have a chance to become competitive with the many-body approaches presented here in more detail. MC methods actually have less difficulties concerning the scaling with the molecular size, and they are rather easily implemented on parallel computers. This may compensate that they are generally rather computer-time consuming.
(d) Pseudopotentials or effective-core potentials (ECP). These are not really methods to treat correlations effects, and are hence not the subject of the present review, but they can simplify ab-initio methods considerably without much loss in accuracy.
(e) Dimensionality scaling [246, 247]. Here one considers a space of dimenion n > 3 and extrapolates finally to n = 3. This is intellectually very appealing. Whether it will gain a noticeable practical importance remains to be seen.
(f) Complementary to methods in which one cares for the energy of a single state, are approaches where energy differences between states are calculated directly. (For a review see [248], as to some fundamental work and more recent advances [249, 250, 251, 252, 253, 254, 255, 256]). From the point of view of electron correlation methodes of this type (often based on propagator, Green’s function or equation-of motion theory) exploit that the contributions to the correlation energy common to the two states don’t enter. The gain is probably not as spectacular as thought originally, but methods of this type will probably continue to play some role, e.g. for the treatment of open-shell states based on a closed-shell reference [252, 253, 254, 255, 256]).
(g) Methods for the treatment of electron correlation which are more popular in solid state theory than for molecules are reviewed in [257].
(h) Other unconventional methods are mentioned in [247, 258].
Possibly methods will become important that have not even be conceived so far.
Acknowledgments
The authors thank again the participants of the 1970 Ischia meeting on electron correlation. Their names, not mentioned earlier [2] are possibly more informative when given now. We remember the following participants
R. Ahlrichs, G. Berthier, W. A. Bingel, B. Cadioli, G. Del Re. P. Durand, M. Gelus, M. Jungen, B. Levy, J. P. Malrieu, R. McWeeny, W. Meyer, V. Staemmler
and apologize to all those whom we may have forgotten.
Some of the just-mentioned authors have collaborated with the present authors on electron correlation. In addition there has been collaboration in this field with many other scientists, especially F. Driessler, W. Klopper, S. Koch, H. Lischka, F. Maeder, J. D. Morgan III, D. Mukherjee, J., H. Reitz, R. Röhse, V. H. Smith and Ch. van Wüllen. For comments on the manuscript the authors are grateful to V. Staemmler, D. Mukherjee, R. Jaquet, and Ch. van Wüllen.