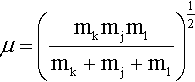1 Introduction

The modem theory of chemical reactions requires the treatment of the quantum mechanics of few bodies, an intrinsically multidimensional, non-separable problem. Accordingly, a proper choice of the coordinate system is of crucial importance for the theoretical approach to molecular dynamics. Introduction of alternative orthogonal coordinates allows the separation of the center of mass and thus the diagonalization of the kinetic energy tensor, leading to an essential simplification of the computational problems connected with the study of chemical reactivity and the mapping of potential energy surfaces [1,2]. The basic geometric theory of the modern approach to the N-body problem is reviewed in ref. [3].

In the following, we emphasize aspects which illustrate the development of the theory as an extension of the elementary theory of angular momentum. As the latter is basically founded on the group theory of rotations in ordinary spaces, tremendous progress has been achieved by properly mapping multidimensional problems on hyperspheres. This article is kept at an elementary level and technicalities are to be found in the quoted references. There it is demonstrated that the theoretical methods based on hyperspherical coordinates have turned out to be essential tools in the quantum mechanical treatment of the interaction between few particles, involving studies both of bound states and of scattering problems.

The recent application of hyperspherical and related coordinates to treat the dynamics on a reactive potential energy surface offers, in fact, the possibility of exploring also those regions where reaction paths present sharp curvatures or bifurcations, taking into account of dynamical quantum effects like tunneling and resonances. Several reviews available [4–10] provide a useful introduction to various aspects of the hyperspherical approach.

In the next two sections of this article we face the problem of separability or “near” separability of variables related to the solution of Schrodinger equation, giving the definition of adiabatic and diabatic representations which applies to the present context. Then we focus our attention on orthogonal coordinate systems starting with the Jacobi vectors for the three body problem and stressing the implication of their choices on the proper handling of the involved angular momenta. In the fifth and sixth sections we give an overview of the hyperspherical coordinates in their different parametrizations and provide the connections with hyperspherical harmonics, which are the eigenfunctions of hyperangular momentum in a hyperspherical diabatic representation. In section 6 we also explore the mapping of potential energy surfaces from the perspective of hyperspherical coordinates, enlightening the characteristics of the regions most relevant for the reaction dynamics.

In the final section we briefly describe some recent developments of the hyperspherical approach, such as the hyperquantization algorithm as an important computational tool for the solution of dynamical problems and the extensions of the hyperspherical method to treat the dynamics of reactions involving polyatomic systems.

2 Separation of radial and angular variables. Orbital angular momentum.

In order to treat properly those atomic and molecular processes, which involve large amplitude motions and even breaking and formation of chemical bonds, one has to face the failure of the nearly harmonic separation on which molecular spectroscopy is rooted. In any case it is basic to try to solve the Schrodinger equation introducing some sort of “near” separability of variables, so to transform a partial differential equation in a set of ordinary coupled differential equations in a variable of the propagation type. In general, this would correspond to find operators which nearly commute with the hamiltonian, giving approximately “good” quantum numbers related with the external or internal angular momenta of the system.

To prepare for proper generalizations, we reconsider a familiar case where exact separability of radial and angular variables is possible: the interaction of two particles, of mass m₁ and m₂, in a central field. Physically, this corresponds to the important example of elastic atom-atom scattering.

In three-dimensional space the positions of the two structureless atoms are specified by six coordinates which, after separating the motion of the center of mass, are reduced to three. Introducing the reduced mass μ of the system (μ = [m₁m₂/(m₁m₂)]^1/2), we obtain a hamiltonian which is the sum of a kinetic part represented by the Laplacian operator acting in a three-dimensional space plus a potential energy V (r), which is a function only of the distance, r, between the two particles:

$\left[-\frac{{\mathrm{\hslash }}^2}{2\mu }{\mathrm{\Delta }}^{\left(3\right)}+\mathrm{V}\left(\mathrm{r}\right)-\mathrm{E}\right]\mathrm{\Psi }=0$

The transformation of the Laplacian in polar coordinates introduces an effective simplification of the Schrödinger equation, here exploiting the separability of the radial coordinate from the angular ones. Here are the known formulas:

${\mathrm{\Delta }}^{\left(3\right)}=\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial y^2}+\frac{{\partial }^2}{\partial z^2}=\frac{{\partial }^2}{\partial {\mathrm{r}}^2}+\frac{2}{\mathrm{r}}\frac{\partial }{\partial \mathrm{r}}-\frac{1}{{\mathrm{r}}^2}{\mathrm{\Lambda }}_{\mathrm{ang}}^{\left(3\right)}$

where

$\mathrm{x}=\mathrm{r}sin\theta cos\varphi ,\mathrm{y}=\mathrm{r}sin\theta sin\varphi ,\mathrm{z}=\mathrm{r}cos\theta$

$\mathrm{r}={\left({\mathrm{x}}^2+{\mathrm{y}}^2+{\mathrm{z}}^2\right)}^{\frac{1}{2}},0\le \theta \le \pi ,0\le \theta <2\pi$

Separate solutions of the angular and radial parts of the equation are to be found. The former can be done analytically, and leads to the spherical harmonics (Y_l,m (θ, ϕ)) as eigenfunctions of the angular Laplacian:

${\mathrm{\Lambda }}_{\mathrm{ang}}^{\left(3\right)}{\mathrm{Y}}_{l,m}\left(\theta ,\varphi \right)=l\left(l+1\right){\mathrm{Y}}_{l,m}\left(\theta ,\varphi \right),l=0,1,2,\dots ,-l\le m\le l$

where l and m represent the “orbital” angular momentum quantum number and its projection on an axis fixed in the center of mass.

The wave function is the product of a spherical harmonic and the radial factor F_l(r) (a vectorial set):

$\mathrm{\Psi }=\frac{1}{\mathrm{r}}{\mathrm{Y}}_{l,m}\left(\theta ,\varphi \right){\mathrm{F}}_l\left(\mathrm{r}\right)$

For a general interaction, one has finally to solve the radial part of the Schrödinger equation

$\left[-\frac{{\mathrm{\hslash }}^2}{2\mu }\left(\frac{{\mathrm{d}}^2}{{\mathrm{dr}}^2}-\frac{l\left(l+1\right)}{{\mathrm{r}}^2}\right)+\mathrm{V}\left(\mathrm{r}\right)-\mathrm{E}\right]{\mathrm{F}}_l\left(\mathrm{r}\right)=0$

If, e.g., V(r) is a harmonic or Morse oscillator, or the Coulomb potential, as for the hydrogen atom, eq. (7) can be solved analytically, otherwise numerical solution is necessary, but involves only a one-dimensional integration and nowadays can be carried out routinely when needed, as for the analysis of elastic scattering experiments in atomic and nuclear physics.

3 Near separability. Adiabatic and diabatic representations.

The consideration that the velocity of electrons is much higher than that of the nuclei (a consequence of their much smaller masses) leads to the Born-Oppenheimer approximation, perhaps the better known example of the near separability of variables. We reconsider it in view of subsequent generalizations. Using the language of classical mechanics, we will speak of adiabatic separability, which can be shown to be related to a semiclassical expansion, i.e. to an asymptotic expansion in ħ. See references [11–14] where we also discuss a “post-adiabatic” representation.

Let us consider again the atom-atom interaction, but permit now the atoms to have a structure. Namely, allow now for inelasticities, and indicate with R the internuclear distance and with r the collection of vectors representing the electron-nucleus distances. We can write down the following Schrödinger equation:

$\left[-\frac{{\mathrm{\hslash }}^2}{2\mu }{\mathrm{\Delta }}^{\left(3\right)}-\frac{{\mathrm{\hslash }}^2}{2{\mathrm{m}}_{\mathrm{e}}}{\mathrm{\Sigma }}_{\mathrm{i}}{{\mathrm{\Delta }}_{\mathrm{i}}}^{\left(3\right)}+\mathrm{V}\left(\mathrm{R},\mathrm{r}\right)-\mathrm{E}\right]\mathrm{\Psi }=0$

where m_e is the mass of the electron.

Solving separately the electronic part of the equation for each fixed configuration of the nuclei, we obtain the spectrum of the electronic adiabatic eigenvalues ∈ _i^a, which depend parametrically on R, and have the meaning of potential energy curves

${\mathrm{H}}_{\mathrm{el}}{\varphi }_{\mathrm{i}}^{\mathrm{a}}\left(\mathrm{R},\mathrm{r}\right)={\in }_{\mathrm{i}}^{\mathrm{a}}\left(\mathrm{R}\right){\varphi }_{\mathrm{i}}^{\mathrm{a}}\left(\mathrm{R},\mathrm{r}\right)$

In practice, one considers only a limited number of the lowest lying eigenvalues and eigenfunctions ϕ_i^a, corresponding to the energy range of interest. It is then possible to factorize the wave function in terms of electronic and nuclear eigenfunctions:

$\mathrm{\Psi }={\mathrm{\Sigma }}_{\mathrm{i}}{\varphi }_{\mathrm{i}}^{\mathrm{a}}\left(\mathrm{r},\mathrm{R}\right){\mathrm{F}}_{\mathrm{i}}^{\mathrm{a}}\left(\mathrm{R}\right)$

where F_i^a(R) are now the solutions of a system of coupled second order ordinary differential equations:

$\left[-\frac{\mathrm{\hslash }}{2\mu }{\left(1\frac{\mathrm{d}}{\mathrm{dR}}+\mathrm{P}\left(\mathrm{R}\right)\right)}^2+\in \left(\mathrm{R}\right)-1\mathrm{E}\right]{\mathrm{F}}^{\mathrm{a}}\left(\mathrm{R}\right)=0$

Such a system is in principle infinite, but, as we have seen, in practice a convenient truncation has to be introduced. According to the Hellmann-Feynman theorem, we can write the coupling terms as follows:

${\mathrm{P}}_{\mathrm{ij}}\left(\mathrm{R}\right)=<{\varphi }_{\mathrm{i}}^{\mathrm{a}}|\frac{\mathrm{d}}{\mathrm{dR}}{\varphi }_{\mathrm{j}}^{\mathrm{a}}>=\frac{1}{{\in }_{\mathrm{i}}-{\in }_{\mathrm{j}}}<{\varphi }_{\mathrm{i}}^{\mathrm{a}}|\frac{\mathrm{dV}}{\mathrm{dR}}|{\varphi }_{\mathrm{j}}^{\mathrm{a}}>=-{\mathrm{P}}_{\mathrm{ij}}\left(\mathrm{R}\right)$

Solving eq. (11) including eq. (12) would amount to “exact” solution of the coupled-channel or close-coupling (CC) formulation in the adiabatic representation. The adiabatic approximation consists in neglecting the coupling terms, as it is done in the Born-Oppenheimer separation.

An alternative development leads to the diabatic representation, which requires the definition of an orthogonal matrix T(R) to interconvert the eigenfunctions corresponding to the two different representations:

${\mathrm{F}}^{\mathrm{a}}={\mathrm{TF}}^{\mathrm{d}}$

and

${\mathrm{T}}^{-1}{\mathrm{T}}^{\prime }=\mathrm{P}$

where the prime denotes differentiation with respect to R, so that, in spite of their innocent look, equations (13) and (14) correspond actually to an often formidable set of differential equations.

The final equation for the diabatic representation is

$\left[-\frac{{\mathrm{\hslash }}^2}{2\mu }1\frac{{\mathrm{d}}^2}{{\mathrm{dR}}^2}+{\mathrm{V}}^{\mathrm{d}}-1\mathrm{E}\right]{\mathrm{F}}^{\mathrm{d}}\left(\mathrm{R}\right)=0$

where

${\mathrm{V}}^{\mathrm{d}}={\mathrm{T}}^{-1}\in \left(R\right)\mathrm{T}$

The main difference between (11) and (15) is that in the former case, the coupling acts in the kinetic energy, while in the latter it acts in the potential energy. This is often convenient for numerical solutions. However T is not unique: solution to the equations (13) and (14) requires specification of boundary conditions and therefore the diabatic representation is not unique as well. This can be in practice a great advantage. A physically motivated diabatic expansion on a mathematically well-behaved orthonormal complete basis set, as the expansions in spherical and hyperspherical harmonics to be considered in the following, leads to analytical evaluation of matrix elements and to the possibility of exploiting powerful numerical techniques. This is the theme of the following sections, as far as chemical reaction theory is concerned.

See [15,16] for the alternative diabatic representations which correspond to the alternative Hund’s angular momentum coupling cases in the spectroscopy and dynamics of a diatomic system.

4 Three-body problem. Orbital and rotational angular momentum.

When molecules undergo large amplitude motions, or even bonds break and form as in a chemical reaction, one doesn’t have any more a privileged interatomic distance and has to consider explicitly the interactions among the various bodies. To begin with, note that for the interaction among three particles it is certainly very difficult to identify a trivially separable variable. Nevertheless it is still possible to reduce the dimensionality of the problem eliminating those coordinates related with the motion of the center of mass.

There are several different representations of the six coordinates necessary to describe the positions of the three particles, but we will treat in detail the Jacobi scheme, not only because it came first chronologically but even because it is nowadays the one more widely employed. Alternatives are discussed elsewhere [1].

In the three body problem we can write down two Jacobi vectors: the first (r) is simply the internuclear distance between two particles and the second (R) connects their center of mass to the third particle.

The resulting hamiltonian will contain as a kinetic term the sum of two three dimensional Laplacians acting on the coordinates of the Jacobi vectors plus a potential energy term describing the interaction between the three particles

$\left[-\frac{{\mathrm{\hslash }}^2}{2\mathrm{M}}{\mathrm{\Delta }}_{\mathrm{R}}^{\left(3\right)}-\frac{{\mathrm{\hslash }}^2}{2\mathrm{m}}{\mathrm{\Delta }}_{\mathrm{r}}^{\left(3\right)}+\mathrm{V}\left(\mathrm{R},\mathrm{r},\theta \right)-\mathrm{E}\right]\mathrm{\Psi }=0$

where

$\mathrm{m}=\frac{{\mathrm{m}}_1{\mathrm{m}}_2}{{\mathrm{m}}_1+{\mathrm{m}}_2}\mathrm{and}\mathrm{M}=\frac{{\mathrm{m}}_3\left({\mathrm{m}}_1+{\mathrm{m}}_2\right)}{{\mathrm{m}}_1+{\mathrm{m}}_2+{\mathrm{m}}_3}$

Expressing the vectors in polar coordinates R = (R,θ_R,ϕ_R) and r = (r,θ_r, ϕ_r), as before we have, as separate eigenfunctions of the angular part of the Laplacians, two spherical harmonics ${\mathrm{Y}}_{l{m}_l}\left({\theta }_R,{\theta }_R\right)$ and ${\mathrm{Y}}_{j{m}_j}\left({\theta }_r,{\theta }_r\right)$, where the quantum numbers of orbital (l and m_l) and rotational (j and m_j) angular momentum appear.

Because of the conservation of the total angular momentum (J = j + 1), we have to search for a proper combination of spherical harmonics. Introducing then the coupling coefficients of quantum mechanical angular momenta (the Clebsch-Gordan coefficients), we obtain a bipolar harmonic

${\mathrm{Y}}_{\mathit{jl}}^{\mathrm{JM}}={\mathrm{\Sigma }}_{m_j{m}_l}<l{m}_{l}j{m}_j|\mathrm{JM}>{\mathrm{Y}}_{l{m}_l}\left({\theta }_{\mathrm{R}},{\varphi }_{\mathrm{R}}\right){\mathrm{Y}}_{j{m}_j}\left({\theta }_{\mathrm{r}},{\varphi }_{\mathrm{rR}}\right)$

After the expansion of the wave function in terms of bipolar harmonics, we obtain:

$\left[-\frac{{\mathrm{\hslash }}^2}{2\mathrm{M}}\frac{{\partial }^2}{\partial {\mathrm{R}}^2}-\frac{{\mathrm{\hslash }}^2}{2\mathrm{m}}\frac{{\partial }^2}{\partial {\mathrm{r}}^2}+\frac{{\mathrm{\hslash }}^2}{2\mathrm{M}}\frac{l\left(l+1\right)}{{\mathrm{R}}^2}+\frac{{\mathrm{\hslash }}^2}{2\mathrm{m}}\frac{j\left(j+1\right)}{{\mathrm{r}}^2}-\mathrm{E}\right]{\mathrm{F}}_{\mathit{jl}}^{\mathrm{J}}={\mathrm{\Sigma }}_{j^{\prime }{l}^{\prime }}{\mathrm{V}}_{\mathit{jl}{j}^{\prime }{l}^{\prime }}^{\mathrm{J}}{\mathrm{F}}_{j^{\prime }{l}^{\prime }}^{\mathrm{J}}$

${\mathrm{V}}_{\mathit{jl}{j}^{\prime }{l}^{\prime }}^{\mathrm{J}}\left(\mathrm{r},\mathrm{R}\right)=<{\mathrm{Y}}_{\mathit{jl}}^{\mathrm{JM}}\left|\mathrm{V}\left(\mathrm{r},\mathrm{R},\theta \right)\right|{\mathrm{Y}}_{j^{\prime }{l}^{\prime }}^{\mathrm{JM}}>$

where < … > implies the integration on the angle θ.

Also the potential energy V (r,R,θ) can be expanded as a function of Legendre polynomials. This expansion allows analytical evaluation of matrix elements according to the algebraic rules for the coupling of angular momenta [17]. Therefore, to solve an “inelastic” problem, where R and r remain appropriate throughout, we may solve first the Schrödinger equation in r, θ_r, ϕ_r, parametrically in R, obtaining the eigenvalues ∈ _jv^J(R) and the eigenfunctions ϕ_jv^J(R, r), where υ is the vibrational quantum number, and then integrate a set of coupled equations in R. Computer programs are available to carry out such calculations of interest for the study of the exchange of rotational and vibrational energy in molecular collisions.

When treating reactions, the situation is obviously more complicated and we have to face the rearrangement problem. We have to take into account the Jacobi rearrangements related to the reactants and products respectively. The main question we should try to answer is whether it can be found a near separable coordinate for rearrangement scattering or in general for any many-body problem, even when one cannot use a manifest difference in masses, as in the Born-Oppenheimer separation. The solution to this problem requires an extension to spaces of mathematically higher dimensionality of the procedure we have been following so far. In such a hyperspace, we are going to introduce the radius of a hypersphere as our key variable.

For a prototypical three body problem, the Helium-like atom, the procedure is well known since the early days of quantum mechanics. More recently, Fano, Macek and Klar [18–23] identified a near separable variable $\rho ={\left({\mathrm{r}}_1^2+{\mathrm{r}}_2^2\right)}^{\frac{1}{2}}\text{,}$, where r₁ and r₂ sure the two Jacobi vectors of the system, named “hyperradius”, corresponding to the radius of a six-dimensional “hypersphere” parameterized by five “hyperangles”. However, note that the hyperradius is independent of the numbering of particles and is therefore very useful for rearrangement problems.

The hyperspherical coordinates, which will be discussed in detail in the present article, represent a generalization to any mass of the near separability for the hyperradius explored for Helium-like atom. Jacobi vectors, besides the reduction of the dimensionality of the problem eliminating the center of mass coordinates, allow us, after a proper mass-scaling, to express the kinetic energy of the system in a diagonal form which depends only on the reduced mass of the system.

If we multiply the vectors R_k and r_k, where k indicates one of the three possible arrangements of the particles (fig. 1), by the mass factor a_k

${\mathrm{a}}_{\mathrm{k}}={\left(\frac{{\mu }_{\mathrm{k},\mathrm{jl}}}{{\mu }_{\mathrm{jl}}}\right)}^{\frac{1}{4}}{\mu }_{\mathrm{k},\mathrm{jl}}=\frac{{\mathrm{m}}_{\mathrm{k}}\left({\mathrm{m}}_{\mathrm{j}}+{\mathrm{m}}_{\mathrm{l}}\right)}{{\mathrm{m}}_{\mathrm{k}}+{\mathrm{m}}_{\mathrm{j}}+{\mathrm{m}}_{\mathrm{l}}}{\mu }_{\mathrm{jl}}=\frac{{\mathrm{m}}_{\mathrm{j}}{\mathrm{m}}_{\mathrm{l}}}{{\mathrm{m}}_{\mathrm{j}}+{\mathrm{m}}_{\mathrm{l}}}$

where we indicate with k the particle connected by the vector R to the center of mass of particles j and i, we obtain the mass-scaled Jacobi vectors X_k and x_k

${\mathsf{X}}_{\mathsf{k}}\mathbf{=}{\mathsf{a}}_{\mathsf{K}}{\mathsf{R}}_{\mathsf{K}}{\mathsf{x}}_{\mathsf{k}}\mathbf{=}{\mathsf{a}}_{\mathsf{k}}^{\mathbf{‐}\mathbf{1}}{\mathsf{r}}_{\mathsf{k}}$

Substituting the previous expressions in the kinetic energy operator in eq. (17), it will result a diagonal expression

$\mathrm{T}=-\frac{{\mathrm{\hslash }}^2}{2\mu }\left({\mathrm{\Delta }}_{{\mathrm{X}}_{\mathrm{k}}}^{\left(3\right)}+{\mathrm{\Delta }}_{{\mathrm{x}}_{\mathrm{k}}}^{\left(3\right)}\right)=\frac{{\mathrm{\hslash }}^2}{2\mu }{\mathrm{\Delta }}^{\left(6\right)}$

where we encounter the reduced mass for the three particles

$\mu ={\left(\frac{{\mathrm{m}}_{\mathrm{k}}{\mathrm{m}}_{\mathrm{j}}{\mathrm{m}}_{\mathrm{l}}}{{\mathrm{m}}_{\mathrm{k}}+{\mathrm{m}}_{\mathrm{j}}+{\mathrm{m}}_{\mathrm{l}}}\right)}^{\frac{1}{2}}$

The procedure can clearly be extended to treat more than three particles, and this is done, e.g. in ref. [24]. It has also to be pointed out the fact that the hyperradius is a measure of the total inertia of the n-body system, and this can be a physical motivation for its candidacy as a proper nearly separable variable, invariant with respect to the choice of the set of Jacobi vectors.

5 Hyperspherical coordinates and harmonics. Hyperangular momentum.

We are now ready to generalize to spaces of higher dimensionality the well known polar representation of the position vector of a particle in a three-dimensional space. A hyperspherical representation of the Jacobi vectors can be developed, corresponding to the projection on a d-dimensional hypersphere, with d = (n-1)D for n particles in a D-dimensional space after the separation of the center of mass. The d hyperspherical coordinates consist of a hyperradius, which does not depend on the particular Jacobi set chosen, and d-1 hyperangles, dependent on the arrangement of the particles.

The case of three particles can be simply represented by the hyperradius ρ, related to the sum of the Jacobi vectors, plus five hyperangles, originating a kinetic energy operator [24,25] consisting of a term depending exclusively on ρ plus a five dimensional Laplacian, Λ(Ω₅), corresponding to a “hyperangular” momentum [26]:

$\mathrm{T}=-\frac{{\mathrm{\hslash }}^2}{2\mu }{\mathrm{\Delta }}^{\left(6\right)}\left(\rho ,{\mathrm{\Omega }}_5\right)=-\frac{{\mathrm{\hslash }}^2}{2\mu }\left[{\rho }^{-5}\frac{\partial }{\partial \rho }\left({\rho }^5\frac{\partial }{\partial \rho }\right)-{\rho }^{-2}\mathrm{\Lambda }\left({\mathrm{\Omega }}_5\right)\right]$

There exist different parametrizations of the hyperangles, such as the commonly used asymmetric or Fock’s parametrization and symmetric or Smith’s, which will be discussed in the next section. The eigenfunctions of the hyperangular momentum are called hyperspherical harmonics and can be easily visualized by the tree method [4,10,24]. To a d-dimensional hypersphere, parameterized by d cartesian coordinates or one hyper radius and d–1 hyperangles, is graphically associated a tree which is composed of d leaves corresponding to the cartesian coordinates and each leaf is connected by a branch to one of the d–1 nodes representing the hyperangles and labeled with the proper quantum numbers.

Starting from a leaf and descending to the root of the tree, through the various nodes, we may find the relationship between coordinates and hyperangles, according to the convention which establishes that the branch converging to a node from the left-hand (right-hand) side corresponds to the cosine (sine) of the hyperangle.

If a hyperspherical parametrization can be represented by a tree, the coordinates can be shown to form an orthogonal set. This implies that the Laplacian on the hypersphere will contain no cross terms, the corresponding Laplace equations are separable and the hyperspherical harmonics can be constructed in closed form [24].

We start considering some examples in two and three-dimensional space and then generalize to spaces of higher dimensionality. On the plane it is possible only one representation visualized by the tree in fig. 2.

The tree represents the correspondence between cartesian and polar coordinates:

$\mathrm{x}=\mathrm{rcos}\varphi \mathrm{y}=\mathrm{rsin}\varphi$

and the corresponding eigenfunction is given by e^im ϕ with m = …,–1,0, + 1,…

In three-dimensional space there are two possible symmetric trees (fig.3), the first corresponding to the usual polar representation related to the spherical harmonics Y_lm(θ, ϕ).

In this case, the correspondence between polar and cartesian coordinates is:

$\begin{array}{ll}\mathrm{x}=\mathrm{rsin}\theta cos\varphi \hfill & \mathrm{x}=\mathrm{rcos}{\theta }^{\prime }sin{\varphi }^{\prime }\hfill \\ \mathrm{y}=\mathrm{rsin}\theta sin\varphi \hfill & \mathrm{y}=\mathrm{rsin}{\theta }^{\prime }\hfill \\ \mathrm{z}=\mathrm{rcos}\theta \hfill & \mathrm{z}=\mathrm{rcos}{\theta }^{\prime }cos{\varphi }^{\prime }\hfill \end{array}$

The orthogonal transformation which allows the connection between Y_lm(θ, ϕ) and Y_lm(θ′, ϕ′) is in this case a Wigner’s rotation matrix. For d greater than three the number of possible representations increases and we can have different hyperspherical harmonics. Transformations allowing the connection among them are orthogonal matrices, whose study is a current important topic of angular momentum theory.

In the four-dimensional case we have many possibilities. Of these, two are basically different. As an example, we show in fig. 4 the trees corresponding to such two different parametrizations (the others are obtained “anagramming” x, y, z and w).

The related hyperspherical harmonics are:

$Y_{\mathit{nlm}}=C_{\mathit{nl}}\left(\chi \right){\mathrm{Y}}_{\mathit{lm}}\left(\theta ,\varphi \right){\mathrm{D}}_{\frac{{\mu }_1+{\mu }_2}{2}\frac{{\mu }_1-{\mu }_2}{2}}^{\frac{\mathrm{u}}{2}}={\mathrm{e}}^{\mathrm{i}{\mu }_1,\alpha }{\mathrm{d}}_{{\mu }_1{\mu }_2}^{\mathrm{n}}\left(\beta \right){\mathrm{e}}^{\mathrm{i}{\mu }_2\mathrm{\gamma }}$

where ϕ = γ and m = μ₂.

To further illustrate the tree-method, consider the six-dimensional hypersphere which parameterizes the components of Jacobi vectors for the three-body problem: the symmetric tree, see fig. 5, corresponds to the hyperspherical harmonics

${\mathrm{Y}}_{\mathrm{\Lambda }{l}_1{l}_2{m}_1{m}_2}\left(\chi ,{\theta }_1,{\theta }_2,{\varphi }_1{\varphi }_2\right)={\mathrm{Y}}_{l_1{l}_2}^{\mathrm{\lambda }}\left(\mathrm{\chi }\right){\mathrm{Y}}_{l_1{m}_1}{\mathrm{Y}}_{l_2{m}_2}$

The quantum number λ is the first example that we encounter of a kind of quantity that can be viewed as the generalization to hyperspace of ordinary angular momentum. They will be called hyperangular (or grandangular) momenta [10,24,26] and the connections among alternative harmonics are related to coupling and recoupling coefficients of hyperangular momentum.

The generalization of the hyperspherical treatment to n particles runs as follows. Considering that n particles in a three-dimensional space, after the separation of the center of mass, can be represented by d = 3(n-1) coordinates parameterized by a d-dimensional hypersphere with d-1 hyperangles and one hyperradius, we can write down explicitly the kinetic energy operator as follows:

$-\frac{{\mathrm{\hslash }}^2}{2\mu }\left[{\rho }^{-\left(\mathrm{d}-1\right)}\frac{\partial }{\partial \rho }{\rho }^{\mathrm{d}-1}\frac{\partial }{\partial \rho }-{\rho }^{-2}\mathrm{\Lambda }\left({\mathrm{\Omega }}_{\mathrm{d}-1}\right)\right]$

where Λ(Ω_d–1) (group-theoretically a quadratic Casimir operator) is the hyperangular Laplacian on the d-dimensional sphere of unit hyperradius.

The hyperspherical harmonics will then be the eigenfunctions of Λ(Ω_d–1):

$\widehat{\mathrm{\Lambda }}{\mathrm{Y}}_{\mathrm{\Lambda },\mu }\left({\mathrm{\Omega }}_{\mathrm{d}-1}\right)=\mathrm{\lambda }\left(\mathrm{\lambda }+\mathrm{d}-2\right){\mathrm{Y}}_{\mathrm{\lambda },\mu }\left({\mathrm{\Omega }}_{\mathrm{d}-1}\right)$

λ being again the hyperangular or grandangular momentum quantum number and μ is here a set of d-1 quantum numbers.

The explicit form of the harmonics depends obviously on the particular parametrization chosen for the coordinates, giving rise to different possibilities, which are formally equivalent, but offer great flexibility to the method.

For the four-body problem in a system of symmetric hyperspherical coordinates the expression of the kinetic energy operator and the kinematic rotations connecting the different reactive channels have been explicitly derived in two recent papers [27,28]. Also, hyperspherical harmonics have recently attracted much attention because of their use as atomic and molecular orbitals in momentum space, allowing the treatment of the many body Coulomb problems via expansions of the Sturmian type over complete orthonormal basis sets, see [10,29–35].

We consider now the consequences of extending the concept of near separability to the hyperspherical parametrization. The hyperradius can be identified as the near separable variable and it is then possible to expand the wave function as a product of a “hyperradial” term and hyperspherical functions [36,37]:

$\mathrm{\Psi }\left(\rho ,{\mathrm{\Omega }}_{\mathrm{d}-1}\right)={\rho }^{-\frac{\mathrm{d}-1}{2}}{\displaystyle \sum _{\mathrm{i}}{\mathrm{F}}_{\mathrm{i}}^{\mathrm{a}}\left(\rho \right){\theta }_{\mathrm{i}}^{\mathrm{a}}}\left(\rho ,{\mathrm{\Omega }}_{\mathrm{d}-1}\right)$

where Ω_d–1 indicates the d-1 hyperangles of the d-dimensional problem, Φ_i(ρ, Ω_d–1) corresponds to the eigenfunctions of d-1 dimensional problem with eigenvalues ∈_i(ρ) depending parametrically on ρ. We thus obtain a set of coupled differential equations

$\left[-\frac{{\mathrm{\hslash }}^2}{2\mu }{\left(1\frac{\mathrm{d}}{\mathrm{d}\rho }+\mathrm{P}\left(\rho \right)\right)}^2+\in \left(\rho \right)-1\mathrm{E}\right]{\mathrm{F}}^{\mathrm{a}}\left(\rho \right)=0$

where ∈(ρ) represents the matrix of adiabatic potential energy curves and P(ρ) is the matrix containing non-adiabatic coupling elements P_ij (ρ), exhibiting maxima at avoided crossings, changes in coupling schemes, ridges between modes [38,39]. An illustration will be provided in the next section, see fig. 7 below.

As in section 3, the diabatic representations are obtained finding the orthogonal matrix T such that $\tilde{\mathbf{T}}{\mathbf{T}}^{\mathbf{\prime }}=\mathbf{P}$. Again, the diabatic representation is not unique because T is defined within an overall ρ-independent orthogonal transformation. In actual calculations, one has to manipulate the potential energy matrix $\mathbf{V}=\mathbf{T}\mathbf{\in }\left(\rho \right)\tilde{\mathbf{T}}$, whose large dimensions are often the bottleneck in practice. Proper choice of T is therefore crucial. The practical implementation (see the final section) of hyperspherical harmonics as the proper diabatic set is of great perspective power.

6 Hyperspherical mapping of potential energy surfaces. Alternative parametrization of hyperangles.

The hyperspherical approach leads to a change in perspective with respect to our views on reactive potential energy surfaces, not only with reference to their representation in terms of coordinates, but also regarding topological features. These are important both as a guide to the numerical implementation and as a tool to understand the qualitative features of the dynamics. The representation of potential energy surfaces in hyperspherical and related coordinates allows us to focus the attention on those regions which are relevant for the numerical implementation of the dynamics and therefore need to be known very accurately [2,9]. If we start by limiting our consideration to a symmetric collinear three particle collision, the easiest to visualize, we may sketch the potential energy contour map as a function of skewed coordinates (fig. 6 a).

The idea of “skewing” the coordinates according to a mass-dependent angle was put forward by the early pioneers of theoretical gas kinetics (Wigner, Polanyi, Eyring …) in the thirties. Such a mass scaling is the first step towards the mass scalings employed in the hyperspherical approach (sect. 4). The dashed line represents the usual minimum energy path connecting the reagents and products channels (see fig. 6 b), the dots correspond to ridges of the potential energy surface and the continuous line follows the increase in hyperradius, starting from the coalescence of particles near the origin and to their alternative rearrangements far from it. It is possible to identify two main kinetic paths (fig. 6 c): the first, given by the evolution of energy minima or “valley bottoms” as a function of ρ, describes at large ρ values the rearrangement channels, while the second is the ridge line, corresponding to the evolution of saddles as a function of ρ.

Ridges play a crucial role in chemical reactions because of the coupling between rearrangement channels leading to non-adiabatic transitions. In correspondence of the “transition state” the valley bottom line undergoes an abrupt transition from single-to double-well situation, bifurcates and continue as a ridge line. Accordingly, the qualitative behaviour of adiabatic potential curves ∈_υ(ρ) drastically changes astride of the ridge (fig. 7 a) and non-adiabatic matrix elements P_υυ′(ρ) show a peak there, as we can see in fig. 7 b [39,40].

If we represent on a plane, which has been named “kinetic plane” [2], all the possible rearrangements of three particles constrained to lay on a line (fig. 8 a), we can identify the kinematic rotation angle Φ, which therefore is a proper generalization to continuous values of the skewing angle, which describes asymptotically the passage through the different rearrangement channels. In fig. 8 b are represented cuts through the potential energy surface at different ρ values which give a useful alternative view of the surface. Curves of fig. 7 are obtained by “quantizing” on these ρ-fixed cuts, obtaining eigenvalues and coupling matrix elements to be entered in eq. (34).

In general, before any numerical calculation, and in order to explore potential energy surfaces of higher dimensionality, it emerges the crucial necessity to consider cuts as these, where some coordinate is held constant or is adjusted to minimize the potential energy [41].

We are now ready for the extension of the previous polar representation of the collinear case in terms of the radial variable ρ and the angle Φ. The case of three particles in three-dimensional space is described, as we have already shown, by a six-dimensional sphere corresponding to a hyperradius and five hyperangles. However, the potential energy surface requires only two angles and, in general, angular momentum conservation can be imposed to restrict the dynamics to a manifold of lower dimensionality. Among the different possible parametrizations we will now consider the most commonly used, i.e. the asymmetric and the symmetric ones.

Symmetric parametrization

The symmetric parametrization, can be obtained taking as internal reference system the one which diagonalizes the inertia tensor and placing the principal axis in correspondence of the maximum inertia one [26,43,44]. In this way we obtain an angle (Θ) correlated with the area of the triangle made up by the three particles, invariant respect with their possible rearrangements (fig. 9), plus an angle (Φ) connected with the shape of the triangle and corresponding to the kinematic rotation angle whose value depends on the particular set of Jacobi vectors considered

${\rho }^2=\left|\mathrm{X}\right|{}^2+\left|\mathrm{x}\right|{}^{2}sin2\mathrm{\Theta }=2\frac{\left|\mathrm{x}\wedge \mathrm{X}\right|}{{\rho }^2}=4\frac{\left|\eta \right|}{{\rho }^2}tan2\theta =2\frac{\left(\mathrm{x}\cdot \mathrm{X}\right)}{\left(\left|\mathrm{x}\right|{}^2-\left|\mathrm{X}\right|{}^2\right)}$

  (37)

Θ = 0 can be shown to correspond to the collinear case, while $\theta =\frac{\mathrm{\pi }}{4}$ to the equilateral triangle. The interconversion formulas between symmetric and asymmetric coordinates are [2]:

$sin2\chi cos\theta =cos2\mathrm{\Theta }sin2\theta sin2\chi sin\mathrm{\Theta }=sin2\theta cos2\chi =cos2\mathrm{\Theta }cos2\theta$

  (38)

All the relevant machinery for handling these coordinates and the explicit relationships with interatomic distances are given in ref. [2]. Symmetric and asymmetric representations for more than three particles are considered elsewhere [1]. For four particles see [27,28,45].

7 Perspectives and concluding remarks.

In this final section we will deal with current research problems. Although numerical implementations of the hyperspherical approach have been extensive, so that now they are considered the main route to full state-to-state information on the dynamics of elementary A + BC type of reactions, they have not been discussed in this paper. However, note that the great power of this approach stems from the fact that, within the framework of the hyperspherical approach to reaction dynamics, it is possible to use angular momentum algebra (or its generalization, see below) to compute matrix elements of the Hamiltonian. The particularly advantageous aspects of the method is that the kinetic energy matrix is universal and sparse: salient features are the block tridiagonal structure and a number of symmetry properties.

Specifically, the technique developed in our group exploits the discrete analogues of orthonormal basis sets usually defined on continuous angular variables. These bases are orthonormal polynomial sets and our representation uses, as their discrete counterparts, polynomials orthogonal on lattice points, the so-called Hahn coefficients [31,41,46–48]. These can be identified, in particular cases, with the Clebsch-Gordan coefficients or vector coupling coefficients in the quantum theory of angular momentum. The algebraic work needed to develop this generalization is an important goal of current research.

Numerical aspects and performances of this ”hyperquantization” algorithm have been demonstrated for a prototypical atom-diatom reaction (F + H₂) [49], including extensions for the treatment of the excited electronic surfaces. Calculations have been carried out on the reaction at total nuclear angular momentum equal to zero, the fine structure of the fluorine atom being explicitly taken into account. The technique presented is shown to be simple and effective for applications to reactive scattering problems, and the results are competitive with those obtained applying other current methods. The theory as well requires substantial effort to provide the ground to further developments. Expansions in alternative hyperspherical harmonics for three-body problems, corresponding to different couplings of particles and angular momenta, allow closed-form expressions for orthogonal transformations between coupling schemes. Similar transformations can also be found for alternative parametrizations of hyperangles [50].

Connections between harmonics are important for providing orthogonal transformations between basis set expansions pertaining to different Jacobi parametrizations. They were first introduced by Raynal and Revai. Their use, especially for nonorthogonal treatments where it may be convenient to expand over different basis sets for entrance and exit channels, is still to be exploited. The extension to more than three particles is the goal of current investigations.

Being the exact quantum mechanical treatment of the dynamics of systems containing more than four atoms presently computationally out of question, only particular cases or approximate methods are nowadays being developed in order to extend the hyperspherical method to complex reactions. Proper formulations of the coordinate systems and relevant hamiltonians have already been referred to [27,28,45], see also [51].

The reaction-volume Hamiltonian approach developed by Billing [52], in analogy with reaction path and surface Hamiltonian developed by Miller [53], consists in the reduction of the reactive process to a three- or four-center problem, focusing the attention on the dynamics of the subsystem constituted by the atoms directly involved in the reaction, while treating the remaining degrees of freedom within a harmonic decoupling scheme. Therefore the accurate hyperspherical method is used only for the reaction centers and the motion of the “spectator” atoms can be followed using the small amplitude approach. As a further example, the reaction OH + H₂ → H₂O + H has been studied [52,54], considering that the initial O-H bond is not directly involved in the rearrangement.

Finally, time dependent methods are yielding interesting views on polyatomic reaction dynamics, although not actually leading to the full state-to-state information. Most promising for the future will be the blending of these methods with the hyperspherical approach under focus in the present paper.