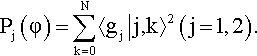1 Introduction

The behavior of molecules in excited electronic states is very different from that in the ground state, as witnessed by the existence of Photochemistry as a separate branch of Chemistry. The prediction of the route actually followed by a given species for its decay, after the absorption of a photon, remains a difficult challenge for Quantum Chemistry, being the result of the competition of different channels, either radiative (fluorescence and phosforescence) or non-radiative (internal conversion, intersystem crossing, photochemical reaction). Some general rules merged already from the first systematic approaches, as the well known Kasha rule [1], stating that, independently of the excitation wavelength, the molecule undergoes a cascade of rapid radiationless decays till it ends in the first singlet or triplet (there is no rule concerning the last decay). A well studied exception to this rule is given by azulene Only recently, however, the scientific community became aware that this general behavior has to be attributed to the occurrence of conical intersections between adiabatic energy surfaces [2–5], an event considered before as rare [6,7].

The study of the radiationless decay mechanism, i.e. of the way a molecule can transform its electronic energy into vibrational (and rotational) energy, has been recognized as a fundamental step towards the comprehension of the behavior of electronically excited molecules. As pointed out by Robinson [8] the problem was clearly stated already in 1929 by O. K. Rice [9–11], but only in the late sixties it became the subject of an huge theoretical and experimental effort, starting from the pioneering work of Kasha, Robinson, Siebrand, Jortner, Rhodes and others, documented for example in the reviews [1,8,12]. Some of the most important progresses realized are shortly resumed in the following few points.

i) After some initial debate it became clear that the radiationless decay is the consequence of the optical preparation of a state which is not a true molecular eigenstate (i.e an eigenstate of the full Hamiltonian). The excited state is an eigenstate of a suitable zero-order Hamiltonian, which does not contains the nuclear kinetic energy, responsible for internal conversion, and the spin-orbit coupling term which allows the intersystem crossing. It was also realized that, in general, preparation and decay are deeply related and can be considered as separate steps only in the case of short light pulses [13–15].

ii) The necessity of solving the time-dependent Schrödinger was clearly stated, thus essentially opening a new field of research, altough the Fermi-golden-rule (which can be derived by first-order time-dependent perturbation theory) was considered sufficient for large molecules.

iii) The Fermi-golden-rule approach, in turn, leaded to put emphasis on Franck-Condon factors, in such a way that the role of high frequency modes (the C-H stretchings) in the decay of aromatic molecules comes into play naturally [16]. It also became clear die different role played by promoting and accepting modes [17]. In close parallelism with the many-phonon approach to the study of lineshapes of impurities in solids, it was also derived an exponential gap law [16], a very useful theoretical instrument.

During the last thirty years the progresses in this field have been continuous, also due to the development of laser sources and of the techniques for doing spectroscopy in the time domain, with a resolution of a few femtoseconds. One may observe, however, that, in general, it remains still hard to extract from the large amount of experimental data, general rules capable of establishing a close correlation between structure and photophysical behavior. Apart from its intrinsic interest, the latter would be of great help for people involved in the material science, to whom is required the design of molecules for specific applications. In the intent of the authors, the present work, devoted to a specific class of molecules, is a modest contribution in that direction.

2 Biaryls and related molecules

Molecules made by (more or less) weakly interacting parts offer interesting possibilities for the study of both electron and excitation transfer processes. The most common situation is that of biaryl compounds, in which two aromatic systems (A and B) are directly linked to give A-B. In a certain range of interaction strength one can imagine that the ground state (as well as some excited states) of A-B can be well represented by mixing a small number of configurations describing the two separate subsystems For example, the ground state may be well described by a linear combination of neutral states |AB〉, some charge-transfer states, either of the kind |A⁺B⁻〉 or |A⁻B⁺〉 and some excitonic states, either |A*B〉 or |AB*〉. Depending on the nature of A and B one may have the predominance of contamination by excitonic or charge transfer configurations. Some general ideas on the origin of different contaminations can be derived assuming that only π electrons play a direct role and then making recourse to the popular PPP model Hamiltonian. The total Hamiltonian is easily partitioned into the sum of two Hamitonians for the separated units A and B plus an interaction term:

$\mathrm{H}={\mathrm{H}}_{\mathrm{A}}+{\mathrm{H}}_{\mathrm{B}}+{\mathrm{V}}_{\mathrm{AB}}$

where:

${\mathrm{H}}_{\mathrm{A}}={\displaystyle \sum _{\mathrm{i}\in \mathrm{A}}{\mathrm{\epsilon }}_{\mathrm{i}}{\mathrm{n}}_{\mathrm{i}}}+{\displaystyle \sum _{\mathrm{i}\ne \mathrm{j}}^{\mathrm{i},\mathrm{j}\in \mathrm{A}}{\mathrm{V}}_{\mathrm{ij}}{\mathrm{n}}_{\mathrm{i}}{\mathrm{n}}_{\mathrm{j}}}+{\displaystyle \sum _{\mathrm{i}\in \mathrm{A}}{\mathrm{U}}_1}{\mathrm{n}}_{1\uparrow }{\mathrm{n}}_{1\downarrow }+{\displaystyle \sum _{\left(\mathrm{i},\mathrm{j}\in \mathrm{A}\right).\mathrm{\sigma }}^{\mathrm{i},\mathrm{j}=\mathrm{n}.\mathrm{n}.}{\mathrm{t}}_{\mathrm{ij}}}{{\mathrm{a}}^{+}}_{\mathrm{i\sigma }}{\mathrm{a}}_{\mathrm{j\sigma }}$

${\mathrm{H}}_{\mathrm{B}}={\displaystyle \sum _{\mathrm{i}\in \mathrm{B}}{\mathrm{\epsilon }}_{\mathrm{i}}{\mathrm{n}}_{\mathrm{i}}}+{\displaystyle \sum _{\mathrm{i}\ne \mathrm{j}}^{\mathrm{i},\mathrm{j}\in \mathrm{B}}{\mathrm{V}}_{\mathrm{ij}}{\mathrm{n}}_{\mathrm{i}}{\mathrm{n}}_{\mathrm{j}}}+{\displaystyle \sum _{\mathrm{i}\in \mathrm{B}}{\mathrm{U}}_1}{\mathrm{n}}_{1\uparrow }{\mathrm{n}}_{1\downarrow }+{\displaystyle \sum _{\left(\mathrm{i},\mathrm{j}\in \mathrm{B}\right).\mathrm{\sigma }}^{\mathrm{i},\mathrm{j}=\mathrm{n}.\mathrm{n}.}{\mathrm{t}}_{\mathrm{ij}}}{{\mathrm{a}}^{+}}_{\mathrm{i\sigma }}{\mathrm{a}}_{\mathrm{j\sigma }}$

${\mathrm{V}}_{\mathrm{AB}}={\displaystyle \sum _{\left(\mathrm{i}\in \mathrm{A},\mathrm{j}\in \mathrm{B}\right).\mathrm{\sigma }}^{\mathrm{i},\mathrm{j}=\mathrm{n}.\mathrm{n}}\left[\left({\mathrm{t}}_{\mathrm{ij}}{{\mathrm{a}}^{+}}_{\mathrm{i\sigma }}{\mathrm{a}}_{\mathrm{j\sigma }}+\mathrm{h}.\mathrm{c}.\right)+{\mathrm{V}}_{\mathrm{ij}}{\mathrm{n}}_{\mathrm{i}}{\mathrm{n}}_{\mathrm{j}}\right]}$

and

${\mathrm{n}}_1={{\mathrm{a}}^{+}}_{1\uparrow }{\mathrm{a}}_{1\uparrow }+{{\mathrm{a}}^{+}}_{\mathrm{i}\downarrow }{{\mathrm{a}}_1}_{\downarrow },\mathrm{n}.\mathrm{n}\text{.}$ indicates nearest neighbours.

The multi-configurational eigenstates of H₀ = H_A + H_B are then used as basis set for handling the full Hamiltonian, eq. (1). We notice that since only the total number of electrons is given, the above eigenstates can be partitioned in sets differing by the total charge on units A (q_A) and units B (q_B) (of course for neutral species q_A = –q_B). Looking at the structure of V_ab one can easily get convinced that the hopping terms give rise to charge-transfer (CT) interactions, whereas the repulsion terms are responsible for excitonic interactions. It is clear, in any case, that what happens is strictly dependent on the particular system under study as well as on the part of the energy spectrum considered; and no general conclusions can then be drawn, without facing the problem of determining the electronic structure through accurate quantum chemical computations. It is worthwhile to mention here that the application of standard computational packages to such problems is not straightforward, since the kind of analysis required here demand, in principle, localization of molecular orbitals. As should also result from the previous discussion, a valence bond approach may also reveal very useful for understanding this kind of processes [18].

Among the more recent studies on the behavior of biaryls upon optical excitation we recall here the experimental-theoretical investigation by Maus and Rettig [19] on the biphenil and its derivatives with a donor group (D) on one ring and an acceptor group (A) on the other. Their optical measures corroborated by CNDO computations are convincingly interpreted as an evidence that, while in the biphenil CT interactions do not play a role at low energy, in the DA compounds the first strong absorption band involves transition to a state which has a partial CT character. The dynamic of the excitation transfer in other biaryls, the 2-2'-binaphtil and in the 9-9'-bifluorene has been studied in various solvents, using femtosecond optical techniques, by the Hochstrasser group [20], with the aim of unraveling the role of the interaction with the solvent in promoting the dephasing of the intramolecular energy transfer.

A considerable amount of work has been also devoted to triphenil-methane dyes, which are known to give rise to fast internal conversion. They may exhibit oscillatory decay under pump and probe experiments [21], whose origin has been tentatively attributed to the fact that what is monitored in optical measurements is not the population of the excited adiabatic state, but that of the diabatic state, which is known to give rise to more persistent oscillations on the basis of computations on model systems with conical intersections [22]. We have not found in the literature, however, any clear interpretation of the electronic transition, especially concerning the degree of charge transfer involved, although some of these dyes are known to give rise to fast intermolecular ET in suitable solvents or when they are adsorbed onto surfaces [23,24].

The betaine-30 is another well studied molecule [25] exhibiting a S₀ → S₁ transition with a marked charge transfer character, which enters in the class discussed here, being basically composed of two triphenil-methane moieties linked together.

The above compounds are a subclass of a larger family, that of molecules undergoing charge transfer processes accompanied by large intramolecular rearrangements, upon optical excitation, which have been extensively studied for both their intrinsic interest [26,27], and as ideal systems for investigating the role of solvation in ET processes [28–31].

In some particular situations the chemical intuition strongly suggests that charge transfer interactions play a major role in determining the nature of the lowest energy states. This is the case, for example, of charged species derived from quinones, as the semiquinone radical anion (I) or from benzoquinone-di-imines, as in the cation radical (II), for which the presence of two dominating VB structures directly suggests a two state model. Even more rich is the situation for the derivatives of the triphenil-methane, like the phenolptalein dianion (III), containing three different aromatic rings, communicating through the central carbon atom. Here one may simplify this complex case assuming (somewhat arbitrarily) that the central atom belongs to the low-lying aromatic system, in such a way that the charge may be in principle assigned to only three subsystems. In the following we introduce a basic model for these cases and show, on the basis of a simple prototypal calculation of the radiationless decay of the excited state for a two-ring system, that they might represents fascinating examples of molecules whose photophysical behavior can be modulated very efficiently through structural modification, which, at first sight, appear to be of minor importance.

3 A simple model

Let us proceed building up the basic model. The cases (I) and (II) can be modeled taking a basis set of two states |A⁻B〉 and |A B⁻〉, whereas for case (III) we need three states |A⁻B C〉, |A B⁻C〉 and |AB C⁻〉 The interaction between the states is assumed to be given by an hopping term modulated by the torsion angle between the rings involved. Hence for (I) and (II) we can write down the electronic Hamiltonian in matrix form (φ is the torsion angle between the aromatic rings A and B and the two states are now labeled 1 and 2):

$\mathrm{H}=\left(\begin{array}{cc}\hfill {\mathrm{\epsilon }}_1\hfill & \hfill \mathrm{tcos}\left(\mathrm{\phi }\right)\hfill \\ \hfill \mathrm{tcos}\left(\mathrm{\phi }\right)\hfill & \hfill {\mathrm{\epsilon }}_2\hfill \end{array}\right)\text{.}$

For the case (III), assuming that the rings A and C communicate only through B one has (φ₁ and φ₂ are the torsion angles between A and B and C and B):

$\mathrm{H}=\left(\begin{array}{ccc}\hfill {\mathrm{\epsilon }}_1\hfill & \hfill \mathrm{tcos}\left({\mathrm{\phi }}_1\right)\hfill & \hfill 0\hfill \\ \hfill \mathrm{tcos}\left({\mathrm{\phi }}_1\right)\hfill & \hfill {\mathrm{\epsilon }}_2\hfill & \hfill \mathrm{tcos}\left({\mathrm{\phi }}_2\right)\hfill \\ \hfill 0\hfill & \hfill \mathrm{tcos}\left({\mathrm{\phi }}_2\right)\hfill & \hfill {\mathrm{\epsilon }}_3\hfill \end{array}\right)$

The above matrix representations utilized electronic states which are purely diabatic, being completely independent from the torsional coordinate(s). They are a very convenient starting point for the study of the full vibronic problem, which is required for investigating the photo-physical behavior of such molecules. The full vibronic Hamiltonian, in fact, is simply obtained adding to the electronic Hamiltonian, eq. (5) or, (6), the proper nuclear kinetic energy operator (along the diagonal). The adiabatic electronic states and curves are obtained as eigenvectors and eigenvalues of the electronic matrix. The figure 1 shows a view of the potential energy curve for both the ground and the excited state (adiabatic) for the Hamiltonians (5) with the following choice of the parameters (in a.u):

$\mathrm{t}=–.0556,{\mathrm{\epsilon }}_1=0,{\mathrm{\epsilon }}_2=0.00167\text{.}$

Figure 1

The figures 2 and 3 depict the ground and the excited state surface, respectively, for the Hamiltonian (6) with (a.u.):

$\mathrm{t}=-.0566,{\mathrm{\epsilon }}_1=0,{\mathrm{\epsilon }}_2=0,{\epsilon }_3=0.00167\text{.}$

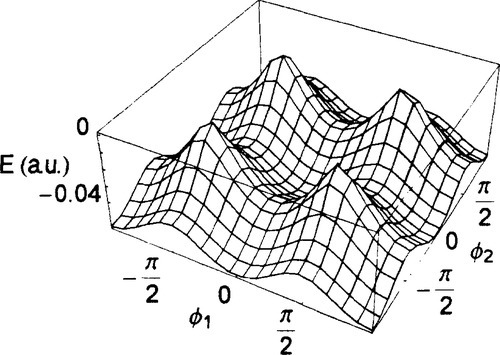
Figure 2

Figure 3

It is clearly seen that the adiabatic surfaces exhibit avoided crossing at the angles for which the hopping terms vanish, i.e. φ = ± π/2 for the mono-dimensional case and and the four points (ϕ_t = ± π / 2, ϕ₂ = ± π / 2) for the bidimensional case.

In the following we will investigate on the simpler two-state case, which can be directly applied to species like (I) and (II). It is worthwhile to remind here that such a study may also serve to shed some light into the behavior of three-state systems for which A=C. In fact, in that case, one may recover a two-state situation by forcing the rings to move in a synchronous manner (i.e. maintaining ϕ₁ = ϕ₂), since, as one can easily realize, for that choice the antisymmetric combination of |A⁻B C〉 and |AB C⁻〉 is decoupled from the problem.

Since we are interested here in the study of the internal conversion from the excited to the ground adiabatic state, we need to tackle the full vibronic problem, whose Hamiltonian can be written as:

$\mathrm{H}=\left(\begin{array}{cc}\hfill {\mathrm{\epsilon }}_1+{\mathrm{T}}_{\mathrm{\phi }}\hfill & \hfill \mathrm{tcos}\left(\mathrm{\phi }\right)\hfill \\ \hfill \mathrm{tcos}\left(\mathrm{\phi }\right)\hfill & \hfill {\mathrm{\epsilon }}_2+{\mathrm{T}}_{\mathrm{\phi }}\hfill \end{array}\right)$

Where (ħ = 1):

$\mathrm{T}=-\frac{1}{2\mathrm{I}}\frac{{\partial }^2}{\partial {\mathrm{\phi }}^2}$

and I is the reduced momentum of inertia for the torsion of the two rings (in the following we take that of a benzene ring).

We notice here that the inclusion of a single nuclear degree of freedom is certainly an oversimplification of the problem. Recently Seidner and Domcke [32] performed some numerical studies on the dynamics of systems involving two diabatic electronic states and a large amplitude torsional angle φ. They assume that the potential energy curve along the torsional angle is different in the two diabatic states, as in many actual cases of photochemical interest, but they claim that the minimal model should include a further harmonic coordinate Q, responsible for the linear inter-electronic coupling (coupling mode). We want to notice here that, while the inclusion of additional modes may certainly result into a more realistic picture, in the present case this in unnecessary if we avoid considering two identical moieties (i.e. ε₁, = ε₂). In fact only in this latter case the adiabatic electronic states, i. e. the eigenstates of the matrix (5), becomes independent from φ by symmetry and, as such, perfectly stationary (the nuclear kinetic energy operator, responsible for non-adiabatic transitions, involves a second order derivative with respect to φ). It is then clear that only in such case is a further coupling mode absolutely needed. With the justification of pursuing the maximum simplicity we then remain here with a single mode (a torsion), leaving to a forthcoming paper a more complete study, including the exploration of the role of additional degrees of freedom. It is then clear that the present model calculation can be directly applied to molecules derived from I and II, with some symmetry-breaking substitution on the rings.

We then move to the next step, the study the dynamical behavior of a suitable excited state, generated by photon absorption from the ground state (both states are in the space spanned by the eigenstates of the full vibronic hamiltonian, eq. (7) In the present case the ground state can be numerically computed by direct diagonalization of a matrix representation of the Hamiltonian in a suitable basis set. For the multi-mode case this is no more possible, in general, due to the explosion of the dimensions and one can make use of Lanczos techniques which are very useful also for the time propagation and have been extensively used in the numerical exploration of systems exhibiting conical intersections or avoided crossings [33–35]. In the following we take the tensorial product of the diabatic electronic states and of the free rotor eigenstates, which are the complex exponential functions:

${\mathrm{\chi }}_{\mathrm{n}}\left(\mathrm{\phi }\right)=1/\sqrt{2\mathrm{\pi }}exp\left[-\mathrm{in}\left(\mathrm{\phi }\right)\right]\left(\mathrm{n}=0,1,\dots \right)\text{.}$

Since in practice we only need the matrix elements of cos[φ], it is convenient to work with real functions:

${\mathrm{\chi }}_{\mathrm{n}}\left(\mathrm{\phi }\right)={\mathrm{N}}_{\mathrm{n}}cos\left[\mathrm{n\phi }\right]\left(\mathrm{n}=0,1,\dots \right):{\mathrm{\psi }}_{\mathrm{n}}\left(\mathrm{\phi }\right)={\mathrm{N}}_{\mathrm{n}}׳sin\left[\mathrm{n\phi }\right]\left(\mathrm{n}=1,2,\dots \right)\text{.}$

where

${\mathrm{N}}_0=1/\sqrt{2\mathrm{\pi }},{\mathrm{N}}_{\mathrm{n}}={\mathrm{N}}_{\mathrm{n}}^{\text{'}}=1/\sqrt{\mathrm{\pi }}\left(\mathrm{n}=1,2,\dots \right)\text{.}$

The matrix elements involving a cosine and a sine function vanish and so the Hamiltonian matrix has two blocks. We have verified that the ground state comes out from the cosine block for which the vibronic Hamiltonian of eq. (7) gives rise to the following matrix representation (each submatrix has dimension N × N, where N is the number of free rotor eigenfunctions utilized:

$\mathbf{H}=\left(\begin{array}{cc}\hfill {\mathbf{H}}^{11}\hfill & \hfill {\mathbf{H}}^{12}\hfill \\ \hfill {\mathbf{H}}^{21}\hfill & \hfill {\mathbf{H}}^{22}\hfill \end{array}\right)\text{,}$

and H¹² = H²¹ are tridiagonal:

${\mathbf{H}}^{12}=\mathrm{t}\left(\begin{array}{rrrrr}\hfill 0& \hfill 1/2& \hfill 0& \hfill 0& \hfill .\\ \hfill 1/2& \hfill 0& \hfill 1/\sqrt{2}& \hfill 0& \hfill .\\ \hfill 0& \hfill 1/\sqrt{2}& \hfill 0& \hfill 1/\sqrt{2}& \hfill .\\ \hfill 0& \hfill 0& \hfill 1/\sqrt{2}& \hfill 0& \hfill .\\ \hfill 0& \hfill 0& \hfill 0& \hfill .& \hfill \text{.}\end{array}\right)$

The diagonalization of the Hamiltonian matrix (12) gives two degenerate ground states, which can be linearly combined to give states localized around φ = 0 and φ = π, respectively. The above degeneration comes out because we have considered the two planar configurations, which are energetically identical in our model, as distinguishable. In the following we will take the state localized near φ = 0 as initial state. We will refer to it as |g〉, which adopting a spinor notation is written as:

$\left|\mathrm{g}\right.〉=\left(\begin{array}{c}\hfill \left|{\mathrm{g}}_1\right.〉\hfill \\ \hfill \left|{\mathrm{g}}_2\right.〉\hfill \end{array}\right)\text{.}$

It is clear that exactly the same results would be obtained by taking the φ = π configuration. It is interesting to notice that adopting a non localized ground state would instead give different results. This latter choice, however, while non violating the quantum mechanics for an isolated system, would contradict the common sense. In practice one can admit, without difficulty, that either the preparation of the system leads to a localized state or that the interaction with the external world operates a wave-packet reduction.

In order to discuss the decay of an optically excited state, we have to make some assumptions on the form of the dipole. As is well known, in fact, the whole time-dependent photo-physical behavior can be simply determined by propagating in time the doorway state, which is obtained by acting with the dipole operator on the ground state (and normalizing). Such excited state can be prepared by photon absorption from a light pulse whose profile in time is a δ, i.e. in practice, a pulse much shorter than the characteristic life-time of the doorway state itself (for example, as we will verify in the following, a sub-picosecond pulse). The output from a time-resolved experiment with a coherent light pulse of arbitrary form and duration can be handled, in the weak-field limit, by simply convoluting the pulse shape with the output for δ excitation. This is however absolutely unnecessary for interpreting the photo-physical behavior upon optical excitation in ordinary conditions, since, even for laser sources, the molecule and the light interacts coherently only for very short times. In the following we will then assume that the basic physics of the problem can be understood simply looking at the time-dependent behavior of the doorway state.

Let us come to the dipole form. Since the two diabatic states depicts a situation in which charge are localized on the two rings, we will assume that they are also eigenstates of the dipole operator, which is directed along the line joining the centers of the rings. Hence, taking the above line as the z axis and assuming that the radiation is polarized along z we may take the dipole matrix as:

$\mathbf{d}=\mathrm{d}\left(\begin{array}{cc}\hfill -1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right)$

and then the doorway state is (apart from the normalization factor):

$\left|\mathrm{w}\right.〉=\mathbf{d}\left|\mathrm{g}\right.〉=\left(\begin{array}{c}\hfill -\left|{\mathrm{g}}_1\right.〉\hfill \\ \hfill \left|{\mathrm{g}}_2\right.〉\hfill \end{array}\right)\text{.}$

The density of probability in the φ space can be computed as a sum of contributions from the two diabatic states In particular for the ground state:

$\mathrm{P}\left(\mathrm{\phi }\right)={\mathrm{P}}_1\left(\mathrm{\phi }\right)+{\mathrm{P}}_2\left(\mathrm{\phi }\right)\text{,}$

where

${\mathrm{P}}_{\mathrm{j}}\left(\mathrm{\phi }\right)={\displaystyle \sum _{\mathrm{k}=0}^{\mathrm{N}}{〈{\mathrm{g}}_{\mathrm{j}}\left|\mathrm{j},\mathrm{k}\right.〉}^2\left(\mathrm{j}=1,2\right)\text{.}}$

Here j labels the diabatic electronic state, while k is the free rotor quantum numbers. As should be clear from eq. (16) the doorway state has exactly the same distribution. It is however much more interesting to look at the corresponding partition with respect to the adiabatic states. This may be easily derived in terms of the orthogonal matrix U(φ) which diagonalizes the electronic Hamiltonian, eq. (5). For a generic state:

$\left|\mathrm{a}\right.〉=\left(\begin{array}{c}\hfill \left|{\mathrm{a}}_1\right.〉\hfill \\ \hfill \left|{\mathrm{a}}_2\right.〉\hfill \end{array}\right)$

with

$\left|{\mathrm{a}}_1\right.〉={\displaystyle \sum _{\mathrm{k}}{\mathrm{C}}_{\mathrm{jk}}}\left|\mathrm{j},\mathrm{k}\right.〉,\left(\mathrm{j}=1,2\right)$

one has:

$\mathrm{P}\left(\mathrm{\phi }\right)={\mathrm{P}}_1^{\mathrm{ad}}\left(\mathrm{\phi }\right)+{\mathrm{P}}_2^{\mathrm{ad}}\left(\mathrm{\phi }\right)\text{,}$

${\mathrm{P}}_{\mathrm{ad},\mathrm{j}}\left(\mathrm{\phi }\right)={\displaystyle \sum _{\mathrm{k}}{\left|〈{\mathrm{j}}_{\mathrm{ad}},\mathrm{k}\left|{\mathrm{a}}_{\mathrm{j}}\right.〉\right|}^2={\displaystyle \sum _{\mathrm{k}}{\left|{\displaystyle \sum _{\mathrm{m}}〈\mathrm{k}\left|({{\mathrm{U}}_{1\mathrm{j}}}^{*}\right|\mathrm{m}〉{\mathrm{C}}_{1\mathrm{m}}+〈\mathrm{k}\left|{{\mathrm{U}}^{*}}_{2\mathrm{j}}\right|\mathrm{m}〉{\mathrm{C}}_{2\mathrm{m}}}\right|}^2\text{.}}}$

Notice that in the final result the integration over electronic states has been explicitly performed and the bracket involves only integration over the torsional angle φ. The numerical analysis performed using eq. (22) reveals that, while the ground state for the full vibronic problem stays onto the potential energy curve for the adiabatic ground state, the doorway state belongs almost completely to the excited adiabatic state. Hence, according to our model, the excitation by a δ -pulse simply transfers the wave-packet to the excited adiabatic state, which is a reasonable result. We also notice that since the doorway state corresponds now to a φ distribution which is sharply peaked around a maximum of the potential energy curve, it would presumably give rise to a highly non-stationary behavior.

4 The time evolution

We then proceed propagating in time the doorway state and computing at any time the population of the excited adiabatic state, which can be evaluated performing a numerical integration of the distribution in eq. (22) over the torsional angle. The time dependent Schrödinger can be solved by matrix diagonalization and the results can be expressed in compact form, as discussed in ref [36]. The results of the calculation (not reported here) are somewhat unexpected. In fact during the time evolution of the doorway state only a negligible fraction of the population is transferred to the adiabatic ground state, mimicking in this respect the behavior of a true stationary state. This behavior depends on the fact that the wave-packet travels through the avoided crossing regions near φ = ± π/2, (see fig. 1), i.e. the regions where non-adiabatic coupling is expected to be more important, with high velocity. From a purely quantum point of view one may say that the time-dependent non-adiabatic matrix elements are small due to the high oscillatory character of the wave function in the φ-space. The semiclassical Landau-Zener formula [37–39] (which is the exact solution for the scattering problem for two electronic states, assuming a classical trajectory of the nuclei and a linear behavior of the diabatic potential curves near the crossing point) also predicts the same behavior if one evaluates the so called two-way probability [39], which takes into account that in one vibrational period the wave-packet travels two times across the intersection point between diabatic curves. In fact, according to this well known theoretical result, the adiabatic transition probability is given by the negative exponential of a term which is inversely proportional to the linear momentum of the nuclei at the time they pass through the intersection point (we are assuming that at t=0 the nuclei have zero momentum. Hence, in our situation, one has an high probability of adiabatic transition during the first passage which is however frustrated by an high probability of the reverse transition during the second passage. It is however worthwhile to mention that, according to recent numerical investigations [33], the Landau-Zener formula becomes progressively less useful when going at high coupling strength.

In practice, we pay here the consequences of our basic assumption concerning the presence of a single mode (the torsion). In fact the initial wave-packet is placed in a region of high potential energy, which is then transformed totally into kinetic energy, since there is no way of transferring it to other degrees of freedom. One expects that this situation will change drastically introducing explicitly one or more other modes[22,32]. It is also possible to mimic the effect of additional internal modes as well as of collisions with solvent molecules moving towards a stochastic approach. The stochastic way of handling the problem has become very popular in the last few years as a powerful tool for investigating the static and dynamic role of the solvent in ET reactions involving large intramolecular rearrangements and the literature on this subject is very extensive (a comprehensive review is [40]). We touch here very marginally the problem just to show how the inclusion of dissipative processes for the torsional motion changes radically the time-dependent behavior of the system. This is accomplished by assuming that the initial distribution (i.e. that corresponding to the doorway state) undergoes a diffusions! motion on the excited adiabatic surface described by a mono-dimensional Fokker-Planck differential equation:

$\frac{\partial }{\partial \mathrm{t}}{\mathrm{P}}_{\mathrm{e}}\left(\mathrm{\phi },\mathrm{t}\right)=\left\{{\mathrm{D}}_{\mathrm{R}}\frac{\partial }{\partial \mathrm{\phi }}\left[\frac{1}{{\mathrm{k}}_{\mathrm{B}}\mathrm{T}}\frac{\partial {\mathrm{E}}_{\mathrm{e}}}{\partial \mathrm{\phi }}+\frac{\partial }{\partial \mathrm{\phi }}\right]-\mathrm{k}\left(\mathrm{\phi }\right)\right\}{\mathrm{P}}_{\mathrm{e}}\left(\mathrm{\phi },\mathrm{t}\right)\text{,}$

where D_R is diffusion coefficient for the torsional coordinate, k_B the Boltzmann constant, T the absolute temperature, E_e(φ)the potential energy curve for the excited adiabatic state and k(φ) the decay rate towards the ground state. It is worthwhile to recall here that equation (23) is often associated in the literature [30,31] to the name of Smoluchowsky, but we prefer to follow the Van Kampen notation [41]. The Fokker-Planck equation can be considered as the master equation associated with a continuous random walk of a particle in a potential. As discussed in ref. [30,31] a more correct approach would include diffusion along a further degree of freedom describing the solvent polarization, also important in determining the exact shape of the adiabatic surfaces for both ground and excited states, but the basic physics is caught by the present simplified model.

The rate k(φ) for a given torsion angle φ has been determined solving numerically the time-dependent Schrodinger equation for a wave-packet sharply localized around φ on the upper adiabatic curve and computing the time-derivative (at t=0) of the probability of being on the excited surface. The computed function k(φ) (not reported here) shows peaks at the angles where the curves exhibit avoided crossings, as expected. According to ref [30] the diffusion coefficient D has been taken as the inverse of the correlation time for the internal rotation $\mathrm{D}=\frac{1}{{\mathrm{\tau }}_{\mathrm{R}}}\text{,}$ and the latter can be estimated from experimental data or taken as an adjustable parameter. We have assumed here τ_R = 150 ps which seems a reasonable value for the torsion of an aromatic ring in water.

The above Fokker-Planck equation can be solved by linear algebraic methods, after making recourse to the matrix representation of the operator acting on the distribution function on the right hand side of eq. (23). For that purpose we made use of the same basis set as for solving the Schrödinger equation for the Hamiltonian in eq. (7). Due to the fact that all the operators (as well as the initial distribution) are even with respect to the inversion φ → –φ we may restrict our basis set to the normalized cos(n φ)functions with n=0, 1, 2,…, N. The proper dimension N is chosen following two criteria: i) the rate k(φ) and the initial distribution P₀(φ) = P(φ, t = 0) should be well represented and ii) the results of the computations should be stable with respect to the enlargement of the basis set. In our example we have taken N=150.

The continuous line in figure (4) shows the population of the excited adiabatic state as a function of time, at room temperature. It is now clear that now the possibility of dissipating the torsional kinetic energy gives rise to a true decay, which is very rapid with respect to the normal fluorescence lifetimes (from 0.1 to 1 nanosecond). We may then expects that molecules like (I) would prefer the radiationless route (internal conversion) for the decay.

Figure 4

As should be clear from the above example, the efficiency of internal conversion is related to the ability of the rings to gives rise to large-amplitude librational motions, since according to our simple model, the initial excited wave-packet is placed far from the zone where non-adiabatic coupling is effective. One may then expects that structural modifications which tend to hinder the torsional motion might be also effective in altering the photo-physical behavior. Let us investigate, for example, the role of a bridge between the two aromatic rings created by o bonds, like for example in IV:

We may maintain our simple two-state picture adding along the diagonal of the matrix (7) a potential energy term taking into account that when the torsion angle increases the σ bridge is stretched. For simplicity we treat this stretching as harmonic, with a force constant of 0.46 a. u. of energy (a. u. of length)^- 2 The resulting adiabatic curves are reported in figure (5). It is evident that now the tendency to give an excited state with minimum at right angle is completely frustrated by the presence of the bridge joining the rings. The doorway state is now located in a region of minimum potential energy, and, during its time evolution, it is not able to reach the avoided crossing regions. As a consequence the population of the excited adiabatic state (dashed line in figure 4) remains essentially constant on the time scale studied here and one may expects that now the fluorescence will become the dominant decay channel. Hence, a change in the molecular structure which a priori could be judged of minor importance (especially due to the fact that we are discussing properties determined mainly by π electrons) results in a drastic variation of the photo-physical behavior.

Figure 5

The results presented here are only intended to draw the main lines of a general scenario concerning molecules in which the photon absorption leads to electron transfer between aromatic rings, which are essentially controlled by a torsional angle, like in biphenil-like compounds. Another interesting class of systems which can be studied along the lines discussed here is that of pairs or even chains of mixed-valent transition metal ions bridged by an organic ligand like pyrazine or bipyridine [42–46], since the dependence of the intersite hopping term of the Hamiltonian on the orientation of the ring(s) introduces an important source of electron-phonon coupling whose role is presently unknown. Of course reliable information on individual system can only be obtained through an accurate quantum chemical study, which should also include solvation effects, since one is dealing with charge transfer processes, to be confronted with experimental data. The present approach can be easily extended to include generic potential energy surfaces and coupling matrix elements. It appears highly suggestive, however, that a very simple basic model seems capable of explaining the behavior of a large class of compounds.

5 Concluding remarks

As a conclusion we mention an old problem for the solution of which one of us (A. L.) spent some time (with scarce success), when he was a young student, as a part of its work for obtaining the degree in Chemistry, under the guide of the person to whom this volume is dedicated. This concerns the striking different photophysical behavior of two similar species, which can be both considered as derivatives of the triphenil-methane: the phenolphtalein (III) and the fluorescein dianions (V) [47]. As is well documented in the literature, the fluorescence quantum yield of the first excited singlet of the fluorescein ion is 1, while that of the phenolphtalein is essentially 0. We firmly believe that the very different efficiency of the radiationless decay channel of such molecules can be explained along the lines sketched here, since, as is clear from a perusal of their structural formulas, the phenolphtalein is characterized by the possibility of large amplitude librational motions of the phenil rings that are not allowed in fluorescein. Of course this is only a working hypothesis that needs to be tested having at hands reliable computations of the electronic structure of the two molecules.