What is a neuron? A neuron is a processing unit that takes an input value and, according to predefined rules, outputs a different value.

In 1943, Warren McCullock and Walter Pitts published an article (W. S. McCulloch and W. Pitts. A Logical Calculus of the Ideas Immanent in Nervous Activity, The Bulletin of Mathematical Biophysics, 5(4):115–133, 1943) in which they described the functioning of a single biological neuron. The components of a biological neuron are the dendrites, the soma (the cell body), the axons, and the synaptic gaps. Under different names, these are also parts of an artificial neuron.

The dendrites bring the input from other neurons to the soma, the neuron's body. The soma is where the inputs are processed and summed together. If the input is over a certain threshold, the neuron will "fire" and transmit a single output that is electrically sent through the axons. Between the axons of the transmitting neurons and the dendrites of the receiving neurons lies the synaptic gap that mediates chemically such impulses, altering their frequencies. In an artificial neural net, we model the frequency through a numerical weight: the higher the frequency, the higher the impulse and, therefore, the higher the weight. We can then establish an equivalence table between biological and artificial neurons (this is a very simplified description, but it works for our purposes):

Schematic correspondence between a biological and an artificial neuron

We can therefore describe an artificial neuron schematically as follows:

At the center of this picture we have the neuron, or the soma, which gets an input (the activation) and sets the neuron's internal state that triggers an output (the activity function). The input comes from other neurons and it is mediated in intensity by the weights (the synaptic gap).

The simple activation value for a neuron is given by , where x_i is the value of each input neuron, and w_i is the value of the connection between the neuron i and the output. In the first chapter, in our introduction to neural networks, we introduced the bias. If we include the bias and want to make its presence explicit, we can rewrite the preceding equation as . The bias effect is to translate the hyperplane defined by the weights so it will not necessarily go through the origin (and hence its name). We should interpret the activation value as the neuron's internal state value.

As we mentioned in the previous chapter, the activation value defined previously can be interpreted as the dot product between the vector w and the vector x. A vector x will be perpendicular to the weight vector w if <w,x> = 0, therefore all vectors x such that <w,x> = 0 define a hyper-plane in Rⁿ (where n is the dimension of x).

Hence, any vector x satisfying <w,x> > 0 is a vector on the side of the hyper-plane defined by w. A neuron is therefore a linear classifier, which, according to this rule, activates when the input is above a certain threshold or, geometrically, when the input is on one side of the hyper-plane defined by the vector of the weights.

A single neuron is a linear classifier

A neural network can have an indefinite number of neurons, but regardless of their number, in classical networks all the neurons will be ordered in layers. The input layer represents the dataset, the initial conditions. For example, if the input is a grey-scale image, the input layer is represented for each pixel by an input neuron with the inner value the intensity of the pixel. It should be noted, however, that the neurons in the input layer are not neurons as the others, as their output is constant and is equal to the value of their internal state, and therefore the input layer is not generally counted. A 1-layer neural net is therefore a simple neural net with just one layer, the output, besides the input layer. From each input neuron we draw a line connecting it with each output neuron and this value is mediated by the artificial synaptic gap, that is the weight w_i,j connecting the input neuron xi to the output neuron y_j. Typically, each output neuron represents a class, for example, in the case of the MNIST dataset, each neuron represents a digit. The 1-layer neural net can therefore be used to make a prediction such as which digit the input image is representing. In fact, the set of output values can be regarded as a measure of the probability that the image represents the given class, and therefore the output neuron with the highest value will represent the prediction of the neural net.

It must be noted that neurons in the same layer are never connected to one another, as in the following figure; instead they are all connected to each of the neurons in the next layer, and so on:

An example of a 1-layer neural network: the neurons on the left represent the input with bias b, the middle column represents the weights for each connection, while the neurons on the right represent the output given the weights w.

This is one of the necessary and defining conditions for classical neural networks, the absence of intra-layers connections, while neurons connect to each and every neuron in adjacent layers. In the preceding figure, we explicitly show the weights for each connection between neurons, but usually the edges connecting neurons implicitly represent the weights. The 1 represents the bias unit, the value 1 neuron with connecting weight equal to the bias that we have introduced earlier.

As mentioned many times, 1-layer neural nets can only classify linearly separable classes; however, there is nothing that can prevent us from introducing more layers between the input and the output. These extra layers are called hidden layers.

Shown is a 3-layer neural network with two hidden layers. The input layer has k input neurons, the first hidden layer has n hidden neurons, and the second hidden layer has m hidden neurons. In principle it is possible to have as many hidden layers as desired. The output, in this example, is the two classes, y₁ and y₂. On top the on always-on bias neuron. Each connection has its own weight w (not depicted for simplicity).

Biologically, neuroscience has identified hundreds, perhaps more than a thousand different types of neurons (refer The Future of the Brain", by Gary Marcus and Jeremy Freeman) and therefore we should be able to model at least some different types of artificial neurons. This can be done by using different types of activity functions, that is, the function defined on the internal state of the neuron represented by the activation calculated on the input from all the input neurons.

The activity function is a function defined on a(x) and it defines the output of the neuron. The most common activity functions used are:

What are the main differences between these activation functions? Often, different activation functions work better for different problems. In general, the identity activity function or threshold function, while widely used at the inception of neural networks with such implementations such as the perceptron or the Adaline (adaptive linear neuron), has recently lost traction in favor of the logistic sigmoid, the hyperbolic tangent, or the ReLU. While the identity function and the threshold function are much simpler, and therefore were the preferred functions when computers did not have quite as much calculation power, it is often preferable to use non-linear functions, such as the sigmoid functions or the ReLU. It should also be noted that if we only used the linear activity function there is no point in adding extra hidden layers, as the composition of linear functions is still just a linear function. The last three activity functions differ in the following ways:

The fact that the gradient may vanish as we increase x and why it is important will be clearer later; for now, let's just mention that the gradient (for example, the derivative) of the function is important for the training of the neural network. This is similar to how, in the linear regression example we introduced in the first chapter, we were trying to minimize the function following it along the direction opposite to its derivative.

The range for the logistic function is (0,1), which is one reason why this is the preferred function for stochastic networks, that is, networks with neurons that may activate based on a probability function. The hyperbolic function is very similar to the logistic function, but its range is (-1, 1). In contrast, the ReLU has a range of (0, ), so it can have a very large output.

However, more importantly, let's look at the derivative for each of the three functions. For a logistic function f, the derivative is f * (1-f), while if f is the hyperbolic tangent, its derivative is (1+f) * (1-f).

If f is the ReLU, the derivative is much simpler and it is simply .

Tip

Let's briefly see how we can calculate the derivative of the logistic sigmoid function. This can be quickly calculated by simply noticing that the derivative with respect to a of the function is given by the following:

When we will talk about back-propagation, we will see that one of the problems for deep networks is that of the vanishing gradient (as mentioned previously), and the advantage of the ReLU activity function is that the derivative is constant and does not tend to 0 as a becomes large.

Typically all neurons in the same layer have the same activity function, but different layers may have different activity functions. But why are neural networks more than 1-layer deep (2-layer or more) so important? As we have seen, the importance of neural networks lies in their predictive power, that is, in their ability to approximate a function defined on the input with the required output. There exists a theorem, called the Universal Approximation Theorem, which states that any continuous functions on compact subsets of R_n can be approximated by a neural network with at least one hidden layer. While the formal proof of such a theorem is too complex to be explained here, we will attempt to give an intuitive explanation only using some basic mathematics, and for this we will make use of the logistic sigmoid as our activity function.

The logistic sigmoid is defined as where . Let's now assume that we have only one neuron x=x_i:

On the left is a standard sigmoid with weight 1 and bias 0. In the center is a sigmoid with weight 10, while on the right is a sigmoid with weight 10 and bias 50.

Then it can be easily shown that if w is very large, the logistic function becomes close to a step function. The larger w is, the more it resembles a step function at 0 with height 1. On the other hand, b will simply translate the function, and the translation will be equal to the negative of the ratio b/w. Let's call t = -b/w.

With this in mind, let's now consider a simple neural net with one input neuron and one hidden layer with two neurons and only one output neuron in the output layer:

X is mapped on the two hidden neurons with weights and biases such that on the top hidden neuron the ratio –b/w is t₁ while on the bottom hidden neuron it is t₂. Both hidden neurons use the logistic sigmoid activation function.

The input x is mapped to two neurons, one with weight and bias such that the ratio is t₁ and the other such that the ratio is t₂. Then the two hidden neurons can be mapped to the output neuron with weights w and –w, respectively. If we apply the logistic sigmoid activity function to each hidden neuron, and the identity function to the output neuron (with no bias), we will get a step function, from t₁ to t₂, and height w, like the one depicted in the following figure. Since the series of step functions like the one in the figure can approximate any continuous function on a compact subset of R, this gives an intuition of why the Universal Approximation Theorem holds (this is, in simplified terms, the content of a mathematical theorem called "The simple function approximation theorem").

With a little more effort, this can be generalized to R_n.

The code to produce the preceding figure is as follows:

#The user can modify the values of the weight w 
#as well as biasValue1 and biasValue2 to observe
#how this plots to different step functions

import numpy 
import matplotlib.pyplot as plt
weightValue = 1000
#to be modified to change where the step function starts
biasValue1 = 5000 
#to be modified to change where the step function ends 
biasValue2 = -5000
  
plt.axis([-10, 10, -1, 10])  

print ("The step function starts at {0} and ends at {1}"
        .format(-biasValue1/weightValue, 
        -biasValue2/weightValue))  

y1 = 1.0/(1.0 + numpy.exp(-weightValue*x - biasValue1)) 
y2 = 1.0/(1.0 + numpy.exp(-weightValue*x - biasValue2)) 
#to be modified to change the height of the step function 
w = 7 
y = y1*w-y2*w  
plt.plot(x, y, lw=2, color='black') 
plt.show()

We have seen how neural networks can map inputs onto determined outputs, depending on fixed weights. Once the architecture of the neural network has been defined (feed-forward, number of hidden layers, number of neurons per layer), and once the activity function for each neuron has been chosen, we will need to set the weights that in turn will define the internal states for each neuron in the network. We will see how to do that for a 1-layer network and then how to extend it to a deep feed-forward network. For a deep neural network the algorithm to set the weights is called the back-propagation algorithm, and we will discuss and explain this algorithm for most of this section, as it is one of the most important topics for multi-layer feed-forward neural networks. First, however, we will quickly discuss this for 1-layer neural networks.

The general concept we need to understand is the following: every neural network is an approximation of a function, therefore each neural network will not be equal to the desired function, and instead it will differ by some value. This value is called the error and the aim is to minimize this error. Since the error is a function of the weights in the neural network, we want to minimize the error with respect to the weights. The error function is a function of many weights; it is therefore a function of many variables. Mathematically, the set of points where this function is zero represents therefore a hypersurface and to find a minimum on this surface we want to pick a point and then follow a curve in the direction of the minimum.

Linear regression

We have already introduced linear regression in the first chapter, but since we are now dealing with many variables, to simplify things we are going to introduce matrix notation. Let x be the input; we can think of x as a vector. In the case of linear regression, we are going to consider a single output neuron y; the set of weights w is therefore a vector of dimension the same as the dimension of x. The activation value is then defined as the inner product <x, w>.

Let's say that for each input value x, we want to output a target value t, while for each x the neural network will output a value y, defined by the activity function chosen, in this case the absolute value of the difference (y-t) represents the difference between the predicted value and the actual value for the specific input example x. If we have m input values x_i, each of them will have a target value t_i. In this case, we calculate the error using the mean squared error , where each y_i is a function of w. The error is therefore a function of w and it is usually denoted with J(w).

As mentioned previously, this represents a hyper-surface of dimension equal to the dimension of w (we are implicitly also considering the bias), and for each w_j we need to find a curve that will lead towards the minimum of the surface. The direction in which a curve increases in a certain direction is given by its derivative with respect to that direction, in this case by the following:

And in order to move towards the minimum we need to move in the opposite direction set by for each w_j.

Let's calculate the following:

If , then and therefore

Tip

The notation can sometimes be confusing, especially the first time one sees it. The input is given by vectors xⁱ, where the superscript indicates the i^th example. Since x and w are vectors, the subscript indicates the j^th coordinate of the vector. yⁱ then represents the output of the neural network given the input xⁱ, while tⁱ represents the target, that is, the desired value corresponding to the input x_i.

In order to move towards the minimum, we need to move each weight in the direction of its derivative by a small amount l, called the learning rate, typically much smaller than 1, (say 0.1 or smaller). We can therefore redefine in the derivative and incorporate the "2 in the learning rate, to get the update rule given by the following:

Or, more generally, we can write the update rule in matrix form as follows:

Here, (also called nabla) represents the vector of partial derivatives. This process is what is often called gradient descent.

Tip

is a vector of partial derivatives. Instead of writing the update rule for w separately for each of its components wj, we can write the update rule in matrix form where, instead of writing the partial derivative for each j, we use to indicate each partial derivative, for each j.

One last note; the update can be done after having calculated all the input vectors, however, in some cases, the weights can be updated after each example or after a defined preset number of examples.

Logistic regression

In logistic regression, the output is not continuous; rather it is defined as a set of classes. In this case, the activation function is not going to be the identity function like before, rather we are going to use the logistic sigmoid function. The logistic sigmoid function, as we have seen before, outputs a real value in (0,1) and therefore it can be interpreted as a probability function, and that is why it can work so well in a 2-class classification problem. In this case, the target can be one of two classes, and the output represents the probability that it be one of those two classes (say t=1).

Tip

Again, the notation can be confusing. t is our target, and it can have, in this example, two values. These two values are often defined to be class 0 and class 1. These values 0 and 1 are not to be confused with the values of the logistic sigmoid function, which is a continuous real-valued function between 0 and 1. The real value of the sigmoid function represents the probability that the output be in class 0 or class 1.

If a is the neuron activation value as defined previously, let's denote with the s(a) the logistic sigmoid function, therefore, for each example x, the probability that the output be the class y, given the weights w, is:

We can write that equation more succinctly as follows:

And since for each sample xⁱ the probabilities P(t_i|x_i, w) are independent, the global probability is as follows:

If we take the natural log of the preceding equation (to turn products into sums), we get the following:

The object is now to maximize this log to obtain the highest probability of predicting the correct results. Usually, this is obtained, as in the previous case, by using gradient descent to minimize the cost function J(w) defined by J(w)= -log(P(y¦ x ,w)).

As before, we calculate the derivative of the cost function with respect to the weights w_j to obtain:

Tip

To understand the last equality, let's remind the reader of the following facts:

Therefore, by the chain rule:

Similarly:

In general, in case of a multi-class output t, with t a vector (t₁, …, t_n), we can generalize this equation using = that brings to the update equation for the weights:

This is similar to the update rule we have seen for linear regression.

Back-propagation

In the case of 1-layer, weight-adjustment is easy, as we can use linear or logistic regression and adjust the weights simultaneously to get a smaller error (minimizing the cost function). For multi-layer neural networks we can use a similar argument for the weights used to connect the last hidden layer to the output layer, as we know what we would like the output layer to be, but we cannot do the same for the hidden layers, as, a priori, we do not know what the values for the neurons in the hidden layers ought to be. What we do, instead, is calculate the error in the last hidden layer and estimate what it would be in the previous layer, propagating the error back from the last to the first layer, hence the name back-propagation.

Back-propagation is one of the most difficult algorithms to understand at first, but all is needed is some knowledge of basic differential calculus and the chain rule. Let's introduce some notation first. We denote with J the cost (error), with y the activity function that is defined on the activation value a (for example, y could be the logistic sigmoid), which is a function of the weights w and the input x. Let's also define w_i,j, the weight between the i^th input value, and the jth output. Here we define input and output more generically than for a 1-layer network: if w_i,j connects a pair of successive layers in a feed-forward network, we denote as "input" the neurons on the first of the two successive layers, and "output" the neurons on the second of the two successive layers. In order not to make the notation too heavy, and have to denote on which layer each neuron is, we assume that the ith input y_i is always in the layer preceding the layer containing the j^th output y_j.

Tip

Note that the letter y is used to both denote an input and the output of the activity function. y_j is the input to the next layer, and y_j is the output of the activity function, but it is then also the input to the next layer. Therefore we can think of the y_j's as functions of the y_j's.

We also use subscripts i and j, where we always have the element with subscript i belonging to the layer preceding the layer containing the element with subscript j.

Figure 10

In this example, layer 1 represents the input, and layer 2 the output, so w_i,j is a number connecting the y_jvalue in a layer, and the y_j value in the following layer.

Using this notation, and the chain-rule for derivatives, for the last layer of our neural network we can write the following:

Since we know that , we have the following:

If y is the logistic sigmoid defined previously, we get the same result we have already calculated at the end of the previous section, since we know the cost function and we can calculate all derivatives.

For the previous layers the same formula holds:

In fact, a j is the activity function, which, as we know, is a function of the weights. The y_j value, which is the activity function of the neuron in the "second" layer, is a function of its activation value, and, of course, the cost function is a function of the activity function we have chosen.

Tip

Even though we have several layers, we always concentrate on pairs of successive layers and so, perhaps abusing the notation somewhat, we always have a "first" layer and a "second" layer, as in Figure 10, which is the "input" layer and the "output" layer.

Since we know that and we know that is the derivative of the activity function that we can calculate, all we need to calculate is the derivative . Let's notice that this is the derivative of the error with respect to the activation function in the "second" layer, and, if we can calculate this derivative for the last layer, and have a formula that allows us to calculate the derivative for one layer assuming we can calculate the derivative for the next, we can calculate all the derivatives starting from the last layer and move backwards.

Let us notice that, as we defined by the y_j, they are the activation values for the neurons in the "second" layer, but they are also the activity functions, therefore functions of the activation values in the first layer. Therefore, applying the chain rule, we have the following:

And once again we can calculate both and , so once we know we can calculate , and since we can calculate for the last layer, we can move backward and calculate for any layer and therefore for any layer.

To summarize, if we have a sequence of layers where

We then have these two fundamental equations, where the summation in the second equation should read as the sum over all the outgoing connections from y j to any neuron in the successive layer.

By using these two equations we can calculate the derivatives for the cost with respect to each layer.

If we set , represents the variation of the cost with respect to the activation value, and we can think of as the error at the y_j neuron. We can then rewrite

This implies that . These two equations give an alternate way of seeing back-propagation, as the variation of the cost with respect to the activation value, and provide a formula to calculate this variation for any layer once we know the variation for the following layer:

We can also combine these equations and show that:

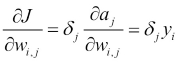
The back-propagation algorithm for updating the weights is then given on each layer by

In the last section, we will provide a code example that will help understand and apply these concepts and formulas.

We mentioned in the previous chapter some examples where machine learning finds its applications. Neural networks, in particular, have many similar applications. We will review some of the applications for which they were used when they became popular in the late 1980's and early 1990's, after back-propagation had been discovered and deeper neural networks could be trained.

It is a well-known fact, and something we have already mentioned, that 1-layer neural networks cannot predict the function XOR. 1-layer neural nets can only classify linearly separable sets, however, as we have seen, the Universal Approximation Theorem states that a 2-layer network can approximate any function, given a complex enough architecture. We will now create a neural network with two neurons in the hidden layer and we will show how this can model the XOR function. However, we will write code that will allow the reader to simply modify it to allow for any number of layers and neurons in each layer, so that the reader can try simulating different scenarios. We are also going to use the hyperbolic tangent as the activity function for this network. To train the network, we will implement the back-propagation algorithm discussed earlier.

We will only need to import one library, numpy, though if the reader wished to visualize the results, we also recommend importing matplotlib. The first lines of code are therefore:

import numpy 
from matplotlib.colors import ListedColormap 
import matplotlib.pyplot as plt 

Next we define our activity function and its derivative (we use tanh(x) in this example):

def tanh(x):     
    return (1.0 - numpy.exp(-2*x))/(1.0 + numpy.exp(-2*x))

def tanh_derivative(x):     
    return (1 + tanh(x))*(1 - tanh(x))

Next we define the NeuralNetwork class:

class NeuralNetwork:

To follow Python syntax, anything inside the NeuralNetwork class will have to be indented. We define the "constructor" of the NeuralNetwork class, that is its variables, which in this case will be the neural network architecture, that is, how many layers and how many neurons per layer, and we will also initialize at random the weights to be between negative 1 and positive 1. net_arch will be a 1-dimensional array containing the number of neurons per each layer: for example [2,4,1] means an input layer with two neurons, a hidden layer with four neurons, and an output layer with one neuron.

Since we are studying the XOR function, for the input layer we need to have two neurons, and for the output layer only one neuron:

    #net_arch consists of a list of integers, indicating 
    #the number of neurons in each layer, i.e. the network 
    #architecture
    def __init__(self, net_arch): 
        self.activity = tanh
        self.activity_derivative = tanh_derivative 
        self.layers = len(net_arch)         
        self.steps_per_epoch = 1000   
        self.arch = net_arch

        self.weights = []         
        #range of weight values (-1,1)         
        for layer in range(self.layers - 1):             
            w = 2*numpy.random.rand(net_arch[layer] + 1, net_arch[layer+1]) - 1
            self.weights.append(w)

In this code, we have defined the activity function to be the hyperbolic tangent and we have defined its derivative. We have also defined how many training steps there should be per epoch. Finally, we have initialized the weights, making sure we also initialize the weights for the biases that we will add later. Next, we need to define the fit function, the function that will train our network. In the last line, nn represents the NeuralNetwork class and predict is the function in the NeuralNetwork class that we will define later:

    #data is the set of all possible pairs of booleans
    #True or False indicated by the integers 1 or 0 
    #labels is the result of the logical operation 'xor' 
    #on each of those input pairs
    def fit(self, data, labels, learning_rate=0.1, epochs=100):
        #Add bias units to the input layer         
        ones = numpy.ones((1, data.shape[0]))        
        Z = numpy.concatenate((ones.T, data), axis=1)
        training = epochs*self.steps_per_epoch
        for k in range(training):             
            if k % self.steps_per_epoch == 0:                  
                print('epochs: {}'.format(k/self.steps_per_epoch))
                for s in data:                     
                    print(s, nn.predict(s))

All we have done here is to add a "1" to the input data (the always-on bias neuron) and set up code to print the result at the end of each epoch to keep track of our progress. We will now go ahead and set up our feed-forward propagation:

               sample = numpy.random.randint(data.shape[0])
               y = [Z[sample]]
               for i in range(len(self.weights)-1):
                   activation = numpy.dot(y[i], self.weights[i])
                   activity = self.activity(activation)
                   #add the bias for the next layer
                   activity = numpy.concatenate((numpy.ones(1), 
                              numpy.array(activity)))
                   y.append(activity)

               #last layer 
               activation = numpy.dot(y[-1], self.weights[-1])
               activity = self.activity(activation)
               y.append(activity)

We are going to update our weights after each step, so we randomly select one of the input data points, then we set up feed-forward propagation by setting up the activation for each neuron, then applying the tanh(x) on the activation value. Since we have a bias, we add the bias to our matrix y that keeps track of each neuron output value.

Now we do our back-propagation of the error to adjust the weights:

               #error for the output layer
               error = labels[sample] - y[-1]
               delta_vec = [error * self.activity_derivative(y[-1])] 
               #we need to begin from the back, 
               #from the next to last layer
               for i in range(self.layers-2, 0, -1):  
                   error = delta_vec[-1].dot(self.weights[i][1:].T) 
                   error = error*self.activity_derivative(y[i][1:])
                   delta_vec.append(error)
               #Now we need to set the values from back to front
               delta_vec.reverse()

               #Finally, we adjust the weights, 
               #using the backpropagation rules
               for i in range(len(self.weights)):
                   layer = y[i].reshape(1, nn.arch[i]+1)
                   delta = delta_vec[i].reshape(1, nn.arch[i+1])
                   self.weights[i] +=learning_rate*layer.T.dot(delta)

This concludes our back-propagation algorithm; all that is left to do is to write a predict function to check the results:

    def predict(self, x):          
        val = numpy.concatenate((numpy.ones(1).T, numpy.array(x)))      
        for i in range(0, len(self.weights)):             
            val = self.activity(numpy.dot(val, self.weights[i]))             
            val = numpy.concatenate((numpy.ones(1).T, 
                                     numpy.array(val)))         
        return val[1]

At this point we just need to write the main function as follows:

    if __name__ == '__main__':  
    numpy.random.seed(0)
    #Initialize the NeuralNetwork with 
    #2 input neurons
    #2 hidden neurons
    #1 output neuron    
    nn = NeuralNetwork([2,2,1])      
    X = numpy.array([[0, 0],
                    [0, 1],
                    [1, 0],
                    [1, 1]])

    #Set the labels, the correct results for the xor operation    
    y = numpy.array([0, 1, 1, 0])      

    #Call the fit function and train the network 
    #for a chosen number of epochs
    nn.fit(X, y, epochs=10)
      
    print "Final prediction"     
    for s in X:         
       print(s, nn.predict(s))

Notice the use of numpy.random.seed(0). This is simply to ensure that the weight initialization is consistent across runs to be able to compare results, but it is not necessary for the implementation of a neural net.

This ends the code, and the output should be a four-dimensional array, such as: (0.003032173692499, 0.9963860761357, 0.9959034563937, 0.0006386449217567) showing that the neural network is learning that the output should be (0,1,1,0).

The reader can slightly modify the code we created in the plot_decision_regions function used earlier in this book and see how different neural networks separate different regions depending on the architecture chosen.

The output picture will look like the following figures. The circles represent the (True, True) and (False, False) inputs, while the triangles represent the (True, False) and (False, True) inputs for the XOR function.

The same figure, on the left zoomed out, and on the right zoomed in on the selected inputs. The neural network learns to separate those points, creating a band containing the two True output values.

Different neural network architectures (for example, implementing a network with a different number of neurons in the hidden layer, or with more than just one hidden layer) may produce a different separating region. In order to do this, the reader can simply change the line in the code nn = NeuralNetwork([2,2,1]). While the first 2 must be kept (the input does not change), the second 2 can be modified to denote a different number of neurons in the hidden layer. Adding another integer will add a new hidden layer with as many neurons as indicated by the added integer. The last 1 cannot be modified. For example, ([2,4,3,1]) will represent a 3-layer neural network, with four neurons in the first hidden layer and three neurons in the second hidden layer.

The reader would then see that, while the solution is always the same, the curves separating the regions will be quite different depending on the architecture chosen. In fact, choosing nn = NeuralNetwork([2,4,3,1]) will give the following figure:

While choosing nn = NeuralNetwork([2,4,1]), for example, would produce the following:

The architecture of the neural network defines therefore the way the neural net goes about to solve the problem at hand, and different architectures provide different approaches (though they may all give the same result) similarly to how human thought processes can follow different paths to reach the same conclusion. We are now ready to start looking more closely at what deep neural nets are and their applications.