Appendix A. More details about differential privacy

As we discussed in chapter 2, differential privacy (DP) is one of the most popular and influential privacy protection schemes. It is based on the concept of making a dataset robust enough that any single substitution in the dataset does not reveal private data. This is typically achieved by calculating the patterns of groups within the dataset, which we call complex statistics, while withholding information about individuals in the dataset. The beauty of differential privacy is its mathematical provability and quantifiability. In the following sections, we will introduce the mathematical foundations and the formal definition of DP. If you are not interested in these mathematical foundations, you can bypass this now and come back to it when necessary.

A.1 The formal definition of differential privacy

Before we introduce the formal definition of DP, let’s look at some essential terms originally defined by Dwork and Roth [1]:

• Probability simplex—Let B denote a discrete set. The probability simplex of B, denoted Δ(B), is defined to be Δ(B) = {x ∈ ℝ^|B| : x_i ≥ 0 for all i and Σ^|B|_i=1 x_i = 1. You can consider the probability simplex to be the space of a given probability distribution.

• Randomized algorithm—A randomized algorithm M with domain A and discrete range B is associated with the mapping M : A→Δ(B). Given an input a ∈ A, the algorithm M outputs M(a) = b with probability (M(a))_b for each b ∈ B. The probability space is over the coin flips of the algorithm M. We discussed how randomization in the algorithm happens with two coin flips in section 2.2.1.

• Database—A database x is a collection of records that form a universe X.

  For instance, let the universe X define the set of unique elements in the database. Then a database could be represented by the histograms of the elements within the database, x ∈ ℕ^|X|, where each entry x_i represents the number of elements in the database x of type i ∈ X.

• Distance between databases—The l₁ norm of a database x is denoted ‖x‖₁ and is defined to be ‖x‖₁ = Σ^|x|_i=1 |xi|. Thus, the l₁ distance between two databases x and y is ‖x - y‖₁.

• Neighboring databases—Two databases, x, y, are defined to be neighboring databases if they differ only in one row. For instance, for a pair of databases x, y ∈ N^|X|, if ‖x - y‖₁ ≤ 1, we consider x, y to be neighboring databases.

Now we are ready to introduce the formal and most general definition of DP. It provides the mathematical guarantee of a randomized algorithm that will behave similarly on neighboring databases.

• (ϵ, δ)-differential privacy—A randomized algorithm M is (ϵ, δ)-DP if for every two neighboring databases, x, y, and for all S ⊆ Range(M ), we have

  Pr[M(x) ∈ S] ≤ e^ε ⋅ Pr[M(y) ∈ S] + δ

  where Pr[⋅] denotes the probability of an event, and Range(M) denotes the set of all possible outputs of the randomized algorithm M. The smaller ϵ and δ are, the closer Pr[M(x) ∈ S] and Pr[M(y) ∈ S] are, and the stronger the privacy protection is. When δ = 0, the algorithm M satisfies ϵ-DP, which is a stronger privacy guarantee than (ϵ, δ)-DP with δ > 0. Usually people call ϵ the privacy budget in the definition of DP. A higher value of ϵ means that one has more privacy budget and thus can tolerate more privacy leakage. A lower value of ϵ means stronger privacy protection is required or provided. The privacy parameter, δ, represents a “failure probability” for the definition. With a probability of 1 - δ, we will get the same guarantee as pure DP (i.e., ϵ-DP, where δ = 0). With a probability of δ > 0, we get no guarantee. In other words,

  • With probability 1 - δ, we have Pr[M(x) ∈ S] ≤ e^ϵ⋅Pr[M(y) ∈ S].

  • With probability δ, we get no guarantee at all.

A.2 Other differential privacy mechanisms

Chapter 2 discussed three of the most popular differential privacy mechanisms: binary, Laplace, and exponential. To recap, randomization in the binary mechanism comes from the binary response (the coin flip), which helps us to perturb the results. The Laplace mechanism achieves DP by adding random noise drawn from a Laplace distribution to the target queries or functions. The exponential mechanism helps us cater to scenarios where the utility is to select the best response but where adding noise directly to the output of the query function would fully destroy the utility. In this section we’ll discuss some other DP mechanisms.

A.2.1 Geometric mechanism

The Laplace mechanism (discussed in section 2.2.2) adds real-value noise to a query function’s outputs. It works best for query functions that output real values, because adding the noise directly to the outputs won’t make the outcomes meaningless. For query functions that output integers, you can still add Laplace noise but apply a discretization mechanism after that. However, this could reduce the outcomes’ utility.

This is where the geometric mechanism comes in [2]. It is designed to add the discrete counterpart of Laplace noise (drawn from the geometric distribution) to query functions that have only integer output values. These are the definitions of geometric distribution and geometric mechanism:

• Geometric distribution—Given a real number α > 1, the geometric distribution denoted as Geom(α) is a symmetric distribution that takes integer values such that the probability mass function at k is ((α – 1) /(α + 1)) ⋅ α^-|k|

  The geometric distribution has properties similar to the Laplace distribution. The variance of random variables drawn from Geom(α) is σ² = 2α/(1 - α)².

• Geometric mechanism—Given a numerical query function f: ℕ^|X| → ℤ^k, the database, x ∈ ℕ^|X| , and the privacy budget ϵ, the geometric mechanism is defined as

  

  where Y₁ are independent and identically distributed random variables drawn from Geom(ϵ/Δf), and Δf is the l₁-sensitivity of query function f.

THEOREM A.1 The geometric mechanism satisfies (ϵ, 0)-DP.

The geometric mechanism could be applied to all the examples involving the Laplace mechanism in section 2.2.2, giving slightly better utility.

A.2.2 Gaussian mechanism

The Gaussian mechanism [1] is another alternative to the Laplace mechanism. Instead of adding Laplace noise, the Gaussian mechanism adds Gaussian noise and provides a slightly relaxed privacy guarantee.

The Gaussian mechanism scales its noise to the l₂ sensitivity (compared with the Laplace mechanism, which scales to the l₁ sensitivity), defined as follows:

• l₂-sensitivity—Given a numerical query function f: ℕ^|X| → ℝ^k, for all pairs of databases, x, y ∈ ℕ^|X|, its l₂-sensitivity is .

We can define the Gaussian mechanism based on Gaussian distribution and l₂-sensitivity as follows:

• Gaussian mechanism—Given a numerical query function f: ℕ^|X| → ℝ^k, the database, x ∈ ℕ^|X| , and the privacy budget ϵ and δ, the Gaussian mechanism is defined as

  

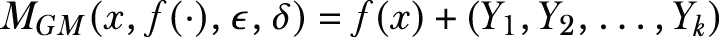
  where Y_i are independent and identically distributed random variables drawn from the Gaussian distribution τ = Δf √(2ln (1.25/ δ)) / ε, and Δf is the l₂-sensitivity of query function f.

Theorem a.2 The Gaussian mechanism satisfies (ϵ, δ)-DP.

Compared with other random noise, adding Gaussian noise has two advantages:

• Gaussian noise is the same as many other sources of noise (e.g., white noise in communication channels).

• The sum of Gaussian random variables results in a new Gaussian random variable.

Those advantages make it easier to analyze and correct privacy-preserving machine learning algorithms that apply the Gaussian mechanism.

A.2.3 Staircase mechanism

The staircase mechanism [3] is a special case of the Laplace mechanism. It aims to optimize the error bounds of the classic Laplace mechanism by tuning the tradeoff between the Laplace mechanism (whose probability density function is continuous) and the geometric mechanism (whose probability density function is discrete).

In the staircase mechanism, we usually define a loss function L(⋅) : ℝ → ℝ, that is a function of the additive noise, where given additive noise n, the loss becomes L(n). Let t ∈ ℝ denote the output of the query function f ( ), and P_t denotes the probability distribution of the random variable that generates the additive noise. Then, the expectation of the loss function would be

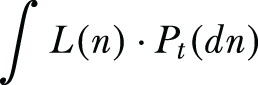
The staircase mechanism aims to minimize the worst-case cost among all possible query output t ∈ ℝ:

For more information about how to formulate and solve such optimization problems, please refer to the original paper by Geng and Viswanath [3].

The staircase mechanism can be specified by three parameters: ϵ, Δf, and γ^*, which is determined by ϵ and the loss function L( ). Figure A.1 illustrates the probability density functions of the Laplace and staircase mechanisms.

Figure A.1 Probability density functions of the Laplace and staircase mechanisms

A.2.4 Vector mechanism

The vector mechanism is designed to perturb vector-valued functions, such as the convex objective functions of many ML algorithms (linear regression, ridge regression, support vector machines, etc.).

The vector mechanism scales its noise to the l₂ sensitivity of a vector-valued function defined as follows:

• l₂-sensitivity of a vector-valued function—Given a vector-valued query function f, its l₂-sensitivity is defined as the maximum change in the l₂ norm of the value of the function when one input changes:

  

Once the l₂-sensitivity of a vector-valued function has been defined (even though formulating such sensitivities in real scenarios, such as ML algorithms, is non-trivial), we could define the vector mechanism using independent and identically distributed random variables drawn from any other mechanisms, such as Lap(Δf/ϵ), where Δf is the l₂-sensitivity of the vector-valued function f.

A.2.5 Wishart mechanism

The Wishart mechanism [4] is designed to achieve DP on second moment matrices, such as covariance matrices. The basic idea is to add a Wishart noise matrix generated from a Wishart distribution to the second moment matrices. Since a Wishart matrix is always positive semidefinite, and can be considered as the scatter matrix of some random Gaussian vectors, it is a natural source of noise to generate the differentially private covariance matrix while maintaining its meaning and utility (because covariance matrices are always positive semidefinite and are also scatter matrices). Figure A.2 illustrates pseudocode for applying the Wishart mechanism on covariance matrices, where Wd(⋅,⋅) is the Wishart distribution.

Figure A.2 Pseudocode for applying the Wishart mechanism

A.3 Formal definitions of composition properties of DP

One very important and useful property of DP is its composition theorems. The rigorous mathematical design of DP enables the analysis and control of cumulative privacy loss over multiple differentially private computations. There are two main composition properties, and we discussed them in detail in section 2.3.3. In this section we’ll explore the mathematical definitions of these properties.

A.3.1 The formal definition of sequential composition DP

The sequential composition property of DP confirms that the cumulative privacy leakage from multiple queries on data is always higher than the single query leakage (figure A.3). For example, if the first query’s DP analysis is performed with a privacy budget of ϵ₁ = 0.1, and the second has a privacy budget of ϵ₂ = 0.2, the two analyses can be viewed as a single analysis with a privacy loss parameter that is potentially larger than ϵ₁ or ϵ₂ but at most ϵ₃ = ϵ₁ + ϵ₂ = 0.3.

Figure A.3 Sequential composition

We’ll start with a simple case, where there are two independent DP algorithms, an (ϵ₁, 0)-DP algorithm M₁ and an (ϵ₂, 0)-DP algorithm M₂. If one applies M₁ and M₂ sequentially (where the output of M₁ becomes the input of M₂), then it follows the two-sequential composition theorem that follows.

Theorem a.3 Two-sequential composition: Let M₁ : ℕ^|X| → R₁ denote a randomized algorithm that is (ϵ₁, 0)-DP, and let M₂ : ℕ^|X| → R₂ denote a randomized algorithm that is (ϵ₂, 0)-DP. The sequential composition of these two, denoted as M_1,2 : ℕ^|X| → R₁ × R₂ by the mapping M_1,2 (x) = (M₁(x), M₂(x)), satisfies (ϵ₁ + ϵ₂, 0)-DP.

Having seen the two-sequential composition theorem, it should not be hard to extend it to a multi-sequential composition theorem that works for multiple independent DP algorithms that cascade sequentially, as follows.

Theorem a.4 Multi-sequential composition 1.0: Let M_i : ℕ^|X| → R_i denote a randomized algorithm that is (ϵ_i, 0)-DP. The sequential composition of k DP algorithms, M_i, i = 1, 2, ... , k, denoted as M_(k) : ℕ^|X| → Π^k_i=1R_i by the mapping M_[k](x) = (M₁(x), M₂(x), ..., M_k(x)) satisfies (Σ^k_i=1 ε_i, 0).

What if δ ≠ 0? What would the sequential composition look like? Take a look at the following theorem.

Theorem a.5 Multi-sequential composition 2.0: Let M_i : ℕ^|X| → R_i denote a randomized algorithm that is (ϵ_i, δ_i)-DP. The sequential composition of k DP algorithms, M_i, i = 1, 2, ... , k, denoted as M_(k) : ℕ^|X| → Π^k_i=1R_i by the mapping M_[k](x) = (M₁(x), M₂(x), ..., M_k(x)) satisfies Σ^k_i=1 ε_i, Σ^k_i=1 δ_i)-DP.

A.3.2 The formal definition of parallel composition DP

Now let’s move to the parallel composition of DP. To summarize, if algorithm F₁(x₁) satisfies ϵ₁-DP, and F₂(x₂) satisfies ϵ₂-DP, where (x₁, x₂) is a nonoverlapping partition of the whole dataset x (figure A.4), the parallel composition of F₁(x₁) and F₂(x₂) satisfies max(ϵ₁, ϵ₂)-DP.

Figure A.4 Parallel composition

Suppose a single database x has been portioned into k disjoint subsets, x_i. Here, “disjoint” ensures that any pair of the subsets, x_i, x_j are independent of each other. In this context there may be k independent DP algorithms, but all of them satisfy the same (ϵ, 0)-DP, and each algorithm M_i exclusively takes care of one subset x_i. The following parallel composition theorem will allow us to combine those k DP algorithms.

Theorem a.6 Parallel composition 1.0: Let M_i : ℕ^|X| → R_i denote a randomized algorithm that is (ϵ, 0)-DP, where i = 1, 2, ... , k. The parallel composition of k DP algorithms, M_i, i = 1, 2, ... , k, denoted as M_(k) : ℕ^|X| → Π^k_i=1R_i by the mapping M_[k](x) = (M₁(x₁), M₂(x₂), ..., M_k(x_k)), where x_i, i = 1, 2, ... , k, represent k disjoint subsets of database x, satisfies (ϵ, 0)-DP.

What if all the DP algorithms use DP budgets, thus satisfying different levels of DP in the parallel composition scenario? The following theorem provides the solution to this situation.

Theorem a.7 Parallel composition 2.0: Let M_i : ℕ^|X| → R_i denote a randomized algorithm that is (ϵ_i, 0)-DP, where i = 1, 2, ... , k. The parallel composition of k DP algorithms, M_i , i = 1, 2, ... , k, denoted as M_(k) : ℕ^|X| → Π^k_i=1R_i by the mapping M_[k](x) = (M₁(x₁), M₂(x₂), ..., M_k(x_k)), where x_i , i = 1, 2, ... , k, represent k disjoint subsets of database x, satisfies (max ϵ_i, 0)-DP.