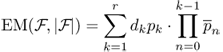2.2 Principles of Local Behavior of GOR

2.2.1 EPA Strictly Increasing Property

Intuitively, increasing the number of forwarding candidates would result in a larger EPA. We present Lemma 2.1 to confirm this intuition.

Definition 2.1 Define EM() be the maximum EPA (defined in Equation (2.1)) achieved by selecting r forwarding candidates from .

Lemma 2.1 (Strictly increasing property) EM is a strictly increasing function of r.

Proof. Assume 1 ≤ m < n ≤ M, and without loss of generality, let be the ordered node set achieving EM with forwarding priority i1 >…> im. We then select a subset with n − m nodes from the remaining node set {im+1, im+2, …, iM}, say . Assume we retain the relay priority of the m nodes in unchanged and give the nodes in lower priorities than those in . Then in , we give the nodes with smaller subscripts higher relay priorities. So we have

Lemma 2.1 basically indicates that the more nodes get involved in GOR, the larger the EPA can be. The maximum EPA can be obtained by involving all the nodes in . Then, how can the candidates be prioritized to maximize the EPA? We answer this question in the following section.

2.2.2 Relay Priority Rule

Theorem 2.1 identifies the upper bound of EPA and the corresponding relay priority rule.

Theorem 2.1 (Relay priority rule) EM can only be obtained by giving the node closer to the destination higher relay priority. That is

2.2

where 0 := 1.

Proof. We prove Theorem 2.1 by induction on r, the size of .

First, when r = 1, obviously Equation (2.2) holds.

Next, we assume Equation (2.2) holds for r = N (N ≥ 1). When , can be divided into with N nodes and with 1 node. Then

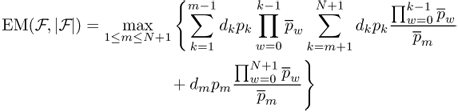
Thus we only need to prove for any integer m (1 ≤ m ≤ N),

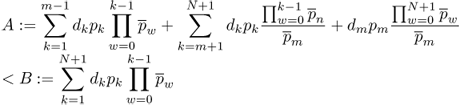
Subtracting A from B, we have

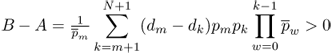
Then Equation (2.2) holds for r = N + 1. So it holds for any r (r ≥ 1).

Theorem 2.1 indicates that when a forwarding candidate set is chosen, the maximum EPA can only be achieved by assigning the relay priority to each node based on its distance from the destination. That is, the furthest node should try to forward the packet first; if it fails (i.e., does not receive the packet correctly), the second furthest node should try next, and so on. The analysis result is the upper bound of the EPA that any GOR can achieve.

Based on the relay priority rule, we will next identify and prove two important principles about the maximum EPA. First, we look at the characteristics of the forwarding candidates that are selected to achieve EM with various sizes r. We prove the containing property for those node sets. Following that, the concavity of the function EM is proved.

2.2.3 Containing Property of Feasible Candidate Set

Let be a feasible ordered node set that achieves the EM. We have the following containing property of 's.

Lemma 2.2 (Containing property) Given the available next-hop node set with M nodes, , , s.t.

2.3

Proof. Let 1 be an ordered node set with M nodes, and with N nodes. and bN = aM. For any node with , we have

2.4

We then prove Lemma 2.2 by induction on r.

First, for an arbitrary N, when r = 1, as , and , it is obvious that the containing property holds.

Then, we assume , an , s.t. , when r = m (m ≥ 1). We first prove for any feasible and , the first node in cannot be the nodes from the second place to the last place in , that is (m + 1)1 ≠ mi, .

We prove this by contradiction. Assume (m + 1)1 = mi. Let node (m + 1)j be the first node in but not in . We have

2.5

then,

2.6

Assume (m + 1)j−1 = ml, and according to inequality (2.4), we have

2.7

where

2.8

2.9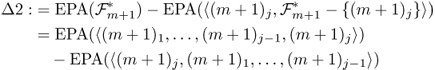

Then combining this with inequality (2.6), we get

2.10

The inequality (2.10) contradicts the fact that is the largest EPA achieved by selecting m + 1 nodes. So the assumption (m + 1)1 = mi is wrong. Therefore (m + 1)1 cannot be mi, 2 ≤ i ≤ m. So there are two cases for (m + 1)1:

From the induction above, we know that for an arbitrary N, we have , s.t. , 1 ≤ r ≤ M.

Lemma 2.2 indicates that an r − 1-node set that achieves EM is a subset of at least one of the feasible r-node sets that achieve EM. It also implies that when more forwarding candidates are selected to increase the maximum EPA, the transmission reliability also increases.

2.2.4 Concavity of Maximum EPA

Following Lemma 2.2, we have the concave property of EM as in Theorem 2.2.

Theorem 2.2 (Concavity of maximum EPA) EM, r, s.t. 1 ≤ r < N.

Proof. According to Lemma 2.2, assume , and . There are two cases for dk and dj.

Combining Lemma 2.1 and Theorem 2.2, we know that giving an available next-hop node set with N nodes, the maximum EPA of selecting r (1 ≤ r ≤ N) nodes is a strictly increasing and concave function of r. This means that although the maximum EPA keeps increasing when more nodes get involved, the speed of the increase slows down. When many nodes are involved, the extra EPA gained becomes marginal.

2.2.5 Reliability Increasing Property

Following the containing property in Lemma 2.2, we have the reliability increasing property in Corollary 2.1.

Denote . Define the one-hop reliability in Equation (2.13) which is the probability of at least one node in correctly receiving the packet sent by node i for one transmission.

2.13

where .

P*(r) is defined in Equation (2.14). This is the maximum one-hop reliability achieved by one of the feasible 's.

2.14

Corollary 2.1 P*(r) defined in Equation (2.14) is an increasing function of r.

Proof. The proof is straightforward following Lemma 2.2. Assume one achieves P*(r), then s.t. . According to the definitions of P*(r) in Equation (2.14) and the one-hop reliability in Equation (2.13), we have

So P*(r) is an increasing function of r.

Corollary 2.1 indicates that the maximum one-hop reliability corresponding to the forwarding candidate set that maximizes the EPA also increases when more forwarding candidates are involved. The increasing of the maximum EPA implies increasing the reliability. Therefore, the EPA is a good metric for balancing the packet advancement and reliability.