| 27 | Logic and Truth Tables |
To gain a true mastery of mathematics, you must become familiar with the laws that govern formal reasoning. Propositional logic is the simplest system. In this chapter, you’ll learn the basics of propositional logic, in which statements are always either “totally true” or “totally false.” You’ll also learn to use truth tables to evaluate complex statements.
SENTENCES
Propositional logic does not involve breaking sentences down into their internal parts. You don’t have to worry about how words are interconnected and how they affect one another within a sentence. A sentence, also called a proposition, is the smallest possible entity in propositional logic.
Sentences are represented by uppercase letters of the alphabet. You might say, “It is raining outside” and represent this by the letter R. Someone else might add, “It’s cold outside” and represent this by the letter C. A third person might say, “The weather forecast calls for snow tomorrow” and represent this by the letter S. Still another person might add, “Tomorrow’s forecast calls for sunny weather” and represent this by B (for “bright”; you’ve already used S).
NEGATION (NOT)
When you write down a letter to stand for a sentence, you assert that the sentence is true. So, for example, if Joanna writes down C in the above situation, she means to say, “It is cold outside.” You might disagree if you grew up in Alaska and Joanna grew up in Hawaii. You might say, “It’s not cold outside.” This can be symbolized as the letter C with a negation symbol in front of it.
There are several ways in which negation, also called the logical NOT operation, can be symbolized. In propositional logic, a common symbol is a drooping minus sign (¬). Let’s use it here. Some texts use a tilde (∼) to represent negation. Others use a minus sign or em dash (¬). Some put a line over the letter representing the sentence; still others use an accent symbol. In our system, the sentence “It’s not cold outside” can be denoted as ¬C.
Suppose someone comes along and says, “You are correct to say ¬C. In fact, I’d say it’s hot outside!” Suppose this is symbolized H. Does H mean the same thing as ¬C? No! You’ve seen days that were neither cold nor hot. There can be in-between states such as “cool” (K), “mild” (M), and “warm” (W). But there is no in-between condition when it comes to C and ¬C. In propositional logic, either it is cold, or else it is not cold. Either it’s hot, or else it is not hot. A proposition is either true, or else it is false (not true). Of course, temperature opinions like this depend on who you ask, so maybe this is not such a good example. But you should get the general idea!
There are logical systems in which in-between states exist. These go by names such as trinary logic or fuzzy logic. But discussions of those types of logic belong in a different book. In this chapter, you can assume that any given proposition is either true or false; there is no “neutral” or “don’t know” truth state, nor any “continuum” of truth values.
CONJUNCTION (AND)
Propositional logic doesn’t bother with how the phrases inside a sentence affect one another, but it is concerned with the ways in which complete sentences interact. Sentences can be combined to make bigger ones, called compound sentences. The truth or falsity of a compound sentence depends on the truth or falsity of its components, and on the ways in which those components are connected.
Suppose someone says, “It’s cold outside, and it’s raining outside.” Using the symbols above, you can write this as
In logic, it’s customary to use a symbol in place of the word AND. There are several symbols in common use, including the ampersand (&), the inverted wedge (^), the asterisk (*), the period (.), the multiplication sign (×), and the raised dot (∙). Let’s use the ampersand. Then the above compound sentence becomes
The formal term for the AND operation is logical conjunction. A compound sentence containing one or more conjunctions is true if (but only if) both or all of its components are true. If any one of the components happens to be false, then the whole compound sentence is false.
DISJUNCTION (OR)
Now imagine that a friend comes along and says, “You are correct in your observations about the weather. It’s cold and raining. I have been listening to the radio, and I heard the weather forecast for tomorrow. It’s supposed to be colder tomorrow than it is today. But it’s going to stay wet. So it might snow tomorrow.”
You say, “It will rain or it will snow tomorrow, depending on the temperature.”
Your friend says, “It might be a mix of rain and snow together, if the temperature is near freezing.”
“So we might get rain, we might get snow, and we might get both,” you say.
“Sure. But the weather experts say we are certain to get precipitation of some sort,” your friend says. “Water is going to fall from the sky tomorrow—maybe liquid, maybe solid, and maybe both.”
In this case, suppose we let R represent the sentence “It will rain tomorrow,” and we let S represent the sentence “It will snow tomorrow.” Then we can say
This is an example of logical disjunction. There are at least two symbols that can represent disjunction: the plus sign (+) and the wedge (∨). Let’s use the wedge. We can now write
A compound sentence in which both, or all, of the components are joined by disjunctions is true if (but only if) at least one of the components is true. A compound sentence made up of disjunctions is false if (but only if) all the components are false.
Logical disjunction, as defined here, is the inclusive OR operation. If all the components are true, then the whole sentence is true. There’s another operation called exclusive OR in which, if all the components are true, the compound sentence is false. So if you say, “It will rain or snow tomorrow,” using the inclusive OR, then your statement is true if you get a mix of rain and snow. But if you use the exclusive OR, you can’t have a mix; it must be one or the other, but not both. Sometimes the exclusive OR operation is called the either-or operation. It’s abbreviated as XOR, and it is important in digital electronic circuit design. From now on, if you see the symbol for the OR operation (or the word “or” in a problem), assume it means the inclusive OR operation.
IMPLICATION (IF/THEN)
Imagine that your conversation about the weather continues, getting more strange with each passing minute. You and your friend are trying to figure out if you should get ready for a snow day tomorrow, or whether rain and gloom are all you’ll have to contend with.
“Does the weather forecast say anything about snow?” you ask.
“Not exactly,” your friend says. “The radio announcer said that there’s going to be precipitation through tomorrow night, and that it’s going to get colder tomorrow. I looked at my car thermometer as she said that, and the outdoor temperature was only a little bit above freezing.”
“If there is precipitation, and if it gets colder, then it will snow,” you say.
“Of course.”
“Unless we get an ice storm.”
“That won’t happen.”
“Okay,” you say. “If there is precipitation tomorrow, and if it is colder tomorrow than it is today, then it will snow tomorrow.” (This is a weird way to talk, but you’re learning logic here, not the art of conversation. Logically rigorous conversation can sound bizarre, even in the “real world.” Have you ever sat in a courtroom during a civil lawsuit between corporations?)
Suppose you use P to represent the sentence “There will be precipitation tomorrow.” In addition, let S represent the sentence “It will snow tomorrow,” and let C represent the sentence “It will be colder tomorrow.” Then in the above conversation, you have made a compound proposition consisting of three sentences, like this:
Another way to write this is
In this context, “implies” means always results in. So in formal logic, “X IMPLIES Y” means “If X, then Y.” Symbolically, the above proposition is written this way:
The double-shafted arrow pointing to the right represents logical implication, also known as the IF/THEN operation. In a logical implication, the “implying” sentence (to the left of the double-shafted arrow) is called the antecedent. In the above example, the antecedent is (P & C). The “implied” sentence (to the right of the double-shafted arrow) is called the consequent. In the above example, the consequent is S.
Some texts use other symbols for logical implication, including the “hook” or “lazy U opening to the left” (⊃), three dots (∴), and a single-shafted arrow pointing to the right (→). Let’s keep using the double-shafted arrow pointing to the right.
LOGICAL EQUIVALENCE (IFF)
Suppose your friend changes the subject and says, “If it snows tomorrow, then there will be precipitation and it will be colder.”
For a moment you hesitate, because this isn’t the way you’d usually think about this kind of situation. But you have to agree. Your friend has made this implication:
Implication holds in both directions here, but there are plenty of scenarios in which implication holds in one direction but not the other.
You and your friend have agreed that both of the following implications are valid:
These two implications can be combined into a conjunction, because you are asserting them both together:
When an implication is valid in both directions, the situation is defined as a case of logical equivalence. The above statement can be shortened to
Mathematicians sometimes shorten the phrase “if and only if” to the single “word” “iff.” So you can also write
The symbol for logical equivalence is a double-shafted, double-headed arrow (⇔)¬There are other symbols that can be used. Sometimes you’ll see an equals sign (=), a three-barred equals sign (≡), or a single-shafted, double-headed arrow (↔) Let’s use the double-shafted, double-headed arrow to symbolize logical equivalence. Symbolically, then, you would write this:
Now look at a situation in which logical implication holds in one direction but not in the other. Consider this statement: “If it is overcast, then there are clouds in the sky.” This statement is always true. Suppose you let O represent the sentence “It is overcast” and K represent the sentence “There are clouds in the sky.” Then you have this, symbolically:
If you reverse this, we get a statement that isn’t necessarily true:
This translates to “If there are clouds in the sky, then it’s overcast.” You have seen days or nights in which there were clouds in the sky, but there were clear spots too, so it was not overcast.
TRUTH TABLES
The outcome, or logic value, of an operation in propositional logic is always either true or false, as you’ve seen. Truth can be symbolized as T, +, or 1, while falsity can be abbreviated as F, −, or 0. Let’s use T and F. They are easy to remember: “T” stands for true and “F” stands for false! When you are performing logic operations, sentences that can attain either T or F logic values (depending on the circumstances) are called variables.
A truth table is a method of denoting all possible combinations of truth values for the variables in a compound sentence. The values for the individual variables, with all possible arrangements, are shown in vertical columns at the left. The truth values for compound sentences, as they are built up from the single-variable (or atomic) propositions, are shown in horizontal rows.
TABLES FOR BASIC LOGIC FUNCTIONS
The simplest truth table is the one for negation, which operates on a single variable. Table 27-1 shows how this works for a single variable called X.

Table 27-1
Truth table for logical negation.
Let X and Y be two logical variables. Conjunction (X & Y) produces results as shown in Table 27-2. This operation produces the truth value T when, but only when, both variables have value T. Otherwise, the operation produces the truth value F.

Table 27-2
Truth table for logical conjunction.
Logical disjunction for two variables (X ∨ Y) breaks down as in Table 27-3. This operation produces the truth value T when either or both of the variables have the truth value T. If both of the variables have the truth value F, then the operation produces the truth value F. Remember, you’re dealing with the inclusive operation (OR) here, not the exclusive operation (XOR)!

Table 27-3
Truth table for logical disjunction.
A logical implication is valid (that is, it has truth value T) whenever the antecedent is false. It is also valid if the antecedent and the consequent are both true. But implication does not hold (that is, it has truth value F) when the antecedent is true and the consequent is false. Table 27-4 shows the truth values for logical implication.

Table 27-4
Truth table for logical implication.
Let’s look at a “word problem” example of a logical implication that is obviously invalid. Let X represent the sentence “The wind is blowing.” Let Y represent the sentence “A hurricane is coming.” Consider this sentence:
Now imagine that it is a windy day. Therefore, variable X has truth value T. But suppose you are in North Dakota, where there are never any hurricanes. Sentence Y has truth value F. Therefore, the statement “If the wind is blowing, then a hurricane is coming” is not valid.
If X and Y are logical variables, then X IFF Y has truth value T when both variables have value T or when both variables have value F. If the truth values of X and Y are different, then X IFF Y has truth value F. This is broken down fully in Table 27-5.

Table 27-5
Truth table for logical equivalence.
THE EQUALS SIGN
In logic, you can use an ordinary equals sign to indicate truth value. If you want to say that a particular sentence K is true, you can write K = T. If you want to say that a variable X always has false truth value, you can write X = F. Be careful about this. Don’t confuse the meaning of the equals sign with the meaning of the double-shafted, double-headed arrow that stands for logical equivalence!
The truth values shown in Tables 27-1 through 27-4 are defined by convention and are based on common sense. Arguably, the same is true for logical equivalence. It seems reasonable to suppose that two logically equivalent statements have identical truth values. How can you prove this? One method is to derive the truth values for logical equivalence based on the truth tables for conjunction and implication. Let’s do it, and show the derivation in the form of a truth table.
Remember that X ⇔ Y means the same thing as (X ⇒ Y) & (Y ⇒ X). You can build up X ⇔ Y in steps, as shown in Table 27-6 as you go from left to right. The four possible combinations of truth values for sentences X and Y are shown in the first (leftmost) and second columns. The truth values for X ⇒Y are shown in the third column, and the truth values for Y ⇒X are shown in the fourth column. To get the truth values for the fifth (rightmost) column, conjunction is applied to the truth values in the third and fourth columns. The complex logical operation (also called a compound logical operation because it’s made up of combinations of the basic ones) in the fifth column is the same thing as X ⇔ Y.
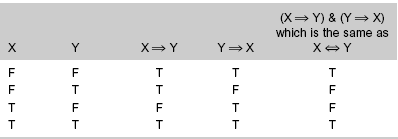
Table 27-6
A truth table proof that logically equivalent statements always have identical truth values.
Q.E.D.
What you have just seen is a mathematical proof of the fact that for any two logical sentences X and Y, the value of X⇔ Y is equal to T when X and Y have the same truth value, and the value of X⇔ Y is equal to F when X and Y have different truth values. Sometimes, when mathematicians finish proofs, they write “Q.E.D.” at the end. This is an abbreviation of the Latin phrase Quod erat demonstradum. It translates to “Which was to be demonstrated.”
PRECEDENCE
When you are reading or constructing logical statements, the operations within parentheses are always performed first. If there are multilayered combinations of sentences (called nesting of operations), then you should use first ordinary parentheses ( ), then brackets [ ], and then braces { }. Alternatively, you can use groups of plain parentheses inside each other, but be sure you end up with the same number of left-hand parentheses and right-hand parentheses in the complete expression.
If there are no parentheses, brackets, or braces in an expression, instances of negation should be performed first. Then conjunctions should be done, then disjunctions, then implications, and finally logical equivalences.
As an example of how precedence works, consider the following compound sentence:
Using parentheses, brackets, and braces to clarify this according to the rules of precedence, you can write it like this:
Now consider a more complex compound sentence, which is so messy that you’ll run out of grouping symbols if you use the “parentheses, brackets, braces” or PBB scheme:
Using plain parentheses only, you can write it this way:
When you count up the number of left-hand parentheses and the number of right-hand parentheses, you’ll see that there are six left-hand ones and six right-hand ones. This should always be true whenever you write, or read, a complicated logical sentence. If the number of opening and closing symbols is not the same, something is wrong.
CONTRADICTION AND DOUBLE NEGATION
A contradiction always results in nonsense, which can be considered to have a truth value of F. This is one of the most interesting and useful laws in all mathematics, and it has been used to prove important facts as well as to construct ridiculous statements and arguments. Symbolically, if X is any logical statement, you can write the rule like this:
This rule is sometimes stated as, “From a contradiction, any false statement whatsoever can follow.” You can then write it this way:
assuming that Q is false. This sort of direct contradiction is often called an absurdity.
Mathematicians sometimes use a process called reductio ad absurdum (Latin for “to reduce to absurdity”) when faced with difficult proofs. You start by assuming that whatever you want to prove is false. Then, from that assumption, you derive a direct contradiction of the form X & ¬X. This demonstrates that the original assumption (that the thing you set out to prove is false) is false! If something is not false, it must be true. This strange twist of logic gives rise to another rule called the law of double negation. The negation of a negation is equivalent to the original expression. That is, if X is any logical variable, then
COMMUTATIVE LAWS
The conjunction of two variables has the same value regardless of the order in which the variables are expressed. If X and Y are logical variables, then X & Y is logically equivalent to Y & X:
The same property holds for logical disjunction:
These are called the commutative law for conjunction and the commutative law for disjunction, respectively. The variables can be commuted (interchanged or reversed in order), and it doesn’t affect the truth value of the resulting sentence.
ASSOCIATIVE LAWS
When there are three variables combined by two conjunctions, it doesn’t matter how the variables are grouped. Suppose you have a compound sentence that can be symbolized as
where X, Y, and Z represent the truth values of three constituent sentences. Then you can consider X & Y as a single variable and combine it with Z, or you can consider Y & Z as a single variable and combine it with X, and the results are logically equivalent:
The same law holds for logical disjunction:
These are called the associative law for conjunction and the associative law for disjunction, respectively.
You must be careful when applying associative laws. All the operations in the compound sentence must be the same. If a compound sentence contains a conjunction and a disjunction, you cannot change the grouping and expect to get the same truth value in all possible cases. For example, the following two compound sentences are not, in general, logically equivalent:

LAW OF IMPLICATION REVERSAL
When one sentence implies another, you can’t reverse the sense of the implication and still expect the result to be valid. When you see X⇒Y, you cannot conclude Y⇒X. Things can work out that way in certain cases, such as when X⇔ Y. But there are plenty of cases where it doesn’t work out.
If you negate both sentences and then reverse the sense of the implication, however, the result is always valid. This can be called the law of implication reversal. It is also known as the law of the contrapositive. To express it symbolically, suppose you are given two logical variables X and Y. Then the following always holds:
Here is an example of the use of words to illustrate an example of the above law “in action.” Let V represent the sentence “Jane is a living vertebrate creature.” Let B represent the sentence “Jane has a brain.” Then V ⇒B reads, “If Jane is a living vertebrate creature, then Jane has a brain.” Applying the law of implication reversal, we can also say with certainty that ¬B ⇒ ¬V. That translates to “If Jane does not have a brain, then Jane is not a living vertebrate creature.”
DE MORGAN’S LAWS
If the conjunction of two sentences is negated as a whole, the resulting compound sentence can be rewritten as the disjunction of the negations of the original two sentences. Expressed symbolically, if X and Y are two logical variables, then the following holds valid in all cases:
This is called De Morgan’s law for conjunction.
A similar rule holds for disjunction. If a disjunction of two sentences is negated as a whole, the resulting compound sentence can be rewritten as the conjunction of the negations of the original two sentences. Symbolically,
This is called De Morgan’s law for disjunction.
You might now begin to appreciate the use of symbols to express complex statements in logic! The rigorous expression of De Morgan’s laws in verbal form is quite a mouthful, but it’s easy to write these rules down as symbols.
DISTRIBUTIVE LAW
A specific relationship exists between conjunction and disjunction, known as the distributive law. It works somewhat like the distributive law that you learned in arithmetic classes—a certain way that multiplication behaves with respect to addition. Do you remember it? It states that if a, b, and c are any three numbers, then
Now think of logical conjunction as the analog of multiplication, and logical disjunction as the analog of addition. Then if X, Y, and Z are any three sentences, the following logical equivalence holds:
This is called the distributive law of conjunction with respect to disjunction.
TRUTH TABLE PROOFS
If you claim that two compound sentences are logically equivalent, then you can prove it by showing that their truth tables produce identical results. Also, if you can show that two compound sentences have truth tables that produce identical results, then you can be sure those two sentences are logically equivalent, as long as all possible combinations of truth values are accounted for.
Tables 27-7A and 27-7B show that the following two general sentences are logically equivalent for any two variables X and Y, proving the commutative law of conjunction for two variables:

Table 27-7
Truth table proof of the commutative law of conjunction. At A, statement of truth values for X & Y At B, statement of truth values for Y & X. The outcomes are identical, demonstrating that they are logically equivalent.
Tables 27-8A and 27-8B show that the following two general sentences are logically equivalent for any two variables X and Y, proving the commutative law of disjunction for two variables:

Table 27-8
Truth table proof of the commutative law of disjunction. At A, statement of truth values statement of truth values for Y ∨ X. The outcomes are identical, demonstrating that they are logically equivalent.
If you’d like a challenging “extra credit” exercise, prove that the commutative rules for conjunction and disjunction work out no matter how many variables there are! Here’s a hint: Try it by “building things up.” Prove that if the rule holds for two variables, then it holds for three. After that, prove that if the rule holds for n variables, then it holds for n + 1 variables. If you can do that, you’ll have successfully employed a rather sophisticated proof technique called mathematical induction.
Tables 27-9A and 27-9B show that the following sentences are logically equivalent for any three variables X, Y, and Z, proving the associative law of conjunction:

Table 27-9A
Derivation of truth values for (X & Y) & Z. Note that the two rightmost columns of this proof make use of the commutative law for conjunction, which has already been proved.

Table 27-9B
Derivation of truth values for X & (Y & Z). The rightmost column of this table has values that are identical with those in the rightmost column of Table 27-9A, demonstrating that the rightmost expressions in the top rows are logically equivalent.
Note that in Table 27-9A, the two rightmost columns make use of the commutative law of conjunction, which has already been proved. Once proven, a statement is called a theorem, and it can be used in future proofs.
Tables 27-10A and 27-10B show that the following sentences are logically equivalent for any three variables X, Y, and Z, proving the associative law of disjunction:
The two rightmost columns in Table 27-10A take advantage of the commutative law for disjunction, which has already been proved.

Table 27-10A
Derivation of truth values for (X ∨ Y) ∨ Z. Note that the two rightmost columns of this proof make use of the commutative law for disjunction, which has already been proved.
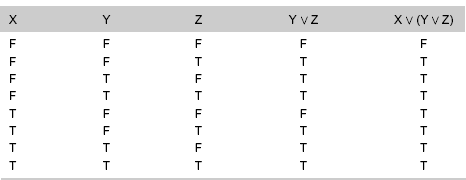
Table 27-10B
Derivation of truth values for X ν (Y ν Z). The rightmost column of this table has values that are identical with those in the rightmost column of Table 27-10A, demonstrating that the rightmost expressions in the top rows are logically equivalent.
Tables 27-11A and 27-11B show that the following sentences are logically equivalent for any two variables X and Y, proving the law of implication reversal:

Table 27-11
Truth table proof of the law of implication reversal. At A, statement X ⇒ Y. At B, derivation of truth values for ¬Y ⇒ ¬X. The outcomes are identical, demonstrating that they are logically equivalent.
Tables 27-12A and 27-12B show that the following sentences are logically equivalent for any two variables X and Y, proving De Morgan’s law for conjunction:

Table 27-12
Truth table proof of De Morgan’s law for conjunction. At A, statement of truth values for ¬(X & Y). At B, derivation of truth values for ¬X ν ¬Y The outcomes are identical, demonstrating that they are logically equivalent.
Tables 27-13A and 27-13B show that the following sentences are logically equivalent for any two variables X and Y, proving De Morgan’s law for disjunction:

Table 27-13
Truth table proof of De Morgan’s law for disjunction. At A, statement of truth values for ¬(X ∨ Y). At B, derivation of truth values for ¬X & ¬Y The outcomes are identical, demonstrating that they are logically equivalent.
Tables 27-14A and 27-14B show that the following two general sentences are logically equivalent for any three variables X, Y, and Z, proving the distributive law of conjunction with respect to disjunction:

Table 27-14A
Derivation of truth values for X & (Y ν Z).

Table 27-14B
Derivation of truth values for (X & Y)
v (X & Z). The rightmost column of this table has values that are identical with those in the rightmost column of Table 27-14A, demonstrating that the rightmost expressions in the top rows are logically equivalent.You can use truth tables to prove any logical proposition, as long as it’s valid, of course! Here is an example:
Tables 27-15A and 27-15B show that the following sentences are logically equivalent for any three variables X, Y, and Z, proving that the proposition is valid:

Table 27-15A
Derivation of truth values for

Table 27-15B
Derivation of truth values for ¬Z ⇒ (¬X ∨ ¬Y). The rightmost column of this table has values that are identical with those in the rightmost column of Table 27-15A, demonstrating that the rightmost expressions in the top rows are logically equivalent.
PROOFS WITHOUT TABLES
You can use the logical rules presented in this chapter, rather than a direct truth table comparison, to prove the following:
First, use De Morgan’s law for conjunction. This states that the following sentences are logically equivalent for any X and Y:
This means that the two expressions are directly interchangeable. Whenever you encounter either of these in any logical sentence, you can “pull it out” and “plug in” the other one. Let’s do that here, changing the logical statement ¬Z ⇒(¬X ν ¬Y) into the logical statement ¬Z⇒ ¬(X & Y). According to the law of implication reversal, this is logically equivalent to
Using the law of double negation on both sides of this expression, you can see that this is logically equivalent to
Q.E.D. !
Now here’s another “extra credit” exercise for you. Prove this the other way without using truth tables. That is, show that the following statement is valid:
QUESTIONS AND PROBLEMS
This is an open-book quiz. You may refer to the text in this chapter (and earlier ones, too, if you want) when figuring out the answers. Take your time! The correct answers are in the back of the book.
1. Under what circumstances is the conjunction of several sentences false? Under what circumstances is the conjunction of several sentences true?
2. Under what circumstances is the disjunction of several sentences false? Under what circumstances is the disjunction of several sentences true?
3. Suppose you see a conjunction, then a double-shafted, double-headed arrow (pointing both left and right), and then a disjunction and a negation. What does the double-shafted, double-headed arrow represent in words?
4. How many possible combinations of truth values are there for a set of four sentences, each of which can attain either the value T or the value F?
5. Suppose you observe, “It is not sunny today, and it’s not warm.” Your friend says, “The statement that it’s sunny or warm today is false.” These two sentences are logically equivalent. What rule does this demonstrate?
6. Suppose someone claims that both of the following statements are valid for all possible truth values of sentences P, Q, and R:
What, if anything, is wrong with this? If something is wrong, show an example demonstrating why.
7. Look at Table 27-16. What is wrong with this truth table?

Table 27-16
Truth table for Probs. 7 and 8.
8. What can be done to make Table 27-16 show a valid derivation?
9. Imagine that someone says to you, “If I am human and I am not human, then the moon is made of Swiss cheese.” What rule of logic does this illustrate?
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
