| 13 | Ratio and Proportion |
Thus far, the concepts of ratio and proportion have been covered with respect to the simple idea of similarity. In this chapter, you’ll learn how ratios and proportions can be used to solve practical problems. You’ll also get a first taste of trigonometry, the branch of mathematics that relates lengths to angles.
FRACTIONS, PROJECTIONS, EXTREMES, AND MEANS
A fraction expresses a ratio or proportion in terms of the relationship between the numerator and denominator. Different numbers can be used to write the same value as a fraction—the same relationship between the numerator and denominator. For example, 1/2 can also be written as 2/4, 3/6, 4/8, or, in general, x/(2x), where x is any positive real number. Proportions can also be denoted by using colons. The foregoing would then be written as 1:2, 2:4, 3:6, 4:8, or, in general, x:2x.
One application that sets the scene for later concepts is the use of ratio or proportion relative to projected images, as shown in Fig. 13-1. This concept is sometimes called the aspect ratio. The old-fashioned standard television (TV) screen aspect ratio is 4:3, meaning 4 units horizontally to 3 units vertically. This aspect ratio is still used in many computers today, although some of the newer computer displays have larger aspect ratios. Movie screens have various aspect ratios, particularly now that wide screens have become popular.

Figure 13-1
An example of ratio or proportion in a projected image. In this case the aspect ratio is 4:3, regardless of the distance from the projector.
Figure 13-2 shows several ways that ratios and proportions can be expressed, along with some of the properties of the variables in these expressions. Note especially how cross products work. In an equation containing two ratios, the left-hand numerator and the right-hand denominator are called the extremes, while the left-hand denominator and the right-hand numerator are called the means. In any equation of this form, the product of the extremes is equal to the product of the means.
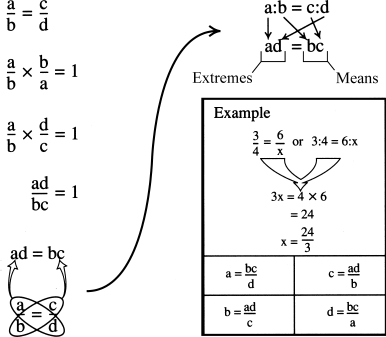
Figure 13-2
Several ways in which ratios and proportions can be written. The product of the extremes always equals the product of the means.
PROPORTIONS IN PRACTICE
Suppose a woman’s will explicitly says that her estate is to be divided among her three daughters in proportion to their ages. The amount of the estate is $78,000, and their ages are 53, 47, and 30. How much does each get?
First, assume that the basis of the proportion is $x per year of age to each person. This means the daughters get $53x, $47x, and $30x, respectively. That adds up to $130x. You know that the total is $78,000. So the equation is
This can be easily solved if you divide through by 130 on each side, getting x = 600. After you substitute into the expressions $53x, $47x, and $30x, the daughters receive $31,800, $28,200, and $18,000 respectively. To check, add these amounts. They sum up to $78,000.
SHAPE AND SIZE
Ratio and proportion form a good basis for showing the distinction between shape and size. This principle can be demonstrated clearly with triangles, the simplest geometric figures having straight edges.
If a triangle is expanded in proportion, the lengths of its respective sides maintain the same ratio (Fig. 13-3). The triangle has the same shape, but it differs in size. Because it has the same shape, it also has the same interior angles. All angles marked (1) are equal, those marked (2) are also equal, as are those marked (3).

Figure 13-3
These three triangles have the same shape even though their sizes differ, because the corresponding angles (1), (2), and (3) are the same. The proportion among the lengths of the three sides is the same in each triangle.
The sides with one crossmark have the same proportion to the sides with two cross-marks in each triangle. The proportion between sides with two and three crossmarks, or between sides with one and three crossmarks, are the same in each triangle, or with any others that have the same shape.
Triangles that have the same shape but not necessarily the same size are called similar triangles. Although their sides might be longer or shorter, they are always in the same proportion. They are “magnified” or “minimized” copies of one another.
ABOUT ANGLES IN TRIANGLES
When two straight lines cross (mathematicians use the word “intersect”), the opposite angles are equal. Figure 13-4A shows how this statement can be demonstrated. Draw square (right-angle) corners at the intersection, based on each of the heavy lines. You can easily see that any pair of angles numbered (1) and (2) has a total angular measure equivalent to two square corners. (This is called a straight angle and has a measure of 180°.) One pair of square corners consists of top angle (2) and left side angle (1). Another pair consists of top angle (2) and right-side angle (1). The total is the same, two square corners, and both use the same angle (2), so the two angles (1) must be the same. Similarly, you can show that the two angles marked (2) are equal.

Figure 13-4
At A, opposite angles have equal measure when two lines intersect. At B, all the angles marked (1) have equal measure, as do all the angles marked (2). At C, the measures of the interior angles in a triangle add up to two square corners (a straight angle).
Next, if two parallel lines intersect a third line (Fig. 13-4B), the angles at the intersections are equal if taken in correct pairs. To show this, complete a rectangle with square corners. As with the single intersection, you can now see that angles numbered (1) are all equal, as are all angles numbered (2).
In any triangle, its three interior angles always add up to two square corners. To show this statement (Fig. 13-4C), extend one side at one corner and draw a line parallel to the opposite side. Because of their positions, relative to parallel lines, corresponding angles marked (1) and (2) are equal. Where the side is extended are three angles numbered (1), (2), and (3) that add up to two square corners. Therefore, the corresponding angles inside the triangle, also numbered (1), (2), and (3), must also add up to two square corners.
USE OF RIGHT TRIANGLES
A right triangle, also called a square-cornered triangle, becomes a very important building block in other shapes and sizes, whether in triangles or in more-complicated shapes. Any acute triangle (one in which all the interior angles are smaller than right angles) can be divided into two right triangles in three different ways, as shown in Fig. 13-5A. In the triangles shown, one such division is done with a thin line, the other two with dashed lines.

Figure 13-5
At A, any acute triangle can be divided into two square-cornered ones in three different ways. At B, the perpendiculars in an acute triangle always intersect at a single point inside the triangle.
If all the angles are acute, all three ways of dividing into two square-cornered triangles are additive, so the original triangle consists of the two square-cornered ones added together. However, if one angle of a triangle is obtuse (wider than a square corner), two of the possible divisions require a difference, rather than a sum. The original triangle is the larger square-cornered triangle minus the smaller one.
An interesting fact about these divisions, which we will not prove here, is that the three dividing lines from the corners of the original triangle, formed by making them perpendicular to the opposite side, always intersect at a single point. “Perpendicular” means the two lines create two square-cornered angles. In an acute triangle, the point of intersection is inside the triangle (Fig. 13-5B). In an obtuse triangle, the point is found only by extending all three perpendiculars (dashed lines). This exercise begins to show the importance of square-cornered (right) triangles as building blocks.
ANGLES IDENTIFIED BY RATIOS
Angles determine the shape of a triangle and also the ratios between the lengths of its sides. Any of the three sides can be changed to alter all three angles, so the relationship between the side ratio and the angle becomes rather involved.
Consider the specific case of a right triangle. Because the measures of its three interior angles add up to two right angles, the other two angles always add up to one right angle. A right triangle that has a fixed measure for one of its acute angles can therefore have only one shape. Regardless of how big (or small) you draw the triangle, the ratio between the lengths of any two sides always is the same for the particular angle of interest. An example of this is shown in Fig. 13-6. The ratio 1/2 identifies the angle, shown by the arc with arrows at each end, uniquely. No other angle can produce a right triangle whose opposite and longest sides have lengths in this same ratio. In the example shown here, the length of the opposite side is always exactly one-half the length of the hypotenuse (longest side).

Figure 13-6
In a right triangle with one acute angle fixed, the ratio of the length of the opposite side to the length of the longest side is constant, regardless of the size of the triangle.
THEOREM OF PYTHAGORAS
Suppose we have a right triangle defined by points A, B, and C whose sides have lengths a, b, and c, respectively. Let c be the length of the side opposite the right angle, which is the hypotenuse (Fig. 13-7). Then the following equation holds:

Figure 13-7
The Theorem of Pythagoras for right triangles.
The converse of this is also true: If there is a triangle whose sides have lengths a, b, and c, and the above equation holds, then that triangle is a right triangle.
This formula can be stated verbally as follows: “The square of the length of the hypotenuse of a right triangle is equal to the sum of the squares of the lengths of the other two sides.” This is called the theorem of Pythagoras or the Pythagorean theorem. It is named after the Greek mathematician Pythagoras of Samos who lived in the 4th century B.C.
NAMES FOR ANGLE RATIOS
As you proceed in studying mathematics, the use of ratios to identify angles assumes an important role. You need names to identify them. These names are the terminology of trigonometry.
The right triangle used to identify the ratios has three sides. The ratio of any two of its three sides uniquely identifies a certain acute angle. In picking those two sides, you have six possible choices. Three of these choices result in the basic trigonometric functions.
The sine is defined as the length of the opposite side divided by the length of the hypotenuse. Each quantity is written with “sin” followed by a letter or symbol to identify that particular angle. In Fig. 13-8, the angle is shown by A, so we write “sin A” to represent the sine of angle A.
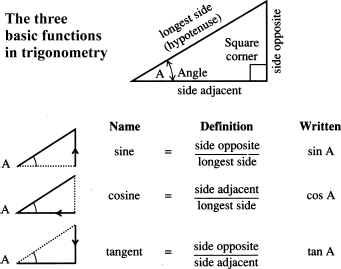
Figure 13-8
The trigonometric functions can be defined as ratios of the lengths of the sides of a right triangle.
The cosine is the length of the adjacent side divided by the length of the hypotenuse. Cosine is abbreviated “cos” so for the cosine of angle A, we write “cos A.”
The tangent uses the length of the opposite side divided by the length of the adjacent side. Tangent is abbreviated “tan,” so we write the tangent of angle A as “tan A.” (If you have previously learned that a tangent is a line that touches the circumference of a circle, this usage is entirely different.)
The little diagrams at the left in Fig. 13-8 show how to remember the relationship of the ratio to the angle. The line with the arrow is the numerator. It leads to the side that forms the denominator. Remember that these names (sine, cosine, and tangent) represent ratios of lengths. A ratio identifies the angles, regardless of how large or how small the triangle happens to be.
SPOTTING THE TRIANGLE
Remembering the ratios in trigonometry requires as much time and practice as learning the multiplication tables in arithmetic. What can be more confusing, needing more care, is spotting the right sides for the ratio when the angle is not in the position used in the previous section. Regardless of where the angle is, you must construct a right triangle (or use one that’s already there) one way or another. Then the ratio follows the definition. A sine, for example, is always the opposite side over the hypotenuse. The other ratios follow similar layouts.
Figure 13-9 shows four possible positions that you might encounter. At A, the triangle is in the “standard orientation” from the previous section. At B, the right angle is on top. At C, the triangle is in the same orientation as at A, but the angle in question is different. At D, the triangle has the angle in question at the bottom, with the right angle at the upper left.

Figure 13-9
It takes some practice to remember trigonometric ratios when the triangles are not oriented in a familiar-looking way.
The little diagrams at the right in Fig. 13-9 show the relationship of each ratio to the angle for the sine, cosine, and tangent. The line with the arrow is the numerator. It leads to the side that forms the denominator.
DEGREE MEASURE OF ANGLES
Degree measure for angles requires a complete circle (rotation) in a flat surface, which is 360 degrees (symbolized 360°). A half rotation is 180°. A quarter rotation, which is a right angle, is 90°. Acute angles are less than 90°, and obtuse angles are more than 90° but less than 180° (Fig. 13-10).

Figure 13-10
Degree measures for angles are based on a full circle of 360 equal increments.
Two other angles of particular interest, 60° and 45°, are based on special triangles. The first is an equilateral triangle, in which all three sides are equally long. It also has all equal angles, each 60°. The other special angle comes from a right triangle in which the two shorter sides have equal lengths. Because the three angles must add up to 180° and one of them is 90°, the other two must each be 45°. This polygon is called a right isosceles triangle. “Isosceles” means “having two equal sides.” These two noteworthy situations are shown in Fig. 13-11.

Figure 13-11
Equilateral (A) and right isosceles (B) triangles give rise to two special angles, 60° and 45°.
THREE APPLICATIONS OF TRIGONOMETRY
Figure 13-12 illustrates three examples of the use of trigonometry to solve practical problems. Use your calculator to find the sines, cosines, and tangents of angles.
Problem 1. Suppose that an observation point at sea level is exactly 20 mi from a mountain peak (Fig. 13-12A). The elevation of the peak above sea level is exactly 5°, viewed from this point. How high is the peak?

Figure 13-12
Three practical problems using trigonometry. See text for discussion.
Solution 1. The relationship involves the adjacent side (a distance of 20 mi), the height, the opposite side, and an angle of 5°. This is the tangent ratio. A calculator tells you that tan 5° = 0.0875, rounded off to four decimal places. The height is therefore 0.0875 times the 20-mi distance. Convert the figure to feet by multiplying by 5280, getting 105,600 ft. Multiply this by 0.0875 and you have the peak height, 9,240 ft.
Problem 2. A skyscraper is viewed from a point on the ground exactly 50 ft away from its vertical wall (Fig. 13-12B). The angle to the horizontal line of sight is exactly 84°. How high is the building? Assume your eyes are at ground level and the ground near the building is perfectly horizontal.
Solution 2. This problem again involves the tangent. A calculator will tell you that tan 84° = 9.5144, rounded off to four decimal places. By multiplying this figure by 50 ft, you can figure that the height of the building is 475.7 ft. You might want to round this off to 476 ft.
Problem 3. A ladder must reach the roof of a building exactly 47 ft high. The slope of the ladder, when resting against the building, should be exactly 70° (Fig. 13-12C). What ladder length is necessary?
Solution 3. The solution here involves the ratio of the opposite side to the hypotenuse, which is the sine, but it’s the inverse. Using a calculator, you can find sin 70° = 0.9397, rounded off to four decimal places. Dividing 47 by 0.9397 gives the needed ladder length as a tiny bit more than 50 ft.
QUESTIONS AND PROBLEMS
This is an open-book quiz. You may refer to the text in this chapter (and earlier ones, too, if you want) when figuring out the answers. Take your time! Consider all values given as exact, so you don’t have to worry about significant figures. The correct answers are in the back of the book.
1. The aspect ratio for a TV picture is 4:3. A wide-screen movie is transmitted so that the picture fills the full height of the TV screen. What proportion of the width must be lost at the sides, if the aspect ratio of the movie picture is 2:1?
2. Another way of transmitting the picture in Prob. 1 is to include the full picture width and mask off an area (top and bottom) where the picture does not fill the TV screen. What proportion of the TV screen will be masked off (top and bottom)?
3. A man wills his estate to his 5 children: 3 boys and 2 girls. It calls for each to get an amount proportional to his or her age at the time of his death. This man is old-fashioned, and he has decided that the boys should get twice the rate for their ages that the girls do. When the will is made, the boys’ ages are 40, 34, and 26, while the girls are aged 37 and 23. If the father dies in the same year, what will each receive from an estate of $22,100?
4. If the father in Prob. 3 lives 10 years after making the will, the estate has not changed in value, and all five children are still living, how much will each get?
5. The two sides of a right triangle that adjoin the right angle are 5 in and 12 in long. What is the length of the hypotenuse?
6. A highway gradient is measured as the rise in altitude divided by the distance along the pavement surface. Suppose that an 8,000-ft length of straight highway maintains a gradient of 1:8 (1 to 8). Find the altitude gained in this distance, and the amount by which the distance measured horizontally falls short of 8,000 ft. Use the Pythagorean theorem.
7. At a distance of 8 mi, the elevation of a mountain peak, viewed from sea level, is 9°. Some distance farther away, still at sea level, the elevation is 5°. What is the height of the peak, and the distance of the second viewpoint?
8. A railroad track stretches for 3 mi at a gradient of 1:42 up, then 5 mi of 1:100 up, then 2 mi level, then 6 mi of 1:250 down, then 4 mi level, and finally 5 mi at 1:125 up. How much higher is the finish point than the starting point?
9. A house is to have a roof slope of 30°, gabled in the middle. The width of the house is 40 ft, and the roof is to extend 2 ft horizontally beyond the wall. What distance from the ridge of the gable to the guttering is required for rafters?
10. By how much could the rafter length be reduced in the house (Prob. 9) by making the roof slope 20° rather than 30°?
11. A house wall is 50 ft high. A ladder used to scale it is 60 ft long. How far from the base of the wall must the ladder be placed for its top to just reach the top of the house wall? Solve this in two ways. First, use trigonometry to derive the answer to four significant figures. Second, use the Pythagorean theorem.
12. In Fig. 13-13, all length units are in centimeters (cm). Assume the lengths and angle measures to be exact. From the data given, use the Pythagorean theorem to derive the length of side x to four significant digits.

Figure 13-13
Illustration for problems 12 through 16.
13. Use trigonometry, not the Pythagorean theorem, to derive the length of side y in Fig. 13-13 to four significant digits.
14. Use trigonometry to derive the measure, in degrees, of angle q in Fig. 13-13 to the nearest one-tenth of a degree.
15. Use trigonometry to derive the measure, in degrees, of angle r in Fig. 13-13 to the nearest one-tenth of a degree.
16. Find the measure of angle r in Fig. 13-13 to the nearest one-tenth of a degree by using a method that does not involve trigonometry.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
