| 26 | Vectors |
You’ve already seen a few examples of vectors in this book. You might reasonably ask, “What, exactly, are vectors, and how do they work?” Technically, a vector is a mathematical expression for a quantity that has two independent properties, usually magnitude (or length) and direction (or orientation). Sometimes rectangular coordinates are used instead of magnitude and direction numbers. A vector quantity always needs two or more numbers to represent it. A scalar quantity needs only one. In this chapter, you’ll learn the basic properties of vectors in two and three dimensions.
MAGNITUDE AND DIRECTION
Vectors are denoted by boldface letters of the alphabet. In the xy plane, vectors a and b can be illustrated as rays from the origin (0,0) to points (xa,ya) and (xb,yb) as shown in Fig. 26-1. The magnitude, or length, of the vector a, written |a| or a, can be found in the xy plane with a distance formula based on the Pythagorean theorem:

Figure 26-1
Two vectors in the Cartesian plane. They can be added using the parallelogram method.
The direction of the vector a, written dir a, is the angle θa that a subtends counterclockwise from the positive x axis. This angle is equal to the arctangent of the ratio of ya to xa :
All possible directions can be represented by restricting the angle to less than a full circle in the counterclockwise direction:
SUM OF TWO VECTORS
The sum of two vectors a and b, where a = (xa,ya) and b = (xb,yb), can be found by adding their x and y components separately. Use this formula for the vectors a and b as shown in Fig. 26-1:
This sum can be found geometrically by constructing a parallelogram with the vectors a and b as adjacent sides. When you do that, the vector a + b is the diagonal of the parallelogram. This technique is called the parallelogram method of vector addition.
Suppose you want to find the sum of two vectors a = (3,−5) and b = (2,6). These are ordered pairs; the first numbers represent the x values, and the second numbers represent the y values. All you must do is to add the x and y components together independently. Writing the vectors as ordered pairs gives

The sum vector a + b therefore has the coordinate values x = 5 and y = 1.
MULTIPLICATION OF A VECTOR BY A SCALAR
To multiply a vector by a scalar quantity such as a real number, multiply both the x and y components of the vector by that scalar. That makes the vector longer or shorter if the real number is positive, but doesn’t change its direction. If the real number is negative, the direction of the vector is exactly reversed, and its length may change as well.
Multiplication by a scalar is commutative. This means that it doesn’t matter whether the scalar comes before or after the vector in the product. If we have a vector a = (xa,ya) and a scalar k, then
You multiply both the x and y values by the scalar k to get the result.
When you multiply a vector by a scalar, it isn’t true vector multiplication because the multiplicand and the multiplier aren’t both vectors. You can multiply vectors by other vectors, however—and things get interesting then! There are two ways to multiply a vector by another vector. The first way gives you a scalar as the product. The second (and somewhat more complicated) way gives you a vector as the product. Let’s look at the first of these two operations now. Later in this chapter, you’ll learn about the second method.
DOT PRODUCT OF TWO VECTORS
Imagine two vectors a = (xa,ya) and b = (xb,yb) such as those shown in Fig. 26-1. If all four of the variables xa, xb, ya, and yb are real numbers, then the dot product, also known as the scalar product and written a · b, of the vectors a and b is a real number and can be found by using this formula:
The dot product of a and b is called “a dot b” in informal talk.
As an example, let’s find the dot product of the two vectors a = (3,−5) and b = (2,6). Use the formula given above.

Now let’s see what happens if the order of the dot product is reversed. Does the value change? If not, the dot product is commutative. Let’s try a general proof. Take the formula above for the dot product, and suppose a = (xa,ya) and b = (xb,yb). First consider the dot product with vector a taken first:
Now evaluate the dot product with b taken first:
You know that ordinary multiplication is commutative for all real numbers. That means you can reverse the factors in both addends. Because xa, ya, xb, and yb are all real numbers, the above formula is equivalent to
But xaxb + yayb is exactly what you get when you work out the expansion of a · b. This proves that, for any two vectors a and b, it is always true that a · b = b · a. The dot product is commutative, just as is plain multiplication of scalars.
MAGNITUDE AND DIRECTION IN THE POLAR PLANE
In the mathematician’s polar coordinate plane, vectors a and b can be denoted as rays from the origin (0,0) to points (θa,ra) and (θb,rb) as shown in Fig. 26-2. The magnitude and direction are defined directly:

Figure 24-2
Two vectors a and b in the polar plane. The direction angles are θa and θb. All angles are expressed in radians. The magnitudes are ra and rb.
The values of the angle and the length are customarily restricted. The angle is expressed counterclockwise and is less than a full circle. The length is positive or zero. Mathematically, you can write these facts as

SUM OF TWO VECTORS IN THE POLAR PLANE
The sum of two vectors in polar coordinates can be found by converting them to their equivalents in the xy plane, adding the vectors according to the formula for the xy plane, and then changing the result back to polar coordinates. To convert the vector a = (θa,ra) in mathematician’s polar coordinates to a = (xa,ya) in rectangular coordinates:
To convert the vector a = (xa,ya) from rectangular coordinates to polar coordinates so a = (θa,ra), use these formulas:

Try a practical problem. Consider the vector a = (xa,ya) = (3,4) in the xy plane. Suppose these values are exact. You want to find the equivalent vector a = θa,ra) in mathematician’s polar coordinates to the nearest angular degree, and to the nearest hundredth of a linear unit. First find the direction angle θa. Because xa > 0, use this formula:

Now solve for ra as follows:

Therefore, a = (θa,ra) = (53°,5.00).
Now work out a problem “the other way.” Consider the vector b = (θb,rb) = (200°,4.55) in mathematician’s polar coordinates. You want to convert this to an equivalent vector b = (xb,yb) in rectangular coordinates to the nearest tenth of a unit. First, solve for xb:

Then solve for yb:

Therefore, b = (xb,yb) = (−4.3, −1.6), with rectangular coordinate values accurate to the nearest tenth of a linear unit.
MULTIPLICATION OF A VECTOR BY A SCALAR IN THE POLAR PLANE
In mathematician’s polar coordinates, imagine some vector a defined as the ordered pair (θ,r) as shown in Fig. 26-3. Suppose a is multiplied by a positive real scalar k. The result is a longer vector if k > 1 and a shorter vector if 0 < k < 1. The following equation can be used:

Figure 26-3
Multiplication of a polar-plane vector a by a positive real number k, and by a negative real number −k. Angles in this drawing are expressed in radians.
If a is multiplied by a negative real scalar −k, then the result is a vector of different length in the opposite direction. The vector is longer if −k < −1 and shorter if −1 < −k < 0. The formula looks like this:
for θ in degrees. For θ in radians, the formula is
The addition of 180° (π rad or a half-circle) to θ reverses the direction of a. The same effect can be produced by subtracting 180° (π rad or a half-circle) from θ. You should add a half-circle if the original angle is less than 180˚ and subtract a half-circle if the original angle is larger than 180°. That will ensure that the final angle is always defined as something nonnegative, but less than a full circle counterclockwise.
DOT PRODUCT OF TWO VECTORS IN POLAR PLANE
The dot product of two vectors is easy to express in mathematician’s polar coordinates if you know their lengths and their directions. Suppose vector a is at an angle of θa counterclockwise from the reference axis, and vector b is at an angle of θb. Let |a| or ra represent the magnitude of vector a, and let |b| or rb represent the magnitude of vector b. Then the dot product of a and b is given by this formula:
Even if you don’t have the exact coordinates of the vectors a and b, you can still find their dot product if you know their lengths ra and rb, and if you also know the angle θ between them. Place the vectors so their back endpoints are both at the coordinate origin. Then a and b define a plane in which the angle can be measured, and the dot product is
MAGNITUDE IN XYZ SPACE
In rectangular xyz space, two vectors a and b can be denoted as rays from the origin (0,0,0) to points (xa,ya,za) and (xb,yb,zb) as shown in Fig. 26-4. The magnitude of a, written |a|, can be found using a three-dimensional extension of the Pythagorean theorem for right triangles. The formula looks like this:

Figure 26-4
Two vectors a and b in xyz-space. They are added using the parallelogram method. This is a perspective drawing, so the parallelogram appears distorted.
If you want a challenge, prove this fact on the basis of the two-dimensional Pythagorean theorem for the magnitude of a vector a in xy space:
Now imagine that you want to find the magnitude of the vector denoted by a = (xa,ya,za) = (1,2,3) in xyz space. Suppose you are told that the values 1, 2, and 3 are exact, and you want to get the answer accurate to four digits after the decimal point. Use the distance formula

DIRECTION IN XYZ SPACE
In three-dimensional xyz space, the direction of a vector a is denoted by measuring or expressing the angles θx, θy and θz that a subtends relative to the positive x, y, and z axes, respectively, as shown in Fig. 26-5. These angles, given in radians as an ordered triple (θx,θy,θz), are called the direction angles of the vector a. So you can write

Figure 26-5
Direction angles of a vector a in xyz-space.
Sometimes the cosines of these angles are specified. These trig ratios are called the direction cosines of a, and are given as an ordered triple (α,β,γ), like this:
where α = cos θχ, β = cos θy, and γ = cos θz.
Direction angles are customarily defined as the smallest possible angle between the vector and the axis in question. Therefore, a direction angle is always positive and cannot exceed π. Formally, the mathematician would say this:
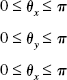
SUM OF TWO VECTORS IN XYZ SPACE
In three-dimensional xyz space, the sum of two vectors a = (xa,ya,za) and b = (xb,yb,zb) is found by simply adding their x values, y values, and z values together, thereby forming a new ordered triple, like this:
This sum can, as in the two-dimensional case, be found geometrically by constructing a parallelogram with a and b as adjacent sides. The sum a + b is determined by the diagonal of the parallelogram, as shown in Fig. 26-4.
MULTIPLICATION OF A VECTOR BY A SCALAR IN XYZ SPACE
Imagine a vector a defined by the coordinates (xa,ya,za) in xyz space. Suppose a is multiplied by some positive real scalar k. Then the following equation holds, an extension of the two-dimensional case:
If a is multiplied by a negative real scalar −k, then
Now imagine that the direction angles of a are represented by (θx,θy,θz) Then the direction angles of ka are also (θx,θy,θz). When you multiply any vector by a positive real number scalar, its direction does not change, no matter how many dimensions it has. But if the scalar is a negative real number (call it −k), the direction angles all change by π, so dir (−ka) is represented by the ordered triple [(θx ± π),(θy ± π),(θz ± π)] Whether π should be added or subtracted from an original angle depends, in each case, on which way will give you a new angle that is positive but not greater than π. The length is multiplied by k (the positive value, with the minus sign removed).
DOT PRODUCT OF TWO VECTORS IN XYZ SPACE
The dot product of two vectors a = (xa,ya,za) and b = (xb,yb,zb) in xyz space is a real number that can be found by a three-dimensional extension of the dot product formula for vectors in the xy plane:
If you don’t have the xyz coordinates of the vectors, but instead you know their magnitudes |a| = ra and |b| = rb as well as the angle θ between them, then you can find their dot product in three dimensions. Position the vectors so their back endpoints are both at the coordinate origin. Then the dot product is found this way:
This formula works in any three-dimensional system of coordinates. It is just as good in spherical or cylindrical coordinates as it is in rectangular xyz space. However, finding the vector magnitudes and the angle between them can sometimes be difficult.
CROSS PRODUCT OF TWO VECTORS
The cross product, also known as the vector product and written a × b, of two vectors a and b is a third vector that is perpendicular to the plane containing both a and b. Cross products are often used in engineering, physics, and electronics.
Suppose that θ is the angle between vectors a and b expressed counterclockwise (as viewed from above, or the direction of the positive z axis) in the plane containing them both, as shown in Fig. 26-6. Let |a| or ra represent the magnitude of vector a, and let |b| or rb represent the magnitude of vector b. Place the vectors so their back endpoints are both at the coordinate origin. Then the magnitude of a × b is the product of the original vector magnitudes and the sine of the angle between them:

Figure 26-6
Vector cross products. The vector b × a has the same magnitude as vector a × b, but points in the opposite direction. Both vectors b × a and a × b are perpendicular to the plane defined by a and b.
What about the direction of the cross-product vector? You can use a little trick called the right-hand rule for cross products to ascertain the direction of a × b. Curl the fingers of your right hand in the sense in which θ, the angle between a and b, is defined. Extend your right thumb. When you hold your hand this way, a × b points in the direction of your thumb. In the example shown by Fig. 26-6, a × b points upward at a right angle to the plane containing both of the original vectors a and b.
When 180° < θ < 360° (π < θ < 2π), the cross-product vector reverses direction compared with the situation when 0° < θ < 180° (0 < θ < π). This is demonstrated by the fact that, in the above formula, sin θ is positive when 0° < θ < 180° (0 < θ < π), but negative when 180° < θ < 360° (π < θ < 2π). When 180° < θ < 360° (π < θ < 2π), the right-hand rule doesn’t work. Instead, you must use your left hand, and curl your fingers into almost a complete circle! An example is the cross product b × a in Fig. 26-6. The angle φ, expressed counterclockwise between these vectors (as viewed from above), is more than 180˚. This reverses the direction of the cross-product vector.
Do you see a pattern here? For any two vectors a and b, the vector b × a is a “mirror image” of a × b, where the “mirror” is the plane containing both vectors. One way to imagine the mirror image is to note that b × a has the same magnitude as a × b, but points in exactly the opposite direction. A less common (but equally valid, at least in theory) way to look at this situation is to imagine that dir b × a is the same as dir a × b, but |b × a| = −|a × b|. Either way, it is apparent that the cross-product operation is not commutative. But it is “inversely commutative”! The following relationship always holds for any two vectors a and b:
NEGATIVE VECTOR MAGNITUDES
Are you confused about the concept of vector magnitude and the fact that absolute-value symbols (the two vertical lines) are sometimes used to denote vector magnitude? From basic algebra, remember that the absolute value of a real number is always positive. But with vectors, negative magnitudes sometimes appear in the equations. What’s going on with that?
Whenever you see a vector whose magnitude is negative, remember that it’s the equivalent of a vector pointing in the opposite direction with positive magnitude having the same absolute value. For example, if someone tells you that a force of −20 newtons is exerted upward by a machine, you know it is the equivalent of 20 newtons exerted downward. If you say that a storm is located 50 kilometers to your southwest, you can also say (although you should expect raised eyebrows in response) that the storm is −50 kilometers to your northeast. A statement in mathematics can sound quite weird but be theoretically valid anyhow.
When a vector with negative magnitude occurs in the final answer to a problem, you can exactly reverse the direction of the vector, and then assign it a positive magnitude equal to −1 times the negative magnitude. This is always a good idea if you can manage it, because it makes more common sense.
Now imagine two vectors a and b in xyz space, represented by the following ordered triples:
You are told that these values are mathematically exact. You want to find an ordered triple (x,y,z) that represents the vector a × b, with values accurate to three significant figures. How do you go about it?
To start out, you should make a rough drawing that shows these two vectors. You’ll get something that looks like Fig. 26-7. Note that both of the vectors are in the xy plane, so you don’t really have to show the z axis to portray the vectors. In Fig. 26-7, the xy plane coincides with the paper. Imagine the positive z axis coming out of the page directly toward you, and the negative z axis pointing straight away from you on the other side of the page.

Figure 26-7
What is the cross product a × b of these two vectors in xyz-space?
Now figure out the direction in which a × b points. Remember that the direction of the cross product of two vectors is always perpendicular to the plane containing the original vectors. Therefore, you know that a × b must point along the z axis. This means that the ordered triple for a × b has to be in the form (0,0,z), where z is some real number. You don’t yet know what this number is, and you had better not jump to any conclusions. Is it positive? Negative? Zero? You must proceed further to find out.
Calculate the magnitudes of the two vectors a and b. To find |a|, use the formula

Similarly, for |b|:

Therefore, |a| |b| = 5 · 5 = 25—exactly! You want three significant figures in the final answer, so you can call it 25.0.
To determine the magnitude of a × b, you must multiply 25.0 by the sine of the angle θ expressed counterclockwise from a to b. When you examine Fig. 26-7, you can see that θ is equal to exactly 270° (three-quarters of a circle) minus the angle between the x axis and the vector a. The angle between the x axis and vector a is the arctangent of 4/3, or approximately 53.13° as determined by using a calculator. Therefore,

This means that the magnitude of a × b is equal to 25.0 · (−0.600), or −15.0. The minus sign means that the cross-product vector points negatively along the z axis. The z coordinate of a × b is equal to −15.0. You know that the x and y coordinates of a × b are both exactly equal to 0, because a × b lies exactly along the z axis. From all this information, you can conclude that a × b = (0.00,0.00,−15.0), with the values each expressed to three significant figures.
QUESTIONS AND PROBLEMS
This is an open-book quiz. You may refer to the text in this chapter (and earlier ones, too, if you want) when figuring out the answers. Take your time! The correct answers are in the back of the book.
1. Find the magnitude of the vector a = (−7,−10) in the xy plane. Assume the values given are exact. Express the answer to three significant figures.
2. Convert the vector a = (−7,−10), as expressed in the xy plane, to polar form as a vector a = (θa,ra). Assume the values given are exact. Express the answer to three significant figures, with θa in degrees.
3. Find the magnitude of the vector b = (8, −1,−6) in xyz space. Assume the values given are exact. Express the answer to four significant figures.
4. Consider the two vectors a = (−7,−10,0) and b = (8,−1,−6) in xyz space. What is their dot product?
5. Imagine that two vectors f and g point in the same direction along a common line in xyz space. Suppose f has magnitude 4, and g has magnitude 7. What is f · g?
6. Imagine that two vectors f and g point in opposite directions along a common line in xyz space. Suppose f has magnitude 4, and g has magnitude 7. What is f · g?
7. Imagine that two vectors f and g are oriented at right angles in xyz space. Suppose vector f has magnitude 4, and vector g has magnitude 7. What is f · g? What is g · f? Does it matter in which sense the rotation from f to g is defined?
8. Imagine that two vectors are oriented at right angles with respect to each other in xyz space. Suppose one of the vectors has magnitude 4, and the other has magnitude 7. What is the magnitude of the cross-product vector? How is this vector oriented with respect to the original two vectors?
9. Consider two vectors a and b that lie in the xy plane portion of xyz space. Suppose a = (2,0,0) and is fixed, pointing along the +x axis. Suppose b has magnitude 2 and rotates counterclockwise in the xy plane, starting at (2,0,0), then going around through (0,2,0), (−2,0,0), and (0,−2,0), finally ending up back at (2,0,0). Describe what happens to a × b with one rotation of b, as you watch from some point high above the xy plane on the +z axis. What happens if b keeps going around and around?
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
