Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

4
Other Topics in Product Development and Optimization: Response Surface and Mixture Designs

4.1 Introduction

In the previous chapter, the case study on the development of an innovative dishwashing product discussed the design and analysis of a general factorial design to identify which formula maximizes the cleaning performance response.

The present chapter extends the topic of design and analysis of factorial designs by introducing two classes of designs particularly suited to fitting and analyzing response surfaces and for optimizing response variables: central composite designs (CCDs) and Box‐Behnken designs.

When the factors represent ingredients or components of a formulation, the total amount of which is fixed and we are interested in evaluating whether one or more responses vary when decreasing or increasing the proportions of the ingredients, mixture experiments can be designed and analyzed to take into account the dependence among components.

The first case study considers the development of a new polymeric membrane, with the goal being to maximize the product's elasticity. Based on previous results, the scientists identify the region of exploration to search for the factor levels that maximize product elasticity. The example shows how to plan a CCD or a Box‐Behnken design in line with specific interests. For the analysis of the design, given that the experimenters are relatively close to the optimum set of factor levels, a second‐order model is fitted to allow the detection of curvatures, if any, in the response surface.

The second example considers a mixture experiment. In the development of a new detergent, the investigators aim to analyze to what extent three different components of a formulation can affect the product's technical performance. The reader is guided through the planning of different kinds of mixture designs depending on the presence or absence of other process variables in the design, or the presence of component bounds or linear constraints among components. The analysis of the selected mixture design closes the chapter.

In short, the chapter deals with the following:

Topics	Stat tools
Central composite designs	4.1
Box‐Behnken designs	4.2
Mixture experiments	4.3
Simplex centroid designs	4.4
Simplex lattice designs	4.5
Constrained simplex designs	4.6
Extreme vertices designs	4.7
Mixture models	4.8

4.2 Case Study for Response Surface Designs: Polymer Project

In the development of a new polymeric membrane, the research team aims to maximize the product's elasticity. Previous research has shown that the concentrations of two additives (factors A, B) and the exposure temperature explain much of the variability in elasticity. The scientists decide that the region of exploration in the search for factor levels that maximize the elasticity of the product should be around (3%, 10%) for the two additives and (40°, 80°) for the temperature. For logistic reasons, investigators need to arrange the experiment in such a way that the combinations of factor levels will be tested by two different operators. As the experimenters are relatively close to having the optimum set of factor levels, a second‐order model will be suitable to study all main effects (both linear and quadratic) and the two‐way interactions between factors. This model will allow the detection of curvatures in the response surface if any.

4.2.1 Plan of the Experimental Design

In Chapter 3, section 3.5, we fit a second‐order model to analyze a general factorial design with continuous factors with more than two levels specified by the experimenters and estimate the response surface in order to identify regions where the responses were close to the optimum. Now, as an alternative approach, we will create the experimental design by using a popular class of response surface designs called CCD (Stat Tool 4.1). Then we will present a variant of the CCD called the face‐centered design, and lastly another standard response surface design named the Box‐Behnken design (Stat Tool 4.2). The experimenters will choose one of the three designs according to the characteristics of each one and the main purposes of the study.

For this study:

The two additives and the temperature represent the key factors.
For factors A and B, the percentages of concentrations 3% and 10% represent the factor levels for the definition of the cube points.
For factor Temperature, the temperatures 40° and 80° represent the factor levels for the definition of the cube points.
The elasticity represents the response variable.
The two operators represent two blocks (Stat Tool 2.4).

To perform the experiment, let's proceed in the following way:

Step 1 – Create a CCD.
Step 2 – Alternatively, create a face‐centered CCD.
Step 3 – Alternatively, create a Box‐Behnken design.
Step 4 – Assign the designed factor‐level combinations (design points) to the experimental units and collect data for the response variable.

4.2.1.1 Step 1 – Create a CCD

Let's begin creating a CCD, considering the three factors A, B, and Temperature.

To create a CCD, go to: Stat > DOE > Response Surface > Create Response Surface Design

Under Type of Design select Central composite and in Number of continuous factors specify 3. Note that you can also consider categorical factors in your design.

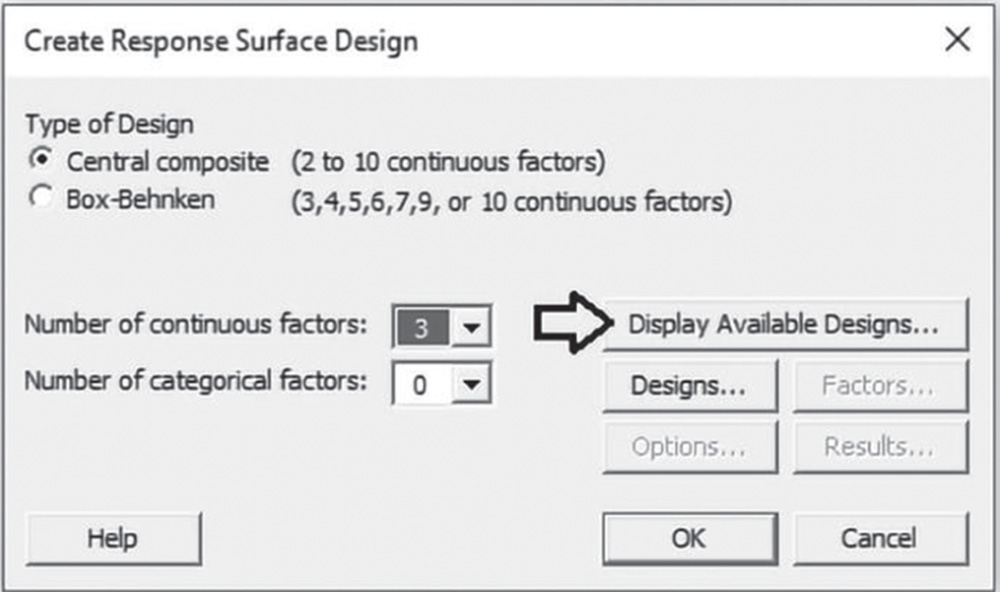
Illustration of Create Response Surface Design dialog box.

Click on Display Available Designs to have an idea of the number of runs based on the design type both with and without blocks and the number of continuous factors in the design. Note that depending on the number of continuous factors, you can create a full or fractional design (Stat Tool 2.2). Click on Designs. In the next dialog box, select the number of experimental runs and the number of blocks for the design. Note that with two blocks (the two operators), the CCD will include 20 runs.

There will be six center points, four of which will be included in the cube block, i.e. in the block with the experimental runs at the high and low levels of the factors. The other two center points will be in the axial block, i.e. the other block with the experimental runs at the axial levels of the factors.

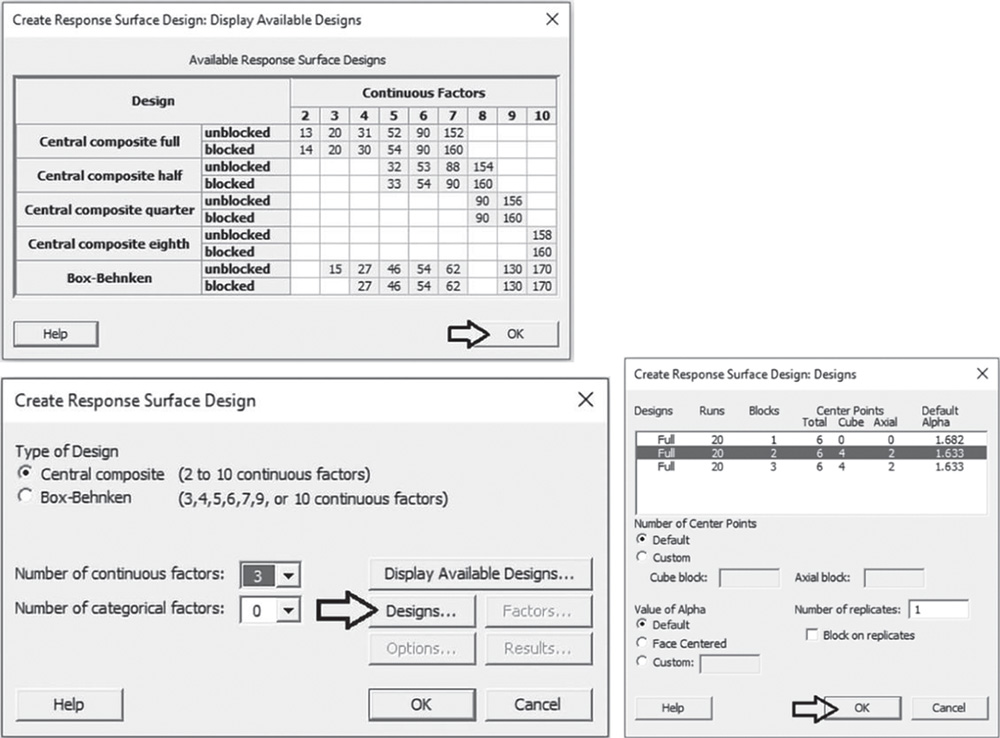
Illustration of Create Response Surface Design and corresponding Display Available Settings and Designs dialog boxes.

Under Number of Center Points leave the selected option Default to ensure that the design preserves some desirable statistical properties. However, Custom can be selected if you want to modify the number of center points in the design and their deployment into the blocks.

Under Value of Alpha check the option Default to ensure that the design preserves some desirable statistical properties. Again, Custom can be selected if you want to modify the value of alpha used to define the axial points. The option Face Centered allows you to create a variant of the CCD called Face Centered CCD (Stat Tool 4.1).

In Number of replicates specify 1 or, depending on available resources, enter how many times to perform each experimental run. Remember you can add replicates to your design later with Stat > DOE > Modify Design. If you specify more than 1 replicate and check the option Block on replicates, Minitab will put each replicate into its own block. If the base design has blocks, then the total number of blocks will be the product of the number of blocks in the base design and the number of replicates. Click OK.

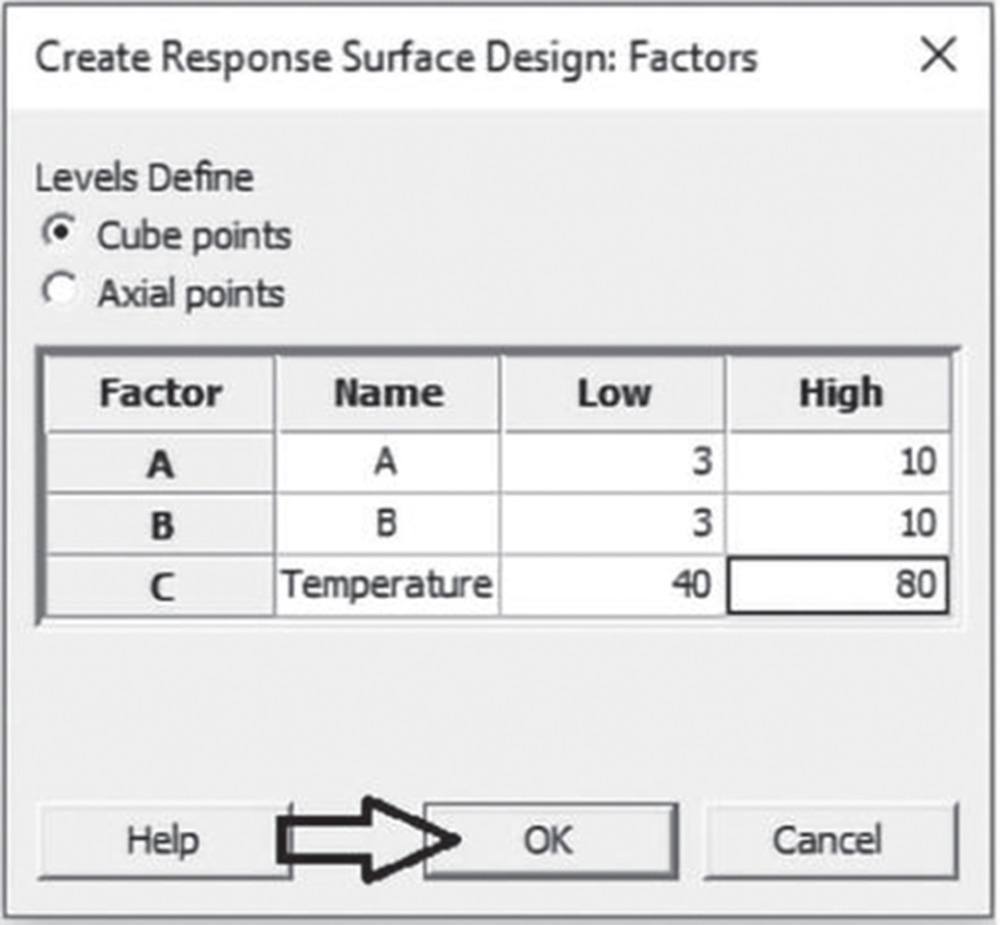
In the main dialog box select Factors. Under Name, Low and High, enter a name for each factor and its high and low levels. By default, Minitab sets the low level of all factors to −1 and the high level to +1. Under Levels Define, choose the appropriate factor setting Cube points or Axial points. In our example, the factor setting represents Cube points. If you have categorical factors, the window will allow you to enter the name, number of levels, and level values.

Illustration of Create Response Surface Design: Factors dialog box.

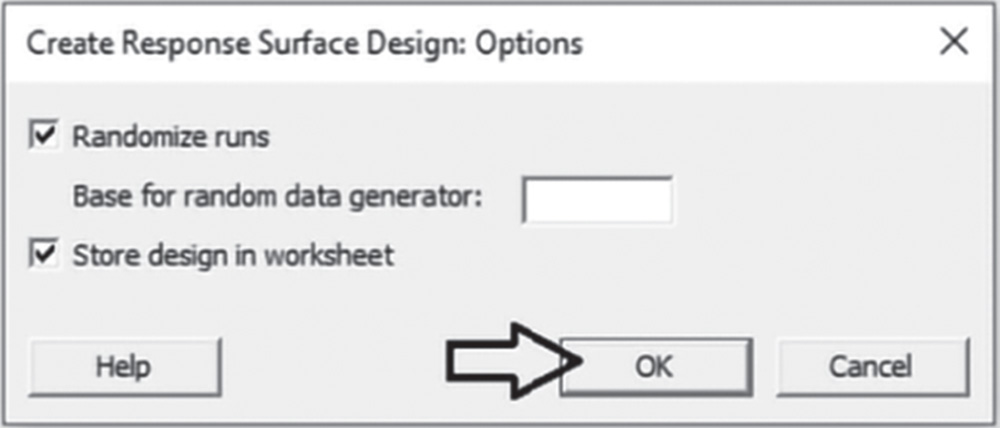
Proceed by clicking Options in the main dialog box and check the option Randomize runs (Stat Tool 2.3). Click OK in the main dialog box and Minitab shows the design of the experiment in the worksheet, and some information in the Session window.

Illustration of Create Response Surface Design and corresponding Options dialog boxes.

You can see that the design includes 20 runs distributed between two blocks. Column PtType shows each design point's type, where the value “0” represents a central point, “1” a cube point, and “−1” an axial point. Block 1 (one of the two operators) is a cube block since it includes cube points with the factors set at their low or high levels. Block 2 is an axial block since it includes axial points. Four center points are in block 1 and two in block 2.

Illustration of a worksheet that displays central composite design.

Stat Tool 4.1 The Central Composite Design (CCD)

The search for a suitable approximating function for the relationship between one or more responses and a set of factors (some being quantitative in nature) is useful to study in depth how factors affect response variables and how to optimize these responses. A response surface represents the functional relationship between responses and factors. Generally, in the mature phase of an experiment, second‐order models, including both linear and quadratic effects and the two‐way interactions between factors, allow the detection of curvatures, if any, in the response surface.

This response surface is represented in Figure 4.1 without curvatures (graph A), when the functional relationship is approximated by a first‐order model, and with curvatures (graph B), when the functional relationship is approximated by a second‐order model.

Figure 4.1 Response surface plot for a first‐order (linear) model (graph A) and for a second‐order model with curvatures (graph B).

A popular class of designs used to fit second‐order models are the CCDs. A CCD is usually used after having performed a factorial or fractional factorial experiment and having identified the key factors. It requires the experimenter to identify only two levels (a low and a high level) for each factor. These levels are not the minimum and maximum admissible values for the factors, but are values around which the experimenter wants to explore the response surface. Generally, the CCD consists of a 2^k factorial design (based on the two levels defined by the experimenter for each factor, with k equal to the number of factors) with the addition of:

a certain number of replicates of the center point (where all the factors are set at their middle value between the low and high levels);
2k axial or star points (where all the factors are set at their middle point except one that is placed at a specific distance “α” from its middle value).

CCDs are especially useful in sequential experiments because you can often build on previous full factorial or fractional factorial designs by adding center points and axial points.

Figure 4.2 shows the CCD for k = 2 and k = 3 with the low and high levels set at “−1” and “+1.”

Figure 4.2 Central composite designs for k = 2 and k = 3.

For example, with two factors A and B, the CCD includes the following:

The factorial design points (−1,−1), (+1,−1), (−1,+1), (+1,+1) represent the vertices of the so‐called “cube” around which the design is built.
Some replicates of the center point (0, 0), with the two factors set at their middle value between the low and high levels.
Four axial points (−α, 0), (α, 0), (0, −α), (0, α), where one factor is set at its middle value and the other factor is set at a distance “α” from its middle value. If “α” is less than 1, the axial points are inside the “cube”; if “α” is greater than 1, the axial points are outside the “cube”; if “α” is equal to 1, the axial points are on the face of the “cube.”

Note that the axial points are usually outside the “cube” (unless you specify an α that is less than or equal to 1). If you are not careful, this could lead to axial points that are not in the region of interest or may be impossible to test.

In many situations, the region of interest in which to explore the relationship between factors and responses, may be imagined as a sphere around the basic factorial design. In these cases, the best choice for the distance “α” for the definition of the axial points is α = , with k equal to the number of factors. This design includes factorial and axial design points lying on the surface of a sphere of radius (Figure 4.3).

Figure 4.3 Spherical CCD for k = 2 with α = .

For a spherical CCD, three to five runs of the center point where all the factors are set at their middle value (for example with k = 2, the point denoted by “0,0”), are generally recommended.

When the region of interest is cuboidal rather than spherical, a useful variation of the central composite design is the face‐centered central composite design, in which α = 1. In this design the axial points are located on the centers of the faces of the cube (Figure 4.4). For a face‐centered CCD, two or three runs of the central point are generally sufficient. The face‐centered CCD requires only three levels of each factor. For this reason it is often used when factor levels are difficult to change.

Figure 4.4 Face‐centered central composite designs for k = 2 and k = 3.

4.2.1.2 Step 2 – Alternatively, Create a Face‐Centered CCD

If you need to evaluate the relationship between the three factors (A, B, Temperature) and elasticity, by exploring a cuboidal region around the basic factorial design, you can create a face‐centered CCD (Stat Tool 4.1).

To create a face‐centered CCD, go to: Stat > DOE > Response Surface > Create Response Surface Design

Under Type of Design select Central composite and in Number of continuous factors specify 3.

Click on Designs. In the next dialog box, select the number of experimental runs and the number of blocks for the design. As outlined in step 1, with two blocks (the two operators), the CCD will include 20 runs. There will be six center points, four of which will be included in the cube block, i.e. in the block with the experimental runs at the high and low levels of the factors. The other two center points will be in the axial block, i.e. the other block with the experimental runs at the axial levels of the factors.

Under Value of Alpha check the option Face Centered.

Illustration of Create Response Surface Design and Designs dialog boxes.

Illustration of Create Response Surface Design and corresponding Factors dialog boxes.

Illustration of Create Response Surface Design: Options dialog box.

Illustration of a worksheet displaying design summary and point types of a central composite design.

4.2.1.3 Step 3 – Alternatively, Create a Box‐Behnken Design

You can decide to evaluate the relationship between the three factors (A, B, Temperature) and elasticity, by creating a Box‐Behnken design (Stat Tool 4.2), which often has fewer design points than CCDs with the same number of factors. The number of blocks (Stat Tool 2.4) that it is possible to include in a Box‐Behnken design depends on the number of factors. Designs with three factors cannot have blocks. For this reason, we now suppose the absence of blocks in our experiment.

To create a Box‐Behnken design, go to: Stat > DOE > Response Surface > Create Response Surface Design

Under Type of Design select Box‐Behnken and in Number of continuous factors specify 3.

Click on Designs. Under Number of Center Points you can leave the selected option Default. However, select Custom if you wish to modify the number of center points in the design. In Number of replicates specify 1 or, depending on available resources, enter how many times to perform each experimental run. Remember you can add replicates to your design later with Stat > DOE > Modify Design. If you specify more than 1 replicate, check the option Block on replicates and Minitab will put each replicate into its own block. If the base design has blocks, then the total number of blocks will be the product of the number of blocks in the base design and the number of replicates. If you have blocks (with more than three factors), then specify the number of blocks and click OK.

Illustration of Create Response Surface Design dialog box that opens another Design dialog box.

In the main dialog box select Factors. Under Name, Low and High, enter a name for each factor and its high and low levels. By default, Minitab sets the low level of all factors to −1 and the high level to +1. If you have categorical factors, the window will allow you to enter the name, number of levels, and level values.

Illustration of Create Response Surface Design dialog box that opens another Factors dialog box.

Proceed by clicking Options in the main dialog box and select Randomize runs (Stat Tool 2.3). Click OK in the main dialog box and Minitab shows the design of the experiment in the worksheet, as well as some information in the Session window.

Illustration of Create Response Surface Design dialog box that opens another Options dialog box.

You can see the design includes 15 runs. Column PtType shows each design point type, where the value “0” represents a central point and “2” an edge mid‐point.

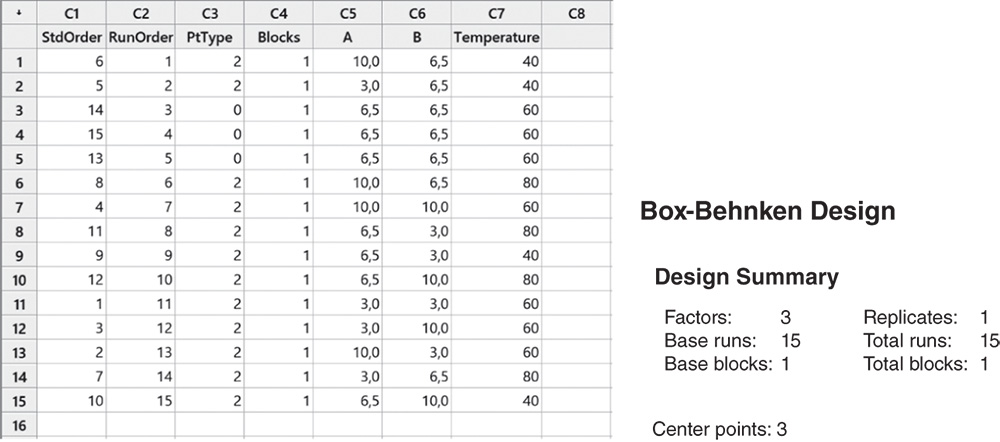
Illustration of a worksheet that displays Design Summary of Box-Behnken Design.

Stat Tool 4.2 The Box‐Behnken Design

The Box‐Behnken design is a three‐level design with no axial points and no cube points. It considers combinations of factor levels where factors are set at their low or high levels and one factor is at its middle value (edge midpoints), and some replicates of the center point. Figure 4.5 shows the Box‐Behnken design with three factors, denoting the low and high values as “−1” and “+1.” Notice that the design includes the edge midpoints lying on a sphere of radius . It often has fewer design points than CCDs with the same number of factors.

Figure 4.5 The Box‐Behnken design for k = 3.

The following table presents a comparison of CCD and Box‐Behnken designs, along with some useful notes for their implementation in Minitab.

Central composite designs	Box‐Behnken designs
For k factors, they consist of: 2^k full factorial (or fractional factorial) 2k axial or star design points (axial runs) a number of center design points	For k factors, they consist of: edge midpoints a number of center design points
They have axial points, which therefore may not be in the region of interest or may be impossible to test.	They do not have axial points; thus, all design points fall within your safe operating zone.
They include runs where all factors are at their extreme setting, such as all at low levels.	They never include runs where all factors are at their extreme setting, such as all at low levels.
In Minitab you can specify 2–10 continuous factors.	In Minitab you can specify 3–10 continuous factors.
In Minitab, starting with the specification of two‐level factors, the design can include up to five levels per factor.	In Minitab, starting with the specification of two‐level factors, the design can include up to three levels per factor.

4.2.1.4 Step 4 – Assign the Designed Factor Level Combinations to the Experimental Units and Collect Data for the Response Variable

Collect the data for the response variables (elasticity) following the order provided in column RunOrder in the chosen design. For example, for the CCD design created in step 1, the first condition for the operator corresponding to block 2 to test will be that with component A at level 6.5, component B at level 6.5 and temperature at 60°.

Once all the designed factor level combinations have been tested, enter the recorded response values (elasticity) in the worksheet containing the design. Now you are ready to proceed with the statistical analysis of the collected data.

4.2.2 Plan of the Statistical Analyses

The main focus of a statistical analysis of a CCD is to study in depth how several factors contribute to the explanation of a response variable and understand how the factors interact with each other. A second important objective is optimization, i.e. the search for those combinations of factor levels that are linked to desirable values of the response.

For these purposes, a second‐order model provides a suitable approximation for the unknown functional relationship between factors and response variables. This is useful for identifying regions of factor levels that optimize response variables.

Let's proceed in the following way:

Step 1 – Perform a descriptive analysis (Stat Tool 1.3) of the response.
Step 2 – Fit a second‐order model to estimate the effects and determine the significant ones.
Step 3 – If need be, reduce the model to include the significant terms.
Step 4 – Optimize the response.
Step 5 – Examine the shape of the response surface and locate the optimum.

For the Polymer Project, the dataset (File: CCD_Polymer_Project.xlsx) opened in Minitab appears as below.

The variables setting is the following:

Columns C1 – C3 are related to the previous creation of the CCD design.
Variables A, B and Temperature are the quantitative factors, each assuming three levels.
Variable Elasticity is the quantitative response variable.

Column	Variable	Type of data	Label
C4	Blocks	Numeric data	The two operators labeled 1 and 2
C5	A	Numeric data	Additive A with levels: 0.78, 6.5, 12.22
C6	B	Numeric data	Additive B with levels: 0.78, 6.5, 12.22
C7	Temperature	Numeric data	Temperature with levels: 27.3°, 60°, 92.7°
C8	Elasticity	Numeric data	Elasticity

CCD_Polymer_Project.xlsx

4.2.2.1 Step 1 – Perform a Descriptive Analysis of the Response Variables

As the response is a quantitative variable, let's use the boxplot to describe how the elasticity occurred in our sample, and calculate means and measures of variability to complete the descriptive analysis.

To display the boxplot, go to: Graph > Boxplot

Under One Y select the graphical option Simple and, in the next dialog box, under Graph variables select “Elasticity.” Then click OK in the dialog box.

To change the appearance of a boxplot, use the tips in Chapter 2, section 2.2.2.1, relating to histograms, as well as the following ones:

To display the boxplot horizontally: double‐click on any scale value on the horizontal axis. A dialog box will open with several options to define. Select from these options: Transpose value and category scales.
To add the mean value to the boxplot: right‐click on the area inside the border of the boxplot, then select Add > Data display > Mean symbol.

Illustration of boxplots dialog box that opens another One Y, Simple dialog box.

To display the descriptive measures (means, measures of variability, etc.), go to:

In the dialog box, select “Elasticity” under Variables, then click Statistics to open a dialog box displaying a range of possible statistics to choose from. In addition to the default options, select Interquartile range and Range.

Illustration of Display Descriptive Statistics dialog box that opens another Statistics dialog box.

4.2.2.1.1 Interpret the Results of Step 1

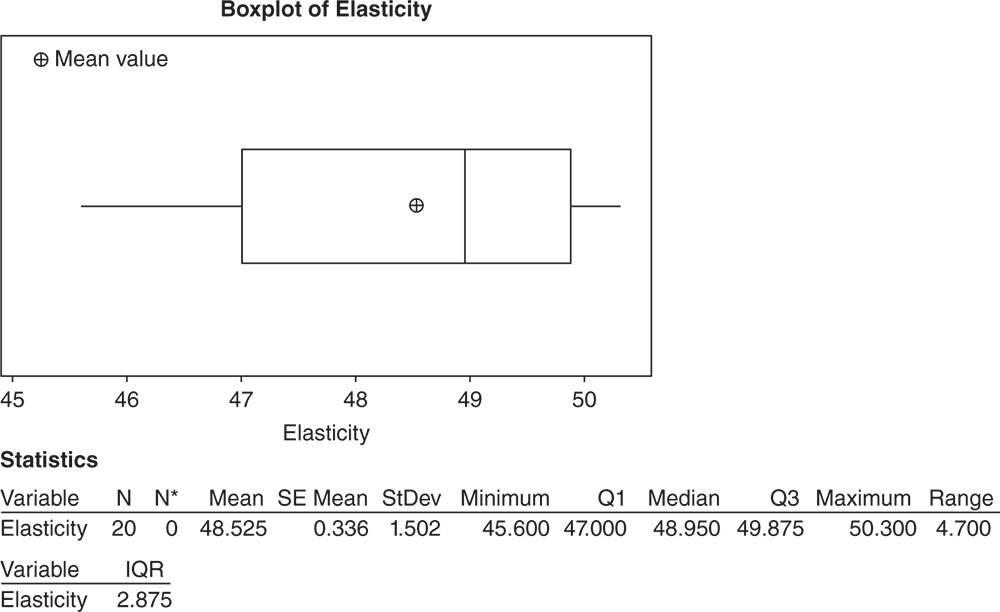
Elasticity data is slightly skewed to the left (Stat Tools 1.4–1.5). About 50% of the trials showed an elasticity value greater than 48.9 (the median, Stat Tool 1.6), and around 25% greater than 49.9 (Q₃, Stat Tool 1.7). With respect to variability, the average distance of the response values from their mean (standard deviation) is about 1.5 (Stat Tool 1.9).

Graphical illustration of Boxplot of Elasticity.

4.2.2.2 Step 2 – Fit a Second‐Order Model to Estimate the Effects and Determine the Significant Ones

Before analyzing the CCD design, we have to specify the factors within Minitab.

To define the CCD design, go to:

Under Continuous Factors, select the factors A, B, and Temperature. If some of your factors are categorical, these should be specified under Categorical Factors. Click on Low/High. For each factor in the list, verify that the high and low settings are correct, and if these levels are in the original units of the data, select Uncoded under Worksheet data are. Click OK.

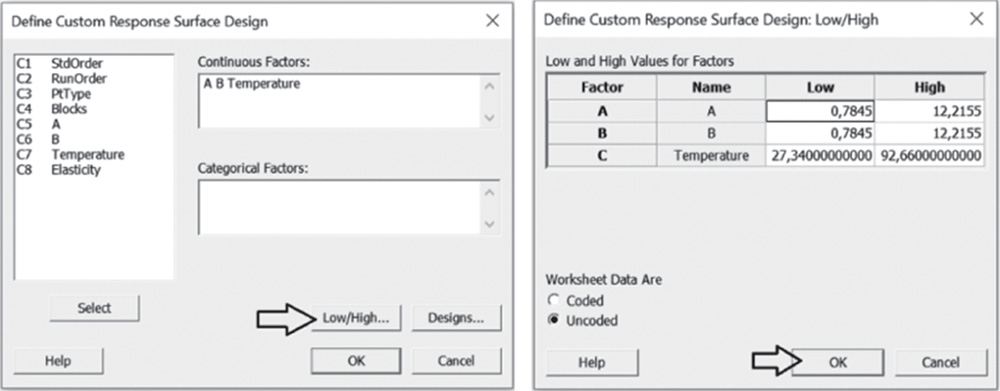
Illustration of Define Custom Response Surface Design dialog box that opens another Low/High dialog box.

In the main dialog box, click on Designs. Specify the columns corresponding to the standard order, run order and point type of the runs. At the bottom of the screen, under Blocks, check the option Specify by column, and in the available space select the column representing the blocking variable. Click OK in each dialog box. Now you are ready to analyze the response surface design.

Illustration of Define Custom Response Surface Design dialog box that opens another Designs dialog box.

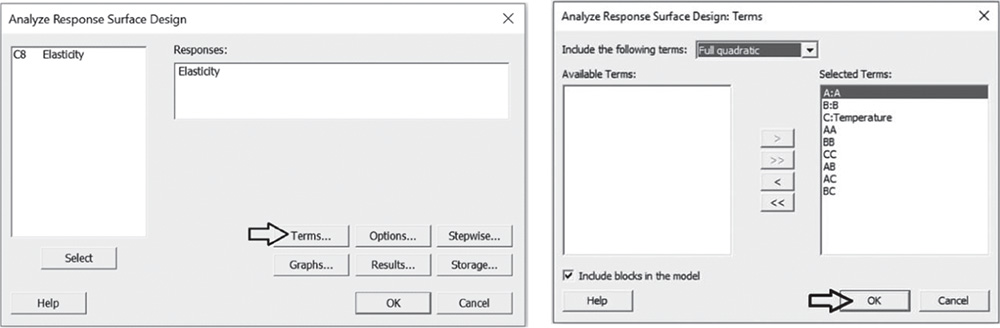
To analyze the response surface design, go to:

Select the response variable “Elasticity” in Responses and click on Terms. At the top of the next dialog box, in Include terms in the model up through order, specify Full quadratic to study all main effects (both linear and quadratic effects) and the two‐way interactions between factors. Select Include blocks in the model to consider blocks in the analysis. Click OK and in the main dialog box, choose Graphs. In Effects plots choose Pareto and Normal. These graphs help you identify the terms (linear and quadratic factor effects and/or interactions) that influence the response and compare the relative magnitude of the effects, along with their statistical significance. Click OK in the main dialog box and Minitab shows the results of the analysis, both in the Session window and through the required graphs.

4.2.2.2.1 Interpret the Results of Step 2

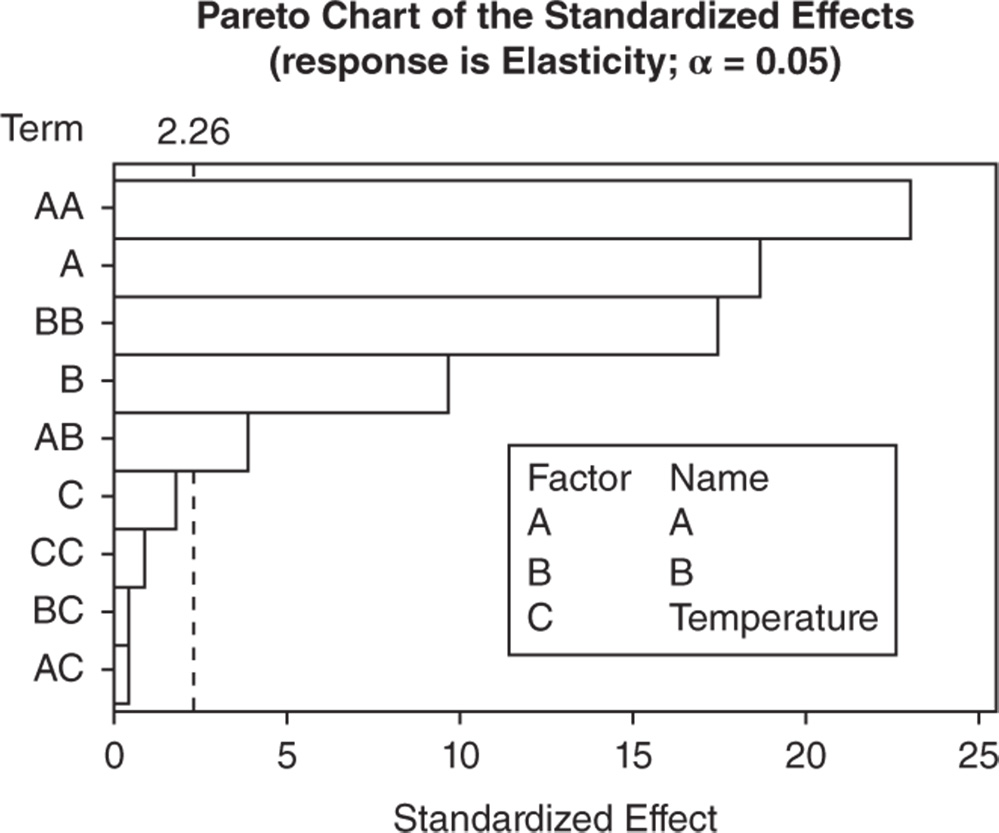
Illustration of Pareto Chart of the Standardized Effects: response is Elasticity; a = 0.05.

First consider the Pareto chart that shows which terms contribute the most to explaining the elasticity. Any bar extending beyond the reference line (considering a significance level equal to 5%) represents a significant effect.

In our example, with the exception of the effects involving temperature, the other main effects, the two‐factor interactions and the quadratic effects are statistically significant at the 0.05 level.

The Pareto chart shows which effects are statistically significant, but you have no information on how these effects affect the response.

Use the normal plot of the standardized effects to evaluate the direction of the effects.

Graphical illustration of Normal Plot of the Standardized Effects: response is Elasticity; a = 0.05.

In the normal plot of the standardized effects, the line represents the situation in which all the effects are 0. Effects that are further from 0 and from the line are statistically significant. Minitab shows statistically significant and nonsignificant effects by giving the points different colors and shapes. In addition, the plot indicates the direction of the effect. Positive effects (displayed on the right of the graph) increase the response when the factor moves from its low value to its high value.

Negative effects (displayed on the left of the graph) decrease the response when moving from the factor's low value to its high value. In our example, the main effects for additives A and B are statistically significant at the 0.05 level. Elasticity seems to increase with higher levels of each additive.

The interaction between the two additives and their quadratic effects are also marked as statistically significant. Later, we will clarify the meaning further.

Response surface regression

ANOVA
Source	DF	Adj SS	Adj MS	F‐Value	p‐Value
Model	10	42.5324	4.2532	125.46	0.000
Blocks	1	0.3000	0.3000	8.85	0.016
Linear	3	15.0789	5.0263	148.27	0.000
A	1	11.8549	11.8549	349.69	0.000
B	1	3.1197	3.1197	92.02	0.000
Temperature	1	0.1044	0.1044	3.08	0.113
Square	3	26.6435	8.8812	261.98	0.000
A*A	1	17.9803	17.9803	530.38	0.000
B*B	1	10.3571	10.3571	305.51	0.000
Temperature*Temperature	1	0.0231	0.0231	0.68	0.430
Two‐way interaction	3	0.5100	0.1700	5.01	0.026
A*B	1	0.5000	0.5000	14.75	0.004
A*Temperature	1	0.0050	0.0050	0.15	0.710
B*Temperature	1	0.0050	0.0050	0.15	0.710
Error	9	0.3051	0.0339
Lack‐of‐fit	5	0.2126	0.0425	1.84	0.287
Pure error	4	0.0925	0.0231
Total	19	42.8375

In the ANOVA table we examine the p‐values to determine whether any factors or interactions, or even blocks, are statistically significant. Remember that the p‐value is a probability that measures the evidence against the null hypothesis. Lower probabilities provide stronger evidence against the null hypothesis.

For the main effects, the null hypothesis is that there is no significant difference in mean elasticity across levels of each factor. As we estimate a full quadratic model, we have two tests for each factor that analyze its linear and quadratic effect on response. The statistical significance of the quadratic effects denotes the presence of curvatures in the response surface.

For the two‐factor interactions, H₀ states that the relationship between a factor and the response does not depend on the other factor in the term.

We usually consider a significance level alpha equal to 0.05, but in an exploratory phase of the analysis we may also consider a significance level equal to 0.10.

When the p‐value is greater than or equal to alpha, we fail to reject the null hypothesis. When it is less than alpha, we reject the null hypothesis and claim statistical significance.

So, if we set the significance level alpha to 0.05, which terms in the model are significant in our example? The answer is: the linear effects of additives A and B; the two‐way interactions between these two factors and their quadratic effects. You may now wish to reduce the model to include only significant terms.

When using statistical significance to decide which terms to keep in a model, it is usually advisable not to remove entire groups of nonsignificant terms at the same time. The statistical significance of individual terms can change because of other terms in the model. To reduce your model, you can use an automatic selection procedure, the stepwise strategy, to identify a useful subset of terms, choosing one of the three commonly used alternatives (standard stepwise, forward selection, and backward elimination).

4.2.2.3 Step 3 – If Need Be, Reduce the Model to Include the Significant Terms

To reduce the model, go to:

Illustration of Analyze Response Surface Design dialog box in which the options Terms is selected.

Select the numeric response variable “Elasticity” under Responses and click on Terms. In Include the following terms, specify Full Quadratic, to study all main effects (both linear and quadratic effects) and the two‐way interactions between factors. Select Include blocks in the model to consider blocks in the analysis. Click OK and in the main dialog box, choose Stepwise. In Method select Backward elimination and in Alpha value to remove specify 0.05, then click OK. In the main dialog box, choose Graphs.

Under Residual plots choose Four in one. Minitab will display several residual plots to examine whether your model meets the assumptions of the analysis (Stat Tools 2.8, 2.9). Click OK in the main dialog box.

Illustration of Analyze Response Surface Design: Terms, Stepwise, Design, and Graphs dialog boxes.

Complete the analysis by adding the factorial plots that show the relationships between the response and the significant terms in the model, displaying how the response mean changes as the factor levels or combinations of factor levels change.

To display factorial plots, go to:

Illustration of Factorial Plots in which the Response selected is Elasticity.

4.2.2.3.1 Interpret the Results of Step 3

By setting the significance level alpha to 0.05, the ANOVA table shows the significant terms in the model. Consider that the stepwise procedure may add nonsignificant terms in order to create a hierarchical model. In a hierarchical model, all lower‐order terms that comprise a higher‐order term also appear in the model.

Response surface regression

Backward elimination of terms α to remove = 0.05 ANOVA
Source	DF	Adj SS	Adj MS	F‐Value	p‐Value
Model	6	42.3949	7.0658	207.53	0.000
Blocks	1	0.3000	0.3000	8.81	0.011
Linear	2	14.9745	7.4873	219.91	0.000
A	1	11.8549	11.8549	348.19	0.000
B	1	3.1197	3.1197	91.63	0.000
Square	2	26.6203	13.3102	390.94	0.000
A*A	1	17.9801	17.9801	528.10	0.000
B*B	1	10.3401	10.3401	303.70	0.000
Two‐way interaction	1	0.5000	0.5000	14.69	0.002
A*B	1	0.5000	0.5000	14.69	0.002
Error	13	0.4426	0.0340
Lack‐of‐fit	9	0.3501	0.0389	1.68	0.324
Pure error	4	0.0925	0.0231
Total	19	42.8375

Model summary

S	R‐sq	R‐sq(adj)	R‐sq(pred)
0.184518	98.97%	98.49%	97.41%

Note that in the ANOVA table, Minitab displays the lack‐of‐fit test when your data contain replicates. This test helps investigators to determine whether the model accurately fits the data. Its null hypothesis states that the model accurately fits the data. As usual, compare the p‐value to your significant level α. If the p‐value is less than α, reject the null hypothesis and conclude that the lack of fit is statistically significant. If the p‐value is larger than α, you fail to reject the null hypothesis and you can conclude that the lack of fit is not statistically significant.

In our example, the p‐value (0.324) is greater than 0.05: we conclude that there is no strong evidence of lack of fit. Lack of fit can occur if important terms such as interactions or quadratic terms are not included in the model or if the fitted model shows several, unusually large residuals (Stat Tool 2.9).

In addition to the results of the analysis of variance, Minitab displays some other useful information in the Model Summary table.

The quantity R‐squared (R‐sq, R²) is interpreted as the percentage of the variability among elasticity data, explained by the terms included in the ANOVA model.

The value of R² varies from 0 to 100%, with larger values being more desirable.

The adjusted R² (R‐sq(adj)) is a variation of the ordinary R² that is adjusted for the number of terms in the model. Use adjusted R² for more complex experiments with several factors, when you want to compare several models with different numbers of terms.

The value of S is a measure of the variability of the errors that we make when we use the ANOVA model to estimate the elasticity data. Generally, the smaller it is, the better the fit of the model to the data.

Before proceeding with the results reported in the Session window, take a look at the residual plots. A residual represents an error, i.e. the distance between an observed value of the response and its value estimated by the ANOVA model. The graphical analysis of residuals based on residual plots helps you to discover possible violations of the underlying ANOVA assumptions (Stat Tools 2.8, 2.9).

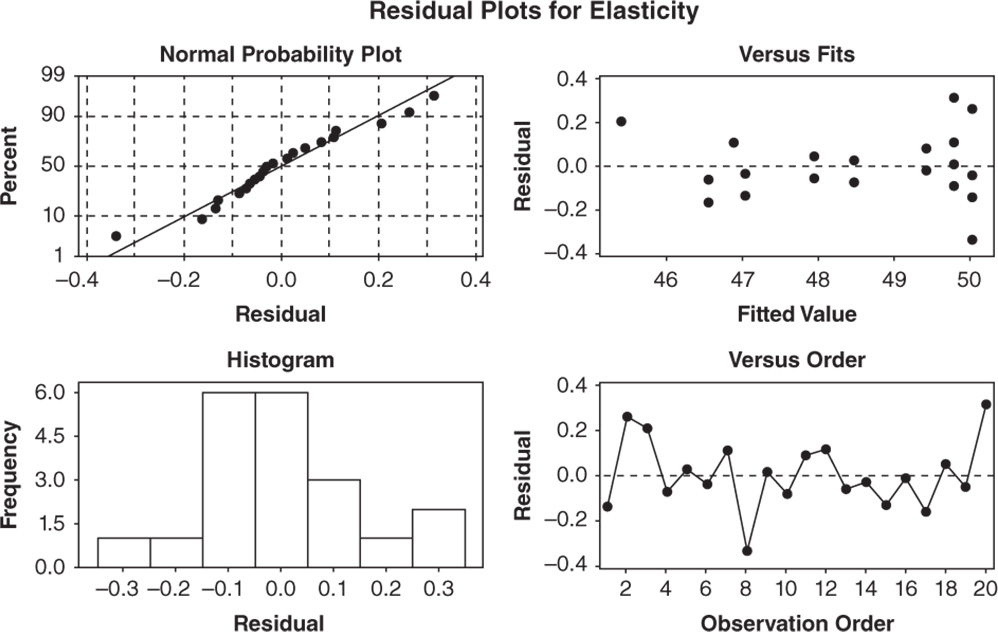
Graphical illustration of Residual Plots for Elasticity: Normal Probability Plot, Versus Fits, Histogram, and Versus Order.

A check of the normality assumption could be made looking at the histogram of the residuals (bottom left), but with small samples, often the histogram has an irregular shape.

The normal probability plot of the residuals may be more useful. Here we can see a tendency of the plot to follow the straight line.

The other two graphs (Residuals versus Fits and Residuals versus Order) seem unstructured, thus supporting the validity of the ANOVA assumptions.

Returning to the Session window, we find a table of coded coefficients followed by a regression equation in uncoded units. In the regression equation, we have a coefficient for each term in the model. They are expressed in uncoded units, i.e. in the original measurement units. These coefficients are also displayed in the Coded Coefficients table, but in coded units (see section 2.2.2.3.1). In the Coded Coefficients table, we find the same results as in the ANOVA table in terms of tests on coefficients and we can evaluate the p‐values to determine whether they are statistically significant. The null hypothesis states that there is no effect on the response. Setting the significance level α at 0.05, if a p‐value is less than α, reject the null hypothesis and conclude that the effect is statistically significant.

Coded coefficients

Term	Coef	SE Coef	t‐Value	p‐Value	VIF
Constant blocks	49.9143	0.0648	769.72	0.000
1	−0.1250	0.0421	−2.97	0.011	1.00
A	1.5398	0.0825	18.66	0.000	1.00
B	0.7899	0.0825	9.57	0.000	1.00
A*A	−3.104	0.135	−22.98	0.000	1.00
B*B	−2.354	0.135	−17.43	0.000	1.00
A*B	0.667	0.174	3.83	0.002	1.00
Regression equation in uncoded units Elasticity = 41.069 + 1.3718 A + 0.9422 B − 0.09501 A * A − 0.07205 B * B + 0.02041 A * B Equation averaged over blocks.

Look at the factorial plots to better understand how the mean elasticity varies as factor levels change.

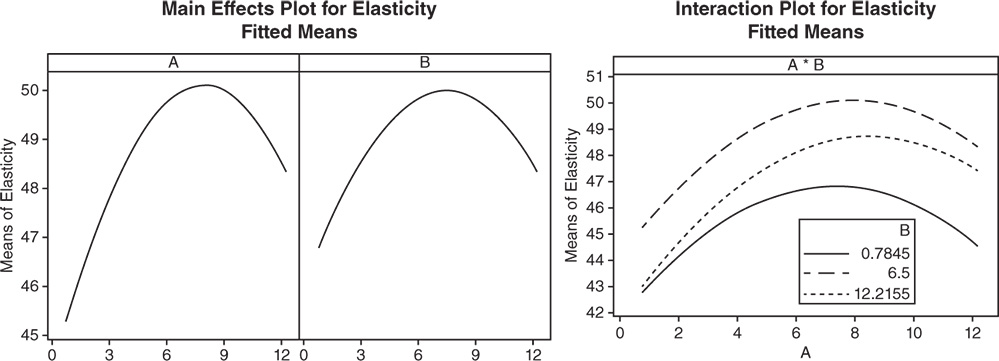Graphical illustration of Main Effects Plot for Elasticity and Interaction Plot for Elasticity. The presence of the quadratic terms A*A and B*B results in a curvature in the factorial plots involving factors A and B. Considering the interaction A*B, the best results in terms of elasticity are obtained when A is around 8 and B is set at its middle value.

4.2.2.4 Step 4 – Optimize the Response

After fitting the response surface model, additional analyses can be carried out to find the optimum set of factor levels that optimizes the response (Stat Tool 3.8).

To optimize the response variable, go to:

In the table, under Goal, select one of the following options for the response:

Do not optimize: Do not include the response in the optimization process.
Minimize: Lower values of the response are preferable.
Target: The response is optimal when values meet a specific target value.
Maximize: Higher values of the response are preferable.

In our case study the goal is to maximize elasticity: choose Maximize from the drop‐down list and click Setup. In the next window you need to specify a response target and lower or upper bounds depending on your goal. Minitab automatically sets the Lower value and the Upper value to the smallest and largest values in the data, but you can change these values depending on your response goal (Stat Tool 3.8).

If your goal is to maximize the response (larger is better), you need to specify the lower bound and a target value. You may want to set the lower value to the smallest acceptable value and the target value at the point of diminishing returns, i.e. a point at which going above its value does not make much difference. If there is no point of diminishing returns, use a very high target value.
If your goal is to target a specific value, you should set the lower value and upper value as points of diminishing returns.
If the goal is to minimize (smaller is better), you need to specify the upper bound and a target value. You may want to set the upper value to the largest acceptable value and the target value at the point of diminishing returns, i.e. a point at which going below its value does not make much difference. If there is no point of diminishing returns, use a very small target value.

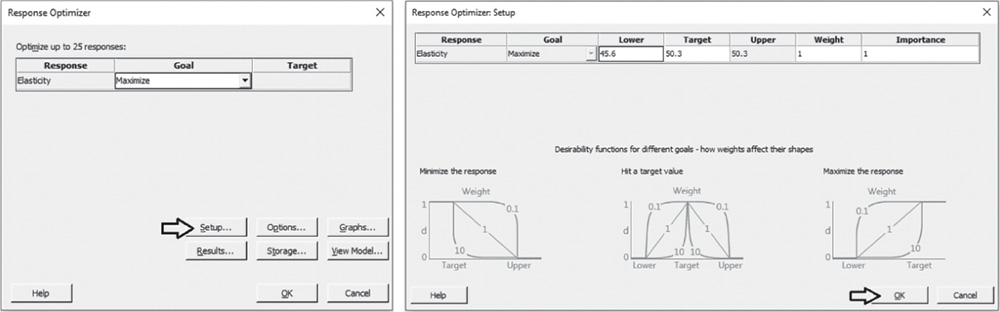Illustration of Response Optimizer and corresponding Setup dialog boxes. In our example, we leave the default values with the lower bound set to the minimum and the target and upper values set to the maximum.

Note that in the process of response optimization, Minitab calculates and uses desirability indicators from 0 to 1 to represent how well a combination of factor levels satisfies the goals you have for the responses. Specifying a different weight varying from 0.1 to 10, you can emphasize or deemphasize the importance of attaining the goals. Furthermore, when you have more than one response, Minitab calculates individual desirabilities for each response and a composite desirability for the entire set of responses. With multiple responses, you may assign a different level of importance to each response by specifying how much effect each response has on the composite desirability.

In our example, leave Weight and Importance equal to 1 and click OK. In the main dialog box select Results and in Number of solutions to display, specify 5. Click OK in each dialog box. In the optimization plot, Minitab will display the optimal solution, i.e. the factor setting that maximizes the composite desirability, while in the Session window we will find a list of five different factor combinations close to the optimal one, which is the first on the list.

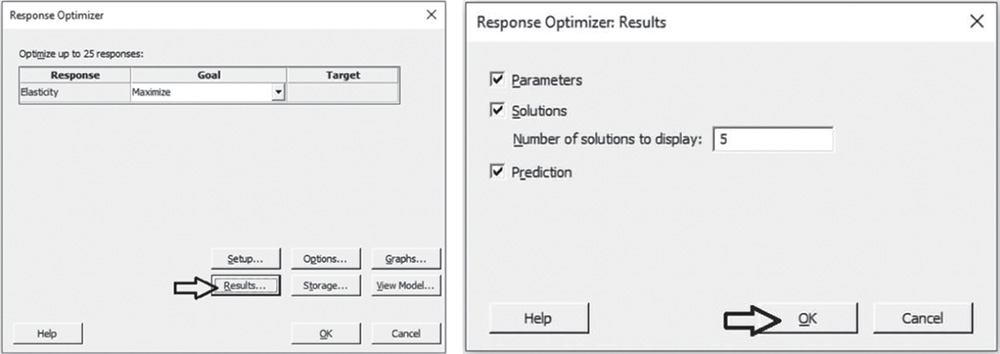
Illustration of Response Optimizer and corresponding Results dialog boxes.

The optimization plot shows how different factor settings affect the response. The vertical lines on the graph represent the current factor settings. The numbers displayed at the top of a column show the current factor level settings (Minitab displays them in red). The horizontal blue lines and numbers represent the responses for the current factor level. The optimal solution is displayed on the graph and serves as the initial point. The settings can then be modified interactively, to determine how different combinations of factor levels affect the response, by moving the red vertical lines corresponding to each factor. To return to the initial settings, right‐click and select Navigation and then Reset to Initial Settings.

4.2.2.4.1 Interpret the Results of Step 4

The optimization plot is a useful tool for exploring the sensitivity of the response variable to changes in the factor settings and in the neighborhood of a local solution – for example, the optimal one.

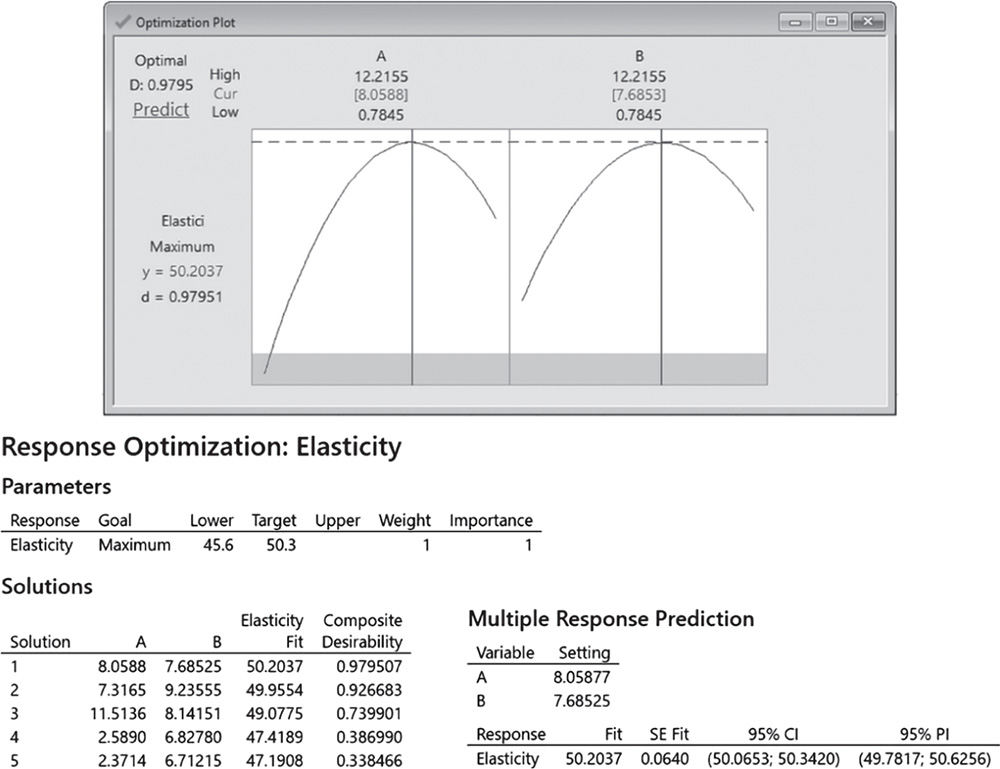
Graphical illustration of Optimization plot for elasticity.

The Session window displays:

Information about the boundaries, weight, and importance for the response variable (Parameters).
The factor settings, the fitted response, and the composite desirability for the required 5 solutions. The first in the list is the optimal solution (Solutions).
The factor settings for the optimal solution and the fitted response with their confidence intervals (Stat Tool 1.14) and prediction intervals (Multiple Response Prediction).

For elasticity data the optimal solution has the additive A set to 8.06 and the additive B to 7.68. For this setting, the fitted response (mean elasticity) is equal to 50.20 (95% CI: 50.06‐50.34). The composite desirability (0.98) is quite close to 1, denoting a satisfactory overall achievement of the specified goal.

4.2.2.5 Step 5 – Examine the Shape of the Response Surface and Locate the Optimum

Graphic techniques such as contour, surface, and overlaid plots help us to examine the shape of the response surface in regions of interest. Through these plots, you can explore the potential relationship between pairs of factors and the responses. You can display a contour, a surface or an overlaid plot considering two factors at a time, while setting the remaining factors to predefined levels. With contour and surface plots, you consider a single response; in overlaid plots, you can consider more than one response.

To display the contour plot, go to: Stat > DOE > Response Surface > Contour Plot

In the dialog box, select the response “Elasticity” in Response. Click Contours, and under Data Display, choose Contour lines. Click OK.

Illustration of Contour plot dialog box where Response is Elasticity.

Illustration of Contour plot: Contours dialog box.

To display the surface plots, go to: Stat > DOE > Response Surface > Surface Plot

In the dialog box, select the reponse “Elasticity” in Response. Click OK.

Illustration of Surface Plot dialog box where Response is Elasticity.

To change the appearance of the surface plot, double‐click on any point inside a surface. In Attributes, under Surface Type, select the option Wireframe instead of the default Surface.

Illustration of Surface Plot of Elasticity vs B; A and Edit Surface dialog boxes.

4.2.2.5.1 Interpret the Results of Step 5

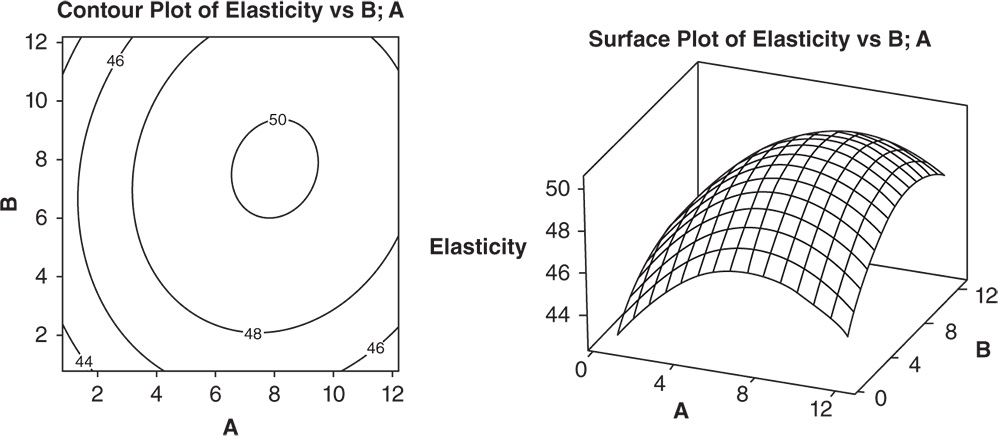
In the contour plot, additives A and B are plotted in the x‐ and y‐axes and elasticity is represented by different level curves. Double‐click on any point in the frame and select Crosshairs to interactively view variations in the response. In the surface plot, elasticity is represented by a smooth surface. It is relatively easy to see that the optimum is very near to 8 for additive A and to 7 for additive B and to explore how the elasticity changes while increasing or decreasing factor levels.

Illustration of Contour Plot of Elasticity vs B; A and Surface Plot of Elasticity vs B; A.

4.3 Case Study for Mixture Designs: Mix‐Up Project

In the development of a new detergent, the research team aims to analyze how three different components can affect the product's technical performance. The three components (A, B, and C) form a mixture of fixed amount. The researchers want to evaluate if changing the proportions of the components inside the mixture will lead to the technical performance (measured as an index assuming values from 0 to 70, with high values representing a better performance) displaying different behavior.

In case study 4.2, we created and analyzed a response surface design in which the levels of each factor can vary independently of the other factors. In this case study, the three components represent ingredients of a mixture and the amount of the mixture is fixed. Consequently, the components are not independent, i.e. if we increase one component, at least one other must decrease. This kind of experiment is called a mixture experiment (Stat Tool 4.3).

4.3.1 Plan of the Experimental Design

We will create the experimental design using either a simplex centroid design (Stat Tool 4.4) or a simplex lattice design (Stat Tool 4.5).

For the present study:

The three components A, B, and C represent the key factors.
The technical performance represents the response variable.

To perform the experiment, let's proceed in the following way:

Step 1 – Create a simplex centroid design for a simple mixture experiment.
Step 2 – Alternatively, create a simplex centroid design for a simple mixture experiment with lower limits for components.
Step 3 – Alternatively, create a simplex centroid design for a mixture‐process variable experiment.
Step 4 – Alternatively, create a simplex centroid design for a mixture‐amount experiment.
Step 5 – Alternatively, create a simplex lattice design for a simple mixture experiment.
Step 6 – Alternatively, create an extreme vertices design with lower and upper limits for components.
Step 7 – Alternatively, create an extreme vertices design with linear constraints for components.
Step 8 – Assign the designed factor level combinations (design points) to the experimental units and collect data for the response variable.

4.3.1.1 Step 1 – Create a Simplex Centroid Design for a Simple Mixture Experiment

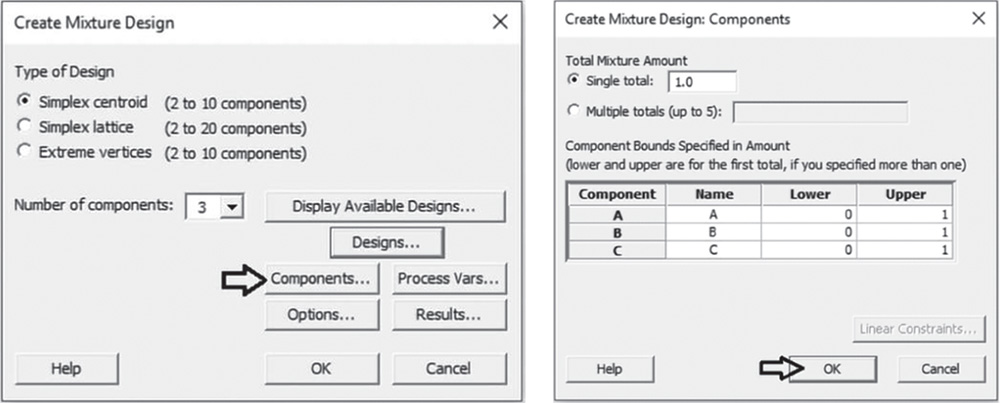
Let's start with a simple mixture experiment in which only the proportions of the three components are expected to be related to the technical performance. For this purpose we will create a simplex centroid design, considering the three factors A, B, and C.

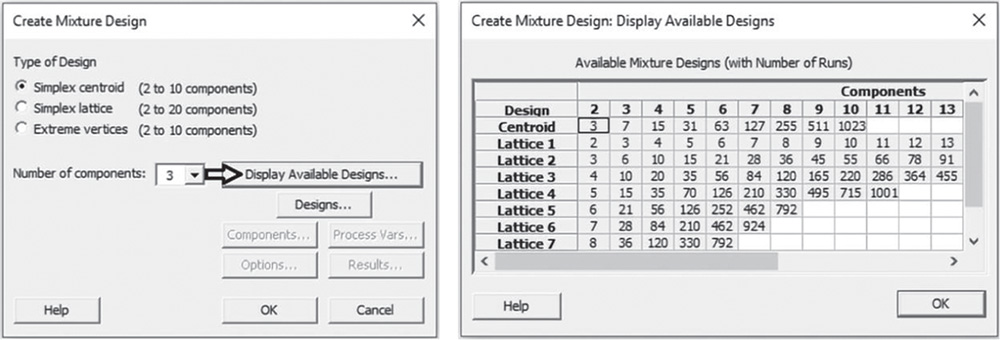
To create a simplex centroid design, go to: Stat > DOE > Mixture > Create Mixture Design

In Type of Design select Simplex centroid and in Number of components specify 3. Click on Display Available Designs to have an indication of the number of runs based on the design type and the number of components in the mixture. Click OK.

Illustration of Create Mixture Design and corresponding Display Available Designs dialog boxes.

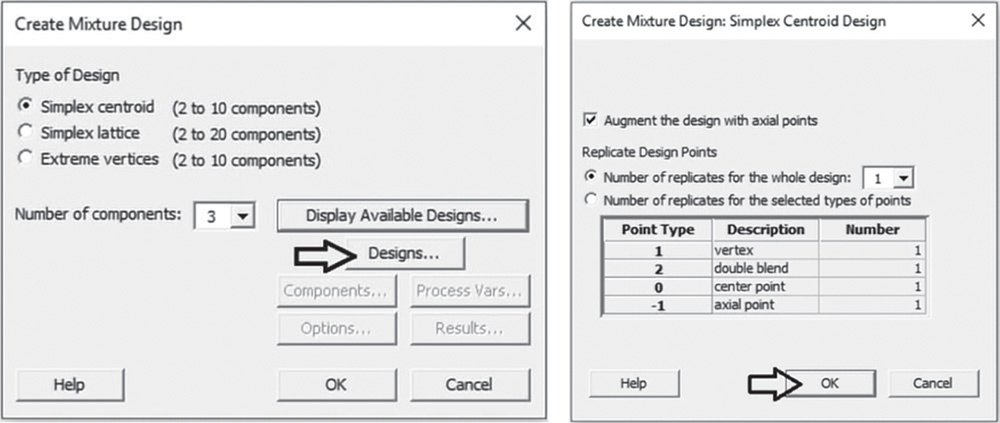
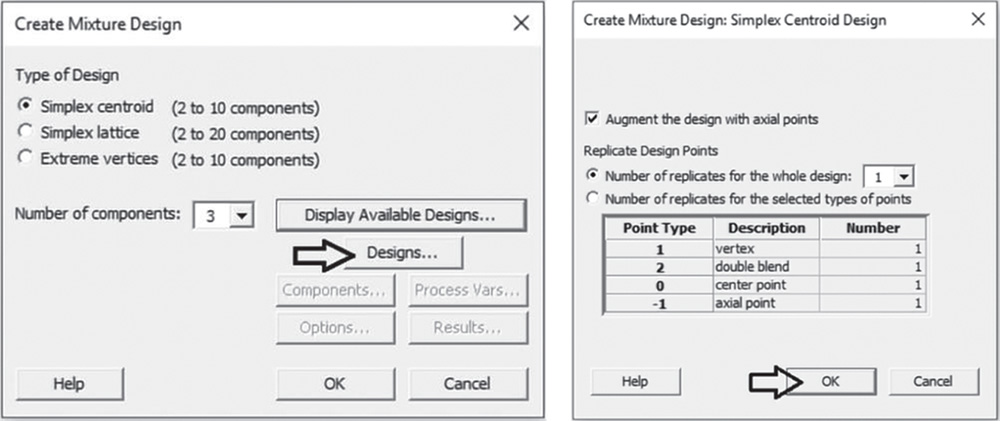
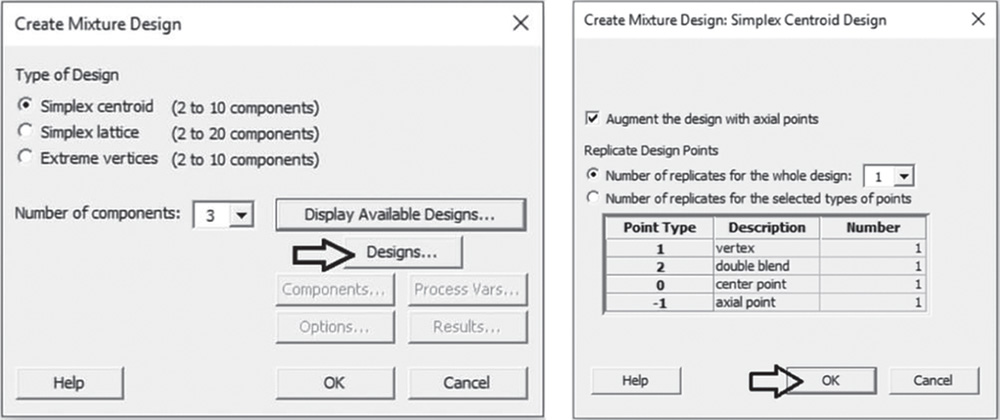
In the main dialog box select Designs. Check the option Augment the design with axial points. In Number of replicates for the whole design specify 1 or, depending on available resources, enter how many times to perform each experimental run. To add replicates for specific design points, for example for a center point or a vertex point, select the option Number of replicates for the selected types of points. Remember, you can add replicates to the whole design later with Stat > DOE > Modify Design. Click OK.

Illustration of Create Mixture Design and corresponding Simplex Centroid Design dialog boxes.

In the main dialog box select Components. Check the option Single total under Total Mixture Amount and leave the default value 1.0 given that the experiment considers a single fixed amount for the mixture and the components are expressed as proportions. Under Name, enter a name for each mixture component. For the moment, suppose that each component can vary from 0 to 1. In steps 2 and 6, we will see how to specify lower and/or upper limits for components. Click OK.

Illustration of Create Mixture Design and corresponding Components dialog boxes.

Proceed by clicking Options in the main dialog box and check the option Randomize runs (Stat Tool 2.3). Click OK in each dialog box and Minitab shows the design of the experiment in the worksheet and some information in the Session window.

Illustration of Create Mixture Design and corresponding Options dialog boxes.

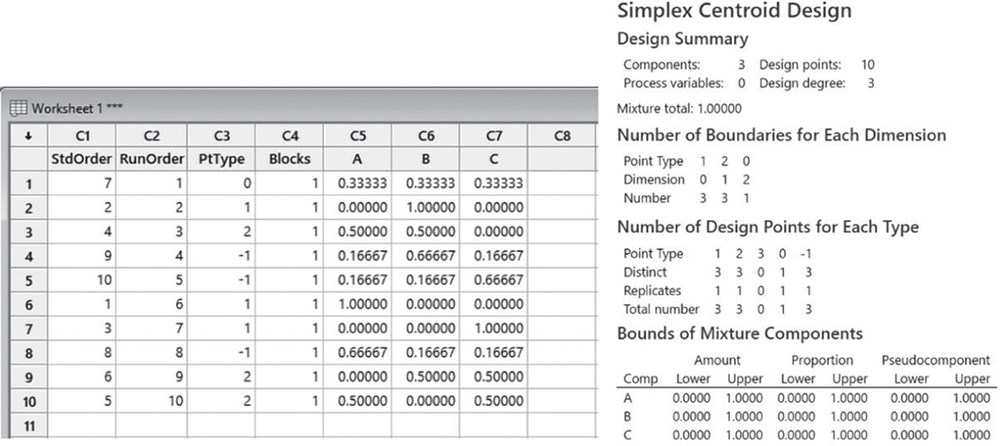
Illustration of worksheet 1 that shows the design summary, number of boundaries for each design, number of design points for each type, and bounds of mixture components of simplex centroid design.

The design includes 10 design points. In the table, Number of Design Points for Each Type, each design point type can be seen. In the design we have three vertices (point type = 1), three double blends (point type = 2), one center point (point type = 0) and three axial points (point type = −1).

You can display the design to graphically check the experimental region.

Go to: Stat > DOE > Mixture > Simplex Design Plot

Under Components, check the option Select a triplet of components for a single plot. If you have more than three components in the mixture, you can select the option Generate plots for all triplets of components. Under Component Unit in Plot(s), check Proportion and under Point Labels, select Point Type. Click OK.

Illustration of a Simplex design plot dialog box and simplex design plot in proportions.

If you hover over the design points, Minitab displays the corresponding mixture. For example, the top vertex corresponds to the pure blend (A = 1, B = 0, C = 0).

Stat Tool 4.3 Mixture Experiments

In a mixture experiment, the factors are ingredients or components of a mixture and these components can't vary independently of each other, i.e. the total amount of the mixture is fixed and if you increase a component, at least one of the other components must decrease. Mixture experiments allow us to study the relationship between mixture components and one or more responses.

In mixture experiments, it is important to clarify if you expect the response(s) to be related:

Only to the mixture of components. In Minitab it is simply a Mixture experiment; or
To the mixture of components and some other factors (process variables) that are not part of the mixture, but might affect its blending properties. For example, the researchers could be interested in evaluating if the temperature is also related to the responses. In Minitab it is a mixture‐process variable experiment and you can include up to seven process variables. These variables must be binary variables assuming two levels.
To the mixture of components and the amount of the mixture. For example, you can test a set of mixtures considering two different total amounts: 20 and 30 g. In Minitab, it is a mixture‐amount experiment and you can specify up to five different total amounts for the mixture.

Regarding the mixture components, they can be considered in the following ways:

In their original measurement unit, i.e. their individual amount. For example, with two components, say A and B, in the mixtures (15 g, 35 g), (20 g, 30 g), and (0 g, 50 g), the components are expressed in their amounts.
As proportions of the total amount (generally recommended). For example, we transform the previous mixtures by dividing each component amount by the total amount of the mixture (50 g). In this way the mixtures are shown as (0.3, 0.7), (0.4, 0.6), and (0, 1), with the components now expressed as proportions.

Suppose we have p components expressed as proportions, and each component can vary from 0 to 1. In a mixture experiment we have the following restrictions:

The factor space, i.e. the set of values that components can assume in a mixture experiment, is called the simplex. With two components x₁ and x₂, the simplex is a segment line represented in Figure 4.6(a) with two vertices representing mixtures where only one component is present. These vertices represent the so‐called pure blends. With three components x₁, x₂, and x₃, the simplex is a triangle represented in Figure 4.6(b) with three vertices representing the pure blends. With four components x₁, x_2, x₃, and x₄, the simplex is a tetrahedron represented in Figure 4.6(c) with four vertices representing the pure blends.

Figure 4.6 The simplex for (a) p = 2, (b) p = 3, and (c) p = 4 mixture components.

In a mixture experiment, the set of mixtures that we can define with the components can be represented as points that lie on the boundaries or inside the simplex.

Creating a mixture design means selecting some points on the boundaries or inside the simplex. This is why the so‐called simplex designs are used to study the effects of mixture components on the response variables.

Statistical software like Minitab can help to make the correct selection. It is therefore important to know how to locate a mixture in the simplex in order to check if the proposed mixture design corresponds adequately to the research needs.

Suppose we have three components in the mixture, expressed as proportions and varying from 0 to 1. A specific mixture will be denoted as (x₁, x₂, x₃). The simplex can be graphically represented by a flat triangle (Figure 4.7, corresponding to the gray oblique triangle shown in Figure 4.6(b).

Figure 4.7 The simplex for p = 3 mixture components.

The three vertices correspond to the pure blends or single‐component: (1, 0, 0), (0, 1, 0), (0, 0, 1).

To locate points inside the simplex, it is useful to draw perpendicular lines from each vertex to the opposite side of the simplex. These lines are called axial axes.

For example, the axial axis of component x₁ goes from the top to the opposite edge midpoint. The four grid lines mark off 20% increments in the component (Figure 4.8).

Figure 4.8 Axial axis for component x₁.

By drawing perpendicular lines from a specific point to each axial axis, it is possible to identify the value of the corresponding component in the mixture.

For example, this point inside the simplex corresponds to the mixture (0.6, 0.2, 0.2). Points located inside the simplex correspond to complete mixtures, where all the components are present (Figure 4.9).

Figure 4.9 Locating design points.

The intersection point of the three axial axes is called centroid and corresponds to the mixture (0.33, 0.33, 0.33), where all the components are present in the same proportion.

Any points along the edges of the simplex represent blends where one of the components is absent (namely the one labeled on the opposite vertex). These are called two‐blend mixtures.

The edge midpoints are two‐blend mixtures in which the two components each make up half of the mixture (Figure 4.10).

Figure 4.10 Edge midpoints.

The edge trisectors are two‐blend mixtures in which one component makes up one‐third and a second component makes up two‐thirds of the mixture (Figure 4.11).

Figure 4.11 Edge trisectors.

Minitab provides three mixture designs to use according to your needs:

Simplex centroid designs
Simplex lattice designs
Extreme vertices designs

In Stat Tools 4.4–4.7, the main characteristics and purposes of each mixture design are presented.

Stat Tool 4.4 Simplex Centroid Designs

A simplex centroid design considers mixtures in which components are of the same amount or proportion.

With three components, expressed as proportions and varying from 0 to 1, the simplex centroid design has the following seven design points (Figure 4.12):

3 vertices (pure mixtures)
3 two‐blend mixtures with two components present in the same proportion
1 centroid

Figure 4.12 Simplex centroid design with p = 3 components.

With four components, the simplex centroid design has 15 design points (Figure 4.13):

4 vertices (pure mixtures);
6 two‐blend mixtures with two components present in the same proportion
4 three‐blend mixtures with three components present in the same proportion
1 centroid

Figure 4.13 Simplex centroid design with p = 4 components.

You will notice that in simplex centroid designs, most of the design points are on the boundaries of the simplex (vertices, edges, faces) and there is only one complete mixture represented by the centroid, where all the components are present.

In order to represent more complete mixtures inside the simplex, with blends consisting of all mixture components, it is possible to augment the basic design with axial points.

Axial points are positioned along the axial axes a certain distance from the centroid. Generally, it is recommended that axial points be placed midway between the centroid of the simplex and each vertex.

For example, with three components, expressed as proportions and varying from 0 to 1, the simplex centroid design augmented with axial points has the following 10 design points (Figure 4.14):

3 vertices (pure mixtures);
3 two‐blend mixtures with two components present in the same proportion
1 centroid
3 three‐blend mixtures corresponding to the axial points

Figure 4.14 Augmented simplex centroid design with p = 3 components.

Generally, an augmented simplex design is superior when it comes to studying the response of complete mixtures in that it can detect and model curvature within the simplex if there is any in the system. Furthermore, the augmented simplex design has more power to detect lack of fit in the fitted model.

4.3.1.2 Step 2 – Alternatively, Create a Simplex Centroid Design for a Simple Mixture Experiment with Lower Limits for Components

Suppose you have to specify a lower limit for some or all components of the mixture. For example, consider the following constraints on the component proportions: A ≱ 0.05; B ≱ 0.25; C ≱ 0.50. When you specify lower limits to some or all components, the experimental region is still a simplex and you can still create a simplex centroid design.

To create a simplex centroid design with lower limits, go to: Stat > DOE > Mixture > Create Mixture Design

Under Type of Design select Simplex centroid and in Number of components specify 3. Select Designs. Check the option Augment the design with axial points. In Number of replicates for the whole design specify 1 or, depending on available resources, enter how many times to perform each experimental run. You can also add replicates for specific design points, for example for a center point or a vertex point, by checking the option Number of replicates for the selected types of points. Remember you can add replicates to the whole design later with Stat > DOE > Modify Design. Click OK.

Illustration of Create Mixture Design dialog box that opens another Simplex centroid design dialog box.

In the main dialog box select Components. Check the option Single total under Total Mixture Amount and leave the default value 1.0 given that the experiment considers a single fixed amount for the mixture and the components are expressed as proportions. Under Name, enter a name for each mixture component. Under Lower, specify the lower limits for each component. Click OK.

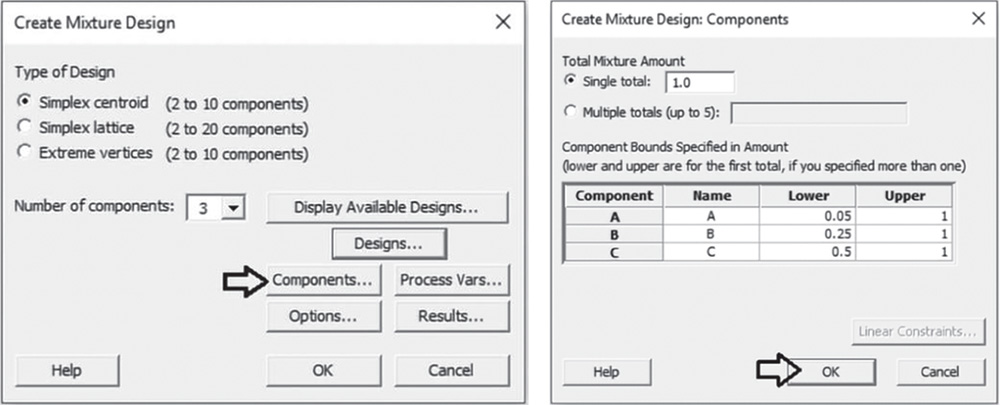
Illustration of Create Mixture Design dialog box that opens another Components dialog box.

Illustration of Create Mixture Design dialog box that opens another Options dialog box.

Illustration of worksheet 2 that displays different parameters of simplex centroid design.

The design includes 10 design points. The table Number of Design Points for Each Type identifies each design point type. Here we have three vertices (point type = 1), three double blends (point type = 2), one center point (point type = 0) and three axial points (point type = −1).

In the table Bounds of Mixture Components, you can see that Minitab adjusted the upper limits of each component to accommodate the specified constraints.

You can display the design to graphically check the experimental region.

Go to: Stat > DOE > Mixture > Simplex Design Plot

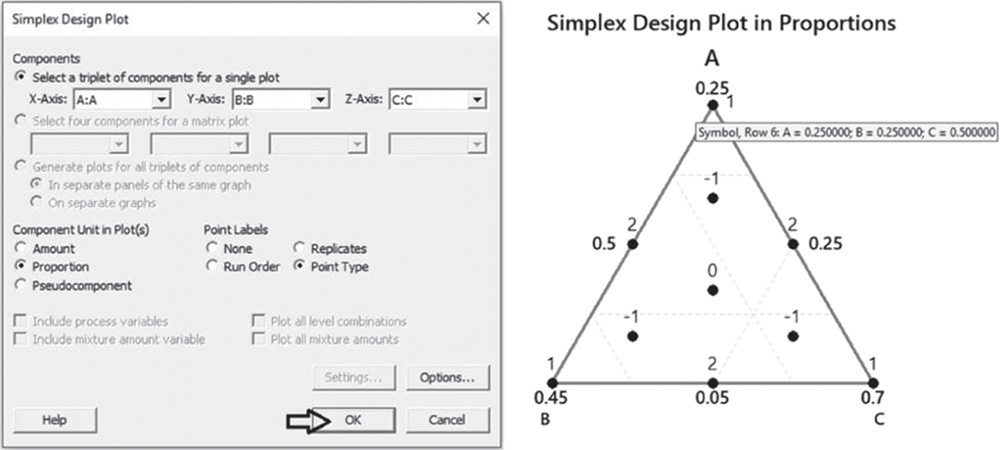
Illustration of simplex design plot dialog box and a triangle representing simplex design plot in proportions.

If you hover over the design points, Minitab displays the corresponding mixture. For example, the top vertex corresponds to the complete blend (A = 0.25, B = 0.25, C = 0.50).

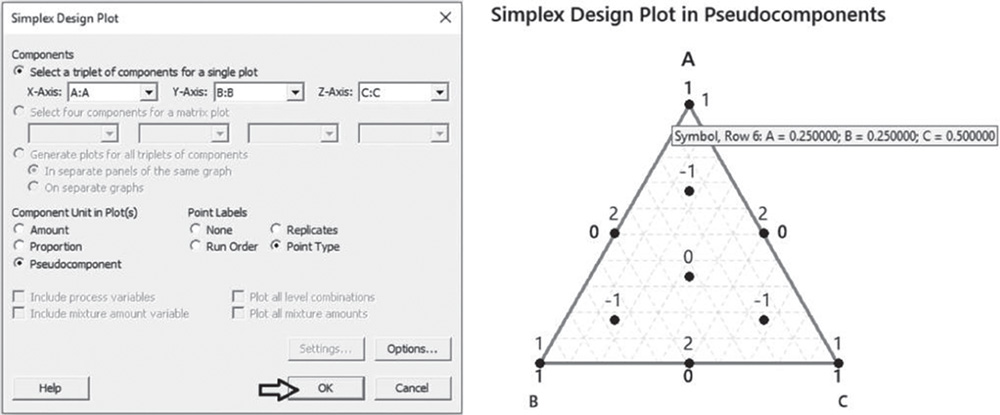
You can also display the design in pseudocomponents rather than in proportions.

Go to: Stat > DOE > Mixture > Simplex Design Plot

Under Components, check the option Select a triplet of components for a single plot. If you have more than three components in the mixture, you can select the option Generate plots for all triplets of components. Under Component Unit in Plot(s), check Pseudocomponent and under Point Labels, select Point Type. Click OK.

If you hover over the design points, Minitab displays the corresponding mixture. Again the top vertex corresponds to the complete blend (A = 0.25, B = 0.25, C = 0.50).

Illustration of simplex design plot dialog box and a triangle representing simplex design plot in pseudocomponents.

4.3.1.3 Step 3 – Alternatively, Create a Simplex Centroid Design for a Mixture‐Process Variable Experiment

Suppose you now suspect the response is related to the proportions inside the mixture and to other factors which are not part of the mixture. These additional factors are called process variables. Minitab allows you to include up to seven process variables but they must be binary, i.e. factors with only two levels. For example, suppose we need to take into account the possible relationship between temperatures of a washing cycle. For this process variable we set the following levels: 30 and 60 °C.

To create a simplex centroid design with process variables, go to: Stat > DOE > Mixture > Create Mixture Design

In Type of Design select Simplex centroid and in Number of components specify 3. Select Designs. Check the option Augment the design with axial points. In Number of replicates for the whole design specify 1 or, depending on available resources, enter how many times to perform each experimental run. You can also add replicates for specific design points, for example for a center point or a vertex point, by checking the option Number of replicates for the selected types of points. Take into account that you can add replicates to the whole design later with Stat > DOE > Modify Design. Click OK.

Illustration of Create Mixture Design dialog box opening another Simplex centroid design dialog box.

In the main dialog box select Components. Check the option Single total under Total Mixture Amount and leave the default value 1.0 given that the experiment considers a single fixed amount for the mixture and the components are expressed as proportions. Under Name, enter a name for each mixture component. Suppose that each component can vary from 0 to 1. You can, however, specify lower limits for some or all of the components as in step 2. Click OK.

Illustration of Create Mixture Design dialog box opening another Components dialog box.

In the main dialog box, select Process Vars. Under Process Variables, select Number and specify 1. Enter the name of the factor and leave the other default options. Note that Minitab codes the low and high levels of the factor as “−1” and “1.”

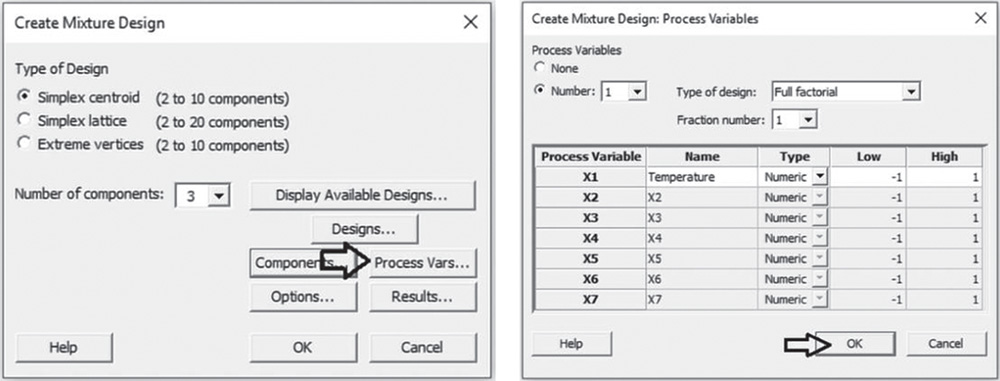
Illustration of Create Mixture Design dialog box opening another Process Variables dialog box.

Illustration of Create Mixture Design dialog box opening another Options dialog box.

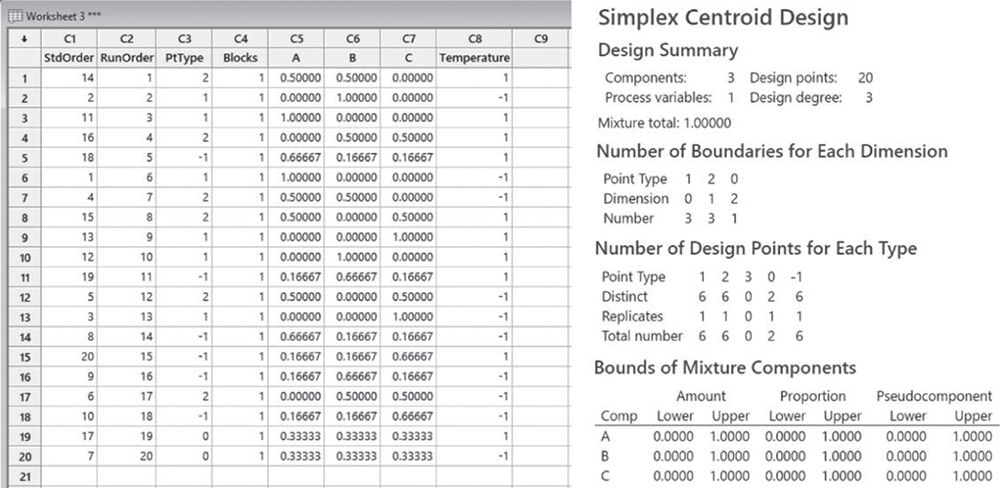
The design includes 20 design points. The table Number of Design Points for Each Type identifies each design point type. In the design we have six vertices (point type = 1), six double blends (point type = 2), two center points (point type = 0), and six axial points (point type = −1).

Illustration of worksheet 3 that shows the different parameters of simplex centroid design.

You can display the design to graphically check the experimental region.

Go to: Stat > DOE > Mixture > Simplex Design Plot

Under Components, check the option Select a triplet of components for a single plot. If you have more than three components in the mixture, you can select the option Generate plots for all triplets of components. Under Component Unit in Plot(s), check Proportion. Check the options Include process variables and Plot all level combinations. Click OK.

Illustration of simplex design plot dialog box and multiple simplex design plot in proportions.

You can see that the simplex centroid design has been generated at each level of the process variable.

4.3.1.4 Step 4 – Alternatively, Create a Simplex Centroid Design for a Mixture‐Amount Experiment

Suppose you now suspect the response is related to both the proportions inside the mixture and the total amount of the mixture. Minitab allows you to specify up to five different amounts. For example, suppose we need to evaluate two different amounts of the mixture equal to 10 and 12 g.

To create a simplex centroid design with multiple mixture amounts, go to: Stat > DOE > Mixture > Create Mixture Design

In Type of Design select Simplex centroid and in Number of components specify 3. Select Designs. Check the option Augment the design with axial points. In Number of replicates for the whole design specify 1 or, depending on available resources, enter how many times to perform each experimental run. You can also add replicates for specific design points, for example for a center point or a vertex point, by checking the option Number of replicates for the selected types of points. Remember that you can add replicates to the whole design later with Stat > DOE > Modify Design. Click OK.

Illustration of Create Mixture Design dialog box that opens Simplex centroid design dialog box.

In the main dialog box select Components. Check the option Multiple totals under Total Mixture Amount and specify the two amounts, 10 and 12 g. Under Name, enter a name for each mixture component. Note that in the table, the amounts for lower and upper limits must be specified only for the first total (10 g). Click OK.

Illustration of Create Mixture Design dialog box that opens Components dialog box.

Illustration of Create Mixture Design dialog box that opens Options dialog box.

Illustration of worksheet 4 that shows the different parameters of simplex centroid design.

You can display the design to graphically check the experimental region.

Go to: Stat > DOE > Mixture > Simplex Design Plot

Under Components, check the option Select a triplet of components for a single plot. If you have more than three components in the mixture, you can select the option Generate plots for all triplets of components. Under Component Unit in Plot(s), check Amount (or Proportion if you want to display the plot in proportions). Check the options Plot all mixture amounts. Click OK.

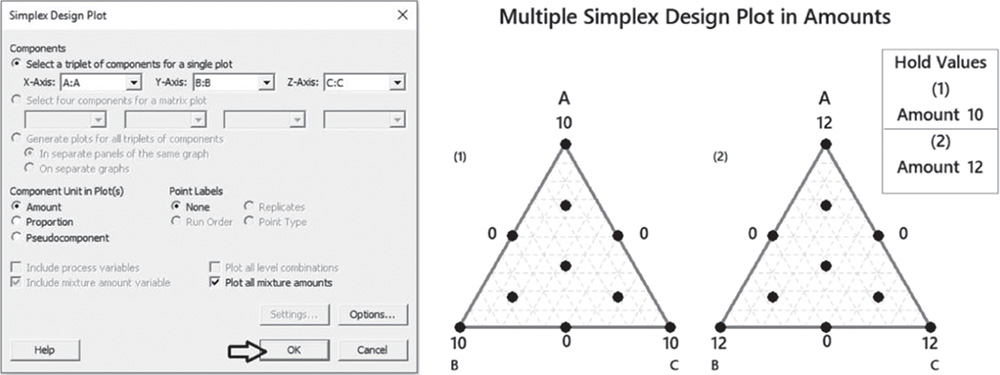
Illustration of simplex design plot dialog box and multiple simplex design plot in amounts.

You can see that the simplex centroid design has been generated at each level of the total amount of the mixture.

4.3.1.5 Step 5 – Alternatively, Create a Simplex Lattice Design for a Simple Mixture Experiment

Let us again consider a simple mixture experiment in which only the proportions of the three components are expected to be related to technical performance. For this purpose we will now create a simplex lattice design (Stat Tool 4.5), considering the three factors A, B, and C.

To create a simplex lattice design, go to: Stat > DOE > Mixture > Create Mixture Design

In Type of Design select Simplex lattice and in Number of components specify 3. Click on Display Available Designs to get an idea of the number of runs based on the design type, the number of components in the mixture and the degree of the lattice. Click OK.

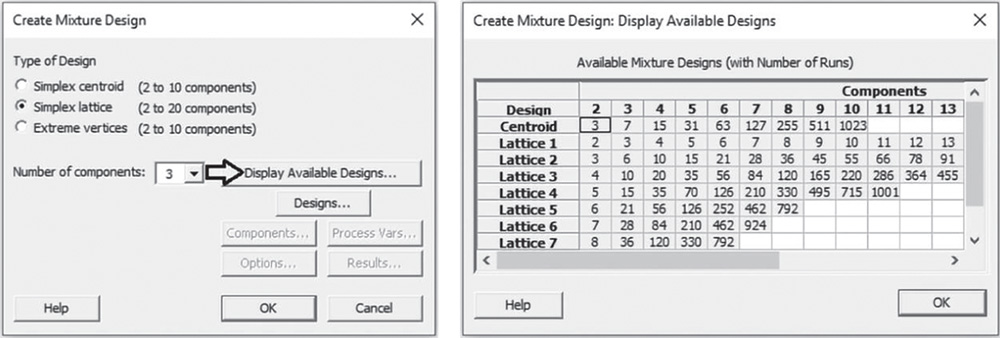Illustration of Create Mixture Design dialog box opening Display Available Designs dialog box. In the main dialog box select Designs. In Degree of lattice specify for example 3 in order to include the edge trisectors that are two‐blend mixtures in which one component makes up one‐third and a different component makes up two‐thirds of the mixture. Check the options Augment the design with center point and Augment the design with axial points. In Number of replicates for the whole design specify 1 or, depending on available resources, enter how many times to perform each experimental run. You can also add replicates for specific design points, for example for a center point or a vertex point, by checking the option Number of replicates for the selected types of points. Remember you can add replicates to the whole design later with Stat > DOE > Modify Design. Click OK.

Illustration of Create Mixture Design dialog box opening Simplex Lattice Design dialog box.

In the main dialog box select Components. Check the option Single total under Total Mixture Amount and leave the default value 1.0, given that the experiment considers a single fixed amount for the mixture and the components are expressed as proportions. Under Name, enter a name for each mixture component. Suppose that each component can vary from 0 to 1. You can, however, specify lower limits for some or all of the components. Click OK.

Illustration of Create Mixture Design dialog box opening Components dialog box.

Illustration of Create Mixture Design dialog box opening Components Options box.

The design includes 13 design points. The table Number of Design Points for Each Type identifies each design point type. In the design we have three vertices (point type = 1), six double blends (point type = 2), one center point (point type = 0) and three axial points (point type = −1).

You can display the design to graphically check the experimental region.

Go to: Stat > DOE > Mixture > Simplex Design Plot

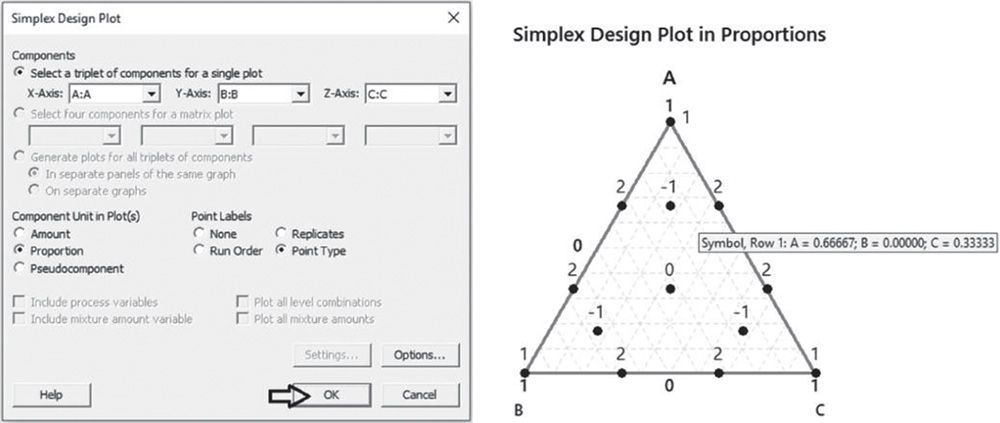
Illustration of worksheet 5 that shows the different parameters of simplex centroid design.

If you hover over the design points, Minitab displays the corresponding mixture. For example, the edge trisector indicated on the right corresponds to the two‐blend mixture (A = 0.67, B = 0, C = 0.33).

Stat Tool 4.5 Simplex Lattice Designs

A simplex lattice design considers design points arranged in a uniform way (lattice) in the simplex. For this kind of mixture designs we have to specify a parameter called the degree of the lattice. In a simplex lattice design for p components with a degree equal to m, the proportions assumed by each component take the m + 1 equally spaced values from 0 to 1:

For example, with three components in the simplex lattice design of degree 3, we have:

The design will consist of the following 10 design points (Figure 4.15):

3 vertices (pure mixtures);
6 two‐blend mixtures corresponding to the edge trisectors;
1 centroid

Figure 4.15 Simplex lattice design of degree 3 with p = 3 components.

Note that for some degrees the simplex lattice design does not include the centroid. In these cases it is possible to augment the basic design with the centroid.

Additionally, in order to have more complete mixtures inside the simplex, where the blends will consist of all mixture components, it is possible to augment the basic design with axial points.

The axial points are positioned along the axial axes a certain distance from the centroid. Generally, it is recommended that axial runs be placed midway between the centroid of the simplex and each vertex.

For example (Figure 4.16), with three components, expressed as proportions and varying from 0 to 1, the simplex lattice design of degree 3 augmented with axial points has the following 13 design points:

3 vertices (pure mixtures);
6 two‐blend mixtures corresponding to the edge trisectors;
1 centroid;
3 three‐blend mixtures corresponding to the axial points

Figure 4.16 Augmented simplex lattice design of degree 3 with p = 3 components.

4.3.1.6 Step 6 – Alternatively, Create an Extreme Vertices Design with Lower and Upper Limits for Components

Suppose that you have to specify lower and upper limits or only upper limits for some or all components of the mixture. For example, consider the following constraints on the component proportions: 0.05 ≤ A ≤ 0.25; 0.25 ≤ B ≤ 0.40; 0.50 ≤ C ≤ 0.70. In this case the experimental region is no longer a simplex and we can use an extreme vertices design (Stat Tool 4.7). Furthermore, suppose that we want to perform a maximum of 14 runs including some replicates.

To create an extreme vertices design, go to: Stat > DOE > Mixture > Create Mixture Design

In Type of Design select Extreme vertices and in Number of components specify 3. Select Designs. In Degree of design specify for example 2. Check the options Augment the design with center point and Augment the design with axial points. In Number of replicates for the whole design specify 1. Click OK.

Stat Tool 4.6 Constrained Simplex Designs

Until now we have considered mixture components expressed in proportions and varying from 0 to 1. Sometimes the researcher needs to specify lower bounds when any of the components must be in the mixture or upper bounds when the mixture cannot contain more than a specified proportion of an ingredient. In these cases the mixture design is said to be constrained.

If the researcher specifies only lower limits for some or all mixture components, the factor space is still a simplex, but it is inscribed inside the original simplex region.

For example, Figure 4.17 shows the simplex (the gray triangle) defined by specifying the following limits for three mixture components: x₁ ≱ 0.1, x₂ ≱ 0.2, x₃ ≱ 0.3. Note that with lower limits, the upper limits are rearranged and it is also possible to express the mixture components as pseudocomponents denoted by .

Figure 4.17 Constrained mixture design.

With the specification of lower limits, it is still possible to create a simplex design (centroid or lattice) because the constrained region is still a simplex.

With upper limits or both lower and upper limits for at least one of the components, the factor space is no longer a simplex. In these cases, extreme vertices designs (Stat Tool 4.7) can be used to select design points in the irregular factor space.

Stat Tool 4.7 Extreme Vertices Designs

In constrained designs (Stat Tool 4.6), the presence of upper bound constraints or both lower and upper bound constraints on the mixture components and/or the specification of linear constraints create a factor space that is no longer a simplex.

With this kind of constraints, you can't create simplex centroid or lattice designs. Instead, extreme vertices designs can be used for this type of mixture problem. Extreme vertices designs cover only a subportion or smaller space within the simplex to take into account component bounds and /or linear constraints.

Notice that when you specify lower and upper limits on:

An individual component, you are setting a component bound, for example: 0.2 ≤ x₁ ≤ 0.6.
A set of components, you are setting a linear constraint, for example: 0.3 ≤ x₁ + x₂ ≤ 0.6. Linear constraints can also be of the type: x₁ ≤ x₂.

For example, Figure 4.18 shows the factor space (the gray region) obtained by specifying the following component bounds: 0.1 ≤ x₁ ≤ 0.6.

Figure 4.18 Constrained mixture design.

Illustration of Create Mixture Design dialog box opening Extreme Vertices Design dialog box.

In the main dialog box select Components. Check the option Single total under Total Mixture Amount and leave the default value 1.0, given that the experiment considers a single fixed amount for the mixture and the components are expressed as proportions. Under Name, enter a name for each mixture component. Under Lower and Upper, specify the lower and upper limits for each component. Click OK.

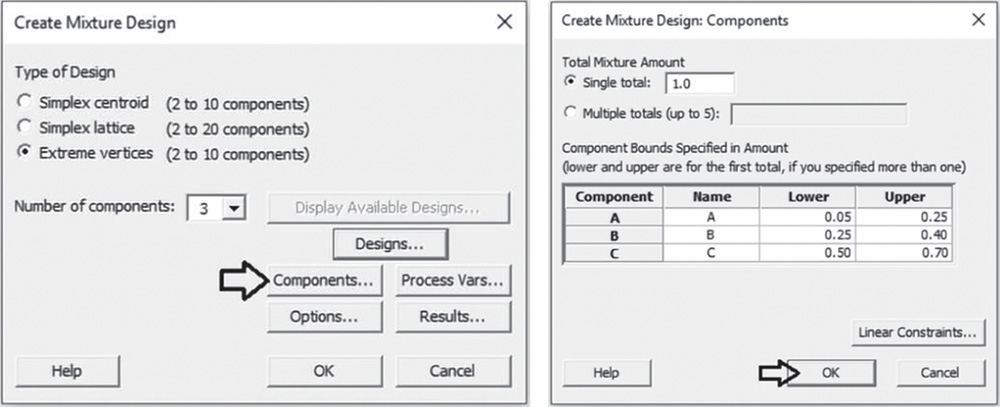
Proceed by clicking Options in the main dialog box and uncheck the option Randomize runs since for the moment, we just want to check the design. Then, when we have decided that the design is suitable for our needs, we will randomize the runs. Click OK in each dialog box and Minitab shows the design of the experiment in the worksheet, as well as some information in the Session window.

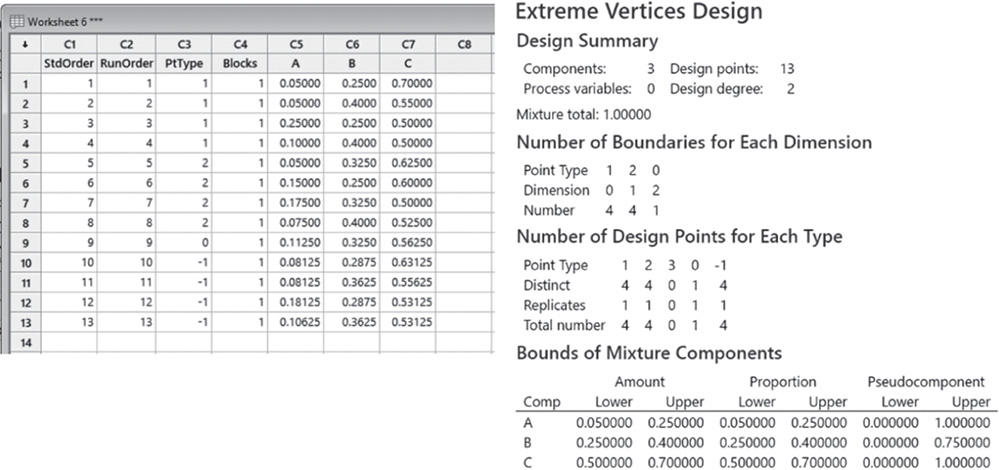
The design includes 13 design points. In the table Bounds of Mixture Components, you can see that Minitab created a pseudocomponent for each component to accommodate the specified constraints.

Illustration of worksheet 6 that shows the different parameters of simplex centroid design.

You can display the design to graphically check the experimental region.

Go to: Stat > DOE > Mixture > Simplex Design Plot

Under Components, check the option Select a triplet of components for a single plot. If you have more than three components in the mixture, you can select the option Generate plots for all triplets of components. Under Component Unit in Plot(s), check Proportion (or Pseudocomponent) and under Point Labels, select Point Type. Click OK.

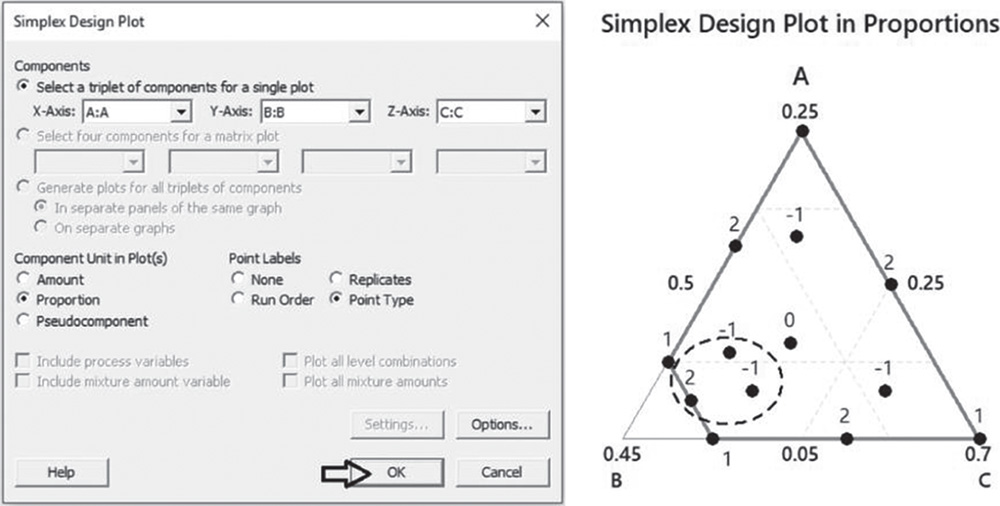
Illustration of Simplex Design Plot dialog box and graphical illustration of simplex design plot in proportions.

You can see that the region is not a simplex. Furthermore, you see that three design points inside the marked dotted oval are very close to each other and to other design points nearby. Given that we have to create a design with 14 design points that includes some replicates, we can try to select an optimal design from the basic extreme vertices design. An optimal design represents a design that is best according to some statistical criterion. It includes only a suitable subset of all combinations of factors (mixtures of components) in order to reduce the number of runs. For this reason, they are often used when there are some constraints in the number of runs to perform.

In our example, it would be desirable to keep all the design points of the basic design except the three points inside the dotted oval and then to augment the design with some replicates to obtain an optimal design with 14 runs. With Minitab, you can create an indicator column that identifies any experimental run that must be in the optimal design. This indicator column specifies a number for each design point. The sign of the number identifies whether an experimental run must be in the optimal design: a positive sign identifies a point that can be left out of the design, while a negative sign denotes a point that must remain in the optimal design.

To better identify the three design points that can be left out of the design, let's again create the simplex plot by displaying the run order of each design point.

Go to: Stat > DOE > Mixture > Simplex Design Plot

Under Components, check the option Select a triplet of components for a single plot. Under Component Unit in Plot(s), check Proportion (or Pseudocomponent) and under Point Labels, select Run Order. Click OK.

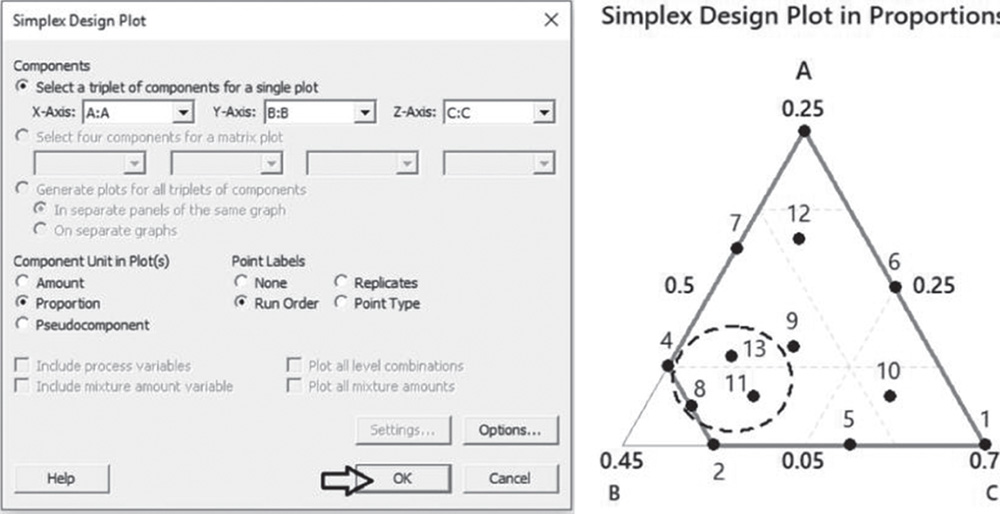
You can see that the three design points that can be left out of the design, have Run Order 8, 11, and 13 in the worksheet of the basic design.

Let's create the indicator column specifying “1” for the three points with Run Order 8, 11, and 13, and “−1” for all the remaining points. The worksheet will appear in the following way:

Illustration of worksheet 6 of a basic design that shows the three design points with Run Order 8, 11, and 13.

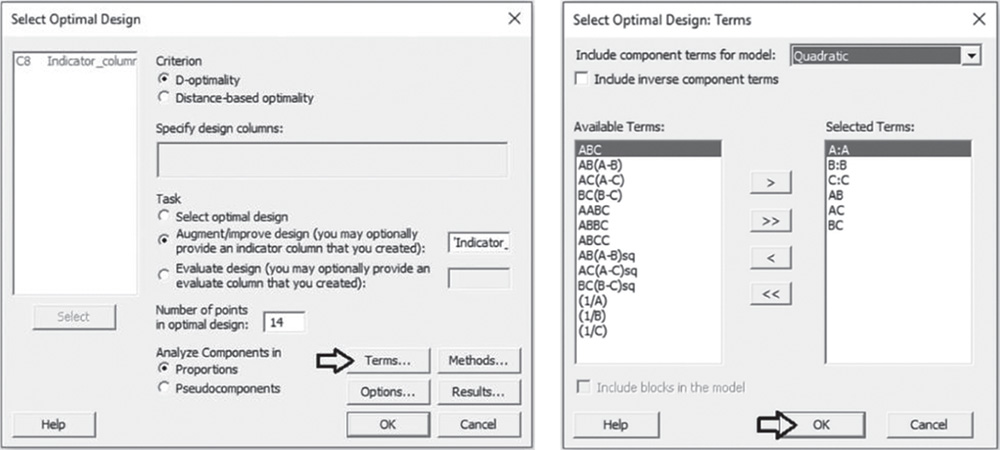
To select the optimal design, go to: Stat > DOE > Mixture > Select Optimal Design

Under Criterion, check the option D‐Optimality. Under Task, choose Augment/improve design and in the blank field select the indicator column. In Number of points in optimal design, specify 14. Click on Terms. In the next dialog box, beside Include component terms for model, specify Quadratic to detect curvatures if present. Click OK in each dialog box and Minitab shows the optimal design in a new worksheet, as well as some information in the Session window.

Illustration of Select Optimal Design dialog box that opens Terms dialog box.

You can display the design to graphically check the experimental region.

Go to: Stat > DOE > Mixture > Simplex Design Plot

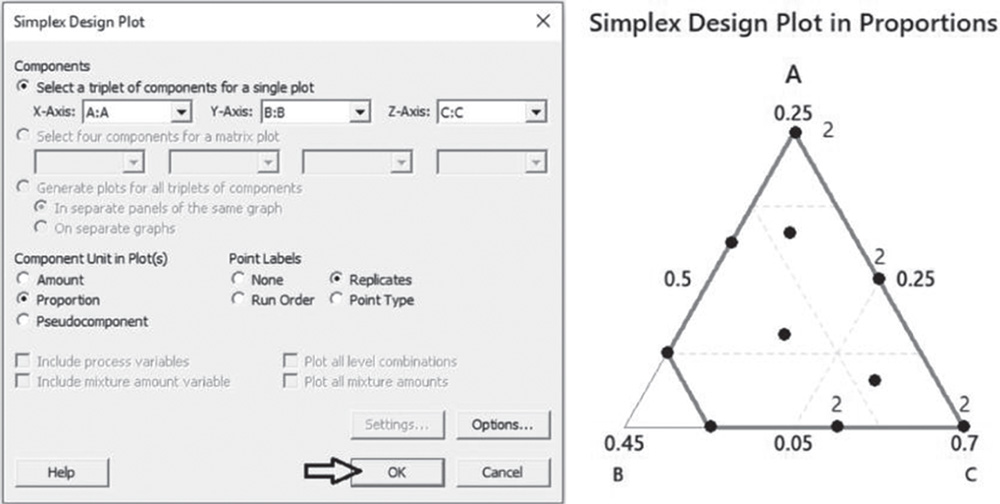
Illustration of Simplex Design Plot dialog box and a corresponding triangle representing simplex design plot in proportions.

You can see that the design includes 10 different design points and four of these runs (two vertices and two edge centers) are replicated and are denoted in the simplex plot by the number “2.”

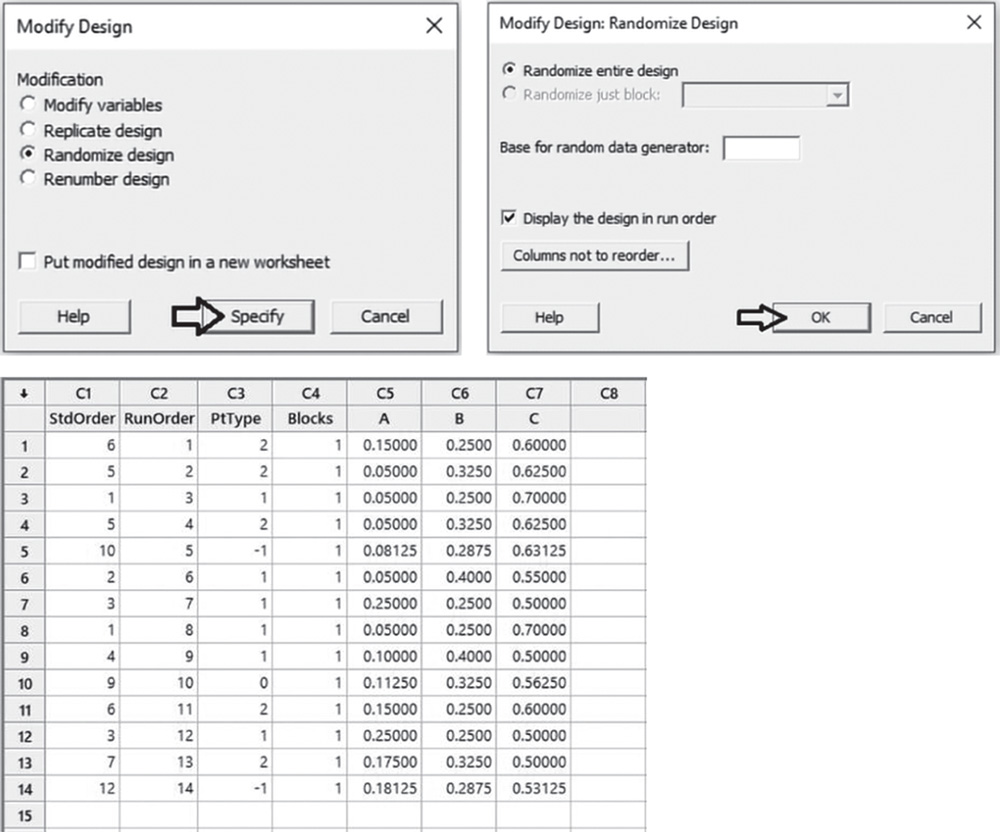
The last step is to randomize the runs. Before this step, we have to renumber the runs.

Go to: Stat > DOE > Modify Design

Under Modification, check the option Renumber design. Click OK.

Illustration of Modify Design dialog box.

Finally to randomize the runs, go to: Stat > DOE > Modify Design

Under Modification, check the option Randomize design. Select Specify and then click OK in each dialog box.

Illustration of Modify Design dialog box that opens Randomize Design dialog box. A corresponding worksheet is seen.

4.3.1.7 Step 7 – Alternatively, Create an Extreme Vertices Design with Linear Constraints for Components

Suppose that you have to specify one or more linear constraints for some or all components of the mixture. For example, suppose that the sum of the proportions of components A and B in the mixture must be between 0.3 and 0.6 (0.3 ≤ A + B ≤ 0.6) and that component C must always be no less than the proportion of component A (C ≱ B). In this case, the experimental region is no longer a simplex and we can use an extreme vertices design (Stat Tool 4.7).

To create an extreme vertices design, go to: Stat > DOE > Mixture > Create Mixture Design

Illustration of Create Mixture Design dialog box that opens Extreme Vertices Design dialog box.

In the main dialog box select Components. Check the option Single total under Total Mixture Amount and leave the default value 1.0, given that the experiment considers a single fixed amount for the mixture and the components are expressed as proportions. Under Name, enter a name for each mixture component. Under Lower and Upper, leave the default values 0 and 1. You can, however, specify lower and/or upper limits for the components. Select Linear Constraints.

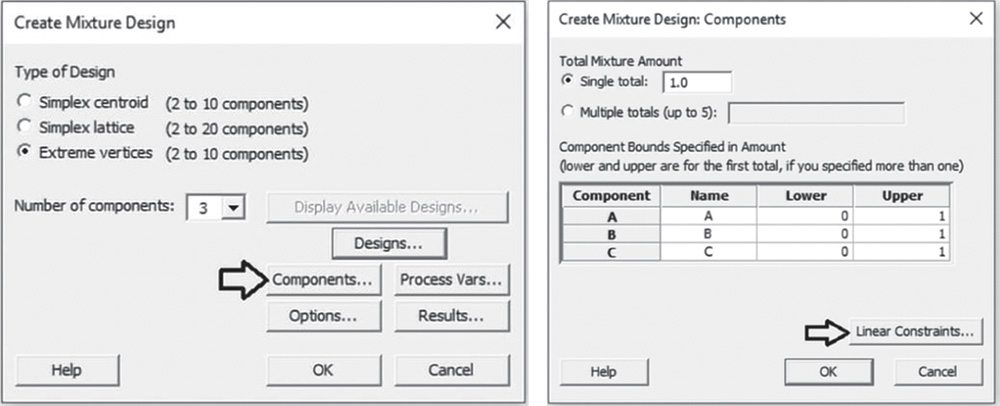
Enter the linear constraints by specifying a coefficient for each component of the mixture and a value for Lower and/or Upper, then click OK.

Illustration of Create Mixture Design: Components: Linear Constraints worksheet.

Proceed by clicking Options in the main dialog box and check the option Randomize runs. Click OK in each dialog box and Minitab shows the design of the experiment in the worksheet, as well as some information in the Session window.

Illustration of Create Mixture Design dialog box that opens corresponding Options dialog box.

The design includes 16 design points. In the table Bounds of Mixture Components, you can see that Minitab created a pseudocomponent for each component to accommodate the specified constraints.

Illustration of worksheet 1 that shows the different parameters of Extreme Vertices Design.

You can display the design to graphically check the experimental region.

Go to: Stat > DOE > Mixture > Simplex Design Plot

Under Components, check the option Select a triplet of components for a single plot. If you have more than three components in the mixture, you can select the option Generate plots for all triplets of components. Under Component Unit in Plot(s), check Proportion (or Pseudocomponent) and under Point Labels, select Point Type. Click OK.

Illustration of simplex design plot and corresponding simplex design plot in proportions diagram.

You can see that the region is not a simplex. If required you can decide to select an optimal design from the basic one as done previously in step 6.

4.3.1.8 Step 8 – Assign the Designed Factor Level Combinations (Design Points) to the Experimental Units and Collect Data for the Response Variable

Collect the data for the response variable, i.e. the technical performance measured on a scale of 0 to 70, following the order given in the column RunOrder in the chosen design. For example, for the extreme vertices design created in step 6, the first mixture to test will be the mixture with component A at level 0.15, component B at 0.25 and C at 0.60, where components are expressed as proportions.

Once all the designed mixtures have been tested, enter the recorded response values (technical performance index) in the worksheet containing the design. Now you are ready to proceed with the statistical analysis of the collected data.

4.3.2 Plan of the Statistical Analyses

Second‐order models can represent a suitable approximation for the unknown functional relationship to study the effects of mixture components on the response variable.

Let's proceed in the following way:

Step 1 – Perform a descriptive analysis (Stat Tool 1.3) of the response variables.
Step 2 – Fit a second‐order model to estimate the effects and determine the significant ones.
Step 3 – Optimize the response.
Step 4 – Examine the shape of the response surface and locate the optimum.

For the Mix‐Up Project, the dataset (File: Mix_Up_Project.xlsx) opened in Minitab appears as below.

The variables setting is the following:

Columns C1–C4 are related to the previous creation of the extreme vertices design.
Variables A, B, and C are the quantitative mixture components.
Variable Tech_Index is the quantitative response variable.

Column	Variable	Type of data	Label
C5	A	Numeric data	Proportion of component A of the mixture
C6	B	Numeric data	Proportion of component B of the mixture
C7	C	Numeric data	Proportion of component C of the mixture
C8	Tech_Index	Numeric data	Technical performance index

Mix_Up_Project.xlsx

4.3.2.1 Step 1 – Perform a Descriptive Analysis of the Response Variables

As the response is a quantitative variable, let's use a boxplot to describe how the technical performance index occurred in our sample, and calculate means and measures of variability to complete the descriptive analysis.

To display the boxplot, go to: Graph > Boxplot

Under One Y, check the graphical option Simple and in the next dialog box, select “Tech_Index” under Graph variables. Then click OK in the dialog box.

To change the appearance of a boxplot, use the tips in Chapter 2, Section 2.2.2.1 to histograms, as well as the following ones:

To display the boxplot horizontally: double‐click on any scale value on the horizontal axis. A dialog box will open with several options to define. Select from these options: Transpose value and category scales.
To add the mean value to the boxplot: right‐click in the area inside the border of the boxplot and select Add > Data display > Mean symbol.

Illustration of Boxplots opening a corresponding One Y, Simple boxplot.

To display the descriptive measures (means, measures of variability, etc.), go to:

In the dialog box, select “Tech_Index” in Variables, then click on Statistics to open a dialog box displaying a range of possible statistics to choose from. In addition to the default options, select Interquartile range and Range.

Illustration of Display Descriptive Statistics dialog box opening a corresponding Statistics dialog box.

4.3.2.1.1 Interpret the Results of Step 1

Technical performance data are slightly skewed with two outliers showing high values of performance. About 50% of the trials showed a performance score greater than 29.9 (the median, Stat Tool 1.6), and around 25%, greater than 34.8 (Q₃, Stat Tool 1.7). With respect to variability, the average distance of the response values from their mean (standard deviation) is about 15.9 (Stat Tool 1.9).

Graphical illustration of Boxplot of Tech_Index.

4.3.2.2 Step 2 – Fit a Second‐Order Model to Estimate the Effects and Determine the Significant Ones

Before analyzing the extreme vertices design, we must specify the mixture components within Minitab.

To define the mixture design, go to:

Under Components, select the factors A, B, and C. If there are any process variables (Section 4.3.1.3, step 3), you have to specify them under Process variables. If you have a mixture‐amount experiment (Section 4.3.1.4, step 4), under Mixture Amount select In Column and specify the column including the different mixture amounts. In our design we don't have process variables and the mixture amount is constant. Therefore, leave the field under Process Variables blank and under Mixture Amount, check the option Constant. Click Lower/Upper. For each component in the list, verify that the high and low limit settings are correct. If you have linear constraints (Section 4.3.1.7, step 7) select Linear Constraints and specify them. In our design we don't have linear constraints. Click OK.

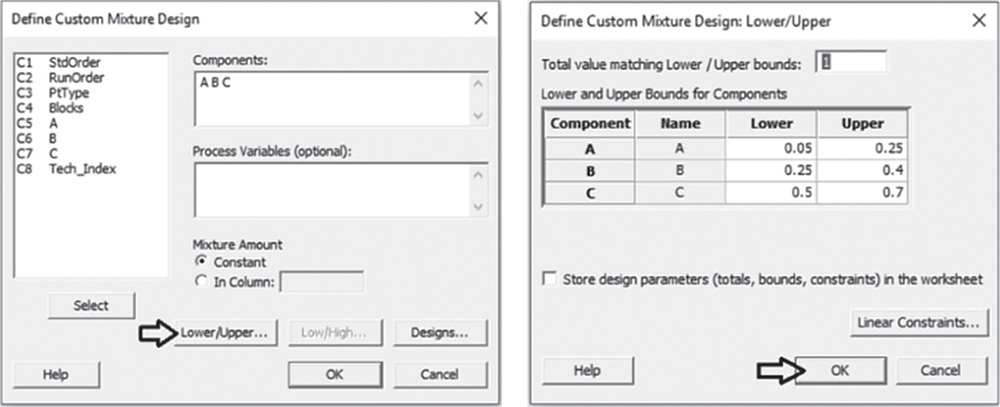
Illustration of Define custom mixture design dialog box that opens Lower/Upper dialog box.

In the main dialog box, click on Designs. Specify the columns corresponding to the standard order, run order, and point type of the runs. Click OK in each dialog box. Now you are ready to analyze the mixture design.

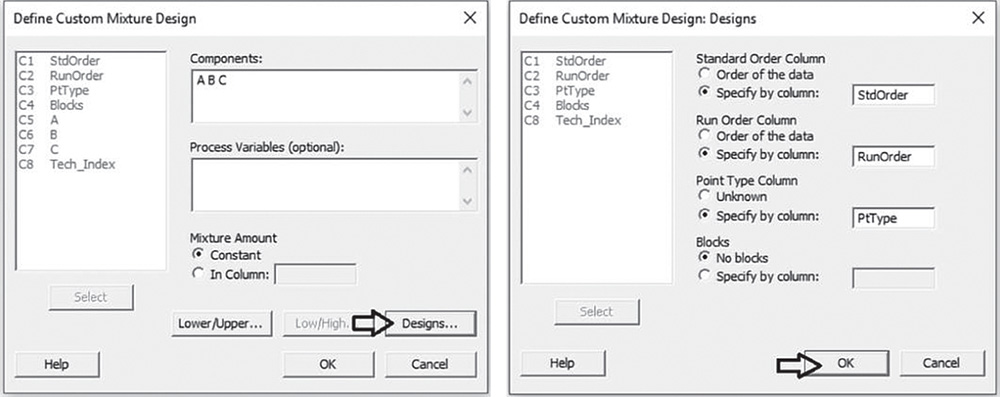
Illustration of Define custom mixture design dialog box that opens Designs dialog box.

To analyze the mixture design, go to:

Select the response variable “Tech_Index” under Responses. Under Type of Model, select Mixture components only. With process variables or different mixture amounts check the corresponding option. Under Analyze Components in, choose Pseudocomponents, then click on Terms. At the top of the next dialog box, in Include component terms for model, specify Quadratic. Click OK and in the main dialog box, choose Graphs. Under Residual Plots, choose Four in one. Click OK in each dialog box and Minitab shows the results of the analysis both in the Session window and through the required graphs.

4.3.2.2.1 Interpret the Results of Step 2

In the ANOVA table, we examine the p‐values to determine whether the associations between any terms in the model and the response are statistically significant. Remember that the p‐value is a probability that measures the evidence against the null hypothesis. Lower probabilities provide stronger evidence against the null hypothesis. The null hypothesis is that there is no association between the term and the response. Usually we consider a significance level α = 0.05, but in an exploratory phase of the analysis we may also consider a significance level equal to 0.10. When the p‐value is greater than or equal to alpha, we fail to reject the null hypothesis. When it is less than alpha, we reject the null hypothesis and claim statistical significance.

Regression for Mixtures: Tech_Index versus A; B; C Analysis of variance for Tech_Index (pseudocomponents)

Source	DF	Seq SS	Adj SS	Adj MS	F‐Value	p‐Value
Regression	5	3083.77	3083.8	616.75	22.85	0.000
Linear	2	2383.49	1572.2	786.09	29.12	0.000
Quadratic	3	700.28	700.3	233.43	8.65	0.007
A*B	1	0.20	163.7	163.68	6.06	0.039
A*C	1	146.25	163.2	163.24	6.05	0.039
B*C	1	553.83	553.8	553.83	20.52	0.002
Residual error	8	215.94	215.9	26.99
Lack‐of‐fit	4	111.67	111.7	27.92	1.07	0.474
Pure error	4	104.27	104.3	26.07
Total	13	3299.71

The table does not display p‐values for the linear terms of the components in mixture experiments because of the dependence between the components. Additionally, the model does not include a constant because it is incorporated into the linear terms.

If an interaction term that includes only mixture components shows a p‐value less than the significance level, the association between the blend of components and the response is statistically significant.

If your model includes process variables, significant interaction terms that include components and the process variables indicate that the effect of the components on the response variable depends on the process variables.

Looking at the ANOVA table, all the interaction terms between mixture components show a p‐value less than 0.05. This means that the mean technical performance index for the two‐blend mixture is statistically different from the value you would obtain by calculating the simple mean of the response variable for each pure mixture.

Note that in the ANOVA table, Minitab displays the lack‐of‐fit test when your data contain replicates. This test helps investigators to determine whether the model accurately fits the data. Its null hypothesis states that the model accurately fits the data. As usual, compare the p‐value to your significant level α. If the p‐value is less than α, reject the null hypothesis and conclude that the lack of fit is statistically significant. If the p‐value is larger than α, you fail to reject the null hypothesis and you can conclude that the lack of fit is not statistically significant.

In our example, the p‐value (0.474) is greater than 0.05: we conclude that there is no strong evidence of lack of fit. Lack‐of‐fit can occur if important terms such as interactions are not included in the model or if the fitted model shows several unusually large residuals (Stat Tool 2.9).

In addition to the results of the analysis of variance, Minitab displays some other useful information in the Model Summary table. Model summary

S	R‐sq	R‐sq(adj)	PRESS	R‐sq(pred)
5.19542	93.46%	89.37%	925.580	71.95%

The quantity R‐squared (R‐sq, R²) is interpreted as the percentage of the variability among technical performance data, explained by the terms included in the ANOVA model.

The value of R² varies from 0 to 100%, with larger values being more desirable.

The value of S is a measure of the variability of the errors that we make when we use the ANOVA model to estimate the performance data. Generally, the smaller it is, the better the fit of the model to the data.

Before proceeding with the results reported in the Session window, take a look at the residual plots. A residual represents an error that is the distance between an observed value of the response and its estimated value by the ANOVA model. The graphical analysis of residuals based on residual plots helps you discover possible violations of the ANOVA underlying assumptions (Stat Tools 2.8, 2.9).

A check of the normality assumption could be made looking at the histogram of the residuals (lower left), but with small samples, often the histogram shows irregular shape.

The normal probability plot of the residuals may be more useful. Here we can see a tendency of the plot to follow the straight line.

Graphical illustration of Residual Plots for Tech_Index.

Estimated regression coefficients for Tech_Index (pseudocomponents)

Term	Coef	SE Coef	t‐Value	p‐Value	VIF
A	26.74	3.60	*	*	1.68
B	37.49	9.09	*	*	5.38
C	64.95	3.59	*	*	1.86
A*B	−66.6	27.1	−2.46	0.039	3.25
A*C	−41.6	16.9	−2.46	0.039	1.65
B*C	−109.9	24.3	−4.53	0.002	3.81

The other two graphs (Residuals versus Fits and Residuals versus Order) seem unstructured, thus supporting the validity of the ANOVA assumptions. In the Residual versus Fits graph, we notice the two ouliers.

Returning to the Session window, we find two tables of coefficients expressed as pseudocomponents and as proportions. Look at the sign of the coefficients of the interactions of two components. Negative coefficients indicate that the two components act against each other. That is, the mean response value for the two‐component blend is less than the value obtained by calculating the simple mean of the response variable for each pure mixture.

Estimated regression coefficients for Tech_Index (component proportions)

Term	Coef
A	463.82
B	1038.56
C	457.53
A*B	−1665.42
A*C	−1040.08
B*C	−2748.19

Positive coefficients indicate that the two components act in synergy. That is, the mean response value for the two‐component blend is greater than the value you would obtain by calculating the simple mean of the response variable for each pure mixture.

4.3.2.3 Step 3 – Optimize the Response

After fitting the model, additional analyses can be carried out to find the optimum set of mixture components that optimizes the response (Stat Tool 3.8).

To optimize the response variable, go to:

In the table, under Goal, select one of the following options for the response:

Do not optimize: Do not include the response in the optimization process.
Minimize: Lower values of the response are preferable.
Target: The response is optimal when values meet a specific target value.
Maximize: Higher values of the response are preferable.

In our case study the goal is to maximize the technical performance: choose Maximize from the drop‐down list and click Setup. In the next window you need to specify a response target and lower or upper bounds depending on your goal (Stat Tool 3.8).

If your goal is to maximize the response (larger is better), you need to specify the lower bound and a target value. You may want to set the lower value to the smallest acceptable value and the target value at the point of diminishing returns, i.e. a point at which going above its value does not make much difference. If there is no point of diminishing returns, use a very high target value.
If your goal is to target a specific value, you should set the lower value and upper value as points of diminishing returns.
If the goal is to minimize (smaller is better), you need to specify the upper bound and a target value. You may want to set the upper value to the largest acceptable value and the target value at the point of diminishing returns, i.e. a point at which going below its value does not make much difference. If there is no point of diminishing returns, use a very small target value.

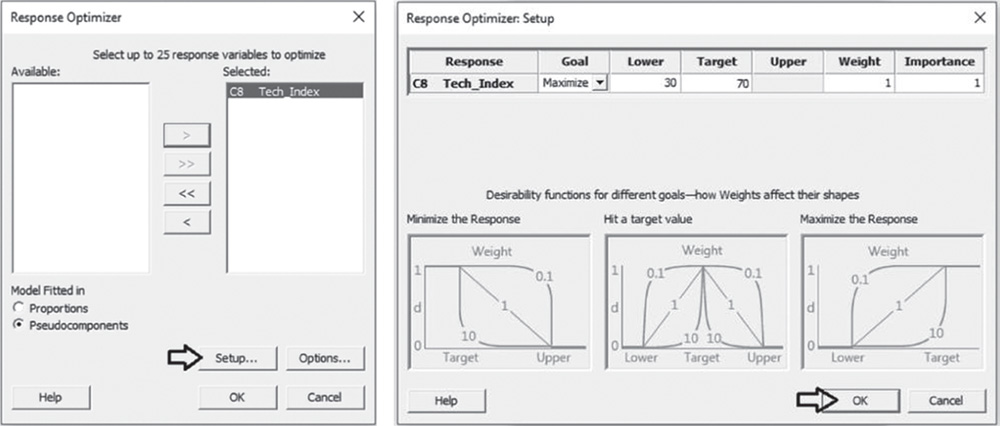
Illustration of Response Optimizer that opens a corresponding Setup dialog box.

In our example, we can set Lower at 30 and the Target at 70.

In our example, leave Weight and Importance equal to 1. Click OK in each dialog box. In the optimization plot, Minitab will display the optimal solution, i.e. the component setting which maximizes the composite desirability.

The optimization plot shows how different component settings affect the response. The vertical lines on the graph represent the current component settings. The numbers displayed at the top of a column show the current mixture (in red). The horizontal blue lines and numbers represent the responses for the current mixture. The optimal solution is plotted on the graph and serves as the initial point. The settings can then be modified interactively, to determine how different mixtures affect the response, by moving the red vertical lines corresponding to each component. To return to the initial settings, right‐click and select Navigation and then Reset to Initial Settings.

4.3.2.3.1 Interpret the Results of Step 3

The optimization plot is a useful tool to explore the sensitivity of the response variable to changes in the component settings and in the neighborhood of a local solution, for example the optimal one.

Graphical illustration of response optimization plot.

The Session window displays:

information about the boundaries, weight, and importance for the response variable (Parameters);
the solution that maximizes the response (Global Solution);
the fitted response for the global solution and the value of the desirability function.

For technical performance data, the global solution has component A set at 0.05, component B at 0.25 and C at 0.70 (components are expressed as proportions). For this mixture the fitted response (mean technical performance index) is equal to 64.9. The composite desirability (0.87) is quite close to 1 denoting a satisfactory overall achievement of the specified goal.

4.3.2.4 Step 4 – Examine the Shape of the Response Surface and Locate the Optimum

Graphic techniques such as contour, surface, and overlaid plots help us to examine the shape of the response surface in regions of interest. Through these plots, you can explore the potential relationship between pairs of factors and the responses. You can display a contour, a surface or an overlaid plot considering two factors at a time, while setting the remaining factors to predefined levels. With contour and surface plots, you consider a single response; in overlaid plots, you can consider more than one response.

To display the contour and surface plots, go to: Stat > DOE > Mixture > Contour/Surface Plots

Choose Contour plot and click Setup. In the dialog box, select the response “Tech_Index” beside Response. Under Components or Process Variables, check the option Select a triplet of components for a single plot. If you have more than three components in the mixture, you can select the option Generate plots for all triplets of components. Under Component Unit in Plot(s), check Proportion. Click Contours, and under Data Display, choose Contour lines and Symbols at design points. Click OK in the last two dialog boxes. In the main dialog box select Surface Plot and click Setup.

Illustration of Contour plots dialog box that opens two Contours dialog boxes.

In the dialog box, select the response “Tech_Index” in Response. Under Components or Process Variables, check the option Select a triplet of components for a single plot. If you have more than three components in the mixture, you can select the option Generate plots for all triplets of components. Under Component Unit in Plot(s), check Proportion. Click OK in each dialog box.

Illustration of Contour/surface plots dialog box that opens Surface dialog box.

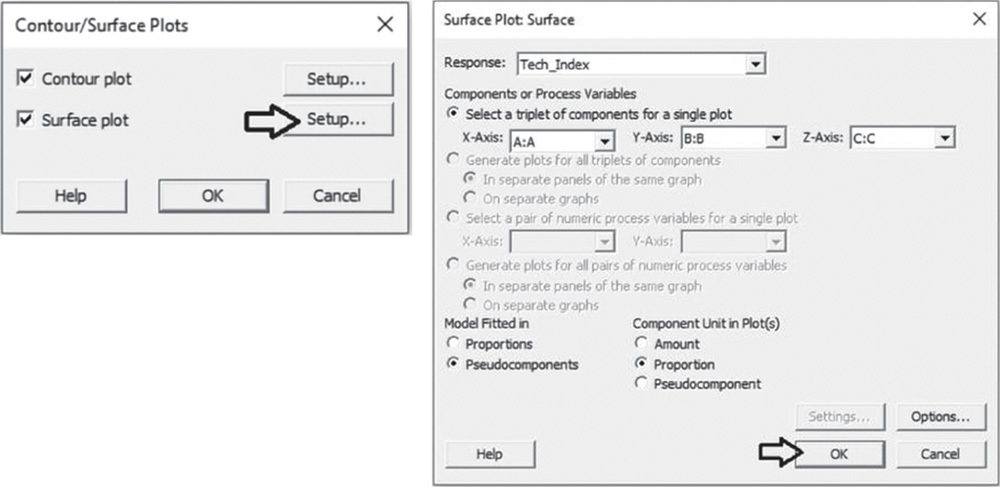
To change the appearance of the surface plot, double‐click on any point inside a surface.

4.3.2.4.1 Interpret the Results of Step 4

In the contour plot, the technical performance index is represented by different level curves. Double‐click on any point in the frame and select Crosshairs to interactively view variations in the response. In the surface plot the performance index is represented by a smooth surface. Both plots show how the component proportions are related to the performance. To maximize performance, researchers should choose proportions for the components in the lower right corner of the design space where the performance index is highest. It is relatively easy to see that the optimum is very close to 8 for additive A and to 7 for additive B, and to explore how the technical performance changes while increasing or decreasing factor levels.

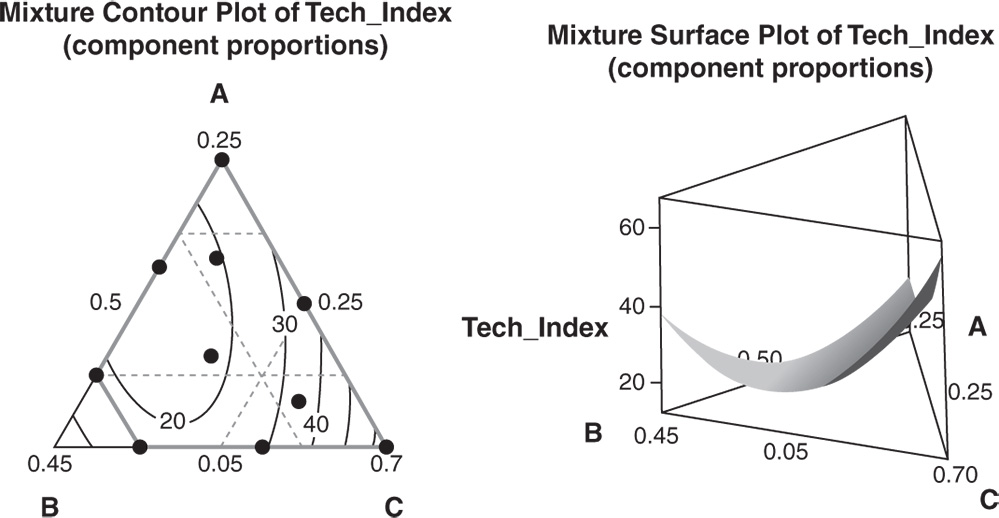
Graphical illustration of Mixture Contour Plot of Tech_Index and Mixture Surface Plot of Tech_Index.

In the contour plot the solid gray contour represents the design space for this mixture design. However, you can see that the plot extends beyond the design space. In the surface plot the boundaries of the design space are not shown. Generally, you should use proportions that are in the design space because the relationships between the variables are uncertain outside the design space.

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 4 Other Topics in Product Development and Optimization: Response Surface and Mixture Designs

Create new playlist

Sign In

Sign Up

4.1 Introduction

4.2 Case Study for Response Surface Designs: Polymer Project

4.2.1 Plan of the Experimental Design

4.2.1.1 Step 1 – Create a CCD

4.2.1.2 Step 2 – Alternatively, Create a Face‐Centered CCD

4.2.1.3 Step 3 – Alternatively, Create a Box‐Behnken Design

4.2.1.4 Step 4 – Assign the Designed Factor Level Combinations to the Experimental Units and Collect Data for the Response Variable

4.2.2 Plan of the Statistical Analyses

4.2.2.1 Step 1 – Perform a Descriptive Analysis of the Response Variables

4.2.2.1.1 Interpret the Results of Step 1

4.2.2.2 Step 2 – Fit a Second‐Order Model to Estimate the Effects and Determine the Significant Ones

4.2.2.2.1 Interpret the Results of Step 2

4.2.2.3 Step 3 – If Need Be, Reduce the Model to Include the Significant Terms

4.2.2.3.1 Interpret the Results of Step 3

4.2.2.4 Step 4 – Optimize the Response

4.2.2.4.1 Interpret the Results of Step 4

4.2.2.5 Step 5 – Examine the Shape of the Response Surface and Locate the Optimum

4.2.2.5.1 Interpret the Results of Step 5

4.3 Case Study for Mixture Designs: Mix‐Up Project

4.3.1 Plan of the Experimental Design

4.3.1.1 Step 1 – Create a Simplex Centroid Design for a Simple Mixture Experiment

4.3.1.2 Step 2 – Alternatively, Create a Simplex Centroid Design for a Simple Mixture Experiment with Lower Limits for Components

4.3.1.3 Step 3 – Alternatively, Create a Simplex Centroid Design for a Mixture‐Process Variable Experiment

4.3.1.4 Step 4 – Alternatively, Create a Simplex Centroid Design for a Mixture‐Amount Experiment

4.3.1.5 Step 5 – Alternatively, Create a Simplex Lattice Design for a Simple Mixture Experiment

4.3.1.6 Step 6 – Alternatively, Create an Extreme Vertices Design with Lower and Upper Limits for Components

4.3.1.7 Step 7 – Alternatively, Create an Extreme Vertices Design with Linear Constraints for Components

4.3.1.8 Step 8 – Assign the Designed Factor Level Combinations (Design Points) to the Experimental Units and Collect Data for the Response Variable

4.3.2 Plan of the Statistical Analyses

4.3.2.1 Step 1 – Perform a Descriptive Analysis of the Response Variables

4.3.2.1.1 Interpret the Results of Step 1

4.3.2.2 Step 2 – Fit a Second‐Order Model to Estimate the Effects and Determine the Significant Ones

4.3.2.2.1 Interpret the Results of Step 2

4.3.2.3 Step 3 – Optimize the Response

4.3.2.3.1 Interpret the Results of Step 3

4.3.2.4 Step 4 – Examine the Shape of the Response Surface and Locate the Optimum

4.3.2.4.1 Interpret the Results of Step 4

Table of Contents for
4 Other Topics in Product Development and Optimization: Response Surface and Mixture Designs