Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

2
The Screening Phase

2.1 Introduction

In the initial stages of development of a new consumer product, a team is generally faced with many options and it is difficult to screen without the risk of missing opportunities to find preferred consumer solutions. When making crucial decisions regarding the next steps to take in product development, it is important to identify suitable statistical tools. Such tools make it possible to combine scientific expertise with data analytics capability and to support the understanding of each factor's relevance in providing an initial indication of possible synergistic effects among different factors. This can generally be achieved with relatively simple techniques, such as factorial designs, and analysis of the results through ANOVA (ANalysis Of VAriance).

This chapter is a guide for developers to properly organize a factorial experimental design through proper randomization, blocking, and replication (Anderson, M. J. and Whitcomb, P. J., 2015). It also provides suggestions on how to reduce variability and analyze data to achieve the best outcome.

A concrete example of product development is provided, looking at an air freshener and consumer preferences regarding constituent oils.

Specifically, this chapter deals with the following:

Topics	Stat tools
Introduction to DOE (Design Of Experiments) and guidelines for planning and conducting experiments	2.1, 2.6
Factors, levels, and responses	2.1
Screening experiments and factorial designs	2.2
Basic principles of factorial designs (randomization, blocking, replication)	2.3, 2.4, 2.5
ANOVA (ANalysis Of VAriance)	2.7
Model assumptions for ANOVA	2.8
Residual analysis	2.9

2.2 Case Study: Air Freshener Project

An air freshener project aims to introduce a new scented oil to provide consistent and long‐lasting fragrance to homes. Six oils have to be tested to determine if there are any consumer perceived differences among different combinations of the fragrances. Expert panelists will test different combinations of oils by assigning them a liking score varying from 1 (dislike extremely) to 5 (like extremely). We need to plan and analyze an experimental study in order to identify which oils affect consumers' preferences.

2.2.1 Plan of the Screening Experiment

During an experiment, investigators select some factors to systematically vary in order to determine their effect on a response variable (Stat Tool 2.1). For the present study:

The six oils represent the key factors.
The liking score represents the response variable.

Stat Tool 2.1 Experiments, Factors, Responses

Experiments are used to study the performance of a process so it can be systematically improved (Box, G. E. P., Hunter, J. S., and Hunter, W. G., 2005). Think about the process as a combination of conditions (procedures, materials, machines, and more) called factors that transforms an input into an output with desirable properties we can measure as response variables. Some of the process conditions are controllable by the experimenter (controllable factors), whereas others are uncontrollable (Figure 2.1).

Figure 2.1 Process variables and conditions.

An experiment is generally a series of trials where the researcher intentionally varies one or more controllable factors, to observe changes in the output response and determine which factors affect the responses.

Factors and responses are statistical variables (Stat Tool 1.1), i.e. characteristics measured or controlled by the researcher on a sample of experimental units (Stat Tool 1.2). For controlled factors the experimenter chooses only a few qualitative categories or numeric values, called levels, to test in the experiment. Responses are quantitative variables, i.e. measurable characteristics on which factors may have an effect.

Example 2.1. In a manufacturing process of plastic textile products, we control two factors on a sample of specimens (experimental units): type of additive (2 levels) and temperature (3 levels), and we measure tensile strength (response) to rate the fibers' ability to withstand stress (Figure 2.2).

Figure 2.2 Response, factors, and levels.

Suppose we know very little about consumers' preferences in relation to these oils and their combinations. At the beginning of an experimental study, if researchers have to investigate many factors, screening experiments based on factorial designs considering k factors, each at only two levels, are widely used to identify the key factors affecting responses. This also reduces the number of experimental conditions to test (also called runs). These designs are called two‐level factorial designs (Stat Tool 2.2) and may be:

Full (all combinations of the factors' levels are tested);
Fractional (only a subset of all combinations is tested).

With fractional factorial designs, the experimenter can further reduce the number of runs to test, if they can reasonably assume that certain high‐order interactions among factors are negligible.

In our example, as the number of potential input factors (the six oils) is large, we consider a two‐level factorial design selecting the two levels: “absent” and “present” for each oil.

We will initially construct a full factorial design and then a fractional design in order to reduce the number of runs.

As two expert panelists will test the selected combinations of oils, assigning them a liking score from 1 to 5, panelists represent a blocking factor with two levels (Stat Tool 2.4): each panelist is a block.

Blocking is a technique for dealing with known and controllable nuisance factors, i.e. variables that probably have some effect on the response but are of no interest to the experimenter. Nuisance factors' levels are called blocks.

When feasible, the experiment should include at least two replicates of the design, i.e. the researcher should run each factor level combination at least twice. Replicates are multiple independent executions of the same experimental conditions (Stat Tool 2.5). As we have two blocks (the two panelists), this leads us to have two replicates of each run.

Stat Tool 2.2 DOE, Factorial Designs, Screening Experiments

DOE (Draper, N. R. and Pukelsheim F., 1996; Montgomery, D. C., 2008) and Statistical Analysis of the experimental data (Yandel, B. S., 1997) are two aspects of any experimental problem: the first refers to the planning of the experiment, the second to the statistical methods to be applied to the collected data to draw valid and objective conclusions.

When we have more than one factor, the correct approach is to plan a factorial experiment in which factors vary simultaneously, instead of one at a time. Factorial designs enable the researcher to investigate whether each factor has an effect on the response (main effect) and whether the factors interact (interaction effect), where an interaction exists between, for example, two factors if the effect of one factor on the response is not the same for all the levels of the other factor.

The experimental conditions, also called treatments or runs, tested on a sample of experimental units, are represented by:

Each level of the factor, with only one factor;
Each combination of factor levels, otherwise.

The entire set of runs is the design. See Figure 2.3 in reference to Example 2.1.

Figure 2.3 Factors, levels, and treatments.

$Illustration of full and fractional designs and treatments.$

Figure 2.4 Full and fractional designs and treatments.

As the number of factors increases, the number of runs increases rapidly, making the experiment too expensive or time consuming to execute. However, the researcher can decide to run all possible treatments by planning a full factorial design or only a suitable subset of the runs with a fractional factorial design (Figure 2.4).

In a full factorial design all main effects and interactions can be estimated, but with many factors and/or many levels, this may result in a prohibitive number of runs (Figure 2.5).

In a fractional factorial design some of the effects will be confounded (aliased), but the number of runs is reduced to a manageable size minimizing time and cost (Kounias, S. and Salmaso, L., 1998).

In the early stages of an experiment, when many factors are likely to be investigated, screening experiments with factorial designs considering k factors, each at only two levels, are widely used to identify the key factors affecting responses. These levels may be quantitative (e.g. two values of temperature) or qualitative (e.g. two machines, “high” and “low” levels of a factor, or the presence or absence of a factor). These are called two‐level factorial designs and may be full (also referred to as 2^k factorial designs) or fractional. After detecting key factors, the experimenter can proceed with a general factorial design increasing the number of levels to optimize responses.

$Schematic of the advantages and disadvantages of full and fractional designs treatments.$

Figure 2.5 Advantages and disadvantages of full and fractional designs treatments.

Stat Tool 2.3 Basic Principles of Factorial Designs: Randomization

The three basic principles of experimental designs are randomization, blocking, and replication.

By randomization we mean that both the allocation of the experimental units to treatments and the order in which the individual runs are to be performed, are randomly determined. Computer software programs help the researcher to plan and construct a factorial design and generally present the runs in random order by default (Figure 2.6).

Figure 2.6 Randomized design for plastic tensile strength (Example 2.1).

Many statistical methods of data analysis require response measurements (also called observations) to be independent. Randomization usually makes this assumption valid.

Randomization also helps in averaging or balancing out effects of extraneous factors (noise factors), that could have an effect on the response and that are difficult to be measured by the experimenter or are not known (Figure 2.7).

Figure 2.7 Advantages of randomization.

Stat Tool 2.4 Basic Principles of Factorial Designs: Blocking

Blocking is a technique for dealing with known and controllable nuisance factors, blocking out their potential effect on the response. A nuisance factor is a factor that probably has some effect on the response, but it's of no interest to the experimenter (e.g. time, batches of material, operators, machines). However, as it can add variability in the response, it needs to be taken into account, and improve the precision in the analysis (Figure 2.8).

Typically, each level of the nuisance factor becomes a block. If a complete replicate of the basic experiment is conducted in each block, the experiment is called randomized complete block design (RCBD) (Figure 2.9).

Figure 2.8 Advantages of blocking.

Figure 2.9 RCBD for plastic tensile strength.

Stat Tool 2.5 Basic Principles of Factorial Designs: Replication

By replication, or replicates, we mean that we assign each factor combination to more than one experimental unit. In other words, replicates are multiple independent executions of the same experimental conditions. They are considered separate runs, processed individually in the experiment, and should be run in random order.

Example 2.1. Plastic tensile strength.
For example, runs 9 and 3 are two replicates of the combination “additive A” and “High temperature” (Figure 2.10).

Figure 2.10 Presence of replications for plastic tensile strength (Example 2.1).

Replication allows the experimenter to obtain an estimate of the experimental error required in the statistical analysis of data in determining whether observed differences are really statistically different. It also allows us to calculate a more precise estimate of the true mean response for factors' levels (Figure 2.11).

Note that a replicate is not a repeated or duplicate measurement of the response. Repeated measurements often reflect the inherent variability in the measurement system.

Example 2.2. The cleaning performance (response) of three formulations of a stain removal product (factor) is measured at four different positions on each piece of a sample of fabrics. The individual measurements for each position on a piece of fabric are not replicates but repeated measurements, because the four positions were processed together in the experiment, receiving the same treatment simultaneously. With repeated measurements, their average is usually the correct response variable to analyze.

Figure 2.11 Advantages of replication.

To create the design for our screening experiment, let's proceed in the following way:

Step 1 – Create a full factorial design.
Step 2 – Alternatively, choose the desired fractional design.
Step 3 – Assign the designed combinations of factor levels to the experimental units and collect data for the response variable.

2.2.1.1 Step 1 – Create a Full Factorial Design

Let's begin to create a full factorial design, considering two levels (absent/present) for each factor and a blocking factor with two blocks (the two panelists).

To create a full factorial design, go to:

Choose 2‐level factorial (default generators) and in Number of factors, specify 6. Click on Designs. In the next dialog box, select Full Factorial. You can see that this design will include 64 factor‐level combinations. In Number of replicates for corner points and in Number of blocks, specify 2. Click OK, and in the main dialog box select Factors. Enter the names of the factors (Oil1 to Oil6); select Text in Type as they are categorical variables, and specify NO and YES in Low and High to represent respectively the “absence” and the “presence” of each factor.

Proceed by clicking Options in the main dialog box and check the option Randomize runs, so that both the allocation of the experimental units and the order of the individual runs will be randomly performed (Stat Tool 2.3). Clicking OK in the main dialog box, Minitab shows the design of the experiment in the worksheet (only the first five runs are shown here as an example), adding some extra columns that are useful for the statistical analysis, and some information on the design in the Session window.

Illustration of the design of the first five runs of an experiment in the worksheet.

2.2.1.2 Step 2 – Alternately, Choose the Desired Fractional Design

Suppose we need to construct a fractional design to reduce the number of runs to test.

To create a fractional factorial design, go to:

Choose 2‐level factorial (default generators) and in Number of factors specify 6. Click on Designs. In the next dialog box, you can select three types of fractional designs, respectively, with 8, 16, and 32 runs for each block. These designs correspond to specific fractions of the full design (e.g. 1/8, 1/4, or 1/2 fraction). Fractional designs can't estimate all the main effects and interactions among factors separately from each other: some effects will be confused (aliased) to other effects. The way in which the effects are aliased is described by the so‐called “Design Resolution.” By choosing fractional designs that have the highest resolution, the experimenter can usually obtain information on the main effects and low‐order interactions, while assuming that certain high‐order interactions are negligible. In our case, let's select, for example, a 1/2 fraction design of Resolution VI. You can see that this design will include 32 factor‐level combinations for each block. In Number of replicates for corner points and in Number of blocks specify 2. Click OK, and in the main dialog box select Factors. Enter the names of the factors (Oil1 to Oil6); select Text in Type, as they are categorical variables, and specify NO and YES in Low and High to represent, respectively, the “absence” and the “presence” of each factor.

Proceed by clicking Options in the main dialog box and check the option Randomize runs as before. Clicking OK in the main dialog box, Minitab shows the design in a new worksheet and more information is in the session panel. Note that for the fractional design, in the Session window the alias structure lists the aliasing between main effects and interaction. For example, A + BCDEF means that factor A (Oil1) is aliased with the four‐order interaction BCDEF; we will estimate the effect of (A + BCDEF), but if we can reasonably assume that the interaction BCDEF is negligible, we will assign the total estimate of the effect to the main effect A.

Illustration of Minitab showing the design in a new worksheet and more information is in the session panel.

2.2.1.3 Step 3 – Assign the Designed Factor Level Combinations to the Experimental Units and Collect Data for the Response Variable

For each block, collect the data for the response variable following the order provided by the column RunOrder in the full or fractional design. For example, in the full factorial design created in step 1, the second panelist (Blocks = 2) will first test the fragrance where Oil2 and Oil5 are present, while Oil1, Oil3, Oil4, and Oil6 are absent. The two panelists will test each run by assigning it a liking score, varying from 1 (dislike extremely) to 5 (like extremely). Once all the designed factor‐level combinations have been tested, enter the recorded response values (liking scores) into the worksheet containing the design. The worksheet will be like the one below (only the first five records are shown here as an example for the fractional design obtained in step 2). Now you are ready to proceed with the statistical analysis of the collected data, but before doing this, have a look at Stat Tool 2.6 to get a summary overview of the main aspects of the design and analysis of experiments.

Stat Tool 2.6 Guidelines for Planning and Conducting Experiments

In Design and Analysis of Experiments (Montgomery, D. C., 2017), the author summarizes a series of steps to follow for a correct statistical approach in designing and analyzing an experiment.

The following diagrams outline some relevant key points.

Develop a clear and generally accepted statement of the problem soliciting input from all concerned parties (engineering, chemists, manufacturing, marketing, management, customers, operating personnel, …).

Characterization or factor screening. In a new process or system, the number of potential input variables (factors) is large. We need to reduce them by identifying the key input factors that affect response variable(s).
Optimization of a mature or reasonably well‐understood system that has been previously characterized.
Confirmation. Is the system performing the same way now as it did in the past?
Discovery. What happens if we explore new operating conditions, materials, variables, etc.?
Stability or robustness. How can we reduce variability in the response variable arising from uncontrolled sources?

Employ a series of smaller experiments, each with a specific objective, rather than a single comprehensive experiment.

Choose the variable that really provides useful information about the process under study.

Multiple responses representing multiple aspects of the process output may be of interest.

In situations where gauge capability is poor or measurement error is large, the experimenter measures the response on each experimental unit several times and uses the average of these repeated measures as the observed response.

Key Factors: Factors of interest.

Factors not of interest: They may have effects on the response that must be accounted for through the blocking technique, randomization, and analysis of covariance.

Two‐level full and fractional factorial designs (factors have only two levels) are often used in factor screening or process characterization to “screen” for the really important factors that influence process output responses. General full factorial designs (factors can have any number of levels) may be used in optimization/confirmatory experiments.

Statistical software packages and MINITAB^® support this phase of the experimental design (Mathews, P. G., 2005; Greenfield, T. and Metcalfe, A., 2007), proposing a selection of designs for consideration and providing worksheets with the order of the randomized runs.

It is important to monitor the process carefully to ensure that everything is being done according to plan and to avoid errors in experimental procedures.

When possible, a few pilot runs prior to conducting the experiment may provide information about the overall experimental design and on consistency of experimental material, measurement system, and experimental error.

They play an important role in data analysis and interpretation.

Many of the questions that the experimenter wants to answer can be solved by hypothesis testing and confidence interval estimation procedures.

It is also helpful to present the results in terms of a model, i.e. an equation derived from the data that expresses the relationship between the response and the important design factors.

Residual analysis and model adequacy checking are also important analysis techniques.

Once the data have been analyzed, the experimenter draws practical conclusions and recommends a course of action.

Recognize the difference between practical and statistical significance. A statistically significant difference may be too small to be of practical value.

The learning process advances by formulating hypotheses, performing experiments to investigate them, formulating new ones on the basis of the results, and so on.

It is usually a mistake to design a single, large, comprehensive experiment at the start of the study.

A sequential approach employing a series of smaller experiments is usually a better strategy.

Use your nonstatistical knowledge of the problem in choosing factors and levels, number of replicates, interpreting the results, and so forth.

Using a designed experiment is no substitute for thinking about the problem.

Do the pre‐experiment planning carefully and select a reasonable design.

Keep the design and analysis as simple as possible.

Do not be overzealous in the use of complex, sophisticated statistical techniques.

Relatively simple design and analysis methods are almost always the best.

2.2.2 Plan of the Statistical Analyses

The main interest in the statistical analysis of a screening experiment is to detect which factors (if any) show a significant contribution to the explanation of the response variable and also something about how the factors interact. For each factor, it is possible to evaluate if the mean response varies between the two factor levels, taking into account the effect of other factors on the response. The appropriate procedure to use for this purpose is the ANOVA (Stat Tool 2.7).

Let's consider the fractional design obtained in step 2 (Section 2.2.1) and suppose to have collected the response data (File: Air_freshener_Project.xlsx). Remember that if the experimenter can reasonably assume that certain high‐order interactions are negligible, a fractional design can give useful information on the main effects and low‐order interactions. The factors identified as important through the statistical analysis of collected data will then be investigated more thoroughly in subsequent experiments.

To analyze our screening experiment, let's proceed in the following way:

Step 1 – Perform a descriptive analysis (Stat Tool 1.3) of the response variable.
Step 2 – Apply the ANOVA to estimate the effects and determine the significant ones.
Step 3 – If required, reduce the model to include the significant terms.

The variables setting is the following:

Columns from C1 to C3 are related to the previous creation of the fractional factorial design.
Column C4 is the blocking factor, assuming values 1 and 2.
Variables OIL1–OIL6 are the categorical factors, each assuming two levels.
Variable “Response” is the response variable, assuming values from 1 to 5.

Column	Variable	Type of data	Label
C4	Block	Numeric data	Blocking factor representing the two panelists 1 and 2
C5–C10	OIL1–OIL6	Categorical data	The six oils for fragrances, each with levels: NO, YES
C11	Response	Numeric data	The liking score, varying from 1 to 5

Air_freshener_Project.xlsx

2.2.2.1 Step 1 – Perform a Descriptive Analysis of the Response Variable

As the response is a quantitative variable, use a dotplot (recommended for small samples with less than 50 observations) or a histogram (for moderate or large datasets with a sample size greater than 20) to describe how the liking scores occurred in our sample. Add a boxplot (for moderate or large datasets) and calculate means and measures of variability to complete the descriptive analysis of the response.

To display the histogram, go to: Graph > Histogram

Check the graphical option Simple, and in the next dialog box select “Response” in Graph variables. Then, select the option Scale and in the next screen Y‐Scale Type to display percentages in the histogram. Then click OK in the main dialog box.

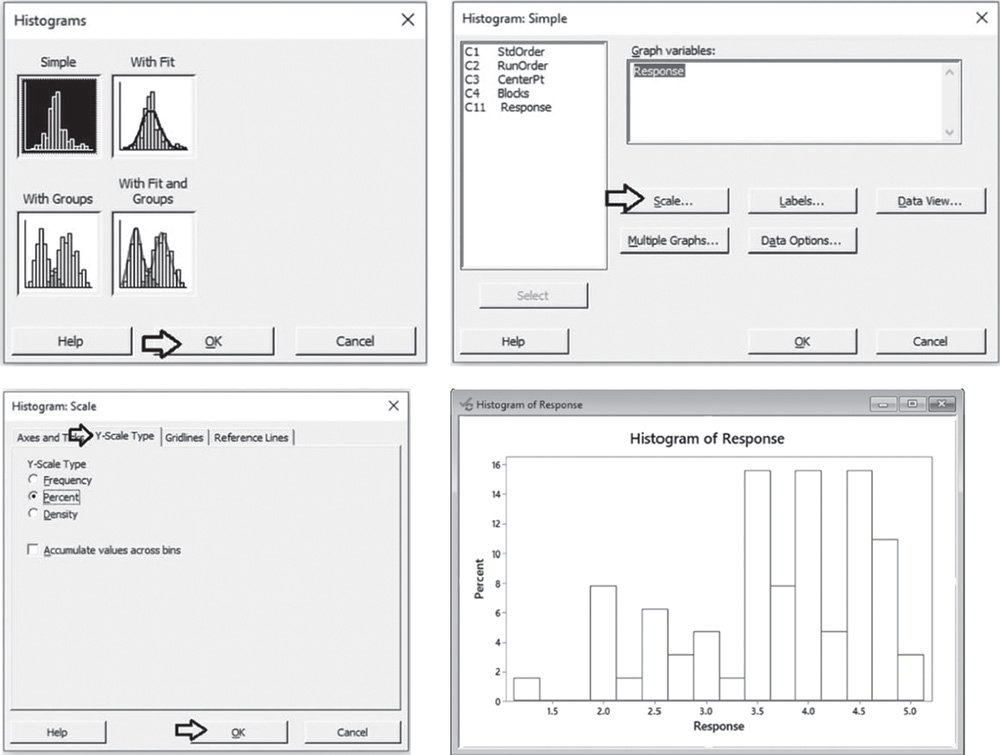
Illustration of percentages displayed in the histogram: Histograms, Histogram Simple, Histogram Scale, and Response Histogram.

To change bar width and number of intervals, double‐click on any bar and select the Binning tab. A dialog box will open with several options to define. Specify 5 in Number of intervals and click OK.

Illustration of a dialog box with several options to define. Number 5 is specified in Number of intervals. On the RHS, a corresponding Response Histogram is seen.

Use the following tips to change the appearance of the histogram:

To change the scale of the horizontal axis: double‐click on any scale value on the horizontal axis. A dialog box will open with several options to define.
To change the scale of the vertical axis: double‐click on any scale value on the vertical axis. A dialog box will open with several options to define.
To change the width and number of intervals of the bars: double‐click on any bar and then select the Binning tab. A dialog box will open with several options to define.
To change the graph window (background and border): double‐ click on the area outside the border of the histogram. A dialog box will open with several options to define.
To add reference lines: right‐click on the area inside the border of the boxplot, then select Add > Data display > Mean symbol.
To change the title, labels, etc.: double‐click on the object to change. A dialog box will open with several options to define.
To insert a text box, lines, points, etc.: from the main menu at the top of the session window, go to Tools > Toolbars > Graph Annotation Tools the Session window.

Illustration of Graph Annotation Tools in the Session window.

To display the boxplot, go to: Graph > Boxplot

Check the graphical option Simple and in the next dialog box, select “Response” in Graph variables. Then click OK in the main dialog box.

Illustration of boxplots and Boxplot: One Y, simple dialog box.

To change the appearance of a boxplot, follow the tips provided for histograms, as well as the following:

To display the boxplot horizontally: double‐click on any scale value on the horizontal axis. A dialog box will open with several options to define. Select from these options: Transpose value and category scales.
To add the mean value to the boxplot: right‐click on the area inside the border of the boxplot, then select Add > Data display > Mean symbol.

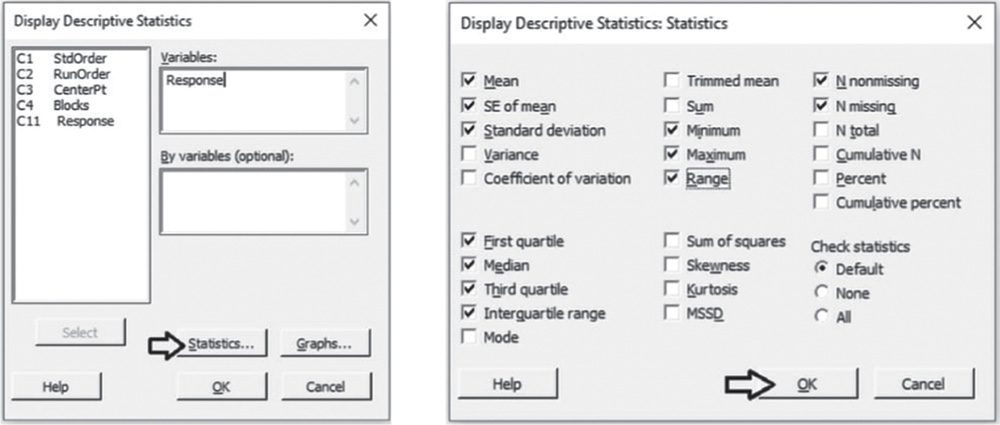
To display the descriptive measures (means, measures of variability, etc.), go to:

Select “Response” in Variables, then click on Statistics to open a dialog box displaying a range of possible statistics to choose from. Leave the default options and select Interquartile range and Range.

Illustration of a dialog box displaying a range of possible statistics to choose from.

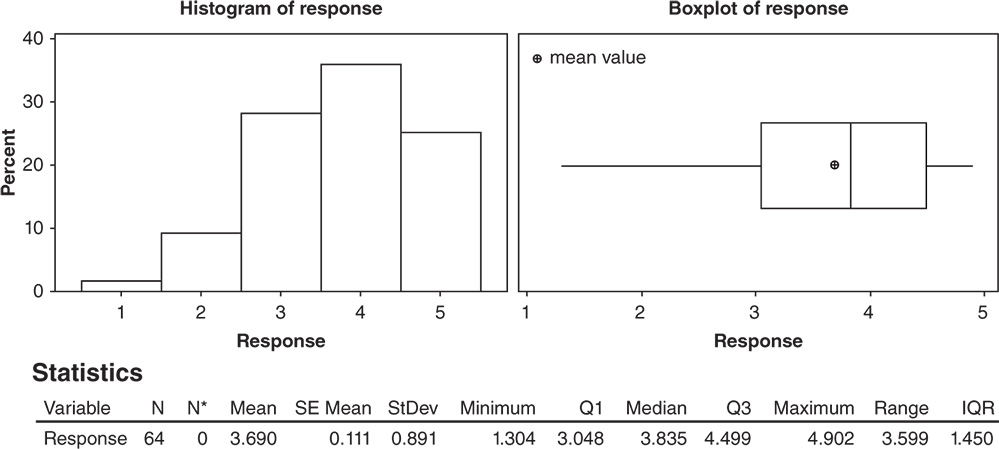
2.2.2.1.1 Interpret the Results of Step 1

Let's describe the shape, central, and non‐central tendency and variability of the distribution of the liking scores, presented in the histogram and boxplot below.

Shape: The distribution of the liking scores is skewed to the left: middle and high scores are more frequent than low scores (Stat Tools 1.4–1.5, 1.11).

Central tendency: The central tendency (the median score) is equal to 3.8: about 50% greater than or equal to 3.8. The mean is equal to 3.69. Mean and median are quite close in value (Stat Tools 1.6, 1.11).

Non‐central tendency: 25% of the scores are less than 3.0 (first quartile Q₁) and 25% are greater than 4.5 (third quartile Q₃) (Stat Tools 1.7, 1.11).

Variability: Observing the length of the boxplot (range) and the width of the box (interquartile range, IQR), the distribution shows high variability. Its scores vary from 1.3 (minimum) to 4.5 (maximum). 50% of middle evaluations vary from 3.0 to 4.5 (IQR = maximum observed difference between evaluations equal to 1.5) (Stat Tools 1.8, 1.11).

The average distance of the scores from the mean (standard deviation) is 0.89: Scores vary on average from (3.69–0.89) = 2.80 to (3.69 + 0.89) = 4.58 (Stat Tool 1.9).

Illustration of a histogram of response and a boxplot of response.

2.2.2.2 Step 2 – Apply the Analysis of Variance to Estimate the Effects and Determine the Significant Ones

The appropriate procedure to analyze a factorial design is the ANOVA (Stat Tool 2.7).

To analyze the screening design, go to:

Select the numeric response variable Response and click on Terms. At the top of the next dialog box, in Include terms in the model up through order, specify 2 to study all main effects and the two‐way interactions. Select Include blocks in the model to consider blocks in the analysis. Click OK and in the main dialog box, choose Graphs. In Effects plots, choose Pareto chart and Normal Plot. These graphs help you identify the terms (factors and/or interactions) that influence the response and compare the relative magnitude of the effects, along with their statistical significance. Click OK in the main dialog box and Minitab shows the results of the analysis both in the session window and through the required graphs.

Illustration of the Analyze Factorial Design dialog box where analysis of variance is applied to estimate the effects and determine the significant ones.

Illustration of Analyze Factorial Design dialog box, Analyze Factorial Design graphs, and Pareto Chart of standardized effects.

2.2.2.2.1 Interpret the Results of Step 2 Let us first consider the Pareto chart that shows which terms contribute the most to explain the response. Any bar extending beyond the reference line (considering a significance level equal to 5%) is related to a significant effect.

In our example, the main effects for Oil2 and Oil5 are statistically significant at 0.05. Furthermore, the interaction between Oil4 and Oil5 is marked as statistically significant, while the interaction between Oil4 and Oil6 is nearly significant. From the Pareto chart, you can detect which effects are statistically significant but you have no information on how these effects affect the response.

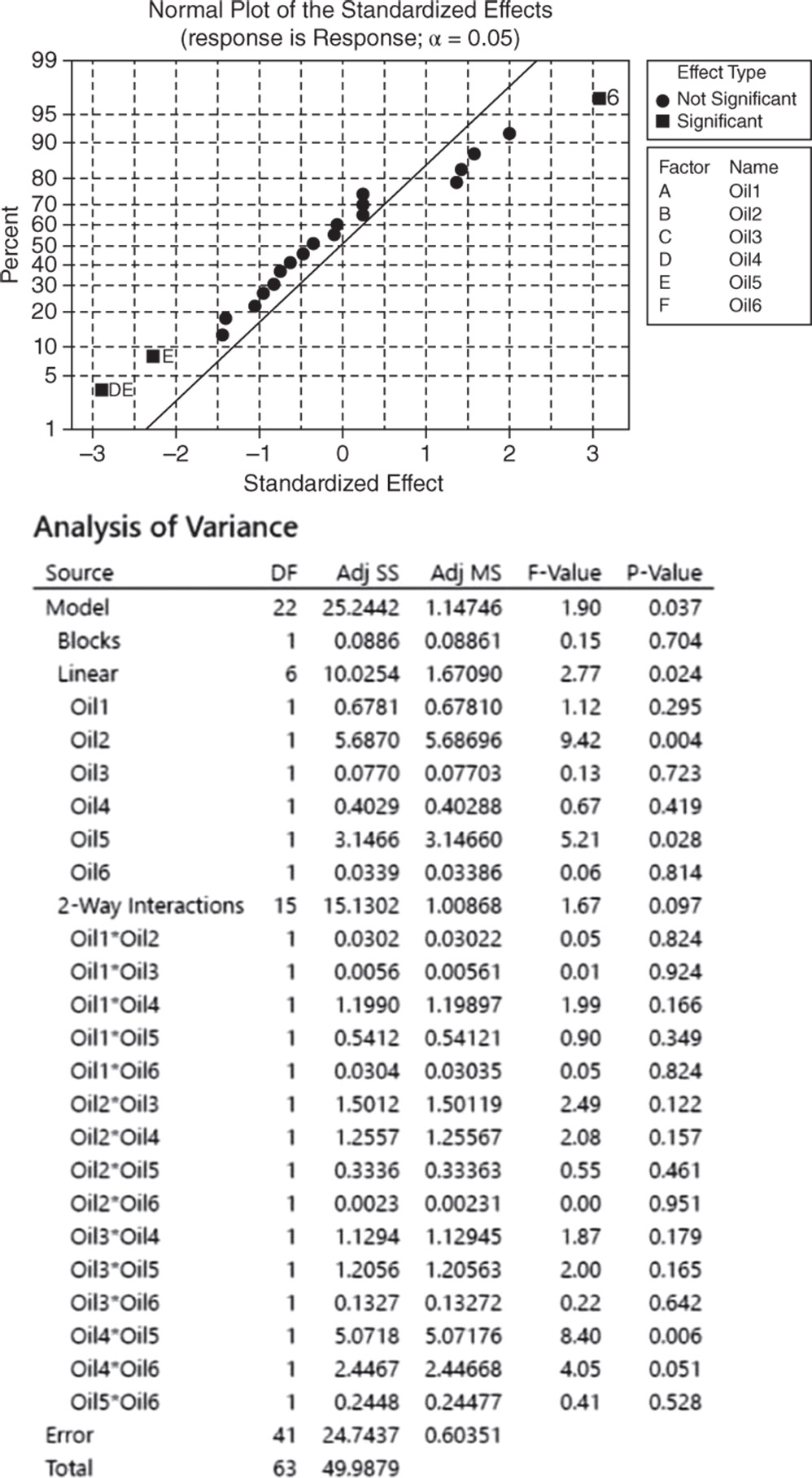
Illustration of normal plot of standardized effects and a table displaying the variance analysis.

Use the normal plot of the standardized effects to evaluate the direction of the effects. In this case, the line represents the situation in which all the effects (main effects and interactions) are 0. Effects that depart from 0 and from the line are statistically significant. Minitab shows statistically significant and nonsignificant effects by giving the points different colors and shapes. In addition, the plot indicates the direction of the effect. Positive effects (displayed on the right side of the line) increase the response when the factor moves from its low value to its high value. Negative effects (displayed on the left side of the graph) decrease the response when moving from the low value to the high value.

In our example, the main effects for Oil2 and Oil5 are statistically significant. The low and high levels represent the absence and presence of the specific oil; therefore, the liking scores seem to increase when Oil2 is present and Oil5 is absent. Furthermore, the interaction between Oil4 and Oil5 is marked as statistically significant.

In the ANOVA table we examine p‐values to determine whether any factors or interactions, or even the blocks, are statistically significant. Remember that the p‐value is a probability that measures the evidence against the null hypothesis. Lower probabilities provide stronger evidence against the null hypothesis. For the main effects, the null hypothesis is that there is not a significant difference in the mean liking score across each factor's low level (absence) and high level (presence). For the two‐factor interactions, H₀ states that the relationship between a factor and the response does not depend on the other factor in the term. With respect to the blocks, the null hypothesis is that the two panelists do not change the response. Usually we consider a significance level alpha equal to 0.05, but in an exploratory phase of the analysis we may also consider a significance level of 0.10.

When the p‐value is greater than or equal to alpha, we fail to reject the null hypothesis. When it is less than alpha, we reject the null hypothesis and claim statistical significance.

So, setting the significance level α = 0.05, which terms in the model are significant in our example? The answer is: Oil2, Oil5 and the interaction between Oil4 and Oil5. Now you may want to reduce the model to include only significant terms.

When using statistical significance to decide which terms to keep in a model, it is usually advisable not to remove entire groups of terms at the same time. The statistical significance of individual terms can change because of the terms in the model. To reduce your model, you can use an automatic selection procedure – the stepwise strategy – to identify a useful subset of terms, choosing one of the three commonly used alternatives (standard stepwise, forward selection, and backward elimination).

Stat Tool 2.7 ANOVA, Analysis Of VAriance

A common task in statistical studies is to compare the mean of a quantitative variable of interest among more than two groups. Use ANOVA to determine whether means of more than two groups differ. Usually, ANOVA is applied in an experimental context. ANOVA requires the following:

A response (quantitative variable) is measured on sample units.
One or more factors (categorical variables or quantitative variables) are controlled by the experimenter and used to identify more than two groups (treatments), related to factor levels or combinations of factor levels.

In other words, for each factor, two or more values (levels) are set by the experimenter. These levels or combinations of levels (when considering more than one factor) are called treatments and define groups across which the means of a response are compared.

For example, a researcher is interested in comparing the mean time of dissolution for three products formulated with three different doses of an additive. Here, the response is the time of dissolution and the factor is the additive dose.

With ANOVA you are studying the relationship between a response variable and one or more controlled factors.

When groups are defined on the basis of a single factor, the ANOVA is called one‐way ANOVA. When groups are defined on the basis of more than one factor, the ANOVA is called multi‐way or multi‐factor ANOVA.

In ANOVA, the F test is applied to determine whether the response means differ among treatments. The null hypothesis H₀ states that all the means are equal. The alternative hypothesis H₁ states that the means are not all equal. If the p‐value of the test is less than the significance level alpha, reject the null hypothesis of equality of means (Stat Tools 1.15, 1.16).

If you reject the null hypothesis, then apply a multiple comparisons procedure to assess how the means differ from one another. One of these procedures is Tukey's multiple comparison procedure, which considers all pairwise comparisons between treatments.

The ANOVA procedure also presents the results in terms of a model, i.e. an equation derived from the data that expresses the relationship between the response and the factors. You can use this model to predict the response for each treatment. These predicted or fitted values are simply the sample averages of the observed response data for each treatment.

Stat Tool 2.8 Model assumptions for ANOVA

The use of ANOVA to formally test for no differences in treatment means requires that certain assumptions be satisfied:

Independent measurements	Each measure of the response variable is taken independently of the other measures.
Normality	For each group, response values are assumed to come from a normal distribution.
Homoscedasticity	There is similar variability of responses across groups.

Example 2.3. A chemist wants to compare the technical performance of three different formulations of a stain‐removal product (factor). Performance (response) is measured as the reflectance (after wash) of a fabric soiled with a specific stain.
Each formulation of the stain‐removal product is randomly applied to a sample of pieces (replicates) of a fabric soiled with a specific stain. Performance is then measured on each piece of fabric, such that each measure is taken independently of the other measures.

For each formulation, experimental data is assumed to come from a normal distribution.

Reflectance should display similar variability across groups (formulations).

We can check these assumptions by performing a residual analysis (Figure 2.12).

Figure 2.12 Model assumptions for ANOVA (Example 2.4).

2.2.2.3 Step 3 – If Required, Reduce the Model to Include the Significant Terms

To reduce the model, go to:

Select the numeric response variable Response and click on Terms. In Include terms in the model up through order, specify 2 to study all main effects and the two‐way interactions. Select Include blocks in the model to consider blocks in the analysis. Click OK and in the main dialog box, choose Stepwise. In Method select Backward elimination and in Alpha to remove specify 0.05, then click OK. In the main dialog box, click Options and in the next dialog box specify in Means table: All terms in the model. Minitab will display the estimated means for the significant effects in the output. Click OK, and in the main dialog box, choose Graphs. Under Residual plots choose Four in one. Minitab will display several residual plots to examine whether your model meets the assumptions of the analysis (Stat Tools 2.8 and 2.9). Click OK in the main dialog box.

Illustration of Analyze Factorial Design minitab displaying several residual plots to examine whether a model meets the assumptions of the analysis.

Illustration of Analyze Factorial Design dialog boxes that display several residual plots to examine whether a model meets the assumptions of the analysis.

Complete the analysis by adding the factorial plots that show the relationships between the response and the significant terms in the model, thus displaying how the response mean changes as the factor levels or combinations of factor levels change.

To display factorial plots, go to:

2.2.2.3.1 Interpret the Results of Step 3

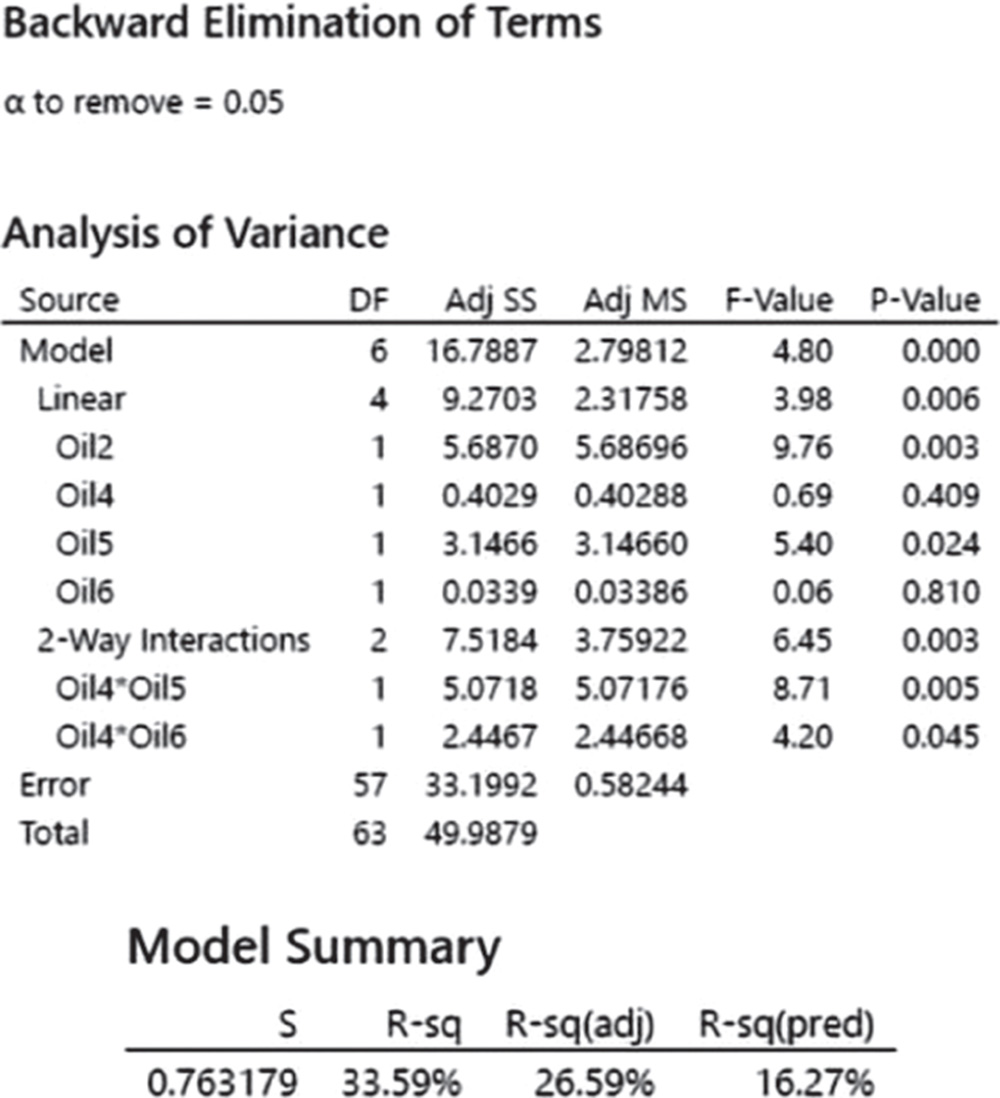
Illustration of a table displaying analysis of variance results.

Setting the significance level alpha to 0.05, the ANOVA table shows the significant terms in the model. Take into account that the stepwise procedure may add nonsignificant terms in order to create a hierarchical model. In a hierarchical model, all lower‐order terms that comprise higher‐order terms also appear in the model. You can see, for example, that the model includes the nonsignificant terms Oil4 and Oil6, because their interaction is present and also significant.

In addition to the results of the ANOVA, Minitab displays some other useful information in the Model Summary table.

The quantity R‐squared (R‐sq, R²) is interpreted as the percentage of the variability among liking scores, explained by the terms included in the ANOVA model.

The value of R² varies from 0% to 100%, with larger values being more desirable.

The adjusted R² (R‐sq(adj)) is a variation of the ordinary R² that is adjusted for the number of terms in the model. Use adjusted R² for more complex experiments with several factors, when you want to compare several models with different numbers of terms.

The value of S is a measure of the variability of the errors that we make when we use the ANOVA model to estimate the liking scores. Generally, the smaller it is, the better the fit of the model to the data.

Before proceeding with the results reported in the session window, take a look at the residual plots. A residual represents an error that is the distance between an observed value of the response and its estimated value by the ANOVA model. The graphical analysis of residuals based on residual plots helps you to discover possible violations of the ANOVA underlying assumptions (Stat Tools 2.8 and 2.9).

A check of the normality assumption could be made by looking at the histogram of the residuals (on the lower left), but with small samples, the histogram often shows irregular shape.

The normal probability plot of the residuals may be more useful. Here we can see a tendency of the plot to bend upward slightly on the right, but the plot is not grossly non‐normal in any case. In general, moderate departures from normality are of little concern in the ANOVA model with fixed effects.

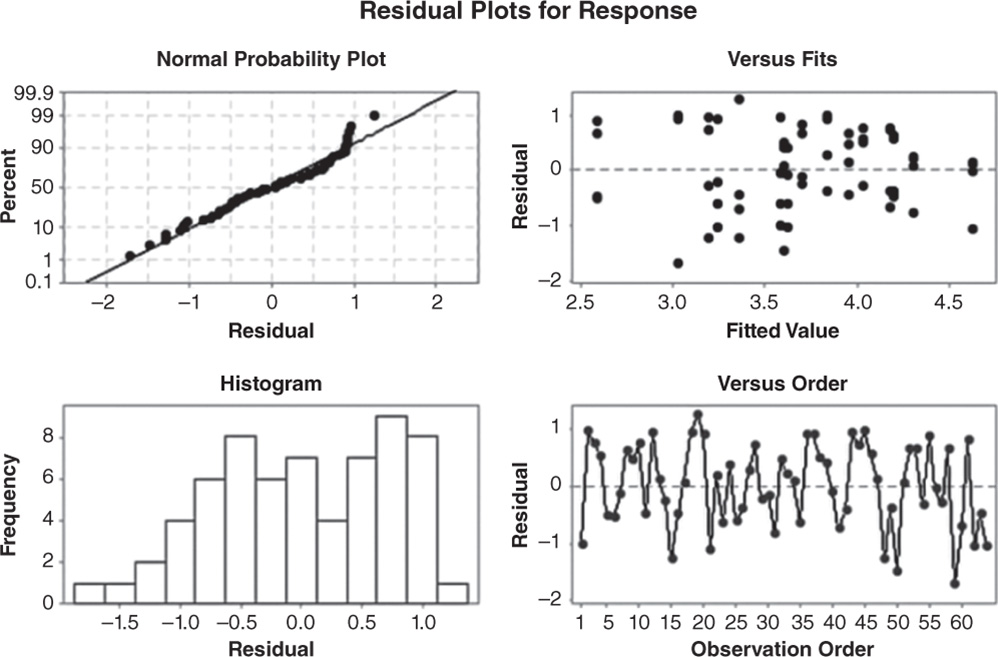
Graphical illustration of four different residual plots for response.

The other two graphs (Residuals vs. Fits and Residuals vs. Order) seem unstructured, thus supporting the validity of the ANOVA assumptions.

Returning to the Session window, we find a table of coded coefficients followed by a regression equation in uncoded units. To understand the meaning of these results and how we can interpret them, consider also the factorial plots and the Mean table.

In ANOVA, we have seen that many of the questions that the experimenter wishes to answer can be solved by several hypothesis tests. It is also helpful to present the results in terms of a regression model, i.e. an equation derived from the data that expresses the relationship between the response and the important design factors.

In the regression equation, the value 3.69 is the intercept. It's the sample response mean. We calculated it in the descriptive phase, considering all 65 observations. Then, in the regression equation we have a coefficient for each term in the model that indicates its impact on the response: a positive impact, if its sign is positive, or a negative impact, if its sign is negative.

In the regression equation, the coefficients are expressed in uncoded units – that is, in the original measurement units. These coefficients are also displayed in the Coded Coefficients table, but in coded units. What are the coded units? Minitab codes the low level of a factor to −1 and the high level of a factor to +1. The data expressed as −1 or + 1 are in coded units.

Coded coefficients

Term	Effect	Coef	SE Coef	t‐Value	p‐Value	VIF
Constant		3.6901	0.0954	38.68	0.000
Oil2	0.5962	0.2981	0.0954	3.12	0.003	1.00
Oil4	−0.1587	−0.0793	0.0954	−0.83	0.409	1.00
Oil5	−0.4435	−0.2217	0.0954	−2.32	0.024	1.00
Oil6	0.0460	0.0230	0.0954	0.24	0.810	1.00
Oil4*Oil5	−0.5630	−0.2815	0.0954	−2.95	0.005	1.00
Oil4*Oil6	0.3910	0.1955	0.0954	2.05	0.045	1.00

Regression Equation in Uncoded Units

Response = 3.6901 + 0.2981 Oil2 − 0.0793 Oil4 − 0.2217 Oil5 + 0.0230 Oil6 − 0.2815 Oil4*Oil5 + 0.1955 Oil4*Oil6

When factors are categorical, the results in coded units or uncoded units are the same. When factors are quantitative, using coded units has a few benefits. One is that we can directly compare the size of the coefficients in the model, since they are on the same scale, thus determining which factor has the biggest impact on the response.

For example (for categorical factors):

Oil2
Uncoded units	Coded units
NO	−1
YES	+1

Earlier, we learned how to examine the p‐values in the ANOVA table to determine whether a factor is statistically related to the response. In the Coded Coefficients table, we find the same results in terms of tests on coefficients and we can evaluate the p‐values to determine whether they are statistically significant. The null hypothesis is that a coefficient is equal to 0 (no effect on the response). Setting the significance level α at 0.05, if a p‐value is less than the α level, reject the null hypothesis and conclude that the effect is statistically significant.

However, how can we interpret the regression coefficients? Looking at the Coded Coefficient table, see, for example, that when Oil2 is present (Oil2 = +1), the mean liking score increases by +0.298. This result is graphically presented in the factorial plots and with further details in the Means table. As Oil2 is not involved in a significant interaction, consider the Main Effects Plot.

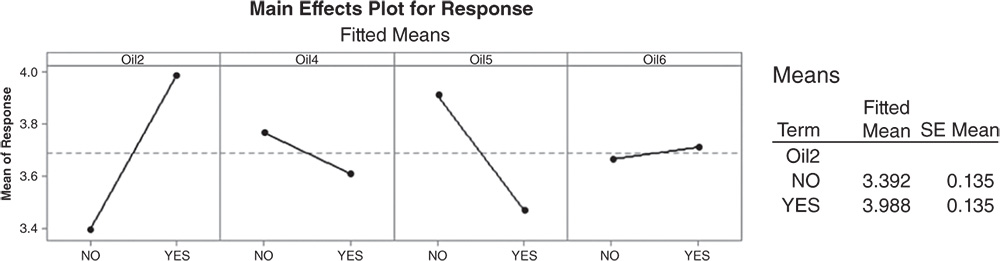
Graphical illustration of main effects plot for response.

Extrapolate the plot related to Oil2 to analyze it in detail. The dashed horizontal line in the middle is the total mean liking score = 3.690. When Oil2 is present, the mean liking score increases by 0.298 (the magnitude of the coefficient) to 3.988 (this can be seen in the Means Table under Fitted Mean), while when absent, the mean liking score decreases by 0.298–3.392.

Illustration of main effects plot for response: fitted means.

So the coefficient in coded units tells us the increase or the decrease with respect to the total mean.

Two times the coefficient is the effect of the factor (see its value in the Coded Coefficients table, under the column Effect).

For Oil5, we have the significance of its main effect and of the interaction between Oil5 and Oil4. The main effect of Oil4 is not statistically significant. The interaction between Oil4 and Oil6 is statistically significant. Look at the interaction plots and the Means table, and consider how the mean liking score varies as the levels of Oil4 and Oil5 change and as the levels of Oil4 and Oil6 change.

Graphical illustration of interaction plot for response.

Considering the Oil4*Oil5 interaction, the best result (the highest mean liking score) is obtained when Oil4 is present and Oil5 is absent (fitted mean liking score = 4.114) and the worst result when both of them are present. For the Oil4*Oil6 interaction, the highest mean liking score is reached when both oils are absent (fitted mean liking score = 3.942), but the second best result is obtained when both oils are present. The interpretation of these results is not so clear. Remember that in a fractional design, we are not able to estimate all the main effects and interactions separately from each other: some of them will be confused (aliased) with others. In the fractional design we are analyzing, for example, factor B (Oil2) is aliased with the four‐order interaction BCDEF; the ANOVA model estimates the effect of (B + ACDEF), but if we can reasonably assume that the interaction ACDEF is negligible, we can assign the total estimate to the main effect B. The three‐ and four‐factor (higher‐order) interactions are rarely considered because they represent complex events, which are sometimes difficult to interpret.

A three‐factor interaction, for example, would mean that the effect of a factor changes as the setting of another factor changes, and that the effect of their two‐factor interaction varies according to the setting of a third factor. As a consequence of this, out of the many factors that are investigated, we expect only a few to be statistically significant, and we can usually focus on the interactions containing factors whose main effects are themselves significant.

Returning to our example, based only on statistical considerations, it would seem reasonable to perform a new experiment to evaluate more deeply the effect of Oil2 and perhaps of Oil4 and Oil6. The likelihood of this interpretation should, however, be judged by the process experts. The experimenter might even think of adding some levels to the factors, considering, for example, three levels representing different concentrations of each oil. From a two‐level fractional design, the researcher could move to a general (i.e. with more than two levels for at least one factor) full or fractional design to further investigate the relationship between oils and the liking scores.

Stat Tool 2.9 Residual Analysis

In the ANOVA procedure, for each group a residual represents an error, i.e. the distance between an observed value of the response and its value estimated by the ANOVA model, which is simply the mean response for that group. The graphical analysis of residuals based on residual plots helps us discover possible violations of the underlying ANOVA assumptions (Stat Tool 2.8).

Randomization and random samples (Stat Tools 2.3, 1.2) are prerequisites of the first assumption of independent measurements. We can plot the residuals in the order that the data were collected and look for any patterns. Structureless plots, showing no obvious patterns, reveal no serious problems of lack of independence. Look at the two residuals versus order plots in Figure 2.13. On the left, the points on the plot are randomly distributed and do not exhibit any patterns. The residuals appear to be independent of one another. The plot on the right, however, displays a recognizable pattern: from the 11th observation onwards, the points gradually increase over time, thus indicating that the residuals may not be independent.

A check of the normality assumption could be made through a normal probability plot of the residuals. If the underlying response distribution is normal, this plot will resemble a straight line. If the residuals approximately follow the straight line on the plot, you don't have a severe violation of the normality assumption. Below are two normal probability plots (Figure 2.14). The one on the left describes residuals that likely follow a normal distribution, where residuals follow approximately a straight line. The one on the right exhibits a pattern that indicates the residuals do not follow a normal distribution.

The normal distribution is bell‐shaped and symmetric and is widely used in statistics to represent quantitative variables showing symmetry and unimodal distributions (Figure 2.15):

Figure 2.13 Residuals versus order plots.

Figure 2.14 Normal probability plots.

Figure 2.15 Normal distribution.

The third assumption states that the response variance across groups (treatment) is constant (homoscedasticity).

To evaluate this assumption, we can plot the residuals versus the fitted values. Notice that the residual values are on the vertical axis and the fitted values are on the horizontal axis.

Remember that the fitted values are obtained using the ANOVA model and are simply the mean response values for each group. Of the two plots in Figure 2.16, the one on the left shows constant variance across groups: the scatter of the points is similar across all groups and shows no patterns. In the plot on the right, the residuals increase systematically with the fitted values, which is sometimes called the funnel effect. Here, the variance is not constant across groups.

Figure 2.16 Residuals versus fitted values plots.

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 2 The Screening Phase

Create new playlist

Sign In

Sign Up