Appendix A

VLC Construction Algorithms

A.1 First RVLC Construction Algorithm

We now introduce the MRG-based algorithm proposed in [21] by slightly paraphrasing it as follows. Continuing the list of definitions in Section 3.3.1, we add:

Definition 12 (Minimum Repetition Gap (MRG) [21]) A codeword c having k bits is represented as c₁c₂ ... c_k. We form a new bit pattern b by concatenating c with a k-bit pattern x yielding the pattern b = cx. Every bit in x can be viewed as ‘0’ or ‘1’ in the following calculation. The minimum repetition gap g of c may be defined as the minimal-length interval that can be created for which it is valid that all the bits in b are repeated every g bits, ie. appear to be repeated every g bits. This may be formulated mathematically as:

For example, given a codeword c = 010, we have k = 3. The resultant 2k-bit long concatenated pattern is formulated as b = 010x₁x₂x₃. We can opt, for example, for setting x = 101, resulting in b₁ = b₃ = b₅ (i.e. x₂) = 0 and b₂ = b₄(x₁) = b₆(x₃) = 1. Therefore, by observing the resultant six-bit pattern of 010101 we infer that the two-bit pattern of 01 repeats itself. Hence we conclude that g is equal to 2 in this case. Alternatively, we may opt for x = 010, in which case we have a six-bit pattern of 010010 emerging, and hence we infer that the three-bit pattern of 010 repeats itself. Therefore we conclude that g is equal to 3 in this case. Thus we have MRG = min {2, 3} = 2.

The RVLC construction method of [21] is based on the following conjecture. For any two candidate codewords c₁ and c₂ at level l, let g₁ and g₂ denote the MRGs of c₁ and c₂, respectively. V(c₁, k) and V(c₂, k) denote the sets of candidate codewords at level k that violate the affix condition for c₁ and c₂. If g₁ ≤ g₂, then |V (c₁, k)|≤|V (c₂, k)| for k ≥ l.

Therefore, if we always choose codewords with the smallest MRGs while satisfying the affix condition, we can make the set of usable candidate codewords for the next levels as large as possible.

Let U = {u₁, ..., u_M} be a M-ary i.i.d. information source with the probability mass function P_u = {p₁, ..., p_M}, p₁ ≥ · · · ≥ p_M. The RVLC construction algorithm of [21] is then summarized as Algorithm A.1.

Algorithm A.1

A.2 Second RVLC Construction Algorithm

In [23] Lakovic and Villasenor improved the above algorithm by establishing the formal relationship between the number of available RVLC codewords of any length and the structure of shorter RVLC codewords that had been selected, and pointed out that the MRG metric was a special case of this relationship. We now re-derive this relationship.

Let a binary codeword w of length i be denoted as w = (w₁w₂ · · · w_i). Define the prefix set P_j(w) as the set of length-j codewords, j > i, which are prefixed by w, and define the suffix set S_j(w) as the set of length-j codewords, j > i, which are suffixed by w. It is obvious that

|P_j(w)| = |S_j(w)| = 2^(j−i).

Assume that W = {w₁, w₂, ..., w_m} is a set of RVLC codewords of lengths l₁ ≤ l₂ ≤ · · · ≤ l_m. Denote with n_a(j) the number of codewords of length j, j > l_m, which are neither prefixed nor suffixed by any codeword from W. Since the total number of length-j codewords is equal to 2^j, it holds that

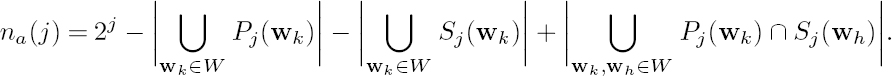
For RVLCs all the prefix sets, as well as all the suffix sets, are disjoint, and therefore

Now define the affix set A_j(w_k, w_h) as the set of codewords of length j, j > max(l_k, l_h), prefixed by w_k and suffixed by w_h:

A_j(w_k, w_h) = P_j(w_k) ∩ S_j(w_h).

Obviously, n_a(j) depends on the cardinalities of affix sets A_j(w_k, w_h), i.e., on the affix index of the set W, defined as

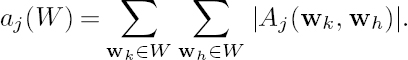
The cardinalities of affix sets A_j(w_k, w_h) are given as follows [27]. For max(l_k, l_h) < j < l_k + l_h,

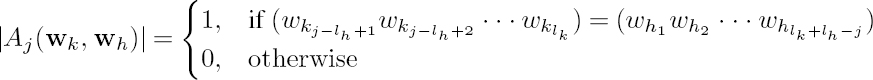
while for l_k + l_h ≤ j,

|A_j(w_k, w_h)| = 2^{j−l_k−l_h}.

With the above formulas, the MRG can be interpreted as follows. The MRG of a length-i codeword w, denoted as g(w), is equal to the minimal positive integer g such that |A_i+g(w, w)| > 0. Algorithm A.1 [21] selects the codewords with the lowest g(w), which contributes to the increase in n_a(i + g), with the lowest g first, because n_a(i + g) depends on |A_{i + g}(w, w)|. However, this algorithm does not consider the elements |A_{i + g}(w_k, w_h)|, w_k ≠ w_h, which have a significant impact on n_a(i + g), and consequently on the coding efficiency. Therefore, Lajovic and Villasenor [23] proposed a new construction algorithm, shown here as Algorithm A.2, that differed from Algorithm A.1

Algorithm A.2 can generate RVLCs with smaller average code lengths than Algorithm A.1; however, the complexity is much higher. At each level i, with n_a(i) ≥ _n(i), Algorithm A.1 considers na(i) MRGs, while Algorithm A.2 considers affix indices.

A.3 Greedy Algorithm and Majority Voting Algorithm (MVA)

Both the greedy algorithm and the MVA may be applied for the construction of a fixed-length code of length n having a given block distance of d from a given set of codewords that may not necessarily contain all possible n tuples. Given a set of codewords W, the greedy algorithm initialises the target codeword set C with an arbitrary codeword in W, and then selects the first available codeword in W that is at a distance of at least d from all the existing codewords in the set C. This procedure is repeated until no more legitimate codewords are available in the set W. This algorithm is easy to implement; however, the number of codewords in the resultant codeword set may be far from the maximum achievable value, since it ignores the effect that the codewords selected at the current stage will limit the number of legitimate codewords at the next stage. By contrast, the MVA is usually capable of generating larger codeword sets by ‘looking’ a step forward. Its procedure can be described as in Algorithm A.3 [30].

Algorithm A.2

Algorithm A.3

The main disadvantage of Algorithm A.3 is that as the number of codewords in W increases it becomes too computationally expensive, and the greedy algorithm will then be preferred.