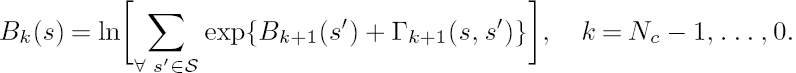Appendix C

APP Channel Equalization

The APP equalizer outputs the channel information, which is expressed as {L_f(d_k)}, associated with all data bits, given N_c received samples hosted by the vector y = y₁^N_c as well as the a priori information {L_b(d_k)} corresponding to all data bits. The feed-forward information L_f(d_k) corresponding to bit d_k is given by

(C.1)

where L(d_k|y) =ln[P(d_k = + 1|y)/P(d_k = −1|y)] represents the a posteriori Logarithmic Likelihood Ratio (LLR) of the data bit d_k, which may be computed using the algorithm described below by following the approaches outlined in [69, 70, 72, 99].

The a posteriori LLR of thedatabit d_k can be expressed in conjunction with the channel states s_k−1 and s_k as

(C.2)

The sequence y1Nc involved in the computation of the probability P(sk−1, sk, y1Nc) can be written in a more detailed form as P(sk−1, sk, y1k−1, yk, yNck+1). Applying the chain rule for joint probabilities, i.e., exploiting that we have P(a, b) = P(a)P(b|a), this expression yields the following decomposition of P(sk−1, sk, y1Nc):

(C.3)

Let us introduce the following definitions:

(C.4)

(C.5)

(C.6)

Then according to [48] the term α_k(s) can be computed via the recursion

(C.7)

associated with the initial values of α₀(q₀) = 1 and α₀(q_i) = 0 for i ≠ 0. The term β_k(s) can be computed via the recursion

(C.8)

in conjunction with the initial values of β_Nc(q₀) = 1 and β_Nc(q_i) = 0 for i ≠ 0. The term γ_k(s_k−1, s_k) represents the transition probability from state s_k−1 to state s_k, which can be further decomposed into

(C.9)

The transition probability γ_k(s_k−1 = q_i, s_k = q_j) is zero if the index pair (i, j) is not in . For pairs (i, j) within , the probability P(s_k = q_j|s_k−1 = q_i) is governed by the corresponding input symbol d_i,j, and p(y_k|s_k−1, s_k) is governed by the corresponding output symbol v_i,j, which can be described as

(C.10)

Given the AWGN channel of Equation (4.49), it follows that p(y_k|ν_k) is given by

(C.11)

From Equation (C.2) and from the decomposition of P(s_k−1, s_k, y₁^N_c) given in Equation (C.3), it follows that

(C.12)

As shown in Equation (C.10), once the channel output samples are available the corresponding values of γ_k(s′, s) can be computed and stored. With the aid of these values, both α_k(s) and β_k(s) of Equations (C.7) and (C.8) can be computed, and, finally, the a posteriori LLR of Equation (C.12) can be obtained. For the sake of reducing the associated complexity, these computations can be performed in the log domain, as follows.

Let us introduce the following notations:

(C.13)

(C.14)

(C.15)

Consequently, A_k(s) can be formed iteratively by:

1. Initialization:

(C.16)

2. Forward Recursion:

(C.17)

B_k(s) of (C.14) can be solved similarly, by:

1. Initialization:

(C.18)

2. Backward Recursion:

(C.19)

Furthermore, given the L-values of the encoded bits d_k, i.e., given the a priori information of L(d_k), and given the channel observations y_k, Γ_k(s′, s) seen in Equation (C.15) can be calculated as follows:

(C.20)

Finally, the a posteriori LLR of Equation (C.12) can be obtained as follows:

(C.21)

The above calculations entail the evaluation of the logarithm of a sum of exponentials. These calculations may be carried out using either either the MAX-Log approximation or the Jacobian logarithm employing a look-up table [250].