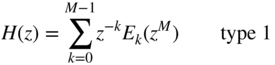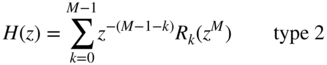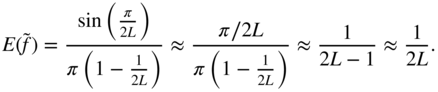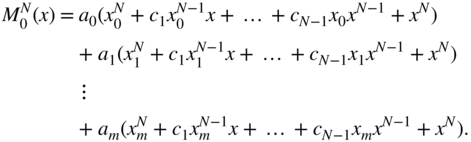Chapter 3
Sampling Rate Conversion
U. Zölzer
Several different sampling rates are established for digital audio applications. For broadcasting, professional, and consumer audio, sampling rates of 32, 48, and 44.1 kHz are used, respectively. Moreover, other sampling rates are derived from different frame rates for film and video. In connecting systems with different uncoupled sampling rates, there is a need for sampling rate conversion. In this chapter, synchronous sampling rate conversion with rational factor 
for coupled clock rates and asynchronous sampling rate conversion will be discussed where the different sampling rates are not synchronized with each other.
3.1 Basics
Sampling rate conversion consists of upsampling and downsampling and anti‐imaging and antialiasing filtering [Cro83, Vai93, Fli00, Opp99]. The discrete‐time Fourier transform of the sampled signal 
with sampling frequency 
(
) is given by
with the Fourier transform 
of the continuous‐time signal 
. For ideal sampling, the condition
holds.
3.1.1 Upsampling and Anti‐Imaging Filtering
For upsampling, the signal
by factor 
between consecutive samples 
, zero samples will be included (see Fig. 3.1). This leads to the upsampled signal
with sampling frequency 
(
) and the corresponding Fourier transform
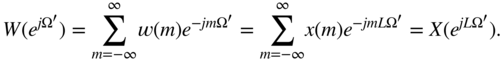
The suppression of the image spectra is achieved by anti‐imaging filtering of 
with 
, such that the output signal is given by
For adjusting the signal power in the baseband, the Fourier transform of the impulse response
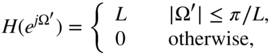
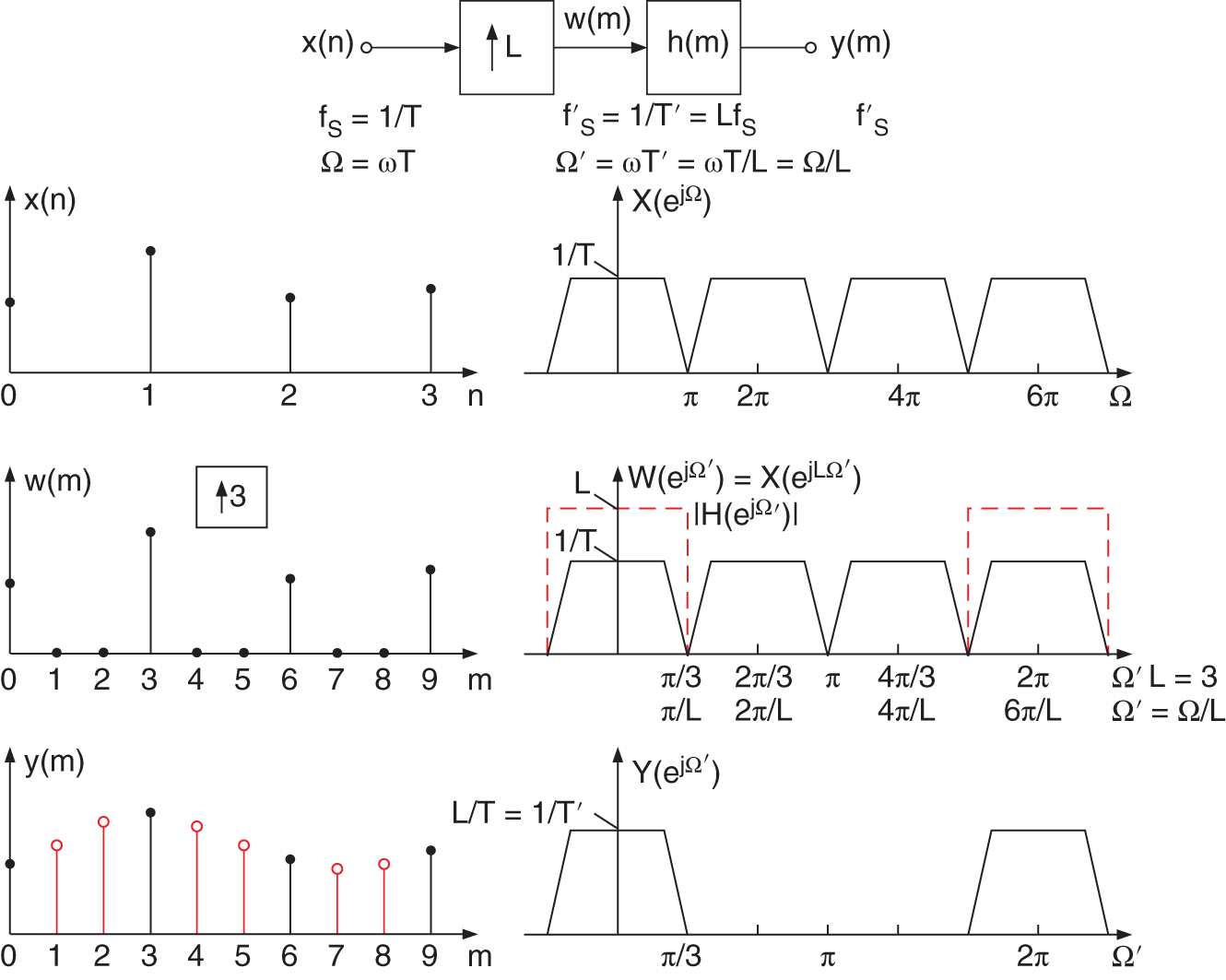
Figure 3.1 Upsampling by L and anti‐imaging filtering in the time and frequency domains.
needs a gain factor 
in the passband, such that the output signal 
has the Fourier transform given by
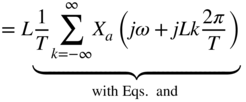
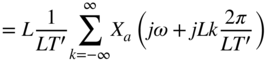
The output signal represents the sampling of the input 
with sampling frequency 
.
3.1.2 Downsampling and Antialiasing Filtering
For downsampling a signal 
by 
, the signal has to be band limited to 
to avoid aliasing after the downsampling operation (see Fig. 3.2). Band limiting is achieved by filtering with 
according to
Downsampling of 
is performed by taking every 
th sample, which leads to the output signal
with the Fourier transform
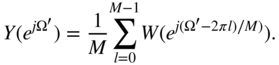
For the baseband spectrum (
and 
), we get
and for the Fourier transform of the output signal, we can derive
Figure 3.2 Antialiasing filtering and downsampling by M in the time and frequency domains.
which represents a sampled signal 
with 
.
3.2 Synchronous Conversion
Sampling rate conversion for coupled sampling rates by a rational factor 
can be performed by the system shown in Fig. 3.3. After upsampling by a factor 
, anti‐imaging filtering at 
is done followed by downsampling by factor 
. Because after upsampling and filtering only every 
th sample is used, it is possible to develop efficient algorithms that reduce the complexity. In this respect, two methods are in use; one is based on a time‐domain interpretation [Cro83] and the other [Hsi87] uses Z‐domain fundamentals. Owing to its computational efficiency, only the method in the Z‐domain will be considered.
Figure 3.3 Sampling rate conversion by factor L/M.
Starting with the finite impulse response 
of length 
and its Z‐transform
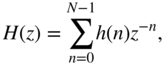
the polyphase representation [Cro83, Vai93, Fli00] with 
components can be expressed as
or
The polyphase decomposition as given in Eqs. (3.22) and (3.24) is denoted as type 1 and 2, respectively. The type‐1 polyphase decomposition corresponds to a commutator model in the anticlockwise direction, whereas the type 2 is in the clockwise direction. The relationship between 
and 
is described by
With the help of the identities [Vai93] shown in Fig. 3.4 and the decomposition (Euclid's theorem)
it is possible to move the inner delay elements of Fig. 3.5. Equation (3.27) is valid if 
and 
are prime numbers. In a cascade of upsampling and downsampling, the order of functional blocks can be exchanged (see Fig. 3.5b).
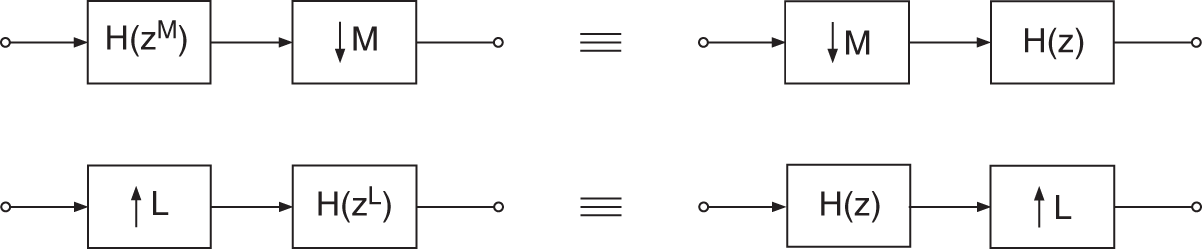
Figure 3.4 Identities for sampling rate conversion.
The use of polyphase decomposition can be demonstrated with the help of an example for 
and 
. This implies a sampling rate conversion from 48 kHz to 32 kHz. Figures 3.6 and 3.7 show two different solutions for polyphase decomposition of sampling rate conversion by 
. Further decompositions of the upsampling decomposition of Fig. 3.7 are demonstrated in Fig. 3.8. First, interpolation is implemented with a polyphase decomposition and the delay 
is decomposed to 
. Then, the downsampler of factor 3 is moved through the adder into the two paths (Fig. 3.8b) and the delays are moved according to the identities of Fig. 3.4. In Fig. 3.8c, the upsampler is exchanged with the downsampler and in a last step (Fig. 3.8d), another polyphase decomposition of 
and 
is carried out. The actual filter operations 
and 
with 
are performed at 
of the input sampling rate.
Figure 3.5 Decomposition in accordance with Euclid's theorem.
Figure 3.6 Polyphase decomposition for downsampling L/M
.
Figure 3.7 Polyphase decomposition for upsampling L/M
.
Figure 3.8 Sampling rate conversion by factor 
.
3.3 Asynchronous Conversion
Plesiochronous systems consist of partial systems with different and uncoupled sampling rates. Sampling rate conversion between such systems can be achieved through a DA conversion with the sampling rate of the first system followed by an AD conversion with the sampling rate of the second system. A digital approximation of this approach is made with a multi‐rate system [Lag81, Lag82a, Lag82b, Lag82c, Lag83, Ram82, Ram84]. Figure 3.9a shows a system for increasing the sampling rate by a factor 
followed by an anti‐imaging filter 
and a resampling of the interpolated signal 
. The samples 
are held for a clock period (see Fig. 3.9c) and then sampled with output clock period 
. The interpolation sampling rate must be increased so that the difference of two consecutive samples 
is smaller than the quantization step 
. The sample‐and‐hold function applied to 
suppresses the spectral images at multiples of 
(see Fig. 3.9b). The obtained signal is a band‐limited continuous‐time signal which can be sampled with output sampling rate 
.
For the calculation of the necessary oversampling rate, the problem is considered in the frequency domain. The sinc function of a sample‐and‐hold system (see Fig. 3.9b) at frequency 
is given by
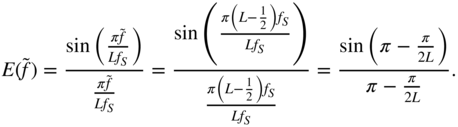
Figure 3.9 Approximation of DA/AD conversions.
With 
, we derive
This value of Eq. (3.29) should be lower than 
and allows the computation of the interpolation factor 
. For a given word length 
and quantization step 
, the necessary interpolation rate 
is calculated by
For a linear interpolation between upsampled samples 
, we can derive
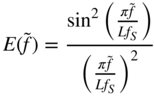
With this, it is possible to reduce the necessary interpolation rate to
Figure (3.10) demonstrates this with a two‐stage block diagram. First, interpolation up to a sampling rate 
is performed by conventional filtering. In the second stage, upsampling by factor 
is done by linear interpolation. The two‐stage approach must satisfy the sampling rate 
.
Figure 3.10 Linear interpolation before virtual sample‐and‐hold function.
The choice of the interpolation algorithm in the second stage enables the reduction of the first oversampling factor.
3.3.1 Single‐stage Methods
Direct conversion methods implement the block diagram [Lag83, Smi84, Par90, Par91a, Par91b, Ada92, Ada93] shown in Fig. 3.9a. The calculation of a discrete sample on an output grid of sampling rate 
from samples 
at sampling rate 
can be written as
where 
. With the transfer function
and the properties
the impulse response is given by
From Eq. (3.37), we can express the delayed signal
as the convolution between 
and 
. Figure 3.11 illustrates this convolution in the time domain for a fixed 
. Fig. 3.12 shows the coefficients 
for discrete 
(
) which are obtained from the intersection of the sinc function with the discrete samples 
.
To limit the convolution sum, the impulse response is windowed, which gives
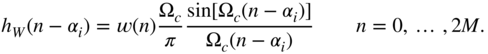
Figure 3.11 Convolution sum (3.42) in the time domain.
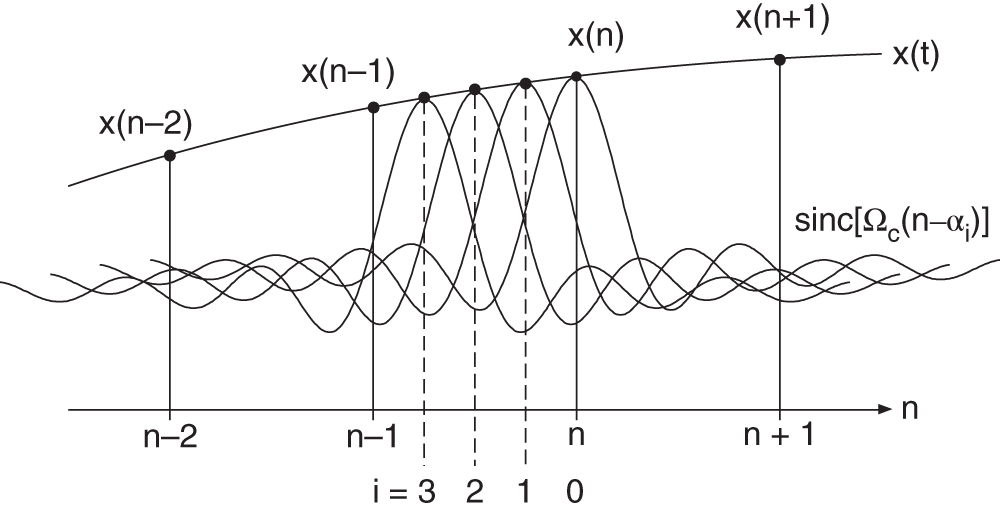
Figure 3.12 Convolution sum (3.42) for different 
.
From this, the sample estimate
results. A graphical interpretation of the time‐variant impulse response which depends on 
is shown in Fig. 3.13. The discrete segmentation between two input samples into 
intervals leads to 
partial impulse responses of length 
.
Figure 3.13 Sinc function and different impulse responses.
If the output sampling rate is smaller than the input sampling rate (
), band limiting (antialiasing) to the output sampling rate has to be done. This can be achieved with factor 
and leads, with the the scaling theorem of the Fourier transform, to
This time scaling of the impulse response has the consequence that the number of coefficients of the time‐variant partial impulse responses is increased. The number of required states also increases. Figure 3.14 shows the time‐scaled impulse response and elucidates the increase of the number 
of the coefficients.
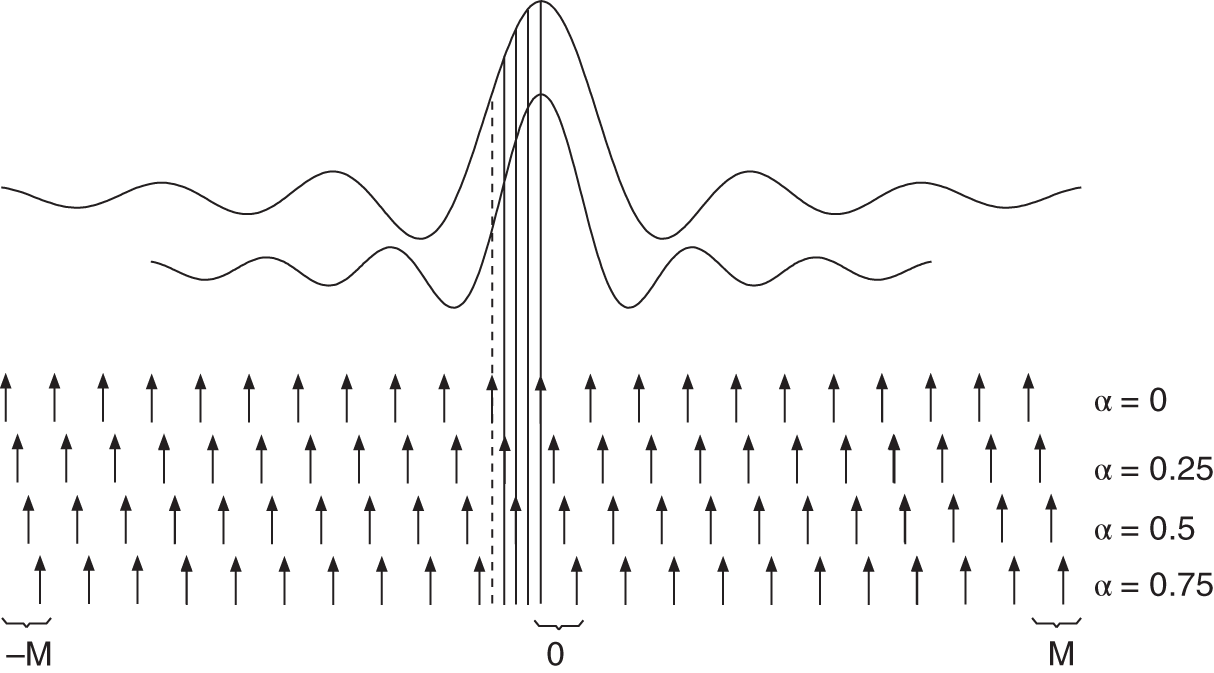
Figure 3.14 Time‐scaled impulse response.
3.3.2 Multistage Methods
The basis of a multistage conversion method [Lag81, Lag82a, Lag82b, Lag82c, Kat85, Kat86] is shown in Fig. 3.15a and will be described in the frequency domain, as shown in Fig. 3.15b–d. The increase of the sampling rate up to the rate 
before the sample‐and‐hold function is done in four stages. In the first two stages, the sampling rate is increased by a factor of two followed by an anti‐imaging filter (see Fig. 3.15b,c), which leads to a four‐times oversampled spectrum (Fig. 3.15d). In the third stage, the signal is upsampled by a factor of 32 and the image spectra are suppressed (see Fig. 3.15d,e). In the fourth stage (Fig. 3.15e), the signal is upsampled to a sampling rate of 
by a factor of 256 and a linear interpolator. The 
‐function of the linear interpolator suppresses the images at multiples of 
up to the spectrum at 
. The virtual sample‐and‐hold function is shown in Fig. 3.15f, where resampling at the output sampling rate is performed. A direct conversion of this kind of cascaded interpolation structure requires anti‐imaging filtering after every upsampling with the corresponding sampling rate. Although the necessary filter order decreases owing to a decrease of requirements for filter design, an implementation of the filters in the third and fourth stages is not possible directly. After a suggestion by Lagadec [Lag82c], the measurement of the ratio of input to output rate is used to control the polyphase filters in the third and fourth stages (see Fig. 3.16a, CON = control) to reduce complexity. Figure 3.16b–d illustrate an interpretation in the time domain. Figure 3.16b shows the interpolation of three samples between two input samples 
with the help of the first and second interpolation stages. The abscissa represents the intervals of the input sampling rate and the sampling rate is increased by a factor of four. In Fig. 3.16c, the four‐times oversampled signal is shown. The abscissa shows the four‐ times oversampled output grid. It is assumed that the output sample 
and input sample 
are identical. The output sample 
is now determined in such a form that, with the interpolator in the third stage, only two polyphase filters just before and after the output sample need to be calculated. Hence, only two out of a total of 31 possible polyphase filters are calculated in the third stage. Fig. 3.16d shows these two polyphase output samples. Between these two samples, the output sample 
is obtained with a linear interpolation on a grid of 255 values.
Figure 3.15 Multistage conversion – frequency‐domain interpretation.
Instead of the third and fourth stages, special interpolation methods can be used to calculate the output 
directly from the four‐times oversampled input signal (see Fig. 3.17) [Sti91, Cuc91, Liu92]. The upsampling factor 
for the last stage is calculated according to 
. Section 3.4 is devoted to different interpolation methods which allow a real‐time calculation of filter coefficients. This can be interpreted as time‐variant filters in which the filter coefficients are derived from the ratio of sampling rates. The calculation of one filter coefficient set for the output sample at the output rate is done by measuring the ratio of input to output sampling rate as described in the next section.
Figure 3.16 Time‐domain interpretation.
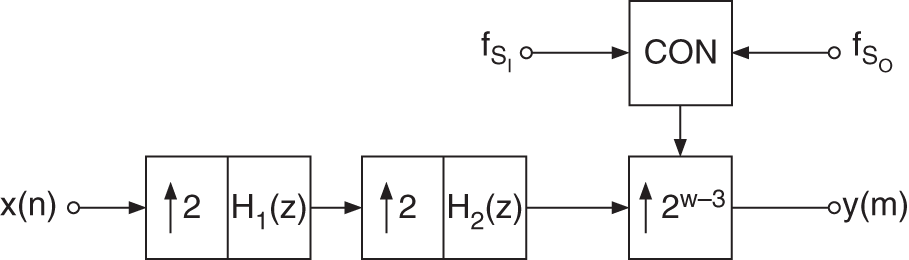
Figure 3.17 Sampling rate conversion with interpolation for calculating coefficients of a time‐variant interpolation filter.
3.3.3 Control of Interpolation Filters
The measurement of the ratio of input and output sampling rates is used to control the interpolation filters [Lag82a]. By increasing the sampling rate by a factor of 
, the input sampling period is divided into 
parts for a signal word‐length of 
bits. The time instant of the output sample is calculated on this grid with the help of the measured ratio of sampling periods 
as follows.
A counter is clocked with 
and reset by every new input sampling clock. A sawtooth curve of the counter output versus time is obtained, as shown in Fig. 3.18. The counter runs from 0 to 
during one input sampling period. At time 
, which corresponds to counter output 
, the output sampling period 
starts, and stops at time 
with counter output 
. The difference between both counter measurements allows for the calculation of the output sampling period 
with a resolution of 
.
Figure 3.18 Calculation of 
.
The new counter measurement is added to the difference of the previous counter measurements. As a result, the new counter measurement is obtained as
The modulo operation can be carried out with an accumulator of word length 
. The resulting time 
determines the time instant of the output sample at the output sampling rate and therefore the choice of the polyphase filter in a single‐stage conversion or the time instant for a multistage conversion.
The measurement of 
is illustrated in Fig. 3.19.
- The input sampling rate
is increased to 
using a frequency multiplier, where 
. This increased input clock by the factor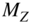 
triggers a 
‐bit counter. The counter output 
is evaluated every 
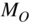output sampling periods. - Counting of
output sampling periods. - Simultaneous counting of the
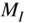input sampling periods.
The time intervals 
and 
(see Fig. 3.19) are given by
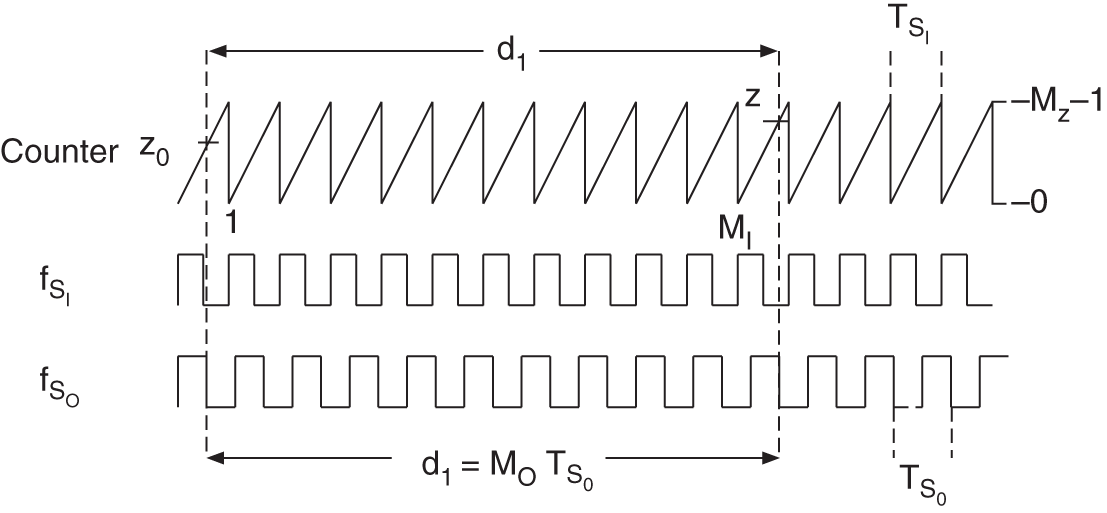
Figure 3.19 Measurement of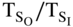 
.
and with the requirement 
, we can write
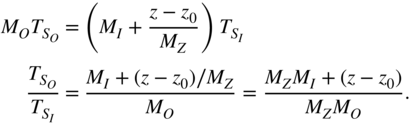
- Example 1:
,
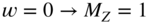(3.50)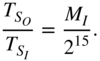
With a precision of 15 bits, the averaging number is chosen as
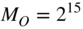and the number 
has to be determined. - Example 2:
,
(3.51)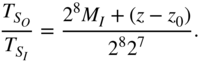
With a precision of 15 bits, the averaging number is chosen as
and the number 
, as well as the counter outputs, has to be determined.
The sampling rates at the input and output of a sampling rate converter can be calculated by evaluating the 8‐bit increment of the counter for each output clock with
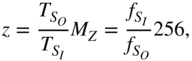
as seen from Table 3.1.
Table 3.1 Counter increments for different sampling rate conversions.
| Conversion/kHz | 8‐bit counter increment | ||
|---|---|---|---|
| 32 |  | 48 | 170 |
| 44.1 |  | 48 | 235 |
| 32 |  | 44.1 | 185 |
| 48 |  | 44.1 | 278 |
| 48 |  | 32 | 384 |
| 44.1 |  | 32 | 352 |
3.4 Interpolation Methods
In the following sections, special interpolation methods are discussed. These methods enable the calculation of time‐variant filter coefficients for sampling rate conversion and need an oversampled input sequence as well as the time instant of the output sample. A convolution of the oversampled input sequence with time‐variant filter coefficients gives the output sample at the output sampling rate. This real‐time computation of filter coefficients is not based on popular filter design methods. On the contrary, methods are presented for calculating filter coefficient sets for every input clock cycle where the filter coefficients are derived from the distance of output samples to the time grid of the oversampled input sequence.
3.4.1 Polynomial Interpolation
The aim of a polynomial interpolation [Liu92] is to determine a polynomial
of 
th order representing exactly a function 
at 
uniformly spaced 
, i.e. 
for 
. This can be written as a set of linear equations:
The polynomial coefficients 
as functions of 
are obtained with the help of Cramer's Rule according to
For uniformly spaced 
with 
, the interpolation of an output sample with distance 
gives
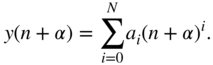
To determine the relationship between the output sample 
and 
, a set of time‐variant coefficients 
needs to be determined such that
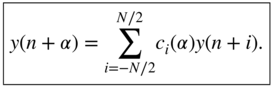
The calculation of time‐variant coefficients 
will be illustrated by an example.
3.4.2 Lagrange Interpolation
Lagrange interpolation for 
samples makes use of the polynomials 
which have the following properties (see Fig. 3.21):
Figure 3.21 Lagrange polynomial.
Based on the zeros of the polynomial 
, it follows that
With 
, the coefficients are given by
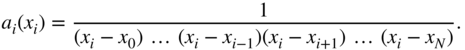
The interpolation polynomial is expressed as
With 
, Eq. (3.66) can be written as
For uniformly spaced samples,
and with the new variable 
, as given by
we get
and hence
For even 
, we can write
and for odd 
,
The interpolation of an output sample is given by
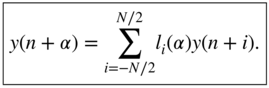
3.4.3 Spline Interpolation
The interpolation using piecewise‐defined functions that only exist over finite intervals is called spline interpolation [Cuc91]. The goal is to compute the sample 
from weighted samples 
.
A B‐spline 
of 
th order using 
samples is defined in the interval 
by
with the truncated power functions
In the following, 
will be considered for 
, where 
for 
and 
for 
. Figure 3.22 shows the truncated power functions and the B‐spline of 
th order. With the definition of the truncated power functions, we can write
and after some calculations, we get
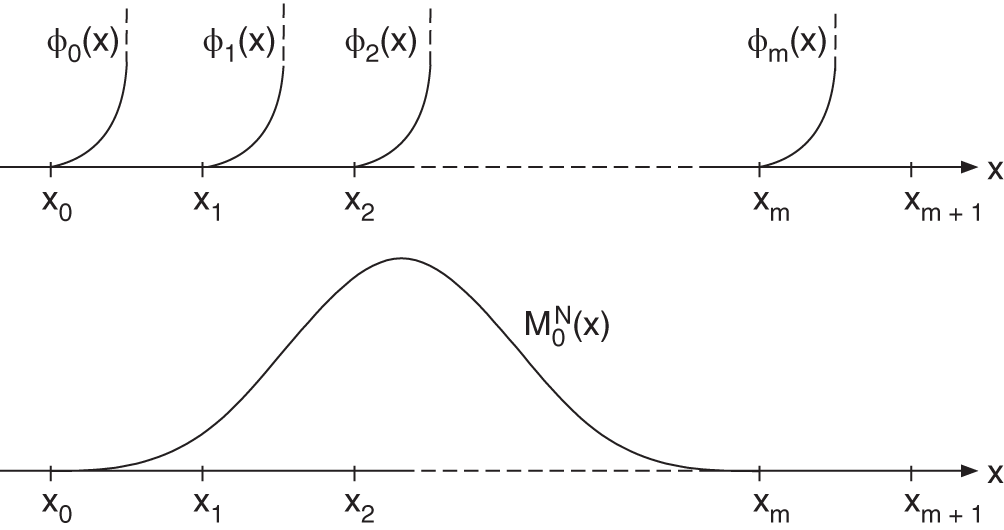
Figure 3.22 Truncated power functions and the B‐spline of Nth order.
With the condition 
for 
, the following set of linear equations can be written with Eq. (3.80) and the coefficients of the powers of 
:
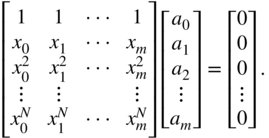
The homogeneous set of linear equations has nontrivial solutions for 
. The minimum requirement results in 
. For 
, the coefficients [Boe93] can be obtained as follows:
Setting the 
th column of the determinant in the numerator of Eq. (3.82) equal to zero corresponds to deleting the column. Computing both determinants of Vandermonde matrices [Bar90] and division leads to the coefficients
and hence
For some 
, we obtain
Because the functions 
decrease with increasing 
, a normalization of the form 
is done, such that for equidistant samples, we get
The next example illustrates the computation of B‐splines.
A linear combination of B‐splines is called a spline. Figure 3.24 shows the interpolation of sample 
for splines of second and third orders. The shifted B‐splines 
are evaluated at the vertical line representing the distance 
. With sample 
and the normalized B‐splines 
, the second‐ and third‐order splines are expressed as
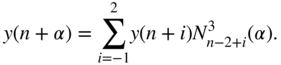
The computation of a second‐order B‐spline at the sample index 
is based on the symmetry properties of the B‐spline, which is depicted in Fig. 3.25. With (Eqs. 3.77) and (3.86), and with the symmetry properties shown in Fig. 3.25, the B‐splines can be written in the form of
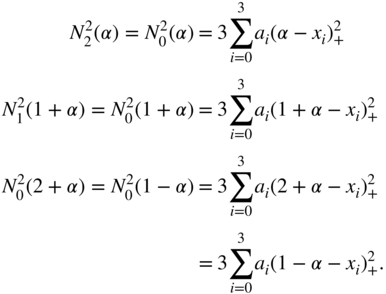
Figure 3.23 Third‐order B‐spline (
, 
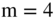, five samples).
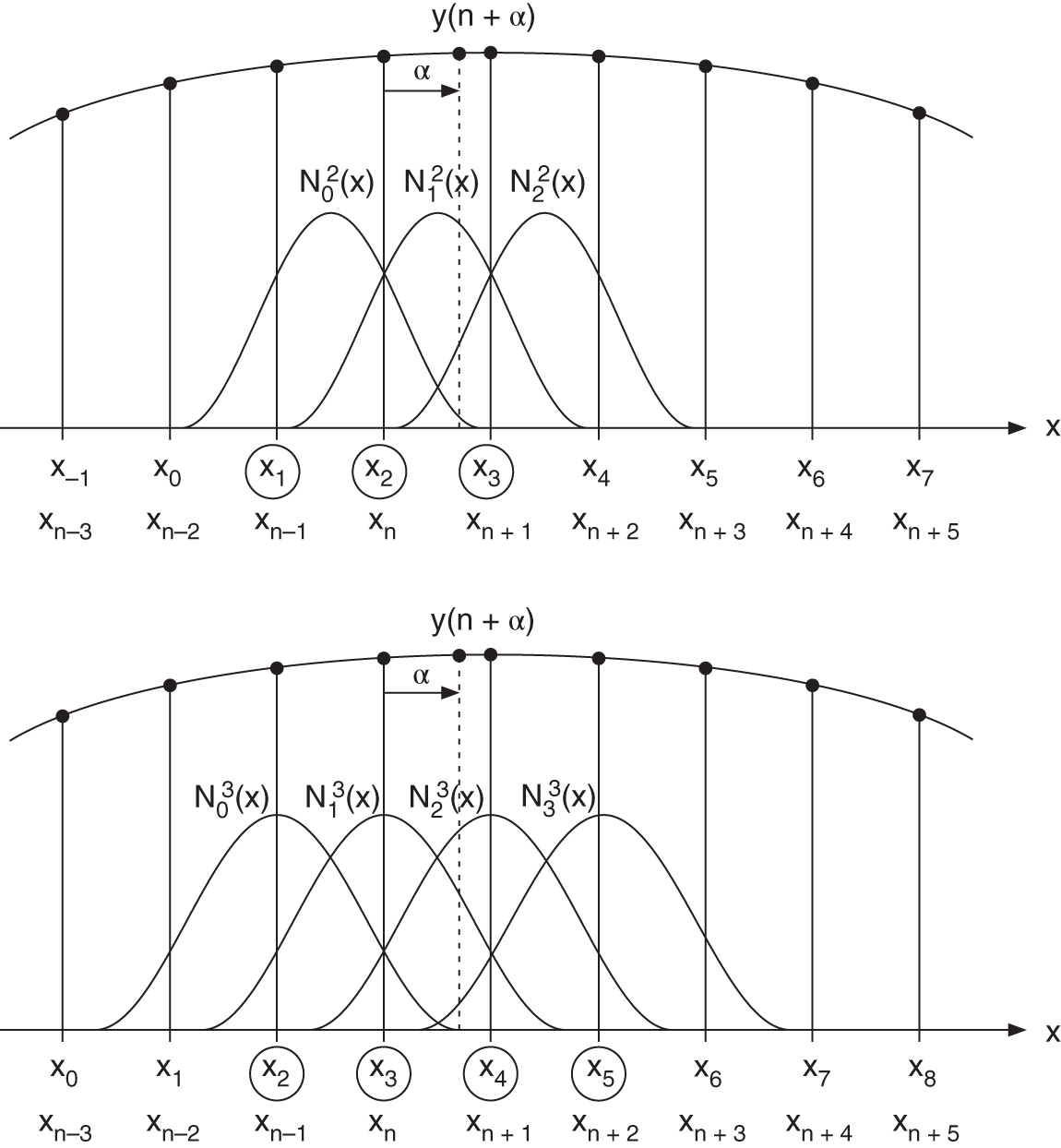
Figure 3.24 Interpolation with B‐splines of second and third orders.
With Eq. (3.83), we get the coefficients
and thus
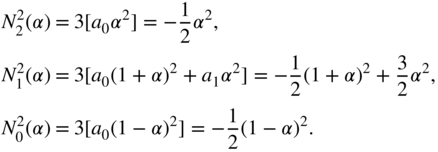
Owing to the symmetrical properties of the B‐splines, the time‐variant coefficients of the second‐order B‐spline can be derived as
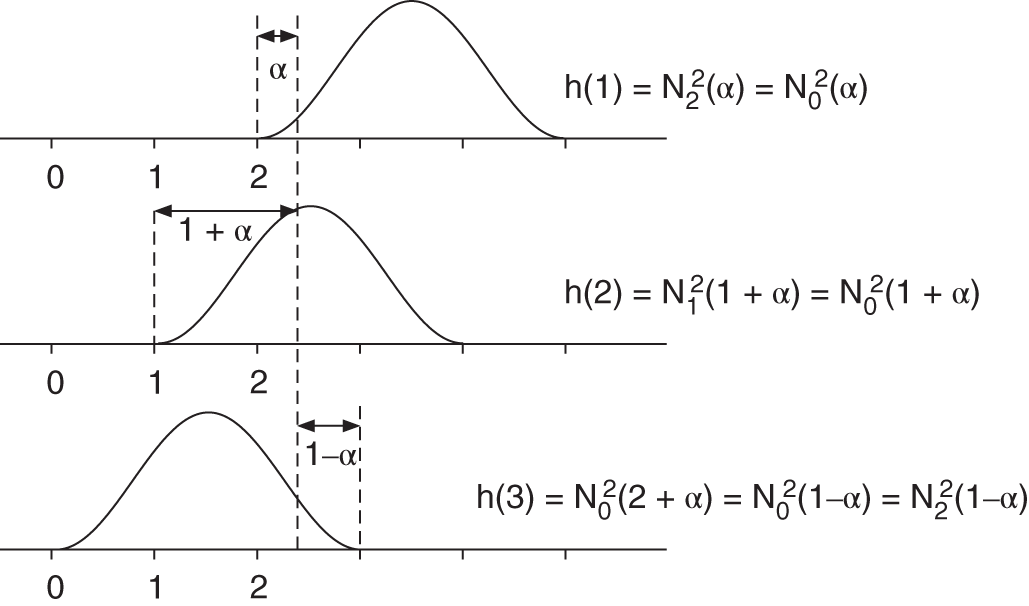
Figure 3.25 Exploiting the symmetry properties of a second‐order B‐spline.
In the same way, the time‐variant coefficients of a third‐order B‐spline are given by
Higher‐order B‐splines are given by
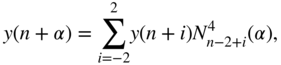
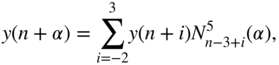
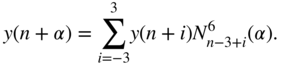
Similar sets of coefficients can be derived here as well. Figure 3.26 illustrates this for fourth‐ and sixth‐order B‐splines.
Generally, for even orders, we get
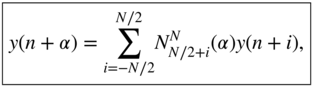
and for odd orders,
Figure 3.26 Interpolation with B‐splines of fourth and sixth order.
For the application of interpolation, the properties in the frequency domain are important. The zero‐order B‐spline is given by
and the Fourier transform gives the 
function in the frequency domain. The first‐order B‐spline, given by
leads to a 
function in the frequency domain. Higher‐order B‐splines can be derived by repeated convolution [Chu92] as given by
Thus, the Fourier transform leads to
With the help of the properties in the frequency domain, the necessary order of the spline interpolation can be determined. Owing to the attenuation properties of the 
function and the simple real‐time calculation of the coefficients, spline interpolation is well suited to time‐variant conversion in the last stage of a multistage sampling rate conversion system [Zöl94].
3.5 Exercises
1. Basics
Consider a simple sampling rate conversion system with a conversion rate of 
. The system consists of two upsampling blocks, each by a factor of 2, and one downsampling block by a factor of 3.
- What are anti‐imaging and anti‐aliasing filters and where do we need them in our system?
- Sketch the block diagram.
- Sketch the input, intermediate, and output spectra in the frequency domain.
- How is the amplitude affected by the up‐ and downsampling and where does it come from?
- Sketch the frequency response of the anti‐aliasing and anti‐imaging filters needed for this upsampling system.
2. Synchronous Conversion
Our system will now be upsampled directly by a factor of 4 and again downsampled by the factor of 3, but with linear interpolation and decimation methods. The input signal is 
.
- What are the impulse responses of the two interpolation filters? Sketch their magnitude responses.
- Plot the signals (input, intermediate, and output signal) in the time domain using Matlab.
- What is the delay resulting from the causal interpolation/decimation filters?
- Show the error introduced by this interpolation/decimation method in the frequency domain.
3. Polyphase Representation
Now we extend our system using a polyphase decomposition of the interpolation/decimation filters.
- Sketch the idea of polyphase decomposition using a block diagram. What is the benefit of such decomposition?
- Calculate the polyphase filters for up‐ and downsampling (using interpolation and decimation).
- Plot with Matlab all resulting signals in the time and frequency domains.
4. Asynchronous Conversion
- What is the basic concept of asynchronous sampling rate conversion?
- Sketch the block diagram and discuss the individual operations.
- What is the necessary oversampling factor
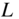for a 20‐bit resolution? - How can we simplify the oversampling operations?
- How can we make use of polyphase filtering?
- Why are half‐band filters an efficient choice for the upsampling operation?
- Which parameters determine the interpolation algorithms in the last stage of the conversion?
References
- [Ada92] R. Adams, T. Kwan: VLSI Architectures for Asynchronous Sample‐Rate Conversion, Proc. 93rd AES Convention, San Francisco, Preprint No. 3355, October 1992.
- [Ada93] R. Adams, T. Kwan: Theory and VLSI Implementations for Asynchronous Sample‐Rate Conversion, Proc. 94th AES Convention, Berlin, Preprint No. 3570, March 1993.
- [Bar90] S. Barnett: Matrices ‐ Methods and Applications, Oxford University Press, 1990.
- [Boe93] W. Boehm, H. Prautzsch: Numerical Methods, AK Peters/Vieweg, 1993.
- [Chu92] C.K. Chui (ed.): Wavelets: A Tutorial in Theory and Applications, Volume 2, Academic Press, Boston, 1992.
- [Cro83] R.E. Crochiere, L.R. Rabiner: Multirate Digital Signal Processing, Prentice‐Hall, Englewood Cliffs, 1983.
- [Cuc91] S. Cucchi, F. Desinan, G. Parladori, G. Sicuranza: DSP Implementation of Arbitrary Sampling Frequency Conversion for High Quality Sound Application, Proc. IEEE ICASSP‐91, Toronto, pp. 3609–3612, May 1991.
- [Fli00] N. Fliege: Multirate Digital Signal Processing, J. Wiley & Sons, Chichester, 2000.
- [Hsi87] C.‐C. Hsiao: Polyphase Filter Matrix for Rational Sampling Rate Conversions, Proc. IEEE ICASSP‐87, Dallas, pp. 2173–2176, April 1987.
- [Kat85] Y. Katsumata, O. Hamada: A Digital Audio Sampling Frequency Converter Employing New Digital Signal Processors, Proc. 79th AES Convention, New York, Preprint No. 2272, October 1985.
- [Kat86] Y. Katsumata, O. Hamada: An Audio Sampling Frequency Conversion Using Digital Signal Processors, Proc. IEEE ICASSP‐86, Tokyo, pp. 33–36, 1986.
- [Lag81] R. Lagadec, H.O. Kunz: A Universal, Digital Sampling Frequency Converter for Digital Audio, Proc. IEEE ICASSP‐81, Atlanta, pp. 595–598, April 1981.
- [Lag82a] R. Lagadec, D. Pelloni, D. Weiss: A Two‐Channel Professional Digital Audio Sampling Frequency Converter, Proc. 71st AES Convention, Montreux, Preprint No. 1882, March 1982.
- [Lag82b] D. Lagadec, D. Pelloni, D. Weiss: A 2‐Channel, 16‐Bit Digital Sampling Frequency Converter for Professional Digital Audio, Proc. IEEE ICASSP‐82, Paris, pp. 93–96, May 1982.
- [Lag82c] R. Lagadec: Digital Sampling Frequency Conversion, Digital Audio, Collected Papers from the AES Premier Conference, pp. 90–96, June 1982.
- [Lag83] R. Lagadec, D. Pelloni, A. Koch: Single‐Stage Sampling Frequency Conversion, Proc. 74th AES Convention, New York, Preprint No. 2039, October 1983.
- [Liu92] G.‐S. Liu, C.‐H. Wei: A New Variable Fractional Delay Filter with Nonlinear Interpolation, IEEE Trans. Circuits and Systems‐II: Analog and Digital Signal Processing, Vol. 39, No.2, pp. 123–126, February 1992.
- [Opp99] A.V. Oppenheim, R.W. Schafer, J.R. Buck: Discret‐time Signal Processing, Prentice‐Hall, 2nd Edition, 1999.
- [Par90] S. Park, R. Robles: A Real‐Time Method for Sample‐Rate Conversion from CD to DAT, Proc. IEEE Int. Conf. Consumer Electronics, Chicago, pp. 360–361, June 1990.
- [Par91a] S. Park: Low Cost Sample Rate Converters, Proc. NAB Broadcast Engineering Conference, Las Vegas, April 1991.
- [Par91b] S. Park, R. Robles: A Novel Structure for Real‐Time Digital Sample‐Rate Converters with Finite Precision Error Analysis, Proc. IEEE ICASSP‐91, Toronto, pp. 3613–3616, May 1991.
- [Ram82] T.A. Ramstad: Sample‐Rate Conversion by Arbitrary Ratios, Proc. IEEE ICASSP‐82, Paris, pp. 101–104, May 1982.
- [Ram84] T.A. Ramstad: Digital Methods for Conversion Between Arbitrary Sampling Frequencies, IEEE Transactions on Acoustics, Speech and Signal Processing, vol. ASSP‐ 32, no. 3, pp. 577–591, June 1984.
- [Smi84] J.O. Smith, P. Gossett: A Flexible Sampling‐Rate Conversion Method, Proc. IEEE ICASSP‐84, pp. 19.4.1–19.4.4, 1984.
- [Sti91] E.F. Stikvoort: Digital Sampling Rate Converter with Interpolation in Continuous Time, Proc. 90th AES Convention, Paris, Preprint No. 3018, Feb. 1991.
- [Vai93] P.P. Vaidyanathan: Multirate Systems and Filter Banks, Prentice‐Hall, Englewood Cliffs, 1993.
- [Zöl94] U. Zölzer, T. Boltze: Interpolation Algorithms: Theory and Application, Proc. 97th AES Convention, San Francisco, Preprint No. 3898, November 1994.