6. Methods: A Deeper Look

Objectives

In this chapter you’ll learn:

• How static methods and fields are associated with an entire class rather than specific instances of the class.

• To use common Math methods available in the Java API.

• To understand the mechanisms for passing information between methods.

• How the method call/return mechanism is supported by the method-call stack and activation records.

• How packages group related classes.

• How to use random-number generation to implement game-playing applications.

• How the visibility of declarations is limited to specific regions of programs.

• What method overloading is and how to create overloaded methods.

• To write and use recursive functions, i.e., functions that call themselves.

The greatest invention of the nineteenth century was the invention of the method of invention.

—Alfred North Whitehead

Call me Ishmael.

—Herman Melville

When you call me that, smile!

—Owen Wister

Answer me in one word.

—William Shakespeare

O! call back yesterday, bid time return.

—William Shakespeare

There is a point at which methods devour themselves.

—Frantz Fanon

Outline

6.1   Introduction

6.2   Program Modules in Java

6.3   static Methods, static Fields and Class Math

6.4   Declaring Methods with Multiple Parameters

6.5   Notes on Declaring and Using Methods

6.6   Method-Call Stack and Activation Records

6.7   Argument Promotion and Casting

6.8   Java API Packages

6.9   Case Study: Random-Number Generation

6.9.1   Generalized Scaling and Shifting of Random Numbers

6.9.2   Random-Number Repeatability for Testing and Debugging

6.10   Case Study: A Game of Chance (Introducing Enumerations)

6.11   Scope of Declarations

6.12   Method Overloading

6.13   Introduction to Recursion

6.14   Recursion Concepts

6.15   Example Using Recursion: Factorials

6.16   Example Using Recursion: Fibonacci Series

6.17   Recursion and the Method-Call Stack

6.18   Recursion vs. Iteration

6.19   (Optional) Software Engineering Case Study: Identifying Class Operations

6.20   Wrap-Up

6.1 Introduction

We introduced methods in Chapter 3. In this chapter, we study methods in more depth. We emphasize how to declare and use methods to facilitate the design, implementation, operation and maintenance of large programs.

You’ll see that it is possible for static methods to be called without the need for an object of the class to exist. You’ll learn how to declare a method with more than one parameter. You’ll also learn how Java is able to keep track of which method is currently executing, how local variables of methods are maintained in memory and how a method knows where to return after it completes execution.

We’ll take a brief diversion into simulation techniques with random-number generation and develop a version of the casino dice game called craps that uses most of the programming techniques you’ve used to this point in the book. In addition, you’ll learn how to declare values that cannot change (i.e., constants) in your programs.

Many of the classes you’ll use or create while developing applications will have more than one method of the same name. This technique, called overloading, is used to implement methods that perform similar tasks for arguments of different types or for different numbers of arguments. The chapter concludes with a discussion of functions that call themselves, either directly, or indirectly (through another function)—a topic called recursion.

6.2 Program Modules in Java

Three kinds of modules exist in Java—methods, classes and packages. Java programs are written by combining new methods and classes that you write with predefined methods and classes available in the Java Application Programming Interface (also referred to as the Java API or Java class library) and in various other class libraries. Related classes are typically grouped into packages so that they can be imported into programs and reused. You’ll see how to group your own classes into packages in Chapter 8. The Java API provides a rich collection of predefined classes that contain methods for performing common mathematical calculations, string manipulations, character manipulations, input/output operations, database operations, networking operations, file processing, error checking and many other useful operations.

Good Programming Practice 6.1

Familiarize yourself with the rich collection of classes and methods provided by the Java API (java.sun.com/javase/6/docs/api/). In Section 6.8, we present an overview of several common packages. In Appendix G, we explain how to navigate the Java API documentation.

Software Engineering Observation 6.1

Don’t try to reinvent the wheel. When possible, reuse Java API classes and methods. This reduces program development time and avoids introducing programming errors.

One motivation for modularizing a program into methods is the divide-and-conquer approach, which makes program development more manageable by constructing programs from small, simple pieces. Another is software reusability—using existing methods as building blocks to create new programs. Often, you can create programs mostly from standardized methods rather than by building customized code. For example, in earlier programs, we did not have to define how to read data values from the keyboard—Java provides these capabilities in class Scanner. A third motivation is to avoid repeating code. Dividing a program into meaningful methods makes the program easier to debug and maintain.

Software Engineering Observation 6.2

To promote software reusability, every method should be limited to performing a single, well-defined task, and the name of the method should express that task effectively. Such methods make programs easier to write, debug, maintain and modify.

Error-Prevention Tip 6.1

A small method that performs one task is easier to test and debug than a larger method that performs many tasks.

Software Engineering Observation 6.3

If you cannot choose a concise name that expresses a method’s task, your method might be attempting to perform too many diverse tasks. It is often appropriate to break such a method into several smaller method declarations.

6.3 static Methods, static Fields and Class Math

As you know, every class provides methods that perform common tasks on objects of the class. For example, to input data from the keyboard, you have called methods on a Scanner object that was initialized in its constructor to obtain input from the standard input stream (System.in). As you’ll learn in Chapter 14, Files and Streams, you can initialize a Scanner to obtain input from other sources, such as a file on disk. One program could have a Scanner object that inputs information from the standard input stream and a second Scanner that inputs information from a file. Each input method called on the standard input stream Scanner would obtain input from the keyboard, and each input method called on the file Scanner would obtain input from the specified file on disk.

Although most methods execute in response to method calls on specific objects, this is not always the case. Sometimes a method performs a task that does not depend on the contents of any object. Such a method applies to the class in which it is declared as a whole and is known as a static method or a class method. It is common for classes to contain convenient static methods to perform common tasks. For example, recall that we used static method pow of class Math to raise a value to a power in Fig. 5.6. To declare a method as static, place the keyword static before the return type in the method’s declaration. You can call any static method by specifying the name of the class in which the method is declared, followed by a dot (.) and the method name, as in

ClassName.methodName( arguments )

We use various Math class methods here to present the concept of static methods. Class Math provides a collection of methods that enable you to perform common mathematical calculations. For example, you can calculate the square root of 900.0 with the static method call

Math.sqrt( 900.0 )

The preceding expression evaluates to 30.0. Method sqrt takes an argument of type double and returns a result of type double. To output the value of the preceding method call in the command window, you might write the statement

System.out.println( Math.sqrt( 900.0 ) );

In this statement, the value that sqrt returns becomes the argument to method println. Note that there was no need to create a Math object before calling method sqrt. Also note that all Math class methods are static—therefore, each is called by preceding the name of the method with the class name Math and the dot (.) separator.

Software Engineering Observation 6.4

Class Math is part of the java.lang package, which is implicitly imported by the compiler, so it is not necessary to import class Math to use its methods.

Method arguments may be constants, variables or expressions. If c = 13.0, d = 3.0 and f = 4.0, then the statement

System.out.println( Math.sqrt( c + d * f ) );

calculates and prints the square root of 13.0 + 3.0 * 4.0 = 25.0—namely, 5.0. Figure 6.1 summarizes several Math class methods. In the figure, x and y are of type double.

Fig. 6.1. Math class methods.

Math Class Constants PI and E

Class Math also declares two fields that represent commonly used mathematical constants: Math.PI and Math.E. The constant Math.PI (3.14159265358979323846) is the ratio of a circle’s circumference to its diameter. The constant Math.E (2.7182818284590452354) is the base value for natural logarithms (calculated with static Math method log). These fields are declared in class Math with the modifiers public, final and static. Making them public allows other programmers to use these fields in their own classes. Any field declared with keyword final is constant—its value cannot be changed after the field is initialized. Both PI and E are declared final because their values never change. Making these fields static allows them to be accessed via the class name Math and a dot (.) separator, just like class Math’s methods. Recall from Section 3.5 that when each object of a class maintains its own copy of an attribute, the field that represents the attribute is also known as an instance variable—each object (instance) of the class has a separate instance of the variable in memory. There are fields for which each object of a class does not have a separate instance of the field. That is the case with static fields, which are also known as class variables. When objects of a class containing static fields are created, all the objects of that class share one copy of the class’s static fields. Together the class variables (i.e., static variables) and instance variables represent the fields of a class. You’ll learn more about static fields in Section 8.11.

Why Is Method main Declared static?

Why must main be declared static? When you execute the Java Virtual Machine (JVM) with the java command, the JVM attempts to invoke the main method of the class you specify—when no objects of the class have been created. Declaring main as static allows the JVM to invoke main without creating an instance of the class. Method main is declared with the header:

public static void main( String args[] )

When you execute your application, you specify its class name as an argument to the command java, as in

java ClassName argument1 argument2 ...

The JVM loads the class specified by ClassName and uses that class name to invoke method main. In the preceding command, ClassName is a command-line argument to the JVM that tells it which class to execute. Following the ClassName, you can also specify a list of Strings (separated by spaces) as command-line arguments that the JVM will pass to your application. Such arguments might be used to specify options (e.g., a file name) to run the application. As you’ll learn in Chapter 7, Arrays, your application can access those command-line arguments and use them to customize the application.

Additional Comments about Method main

In earlier chapters, every application had one class that contained only main and possibly a second class that was used by main to create and manipulate objects. Actually, any class can contain a main method. In fact, each of our two-class examples could have been implemented as one class. For example, in the application in Fig. 5.9 and Fig. 5.10, method main (lines 6–16 of Fig. 5.10) could have been taken as is and placed in class GradeBook (Fig. 5.9). You would then execute the application by typing the command java GradeBook in the command window—the application results would be identical to those of the two-class version. You can place a main method in every class you declare. The JVM invokes the main method only in the class used to execute the application. Some programmers take advantage of this to build a small test program into each class they declare.

6.4 Declaring Methods with Multiple Parameters

We now show how to write methods with multiple parameters. The application in Fig. 6.2 and Fig. 6.3 uses a programmer-declared method called maximum to determine and return the largest of three double values that are input by the user. When the application begins execution, class MaximumFinderTest’s main method (lines 7–11 of Fig. 6.3) creates one object of class MaximumFinder (line 9) and calls the object’s determineMaximum method (line 10) to produce the program’s output. In class MaximumFinder (Fig. 6.2), lines 14–18 of method determineMaximum prompt the user to enter three double values, then read them from the user. Line 21 calls method maximum (declared in lines 28–41) to determine the largest of the three double values passed as arguments to the method. When method maximum returns the result to line 21, the program assigns maximum’s return value to local variable result. Then line 24 outputs the maximum value. At the end of this section, we’ll discuss the use of operator + in line 24.

Fig. 6.2. Programmer-declared method maximum that has three double parameters.

Fig. 6.3. Application to test class MaximumFinder.

Consider the declaration of method maximum (lines 28–41). Line 28 indicates that the method returns a double value, that the method’s name is maximum and that the method requires three double parameters (x, y and z) to accomplish its task. When a method has more than one parameter, the parameters are specified as a comma-separated list. When maximum is called from line 21, the parameter x is initialized with the value of the argument number1, the parameter y is initialized with the value of the argument number2 and the parameter z is initialized with the value of the argument number3. There must be one argument in the method call for each parameter (sometimes called a formal parameter) in the method declaration. Also, each argument must be consistent with the type of the corresponding parameter. For example, a parameter of type double can receive values like 7.35, 22 or –0.03456, but not Strings like "hello" nor the boolean values true or false. Section 6.7 discusses the argument types that can be provided in a method call for each parameter of a primitive type.

To determine the maximum value, we begin with the assumption that parameter x contains the largest value, so line 30 declares local variable maximumValue and initializes it with the value of parameter x. Of course, it is possible that parameter y or z contains the actual largest value, so we must compare each of these values with maximumValue. The if statement at lines 33–34 determines whether y is greater than maximumValue. If so, line 34 assigns y to maximumValue. The if statement at lines 37–38 determines whether z is greater than maximumValue. If so, line 38 assigns z to maximumValue. At this point the largest of the three values resides in maximumValue, so line 40 returns that value to line 21. When program control returns to the point in the program where maximum was called, maximum’s parameters x, y and z no longer exist in memory. Note that methods can return at most one value, but the returned value could be a reference to an object that contains many values.

Note that result is a local variable in determineMaximum because it is declared in the block that represents the method’s body. Variables should be declared as fields of a class only if they are required for use in more than one method of the class or if the program should save their values between calls to the class’s methods.

Common Programming Error 6.1

Declaring method parameters of the same type as float x, y instead of float x, float y is a syntax error—a type is required for each parameter in the parameter list.

Software Engineering Observation 6.5

A method that has many parameters may be performing too many tasks. Consider dividing the method into smaller methods that perform the separate tasks. As a guideline, try to fit the method header on one line if possible.

Implementing Method maximum by Reusing Method Math.max

Recall from Fig. 6.1 that class Math has a max method that can determine the larger of two values. The entire body of our maximum method could also be implemented with two calls to Math.max, as follows:

return Math.max( x, Math.max( y, z ) );

The first call to Math.max specifies arguments x and Math.max( y, z ). Before any method can be called, its arguments must be evaluated to determine their values. If an argument is a method call, the method call must be performed to determine its return value. So, in the preceding statement, Math.max( y, z ) is evaluated first to determine the maximum of y and z. Then the result is passed as the second argument to the other call to Math.max, which returns the larger of its two arguments. This is a good example of software reuse—we find the largest of three values by reusing Math.max, which finds the largest of two values. Note how concise this code is compared to lines 30–40 of Fig. 6.2.

Assembling Strings with String Concatenation

Java allows String objects to be created by assembling smaller strings into larger strings using operator + (or the compound assignment operator +=). This is known as string concatenation. When both operands of operator + are String objects, operator + creates a new String object in which the characters of the right operand are placed at the end of those in the left operand. For example, the expression "hello " + "there" creates the String "hello there".

In line 24 of Fig. 6.2, the expression "Maximum is: " + result uses operator + with operands of types String and double. Every primitive value and object in Java has a String representation. When one of the + operator’s operands is a String, the other is converted to a String, then the two are concatenated. In line 24, the double value is converted to its String representation and placed at the end of the String "Maximum is: ". If there are any trailing zeros in a double value, these will be discarded when the number is converted to a String. Thus, the number 9.3500 would be represented as 9.35 in the resulting String.

For primitive values used in string concatenation, the primitive values are converted to Strings. If a boolean is concatenated with a String, the boolean is converted to the String "true" or "false". All objects have a method named toString that returns a String representation of the object. When an object is concatenated with a String, the object’s toString method is implicitly called to obtain the String representation of the object. You’ll learn more about the method toString in Chapter 7.

When a large String literal is typed into a program’s source code, programmers sometimes prefer to break that String into several smaller Strings and place them on multiple lines of code for readability. In this case, the Strings can be reassembled using concatenation. We discuss the details of Strings in Chapter 25, Strings, Characters and Regular Expressions.

Common Programming Error 6.2

It is a syntax error to break a String literal across multiple lines in a program. If a String does not fit on one line, split the String into several smaller Strings and use concatenation to form the desired String.

Common Programming Error 6.3

Confusing the + operator used for string concatenation with the + operator used for addition can lead to strange results. Java evaluates the operands of an operator from left to right. For example, if integer variable y has the value 5, the expression "y + 2 = " + y + 2 results in the string "y + 2 = 52", not "y + 2 = 7", because first the value of y (5) is concatenated with the string "y + 2 = ", then the value 2 is concatenated with the new larger string "y + 2 = 5". The expression "y + 2 = " + (y + 2) produces the desired result "y + 2 = 7".

6.5 Notes on Declaring and Using Methods

There are three ways to call a method:

1. Using a method name by itself to call another method of the same class—such as maximum( number1, number2, number3 ) in line 21 of Fig. 6.2.

2. Using a variable that contains a reference to an object, followed by a dot (.) and the method name to call a method of the referenced object—such as the method call in line 10 of Fig. 6.3, maximumFinder.determineMaximum(), which calls a method of class MaximumFinder from the main method of MaximumFinderTest.

3. Using the class name and a dot (.) to call a static method of a class—such as Math.sqrt( 900.0 ) in Section 6.3.

Note that a static method can call only other static methods of the same class directly (i.e., using the method name by itself) and can manipulate only static fields in the same class directly. To access the class’s non-static members, a static method must use a reference to an object of the class. Recall that static methods relate to a class as a whole, whereas non-static methods are associated with a specific instance (object) of the class and may manipulate the instance variables of that object. Many objects of a class, each with its own copies of the instance variables, may exist at the same time. Suppose a static method were to invoke a non-static method directly. How would the method know which object’s instance variables to manipulate? What would happen if no objects of the class existed at the time the non-static method was invoked? Clearly, such a situation would be problematic. Thus, Java does not allow a static method to access non-static members of the same class directly.

There are three ways to return control to the statement that calls a method. If the method does not return a result, control returns when the program flow reaches the method-ending right brace or when the statement

return;

is executed. If the method returns a result, the statement

return expression;

evaluates the expression, then returns the result to the caller.

Common Programming Error 6.4

Declaring a method outside the body of a class declaration or inside the body of another method is a syntax error.

Common Programming Error 6.5

Omitting the return-value-type in a method declaration is a syntax error.

Common Programming Error 6.6

Placing a semicolon after the right parenthesis enclosing the parameter list of a method declaration is a syntax error.

Common Programming Error 6.7

Redeclaring a method parameter as a local variable in the method’s body is a compilation error.

Common Programming Error 6.8

Forgetting to return a value from a method that should return a value is a compilation error. If a return-value-type other than void is specified, the method must contain a return statement that returns a value consistent with the method’s return-value-type. Returning a value from a method whose return type has been declared void is a compilation error.

6.6 Method-Call Stack and Activation Records

To understand how Java performs method calls, we first need to consider a data structure (i.e., collection of related data items) known as a stack. Stacks are known as last-in, first-out (LIFO) data structures—the last item pushed (inserted) on the stack is the first item popped (removed) from the stack.

When a program calls a method, the called method must know how to return to its caller, so the return address of the calling method is pushed onto the program execution stack (sometimes referred to as the method-call stack). If a series of method calls occurs, the successive return addresses are pushed onto the stack in last-in, first-out order so that each method can return to its caller.

The program execution stack also contains the memory for the local variables used in each invocation of a method during a program’s execution. This data, stored as a portion of the program execution stack, is known as the activation record or stack frame of the method call. When a method call is made, the activation record for that method call is pushed onto the program execution stack. When the method returns to its caller, the activation record for this method call is popped off the stack and those local variables are no longer known to the program. If a local variable holding a reference to an object is the only variable in the program with a reference to that object, when the activation record containing that local variable is popped off the stack, the object can no longer be accessed by the program and will eventually be deleted from memory by the JVM during “garbage collection.” We’ll discuss garbage collection in Section 8.10.

Of course, the amount of memory in a computer is finite, so only a certain amount of memory can be used to store activation records on the program execution stack. If more method calls occur than can have their activation records stored on the program execution stack, an error known as a stack overflow occurs.

6.7 Argument Promotion and Casting

Another important feature of method calls is argument promotion—converting an argument’s value to the type that the method expects to receive in its corresponding parameter. For example, a program can call Math method sqrt with an integer argument even though the method expects to receive a double argument (but, as we’ll soon see, not vice versa). The statement

System.out.println( Math.sqrt( 4 ) );

correctly evaluates Math.sqrt( 4 ) and prints the value 2.0. The method declaration’s parameter list causes Java to convert the int value 4 to the double value 4.0 before passing the value to sqrt. Attempting these conversions may lead to compilation errors if Java’s promotion rules are not satisfied. The promotion rules specify which conversions are allowed—that is, which conversions can be performed without losing data. In the sqrt example above, an int is converted to a double without changing its value. However, converting a double to an int truncates the fractional part of the double value—thus, part of the value is lost. Converting large integer types to small integer types (e.g., long to int) may also result in changed values.

The promotion rules apply to expressions containing values of two or more primitive types and to primitive-type values passed as arguments to methods. Each value is promoted to the “highest” type in the expression. (Actually, the expression uses a temporary copy of each value—the types of the original values remain unchanged.) Figure 6.4 lists the primitive types and the types to which each can be promoted. Note that the valid promotions for a given type are always to a type higher in the table. For example, an int can be promoted to the higher types long, float and double.

Fig. 6.4. Promotions allowed for primitive types.

Converting values to types lower in the table of Fig. 6.4 will result in different values if the lower type cannot represent the value of the higher type (e.g., the int value 2000000 cannot be represented as a short, and any floating-point number with digits after its decimal point cannot be represented in an integer type such as long, int or short). Therefore, in cases where information may be lost due to conversion, the Java compiler requires you to use a cast operator (introduced in Section 4.7) to explicitly force the conversion to occur—otherwise a compilation error occurs. This enables you to “take control” from the compiler. You essentially say, “I know this conversion might cause loss of information, but for my purposes here, that’s fine.” Suppose method square calculates the square of an integer and thus requires an int argument. To call square with a double argument named doubleValue, we would be required to write the method call as

square( (int) doubleValue )

This method call explicitly casts (converts) the value of doubleValue to an integer for use in method square. Thus, if doubleValue’s value is 4.5, the method receives the value 4 and returns 16, not 20.25.

Common Programming Error 6.9

Converting a primitive-type value to another primitive type may change the value if the new type is not a valid promotion. For example, converting a floating-point value to an integral value may introduce truncation errors (loss of the fractional part) into the result.

6.8 Java API Packages

As we have seen, Java contains many predefined classes that are grouped into categories of related classes called packages. Together, we refer to these packages as the Java Application Programming Interface (Java API), or the Java class library.

Throughout the text, import declarations specify the classes required to compile a Java program. For example, a program includes the declaration

import java.util.Scanner;

to specify that the program uses class Scanner from the java.util package. This allows you to use the simple class name Scanner, rather than the fully qualified class name java.util.Scanner, in the code. A great strength of Java is the large number of classes in the packages of the Java API. Some key Java API packages are described in Fig. 6.5, which represents only a small portion of the reusable components in the Java API. When learning Java, spend a portion of your time browsing the packages and classes in the Java API documentation (java.sun.com/javase/6/docs/api/).

Fig. 6.5. Java API packages (a subset).

The set of packages available in Java SE 6 is quite large. In addition to the packages summarized in Fig. 6.5, Java SE 6 includes packages for complex graphics, advanced graphical user interfaces, printing, advanced networking, security, database processing, multimedia, accessibility (for people with disabilities) and many other capabilities. For an overview of the packages in Java SE 6, visit

java.sun.com/javase/6/docs/api/overview-summary.html

Many other packages are also available for download at java.sun.com.

You can locate additional information about a predefined Java class’s methods in the Java API documentation at java.sun.com/javase/6/docs/api/. When you visit this site, click the Index link to see an alphabetical listing of Java API classes, interfaces and methods. Locate the class name and click its link to see the class’s description. Click the METHOD link to see a table of the class’s methods. Each static method is listed with the word “static” preceding the method’s return type. For a more detailed overview of navigating the Java API documentation, see Appendix G.

Good Programming Practice 6.2

The online Java API documentation is easy to search and provides many details about each class. As you learn a class in this book, you should get in the habit of looking at the class in the online documentation for additional information.

6.9 Case Study: Random-Number Generation

We now take a brief and, hopefully, entertaining diversion into simulation and game playing. In this and the next section, we develop a nicely structured game-playing program with multiple methods. The program uses most of the control statements presented thus far in the book and introduces several new programming concepts.

There is something in the air of a casino that invigorates people—from the high rollers at the plush mahogany-and-felt craps tables to the quarter poppers at the one-armed bandits. It is the element of chance, the possibility that luck will convert a pocketful of money into a mountain of wealth. The element of chance can be introduced in a program via an object of class Random (package java.util) or via the static method random of class Math. Objects of class Random can produce random boolean, byte, float, double, int, long and Gaussian values, whereas Math method random can produce only double values in the range 0.0 ≤ x < 1.0, where x is the value returned by method random. In the next several examples, we use objects of class Random to produce random values.

A new random-number generator object can be created as follows:

Random randomNumbers = new Random();

The random-number generator object can then be used to generate random boolean, byte, float, double, int, long and Gaussian values—we discuss only random int values here. For more information on the Random class, see java.sun.com/javase/6/docs/api/java/util/Random.html.

Consider the following statement:

int randomValue = randomNumbers.nextInt();

Method nextInt of class Random generates a random int value from –2,147,483,648 to +2,147,483,647. If the nextInt method truly produces values at random, then every value in that range should have an equal chance (or probability) of being chosen each time method nextInt is called. The values returned by nextInt are actually pseudorandom numbers—a sequence of values produced by a complex mathematical calculation. The calculation uses the current time of day (which, of course, changes constantly) to seed the random-number generator such that each execution of a program yields a different sequence of random values.

The range of values produced directly by method nextInt often differs from the range of values required in a particular Java application. For example, a program that simulates coin tossing might require only 0 for “heads” and 1 for “tails.” A program that simulates the rolling of a six-sided die might require random integers in the range 1–6. A program that randomly predicts the next type of spaceship (out of four possibilities) that will fly across the horizon in a video game might require random integers in the range 1–4. For cases like these, class Random provides another version of method nextInt that receives an int argument and returns a value from 0 up to, but not including, the argument’s value. For example, to simulate coin tossing, you might use the statement

int randomValue = randomNumbers.nextInt( 2 );

which returns 0 or 1.

Rolling a Six-Sided Die

To demonstrate random numbers, let us develop a program that simulates 20 rolls of a six-sided die and displays the value of each roll. We begin by using nextInt to produce random values in the range 0–5, as follows:

face = randomNumbers.nextInt( 6 );

The argument 6—called the scaling factor—represents the number of unique values that nextInt should produce (in this case six—0, 1, 2, 3, 4 and 5). This manipulation is called scaling the range of values produced by Random method nextInt.

A six-sided die has the numbers 1–6 on its faces, not 0–5. So we shift the range of numbers produced by adding a shifting value—in this case 1—to our previous result, as in

face = 1 + randomNumbers.nextInt( 6 );

The shifting value (1) specifies the first value in the desired set of random integers. The preceding statement assigns face a random integer in the range 1–6.

Figure 6.6 shows two sample outputs which confirm that the results of the preceding calculation are integers in the range 1–6, and that each run of the program can produce a different sequence of random numbers. Line 3 imports class Random from the java.util package. Line 9 creates the Random object randomNumbers to produce random values. Line 16 executes 20 times in a loop to roll the die. The if statement (lines 21–22) in the loop starts a new line of output after every five numbers.

Fig. 6.6. Shifted and scaled random integers.

Rolling a Six-Sided Die 6000 Times

To show that the numbers produced by nextInt occur with approximately equal likelihood, let us simulate 6000 rolls of a die with the application in Fig. 6.7. Each integer from 1 to 6 should appear approximately 1000 times.

Fig. 6.7. Rolling a six-sided die 6000 times.

As the two sample outputs show, scaling and shifting the values produced by method nextInt enables the program to realistically simulate rolling a six-sided die. The application uses nested control statements (the switch is nested inside the for) to determine the number of times each side of the die occurred. The for statement (lines 21–47) iterates 6000 times. During each iteration, line 23 produces a random value from 1 to 6. That value is then used as the controlling expression (line 26) of the switch statement (lines 26–46). Based on the face value, the switch statement increments one of the six counter variables during each iteration of the loop. When we study arrays in Chapter 7, we’ll show an elegant way to replace the entire switch statement in this program with a single statement! Note that the switch statement has no default case, because we have a case for every possible die value that the expression in line 23 could produce. Run the program several times, and observe the results. As you’ll see, every time you execute this program, it produces different results.

6.9.1 Generalized Scaling and Shifting of Random Numbers

Previously, we demonstrated the statement

face = 1 + randomNumbers.nextInt( 6 );

which simulates the rolling of a six-sided die. This statement always assigns to variable face an integer in the range 1 ≤ face ≤ 6. The width of this range (i.e., the number of consecutive integers in the range) is 6, and the starting number in the range is 1. Referring to the preceding statement, we see that the width of the range is determined by the number 6 that is passed as an argument to Random method nextInt, and the starting number of the range is the number 1 that is added to randomNumberGenerator.nextInt( 6 ). We can generalize this result as

number = shiftingValue + randomNumbers.nextInt( scalingFactor );

where shiftingValue specifies the first number in the desired range of consecutive integers and scalingFactor specifies how many numbers are in the range.

It is also possible to choose integers at random from sets of values other than ranges of consecutive integers. For example, to obtain a random value from the sequence 2, 5, 8, 11 and 14, you could use the statement

number = 2 + 3 * randomNumbers.nextInt( 5 );

In this case, randomNumberGenerator.nextInt( 5 ) produces values in the range 0–4. Each value produced is multiplied by 3 to produce a number in the sequence 0, 3, 6, 9 and 12. We then add 2 to that value to shift the range of values and obtain a value from the sequence 2, 5, 8, 11 and 14. We can generalize this result as

number = shiftingValue +
      differenceBetweenValues * randomNumbers.nextInt( scalingFactor );

where shiftingValue specifies the first number in the desired range of values, differenceBetweenValues represents the difference between consecutive numbers in the sequence and scalingFactor specifies how many numbers are in the range.

6.9.2 Random-Number Repeatability for Testing and Debugging

As we mentioned earlier in Section 6.9, the methods of class Random actually generate pseudorandom numbers based on complex mathematical calculations. Repeatedly calling any of Random’s methods produces a sequence of numbers that appears to be random. The calculation that produces the pseudorandom numbers uses the time of day as a seed value to change the sequence’s starting point. Each new Random object seeds itself with a value based on the computer system’s clock at the time the object is created, enabling each execution of a program to produce a different sequence of random numbers.

When debugging an application, it is sometimes useful to repeat the exact same sequence of pseudorandom numbers during each execution of the program. This repeatability enables you to prove that your application is working for a specific sequence of random numbers before you test the program with different sequences of random numbers. When repeatability is important, you can create a Random object as follows:

Random randomNumbers = new Random( seedValue );

The seedValue argument (of type long) seeds the random-number calculation. If the same seedValue is used every time, the Random object produces the same sequence of random numbers. You can set a Random object’s seed at any time during program execution by calling the object’s setSeed method, as in

randomNumbers.setSeed( seedValue );

Error-Prevention Tip 6.2

While a program is under development, create the Random object with a specific seed value to produce a repeatable sequence of random numbers each time the program executes. If a logic error occurs, fix the error and test the program again with the same seed value—this allows you to reconstruct the same sequence of random numbers that caused the error. Once the logic errors have been removed, create the Random object without using a seed value, causing the Random object to generate a new sequence of random numbers each time the program executes.

6.10 Case Study: A Game of Chance (Introducing Enumerations)

A popular game of chance is a dice game known as craps, which is played in casinos and back alleys throughout the world. The rules of the game are straightforward:

You roll two dice. Each die has six faces, which contain one, two, three, four, five and six spots, respectively. After the dice have come to rest, the sum of the spots on the two upward faces is calculated. If the sum is 7 or 11 on the first throw, you win. If the sum is 2, 3 or 12 on the first throw (called “craps”), you lose (i.e., the “house” wins). If the sum is 4, 5, 6, 8, 9 or 10 on the first throw, that sum becomes your “point.” To win, you must continue rolling the dice until you “make your point” (i.e., roll that same point value). You lose by rolling a 7 before making the point.

The application in Fig. 6.8 and Fig. 6.9 simulates the game of craps, using methods to define the logic of the game. In the main method of class CrapsTest (Fig. 6.9), line 8 creates an object of class Craps (Fig. 6.8) and line 9 calls its play method to start the game. The play method (Fig. 6.8, lines 21–65) calls the rollDice method (Fig. 6.8, lines 68–81) as necessary to roll the two dice and compute their sum. Four sample outputs in Fig. 6.9 show winning on the first roll, losing on the first roll, winning on a subsequent roll and losing on a subsequent roll, respectively.

Fig. 6.8. Craps class simulates the dice game craps.

Fig. 6.9. Application to test class Craps.

Let’s discuss the declaration of class Craps in Fig. 6.8. In the rules of the game, the player must roll two dice on the first roll, and must do the same on all subsequent rolls. We declare method rollDice (lines 68–81) to roll the dice and compute and print their sum. Method rollDice is declared once, but it is called from two places (lines 26 and 50) in method play, which contains the logic for one complete game of craps. Method rollDice takes no arguments, so it has an empty parameter list. Each time it is called, rollDice returns the sum of the dice, so the return type int is indicated in the method header (line 68). Although lines 71 and 72 look the same (except for the die names), they do not necessarily produce the same result. Each of these statements produces a random value in the range 1–6. Note that randomNumbers (used in lines 71–72) is not declared in the method. Rather it is declared as a private instance variable of the class and initialized in line 8. This enables us to create one Random object that is reused in each call to rollDice.

The game is reasonably involved. The player may win or lose on the first roll, or may win or lose on any subsequent roll. Method play (lines 21–65 of Fig. 6.8) uses local variable myPoint (line 23) to store the “point” if the player does not win or lose on the first roll, local variable gameStatus (line 24) to keep track of the overall game status and local variable sumOfDice (line 26) to hold the sum of the dice for the most recent roll. Note that myPoint is initialized to 0 to ensure that the application will compile. If you do not initialize myPoint, the compiler issues an error, because myPoint is not assigned a value in every case of the switch statement, and thus the program could try to use myPoint before it is assigned a value. By contrast, gameStatus does not require initialization because it is assigned a value in every case of the switch statement—thus, it is guaranteed to be initialized before it is used.

Note that local variable gameStatus (line 24) is declared to be of a new type called Status, which we declared at line 11. Type Status is declared as a private member of class Craps, because Status will be used only in that class. Status is a programmerdeclared type called an enumeration, which, in its simplest form, declares a set of constants represented by identifiers. An enumeration is a special kind of class that is introduced by the keyword enum and a type name (in this case, Status). As with any class, braces ({ and }) delimit the body of an enum declaration. Inside the braces is a comma-separated list of enumeration constants, each representing a unique value. The identifiers in an enum must be unique. (You’ll learn more about enumerations in Chapter 8.)

Good Programming Practice 6.3

Use only uppercase letters in the names of enumeration constants. This makes the constants stand out and reminds you that enumeration constants are not variables.

Variables of type Status can be assigned only one of the three constants declared in the enumeration (line 11) or a compilation error will occur. When the game is won, the program sets local variable gameStatus to Status.WON (lines 33 and 54). When the game is lost, the program sets local variable gameStatus to Status.LOST (lines 38 and 57). Otherwise, the program sets local variable gameStatus to Status.CONTINUE (line 41) to indicate that the game is not over and the dice must be rolled again.

Good Programming Practice 6.4

Using enumeration constants (like Status.WON, Status.LOST and Status.CONTINUE) rather than literal integer values (such as 0, 1 and 2) can make programs easier to read and maintain.

Line 26 in method play calls rollDice, which picks two random values from 1 to 6, displays the value of the first die, the value of the second die and the sum of the dice, and returns the sum of the dice. Method play next enters the switch statement at lines 29–45, which uses the sumOfDice value from line 26 to determine whether the game has been won or lost, or whether it should continue with another roll. The sums of the dice that would result in a win or loss on the first roll are declared as public final static int constants in lines 14–18. These are used in the cases of the switch statement. The identifier names use casino parlance for these sums. Note that these constants, like enum constants, are declared with all capital letters by convention, to make them stand out in the program. Lines 31–34 determine whether the player won on the first roll with SEVEN (7) or YO_LEVEN (11). Lines 35–39 determine whether the player lost on the first roll with SNAKE_EYES (2), TREY (3), or BOX_CARS (12). After the first roll, if the game is not over, the default case (lines 40–44) sets gameStatus to Status.CONTINUE, saves sumOfDice in myPoint and displays the point.

If we are still trying to “make our point” (i.e., the game is continuing from a prior roll), the loop in lines 48–58 executes. Line 50 rolls the dice again. In line 53, if sumOfDice matches myPoint, line 54 sets gameStatus to Status.WON, then the loop terminates because the game is complete. In line 56, if sumOfDice is equal to SEVEN (7), line 57 sets gameStatus to Status.LOST, and the loop terminates because the game is complete. When the game completes, lines 61–64 display a message indicating whether the player won or lost, and the program terminates.

Note the use of the various program-control mechanisms we have discussed. The Craps class in concert with class CrapsTest uses two methods—main, play (called from main) and rollDice (called twice from play)—and the switch, while, if...else and nested if control statements. Note also the use of multiple case labels in the switch statement to execute the same statements for sums of SEVEN and YO_LEVEN (lines 31–32) and for sums of SNAKE_EYES, TREY and BOX_CARS (lines 35–37).

You might be wondering why we declared the sums of the dice as public final static int constants rather than as enum constants. The answer lies in the fact that the program must compare the int variable sumOfDice (line 26) to these constants to determine the outcome of each roll. Suppose we were to declare enum Sum containing constants (e.g., Sum.SNAKE_EYES) representing the five sums used in the game, then use these constants in the cases of the switch statement (lines 29–45). Doing so would prevent us from using sumOfDice as the switch statement’s controlling expression, because Java does not allow an int to be compared to an enumeration constant. To achieve the same functionality as the current program, we would have to use a variable currentSum of type Sum as the switch’s controlling expression. Unfortunately, Java does not provide an easy way to convert an int value to a particular enum constant. Translating an int into an enum constant could be done with a separate switch statement. Clearly this would be cumbersome and not improve the readability of the program (thus defeating the purpose of using an enum).

6.11 Scope of Declarations

You have seen declarations of various Java entities, such as classes, methods, variables and parameters. Declarations introduce names that can be used to refer to such Java entities. The scope of a declaration is the portion of the program that can refer to the declared entity by its name. Such an entity is said to be “in scope” for that portion of the program. This section introduces several important scope issues. (For more scope information, see the Java Language Specification, Section 6.3: Scope of a Declaration, at java.sun.com/docs/books/jls/second_edition/html/names.doc.html#103228.)

The basic scope rules are as follows:

1. The scope of a parameter declaration is the body of the method in which the declaration appears.

2. The scope of a local-variable declaration is from the point at which the declaration appears to the end of that block.

3. The scope of a local-variable declaration that appears in the initialization section of a for statement’s header is the body of the for statement and the other expressions in the header.

4. The scope of a method or field of a class is the entire body of the class. This enables non-static methods of a class to use the class’s fields and other methods.

Any block may contain variable declarations. If a local variable or parameter in a method has the same name as a field, the field is “hidden” until the block terminates execution—this is called shadowing. In Chapter 8, we discuss how to access shadowed fields.

Common Programming Error 6.10

A compilation error occurs when a local variable is declared more than once in a method.

Error-Prevention Tip 6.3

Use different names for fields and local variables to help prevent subtle logic errors that occur when a method is called and a local variable of the method shadows a field of the same name in the class.

The application in Fig. 6.10 and Fig. 6.11 demonstrates scoping issues with fields and local variables. When the application begins execution, class ScopeTest’s main method (Fig. 6.11, lines 7–11) creates an object of class Scope (line 9) and calls the object’s begin method (line 10) to produce the program’s output (shown in Fig. 6.11).

Fig. 6.10. Scope class demonstrating scopes of a field and local variables.

Fig. 6.11. Application to test class Scope.

In class Scope, line 7 declares and initializes the field x to 1. This field is shadowed (hidden) in any block (or method) that declares a local variable named x. Method begin (lines 11–23) declares a local variable x (line 13) and initializes it to 5. This local variable’s value is output to show that the field x (whose value is 1) is shadowed in method begin. The program declares two other methods—useLocalVariable (lines 26–35) and useField (lines 38–45)—that each take no arguments and do not return results. Method begin calls each method twice (lines 17–20). Method useLocalVariable declares local variable x (line 28). When useLocalVariable is first called (line 17), it creates local variable x and initializes it to 25 (line 28), outputs the value of x (lines 30–31), increments x (line 32) and outputs the value of x again (lines 33–34). When uselLocalVariable is called a second time (line 19), it re-creates local variable x and re-initializes it to 25, so the output of each useLocalVariable call is identical.

Method useField does not declare any local variables. Therefore, when it refers to x, field x (line 7) of the class is used. When method useField is first called (line 18), it outputs the value (1) of field x (lines 40–41), multiplies the field x by 10 (line 42) and outputs the value (10) of field x again (lines 43–44) before returning. The next time method useField is called (line 20), the field has its modified value, 10, so the method outputs 10, then 100. Finally, in method begin, the program outputs the value of local variable x again (line 22) to show that none of the method calls modified begin’s local variable x, because the methods all referred to variables named x in other scopes.

6.12 Method Overloading

Methods of the same name can be declared in the same class, as long as they have different sets of parameters (determined by the number, types and order of the parameters)—this is called method overloading. When an overloaded method is called, the Java compiler selects the appropriate method by examining the number, types and order of the arguments in the call. Method overloading is commonly used to create several methods with the same name that perform the same or similar tasks, but on different types or different numbers of arguments. For example, Math methods abs, min and max (summarized in Section 6.3) are overloaded with four versions each:

1. One with two double parameters.

2. One with two float parameters.

3. One with two int parameters.

4. One with two long parameters.

Our next example demonstrates declaring and invoking overloaded methods. We present examples of overloaded constructors in Chapter 8.

Declaring Overloaded Methods

In our class MethodOverload (Fig. 6.12), we include two overloaded versions of a method called square—one that calculates the square of an int (and returns an int) and one that calculates the square of a double (and returns a double). Although these methods have the same name and similar parameter lists and bodies, you can think of them simply as different methods. It may help to think of the method names as “square of int” and “square of double,” respectively. When the application begins execution, class MethodOverloadTest’s main method (Fig. 6.13, lines 6–10) creates an object of class MethodOverload (line 8) and calls the object’s method testOverloadedMethods (line 9) to produce the program’s output (Fig. 6.13).

Fig. 6.12. Overloaded method declarations.

Fig. 6.13. Application to test class MethodOverload.

In Fig. 6.12, line 9 invokes method square with the argument 7. Literal integer values are treated as type int, so the method call in line 9 invokes the version of square at lines 14–19 that specifies an int parameter. Similarly, line 10 invokes method square with the argument 7.5. Literal floating-point values are treated as type double, so the method call in line 10 invokes the version of square at lines 22–27 that specifies a double parameter. Each method first outputs a line of text to prove that the proper method was called in each case. Note that the values in lines 10 and 24 are displayed with the format specifier %f and that we did not specify a precision in either case. By default, floating-point values are displayed with six digits of precision if the precision is not specified in the format specifier.

Distinguishing Between Overloaded Methods

The compiler distinguishes overloaded methods by their signature—a combination of the method’s name and the number, types and order of its parameters. If the compiler looked only at method names during compilation, the code in Fig. 6.12 would be ambiguous—the compiler would not know how to distinguish between the two square methods (lines 14–19 and 22–27). Internally, the compiler uses longer method names that include the original method name, the types of each parameter and the exact order of the parameters to determine whether the methods in a class are unique in that class.

For example, in Fig. 6.12, the compiler might use the logical name “square of int” for the square method that specifies an int parameter and “square of double” for the square method that specifies a double parameter (the actual names the compiler uses are messier). If method1’s declaration begins as

void method1( int a, float b )

then the compiler might use the logical name “method1 of int and float.” If the parameters are specified as

void method1( float a, int b )

then the compiler might use the logical name “method1 of float and int.” Note that the order of the parameter types is important—the compiler considers the preceding two method1 headers to be distinct.

Return Types of Overloaded Methods

In discussing the logical names of methods used by the compiler, we did not mention the return types of the methods. This is because method calls cannot be distinguished by return type. The program in Fig. 6.14 illustrates the compiler errors generated when two methods have the same signature and different return types. Overloaded methods can have different return types if the methods have different parameter lists. Also, overloaded methods need not have the same number of parameters.

Fig. 6.14. Overloaded method declarations with identical signatures cause compilation errors, even if the return types are different.

Common Programming Error 6.11

Declaring overloaded methods with identical parameter lists is a compilation error regardless of whether the return types are different.

6.13 Introduction to Recursion

The programs we’ve discussed so far are generally structured as methods that call one another in a disciplined, hierarchical manner. For some problems, however, it is useful to have a method call itself. Such a method is known as a recursive method. A recursive method can be called either directly or indirectly through another method. We now consider recursion conceptually, then present several programs containing recursive methods.

6.14 Recursion Concepts

Recursive problem-solving approaches have a number of elements in common. When a recursive method is called to solve a problem, the method actually is capable of solving only the simplest case(s), or base case(s). If the method is called with a base case, the method returns a result. If the method is called with a more complex problem, the method typically divides the problem into two conceptual pieces—a piece that the method knows how to do and a piece that it does not know how to do. To make recursion feasible, the latter piece must resemble the original problem, but be a slightly simpler or smaller version of it. Because this new problem looks like the original problem, the method calls a fresh copy of itself to work on the smaller problem—this is referred to as a recursive call and is also called the recursion step. The recursion step normally includes a return statement, because its result will be combined with the portion of the problem the method knew how to solve to form a result that will be passed back to the original caller. This concept of separating the problem into two smaller portions is a form of the divide-and-conquer approach introduced in Section 6.2.

The recursion step executes while the original call to the method is still active (i.e., while it has not finished executing). It can result in many more recursive calls as the method divides each new subproblem into two conceptual pieces. For the recursion to eventually terminate, each time the method calls itself with a simpler version of the original problem, the sequence of smaller and smaller problems must converge on a base case. At that point, the method recognizes the base case and returns a result to the previous copy of the method. A sequence of returns ensues until the original method call returns the final result to the caller.

A recursive method may call another method, which may in turn make a call back to the recursive method. Such a process is known as an indirect recursive call or indirect recursion. For example, method A calls method B, which makes a call back to method A. This is still considered recursion, because the second call to method A is made while the first call to method A is active—that is, the first call to method A has not yet finished executing (because it is waiting on method B to return a result to it) and has not returned to method A’s original caller.

To better understand the concept of recursion, consider an example of recursion that is quite common to computer users—the recursive definition of a directory on a computer. A computer normally stores related files in a directory. A directory can be empty, can contain files and/or can contain other directories (usually referred to as subdirectories). Each of these subdirectories, in turn, may also contain both files and directories. If we want to list each file in a directory (including all the files in the directory’s subdirectories), we need to create a method that first lists the initial directory’s files, then makes recursive calls to list the files in each of that directory’s subdirectories. The base case occurs when a directory is reached that does not contain any subdirectories. At this point, all the files in the original directory have been listed and no further recursion is necessary.

6.15 Example Using Recursion: Factorials

Let’s write a recursive program to calculate the factorial of a positive integer n—written n! (and pronounced “n factorial”)—which is the product

n · (n – 1) · (n – 2) · ... · 1

with 1! equal to 1 and 0! defined to be 1. For example, 5! is the product 5 · 4 · 3 · 2 · 1, which is equal to 120.

The factorial of integer number (where number ≥ 0) can be calculated iteratively (non-recursively) using a for statement as follows:

A recursive declaration of the factorial method is arrived at by observing the following relationship:

n ! = n · (n – 1)!

For example, 5! is clearly equal to 5 · 4!, as is shown by the following equations:

5! = 5 · 4 · 3 · 2 · 1

5! = 5 · (4 · 3 · 2 · 1)

5! = 5 · (4!)

The evaluation of 5! would proceed as shown in Fig. 6.15. Figure 6.15(a) shows how the succession of recursive calls proceeds until 1! (the base case) is evaluated to be 1, which terminates the recursion. Figure 6.15(b) shows the values returned from each recursive call to its caller until the final value is calculated and returned.

Fig. 6.15. Recursive evaluation of 5!.

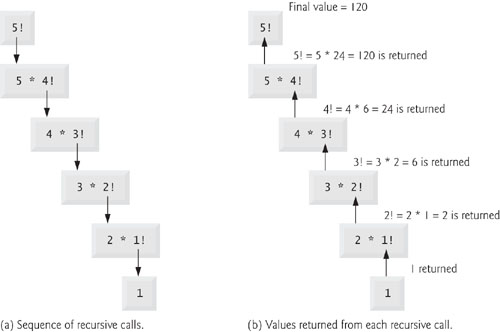
Figure 6.16 uses recursion to calculate and print the factorials of the integers from 0–10. The recursive method factorial (lines 7–13) first tests to determine whether a terminating condition (line 9) is true. If number is less than or equal to 1 (the base case), factorial returns 1, no further recursion is necessary and the method returns. If number is greater than 1, line 12 expresses the problem as the product of number and a recursive call to factorial evaluating the factorial of number - 1, which is a slightly smaller problem than the original calculation, factorial( number ).

Fig. 6.16. Factorial calculations with a recursive method.

Common Programming Error 6.12

Either omitting the base case or writing the recursion step incorrectly so that it does not converge on the base case can cause a logic error known as infinite recursion, where recursive calls are continuously made until memory has been exhausted. This error is analogous to the problem of an infinite loop in an iterative (nonrecursive) solution.

Method displayFactorials (lines 16–21) displays the factorials of 0–10. The call to method factorial occurs in line 20. Method factorial receives a parameter of type long and returns a result of type long. Figure 6.17 tests our factorial and displayFactorials methods by calling displayFactorials (line 10). The output of Fig. 6.17 shows that factorial values become large quickly. We use type long (which can represent relatively large integers) so the program can calculate factorials greater than 12!. Unfortunately, the factorial method produces large values so quickly that factorial values soon exceed the maximum value that can be stored even in a long variable.

Fig. 6.17. Testing the factorial method.

Due to the limitations of integral types, float or double variables may ultimately be needed to calculate factorials of larger numbers. This points to a weakness in most programming languages—namely, that the languages are not easily extended to handle unique application requirements. Java is an extensible language that allows us to create arbitrarily large integers if we wish. In fact, package java.math provides classes BigInteger and BigDecimal explicitly for arbitrary precision mathematical calculations that cannot be performed with primitive types. For more information on these classes visit, java.sun.com/javase/6/docs/api/java/math/BigInteger.html and java.sun.com/javase/6/docs/api/java/math/BigDecimal.html, respectively.

6.16 Example Using Recursion: Fibonacci Series

The Fibonacci series,

0, 1, 1, 2, 3, 5, 8, 13, 21, ...

begins with 0 and 1 and has the property that each subsequent Fibonacci number is the sum of the previous two Fibonacci numbers. This series occurs in nature and describes a form of spiral. The ratio of successive Fibonacci numbers converges on a constant value of 1.618..., a number that has been called the golden ratio or the golden mean. Humans tend to find the golden mean aesthetically pleasing. Architects often design windows, rooms and buildings whose length and width are in the ratio of the golden mean. Postcards are often designed with a golden-mean length-to-width ratio.

The Fibonacci series may be defined recursively as follows:

fibonacci(0) = 0

fibonacci(1) = 1

fibonacci(n) = fibonacci(n – 1) + fibonacci(n – 2)

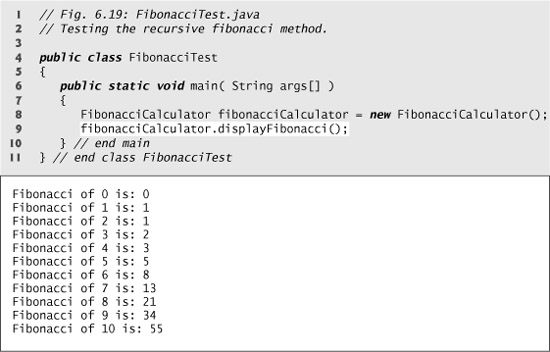
Note that there are two base cases for the Fibonacci calculation: fibonacci(0) is defined to be 0, and fibonacci(1) is defined to be 1. The program in Fig. 6.18 calculates the ith Fibonacci number recursively, using method fibonacci (lines 7–13). Method displayFibonacci (lines 15–20) tests fibonacci, displaying the Fibonacci values of 0–10. The variable counter created in the for header in line 17 indicates which Fibonacci number to calculate for each iteration of the for statement. Fibonacci numbers tend to become large quickly. Therefore, we use type long as the parameter type and the return type of method fibonacci. Line 9 of Fig. 6.19 calls method displayFibonacci (line 9) to calculate the Fibonacci values.

Fig. 6.18. Fibonacci numbers generated with a recursive method.

Fig. 6.19. Testing the fibonacci method.

The call to method fibonacci (line 19 of Fig. 6.18) from displayFibonacci is not a recursive call, but all subsequent calls to fibonacci performed from the body of fibonacci (line 12 of Fig. 6.18) are recursive, because at that point the calls are initiated by method fibonacci itself. Each time fibonacci is called, it immediately tests for the base cases—number equal to 0 or number equal to 1 (line 9). If this condition is true, fibonacci simply returns number because fibonacci( 0 ) is 0, and fibonacci( 1 ) is 1. Interestingly, if number is greater than 1, the recursion step generates two recursive calls (line 12), each for a slightly smaller problem than the original call to fibonacci.

Figure 6.20 shows how method fibonacci evaluates fibonacci( 3 ). Note that at the bottom of the figure, we are left with the values 1, 0 and 1—the results of evaluating the base cases. The first two return values (from left to right), 1 and 0, are returned as the values for the calls fibonacci( 1 ) and fibonacci( 0 ). The sum 1 plus 0 is returned as the value of fibonacci( 2 ). This is added to the result (1) of the call to fibonacci( 1 ), producing the value 2. This final value is then returned as the value of fibonacci( 3 ).

Fig. 6.20. Set of recursive calls for fibonacci( 3 ).

Figure 6.20 raises some interesting issues about the order in which Java compilers evaluate the operands of operators. This order is different from the order in which operators are applied to their operands—namely, the order dictated by the rules of operator precedence. From Figure 6.20, it appears that while fibonacci( 3 ) is being evaluated, two recursive calls will be made—fibonacci( 2 ) and fibonacci( 1 ). But in what order will these calls be made? The Java language specifies that the order of evaluation of the operands is from left to right. Thus, the call fibonacci( 2 ) is made first and the call fibonacci( 1 ) is made second.

A word of caution is in order about recursive programs like the one we use here to generate Fibonacci numbers. Each invocation of the fibonacci method that does not match one of the base cases (0 or 1) results in two more recursive calls to the fibonacci method. Hence, this set of recursive calls rapidly gets out of hand. Calculating the Fibonacci value of 20 with the program in Fig. 6.18 requires 21,891 calls to the fibonacci method; calculating the Fibonacci value of 30 requires 2,692,537 calls! As you try to calculate larger Fibonacci values, you’ll notice that each consecutive Fibonacci number results in a substantial increase in calculation time and in the number of calls to the fibonacci method. For example, the Fibonacci value of 31 requires 4,356,617 calls, and the Fibonacci value of 32 requires 7,049,155 calls! As you can see, the number of calls to fibonacci increases quickly—1,664,080 additional calls between Fibonacci values of 30 and 31 and 2,692,538 additional calls between Fibonacci values of 31 and 32! The difference in the number of calls made between Fibonacci values of 31 and 32 is more than 1.5 times the difference in the number of calls for Fibonacci values between 30 and 31. Problems of this nature can humble even the world’s most powerful computers. [Note: In the field of complexity theory, computer scientists study how hard algorithms work to complete their tasks.]

Performance Tip 6.1

Avoid Fibonacci-style recursive programs, because they result in an exponential “explosion” of method calls.

6.17 Recursion and the Method-Call Stack

In Section 6.6, the stack data structure was introduced in the context of understanding how Java performs method calls. We discussed both the method-call stack (also known as the program execution stack) and activation records. In this section, we’ll use these concepts to demonstrate how the program execution stack handles recursive method calls.

Let’s begin by returning to the Fibonacci example—specifically, calling method fibonacci with the value 3, as in Fig. 6.20. To show the order in which the method calls’ activation records are placed on the stack, we have lettered the method calls in Fig. 6.21.

Fig. 6.21. Method calls made within the call fibonacci( 3 ).

When the first method call (A) is made, an activation record is pushed onto the program execution stack which contains the value of the local variable number (3, in this case). The program execution stack, including the activation record for method call A, is illustrated in part (a) of Fig. 6.22. [Note: We use a simplified stack here. In an actual computer, the program execution stack and its activation records would be more complex than in Fig. 6.22, containing such information as where the method call is to return to when it has completed execution.]

Fig. 6.22. Method calls on the program execution stack.

Within method call A, method calls B and E are made. The original method call has not yet completed, so its activation record remains on the stack. The first method call to be made from within A is method call B, so the activation record for method call B is pushed onto the stack on top of the activation record for method call A. Method call B must execute and complete before method call E is made. Within method call B, method calls C and D will be made. Method call C is made first, and its activation record is pushed onto the stack [part (b) of Fig. 6.22]. Method call B has not yet finished, and its activation record is still on the method-call stack. When method call C executes, it does not make any further method calls, but simply returns the value 1. When this method returns, its activation record is popped off the top of the stack. The method call at the top of the stack is now B, which continues to execute by performing method call D. The activation record for method call D is pushed onto the stack [part (c) of Fig. 6.22]. Method call D completes without making any more method calls, and returns the value 0. The activation record for this method call is then popped off the stack. Now, both method calls made from within method call B have returned. Method call B continues to execute, returning the value 1. Method call B completes and its activation record is popped off the stack. At this point, the activation record for method call A is at the top of the stack and the method continues its execution. This method makes method call E, whose activation record is now pushed onto the stack [part (d) of Fig. 6.22]. Method call E completes and returns the value 1. The activation record for this method call is popped off the stack, and once again method call A continues to execute. At this point, method call A will not be making any other method calls and can finish its execution, returning the value 2 to A’s caller (fibonacci(3) = 2). A’s activation record is popped off the stack. Note that the executing method is always the one whose activation record is at the top of the stack, and the activation record for that method contains the values of its local variables.

6.18 Recursion vs. Iteration

In the preceding sections, we studied methods factorial and fibonacci, which can easily be implemented either recursively or iteratively. In this section, we compare the two approaches and discuss why the programmer might choose one approach over the other in a particular situation.

Both iteration and recursion are based on a control statement: Iteration uses a repetition statement (e.g., for, while or do...while), whereas recursion uses a selection statement (e.g., if, if...else or switch). Both iteration and recursion involve repetition: Iteration explicitly uses a repetition statement, whereas recursion achieves repetition through repeated method calls. Iteration and recursion each involve a termination test: Iteration terminates when the loop-continuation condition fails, whereas recursion terminates when a base case is reached. Iteration with counter-controlled repetition and recursion each gradually approach termination: Iteration keeps modifying a counter until the counter assumes a value that makes the loop-continuation condition fail, whereas recursion keeps producing smaller versions of the original problem until the base case is reached. Both iteration and recursion can occur infinitely: An infinite loop occurs with iteration if the loop-continuation test never becomes false, whereas infinite recursion occurs if the recursion step does not reduce the problem each time in a manner that converges on the base case, or if the base case is not tested.

To illustrate the differences between iteration and recursion, let’s examine an iterative solution to the factorial problem (Figs. 6.23–6.24). Note that a repetition statement is used (lines 12–13 of Fig. 6.23) rather than the selection statement of the recursive solution (lines 9–12 of Fig. 6.16). Note that both solutions use a termination test. In the recursive solution, line 9 tests for the base case. In the iterative solution, line 12 tests the loop-continuation condition—if the test fails, the loop terminates. Finally, note that instead of producing smaller versions of the original problem, the iterative solution uses a counter that is modified until the loop-continuation condition becomes false.

Fig. 6.23. Iterative factorial solution.

Fig. 6.24. Testing the iterative factorial solution.

Recursion has many negatives. It repeatedly invokes the mechanism, and consequently the overhead, of method calls. This repetition can be expensive in terms of both processor time and memory space. Each recursive call causes another copy of the method (actually, only the method’s variables, stored in the activation record) to be created—this set of copies can consume considerable memory space. Since iteration occurs within a method, repeated method calls and extra memory assignment are avoided. So why choose recursion?

Software Engineering Observation 6.6

Any problem that can be solved recursively can also be solved iteratively (nonrecursively). A recursive approach is normally preferred over an iterative approach when the recursive approach more naturally mirrors the problem and results in a program that is easier to understand and debug. A recursive approach can often be implemented with fewer lines of code. Another reason to choose a recursive approach is that an iterative one might not be apparent.

Performance Tip 6.2

Avoid using recursion in situations requiring high performance. Recursive calls take time and consume additional memory.

Common Programming Error 6.13

Accidentally having a nonrecursive method call itself either directly or indirectly through another method can cause infinite recursion.

6.19 (Optional) Software Engineering Case Study: Identifying Class Operations

In the Software Engineering Case Study sections at the ends of Chapters 3–5, we performed the first few steps in the object-oriented design of our ATM system. In Chapter 3, we identified the classes that we’ll need to implement and created our first class diagram. In Chapter 4, we described some attributes of our classes. In Chapter 5, we examined objects’ states and modeled objects’ state transitions and activities. In this section, we determine some of the class operations (or behaviors) that are needed to implement the ATM system.

Identifying Operations

An operation is a service that objects of a class provide to clients (users) of the class. Consider the operations of some real-world objects. A radio’s operations include setting its station and volume (typically invoked by a person adjusting the radio’s controls). A car’s operations include accelerating (invoked by the driver pressing the accelerator pedal), decelerating (invoked by the driver pressing the brake pedal or releasing the gas pedal), turning and shifting gears. Software objects can offer operations as well—for example, a software graphics object might offer operations for drawing a circle, drawing a line, drawing a square and the like. A spreadsheet software object might offer operations like printing the spreadsheet, totaling the elements in a row or column and graphing information in the spreadsheet as a bar chart or pie chart.

We can derive many of the operations of each class by examining the key verbs and verb phrases in the requirements document. We then relate each of these to particular classes in our system (Fig. 6.25). The verb phrases in Fig. 6.25 help us determine the operations of each class.

Fig. 6.25. Verbs and verb phrases for each class in the ATM system.

Modeling Operations

To identify operations, we examine the verb phrases listed for each class in Fig. 6.25. The “executes financial transactions” phrase associated with class ATM implies that class ATM instructs transactions to execute. Therefore, classes BalanceInquiry, Withdrawal and Deposit each need an operation to provide this service to the ATM. We place this operation (which we have named execute) in the third compartment of the three transaction classes in the updated class diagram of Fig. 6.26. During an ATM session, the ATM object will invoke these transaction operations as necessary.

Fig. 6.26. Classes in the ATM system with attributes and operations.

The UML represents operations (which are implemented as methods in Java) by listing the operation name, followed by a comma-separated list of parameters in parentheses, a colon and the return type:

operationName( parameter1, parameter2, ..., parameterN ) : return type

Each parameter in the comma-separated parameter list consists of a parameter name, followed by a colon and the parameter type:

parameterName : parameterType

For the moment, we do not list the parameters of our operations—we’ll identify and model the parameters of some of the operations shortly. For some of the operations, we do not yet know the return types, so we also omit them from the diagram. These omissions are perfectly normal at this point. As our design and implementation proceed, we’ll add the remaining return types.

Figure 6.25 lists the phrase “authenticates a user” next to class BankDatabase—the database is the object that contains the account information necessary to determine whether the account number and PIN entered by a user match those of an account held at the bank. Therefore, class BankDatabase needs an operation that provides an authentication service to the ATM. We place the operation authenticateUser in the third compartment of class BankDatabase (Fig. 6.26). However, an object of class Account, not class BankDatabase, stores the account number and PIN that must be accessed to authenticate a user, so class Account must provide a service to validate a PIN obtained through user input against a PIN stored in an Account object. Therefore, we add a validatePIN operation to class Account. Note that we specify a return type of Boolean for the authenticateUser and validatePIN operations. Each operation returns a value indicating either that the operation was successful in performing its task (i.e., a return value of true) or that it was not (i.e., a return value of false).

Figure 6.25 lists several additional verb phrases for class BankDatabase: “retrieves an account balance,” “credits a deposit amount to an account” and “debits a withdrawal amount from an account.” Like “authenticates a user,” these remaining phrases refer to services that the database must provide to the ATM, because the database holds all the account data used to authenticate a user and perform ATM transactions. However, objects of class Account actually perform the operations to which these phrases refer. Thus, we assign an operation to both class BankDatabase and class Account to correspond to each of these phrases. Recall from Section 3.9 that, because a bank account contains sensitive information, we do not allow the ATM to access accounts directly. The database acts as an intermediary between the ATM and the account data, thus preventing unauthorized access. As we’ll see in Section 7.13, class ATM invokes the operations of class BankDatabase, each of which in turn invokes the operation with the same name in class Account.

The phrase “retrieves an account balance” suggests that classes BankDatabase and Account each need a getBalance operation. However, recall that we created two attributes in class Account to represent a balance—availableBalance and totalBalance. A balance inquiry requires access to both balance attributes so that it can display them to the user, but a withdrawal needs to check only the value of availableBalance. To allow objects in the system to obtain each balance attribute individually, we add operations getAvailableBalance and getTotalBalance to the third compartment of classes BankDatabase and Account (Fig. 6.26). We specify a return type of Double for these operations because the balance attributes which they retrieve are of type Double.

The phrases “credits a deposit amount to an account” and “debits a withdrawal amount from an account” indicate that classes BankDatabase and Account must perform operations to update an account during a deposit and withdrawal, respectively. We therefore assign credit and debit operations to classes BankDatabase and Account. You may recall that crediting an account (as in a deposit) adds an amount only to the totalBalance attribute. Debiting an account (as in a withdrawal), on the other hand, subtracts the amount from both balance attributes. We hide these implementation details inside class Account. This is a good example of encapsulation and information hiding.

If this were a real ATM system, classes BankDatabase and Account would also provide a set of operations to allow another banking system to update a user’s account balance after either confirming or rejecting all or part of a deposit. Operation confirmDepositAmount, for example, would add an amount to the availableBalance attribute, thus making deposited funds available for withdrawal. Operation rejectDepositAmount would subtract an amount from the totalBalance attribute to indicate that a specified amount, which had recently been deposited through the ATM and added to the totalBalance, was not found in the deposit envelope. The bank would invoke this operation after determining either that the user failed to include the correct amount of cash or that any checks did not clear (i.e., they “bounced”). While adding these operations would make our system more complete, we do not include them in our class diagrams or our implementation because they are beyond the scope of the case study.

Class Screen “displays a message to the user” at various times in an ATM session. All visual output occurs through the screen of the ATM. The requirements document describes many types of messages (e.g., a welcome message, an error message, a thank you message) that the screen displays to the user. The requirements document also indicates that the screen displays prompts and menus to the user. However, a prompt is really just a message describing what the user should input next, and a menu is essentially a type of prompt consisting of a series of messages (i.e., menu options) displayed consecutively. Therefore, rather than assign class Screen an individual operation to display each type of message, prompt and menu, we simply create one operation that can display any message specified by a parameter. We place this operation (displayMessage) in the third compartment of class Screen in our class diagram (Fig. 6.26). Note that we do not worry about the parameter of this operation at this time—we model the parameter later in this section.

From the phrase “receives numeric input from the user” listed by class Keypad in Fig. 6.25, we conclude that class Keypad should perform a getInput operation. Because the ATM’s keypad, unlike a computer keyboard, contains only the numbers 0–9, we specify that this operation returns an integer value. Recall from the requirements document that in different situations the user may be required to enter a different type of number (e.g., an account number, a PIN, the number of a menu option, a deposit amount as a number of cents). Class Keypad simply obtains a numeric value for a client of the class—it does not determine whether the value meets any specific criteria. Any class that uses this operation must verify that the user entered an appropriate number in a given situation, then respond accordingly (i.e., display an error message via class Screen). [Note: When we implement the system, we simulate the ATM’s keypad with a computer keyboard, and for simplicity we assume that the user does not enter non-numeric input using keys on the computer keyboard that do not appear on the ATM’s keypad.]

Figure 6.25 lists “dispenses cash” for class CashDispenser. Therefore, we create operation dispenseCash and list it under class CashDispenser in Fig. 6.26. Class CashDispenser also “indicates whether it contains enough cash to satisfy a withdrawal request.” Thus, we include isSufficientCashAvailable, an operation that returns a value of UML type Boolean, in class CashDispenser. Figure 6.25 also lists “receives a deposit envelope” for class DepositSlot. The deposit slot must indicate whether it received an envelope, so we place an operation isEnvelopeReceived, which returns a Boolean value, in the third compartment of class DepositSlot. [Note: A real hardware deposit slot would most likely send the ATM a signal to indicate that an envelope was received. We simulate this behavior, however, with an operation in class DepositSlot that class ATM can invoke to find out whether the deposit slot received an envelope.]

We do not list any operations for class ATM at this time. We are not yet aware of any services that class ATM provides to other classes in the system. When we implement the system with Java code, however, operations of this class, and additional operations of the other classes in the system, may emerge.

Identifying and Modeling Operation Parameters

So far, we have not been concerned with the parameters of our operations—we have attempted to gain only a basic understanding of the operations of each class. Let’s now take a closer look at some operation parameters. We identify an operation’s parameters by examining what data the operation requires to perform its assigned task.

Consider the authenticateUser operation of class BankDatabase. To authenticate a user, this operation must know the account number and PIN supplied by the user. Thus we specify that operation authenticateUser takes integer parameters userAccountNumber and userPIN, which the operation must compare to the account number and PIN of an Account object in the database. We prefix these parameter names with “user” to avoid confusion between the operation’s parameter names and the attribute names that belong to class Account. We list these parameters in the class diagram in Fig. 6.27 that models only class BankDatabase. [Note: It is perfectly normal to model only one class in a class diagram. In this case, we are most concerned with examining the parameters of this one class in particular, so we omit the other classes. In class diagrams later in the case study, in which parameters are no longer the focus of our attention, we omit these parameters to save space. Remember, however, that the operations listed in these diagrams still have parameters.]

Fig. 6.27. Class BankDatabase with operation parameters.

Recall that the UML models each parameter in an operation’s comma-separated parameter list by listing the parameter name, followed by a colon and the parameter type (in UML notation). Figure 6.27 thus specifies that operation authenticateUser takes two parameters—userAccountNumber and userPIN, both of type Integer. When we implement the system in Java, we’ll represent these parameters with int values.

Class BankDatabase operations getAvailableBalance, getTotalBalance, credit and debit also each require a userAccountNumber parameter to identify the account to which the database must apply the operations, so we include these parameters in the class diagram of Fig. 6.27. In addition, operations credit and debit each require a Double parameter amount to specify the amount of money to be credited or debited, respectively.

The class diagram in Fig. 6.28 models the parameters of class Account’s operations. Operation validatePIN requires only a userPIN parameter, which contains the user-specified PIN to be compared with the PIN associated with the account. Like their counterparts in class BankDatabase, operations credit and debit in class Account each require a Double parameter amount that indicates the amount of money involved in the operation. Operations getAvailableBalance and getTotalBalance in class Account require no additional data to perform their tasks. Note that class Account’s operations do not require an account number parameter to distinguish between Accounts, because these operations can be invoked only on a specific Account object.

Fig. 6.28. Class Account with operation parameters.

Figure 6.29 models class Screen with a parameter specified for operation displayMessage. This operation requires only a String parameter message that indicates the text to be displayed. Recall that the parameter types listed in our class diagrams are in UML notation, so the String type listed in Fig. 6.29 refers to the UML type. When we implement the system in Java, we’ll in fact use the Java class String to represent this parameter.

Fig. 6.29. Class Screen with operation parameters.

The class diagram in Fig. 6.30 specifies that operation dispenseCash of class CashDispenser takes a Double parameter amount to indicate the amount of cash (in dollars) to be dispensed. Operation isSufficientCashAvailable also takes a Double parameter amount to indicate the amount of cash in question.

Fig. 6.30. Class CashDispenser with operation parameters.

Note that we do not discuss parameters for operation execute of classes BalanceInquiry, Withdrawal and Deposit, operation getInput of class Keypad and operation isEnvelopeReceived of class DepositSlot. At this point in our design process, we cannot determine whether these operations require additional data to perform their tasks, so we leave their parameter lists empty. As we progress through the case study, we may decide to add parameters to these operations.

In this section, we have determined many of the operations performed by the classes in the ATM system. We have identified the parameters and return types of some of the operations. As we continue our design process, the number of operations belonging to each class may vary—we might find that new operations are needed or that some current operations are unnecessary—and we might determine that some of our class operations need additional parameters and different return types.

Software Engineering Case Study Self-Review Exercises

6.1 Which of the following is not a behavior?

a. reading data from a file

b. printing output

c. text output

d. obtaining input from the user

6.2 If you were to add to the ATM system an operation that returns the amount attribute of class Withdrawal, how and where would you specify this operation in the class diagram of Fig. 6.26?

6.3 Describe the meaning of the following operation listing that might appear in a class diagram for an object-oriented design of a calculator:

add( x : Integer, y : Integer ) : Integer

Answers to Software Engineering Case Study Self-Review Exercises

6.1 c.

6.2 To specify an operation that retrieves the amount attribute of class Withdrawal, the following operation listing would be placed in the operation (i.e., third) compartment of class Withdrawal:

getAmount( ) : Double

6.3 This operation listing indicates an operation named add that takes integers x and y as parameters and returns an integer value.

6.20 Wrap-Up

In this chapter, you learned more about the details of method declarations. You also learned the difference between non-static and static methods and how to call static methods by preceding the method name with the name of the class in which it appears and the dot (.) separator. You learned how to use operator + to perform string concatenations. You learned how to declare named constants using both enum types and public final static variables. You saw how to use class Random to generate sets of random numbers that can be used for simulations. You also learned about the scope of fields and local variables in a class. Finally, you learned that multiple methods in one class can be overloaded by providing methods with the same name and different signatures. Such methods can be used to perform the same or similar tasks using different types or different numbers of parameters.

In Chapter 7, you’ll learn how to maintain lists and tables of data in arrays. You’ll see a more elegant implementation of the application that rolls a die 6000 times and two enhanced versions of our GradeBook case study that you studied in Chapters 3–5. You’ll also learn how to access an application’s command-line arguments that are passed to method main when an application begins execution.