| 24 | Logarithms and Exponentials |
A logarithm (sometimes called a log) of a quantity is a power to which a positive real number constant is raised to obtain that quantity. An exponential of a quantity is the result of raising a positive real number constant to a power equal to that quantity. The constant is known as the base of the logarithmic function or the exponential function. The two most common bases for logarithmic and exponential functions are 10 and e, where e is an irrational number approximately equal to 2.71828. The number e is also known as Euler’s constant and the exponential constant.
THE LOGARITHM BASE
Suppose you raise a positive real number b to some real number power y, getting another real number x as the result. A mathematician would say that this relationship exists among the three real numbers b, and x, and y, where b > 0:
The exponent y in this expression is the base-b logarithm of x. This expression can also be written as follows:
You can raise nonpositive numbers to real powers, but when it comes to logarithms, this is rarely done. You probably aren’t going to come across “base-negative-10” or “base-negative-2” logarithms. The trouble with negative numbers as log bases is that they go outside the set of real numbers. For example,
This is a valid equation, but you won’t be likely to hear anyone say that 1/2 is the base-(−9) logarithm of i3 unless you’re in the company of theoreticians!
COMMON LOGARITHMS
Base-10 logarithms are also known as common logarithms or common logs. In equations, common logs are denoted by writing “log” followed by a subscript 10, and then the number, called the argument, for which you want to find the logarithm. Here are a few examples that you can verify with your calculator:

The squiggly equals sign means “is approximately equal to.” You will often see it in engineering papers, articles, and books.
The first equation above is simply another way of saying that 102 = 100. In that equation, 100 is the argument, or value on which the log function depends. It’s another expression for the independent variable. You would say, “The common log of 100 is equal to 2.” In the second equation, you are in effect saying that 101.653 ≈ 45, and you could also say, “The common log of 45 is approximately equal to 1.653.” And so it goes. Exponents, when expressed as logarithms, don’t have to be whole numbers or fractions. They don’t even have to be rational numbers. You can have exponents that are irrational, such as π, e, or the square root of 2.
Figure 24-1 is a partial linear-coordinate graph of the function y = log10 x. Figure 24-2 is a partial graph of the same function in semilog coordinates, where one graph scale is linear and the other is graduated according to the common log function. Regardless of the base, log functions are defined only for positive arguments in the real numbers.

Figure 24-1
Partial linear-coordinate graph of the common logarithm function. As x approaches 0, the value of y becomes arbitrarily large in the negative sense. As x increases without limit, so does y.

Figure 24-2
Partial semilog-coordinate graph of the common logarithm function. In this illustration, the y axis intersects the x axis at the point where x = 0.1.
Here are a couple of function-related terms you should be familiar with. The set of x values for which any function y = f (x) is defined is called the domain of the function. The set of all the possible y (or “output”) values that you can get when you “input” some x value in the domain is known as the range of the function. In any log function with a positive real base, when the domain is the set of positive real numbers, the range is the entire set of real numbers.
NATURAL LOGARITHMS
Base-e logarithms are also called natural logs or Napierian logs. In equations, the natural log function is usually denoted by writing “ln” or “loge” followed by the argument.
Here’s a little trick you can use to get a good display of e on your calculator, if it doesn’t have a key that gives it directly. Enter the number 1, then hit the inverse function key or put a check in the appropriate box if you’re using the calculator in a computer (it might be labeled “Inv” or “Rev”). Then hit the “ln” or “loge” key. If you have a computer with a scientific calculator, you should get a readout something like this:
And now, a warning! In some texts, the natural log function is denoted by writing “log” (without a subscript) followed by the argument, but in other texts and in most calculators, “log” means the common log function! To avoid confusion, it’s a good idea to include the base as a subscript whenever you write “log” to represent a log function. If you aren’t sure what the “log” key on a calculator does, conduct some tests to find out. You don’t want to get natural logs from your calculator when you want common logs, or vice versa!
Now look at an example of a simple, approximate equation using the natural log function:
If you want to be theoretically precise with this statement, you can substitute e4 for 54.59815 and write it as follows:
These equations reflect the fact that e4 = 54.59815. That’s an exponential equation; you’ll learn more about them later in this chapter. Here are some more equations using the natural log function:

Figure 24-3 is a partial linear coordinate graph of y = ln x. Figure 24-4 is a partial graph of the same function in semilog coordinates. As with the base-10 log function, the domain is limited to the set of positive real numbers, and the range extends over the set of all real numbers.

Figure 24-3
Partial linear-coordinate graph of the natural logarithm function. As x approaches 0, the value of y becomes arbitrarily large in the negative sense. As x increases without limit, so does y.

Figure 24-4
Partial semilog-coordinate graph of the natural logarithm function. In this illustration, the y axis intersects the × axis at the point where × = 0.1.
The curves for log functions of different bases look similar. The exact values for specific arguments vary, but the functions always “blow up negatively” (you could also say they “blow down”!) as the argument approaches 0 from the positive direction, and they always increase without limit as the argument approaches positive infinity. If you want visible evidence of this, draw some expanded graphs of common log and natural log functions. Most calculators give you values for both functions, so it’s easy to plot the points and connect them to get smooth curves.
BASIC PROPERTIES OF LOGARITHMS
With logarithms, you can convert multiplication problems into addition problems, division into subtraction, powers into products, and roots into quotients.
Suppose that x and y are positive real numbers. The logarithm of the product is equal to the sum of the logarithms of the individual numbers:
Here, and in some of the formulas that follow, the base b means that it works regardless of the log base. It can be a common log, a natural log, or a logarithm of any other base; it doesn’t matter. Now look at a numeric example of the above principle. Consider the arguments exact. Use your calculator to follow along.
Work out both sides and approximate the results to four significant figures:
You shouldn’t expect to get perfect answers every time you use logarithms, because the results are almost always irrational numbers. That means they are nonterminating, nonrepeating decimals. Approximation is the best you can do. Sometimes approximations agree exactly to a certain number of significant figures, but often they do not.
Here’s a counterpart of the above property for division. Let x and y be positive real numbers. Then the logarithm of their ratio (or quotient) is equal to the difference of the logarithms of the individual numbers:
You can work out an example using the same numerical arguments as before. Again, follow along with your calculator:
Working out both sides and approximating the results to four significant figures, we find
Logarithms simplify the raising of a number to a power. This is useful when the argument does not have two whole numbers. Let x be a positive real number, and let y be any real number (positive, negative, or zero). Then the logarithm of x raised to the power y can be reduced to a product:
Here is a worked-out example using the same arguments as before, carried out to four significant figures:

This time, the answers agree perfectly to four significant figures!
Now try an example in which neither of the numbers in the input argument is whole. Again, go to four significant figures and follow along with a calculator. But this time, leave the left-hand side just as it is, at least for the moment.

Set this result aside, but don’t put it out of your mind altogether. You’ll return to it a little later in this chapter.
The logarithm (to any base b) of the reciprocal of a number is equal to the negative of the logarithm of that number. Stated formally, if x is a positive real number, then
This is a special case of division simplifying to subtraction. Here is a numerical example. Suppose x = 3 (exactly) and you use natural logs, as follows:
Using your calculator, you can evaluate both expressions. This time, go to 10 significant figures, just for fun!
Again, as luck would have it, the results agree exactly.
What happens when you have a reciprocal in an exponent? Suppose x is a positive real number, and y is any real number except zero. Then the logarithm (to any base b) of the yth root of x (also denoted as x to the 1/y power) is equal to the log of x, divided by y:
Try this with x = 8 and y = 1/3, considering both values exact and using natural logs evaluated to six significant figures. You get
You know that the cube root of 8 is equal to 2. Therefore,

Once again, the error is too small to show up.
Using your calculator, you can invent plenty of examples that show how these equations work with actual number values. Remember that multiplication is a way of adding things over and over, and division is repeated subtraction. Raising to a power is repeated multiplication, and taking a root is repeated division. These facts show up in the behavior of logarithmic functions.
CONVERSION OF LOG FUNCTIONS
Here are a couple of rules you can use to convert from natural logs to common logs and vice versa. You’ll sometimes have to do this, especially if you get into physics or engineering.
Let x be a positive real number. The common logarithm of x can be expressed in terms of the natural logarithms of x and 10 as follows:

Try an example. Let x = 3.537. Working to four significant figures, use your calculator to find
Now multiply by 0.4342945 and round to four significant figures.
Compare this with the common log of 3.537 as your calculator determines it, rounding off to four significant figures.
There’s a little error here—just enough to remind you that you’re dealing with irrational numbers, and approximations are the rule.
Now go the other way. Suppose x is a positive real number. The natural logarithm of x can be expressed in terms of the common logarithms of x and e as follows:

Let’s put a number into this formula and test it. Suppose x = 238.9. Working with your calculator to four significant figures, you find
Now multiply by 2.302585 and round to four significant figures.
Compare this with the natural log of 238.9 as your calculator “sees” it, rounded off to four significant figures. You should get
LOGARITHM COMPARISONS
Compare the common logarithms of 0.01, 0.1, 1, 10, and 100. Remember, the common log of a number is the power of 10 that produces that number. Note that 0.01 = 10−2, 0.1 = 10 −1, 1 = 100, 10 = 101, and 100 = 102. Therefore,

These values are all exact! But now suppose you want to compare the base-e logarithms (or natural logarithms) of these same five arguments. The base-e logarithm of a number is the power of e that produces that number. You must use a calculator to find them. The results are as follows, to four significant figures in each case except the natural log of 1, which is an exact value:

The log of 1 is always equal to 0, no matter what the base. This is a reflection of the fact that any positive real number raised to the zeroth power is equal to 1.
What about the logarithm of 0, or of any negative number? These are not defined in the set of real numbers, no matter what the base. To understand why, look at what happens if you try to calculate the base-b logarithm of −2. Remember that b must be a positive real number. Suppose logb (−2) = y. This can be rewritten in the form by = −2. What is the value of y? No real number will work here. Regardless of what real number you choose for y, the value of by is always positive. If you change −2 to any other negative number, or to 0, you run into the same problem. It’s impossible to find any real number y such that by is less than or equal to 0.
THE EXPONENTIAL BASE
Logarithms can be “undone” by exponential functions. An exponential function has a base and an exponent, just as a logarithm has. In fact, an exponential function is an “inside-out” way of looking at a logarithmic function! Suppose you have three real numbers h, x, and y, where b > 0, and you raise b to the x th power to get y, like this:
Then y is the hase-b exponential of x In the expression 102 = 100, 10 is the base and 100 is the exponential. In the expression e3 = 20.0855, e is the base and 20.0855 is the exponential. The two most often used exponential bases are the same as the two most often used log bases: 10 and e.
It’s possible to raise imaginary numbers to real number powers and get negative numbers; you’ve already learned about this. You could talk about base-i exponentials, for example, and make mathematical sense. Consider this:
This is true, as you have already learned. But you won’t be likely to hear anybody state this fact as “Minus 1 is the base-i exponential of 2,” unless you find yourself in the company of theoreticians! This book does not deal with exponential functions that involve complex numbers.
COMMON EXPONENTIALS
Base-10 exponentials are also known as common exponentials. Here are a few examples that you can verify with your calculator:

In the first equation, 2 is the argument, or value on which the exponential function depends, and 100 is the resultant. You would say, “The common exponential of 2 is equal to 100.” In the second equation, you would say, “The common exponential of 1.478 is approximately 30.06.” As with logarithms, the arguments in an exponential function need not be whole numbers. They can even be irrational; you could speak of 10w, for example. It happens to be approximately equal to 1,385.
Figure 24-5 is a partial linear coordinate graph of the function y = 10x. Figure 24-6 is a partial graph of the same function in semilog coordinates. The domain of the common exponential function encompasses the entire set of real numbers. The range is limited to the positive real numbers. This reflects the fact that you can never raise a real number to any real power and get a negative number.
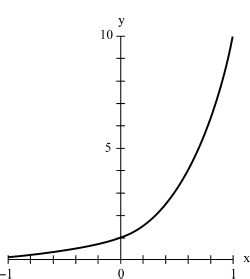
Figure 24-5
Partial linear-coordinate graph of the common exponential function. As x becomes arbitrarily large in the negative sense, the value of y approaches 0. As × increases without limit, so does y.

Figure 24-6
Partial semilog graph of the common exponential function. In this illustration, the x axis intersects the y axis at the point where y = 0.1.
NATURAL EXPONENTIALS
Base-e exponentials are also known as natural exponentials. Here are some examples, using the same arguments as in the previous section:

Figure 24-7 is a partial linear coordinate graph of the function y = ex. Figure 24-8 is a partial graph of the same function in semilog coordinates. As with the base-10 exponential function (or an exponential function of any other base), the domain encompasses the entire set of real numbers, and the range is limited to the positive real numbers.

Figure 24-7
Partial linear-coordinate graph of the natural exponential function. As × becomes arbitrarily large in the negative sense, the value of y approaches 0. As × increases without limit, so does y.

Figure 24-8
Partial semilog graph of the natural exponential function. In this illustration, the x axis intersects the y axis at the point where y = 0.1.
ALTERNATIVE EXPRESSIONS
Sometimes, the common exponential of a quantity is called the common antilogarithm (antilog10) or the common inverse logarithm (log−1) of that number. The natural exponential of a quantity is sometimes called the natural antilogarithm (antiln) or the natural inverse logarithm (ln−1) of that number.
LOGARITHMS VS. EXPONENTIALS
The exponential function is the inverse of the logarithm function, and vice versa. When two functions are inverses, they “undo” each other if both functions are defined for all the arguments of interest. For any real number x, and for any positive real number y, the following equations hold. Let the abbreviation “log” represent a logarithm to any base b for simplicity of notation, avoiding the need for putting a subscript within a superscript in the second equation. Then
and
Now work out an example of how a common antilog can be used to find the value of one nonwhole number raised to the power of another nonwhole number. Recall the example set out earlier in this chapter:

If you get rid of all the intermediate expressions, you have
Take the common antilog of both sides.
Now use your calculator to find the common antilog of 0.4536, and simplify the left-hand side of the equation according to the principle just mentioned in which the antilog “undoes” the log function.
You can use the “xy” key (or “x^y” or whatever it is called, where the first input number is raised to the power of the second) to verify
Good luck shows itself again here! The calculations agree to four significant figures. This should not come as a surprise when you realize that the “log-antilog” scheme is the way most calculators work to evaluate powers where the numbers are not whole. Before the invention of logs and antilogs, expressions such as 2.6351.078 were confusing and mysterious!
Try this same exercise using the base-e log and antilog functions instead of the base-10 functions. You’ll get the same result. In fact, you can use logs and antilogs of any base to evaluate any number raised to the power of any other number, as long as the log and the antilog are both defined for all the arguments.
BASIC PROPERTIES OF EXPONENTIALS
In all the following rules, b is a positive real number that represents the exponential base. In most real-life applications of exponential functions, b is equal to 10 (in the case of the common exponential function) or e (for the natural exponential function). However, once in a while you’ll come across a situation where b is some other number such as 2, which could represent a base for binary exponential functions.
Suppose x is some real number. The reciprocal of the exponential of x is equal to the exponential of the negative of x as follows:
You should recognize this from your work with powers and roots. Here’s a familiar example. You know that 1/8 is equal to 1 / (23). This is the same as saying that 1/8 is equal to 2−3. You also know that 1/100 equals 1 / (102), which is the same as saying that 1/100 equals 10−2. Now consider this:

Compare the above with the result of entering −3 into a scientific calculator, then hitting “Inv,” then hitting “ln,” and finally rounding off to four significant figures:
Exponential functions can express the relationship between sums and products, just as logarithms do. Let x and y be real numbers. The product of the exponentials of x and y is equal to the exponential of the sum of x and y:
To demonstrate, let b = 10, x = 4, and y = −6. Plug in the numbers on the left-hand side of the equation and evaluate.
Now evaluate the right-hand side:

The results agree! You’ll find that this is always true no matter what base and arguments you use, as long as the base is positive. Of course, if you get nonterminating decimals for any of the values in the calculation, you should expect some approximation error.
Let x and y be real numbers. Then the ratio of the exponential of x to the exponential of y is equal to the exponential of the difference between x and y:
Using the same numerical values as before, you can demonstrate this. Plug in the numbers on the left-hand side of the equation and evaluate.

Now evaluate the right-hand side:
Here’s a more complicated property of exponentials. At least, it looks complicated until you get used to working it out. Let x and y be real numbers, with the restriction that y cannot be equal to 0. Then the exponential of x/y is equal to the exponential of 1/y with base bx:
Try an example where the base b is equal to 10, with exponents x = 4 and y = 7. Evaluating the left-hand side first, letting 4/7 = 0.5714, and using the “xy “ or “xAy” function key on your calculator, you should get
Alternatively, you can enter 0.5714, hit the “Inv” key, and then hit “log” to find 10 to the power of 0.5714. Now plug the numbers into the right-hand side of the general equation and work it out.
To do this on your calculator, first figure 1/7 to four significant figures. You should get 0.1429. Then enter 10,000, hit the “xy” or “x^y” key, and enter 0.1429. The result should be 3.729. There’s a significant discrepancy here (2 parts in 10,000) because you’ve taken a rounding error to the 7th power.
Exponentials can show the relationship between a “power of a power” and a product. Suppose x and y are real numbers. Then the y th power of the exponential of x is equal to the exponential of the product xy.
To demonstrate this, let b = e, x = 2, and y = 3. Evaluate the left-hand side first.

Now the right-hand side:

If you want a more exact and simple example, use b = 10 instead of b = e. In that case, the left-hand side works out like this:
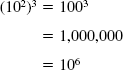
Now the right-hand side:
Let’s mix common and natural exponentials and see what happens! Suppose x is a real number representing the argument of an exponential function in base 10 and also in base e. The product of the common and natural exponentials of x is equal to the exponential of x to the base 10 e, as follows:
This can be illustrated with a numerical example. Go to six significant figures. Set x = 4 (exactly). Then the left-hand side of the above equation works out like this:

Now do the right-hand side, rounding off to six significant figures:

How about ratios of mixed common and natural exponentials? If x is a real number, then the ratio of the common exponential of x to the natural exponential of x is equal to the exponential of x to the base 10/e:
Work this out using x = 4, as in the previous example, and go to six significant figures. First, work on the left-hand side:

Next, do the right-hand side:

Now invert this ratio. Suppose x is a real number. The ratio of the natural exponential of x to the common exponential of x is equal to the exponential of x to the base e/10:
Again, use x = 4 and go through this with your calculator, rounding to six significant figures. Here’s the left-hand side:

And the right-hand side:

EXPONENTIAL COMPARISONS
Suppose you want to compare the values of e−2, e−1, e0, e1, and e2. Assume the exponents given here are exact. You want to express each answer to five significant figures. To determine the values of natural exponentials, you must use a calculator that has this function. The key is often labeled ex. With some calculators, it is necessary to hit an “Inv” key followed by a “ln” or “loge” key. Here are the values of the above exponentials, rounded off to five significant figures:

Now suppose you want to find the number whose common exponential function value is exactly 1,000,000 and also the number whose common exponential function value is exactly 0.0001. The argument 6 produces the common exponential value 1,000,000. This can be demonstrated by the fact that 106 = 1,000,000. The argument −4 produces the common exponential value 0.0001. This is shown by the fact that 10−4 = 0.0001.
How about the number whose natural exponential function value is exactly 1,000,000 and the number whose natural exponential function value is exactly 0.0001? To solve this problem, you must be sure you know what you’re trying to get! Suppose you call the solution x In the first case, solve the following equation for x
Taking the natural logarithm of each side, you obtain the following:
This simplifies to a matter of finding a natural logarithm with a calculator. To four significant figures
In the second case, you must solve the following equation for x:
Taking the natural logarithm of each side gives
This simplifies, as in the first case, to a matter of finding a natural logarithm with a calculator. Again to four significant figures
NUMERICAL ORDERS OF MAGNITUDE
You will sometimes hear the expression “order of magnitude” for a positive real number base b. Usually, b = 10. Sometimes b can be another number such as 2. An order of magnitude is a difference of 1 in the exponent of the base b.
For example, note that 10−2 = 0.01 and 103 = 1000. This means that in the base 10, the number 1000 is 5 orders of magnitude greater than the number 0.01, because the power of 10 for 1000 is 5 greater than the power of 10 for 0.01.
Here are some power-of-10 numbers, listed in ascending order. Each time you go down one line, the order of magnitude increases by 1:

Now look at powers of 2. An increase of 1 order of magnitude in base 2 is the equivalent of multiplying a given number by 2 (doubling it). Thus, starting with 20 = 1, you can build up like this:

and so on. A decrease of 1 order of magnitude in base 2 is the equivalent of dividing a given number by 2 (halving it). Again starting with 20 = 1, you get

and so on. Orders of magnitude in base 2 are unique because of their repetitive doubling and halving properties. This makes them useful in digital electronics and computing applications.
QUESTIONS AND PROBLEMS
This is an open-book quiz. You may refer to the text in this chapter (and earlier ones, too, if you want) when figuring out the answers. Take your time! Consider all values given as exact, so you don’t have to worry about significant figures. The correct answers are in the back of the book.
1. Consider the two numbers x = 2.3713018568 and y = 0.902780337. Find the product xy, using common logarithms, to four significant figures. (Ignore, for the moment, the fact that a calculator can easily be used to solve this problem without using logarithms in any form.)
2. Approximate the product of the two numbers xy from Prob. 1, but use natural logarithms instead. Show that the result is the same. Express the answer to four significant figures.
3. The power gain of an electronic circuit, in units called decibels (dB), can be calculated according to
where Pout is the output signal power and Pin is the input signal power, both specified in watts. Suppose the audio input to the left channel of a high-fidelity amplifier is 0.535 watt, and the output is 23.7 watts. What is the power gain of this circuit in decibels? Round off the answer to three significant figures.
4. Suppose the audio output signal in the scenario of Prob. 3 is run through a long length of speaker wire, so that instead of the 23.7 watts that appears at the left-channel amplifier output, the speaker only gets 19.3 watts. What is the power gain of the length of speaker wire, in decibels? Round off the answer to three significant figures.
5. If a positive real number increases by a factor of exactly 10, how does its common (base-10) logarithm change?
6. Show that the solution to Prob. 5 is valid for all positive real numbers.
7. If a positive real number decreases by a factor of exactly 100 (becomes 1/100 as great), how does its common logarithm change?
8. Show that the solution to Prob. 7 is valid for all positive real numbers.
9. If a positive real number is divided by a factor of exactly 357, how does its natural (base-e) logarithm change? Express the answer to five significant figures.
10. Show that the solution to Prob. 9 is valid for all positive real numbers.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
