| 4 | Division |
Before the days of electronic calculators and computers, division was a shortcut for counting out. To divide 28 items among 4 people, you would keep giving one to each of the four until the items were all gone, and then you would see how many each person had. Figure 4-1 shows two ways of how this could be done. Division is symbolized by using the division sign (÷) and the equation in this case is written 28 ÷ 4 = 7. In a division problem written in this way, the first number (in this case 28) is called the dividend, the second number (in this case 4) is called the divisor, and the answer (in this case 7) is called the quotient.

Figure 4-1
Two ways in which 28 items can be divided among four people so each person gets seven items.
LET’S THINK LIKE A CALCULATOR
A calculator uses a repeated process of subtraction to perform division. Let’s think like a calculator for a moment and see how this works when we want to divide 45,355 by 193. You can follow along here by reading down the columns in Fig. 4-2.

Figure 4-2
A pictorial representation of the way a calculator divides 45,355 by 193 to get a quotient of 235.
First, note that 100 × 193 = 19,300. Subtracting 193 from 45,355 over and over a total of 100 times leaves us with 26,055. Now 26,055 is greater than 19,300, so we can subtract 193 over and over, 100 more times, leaving us with 6,755. So far, we have subtracted 193 from 45,355 a total of 200 times. Now, let’s start taking away 193 × 10, which is 1,930, over and over. When we begin with 6,755 and do this, we get, in succession, 4,825, 2,895, and 965, while adding 10 to the quotient column (called a register in calculator parlance) each time. So far, we have taken away 193 from 45,355 a total of 230 times. To finish, we subtract 193 five more times, leaving us with 0. Now we are all done with the process. We have subtracted 193 from 45,355 a total of 235 times, and there’s nothing left over. That means 45,355 ÷ 193 = 235.
Some students say that 193 “goes into” 45,355 exactly 235 times. When I did that in elementary school, my teachers scolded me, saying that “goes into” was a bad expression. But it helped me to understand division. You might prefer to say that 193 “comes out of” 45,355 exactly 235 times.
DIVISION “UNDOES” MULTIPLICATION
Just as a calculator performs multiplication by repeated addition, it also performs division by repeated subtraction. In fact, this pattern in mathematics is useful to follow through. Each process that we learn has a reverse, and each reverse process provides a way to check the one it reverses:

We can say that subtraction is the opposite of addition in some ways, and division is the opposite of multiplication in some ways. But that doesn’t mean that these pairs of operations have identical properties. They are not mirror-image operations; some big differences exist! You can add or multiply two numbers in either order, and it doesn’t matter. But the order is critical in subtraction and division. For example, the following statements are true:
But these statements are false:
ALTERNATIVE NOTATION
Mathematicians, scientists, and engineers often use a forward slash to represent division, and you should get used to this notation. Here are a few examples:

If an expression looks too “scrunched up” without spaces between the slash and the numbers, you can add spaces on either side of the slash. This is not a bad idea, especially if either or both of the numbers are long.
DIVIDING INTO LONGER NUMBERS
Now let’s try another division problem: 1,743/7. You might find it helpful to have a multiplication table for the divisor, in this case 7, at the side. This table enables you to subtract the number in the quotient all in one “bite,” rather than one piece at a time as a calculator does. The remainder each time is less than the divisor, so “bring down” the next digit or figure and continue for the next place in the quotient. Figure 4-3 shows what you really do, and then how it is usually written.

Figure 4-3
In division, we start with the larger number and work toward smaller ones. In this example, we divide 1,743 by 7 to get a quotient of 249.
MULTIPLICATION CHECKS DIVISION
You can always check division by multiplication (Fig. 4-4), whether you do it the old-fashioned way or on a calculator. Using a calculator, you punch in the number 1,743, then the “divided by” button (marked “÷” or “/”), then the number 7, and finally the equals button (marked “=”). The calculator reads 249. Now, with 249 still reading, punch the “times” button (marked “×”), then the number 7, and finally the = button. You should get back the original number: 1,743.

Figure 4-4
You can check your division by multiplying. When you multiply the quotient by the divisor, you should get the dividend (the original number) back.
This procedure confirms that you hit the correct keys. If the last figure isn’t the one you began with, you probably hit a wrong button somewhere. Try again!
MORE ABOUT HOW A CALCULATOR DOES IT
Look back to the section “Let’s think like a calculator.” How does the calculator “know” that its first subtraction must be 100 times the divisor? To figure this out, it begins with 1 times the divisor (or the divisor itself), then tries 10 times the divisor (1,930), and then 100 times the divisor (19,300). If it finds that the dividend is larger, it will increase to 1000 times the divisor (193,000). If it finds that the divisor is larger, it will drop back to 100 times. After subtracting 100 times the divisor twice, it tries the third time, finds that the division is bigger, so it drops back to 10 times the divisor. The same thing happens when it has subtracted 10 times the divisor a total of three times. The fourth time it finds that the divisor is bigger, so it drops back to the divisor itself, as shown in Fig. 4-5. It “grinds away” at the problem, putting the quotient together in a register called the quotient accumulator.

Figure 4-5
Here is how a calculator figures out which numbers to take away as it divides 45,355 by 193.
DIVIDING BY LARGER NUMBERS (THE PEOPLE WAY)
Figure 4-6A shows an example of why we suggested having a multiplication table handy when doing division “by hand,” a process that has traditionally been called long division. In this example, we divide 14,996 by 23. The divisor, 23, is not in your regular multiplication table. But you can make one up, getting something like the table at left. Then you can see at a glance which digits you should use to do the long division.
In this example, we might first try to divide 149 by 7. But when we multiply 23 by 7, we get 161. That number is bigger than 149, so we try multiplying 23 by 6, which is 138. Then 138 is larger than 119, so we try 5 times. Finally, the last digit (conveniently) is exactly twice.
With multiple-digit numbers such as 23 as divisors, it’s more important to check our techniques because we have more chances of making a mistake. These mistakes occur both when we do it “by hand” and when we use a calculator. Figure 4-6B illustrates how multiplication “by hand” (or long multiplication) can be used to check the long division problem we just finished.
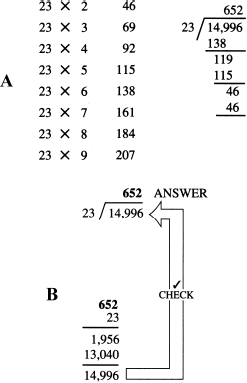
Figure 4-6
At A, we can make a table of multiples of the divisor to help us do long division when the divisor has more than one digit. At B, we use long multiplication to be sure we did the division problem correctly.
DIVISION BY FACTORS
You can sometimes solve multiplication problems by using factors. It also works in division, if the divisor can be factored into a product of two whole numbers. To see an example of how this can be done, examine Fig. 4-7, where we find the quotient 37,996/28. In this case, the divisor, 28, factors into 4 × 7. So you can divide the dividend by 4, and then divide the result by 7 to get the final quotient. (You could divide by 7 first and then by 4, and things would end up the same, although the intermediate quotient would be 5,428 instead of 9,499.) You can use long division, and also multiplication by factors, to check the answer.

Figure 4-7
An example of division by factors, and two methods of checking the answer. Here, we divide 37,996 by 4 to get 9,499, and then divide that result by 7 to get 1,357.
WHEN A REMAINDER IS LEFT
What happens when division doesn’t produce a whole number? Try it on a calculator and you’ll see. Instead of a whole number, you get some digits, then a decimal point, and then some more digits. If you do long division, you get a remainder.
Figure 4-8 shows how we find the quotient 10,050/37 by using long division. We get a whole number, 271, and a remainder of 23. Now you ask, “What does that mean? My calculator doesn’t show things that way!” Well, the remainder indicates how many parts of the divisor are left over in addition to the whole-number part of the quotient.

Figure 4-8
Division doesn’t always produce a whole-number quotient. In this example, dividing 10,050 by 37 gives us 271 with a remainder of 23.
In the example of Fig. 4-8, we have a remainder of 23 and a divisor of 37. That translates to a fraction: 23/37. Our quotient is therefore 271 and 23/37, written like this:
271-23/37
The dash here is not a minus sign! It just serves to separate the whole-number part from the fractional part. Sometimes the dash is left out and a space is put there instead. Fractions can also be written with the numerator on top, then a horizontal line under the numerator instead of a slash after it, and then the denominator underneath the line. The first or top number in the fraction (in this case 23) is called the numerator. The second or bottom number (in this case 37) is called the denominator.
If you use your calculator, you will see that dividing 23 by 37 gives you a bunch of numbers after a decimal point, like this:
23/37 = .621621621621 …
On some calculators you will see a 0 in front, like this:
23/37 = 0.621621621621 …
Now try dividing the original dividend, 10,050, by 37 on a calculator. You will get
10,050/37 = 271.621621621 …
That means 271 plus 0.621621621 … . The remainder of 23 means 23 parts out of 37, which is equivalent to the decimal number 0.621621621 … . The three dots mean that the numbers “621” keep repeating in that order, over and over, forever! That’s called a recurring decimal. Some texts call it a repeating decimal.
HOW A CALCULATOR HANDLES FRACTIONS
Now, let’s look more closely at what a calculator does with fractions. If you divide 25 by 6, it will read out 4.16666 … . Figure 4-9 shows what goes on inside the little thing’s “brain.” As you move down until the quotient accumulator reads 4, it follows what you already know. However, it doesn’t stop. Had you punched in 2500 divided by 6, it would read 416.6666 … . Expressed as a whole number and a fraction, that’s 416-2/3.

Figure 4-9
Here is the process a calculator goes through when you tell it to divide 25 by 6.
A division problem such as 25/6, when done in decimal form, never ends. Each recurring 4 in the quotient accumulator can be divided by another 6. A real calculator stops when it runs out of digits to display. Depending on the type of calculator you have, it will either leave the last digit as a 6 or round it up to a 7. If the calculator didn’t know better, it would get “hung up” in the calculation process and spit out 6s until you switched it off or its battery died!
DECIMAL EQUIVALENTS OF FRACTIONS
We have seen how a calculator turns a fraction into a decimal. That’s what it does naturally, if you want to believe that there is anything “natural” about a calculator! Now, let’s look at what a calculator does with some simple fractions. Here are a few that convert to relatively simple decimals. You can use your own calculator to verify these:

MORE DIFFICULT FRACTIONS
The above fractions are easy. The harder ones are those that always run off the end of the calculator’s space. The whole number and fraction 416-2/3 is a good example. Here’s another one that looks simple: 1/3.
When you divide 3 into 1, after bringing down zero after zero, you get an unending string of 3s. Earlier generations had a useful trick to avoid having to keep writing 3s; they put a dot over the 3 to indicate that it keeps repeating. Sometimes they put a line over it instead of a dot. Here are some more fractions that end up with one number that keeps repeating. Again, you can use your calculator to check them, as follows:

WHERE GROUPS OF DIGITS REPEAT
In all the fractions in the last section, the decimal equivalent, which is what your calculator always gives you, ends up with one figure that kept repeating. Another kind of fraction first shows up in the decimal equivalent for 1/7. Here, a sequence of six digits repeats. Try dividing it out with a calculator that displays plenty of digits, such as the one on your computer! You should get this:
The sequence that repeats here is 142857, always in the same order. Try some others now. See what happens when you divide out the following quotients. How many digits are in the sequence that repeats? You might need a calculator that can display a lot of digits to see the pattern, but there will always be one!

Do you notice something in common about the last four examples above?
CONVERTING RECURRING DECIMALS TO FRACTIONS
Although recurring decimals are easier to handle when you know what they mean, using old-fashioned fractions is often easier. How can we convert a recurring decimal to a fraction? There’s a neat little trick that works for decimal numbers less than 1—that is, numbers that you write down as a zero followed by a decimal point and then a group of digits that keeps recurring. We can call this general rule the “law of the nines.”
First, find the pattern that repeats, and write it down. For example, you might see the following decimal:
Here, the sequence of digits that repeats is 6738. Now put this in the numerator of a fraction, and then put an equal number of 9s in the denominator. In this case, you get 6,738/9,999. This is the fractional equivalent of the above decimal number. Check it out with your calculator. Punch in the digits 6, 7, 3, and 8; then press the “divide by” key, then the digits 9, 9, 9, and 9, and finally the “equals” key. Here are some more examples:

You will recognize these as the last four numbers from the previous section.
QUESTIONS AND PROBLEMS
This is an open-book quiz. You may refer to the text in this chapter (and earlier ones, too, if you want) when figuring out the answers. Take your time! The correct answers are in the back of the book.
1. Perform the following divisions and check your answers by multiplication.
(a) 343 ÷ 7
(b) 729 ÷ 9
(c) 4,928 ÷ 8
(d) 3,265 ÷ 5
(e) 6,243 ÷ 3
(f) 7,862 ÷ 2
(g) 3,936 ÷ 4
(h) 3,924 ÷ 6
(i) 3,081 ÷ 13
(j) 16,324 ÷ 11
(k) 6,443 ÷ 17
(l) 8,341 ÷ 19
2. Perform the following divisions by successive (division by factors) and long division. If your answers do not agree, check them with long multiplication.
(a) 3,600 ÷ 15
(b) 15,813 ÷ 21
(c) 73,625 ÷ 25
(d) 10,136 ÷ 28
3. Perform the following divisions and write the remainder as a fraction, using whichever method of conversion you like best.
(a) 3,459 ÷ 7
(b) 23,431 ÷ 8
(c) 13,263 ÷ 9
(d) 14,373 ÷ 3
(e) 29,336 ÷ 6
(f) 8,239 ÷ 17
(g) 34,343 ÷ 28
(h) 92,929 ÷ 29
4. A profit of $14,000,000 has to be shared among holders of 2,800,000 shares of stock. What is the profit per share?
5. The total operating cost for a commuter airline flight between two cities is estimated as $8,415. What fare should be charged so that a flight with 55 passengers just meets the operating cost?
6. A machine needs a special tool that costs $5,000 to make a certain part. When equipped with this tool, the machine makes parts for 25 cents each. But the price must also pay for the tool. If the tool cost is to be paid for out of the first 10,000 parts made, what will be the cost of each part?
7. A freight car carries 58 tons (a ton here is defined as 2000 pounds), including its own weight, and runs on 8 wheels. Its suspension distributes the weight equally among the wheels. What is the weight on each wheel?
8. A man makes 1,200 production units of a certain part in 8 hours. How much time is spent making each part?
9. A package of 10,000 small parts weighs 1,565 pounds. The empty package weighs 2.5 pounds. How much does each part weigh? (Hint: convert pounds to ounces.)
10. Another package weighs 2,960 pounds full and 5 pounds empty. One part weighs 3 ounces. How many parts are in the full package?
11. A narrow strip of land exactly 1 mile long is to be divided into 33 lots of equal width. How wide is each lot?
12. On a test run, a car travels 462 miles on 22 gallons of gas. Assuming performance is uniform, how far does it go on each gallon of gas?
13. A particular mixture is usually made up 160 gallons at a time. It uses 75 gallons of ingredient 1; 50 gallons of ingredient 2; 25 gallons of ingredient 3; and 10 gallons of ingredient 4. If only 1 gallon is required, what amounts of each ingredient should be used?
14. Find the simplest fractional equivalents of the following decimals. By “simplest,” we mean that the numerator and denominator should both be as small as possible so the fraction “divides out” into the decimal expression shown.
(a) 0.125
(b) 0.7
(c) 0.375
(d) 0.95
15. Find fractional equivalents of the following decimals. Check each by dividing back to decimal form again. You don’t have to find the simplest expressions here.
(a) 0.416416416 …
(b) 0.212121 …
(c) 0.189189189 …
(d) 0.489248924892 …
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
