Appendix C. Algebraic Preliminaries

C.1 Construction of Galois Fields GF(2^m) FromGF(2)

Consider adding powers of α, α², α³,… to the binary Galois field with multiplication (*) defined as:

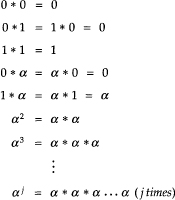
It can be shown from this definition that

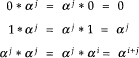
Definition: Degree of a polynomial p(x) is the power of the highest power of x with a nonzero coefficient.

Definition: Irreducible Polynomial—A polynomial p(x) over GF(2) of degree m is irreducible over GF(2) if p (x) is not divisible by any polynomial over GF(2) of degree less than m but greater than zero.

Fact: It can be proved [Lin+83¹] that any irreducible polynomial over GF(2) of degree m divides x^2m-1 + 1.

¹ Lin, Shu, and Daniel J. Costello, Jr., Error Control Coding Fundamentals and Applications. New York: Prentice-Hall, 1983.

Definition: Primitive Polynomial—An irreducible polynomial p(x) of degree m is primitive if the smallest positive integer η for which p(x) divides x^η + 1 is η = 2^m – 1.

We can now define a new field F with elements

We can then create restrictions on α so that F contains only 2^m elements. Let p(x) be a primitive polynomial of degree m over GF(2). Assume p(x) = 0. Since p (x) divides x^2m-1 + 1, we have

Let x = α, so

Because p(x) = 0,

Thus, if p(x) = 0, the set F* = {0, 1, α, α², … , α^2m-2] is finite and has 2^m elements.

C.2 Basic Properties of the Galois Field GF(2^m)

1. As with real polynomials, a polynomial from GF(2) may not have roots from GF(2). However, whereas polynomials with real coefficients have complex valued roots, a polynomial with coefficients from GF(2) has roots from an extension field of GF(2).

2. If f(x) is a polynomial with coefficients from GF(2) and β is an element of an extension field of GF(2), then β² is also a root of f(x).
Definition: Conjugate of β—The element β²¹ is called a conjugate of β.

3. The 2^m – 1 nonzero elements of GF(2^m) form all the roots of x^2m-1 = 1. The elements of GF(2^m) form all the roots of x^2m + x.

4. Since any element p in GF(2^m) is a root of x^2m + x, β may be a root of a polynomial over GF(2) with a degree of less than 2^m. Let ø(x) be the polynomial of smallest degree over GF(2) such that φ (β) = 0.
Definition: Minimal Polynomial—The polynomial φ (x) = y is called the minimal polynomial of β.

5. The minimal polynomial φ(x) of a field element β is irreducible.

6. Let f(x) be a polynomial over GF(2) and φ(x) be the minimal polynomial of a field element β. If β is a root of f(x), then f(x) is divisible by φ(x).

7. The minimal polynomial φ(x) of an element β in GF(2^m) divides x^2m + x.

8. Let f(x) be an irreducible polynomial over GF(2) and β be an element in GF(2^m). Let φ(x) be the minimal polynomial of β. If f(β) = 0, then φ(x) = f(x). Thus, β and its conjugates β², β²², … , β^2e-1 are roots of φ(x).

9. Let β be an element in GF(2) and e the smallest integer such that β^2e = β. Then

is an irreducible polynomial over GF(2)

10. Let φ(x) be the minimal polynomial of an element β in GF(2^m). Let e be the smallest integer such that β^2e = β. Then

11. Let φ(x) be the minimal polynomial of an element β in GF(2^m). Let e be the degree of φ(x). Then e is the smallest integer such that β^2e = β. More-over, e ≤ m.

12. If β is a primitive element of GF(2^m), all of its conjugates are also primitive elements of GF(2^m).

13. If β is an element of order n in GF(2^m), all of its conjugates have the same order n.