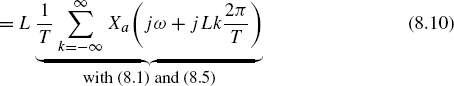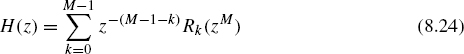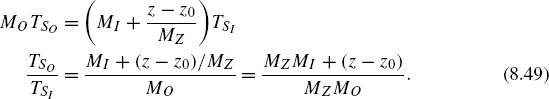Chapter 8
Sampling Rate Conversion
Several different sampling rates are established for digital audio applications. For broadcasting, professional and consumer audio, sampling rates of 32, 48 and 44.1 kHz are used. Moreover, other sampling rates are derived from different frame rates for film and video. In connecting systems with different uncoupled sampling rates, there is a need for sampling rate conversion. In this chapter, synchronous sampling rate conversion with rational factor L/M for coupled clock rates and asynchronous sampling rate conversion will be discussed where the different sampling rates are not synchronized with each other.
8.1 Basics
Sampling rate conversion consists out of upsampling and downsampling and anti-imaging and anti-aliasing filtering [Cro83, Vai93, Fli00, Opp99]. The discrete-time Fourier transform of the sampled signal x(n) with sampling frequency fS = 1/T (ΩS = 2πfS) is given by
with the Fourier transform Xa(jΩ) of the continuous-time signal x(t). For ideal sampling the condition
holds.
8.1.1 Upsampling and Anti-imaging Filtering
For upsampling the signal
by a factor L between consecutive samples L − 1 zero samples will be included (see Fig. 8.1). This leads to the upsampled signal
with sampling frequency ![]() and the corresponding Fourier transform
and the corresponding Fourier transform
The suppression of the image spectra is achieved by anti-imaging filtering of w(m) with h(m), such that the output signal is given by
To adjust the signal power in the base-band the Fourier transform of the impulse-response
needs a gain factor L in the pass-band, such that the output signal y(m) has the Fourier transform given by
The output signal represents the sampling of the input x(t) with sampling frequency ![]() = LfS.
= LfS.
8.1.2 Downsampling and Anti-aliasing Filtering
For downsampling a signal x(n) by M the signal has to be band-limited to π/M in order to avoid aliasing after the downsampling operation (see Fig. 8.2). Band-limiting is achieved by filtering with H(ejΩ) according to

Figure 8.1 Upsampling by L and anti-imaging filtering in time and frequency domain.
Downsampling of w(m) is performed by taking every Mth sample, which leads to the output signal
with the Fourier transform
For the base-band spectrum (|Ω′| ≤ π and l = 0) we get
and for the Fourier transform of the output signal we can derive
which represents a sampled signal y(n) with ![]() .
.

Figure 8.2 Anti-aliasing filtering and downsampling by M in time and frequency domain.
8.2 Synchronous Conversion
Sampling rate conversion for coupled sampling rates by a rational factor L/M can be performed by the system shown in Fig. 8.3. After upsampling by a factor L, anti-imaging filtering at LfS is carried out, followed by downsampling by factor M. Since after upsampling and filtering only every Mth sample is used, it is possible to develop efficient algorithms that reduce complexity. In this respect two methods are in use: one is based on a time-domain interpretation [Cro83] and the other [Hsi87] uses Z-domain fundamentals. Owing to its computational efficiency, only the method in the Z-domain will be considered.

Figure 8.3 Sampling rate conversion by factor L/M.
Starting with the finite impulse response h(n) of length N and its Z-transform
the polyphase representation [Cro83, Vai93, Fli00] with M components can be expressed as
with
or
with
The polyphase decomposition as given in (8.22) and (8.24) is referred to as type 1 and 2, respectively. The type 1 polyphase decomposition corresponds to a commutator model in the anti-clockwise direction whereas the type 2 is in the clockwise direction. The relationship between R(z) and E(z) is described by
With the help of the identities [Vai93] shown in Fig. 8.4 and the decomposition (Euclid's theorem)
it is possible to move the inner delay elements of Fig. 8.5. Equation (8.27) is valid if M and L are prime numbers. In a cascade of upsampling and downsampling, the order of functional blocks can be exchanged (see Fig. 8.5b).
The use of polyphase decomposition can be demonstrated with the help of an example for L = 2 and M = 3. This implies a sampling rate conversion from 48 kHz to 32 kHz. Figures 8.6 and 8.7 show two different solutions for polyphase decomposition of sampling rate conversion by 2/3. Further decompositions of the upsampling decomposition of Fig. 8.7 are demonstrated in Fig. 8.8. First, interpolation is implemented with a polyphase decomposition and the delay z−1 is decomposed to z−1 = z−2z3. Then, the downsampler of factor 3 is moved through the adder into the two paths (Fig. 8.8b) and the delays are moved according to the identities of Fig. 8.4. In Fig. 8.8c, the upsampler is exchanged with the downsampler, and in a final step (Fig. 8.8d) another polyphase decomposition of E0(z) and E1(z) is carried out. The actual filter operations E0k(z) and E1k(z) with k = 0, 1, 2 are performed at ![]() of the input sampling rate.
of the input sampling rate.

Figure 8.4 Identities for sampling rate conversion.

Figure 8.5 Decomposition in accordance with Euclid's theorem.
8.3 Asynchronous Conversion
Plesiochronous systems consist of partial systems with different and uncoupled sampling rates. Sampling rate conversion between such systems can be achieved through a DA conversion with the sampling rate of the first system followed by an AD conversion with the sampling rate of the second system. A digital approximation of this approach is made with a multirate system [Lag81, Lag82a, Lag82b, Lag82c, Lag83, Ram82, Ram84]. Figure 8.9a shows a system for increasing the sampling rate by a factor L followed by an anti-imaging filter H(z) and a resampling of the interpolated signal y(k). The samples y(k) are held for a clock period (see Fig. 8.9c) and then sampled with output clock period TSO = 1/fSO. The interpolation sampling rate must be increased sufficiently that the difference of two consecutive samples y(k) is smaller than the quantization step Q. The sample-and-hold function applied to y(k) suppresses the spectral images at multiples of LfS (see Fig. 8.9b). The signal obtained is a band-limited continuous-time signal which can be sampled with output sampling rate fSO.

Figure 8.6 Polyphase decomposition for downsampling L/M = 2/3.

Figure 8.7 Polyphase decomposition for upsampling L/M = 2/3.
For the calculation of the necessary oversampling rate, the problem is considered in the frequency domain. The sinc function of a sample-and-hold system (see Fig. 8.9b) at frequency ![]() is given by
is given by

Figure 8.8 Sampling rate conversion by factor 2/3.
With sin (α − β) = sin(α) cos(β) − cos(α) sin(β) we derive
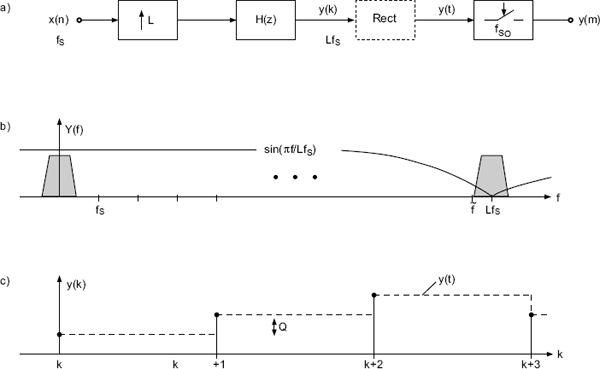
Figure 8.9 Approximation of DA/AD conversions.
This value of (8.29) should be lower than ![]() and allows the computation of the interpolation factor L. For a given word-length w and quantization step Q, the necessary interpolation rate L is calculated by
and allows the computation of the interpolation factor L. For a given word-length w and quantization step Q, the necessary interpolation rate L is calculated by
For a linear interpolation between upsampled samples y(k), we can derive
With this it is possible to reduce the necessary interpolation rate to
Figure 8.10 demonstrates this with a two-stage block diagram. First, interpolation up to a sampling rate L1fS is performed by conventional filtering. In a second stage upsampling by factor L2 is done by linear interpolation. The two-stage approach must satisfy the sampling rate LfS = (L1L2) fS.
The choice of the interpolation algorithm in the second stage enables the reduction of the first oversampling factor. More details are discussed in Section 8.2.2.

Figure 8.10 Linear interpolation before virtual sample-and-hold function.
8.3.1 Single-stage Methods
Direct conversion methods implement the block diagram [Lag83, Smi84, Par90, Par91a, Par91b, Ada92, Ada93] shown in Fig. 8.9a. The calculation of a discrete sample on an output grid of sampling rate fSO from samples x(n) at sampling rate fSI can be written as
where 0 ≤ α < 1. With the transfer function
and the properties
the impulse response is given by
From (8.37) we can express the delayed signal
as the convolution between x(n) and h(n − α). Figure 8.11 illustrates this convolution in the time domain for a fixed α. Figure 8.12 shows the coefficients h(n − αi) for discrete αi (i = 0,…, 3) which are obtained from the intersection of the sinc function with the discrete samples x(n).

Figure 8.11 Convolution sum (8.42) in the time domain.
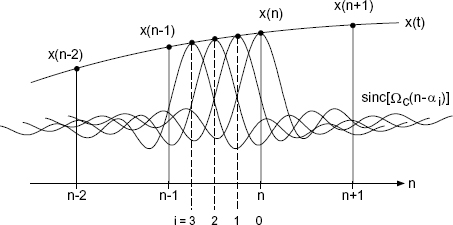
Figure 8.12 Convolution sum (8.42) for different αi.
In order to limit the convolution sum, the impulse response is windowed, which gives
From this, the sample estimate
results. A graphical interpretation of the time-variant impulse response which depends on αi is shown in Fig. 8.13. The discrete segmentation between two input samples into N intervals leads to N partial impulse responses of length 2M + 1.
If the output sampling rate is smaller than the input sampling rate (fSO < fSI), band-limiting (anti-aliasing) to the output sampling rate has to be done. This can be achieved with factor β = fSO/fSI and leads, with the scaling theorem of the Fourier transform, to
This time-scaling of the impulse response has the consequence that the number of coefficients of the time-variant partial impulse responses is increased. The number of required states also increases. Figure 8.14 shows the time-scaled impulse response and elucidates the increase in the number M of the coefficients.

Figure 8.13 Sinc function and different impulse responses.

Figure 8.14 Time-scaled impulse response.
8.3.2 Multistage Methods
The basis of a multistage conversion method [Lag81, Lag82, Kat85, Kat86] is shown in Fig. 8.15a and will be described in the frequency domain as shown in Fig. 8.15b–d. Increasing the sampling rate up to LfS before the sample-and-hold function is done in four stages. In the first two stages, the sampling rate is increased by a factor of 2 followed by an anti-imaging filter (see Fig. 8.15b, c), which leads to a four times oversampled spectrum (Fig. 8.15d). In the third stage, the signal is upsampled by a factor of 32 and the image spectra are suppressed (see Fig. 8.15d, e). In the fourth stage (Fig. 8.15e) the signal is upsampled to a sampling rate of LfS by a factor of 256 and a linear interpolator. The sinc2 function of the linear interpolator suppresses the images at multiples of 128fS up to the spectrum at LfS. The virtual sample-and-hold function is shown in Fig. 8.15f, where resampling at the output sampling rate is performed. A direct conversion of this kind of cascaded interpolation structure requires anti-imaging filtering after every upsampling with the corresponding sampling rate. Although the necessary filter order decreases owing to a decrease in requirements for filter design, an implementation of the filters in the third and fourth stages is not possible directly. Following a suggestion by Lagadec [Lag82c], the measurement of the ratio of input to output rate is used to control the polyphase filters in the third and fourth stages (see Fig. 8.16a, CON = control) to reduce complexity. Figures 8.16b–d illustrate an interpretation in the time domain. Figure 8.16b shows the interpolation of three samples between two input samples x(n) with the help of the first and second interpolation stage. The abscissa represents the intervals of the input sampling rate and the sampling rate is increased by factor of 4. In Fig. 8.16c the four times oversampled signal is shown. The abscissa shows the four times oversampled output grid. It is assumed that output sample y(m = 0) and input sample x(n = 0) are identical. The output sample y(m = 1) is now determined in such a form that with the interpolator in the third stage only two polyphase filters just before and after the output sample need to be calculated. Hence, only two out of a total of 31 possible polyphase filters are calculated in the third stage. Figure 8.16d shows these two polyphase output samples. Between these two samples, the output sample y(m = 1) is obtained with a linear interpolation on a grid of 255 values.
Instead of the third and fourth stages, special interpolation methods can be used to calculate the output y(m) directly from the four times oversampled input signal (see Fig. 8.17) [Sti91, Cuc91, Liu92]. The upsampling factor L3 = 2w−3 for the last stage is calculated according to L = 2w−1 = L1L2L3 = 22L3. Section 8.4 is devoted to different interpolation methods which allow a real-time calculation of filter coefficients. This can be interpreted as time-variant filters in which the filter coefficients are derived from the ratio of sampling rates. The calculation of one filter coefficient set for the output sample at the output rate is done by measuring the ratio of input to output sampling rate as described in the next section.
8.3.3 Control of Interpolation Filters
The measurement of the ratio of input and output sampling rate is used for controlling the interpolation filters [Lag82a]. By increasing the sampling rate by a factor of L the input sampling period is divided into L = 2w−1 = 215 parts for a signal word-length of w = 16 bits. The time instant of the output sample is calculated on this grid with the help of the measured ratio of sampling periods TSO/TSI as follows.
A counter is clocked with LfSI and reset by every new input sampling clock. A sawtooth curve of the counter output versus time is obtained as shown in Fig. 8.18. The counter runs from 0 to L − 1 during one input sampling period. The output sampling period TSO starts at time ti−2, which corresponds to counter output zi−2, and stops at time ti−1, with counter output zi−1. The difference between both counter measurements allows the calculation of the output sampling period TSO with a resolution of LfSI.

Figure 8.15 Multistage conversion – frequency-domain interpretation.
The new counter measurement is added to the difference of previous counter measurements. As a result, the new counter measurement is obtained as
The modulo operation can be carried out with an accumulator of word-length w − 1 = 15. The resulting time ti determines the time instant of the output sample at the output sampling rate and therefore the choice of the polyphase filter in a single-stage conversion or the time instant for a multistage conversion.

Figure 8.16 Time-domain interpretation.

Figure 8.17 Sampling rate conversion with interpolation for calculating coefficients of a time-variant interpolation filter.
The measurement of TSO/TSI is illustrated in Fig. 8.19:
- The input sampling rate fSI is increased to MZ fSI using a frequency multiplier where MZ = 2w. This input clock increase by the factor MZ triggers a w-bit counter. The counter output z is evaluated every MO output sampling periods.
- Counting of MO output sampling periods.
- Simultaneous counting of the MI input sampling periods.

Figure 8.18 Calculation of ti.

Figure 8.19 Measurement of TSO/TSI.
The time intervals d1 and d2 (see Fig. 8.19) are given by
and with the requirement d1 = d2 we can write
- Example 1: w = 0 → MZ = 1
With a precision of 15 bits, the averaging number is chosen as MO = 215 and the number MI has to be determined.
- Example 2: w = 8 → MZ = 28
With a precision of 15 bits, the averaging number is chosen as MO = 27 and the number MI and the counter outputs have to be determined.
The sampling rates at the input and output of a sampling rate converter can be calculated by evaluating the 8-bit increment of the counter for each output clock with
as seen from Table 8.1.
Table 8.1 Counter increments for different sampling rate conversions.
| Conversion/kHz | 8-bit counter increment |
| 32 → 48 | 170 |
| 44.1 → 48 | 235 |
| 32 → 44.1 | 185 |
| 48 → 44.1 | 278 |
| 48 → 32 | 384 |
| 44.1 → 32 | 352 |
8.4 Interpolation Methods
In the following sections, special interpolation methods are discussed. These methods enable the calculation of time-variant filter coefficients for sampling rate conversion and need an oversampled input sequence as well as the time instant of the output sample. A convolution of the oversampled input sequence with time-variant filter coefficients gives the output sample at the output sampling rate. This real-time computation of filter coefficients is not based on popular filter design methods. On the contrary, methods are presented for calculating filter coefficient sets for every input clock cycle where the filter coefficients are derived from the distance of output samples to the time grid of the oversampled input sequence.
8.4.1 Polynomial Interpolation
The aim of a polynomial interpolation [Liu92] is to determine a polynomial
of Nth order representing exactly a function f(x) at N + 1 uniformly spaced xi, i.e. pN(xi) = f(xi) = yi for i = 0,…, N. This can be written as a set of linear equations
The polynomial coefficients ai as functions of y0,…,yN are obtained with the help of Cramer's rule according to
For uniformly spaced xi = i with i = 0, 1,…, N the interpolation of an output sample with distance α gives
In order to determine the relationship between the output sample y(n + α) and yi, a set of time-variant coefficients ci needs to be determined such that
The calculation of time-variant coefficients ci(α) will be illustrated by an example.
Example: Figure 8.20 shows the interpolation of an output sample of distance α with N = 2 and using three samples which can be written as

Figure 8.20 Polynomial interpolation with three samples.
The samples y(n + i), with i = −1, 0, 1, can be expressed as
or in matrix notation
The coefficients ai as functions of yi are then given by
such that
is valid. The output sample y(n + α) can be written as
Equation (8.62) with ai from (8.61) leads to
Comparing the coefficients from (8.63) and (8.64) for n = 0 gives the coefficients

8.4.2 Lagrange Interpolation
Lagrange interpolation for N + 1 samples makes use of the polynomials li(x) which have the following properties (see Fig. 8.21):
Based on the zeros of the polynomial li(x), it follows that
With li(xi) = 1 the coefficients are given by
The interpolation polynomial is expressed as
With ![]() , (8.66) can be written as
, (8.66) can be written as
For uniformly spaced samples
and with the new variable α as given by
and hence
For even N we can write
and for odd N,
The interpolation of an output sample is given by

Figure 8.21 Lagrange polynomial.
Example: For N = 2, 3 samples,

8.4.3 Spline Interpolation
The interpolation using piecewise defined functions that only exist over finite intervals is called spline interpolation [Cuc91]. The goal is to compute the sample y(n + α) = ![]() from weighted samples y(n + i).
from weighted samples y(n + i).
A B-spline ![]() of Nth order using m + 1 samples is defined in the interval [xk,…, xk+m] by
of Nth order using m + 1 samples is defined in the interval [xk,…, xk+m] by
with the truncated power functions
In the following ![]() will be considered for k = 0 where
will be considered for k = 0 where ![]() for x < x0 and
for x < x0 and ![]() . Figure 8.22 shows the truncated power functions and the B-spline of Nth order. With the definition of the truncated power functions we can write
. Figure 8.22 shows the truncated power functions and the B-spline of Nth order. With the definition of the truncated power functions we can write
and after some calculations we get

Figure 8.22 Truncated power functions and the B-spline of Nth order.
With the condition ![]() , the following set of linear equations can be written with (8.80) and the coefficients of the powers of x:
, the following set of linear equations can be written with (8.80) and the coefficients of the powers of x:
The homogeneous set of linear equations has non-trivial solutions for m>N. The minimum requirement results in m = N + 1. For m = N + 1, the coefficients [Boe93] can be obtained as follows:
Setting the ith column of the determinant in the numerator of (8.82) equal to zero corresponds to deleting the column. Computing both determinants of Vandermonde matrices [Bar90] and division leads to the coefficients
and hence
For some k we obtain
Since the functions ![]() decrease with increasing N, a normalization of the form
decrease with increasing N, a normalization of the form ![]()
![]() is done, such that for equidistant samples we get
is done, such that for equidistant samples we get
The next example illustrates the computation of B-splines.
Example: For N = 3, m = 4, and five samples the coefficients according to (8.83) are given by

Figure 8.23a, b shows the truncated power functions and their summation for calculating ![]() . In Fig. 8.23c the horizontally shifted
. In Fig. 8.23c the horizontally shifted ![]() are depicted.
are depicted.
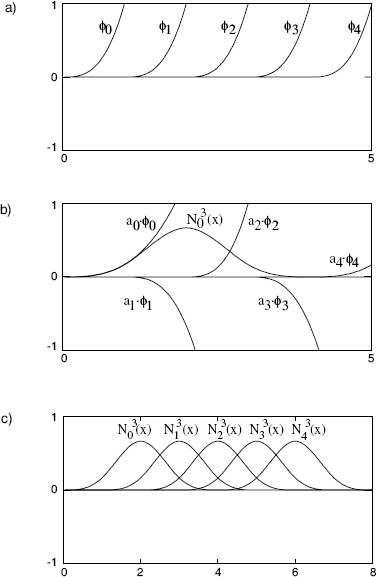
Figure 8.23 Third-order B-spline (N = 3, m = 4, 5 samples).

Figure 8.24 Interpolation with B-splines of second and third order.
A linear combination of B-splines is called a spline. Figure 8.24 shows the interpolation of sample y(n + α) for splines of second and third order. The shifted B-splines ![]() are evaluated at the vertical line representing the distance α. With sample y(n) and the normalized B-splines
are evaluated at the vertical line representing the distance α. With sample y(n) and the normalized B-splines ![]() , the second- and third-order splines are respectively expressed as
, the second- and third-order splines are respectively expressed as
and
The computation of a second-order B-spline at the sample index α is based on the symmetry properties of the B-spline, as depicted in Fig. 8.25. With (8.77), (8.86) and the symmetry properties shown in Fig. 8.25, the B-splines can be written in the form
With (8.83) we get the coefficients
and thus

Figure 8.25 Exploiting the symmetry properties of a second-order B-spline.
Owing to the symmetrical properties of the B-splines, the time-variant coefficients of the second-order B-spline can be derived as
In the same way the time-variant coefficients of a third-order B-spline are given by
Higher-order B-splines are given by
Similar sets of coefficients can be derived here as well. Figure 8.26 illustrates this for fourth- and sixth-order B-splines.
Generally, for even orders we get
and for odd orders
For the application of interpolation the properties in the frequency domain are important. The zero-order B-spline is given by
and the Fourier transform gives the sinc function in the frequency domain. The first-order B-spline given by

Figure 8.26 Interpolation with B-splines of fourth and sixth order.
leads to a sinc2 function in the frequency domain. Higher-order B-splines can be derived by repeated convolution [Chu92] as given by
Thus, the Fourier transform leads to
With the help of the properties in the frequency domain, the necessary order of the spline interpolation can be determined. Owing to the attenuation properties of the sincN + 1(f) function and the simple real-time calculation of the coefficients, spline interpolation is well suited to time-variant conversion in the last stage of a multistage sampling rate conversion system [Zöl94].
8.5 Exercises
1. Basics
Consider a simple sampling rate conversion system with a conversion rate of ![]() . The system consists of two upsampling blocks, each by 2, and one downsampling block by 3.
. The system consists of two upsampling blocks, each by 2, and one downsampling block by 3.
- What are anti-imaging and anti-aliasing filters and where do we need them in our system?
- Sketch the block diagram.
- Sketch the input, intermediate and output spectra in the frequency domain.
- How is the amplitude affected by the up- and downsampling and where does it come from?
- Sketch the frequency response of the anti-aliasing and anti-imaging filters needed for this upsampling system.
2. Synchronous Conversion
Our system will now be upsampled directly by a factor of 4, and again downsampled by a factor of 3, but with linear interpolation and decimation methods. The input signal is x(n) = sin(nπ/6), n = 0,…, 48.
- What are the impulse responses of the two interpolation filters? Sketch their magnitude responses.
- Plot the signals (input, intermediate and output signal) in the time domain using Matlab.
- What is the delay resulting from the causal interpolation/decimation filters?
- Show the error introduced by this interpolation/decimation method, in the frequency domain.
3. Polyphase Representation
Now we extend our system using a polyphase decomposition of the interpolation/decimation filters.
- Sketch the idea of polyphase decomposition using a block diagram. What is the benefit of such decomposition?
- Calculate the polyphase filters for up- and downsampling (using interpolation and decimation).
- Use Matlab to plot all resulting signals in the time and frequency domain.
4. Asynchronous Conversion
- What is the basic concept of asynchronous sampling rate conversion?
- Sketch the block diagram and discuss the individual operations.
- What is the necessary oversampling factor L for a 20-bit resolution?
- How can we simplify the oversampling operations?
- How can we make use of polyphase filtering?
- Why are halfband filters an efficient choice for the upsampling operation?
- Which parameters determine the interpolation algorithms in the last stage of the conversion?
References
[Ada92] R. Adams, T. Kwan: VLSI Architectures for Asynchronous Sample-Rate Conversion, Proc. 93rd AES Convention, Preprint No. 3355, San Francisco, October 1992.
[Ada93] R. Adams, T. Kwan: Theory and VLSI Implementations for Asynchronous Sample-Rate Conversion, Proc. 94th AES Convention, Preprint No. 3570, Berlin, March 1993.
[Bar90] S. Barnett: Matrices – Methods and Applications, Oxford University Press, Oxford, 1990.
[Boe93] W. Boehm, H. Prautzsch: Numerical Methods, Vieweg, Wiesbaden, 1993.
[Chu92] C. K. Chui, Ed.: Wavelets: A Tutorial in Theory and Applications, Volume 2, Academic Press, Boston, 1992.
[Cro83] R. E. Crochiere, L. R. Rabiner: Multirate Digital Signal Processing, Prentice Hall, Englewood Cliffs, NJ, 1983.
[Cuc91] S. Cucchi, F. Desinan, G. Parladori, G. Sicuranza: DSP Implementation of Arbitrary Sampling Frequency Conversion for High Quality Sound Application, Proc. IEEE ICASSP-91, pp. 3609–3612, Toronto, May 1991.
[Fli00] N. Fliege: Multirate Digital Signal Processing, John Wiley & Sons Ltd, Chichester, 2000.
[Hsi87] C.-C. Hsiao: Polyphase Filter Matrix for Rational Sampling Rate Conversions, Proc. IEEE ICASSP-87, pp. 2173–2176, Dallas, April 1987.
[Kat85] Y. Katsumata, O. Hamada: A Digital Audio Sampling Frequency Converter Employing New Digital Signal Processors, Proc. 79th AES Convention, Preprint No. 2272, New York, October 1985.
[Kat86] Y. Katsumata, O. Hamada: An Audio Sampling Frequency Conversion Using Digital Signal Processors, Proc. IEEE ICASSP-86, pp. 33–36, Tokyo, 1986.
[Lag81] R. Lagadec, H. O. Kunz: A Universal, Digital Sampling Frequency Converter for Digital Audio, Proc. IEEE ICASSP-81, pp. 595–598, Atlanta, April 1981.
[Lag82a] R. Lagadec, D. Pelloni, D. Weiss: A Two-Channel Professional Digital Audio Sampling Frequency Converter, Proc. 71st AES Convention, Preprint No. 1882, Montreux, March 1982.
[Lag82b] D. Lagadec, D. Pelloni, D. Weiss: A 2-Channel, 16-Bit Digital Sampling Frequency Converter for Professional Digital Audio, Proc. IEEE ICASSP-82, pp. 93–96, Paris, May 1982.
[Lag82c] R. Lagadec: Digital Sampling Frequency Conversion, Digital Audio, Collected Papers from the AES Premier Conference, pp. 90–96, June 1982.
[Lag83] R. Lagadec, D. Pelloni, A. Koch: Single-Stage Sampling Frequency Conversion, Proc. 74th AES Convention, Preprint No. 2039, New York, October 1983.
[Liu92] G.-S. Liu, C.-H. Wei: A New Variable Fractional Delay Filter with Nonlinear Interpolation, IEEE Trans. Circuits and Systems-II: Analog and Digital Signal Processing, Vol. 39, No. 2, pp. 123–126, February 1992.
[Opp99] A. V. Oppenheim, R. W. Schafer, J. R. Buck: Discrete Time Signal Processing, 2nd edn, Prentice Hall, Upper Saddle River, NJ, 1999.
[Par90] S. Park, R. Robles: A Real-Time Method for Sample-Rate Conversion from CD to DAT, Proc. IEEE Int. Conf. Consumer Electronics, pp. 360–361, Chicago, June 1990.
[Par91a] S. Park: Low Cost Sample Rate Converters, Proc. NAB Broadcast Engineering Conference, Las Vegas, April 1991.
[Par91b] S. Park, R. Robles: A Novel Structure for Real-Time Digital Sample-Rate Converters with Finite Precision Error Analysis, Proc. IEEE ICASSP-91, pp. 3613–3616, Toronto, May 1991.
[Ram82] T. A. Ramstad: Sample-Rate Conversion by Arbitrary Ratios, Proc. IEEE ICASSP-82, pp. 101–104, Paris, May 1982.
[Ram84] T. A. Ramstad: Digital Methods for Conversion between Arbitrary Sampling Frequencies, IEEE Trans. on Acoustics, Speech and Signal Processing, Vol. ASSP-32, No. 3, pp. 577–591, June 1984.
[Smi84] J. O. Smith, P. Gossett: A Flexible Sampling-Rate Conversion Method, Proc. IEEE ICASSP-84, pp. 19.4.1–19.4.4, 1984.
[Sti91] E. F. Stikvoort: Digital Sampling Rate Converter with Interpolation in Continuous Time, Proc. 90th AES Convention, Preprint No. 3018, Paris, February 1991.
[Vai93] P. P. Vaidyanathan: Multirate Systems and Filter Banks, Prentice Hall, Englewood Cliffs, NJ, 1993.
[Zöl94] U. Zölzer, T. Boltze: Interpolation Algorithms: Theory and Application, Proc. 97th AES Convention, Preprint No. 3898, San Francisco, November 1994.